附表4 F值表
第8章思考与练习0801217
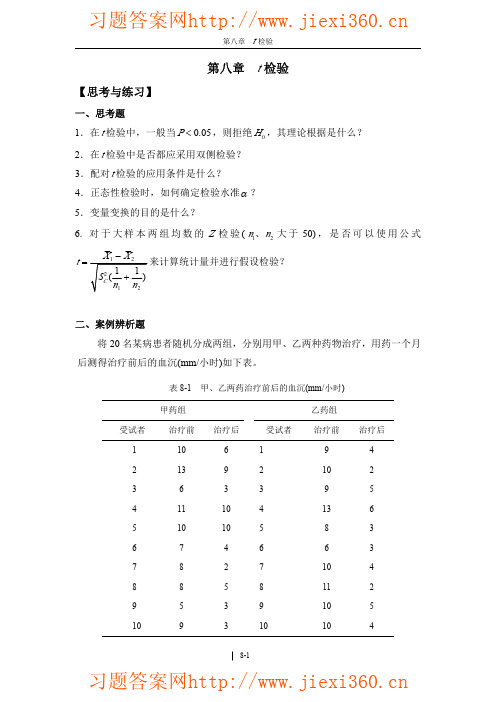
Z KURT = 0.360 1.334 < 1.96 Z KURT = 0.232 1.334 < 1.96
故,甲药,、乙药两组资料的差值 d1、d 2 均服从正态分布。 (2) 方差齐性检验 1) 建立检验假设,确定检验水准
2 ,两差值总体方差相等 H 0 :σ 12 = σ 2
2 ,两差值总体方差不等 H1:σ 12 ≠ σ 2
g d Valid N (listwise) d Valid N (listwise)
Group Statist ic s Std. Error Std. Deviation Mean 1.93218 .61101 1.81353 .57349
g d
N 10 10
Mean 3.2000 5.8000
8-3
习题答案网
习题答案网
第八章
t 检验
7. 为研究两种方法的检测效果,将 24 名患者配成 12 对,采用配对 t 检验进行统 计分析,则其自由度为: A. 24 B. 12 C. 11 D. 23 E. 2 四、综合分析题 1. 大量研究表明健康成年男子脉搏的均数为 72 次/min。某医生在某山区随机调 查了 16 名健康成年男子,测得其脉搏(次/min)资料如下: 69 72 74 68 73 74 80 73 75 74 73 75 74 79 72 74
Z KURT = 1.403 1.334 < 1.96 Z KURT = 0.751 1.334 < 1.96
Z SKEW = 0.088 0.687 < 1.96
故,甲、乙两组资料均服从正态分布。 (2) 假设检验
2 2 由甲、乙两组数据得: X甲 = 5.5, X 乙 = 3.8, S甲 = 3.12 , S乙 = 1.32
医学统计学:04 方差分析

1.4 f( F)
1.2
1.0
0.8
0.6
0.4
0.2
0.0
0
1
F 分布曲线
1 1, 2 5
1 5, 2 5
1 10,2 10
2F
3
4
F 界值表
附表4 F界值表(方差分析用,单侧界值) 上行:P=0.05 下行:P=0.01
分母自由度
υ2
1
161 1
4052
18.51 2
98.49
4.21 27
• 随机区组设计又称随机单位组设计、配伍组设计,也叫双因 素方差分析(two--way ANOVA)。是配对设计的扩展。
具体做法:
① 将受试对象按性质(如性别、年龄、病情等) (这些性质是
非处理因素,可能影响试验结果)相同或相近者组成m个单位 组(配伍组),每个单位组中有k个受试对象,分别随机地分 配到k个处理组。
2
7
33.4
18
2
8
38.3
19
2
9
38.4
20
2
10
39.8
21
3
1
32.9
22
3
2
37.9
23
3
3
30.5
24
3
4
31.1
25
3
5
34.7
26
3
6
37.6
27
3
7
40.2
28
3
8
38.1
29
3
9
32.4
30
3
10
35.6
35.51667
(Xij X )2
假设检验原理和实现
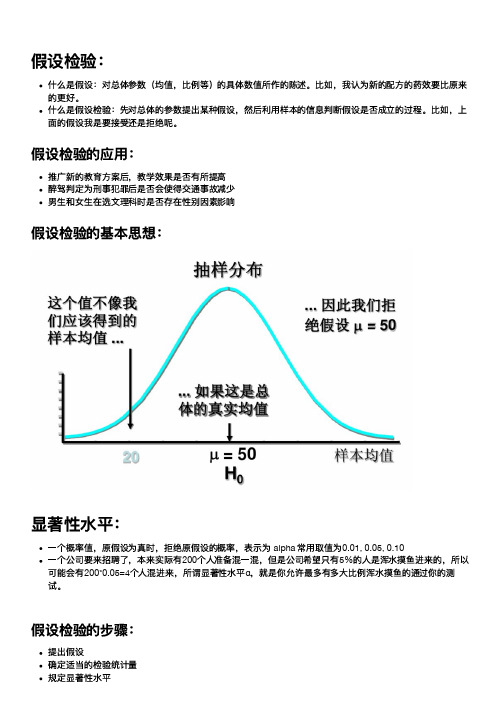
假设检验:什么是假设:对总体参数(均值,⽐例等)的具体数值所作的陈述。
⽐如,我认为新的配⽅的药效要⽐原来的更好。
什么是假设检验:先对总体的参数提出某种假设,然后利⽤样本的信息判断假设是否成⽴的过程。
⽐如,上⾯的假设我是要接受还是拒绝呢。
假设检验的应⽤:推⼴新的教育⽅案后,教学效果是否有所提⾼醉驾判定为刑事犯罪后是否会使得交通事故减少男⽣和⼥⽣在选⽂理科时是否存在性别因素影响假设检验的基本思想:显著性⽔平:⼀个概率值,原假设为真时,拒绝原假设的概率,表示为 alpha 常⽤取值为0.01, 0.05, 0.10⼀个公司要来招聘了,本来实际有200个⼈准备混⼀混,但是公司希望只有5%的⼈是浑⽔摸⻥进来的,所以可能会有200*0.05=4个⼈混进来,所谓显著性⽔平α,就是你允许最多有多⼤⽐例浑⽔摸⻥的通过你的测试。
假设检验的步骤:提出假设确定适当的检验统计量规定显著性⽔平计算检验统计量的值做出统计决策原假设与备择建设:待检验的假设⼜叫原假设,也可以叫零假设,表示为H0。
(零假设其实就是表示原假设⼀般都是说没有差异,没有改变。
)与原假设对⽐的假设叫做备择假设,表示为H1⼀般在⽐较的时候,主要有等于,⼤于,⼩于检验统计量:计算检验的统计量根据给定的显著性⽔平,查表得出相应的临界值将检验统计量的值与显著性⽔平的临界值进⾏⽐较得出拒绝或不拒绝原假设的结论检验中常说的⼩概率:在⼀次试验中,⼀个⼏乎不可能发⽣的事件发⽣的概率在⼀次试验中⼩概率事件⼀旦发⽣,我们就有理由拒绝原假设⼩概率由我们事先确定P值:是⼀个概率值如果原假设为真,P-值是抽样分布中⼤于或⼩于样本统计量的概率左侧检验时,P-值为曲线上⽅⼩于等于检验统计量部分的⾯积右侧检验时,P-值为曲线上⽅⼤于等于检验统计量部分的⾯积左侧检验与右侧检验当关键词有不得少于/低于的时候⽤左侧,⽐如灯泡的使⽤寿命不得少于/低于700⼩时时当关键词有不得多于/⾼于的时候⽤右侧,⽐如次品率不得多于/⾼于5%时双侧检验单侧检验指按分布的⼀侧计算显著性⽔平概率的检验。
方差齐性检验

但是,方差齐性检验也可以在 F 检验结果为多个样本所属总体平均数差异显著的情况下进行,因为 F 检验之后,如果多个样本所属总体平均数差异不显著,就不必再进行方差齐性检验。
Levene 方差齐性检验也称为Levene 检验(Levene's Test). 由H.Levene 在1960 年提出[1] .M.B.Brown 和A.B.Forsythe 在1974年对Levene 检验进行了扩展[2], 使对原始数据的数据转换不但可以使用数据与算术平均数的绝对差, 也可以使用数据与中位数和调整均数(trimmed mean) 的绝对差. 这就使得Levene 检验的用途更加广泛.Levene 检验主要用于检验两个或两个以上样本间的方差是否齐性. 要求样本为随机样本且相互独立. 国内常见的Bartlett 多样本方差齐性检验主要用于正态分布的资料,对于非正态分布的数据, 检验效果不理想.Levene 检验既可以用于正态分布的资料, 也可以用于非正态分布的资料或分布不明的资料, 其检验效果比较理想.方差分析的条件之一为方差齐,即各总体方差相等。
因此在方差分析之前,应首先检验各样本的方差是否具有齐性。
常用方差齐性检验( test for homogeneity of variance )推断各总体方差是否相等。
本节将介绍多个样本的方差齐性检验,本法由Bartlett 于1937 年提出,称Bartlett 法。
该检验方法所计算的统计量服从分布。
用自由度查界值表,若值大于等于界值,则P值小于等于相应的概率,反之,P值大于相应的概率。
如果未经校正的值小于界值,则校正后的值更小,可不必再计算校正值。
J J例5.7对照组、A降脂药组、B降脂药组和C降脂药组家兔的血清胆固醇含量 (mmol/L)的均数分别为5.845 、2.853 、2.972 和1.768 ,方差分别为5.941、2.370 、0.517 和0.581 ,样本含量分别为6、6、 6 和7,问四样本的方差是否齐同?J J本例自由度为,查界值表,得0.025>P>0.01 ,按=0.05水准拒绝H0,接受H1,可以认为四总体方差不同或不全相同。
