管理运筹学作业 韩伯棠第3版高等教育出版社课后答案
管理运筹学(第3版)章后习题解析(下)
− 0.2 x1 − 0.2 x2 + 0.8 x3 − d 3+ + d3− = 0
+ − 2.5 x1 + 0.5 x2 + 0.3x3 − d 4 + d4 = 20
d1− = 0
− d2 =0
d3+ = 0 x1 , x2 , x3 , di+ , di− ≥ 0, i = 1, 2,3, 4
1．解： 最优解为 A―B2―C1―D1―E 或 A―B3―C1―D1―E 或 A―B3―C2―D2―E。 最优值为 13。 2．解： 最优解是项目 A 为 300 万元，项目 B 为 0 万元、项目 C 为 100 万元。 最优值 z=71+49+70=190 万元。 3．解： ， 设每个月的产量是 xi 百台（i=1, 2, 3, 4） 最优解：x1=4，x2＝0，x3＝4，x4＝3。即第一个月生产 4 百台，第二个月生产 0 台，第三 个月生产 4 百台，第四个月生产 3 百台。 最优值 z=252 000 元。 4．解： 最优解为运送第一种产品 5 件。 最优值 z=500 元。 5．解： 最大利润 2 790 万元。最优安排如表 10-1 所示。
表 10-1 年 1 2 3 4 5 度 年初完好设备 125 100 80 64 32 高负荷工作设备数 0 0 0 64 32 低负荷工作设备数 125 100 80 0 0
6．解： 最优解（0，200，300，100）或（200，100，200，100）或者（100，100，300，100）或 （200，200，0，200） 。总利润最大增长额为 134 万。 7．解： 在一区建 3 个分店，在二区建 2 个分店，不在三区建立分店。最大总利润为 32。 8．解： 最优解为第一年继续使用，第二年继续使用，第三年更新，第四年继续使用，第五年继续 使用，总成本=450 000 元。 9．解： 最优采购策略为若第一、二、三周原料价格为 500 元，则立即采购设备，否则在以后的几 周内再采购；若第四周原料价格为 500 元或 550 元，则立即采购设备，否则等第五周再采购；
韩伯棠管理运筹学(第三版)_第五章_单纯形法
一、找出一个初始基本可行解（可行域边 找出一个初始基本可行解（ 界上一个点） 界上一个点）
• • • • • • • • • • • • 在第二章的例1中我们得到以下数学模型： 在第二章的例 中我们得到以下数学模型： 中我们得到以下数学模型 目标函数： 目标函数： max Z=50X1+100X2 约束条件： X1+X2≤300， 约束条件： ， 2 X1+X2≤400， ， X2≤250, X1≥0, X2≥0. 加上松弛变量后得到如下标准型： 加上松弛变量后得到如下标准型： 目标函数：max Z=50X1+100X2 目标函数： 约束条件： 约束条件： X1+X2+S1=300, 2X1+X2+S2=400, X2+S3=250, X1,X2,S1,S2,S3≥0
可 行 解
基 本 可 行 解
基 本 解
非可行解
关于基本解， 关于基本解，可行解和基本可行 解的概念： 解的概念：
• 注意首先要把模型变成标准型再判断。 注意首先要把模型变成标准型再判断。 • 可行解： 可行解： • 满足约束条件（包括非负性）的解称为可行解， 满足约束条件（包括非负性）的解称为可行解， 但不一定含有基。 但不一定含有基。 • 基本解： 基本解： • 找出一个基，令非基变量为 ，再求出解，此 找出一个基，令非基变量为0，再求出解， 解不一定满足非负性。 解不一定满足非负性。 • 基本可行解： 基本可行解： • 既满足非负性又满足基本解的解称为基本可行 解。
则约束条件组成的线性方程组的系数矩阵为： 则约束条件组成的线性方程组的系数矩阵为：
1 1 1 0 0 A = ( p1, p2 , p3 , p4 , p5 ) = 2 1 0 1 0 0 1 0 0 1
韩伯棠管理运筹学(第三版)_第七章_运输问题
B2 c12 c22
Bn c1n c2n
A1 A2
Am 销量
cm1 b1
cm2 b2 … …
cmn
m i 1
am
n ji
bn a i b j
10
求使总的运输费用最小的调运方案？
§1
n
运 输 模 型
m
运输问题线性规划模型
min s
n
cij xij
j 1 i 1
运筹学
J a
30° C 40° C 60° C 95° C
PERSIL
J a
30° C 40° C 60° C 95° C
统筹安排 成本最低
REWE
PERSIL
第七章 运输问题
1
第五章
运 输 问 题
• §1 运 输 模 型 • §2 运输问题的计算机求解 • §3 运输问题的应用 • §4* 运输问题的表上作业法
A2
6
6
4
5
6
5
200
300 500 650
销量
250
200
200
思考题
在例3中，即某公司从两个产地 A1、A2将物品 运往三个销地B1、B2、B3，各产地的产量、各 销地的销量和各产地运往各销地每件物品的运 费如下表所示，如果增加条件：B3的需求不能 满足则需以高价（每单位10元）在本地购买， 问：应如何调运可使总运输费用最小？
§1
整理得：
运 输 模 型
Min f = 6x11+ 4x12+ 6x13+ 6x21+ 5x22+ 5x23 s.t. x11+ x12 + x13 = 200 x21 + x22+ x23 = 300 x11 + x21 = 150
管理运筹学(第3版)章后习题解析(上、下合集)课后习题答案
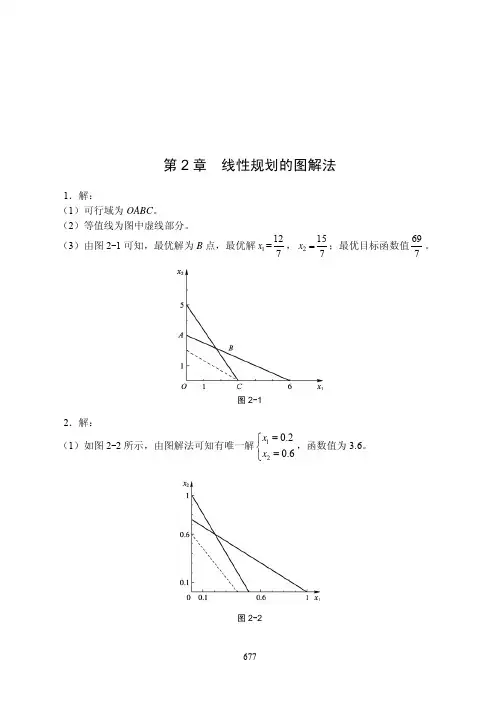
用图解法求解如图 9-2 所示。
717
图 9-2
如图 9-2 所示，解为区域 ABCD，有无穷多解。 （2）由图 9-2 可知，如果不考虑目标 1 和目标 2，仅仅把它们加工时间的最大限度分别为 60 和 180 小时作为约束条件，而以利润最大化为目标，那么最优解为 C 点（360，0） ，即生产 产品 A360 件，最大利润为 1 420 元。结果与（1）是不相同的，原因是追求利润最大化而不仅 仅是要求利润不少于 1 300 元。 （3）如果设目标 3 的优先权为 P1，目标 1 和目标 2 的优先权为 P2，则由图 9-2 可知，满意 解的区域依然是 ABCD，有无穷多解，与（1）的解是相同的，原因是（1）和（3）所设定的目 标只是优先级别不同，但都能够依次达到。 5．解： 设该纸张制造厂需要生产一般类型纸张 x1 吨，生产特种纸张 x2 吨。 （1）目标规划模型如下。 min s.t
716
+ − + − = 0, d 2 = 0,d 3+ = 0, d3− = 4.211, d 4 = 14.316, d 4 = 0。 得 x1 = 9.474, x2 = 20, x3 = 2.105, d1+ = 0, d1− = 0, d 2
所以，食品厂商为了依次达到 4 个活动目标，需在电视上发布广告 9.474 次，报纸上发布 广告 20 次，广播中发布广告 2.105 次。 （使用管理运筹学软件可一次求解上述问题） 3．解： （1） 设该化工厂生产 x1 升粘合剂 A 和 x2 升粘合剂 B。 则根据工厂要求， 建立以下目标规划模型。 min s.t
s.t x1 ≤ 10 x2 ≤ 20 x3 ≤ 15 20 x1 + 10 x2 + 5 x3 − d1+ + d1− = 400
《管理运筹学》课后习题答案59页word
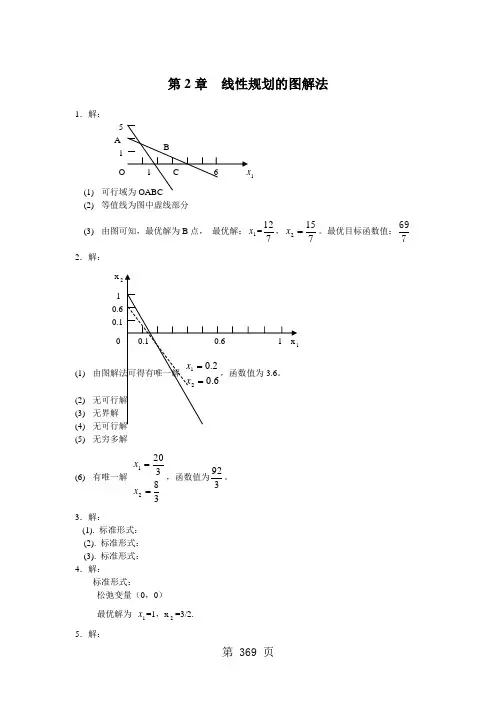
第2章 线性规划的图解法1．解： 5 A 11 (1) (2) 等值线为图中虚线部分(3) 由图可知，最优解为B 点， 最优解：1x =712，7152=x 。
最优目标函数值：7692．解： x 2 1 0(1) (2) (3) 无界解 (4) (5)无穷多解(6) 有唯一解 3832021==x x ，函数值为392。
3．解：(1). 标准形式： (2). 标准形式：(3). 标准形式： 4．解：标准形式：松弛变量（0，0） 最优解为 1x =1，x 2=3/2. 5．解：标准形式：剩余变量（0.0.13） 最优解为 x 1=1，x 2=5. 6．解：(1) 最优解为 x 1=3，x 2=7. (2) 最优解为 x 1=8，x 2=0. (3) 不变化。
因为当斜率31121-≤-≤-c c ,最优解不变,变化后斜率为1,所以最优解不变. 7．解：模型：(1) 1501=x ，702=x ，即目标函数最优值是103000 (2) 2，4有剩余，分别是330，15，均为松弛变量. (3) 50，0，200，0。
(4) 在[]500,0变化，最优解不变。
在400到正无穷变化，最优解不变. (5) 因为143045021-≤-=-c c ,所以原来的最优产品组合不变. 8．解：(1) 模型：b a x x f 38min +=基金a,b 分别为4000，10000,回报率为60000。
(2) 模型变为：b a x x z 45max +=推导出：180001=x 30002=x ，故基金a 投资90万，基金b 投资30万。
第3章 线性规划问题的计算机求解1．解：(1) 1501=x ，702=x 。
目标函数最优值103000。
(2) 1，3车间的加工工时已使用完；2，4车间的加工工时没用完；没用完的加工工时数为2车间330小时,4车间15小时. (3) 50，0，200，0含义：1车间每增加1工时，总利润增加50元；3车间每增加1工时，总利润增加200元；2车间与4车间每增加一个工时，总利润不增加。
《管理运筹学》第三版(韩伯棠 )课后习题答案 高等教育出版社
a、 在满足对职工需求的条件下，在 10 时安排 8 个临时工，12 时新安排 1 个临时工，13 时新安排 1 个临时工，15 时新安排 4 个临时工，17 时新 安排 6 个临时工可使临时工的总成本最小。
50xa + 100xb ≤ 1200000 5xa + 4xb ≥ 60000 100xb ≥ 300000 xa , xb ≥ 0 基金 a,b 分别为 4000，10000。 回报率：60000
b 模型变为： max z = 5xa + 4xb
50xa + 100xb ≤ 1200000 100xb ≥ 300000 xa , xb ≥ 0
xi ≥ 0, yi ≥ 0 i=1,2,…,11
稍微变形后，用管理运筹学软件求解可得：总成本最小为 264 元。 安排如下：y1=8（ 即在此时间段安排 8 个 3 小时的班），y3=1，y5=1，y7=4，x8=6 这样能比第一问节省：320-264=56 元。
x2＋x3＋x4＋x5＋1 ≥ 3 x3＋x4＋x5＋x6＋2 ≥ 3 x4＋x5＋x6＋x7＋1 ≥ 6 x5＋x6＋x7＋x8＋2 ≥ 12 x6＋x7＋x8＋x9＋2 ≥ 12 x7＋x8＋x9＋x10＋1 ≥ 7 x8＋x9＋x10＋x11＋1 ≥ 7 x1，x2，x3，x4，x5，x6，x7，x8，x9，x10，x11≥ 0 用管理运筹学软件我们可以求得此问题的解为：
b、 这时付给临时工的工资总额为 80 元，一共需要安排 20 个临时工的班 次。
约束 -------
1 2 3 4 5 6 7 8 9 10 11
韩伯棠管理运筹学(第三版)_第七章_运输问题
§2
运输问题的计算机求解
将上述问题用以下运价表： 销地 产地 1 2 3 销量 1 6 8 5 22 2 7 4 9 13 3 5 2 10 12 4 3 7 6 13 产量 14 27 19
14
§2 运输问题的计算机求解
运行管理运筹学计算机软件：
点击运输问题模块
15
§2 运输问题的计算机求解
运筹学
J a
30° C 40° C 60° C 95° C
PERSIL
J a
30° C 40° C 60° C 95° C
统筹安排 成本最低
REWE
PERSIL
第七章 运输问题
1
第五章
运 输 问 题
• §1 运 输 模 型 • §2 运输问题的计算机求解 • §3 运输问题的应用 • §4* 运输问题的表上作业法
8
§1
B1
运 输 模 型
B2 … Bn 产量
运输问题及其数学模型
产地 销地
A1 A2
a1
Am 销量 b1
运价
m
a2
am b2 … bn
a b
i 1 i ji
n
j
产销平衡
9
§1
B1 c11 c21
运 输 模 型
… … … 产量 a1 a2
产 销 平 衡 表
运输问题及其数学模型
产地
销地
产量 50 60 50 50 210 50 210
最低要求必须满足，因此把相应的虚设产地运 费取为M, 而最高要求与最低要求的差允许按 需要安排，因此把相应的虚设产地运费取为 0 。 对应 4”的销量 50 是考虑问题本身适当取的数 据,根据产销平衡要求确定D的产量为 50 .
管理运筹学第三版习题答案(全)
第2章 线性规划的图解法1．解：x`A 1 (1) 可行域为OABC(2) 等值线为图中虚线部分(3) 由图可知，最优解为B 点， 最优解：1x =712，7152=x 。
最优目标函数值：7692．解： x 2 10 1(1) 由图解法可得有唯一解 6.02.021==x x ，函数值为3.6。
(2) 无可行解 (3) 无界解 (4) 无可行解 (5)无穷多解(6) 有唯一解 3832021==x x ，函数值为392。
3．解：(1). 标准形式：3212100023max s s s x x f ++++=,,,,9221323302932121321221121≥=++=++=++s s s x x s x x s x x s x x(2). 标准形式：21210064min s s x x f +++= 0,,,46710263212121221121≥=-=++=--s s x x x x s x x s x x(3). 标准形式：21''2'2'10022min s s x x x f +++-=,,,,30223505527055321''2'2'12''2'2'1''2'2'11''2'21≥=--+=+-=+-+-s s x x x s x x x x x x s x x x4．解：标准形式：212100510max s s x x z +++= 0,,,8259432121221121≥=++=++s s x x s x x s x x松弛变量（0，0） 最优解为 1x =1，x 2=3/2.标准形式：32121000811min s s s x x f ++++=,,,,369418332021032121321221121≥=-+=-+=-+s s s x x s x x s x x s x x剩余变量（0.0.13） 最优解为 x 1=1，x 2=5.6．解：(1) 最优解为 x 1=3，x 2=7. (2) 311<<c (3) 622<<c (4)4621==x x(5) 最优解为 x 1=8，x 2=0. (6) 不变化。
韩伯棠管理运筹学(第三版)_第十二章_排序与统筹
寻找例2的最优解： 寻找例 的最优解：我们在上表中找到所列出的最 的最优解 短加工时间是0.25,它是第二道工序磨床加工零件 的所 它是第二道工序磨床加工零件2的所 短加工时间是 它是第二道工序磨床加工零件 需时间，由于这个时间与磨床有关，故我们把零件2放 需时间，由于这个时间与磨床有关，故我们把零件 放 在加工顺序的末尾，即第五位，并在表中划去零件2 在加工顺序的末尾，即第五位，并在表中划去零件 所 在行。如表中红色线条所示。 在行。如表中红色线条所示。
12
§1 车间作业计划模型
车床 磨床 零 第一工序) 第二工序) 件 (第一工序 (第二工序 第一工序 第二工序 1 1.5 0.5 2 2.0 0.25 3 1.0 1.75 车床 磨床 零 第一工序) 第二工序) 件 (第一工序 (第二工序 第一工序 第二工序 4 1.25 2.5 5 0.75 1.25
7
§1 车间作业计划模型
零件 车床 磨床 零件 车床 磨床 1 1.5 0.5 4 1.25 2.5 2 2.0 0.25 5 0.75 1.25 3 1.0 1.75 由于每个零件必须先进行车床加工， 解 ： 由于每个零件必须先进行车床加工 ， 再进行 磨床加工， 磨床加工 ， 所以在车床上加工零件的顺序与在磨床 上加工零件的顺序是一样的。 上加工零件的顺序是一样的 。 如果这些零件在车床 上和磨床上加工顺序都为1， ， ， ， 。 上和磨床上加工顺序都为 ，2，3，4，5。我们用图 12-1中的线条图来表示各零件加工的开始时间与完成 中的线条图来表示各零件加工的开始时间与完成 时间， 这种图是由一根时间轴和车床、 时间 ， 这种图是由一根时间轴和车床 、 磨床在每个 时间段的状况的图形所构成。 时间段的状况的图形所构成。
韩伯棠管理运筹学(第三版)_第四章_线性规划在工商管理中的应用
解: 函数值=36, X1=3,x2=5, x3=12,X4=0, x5=11,x6=0 X7=5, 则周1休息人数为 周3上班的+周2上 班的=12+5=17,与 法一是一样的周1 开始休息仍为175=12人 12
§4.2、生产计划的问题
例3
．明兴公司面临一个是外包协作还 是自行生产的问题。该公司生产甲、乙、 丙三种产品，这三种产品都要经过铸造、 机加工和装配三个车间。甲、乙两种产品 的铸件可以外包协作，亦可以自行生产， 但产品丙必须本厂铸造才能保证质量。有 关情况见表4—3；公司中可利用的总工时 为：铸造8000小时，机加工12000小时和装 配10000小时。公司为了获得最大利润，甲、 乙、丙三种产品各生产多少件?甲、乙两种 产品的铸造应多少由本公司铸造?应多少由 外包协作？
工时与成本
甲
乙
丙
每件铸造工时(小时) 每件机加工工时(小时) 每件装配工时（小时)
5 6 3
10 4 2
7 8 2
建立数学模型如下： 目标函数： max 15X1+10X2+7X3+13X4+9X5 约束条件： 5X1+10X2+7X3≤8000(这里没包括外协铸造时间)， 6X1+4X2+8X3+6X4+4X5≤12000(机加工)， 3X1+2X2+2X3+3X4+2X5≤10000(装配)， X1，X2，X3，X4，X5≥0 用“管理运筹学”软件进行计算，计算机计算结果显示 在图4-1中。详见上机计算……。
7
目标函数 :
约束条件 : x1 x2 x3 x4 x5 28
喂！请问数学模型？
韩伯棠教授《管理运筹学》第三版习总复习
一、管理运筹学的定义运筹学（Operational Research，简称OR) ，英文直译为“运作研究”。
管理运筹学是应用分析、试验、量化的方法，对经济管理系统中的人力、物力、财力等资源进行统筹安排，为决策者提供有依据的最优方案，以实现最有效的管理。
——《中国企业管理百科全书》绪论二、管理运筹学Ⅰ的主要分支线性规划(Linear Programming，简称LP)整数规划(Integral Programming，简称IP)目标规划(Objective Programming，简称OP)动态规划(Dynamic Programming，简称DP)图与网络(Graph and Network)三、管理运筹学的工作步骤提出问题、分析问题建立模型求解解的检验、控制、实施四、运筹学方法的特点1. 最优化方法2. 定量的方法线性规划(LP)一、问题的提出1.生产计划安排问题：合理利用人力、物力、财力等，在资源有限的约束条件下,寻求使得获利最大的最优生产计划方案。
2.人力资源分配的问题：在满足工作的需要的条件下，寻求使用最少的劳动力的最优分配方案。
3.套裁下料问题：在保证正常生产，完成生产任务的条件下，寻求使用原料最省的最优下料方案。
4.投资问题：在投资额限制的条件下，从多个投资项目中选取使得投资回报最大的最优投资方案。
5.运输问题：寻求使得总运费最小的最优调运方案。
二、建模1.一般步骤:分析问题，设出决策变量根据所提问题列出目标函数根据已知条件列出所有约束条件数学模型的一般形式★矩阵形式：假设有n个决策变量，m个约束条件。
目标函数：Max （Min）z = CX约束条件：AX ≤（=, ≥）b.X≥0其中，C=(c1 , c2 , …, cn )(价值向量)X= (x1 , x2 , …, xn )T(决策变量向量)b=(b1 , b2 , …, bm )T (限定向量)a11 a12 (1)a21 a22 …a2n (约束条件系数矩阵) Am×n = ……am1 am2 …amn数学模型的特点（1）由目标函数和约束条件构成；（2）目标函数只有两种情况：求极小或求极大。
韩伯棠管理运筹学(第三版)_第六章_单纯形法的灵敏度分析与对偶
2．在最终的单纯形表中，XK是基变量。
• 当CK变成Ck+△Ck时，同上一样，可知在最终的单纯形表中的 约束方程的增广矩阵不变，但是基变量在目标函数中的系数CB 变了，则Zj (j=1,2,…,n)一般也变了，不妨设CB=(CB1,CB2,…, CK, …,CBm) , 当CB 变成 (CB1,CB2,…,（ CK+ΔCk) , …,CBm) , 则：
x1
x2
s1
s2
s3
2
50 1 0 0
50 0
100 0 0 1
0 1 -2 0
0 0 1 0
0 0
0 -1 1 1
50 -50
b
50 50 250
Z= 27500
100 50 0 -50
先对非基变量s1的目标函数的系数C3进行灵敏度 分析。这里σ3=-50，所以当C3 的增量ΔC3≤-(-50)即 ΔC3≤50时，最优解不变，也就是说S1的目标函数的系数 C′3=C3+△C3≤0+50=50时，最优解不变。 再对基变量x1的目标函数的系数C1进行灵敏度分析。
在a11, a12 , a13, a14 , a15中, 知道除了a11外有a13 0, a15 0, j 3 50 可知, 50, 有 min a1 j 0 min 50 50, a13 1 a1 j j 5 50 同样有 : max a1 j 0 max max( ) 50, 1 a1 j a15 这样可知当 50 C1 50时, 也就是x1的目标函数c1有 : 50 50 c1 c1 c1 50 50,即0 c1 100的最优解不变.
管理运筹学第三版课后答案汇总
第 4 章线性规划在工商管理中的应用1、解：为了用最少的原材料得到 10 台锅炉，需要混合使用 14 种下料方案设按 14 种方案下料的原材料的根数分别为 x 1，x 2，x 3，x 4，x 5，x 6，x 7，x 8，x 9， x 10，x 11，x 12，x 13，x 14，则可列出下面的数学模型： min f ＝x 1+x 2+x 3+x 4+x 5+x 6+x 7+x 8+x 9+x 10+x 11+x 12+x 13+x 14 s ．t ． 2x 1＋x 2＋x 3＋x 4 ≥ 80x 2＋3x 5＋2x 6＋2x 7＋x 8＋x 9＋x 10≥ 350 x 3＋x 6＋2x 8＋x 9＋3x 11＋x 12＋x 13≥ 420x 4＋x 7＋x 9＋2x 10＋x 12＋2x 13＋3x 14 ≥ 10x 1，x 2，x 3，x 4，x 5，x 6，x 7，x 8，x 9，x 10，x 11，x 12，x 13，x 14≥ 0 用管理运筹学软件我们可以求得此问题的解为：x 1＝40，x 2＝0，x 3＝0，x 4＝0，x 5＝116.667，x 6＝0，x 7＝0，x 8＝0， x 9＝0，x 10＝0，x 11＝140，x 12＝0，x 13＝0，x 14＝3.333 最优值为 300。
2、解：从上午 11 时到下午 10 时分成 11 个班次，设 x i 表示第 i 班次安排的临时工的人数，则可列出下面的数学模型：min f＝16（x 1+x 2+x 3+x 4+x 5+x 6+x 7+x 8+x 9+x 10+x 11） s ．t ． x 1＋1 ≥ 9x 1＋x 2＋1 ≥ 9x 1＋x 2＋x 3＋2 ≥ 9x 1＋x 2＋x 3＋x 4＋2 ≥ 3x 2＋x 3＋x 4＋x 5＋1 ≥ 3 x 3＋x 4＋x 5＋x 6＋2 ≥ 3 x 4＋x 5＋x 6＋x 7＋1 ≥ 6 x 5＋x 6＋x 7＋x 8＋2 ≥ 12 x 6＋x 7＋x 8＋x 9＋2 ≥ 12 x 7＋x 8＋x 9＋x 10＋1 ≥ 7 x 8＋x 9＋x 10＋x 11＋1 ≥ 7x 1，x 2，x 3，x 4，x 5，x 6，x 7，x 8，x 9，x 10，x 11≥ 0 用管理运筹学软件我们可以求得此问题的解为：x 1＝8，x 2＝0，x 3＝1，x 4＝1，x 5＝0，x 6＝4，x 7＝0，x 8＝6，x 9＝0，x 10＝0，x 11＝0 最优值为 320。
韩伯棠管理运筹学(第三版)_第十六章_决策分析
S1（大批量生产） S2（中批量生产） S3（小批量生产）
N1
p = 1/2
30 20 10
N2
p = 1/2
-6 -2 5
（需求量大） （需求量小）
收益期望值 E (Si)
12(max) 9 7.5
13
练习、电视机厂，99年产品更新方案： A1：彻底改型 A2：只改机芯，不改外壳 A3：只改外壳，不改机芯 问：如何决策？ 价格 方案 A1 A2 A3 高 S1 20 9 6 中 S2 1 8 5 低 S3 (万元) -6 0 4
1 Vi 3
aij
i 1
3
A3
5
5 maxV = 5 2 2 i 5 i 3 3 5
选择方案A2
§1 不确定情况下的决策
四、乐观系数(折衷)准则(Hurwicz胡魏兹准则) 决策者取乐观准则和悲观准则的折衷： 先确定一个乐观系数 （01），然后计算： CVi = max [(Si, Nj)] +（1- ）min [(Si, Nj)]
23
天气 利润 方案 蔬菜: A1 小麦: A2 棉花: A3
旱 0.2 1000 2000 3000
正常 期望值法 0.7 4000 5000 6000
多雨 0.1 7000 3000 2000
解：计算各方案的益损期望值：
E ( A1 ) 1000 0.2 4000 0.7 7000 0.1 3700 E ( A2 ) 2000 0.2 5000 0.7 3000 0.1 4200 E ( A3 ) 3000 0.2 6000 0.7 2000 0.1 5000
8
运筹学第三版习题答案
运筹学第三版习题答案
《运筹学第三版习题答案》
运筹学是一门研究如何有效地组织和管理资源，以达到最优解的学科。
第三版习题答案是这门学科的重要参考资料，它包含了大量的问题和答案，帮助学生更好地理解和掌握运筹学的知识。
在运筹学中，我们需要运用数学和逻辑推理来解决各种实际问题，比如资源分配、生产计划、物流管理等。
通过对这些问题的分析和建模，可以找到最优的解决方案，从而提高效率和降低成本。
而第三版习题答案则为我们提供了一系列实例和解决方法，帮助我们更好地理解和应用运筹学的理论。
在学习运筹学的过程中，我们常常会遇到各种各样的问题，有些问题可能会让我们感到困惑和无从下手。
而第三版习题答案则为我们提供了宝贵的参考，帮助我们更好地理解问题的本质，掌握解决问题的方法。
通过对习题答案的学习和思考，我们可以提高自己的分析和解决问题的能力，为将来的实际工作做好准备。
除此之外，第三版习题答案还可以帮助我们检验自己的学习成果。
通过做习题和对照答案，我们可以及时发现自己的不足之处，及时调整学习方法和提高学习效率。
这对于我们的学习和成长都是非常有益的。
总的来说，第三版习题答案是运筹学学习过程中的重要工具，它不仅可以帮助我们更好地理解和掌握运筹学的知识，还可以帮助我们提高解决问题的能力和检验学习成果。
希望大家在学习运筹学的过程中，能够善加利用这份宝贵的资料，不断提高自己的能力和水平。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
课程：管理运筹学管理运筹学作业第二章线性规划的图解法P23：Q2：（1）－（6）；Q3：(2)Q2：用图解法求解下列线性规划问题，并指出哪个问题具有唯一最优解，无穷多最优解，无界解或无可行解。
（1）Min f＝6X1+4X2约束条件：2X1+X2>=1,3X1+4X2>=3X1, X2>=0解题如下：如图1Min f＝3.6X1=0.2, X2=0.6本题具有唯一最优解。
图1（2）Max z＝4X1+8X2约束条件：2X1+2X2<=10-X1+X2>=8X1,X2>=0解题如下：如图2：Max Z 无可行解。
图2（3） Max z ＝X1+X2 约束条件 8X1+6X2>=24 4X1+6X2>=-12 2X2>=4 X1,X2>=0 解题如下：如图3： Max Z=有无界解。
图3（4） Max Z ＝3X1-2X2 约束条件：X1+X2<=1 2X1+2X2>=4 X1,X2>=0 解题如下：如图4： Max Z 无可行解。
图4(5)Max Z＝3X1+9X2 约束条件：X1+3X2<=22-X1+X2<=4X2<=62X1-5X2<=0X1,X2>=0解题如下：如图5：Max Z =66；X1=4 X2=6本题有唯一最优解。
图5(6)Max Z=3X1+4X2 约束条件：-X1+2X2<=8X1+2X2<=122X1+X2<=162X1-5X2<=0X1,X2>=0解题如下：如图6Max Z =30.669X1=6.667 X2=2.667本题有唯一最优解。
图6Q3：将线性规划问题转化为标准形式（2）min f＝4X1+6X2约束条件：3X1-2X2>=6X1+2X2>=107X1-6X2=4X1,X2>=0解题如下：1）目标函数求最小值化为求最大值：目标函数等式左边min改为max，等式右边各项均改变正负号。
2）决策变量非负化：若Xi≤0，令Xi=－Xia，（Xia≥0）；若Xi无约束，令Xi=Xia－Xib，（Xia≥0，Xib≥0）；将上述替换变量代入目标函数和约束条件。
3）约束条件不等式化为等式：不等号为≤的，不等式左边加松弛变量；不等号为≥的，不等式左边减剩余变量。
4）常数项为非负。
本题标准化如下：令：z＝-f，则：Max z＝min (-f)= -4X1-6X2+0X3+0X4所以：Max z＝-4X1-6X2+0X3+0X4约束条件：3X1-2X2-X3+0X4＝6X1+2X2+0X3-X4=107X1-6X2+0X3+0X4=4X1,X2,X3,X4>=0第三章线性规划问题的计算机求解P37: Q4; P38:Q5Q4：考虑下面的线性规划问题：Max Z＝2X1+X2-X3+X4约束条件：X1-X2+2X3+X4>=2X1-3X2+X3-X3-X4<=42X2+X3+2X4<=3X1,X2,X3,X4>=0计算机结果输出如下：**********************最优解如下*************************目标函数最优值为: 18.5变量最优解相差值------- -------- --------x1 8.5 0x2 1.5 0x3 0 4.5x4 0 4约束松弛/剩余变量对偶价格------- ------------- --------1 5 02 0 23 0 3.5目标函数系数范围:变量下限当前值上限------- -------- -------- --------x1 .2 2 无上限x2 -3 1 无上限x3 无下限 1 5.5x4 无下限 1 5常数项数范围:约束下限当前值上限------- -------- -------- --------1 无下限2 72 -1 4 无上限3 0 3 无上限回答下列问题：（1）请指出其最优解及其最优目标值。
（2）那些约束条件起到了约束作用，它们的对偶价格各为多少，请给予说明。
（3）如果请你选择一个约束条件，将它的常数项增加一个单位，你将选择哪一个约束条件，这时候最优目标函数值是多少？（4）请问在目标函数中X3的系数在什么范围内变化时，其最优解不变，这时其最优目标函数值是否会发生变化，为什么？（5）请问在目标函数中X1的系数在什么范围内变化时，其最优解不变，这时其最优目标函数值是否会发生变化，为什么？解题如下：答：（1）其最优解是X1=8.5;X2=1.5;X3=0;X4=0；最优目标值是MaxZ=18.5（2）约束条件2、3起到了约束的作用，它们的对偶价格分别为2和3.5。
（3）因为求目标函数值MaxZ，因选择约束条件3的对偶价格为3.5，当该约束条件改善一个单位时，目标函数最大值改善3.5。
这时目标函数最大值为18.5+3.5＝22。
（4）计算机输出结果可知，当X3的系数在（－∞，5.5）范围内变化时，其最优解不变。
且这时其最优目标函数值不会发生变化。
因为输出结果中X3=0。
（5）计算机输出结果可知，当X1的系数在（0.2，∞）范围内变化时，其最优解不变。
因X1=8.5为最优解，因此目标函数值会随着X1的变化而改变。
Q5、考虑下面线性规划问题：MinZ＝16X1+16X2+17X3;约束条件：X1+X2<=300.5X1-X2+6X3>=153X1+4X2-X3>=20X1,X2,X3>=0计算机输出结果如下：**********************最优解如下*************************目标函数最优值为: 148.916变量最优解相差值------- -------- --------x1 7.297 0x2 0 .703x3 1.892 0约束松弛/剩余变量对偶价格------- ------------- --------1 22.703 02 0 -3.6223 0 -4.73目标函数系数范围:变量下限当前值上限------- -------- -------- --------x1 1.417 16 16.565x2 15.297 16 无上限x3 14.4 17 192常数项数范围:约束下限当前值上限------- -------- -------- --------1 7.297 30 无上限2 3.333 15 4353 -2.5 20 90回答如下问题：（1）第二个约束方程的对偶价格是一个负数（-3.622），它的含义是什么？（2）X2的相差值为0.703，它的含义是什么。
（3）当目标函数中X1的系数从16降为15，而X2的系数从16升为18时，最优解是否会发生变化？会发生变化。
（4）当第一个约束条件的常数项从30变为15，而第二个常数项从15变为80时，你能断定其对偶价格是否会发生变化，为什么？会。
384.32解题如下：答：（1）第二个约束方程的对偶价格是一个负数（-3.622），其含义是如果把约束条件2的下限15增加1，那么最优目标函数值将增加3.622。
即148.916+3.622＝152.538 （2）决策变量最优解非零，则相差值为0；决策变量最优解为零，则存在正数相差值。
相差值表示为使得相应的决策变量参加最优生产组合（最优解取正），其价值系数至少需要增加的量（max型目标函数）或其价值系数至少需要减少的量（min型目标函数）。
X2的相差值为0.703，它的含义是X2的系统需要减少0.703，即16－0.703＝15.297，此时的目标函数值为148.919.(3) 当目标函数中X1的系数从16降为15，而X2的系数从16升为18时，最优解不会发生变化，但是目标函数最优值会发生变化。
因为X1在（1.417, 16.565）和X2在(15.297, )范围内变化时，最优解不会发生变化。
只是会影响目标函数最优值变化。
（4）当第一个约束条件的常数项从30变为15，而第二个常数项从15变为80时，对偶价格不会发生变化。
对偶价格是某种资源在最佳生产组合的基础上，每增加一个单位产生的最优目标值的改进量。
常数项的变化只对目标函数最优解产生影响，对偶价格不会产生变化。
第四章线性规划在工商管理中的应用作业：P57-58，Q2,Q3Q2：某快餐店座落在一个旅游景点中。
该景点远离市区，平时顾客不多，而在每个周六顾客猛增。
该店主要为顾客提供低价位的快餐服务。
该店雇佣2名正式工，每天工作8小时。
其余工作由临时工担任，临时工每天工作4小时。
周六营业时间11:00a.m-22:00p.m。
根据就餐情况，在周六每个营业小时所需的职工数如表（包括正式工和临时工）。
已知一名正式工从11点上班，工作4小时后休息1小时，而后在工作4小时。
另外一名正式工13点上班，工作4小时后，休息1小时，在工作4小时。
又知临时工每小时工资4元。
（1）、满足对职工需求的条件下，如何安排临时工的班次，使得临时工成本最小。
（2）、这时付给临时工的工资总额是多少，一共需要安排多少临时工班次。
请用剩余变量来说明应该安排一些临时工的3小时工作时间的班次，可使得总成本更小。
（3）、如果临时工每班工作时间可以是3小时，也可以是4小时，那么如何安排临时工的班次，使得临时工总成本最小。
这样比（1）节省多少费用，这时要安排多少临时工班次。
解题如下：(1)临时工的工作时间为4小时，正式工的工作时间也是4小时，则第五个小时需要新招人员，临时工只要招用，无论工作多长时间，都按照4小时给予工资。
每位临时工招用以后，就需要支付16元工资。
从上午11时到晚上10时共计11个班次，则设Xi(i=1,2,…,11)个班次招用的临时工数量，如下为最小成本：minf＝16（X1+X2+X3+X4+X5+X6+X7+X8+X9+X10+X11)两位正式工一个在11－15点上班，在15－16点休息，然后在16－20点上班。
另外一个在13－17点上班，在17－18点休息，18－22点上班。
则各项约束条件如下：X1+1>=9X1+X2+1>=9X1+X2+X3+2>=9X1+X2+X3+X4+2>=3X2+X3+X4+X5+1>=3X3+X4+X5+X6+2>=3X4+X5+X6+X7+2>=6X5+X6+X7+X8+1>=12X6+X7+X8+X9+2>=12X7+X8+X9+X10+1>=7X8+X9+X10+X11+1>=7Xi>=0(i＝1,2, (11)运用计算机解题，结果输出如下;**********************最优解如下*************************目标函数最优值为: 320变量最优解相差值------- -------- --------x1 8 0x2 0 0x3 1 0x4 0 0x5 1 0x6 4 0x7 0 0x8 6 0x9 0 0x10 0 1x11 0 1目标函数最优值为: 320这时候临时工的安排为：变量班次临时工班次时间------- -------- --------x1 8 11：00－12：00x2 0 12：00－13：00x3 1 13：00－14：00x4 0 14：00－15：00x5 1 15：00－16：00x6 4 16：00－17：00x7 0 17：00－18：00x8 6 18：00－19：00x9 0 19：00－20：00x10 0 20：00－21：00x11 0 21：00－22：00（2）付出工资总额为：Minf＝16（X1+X2+X3+X4+X5+X6+X7+X8+X9+X10+X11)＝16（8+0+1+0+1+4+0+6+0+0+0)=320元共需要安排20个临时工班次。