MBA管理运筹学课后习题答案
管理运筹学课后习题答案

管理运筹学课后习题答案管理运筹学课后习题答案一、线性规划线性规划是管理运筹学中的一种重要方法,它通过建立数学模型,寻找最优解来解决实际问题。
下面我们来讨论一些常见的线性规划习题。
1. 一家工厂生产两种产品A和B,每单位产品A需要3小时的加工时间和2小时的装配时间,每单位产品B需要2小时的加工时间和4小时的装配时间。
工厂每天有8小时的加工时间和10小时的装配时间。
已知产品A的利润为300元,产品B的利润为400元。
如何安排生产,使得利润最大化?解答:设生产产品A的数量为x,生产产品B的数量为y。
根据题目中的条件,可以得到以下线性规划模型:目标函数:max 300x + 400y约束条件:3x + 2y ≤ 82x + 4y ≤ 10x, y ≥ 0通过求解上述线性规划模型,可以得到最优解,即生产4个产品A和1个产品B时,利润最大化,为2000元。
2. 一家超市有两种品牌的洗衣液,品牌A和品牌B。
品牌A每瓶售价20元,每瓶利润为5元;品牌B每瓶售价25元,每瓶利润为7元。
超市每天销售洗衣液的总利润不能超过100元,并且每天至少要销售10瓶洗衣液。
如何安排销售,使得利润最大化?解答:设销售品牌A的瓶数为x,销售品牌B的瓶数为y。
根据题目中的条件,可以得到以下线性规划模型:目标函数:max 5x + 7y约束条件:20x + 25y ≤ 100x + y ≥ 10x, y ≥ 0通过求解上述线性规划模型,可以得到最优解,即销售5瓶品牌A和5瓶品牌B时,利润最大化,为60元。
二、排队论排队论是管理运筹学中研究排队系统的一种方法,它通过数学模型和概率统计来分析和优化排队系统。
下面我们来讨论一些常见的排队论习题。
1. 一家银行有两个窗口,每个窗口的服务时间服从指数分布,平均服务时间分别为3分钟和4分钟。
顾客到达的间隔时间也服从指数分布,平均间隔时间为2分钟。
如果顾客到达时,两个窗口都有空闲,顾客会随机选择一个窗口进行服务。
《管理运筹学》(第二版)课后习题参考标准答案

《管理运筹学》(第二版)课后习题参考答案第1章线性规划(复习思考题)1.什么是线性规划?线性规划的三要素是什么?答:线性规划(Linear Programming,LP)是运筹学中最成熟的一个分支,并且是应用最广泛的一个运筹学分支。
线性规划属于规划论中的静态规划,是一种重要的优化工具,能够解决有限资源的最佳分配问题。
建立线性规划问题要具备三要素:决策变量、约束条件、目标函数。
决策变量是决策问题待定的量值,取值一般为非负;约束条件是指决策变量取值时受到的各种资源条件的限制,保障决策方案的可行性;目标函数是决策者希望实现的目标,为决策变量的线性函数表达式,有的目标要实现极大值,有的则要求极小值。
2.求解线性规划问题时可能出现几种结果,哪种结果说明建模时有错误?答:(1)唯一最优解:只有一个最优点;(2)多重最优解:无穷多个最优解;(3)无界解:可行域无界,目标值无限增大;(4)没有可行解:线性规划问题的可行域是空集。
当无界解和没有可行解时,可能是建模时有错。
3.什么是线性规划的标准型?松弛变量和剩余变量的管理含义是什么?答:线性规划的标准型是:目标函数极大化,约束条件为等式,右端常数项0b,≥i决策变量满足非负性。
如果加入的这个非负变量取值为非零的话,则说明该约束限定没有约束力,对企业来说不是紧缺资源,所以称为松弛变量;剩余变量取值为非零的话,则说明“≥”型约束的左边取值大于右边规划值,出现剩余量。
4.试述线性规划问题的可行解、基础解、基可行解、最优解的概念及其相互关系。
答:可行解:满足约束条件0bAX,的解,称为可行解。
=X≥基可行解:满足非负性约束的基解,称为基可行解。
可行基:对应于基可行解的基,称为可行基。
最优解:使目标函数最优的可行解,称为最优解。
最优基:最优解对应的基矩阵,称为最优基。
它们的相互关系如右图所示:5.用表格单纯形法求解如下线性规划。
32124max x x x Z ++=s .t . ⎪⎩⎪⎨⎧≥≤++≤++0,,86238321321321x x x x x x x x x解:标准化 32124m a x x x x Z ++=s .t . ⎪⎩⎪⎨⎧≥=+++=+++0,,,,862385432153214321x x x x x x x x x x x x x 列出单纯形表故最优解为T X )6,0,2,0,0(*=,即2,0,0321===x x x ,此时最优值为4*)(=X Z . 6.表1—15中给出了求极大化问题的单纯形表,问表中d c c a a ,,,,2121为何值及变量属于哪一类型时有:(1)表中解为唯一最优解;(2)表中解为无穷多最优解之一;(3)下一步迭代将以1x 代替基变量5x ;(4)该线性规划问题具有无界解;(5)该线性规划问题无可行解。
管理运筹学第二版课后习题参考答案

《管理运筹学》(第二版)课后习题参考答案第1章 线性规划(复习思考题)1.什么是线性规划?线性规划的三要素是什么?答:线性规划(Linear Programming ,LP )是运筹学中最成熟的一个分支,并且是应用最广泛的一个运筹学分支。
线性规划属于规划论中的静态规划,是一种重要的优化工具,当无界解和没有可行解时,可能是建模时有错。
3.什么是线性规划的标准型?松弛变量和剩余变量的管理含义是什么?答:线性规划的标准型是:目标函数极大化,约束条件为等式,右端常数项0 i b ,决策变量满足非负性。
如果加入的这个非负变量取值为非零的话,则说明该约束限定没有约束力,对企业来说不是紧缺资源,所以称为松弛变量;剩余变量取值为非零的话,则说明“≥”型约束的左边取值大于右边规划值,出现剩余量。
4.试述线性规划问题的可行解、基础解、基可行解、最优解的概念及其相互关系。
答:可行解:满足约束条件0≥=X b AX ,的解,称为可行解。
基可行解:满足非负性约束的基解,称为基可行解。
可行基:对应于基可行解的基,称为可行基。
最优解:使目标函数最优的可行解,称为最优解。
最优基:最优解对应的基矩阵,称为最优基。
它们的相互关系如右图所示:5.用表格单纯形法求解如下线性规划。
s .t . ⎪⎩⎪⎨⎧≥≤++≤++0,,86238321321321x x x x x x x x x解:标准化 32124max x x x Z ++=s .t . ⎪⎩⎪⎨⎧≥=+++=+++0,,,,862385432153214321x x x x x x x x x x x x x 列出单纯形表于哪一类型时有:(1)表中解为唯一最优解;(2)表中解为无穷多最优解之一;(3)下一步迭代将以1x 代替基变量5x ;(4)该线性规划问题具有无界解;(5)该线性规划问题无可行解。
表1—15 某极大化问题的单纯形表7.用大M 法求解如下线性规划。
s .t . ⎪⎪⎩⎪⎪⎨⎧≥=++≤++≤++0,,101632182321321321321x x x x x x x x x x x x解:加入人工变量,进行人造基后的数学模型如下:s .t . ⎪⎪⎩⎪⎪⎨⎧=≥=+++=+++=+++)6,,2,1(0101632182632153214321 i x x x x x x x x x x x x x i列出单纯形表x为“第i电站向第j城市分配的电量”(i=1,2; j=1,2,3),建立模型如下:解:设ijs .t . ⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧==≥≤+≥+=+≤+≥+=++=++3,2,1;2,1,035027025032029045040023132313221221112111232221131211j i x x x x x x x x x x x x x x x x x ij10s .t . ⎪⎪⎪⎪⎩⎨=≥≤≤≤4,3,2,1,0,,101520)3()2()1()1(4)1(3)1(2i x x x x x x i i i 通过LINGO 软件计算得:44,12,0,20,10)2(1)2(1)1(3)1(2)1(1=====x x x x x . 10.某家具制造厂生产五种不同规格的家具。
《管理运筹学》第四版课后习题答案

《管理运筹学》第四版课后习题解析(上)第2章线性规划的图解法1.解:(1)可行域为OABC。
(2)等值线为图中虚线部分。
? (3)由图2-1可知,最优解为B 点,最优解 x =12, x ??15 727图2-1 ;最优目标函数值 69。
72.解:(1)如图2-2所示,由图解法可知有唯一解?x 1 ??0.2,函数值为3.6。
?x 2图2-2(2)无可行解。
(3)无界解。
(4)无可行解。
? (5)无穷多解。
?x ? (6)有唯一解 ??1? 203,函数值为 92 。
8 3x ? ??2 33.解: (1)标准形式max f ??3x 1 ??2x 2 ??0s 1 ??0s 2 ??0s 39x 1 ??2x 2 ??s 1 ??30 3x 1 ??2x 2 ??s 2 ??13 2x 1 ??2x 2 ??s 3 ??9 x 1, x 2 , s 1, s 2 , s 3 ≥ 0(2)标准形式min f ??4x 1 ??6x 2 ??0s 1 ??0s 23x 1 ??x 2 ??s 1 ??6x 1 ??2x 2 ??s 2 ??10 7x 1 ??6x 2 ??4x 1, x 2 , s 1, s 2 ≥ 0(3)标准形式min f ??x 1????2x 2????2x 2??????0s 1 ??0s 2?3x 1 ??5x 2????5x 2??????s 1 ??70 2x 1????5x 2????5x 2??????50 3x 1????2x 2????2x 2??????s 2 ??30 x 1?, x 2??, x 2????, s 1, s 2 ≥ 0 4.解: 标准形式max z ??10x 1 ??5x 2 ??0s 1 ??0s 23x 1 ??4x 2 ??s 1 ??95x 1 ??2x 2 ??s 2 ??8x1, x2 , s1, s2 ≥0≤松弛变量(0,0)最优解为 x 1 =1,x 2=3/2。
《管理运筹学》第二课后习题答案

《管理运筹学》(第二版)课后习题参考答案第1章 线性规划(复习思考题)1.什么是线性规划?线性规划的三要素是什么?答:线性规划(Linear Programming ,LP )是运筹学中最成熟的一个分支,并且是应用最广泛的一个运筹学分支。
线性规划属于规划论中的静态规划,是一种重要的优化工具,能够解决有限资源的最佳分配问题。
建立线性规划问题要具备三要素:决策变量、约束条件、目标函数。
决策变量是决策问题待定的量值,取值一般为非负;约束条件是指决策变量取值时受到的各种资源条件的限制,保障决策方案的可行性;目标函数是决策者希望实现的目标,为决策变量的线性函数表达式,有的目标要实现极大值,有的则要求极小值。
2.求解线性规划问题时可能出现几种结果,哪种结果说明建模时有错误? 答:(1)唯一最优解:只有一个最优点; (2)多重最优解:无穷多个最优解;(3)无界解:可行域无界,目标值无限增大; (4)没有可行解:线性规划问题的可行域是空集。
当无界解和没有可行解时,可能是建模时有错。
3.什么是线性规划的标准型?松弛变量和剩余变量的管理含义是什么?答:线性规划的标准型是:目标函数极大化,约束条件为等式,右端常数项0≥i b ,决策变量满足非负性。
如果加入的这个非负变量取值为非零的话,则说明该约束限定没有约束力,对企业来说不是紧缺资源,所以称为松弛变量;剩余变量取值为非零的话,则说明“≥”型约束的左边取值大于右边规划值,出现剩余量。
4.试述线性规划问题的可行解、基础解、基可行解、最优解的概念及其相互关系。
答:可行解:满足约束条件0≥=X b AX ,的解,称为可行解。
基可行解:满足非负性约束的基解,称为基可行解。
可行基:对应于基可行解的基,称为可行基。
最优解:使目标函数最优的可行解,称为最优解。
最优基:最优解对应的基矩阵,称为最优基。
它们的相互关系如右图所示:5.用表格单纯形法求解如下线性规划。
s .t . ⎪⎩⎪⎨⎧≥≤++≤++0,,86238321321321x x x x x x x x x解:标准化 32124m a xx x x Z ++= s .t . ⎪⎩⎪⎨⎧≥=+++=+++0,,,,862385432153214321x x x x x x x x x x x x x 列出单纯形表故最优解为T X )6,0,2,0,0(*=,即2,0,0321===x x x ,此时最优值为4*)(=X Z . 6.表1—15中给出了求极大化问题的单纯形表,问表中d c c a a ,,,,2121为何值及变量属于哪一类型时有:(1)表中解为唯一最优解;(2)表中解为无穷多最优解之一;(3)下一步迭代将以1x 代替基变量5x ;(4)该线性规划问题具有无界解;(5)该线性规划问题无可行解。
《管理运筹学》第四版课后习题答案
(4)3 车间 ,因为增加的利 润最大。
(5)在400 到正无 穷的范 围内 变化,最优产 品的 组合不 变。
(6)不变,因为在 0,500 的范 围内。
(7)所谓的上限和下限 值指当 约束条件的右 边值 在 给定范 围 内变化 时,约束条件 1 的右 边值 在 200,440 变化,对 偶价格仍 为 50(同理解释 其他 约 束条件)。
当 c1 不变时 ,c2 在 负无穷 到 6.4 的范 围内变 化,最优 解不 变。 (5)约 束条件 1 的右 边值 在 780 000,1500 000 变化,对偶价格仍 为 0.057(其他同理) 。 (6)不能,因为允 许减少的百分比与允 许 增加的百分比之和 4 2 100% ,理由
4.25 3.6
11.解: 设圆 桌和衣柜的生 产件数分 别为 x、y,所获 利润为 z,则 z=6x+10y.
0.18x 0.08x
x0 y0
0.09 y 0.28 y
72 2x y 800
56 2x 7 y 即 x0
1400 作出可行域.平移 6x+ 10y=0 ,如图
y0
2x y 800
x 350
得
即 C(350,100) .当直线 6x+ 10y=0 即 3x+ 5y=0 平移
x1
0.2
,函数值为 3.6。
x2 0.6
图 2-2
(2)无可行解。 (3)无界解。 (4)无可行解。
(5)无穷多解。
x1
(6)有唯一解
x2
20
3 ,函数值为 92 。
8
3
3
3.解: (1)标 准形式
max f 3x1 2x2 0s1 0s2 0s3
管理运筹学课后答案
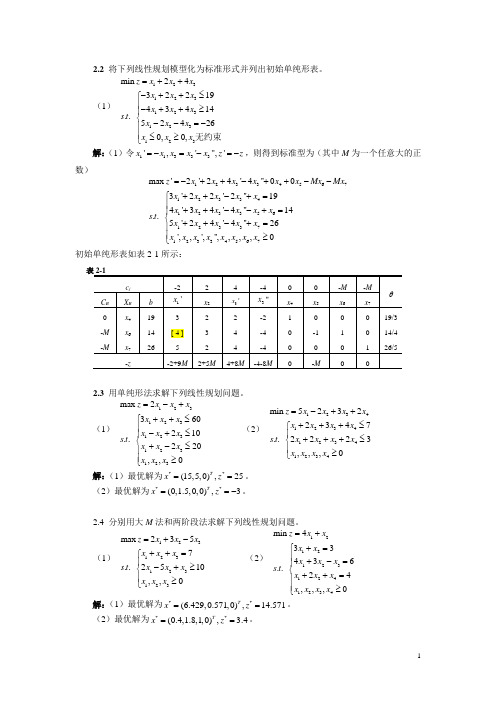
2.2 将下列线性规划模型化为标准形式并列出初始单纯形表。
(1)123123123123123min 243221943414..524260,0,z x x x x x x x x x s t x x x x x x =++-++≤⎧⎪-++≥⎪⎨--=-⎪⎪≤≥⎩无约束 解:(1)令11333','",'x x x x x z z =-=-=-,则得到标准型为(其中M 为一个任意大的正数)12334567123341233561233712334567max '2'24'4''003'22'2''194'34'4''14..5'24'4''26',,','',,,,0z x x x x x x Mx Mx x x x x x x x x x x x s t x x x x x x x x x x x x x =-++-++--++-+=⎧⎪++--+=⎪⎨++-+=⎪⎪≥⎩初始单纯形表如表2-1所示:表2-1c j-22 4-4 0 0 -M -M θC B X B b 1'xx 2 3'x3''xx 4 x 5 x 6 x 7 0 x 4 19 3 2 2 -2 1 0 0 0 19/3 -M x 6 14 [ 4 ] 3 4 -4 0 -1 1 0 14/4 -Mx 7 265 2 4-40 0 0 1 26/5 -z-2+9M2+5M4+8M -4-8M-M2.3 用单纯形法求解下列线性规划问题。
(1)123123123123123max 2360210..220,,0z x x x x x x x x x s t x x x x x x =-+++≤⎧⎪-+≤⎪⎨+-≤⎪⎪≥⎩ (2) 1234123412341234min 52322347..2223,,,0z x x x x x x x x s t x x x x x x x x =-+++++≤⎧⎪+++≤⎨⎪≥⎩解:(1)最优解为**(15,5,0),25T x z ==。
MBA管理运筹学课后部分作业答案

* f2(s2,x2) 0.5s2+ f 3 ( s2 )
3+x2+0.5s2+ f 3* ( s2 )
f 2* ( s2 )
s2 0 1 2 16 16.5 16.5 x2 0 1 2 3 17 17 15 4 17.5 15.5 16 5 16 16.5 17 6 17 17.5 16 15.5 15
变换标准型,找出最大元素为1000,用1000减 去各个元素得:
100 200 100 600 0
600 500 300 200 500
400 100 700 700
200 0 500 400
500 100 400 0 200 100 500 100 200 0
400 100
0 200 0 500 0
45+125 70+95
170
1
• • • •
顺序递推,得出结论 由表可知,当x1=1,x2=3,x3=1时各商场的增加额最大 最大值 f1*=170(万元) 即该公司应分配给甲、乙、丙3个商场以1,3,1个人员。这样增加额最大,为 170万元。 3
7-6 某厂生产一种机械设备。据市场调查,今后4个时期该 产品需求量依次为2、3、2、4台。该厂每期最大生产能力 为6台;每期固定生产费用为3万元(若不生产则为0), 单台成本1万元,每期贮存保养费为每台0.5万元。若第1期 初和第4期末均无库存,试确定各期产量,使总费用最少。 解:1. 建立模型 令k=1、2、3、4表示4个时期的序号 设Sk=第K时期初(或第k-1时期末的库存量) Xk——第k时期的产量 dk表第k时期的需求量,则状态转移方程为: Sk+1=Sk+Xk-dk 设:Uk(Sk,Xk)——第k时期生产费用; fk (Sk,Xk)——第k月初到第4月末的生产费用 * f k k,Xk)——第k月初到底4月末的最低生产费用 (S
