混凝土单筋矩形截面计算
合集下载
矩形截面钢筋混凝土拉弯构件计算
综合检算 一、输入数据
1、矩形截面宽b 2、截面全高h 3、钢筋弹性模量与混凝土受压弹性模量之比n 受拉侧钢筋直径 受拉侧钢筋根数 n 4、一侧受拉钢筋面积Ag 受压侧钢筋直径 受压侧钢筋根数 n 5、另一侧受压钢筋面积Ag´ 6、钢筋Ag重心至边缘距离a 7、钢筋Ag´重心至边缘距离a´ 8、轴向拉力N 9、初始弯矩M 10、初始偏心矩e0 单位 m m m m^2 m m^2 m m MN MN.m m
三、裂缝检算
钢筋表面系数(光筋1.0,肋筋0.8) 系数(光筋0.5,肋筋0.3) 活载弯矩 恒载弯矩 全部计算荷载弯矩 中性轴到受拉筋与受拉边之比(梁1.1,板1.2) 受拉钢筋重心处的钢筋应力 钢筋的弹性模量 受拉钢筋直径 受拉钢筋的有效配筋率 单根受拉根数 两根一束受拉根数 三根一束的受拉根数 单根1.0 两根一束0.85 三根一束0.7 单根钢筋的截面积 Acl=2ab 钢筋重心到拉边距离 截面宽度 裂缝宽度 K1 K2 α M1 M2 M γ σs Es d μ z n1 n2 n3 β 1 β 2 β 3 Asl Acl a b ωf 0.8 0.8 0.8 0.8 1.320 1.603 1.769 1.735 0.3 0.3 0.3 0.3 1.422 -0.0545 -0.0918 -0.08643 0.16 0.16 0.16 0.16 1.582 0.1055 0.0682 0.07357 1.2 1.2 1.2 1.2 81.435 101.468 102.272 149.327 210000 210000 210000 210000 20 20 20 16 0.392699082 0.020943951 0.013089969 0.022340214 150 8 5 10 0 0 0 0 0 0 0 0 1 1 1 1 0.85 0.85 0.85 0.85 0.7 0.7 0.7 0.7 0.000314159 0.000314159 0.000314159 0.000201062 0.12 0.12 0.12 0.09 0.06 0.06 0.06 0.045 1 1 1 1 0.0519 0.1417 0.1818 0.2089
1、矩形截面宽b 2、截面全高h 3、钢筋弹性模量与混凝土受压弹性模量之比n 受拉侧钢筋直径 受拉侧钢筋根数 n 4、一侧受拉钢筋面积Ag 受压侧钢筋直径 受压侧钢筋根数 n 5、另一侧受压钢筋面积Ag´ 6、钢筋Ag重心至边缘距离a 7、钢筋Ag´重心至边缘距离a´ 8、轴向拉力N 9、初始弯矩M 10、初始偏心矩e0 单位 m m m m^2 m m^2 m m MN MN.m m
三、裂缝检算
钢筋表面系数(光筋1.0,肋筋0.8) 系数(光筋0.5,肋筋0.3) 活载弯矩 恒载弯矩 全部计算荷载弯矩 中性轴到受拉筋与受拉边之比(梁1.1,板1.2) 受拉钢筋重心处的钢筋应力 钢筋的弹性模量 受拉钢筋直径 受拉钢筋的有效配筋率 单根受拉根数 两根一束受拉根数 三根一束的受拉根数 单根1.0 两根一束0.85 三根一束0.7 单根钢筋的截面积 Acl=2ab 钢筋重心到拉边距离 截面宽度 裂缝宽度 K1 K2 α M1 M2 M γ σs Es d μ z n1 n2 n3 β 1 β 2 β 3 Asl Acl a b ωf 0.8 0.8 0.8 0.8 1.320 1.603 1.769 1.735 0.3 0.3 0.3 0.3 1.422 -0.0545 -0.0918 -0.08643 0.16 0.16 0.16 0.16 1.582 0.1055 0.0682 0.07357 1.2 1.2 1.2 1.2 81.435 101.468 102.272 149.327 210000 210000 210000 210000 20 20 20 16 0.392699082 0.020943951 0.013089969 0.022340214 150 8 5 10 0 0 0 0 0 0 0 0 1 1 1 1 0.85 0.85 0.85 0.85 0.7 0.7 0.7 0.7 0.000314159 0.000314159 0.000314159 0.000201062 0.12 0.12 0.12 0.09 0.06 0.06 0.06 0.045 1 1 1 1 0.0519 0.1417 0.1818 0.2089
单筋截面计算
3.3单筋矩形截面受弯承载能力计算
（2）查表计算 ①求αs
αs = M／ α1 f cb h0 2 ②查表求ξ 、γs ，教材表3-7（若ξ ＞ξb ，应加大截面尺寸，或改双筋 ③求As
As = M ／fy h0 γs
或 As = ξb h0 α1 f c／fy ④选配钢筋（和公式法相同） 一般情况下接近计算值，范围为5%。 ⑤验算配筋率（和公式法相同）
ρ ≥ ρ min 或 AS ≥ ρ min bh （3-15） 上式说明检验最小配筋率ρ min 时，构件截面应采用全截面面积
3.3单筋矩形截面受弯承载能力计算
（2）基本公式的应用
a.计算表格的编制
上面推导的公式虽可直接计算，但还不方便，设计中为了 方便，常将公式进行改写，并制成表格使用。
令：αs=ξ（1－0.5 ξ ）代入（3-11）
◆设计过程应为： αs → ξ → γs → As
3.3单筋矩形截面受弯承载能力计算
◆截面设计步骤 已知弯矩设计值M，混凝土等级和钢筋级别，截面尺寸b、h0。求所
需受拉钢筋面积As。 (1)公式法求解步骤 ①将已知条件代入下列公式求解x及As
α1 f cb x= fyAs M = α1 f cb x（h0-0.5x）= fyAs （h0-0.5x） ②选配钢筋
则有： M = α1 f cb h0 2 αs
αs = M／ α1 f cb h0 2
（3－16）
再令：γs=1－0.5 ξ代入（3-12）
则有：M= fyAs h0 γs
As = M ／fy h0 γs
（3－17）
由αs=ξ（1－0.5 ξ ）可得： ξ=1－（1－2 αs ）0.5
3.3单筋矩形截面受弯承载能力计算
6单筋矩形截面
2某教学楼钢筋混凝土矩形截面简支梁，安全等级为二级，截面尺寸 b×h=250×550mm，承受恒载标准值10kN/m（不包括梁的自重），活荷载标准 值12kN/m，计算跨度=6m，采用C20级混凝土，HRB335级钢筋。试确定纵向 受力钢筋的数量。
3. 计算x，并判断是否属超筋梁
2M 2 148.165106 2 x h0 h 510 510 1 f c b 1.0 9.6 250
2）复核己知截面的承载力 己知：构件截面尺寸b×h，钢筋截面面积As，混凝土强度等级fc，钢筋级别 fy ，弯矩设计值M 。 求：复核截面是否安全 、弯矩承载力Mu= ？
计算步骤如下：
①确定截面有效高度h0 ②判断梁的类型 As f y
x
1 f c b
若As minbh，且x b h0 为适筋梁；
若x b h0 为超筋梁；若As minbh 为少筋梁。
③计算截面受弯承载力Mu
适筋梁 M u As f y h0 x 2
2 超筋梁 M M f bh u u, max 1 c 0 b (1 0.5b )
对少筋梁，应将其受弯承载力降低使用（已建成工程）或修改设计。 ④判断截面是否安全 若M ≤Mu ，则截面安全。
防止少筋的条件：
x xb b h0
min
AS AS ,min minbh
取x =ξbh0 ，即得到单筋矩形截面所能承受的最大弯矩的表达式：
2 M u,max 1 f c bh0 b (1 0.5 b )
混凝土受压区高度计算式： x h0
2M h 1 f c b
③ 少筋梁
配筋率小于最小配筋率的梁为少筋梁。 破坏特征：梁破坏时， 裂缝往往集中出现一条， 不但开展宽度大，而且 沿梁高延伸较高。一旦 出现裂缝，钢筋的应力 就会迅速增大并超过屈 服强度而进入强化阶段， 甚至被拉断。属于“脆 性破坏”
钢筋混凝土受弯构件正截面承载力计算—单筋矩形截面梁计算
受压混凝土的应力－应变关系
计算原则
2）等效矩形应力图
简化原则：受压区混凝土的合力大小不变；受压区混凝土的合力作用点不变。
等效矩形应力图形的混凝土受压区高度 x 1xn ，等效矩形应力图形的应力值 为 1 fc， 1、1 的值见下表。
表 1、1 值
混凝土强 度等级
≤C50
C55
C60
C65
C70
C75
（2）求跨中截面的最大弯矩设计值。
因仅有一个可变荷载，故弯矩设计值应有取下列两者中的较大值：
M 1 1.2g 1.4q l 2
8
1 1.2 5 1.4 10 5.02 62.5
8
M 1 1.35g 1.4 0.7q l 2
8
1 1.35 5 1.4 0.7 10 5.02 51.7
需要加固、补强
计算原则
1）基本假定
01 平截面假定。
02
钢筋的应力 s 等于钢筋应变 s 与其弹性模量 Es 的乘积，但不得大
于其强度设计值 fy，即
s sEs fv
03 不考虑截面受拉区混凝土的抗拉强度。
计算原则
04
受压混凝土采用理想化的应力－应变关系，当混凝土强度等级为
C50及以下时，混凝土极限压应变 cu=0.0033。
（1）受拉钢筋为4 25，As=1964 mm2； （2）受拉钢筋为3 18，As=763 mm²。
单筋矩形截面梁计算
解 查表得：
fc 9.6N/mm2
ft 1.10N/mm2
f y 300N/mm2 c 1.0
b 0.550
c 30mm
单筋矩形截面梁计算
（1）
d
25
h0 h c 2 450 30 2 408
单筋矩形截面梁、板正截面受弯承载力计算教学课件.
0.96
0.76
0.95
0.73
0.94
0.74
水工混凝土结构
1.3 相对受压区计算高度
相对受压区计算高度是等效矩形混凝土受压区计算高度x
与截面有效高度h0的比值，用ξ= x/h0表示。 当梁发生界限破坏时，即受拉钢筋屈服的同时，受压区
混凝土也达到极限压应变εcu。这时混凝土受压区计算高度xb
与截面有效高度h0的比值，称为相对界限受压区计算高度ξb， ξb= xb/h0。这一临界破坏状态，就是适筋梁与超筋梁的界限。
HPB235
≤C50 HRB335 HRB400 RRB400
0.614
0.550 0.518
0.425
0.399 0.384
0.522
0.468 0.440
0.386
0.358 0.343
水工混凝土结构
1.4 受拉钢筋配筋率 受拉钢筋的配筋率ρ是指受拉钢筋截面面积As与截面有效 截面面积bh0比值的百分率，即ρ =As /（bh0 ）×100﹪。 通常用ρmax表示受拉钢筋的最大配筋率； 用ρmin表示受拉钢筋的最小配筋率。 当ρ＞ρmax时，将发生超筋破坏； 当ρ＜ρmin时，将发生少筋破坏； 当ρmin≤ρ≤ρmax时，将发生适筋破坏。 为避免发生超筋破坏与少筋破坏，截面设计时，应控制 受拉纵筋的配筋率ρ在ρmin～ρmax范围内。
水工混凝土结构
2015.03
钢筋混凝土梁板设计
单筋矩形截面梁、板正截面承载力计算
1 正截面承载力计算的一般规定
1.1 计算方法的基本假定
(1) 截面应变保持为平面：
c
x
c
y
c
4.4单筋矩形截面受弯构件正截面承载力计算-PPT课件
γs——截面内力臂系数。
43
第三章 受弯构件正截面承载力计算
αs、γs均为ξ 的函数，可编制成计算表格供查用。 但通常采用如下方法计算：
①计算αs ②计算ξ 或γs
M s 2 1 f cbho
1 1 2 s
γs＝1－0.5ξ
44
第三章 受弯构件正截面承载力计算
③ 求纵向钢筋面积As 若 ξ ≤ξ 或
40
第三章 受弯构件正截面承载力计算
2）求纵向受拉钢筋面积As
1 f c bx As 若 x≤ξ bho，则 fy 若 x＞ξ bho，则属于超筋梁，应加大截面尺寸或提 高混凝土强度等级，并重新设计计算。
fyA 1 fcbx s
3）验算最小配筋率ρmin As≥ρminbh 若 或按 As＜ρminbh，应适当减少截面尺寸， As＝ρminbh 配筋。
能力的不足。 ② 在不同荷载组合情况下，其中在某一组合情况下截面承受 正弯矩，另一种组合情况下可能承受负弯矩，即梁截面承 受异号弯矩。
③ 在抗震结构中要求框架梁必须配置一定比例的受压钢筋， 受压钢筋可以提高截面的延性。
48
二、纵向受压钢筋的抗压强度设计取值 混凝土受压高度x满足下述条件，且配置必要的封 闭箍筋，则纵向受压钢筋的应力可取《规范》规定的 设计强度值ƒy＇ ' x 2a
b
则
As bh o
1 fc
fy
M As f y rs h o
若ξ ＞ξ b，则为超筋梁，应重新计算。
④ 验算最小配筋率
As≥ρminbh
45
2. 截面复核
己知：截面尺寸b×h，截面配筋As，材料强度fc、fy ，弯矩设计值M 求：复核截面是否安全 、弯矩承载力Mu= ？
43
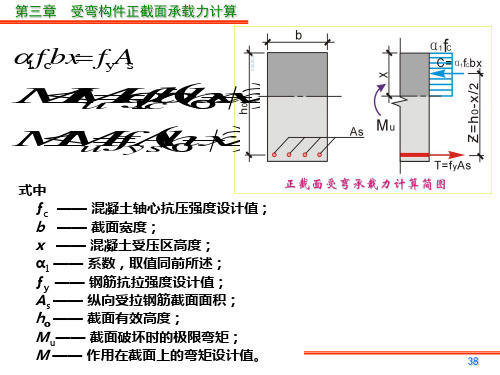
第三章 受弯构件正截面承载力计算
αs、γs均为ξ 的函数，可编制成计算表格供查用。 但通常采用如下方法计算：
①计算αs ②计算ξ 或γs
M s 2 1 f cbho
1 1 2 s
γs＝1－0.5ξ
44
第三章 受弯构件正截面承载力计算
③ 求纵向钢筋面积As 若 ξ ≤ξ 或
40
第三章 受弯构件正截面承载力计算
2）求纵向受拉钢筋面积As
1 f c bx As 若 x≤ξ bho，则 fy 若 x＞ξ bho，则属于超筋梁，应加大截面尺寸或提 高混凝土强度等级，并重新设计计算。
fyA 1 fcbx s
3）验算最小配筋率ρmin As≥ρminbh 若 或按 As＜ρminbh，应适当减少截面尺寸， As＝ρminbh 配筋。
能力的不足。 ② 在不同荷载组合情况下，其中在某一组合情况下截面承受 正弯矩，另一种组合情况下可能承受负弯矩，即梁截面承 受异号弯矩。
③ 在抗震结构中要求框架梁必须配置一定比例的受压钢筋， 受压钢筋可以提高截面的延性。
48
二、纵向受压钢筋的抗压强度设计取值 混凝土受压高度x满足下述条件，且配置必要的封 闭箍筋，则纵向受压钢筋的应力可取《规范》规定的 设计强度值ƒy＇ ' x 2a
b
则
As bh o
1 fc
fy
M As f y rs h o
若ξ ＞ξ b，则为超筋梁，应重新计算。
④ 验算最小配筋率
As≥ρminbh
45
2. 截面复核
己知：截面尺寸b×h，截面配筋As，材料强度fc、fy ，弯矩设计值M 求：复核截面是否安全 、弯矩承载力Mu= ？
混凝土结构1-2单筋矩形截面梁板设计
三、梁的钢筋构造
纵向钢筋
梁
中
钢
筋
箍筋
构
架
弯起钢筋
纵向受力钢筋 架立钢筋
腰筋及拉筋
（一）纵向钢筋
1.纵向受力钢筋
钢筋直径与根数： （1）纵向受力钢筋的常用直径为12～28mm。截面一侧
（受拉或受压）钢筋的直径最好相同，为节约钢材，也可选 用两种不同直径的钢筋，其直径相差宜在2～6mm范围内。
（2）梁内纵向受力钢筋至少为2根，以形成钢筋骨架的 需要。纵向受力钢筋的根数也不宜太多，否则会增大钢筋加 工的工作量，给混凝土浇捣带来困难。
架立钢筋
腰 筋
拉筋
（二）箍筋
箍筋的形状和肢数
作用 ：①固定纵筋的位置； ②提高梁的抗剪能力；
③提高梁的抗扭能力。 形状 ：封闭式和开口式
肢数 ：双肢或四肢
图2-7 箍筋的肢数 （a）双肢箍筋；（b）四肢箍筋
箍筋的强度 考虑到高强度的钢筋延性较差，施工时成型困难，箍筋一
般采用HPB235钢筋，也可采用HRB335级。
3.最小间距：受力钢筋最小间距为 70mm。
四、板内钢筋构造
板
受力钢筋
图示
分布钢筋
1.作用： ① 将板面荷载均匀地传递给受力钢筋； ② 防止因温度变化或混凝土收缩等原因，沿板跨方向产生裂缝； ③ 固定受力钢筋处于正确位置。
2.面积：每米板宽内分布钢筋的截面面积不小于受力钢筋截面面 积的15%（集中荷载时为25%）。
钢筋间距和布置 ： （1）梁内纵向钢筋之间的水平净距e在下部不应小于d
（d为纵筋的最大直径），同时不应小于25mm。 （2）在上部不应小于1.5d，同时不应小于30mm和最大
骨料粒径的1.5倍。 （3）梁内纵向钢筋应尽可能布置为一层。 当纵筋根数较多，若布置一层不能满足钢筋的间距、
3.2 正截面承载力计算
3.2 正截面承载力计算钢筋混凝土受弯构件通常承受弯矩和剪力共同作用，其破坏有两种可能：一种是由弯矩引起的，破坏截面与构件的纵轴线垂直，称为沿正截面破坏；另一种是由弯矩和剪力共同作用引起的，破坏截面是倾斜的，称为沿斜截面破坏。
所以，设计受弯构件时，需进行正截面承载力和斜截面承载力计算。
一、单筋矩形截面1.单筋截面受弯构件沿正截面的破坏特征钢筋混凝土受弯构件正截面的破坏形式与钢筋和混凝土的强度以及纵向受拉钢筋配筋率ρ有关。
ρ用纵向受拉钢筋的截面面积与正截面的有效面积的比值来表示，即ρ＝As/(bh0)，其中A s为受拉钢筋截面面积；b为梁的截面宽度；h0为梁的截面有效高度。
根据梁纵向钢筋配筋率的不同，钢筋混凝土梁可分为适筋梁、超筋梁和少筋梁三种类型，不同类型梁的具有不同破坏特征。
①适筋梁配置适量纵向受力钢筋的梁称为适筋梁。
适筋梁从开始加载到完全破坏，其应力变化经历了三个阶段，如图3.2.1。
第I阶段（弹性工作阶段）：荷载很小时，混凝土的压应力及拉应力都很小，应力和应变几乎成直线关系，如图3.2.1a。
当弯矩增大时，受拉区混凝土表现出明显的塑性特征，应力和应变不再呈直线关系，应力分布呈曲线。
当受拉边缘纤维的应变达到混凝土的极限拉应变εtu时，截面处于将裂未裂的极限状态，即第Ⅰ阶段末，用Ⅰa表示，此时截面所能承担的弯矩称抗裂弯矩M cr，如图3.2.1b。
Ⅰa阶段的应力状态是抗裂验算的依据。
第Ⅱ阶段（带裂缝工作阶段）：当弯矩继续增加时，受拉区混凝土的拉应变超过其极限拉应变εtu，受拉区出现裂缝，截面即进入第Ⅱ阶段。
裂缝出现后，在裂缝截面处，受拉区混凝土大部分退出工作，拉力几乎全部由受拉钢筋承担。
随着弯矩的不断增加，裂缝逐渐向上扩展，中和轴逐渐上移，受压区混凝土呈现出一定的塑性特征，应力图形呈曲线形，如图3.2.1c。
第Ⅱ阶段的应力状态是裂缝宽度和变形验算的依据。
当弯矩继续增加，钢筋应力达到屈服强度f y，这时截面所能承担的弯矩称为屈服弯矩M y。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第4章 受弯构件正截面承载力
1 基本计算公式
精选ppt
1
4.4 单筋矩形截面受弯承载力计算
第4章 受弯构件正截面承载力
2 适用条件
防止发生超筋破坏
xbh0 或 b
As
bh0
max
b
1 fc
fy
MMu smax 1fcbh02
或 s smax
防止发生少筋破坏
As mibn h
精选ppt
2
4.4 单筋矩形截面受弯承载力计算
（2）当 x bh0时，说明是超筋梁，取 x bh0，M u sm ax 1fcbh02；
（3）当 As minbh时，说明是少筋梁，分别按素混凝土构件和钢筋
混凝土构件计算 M
，取小值。
u
精选ppt
4
4.4 单筋矩形截面受弯承载力计算
第4章 受弯构件正截面承载力
4 截面设计
已知：M 、b 、h 、f y 、f c 、 s 求： A s 未知数：x 、A s 。 基本公式：
单筋矩形截面计算框图
精选ppt
3
第4章 受弯构件正截面承载力
3 截面复核
已知：b 、h 、A s 、f y 、f c 、M u、 s 求： M u 未知数： x 、M u
基本公式： 1fcbxfyA s MM u1fcbx(h02 x)fyA s(h02 x)
（1）当 x bh0且 As mibn h时，用基本公式直接计算 M u ；
精选ppt
7
精选ppt
8
精选ppt
9
第4章 受弯构件正截面承载力（选讲）
应用（选讲）
精选ppt
10
4.4 单筋矩形截面受弯承载力计算
（1） s
M = 1 fcbh0梁，改用双筋梁或增大截面尺寸重新计算；
（3）当 b时，用基本公式直接计算 A s；
（4）如果 As minbh，说明是少筋梁， 取 As minbh。
精选ppt
5
4.4 单筋矩形截面受弯承载力计算
精选ppt
6
1 基本计算公式
精选ppt
1
4.4 单筋矩形截面受弯承载力计算
第4章 受弯构件正截面承载力
2 适用条件
防止发生超筋破坏
xbh0 或 b
As
bh0
max
b
1 fc
fy
MMu smax 1fcbh02
或 s smax
防止发生少筋破坏
As mibn h
精选ppt
2
4.4 单筋矩形截面受弯承载力计算
（2）当 x bh0时，说明是超筋梁，取 x bh0，M u sm ax 1fcbh02；
（3）当 As minbh时，说明是少筋梁，分别按素混凝土构件和钢筋
混凝土构件计算 M
，取小值。
u
精选ppt
4
4.4 单筋矩形截面受弯承载力计算
第4章 受弯构件正截面承载力
4 截面设计
已知：M 、b 、h 、f y 、f c 、 s 求： A s 未知数：x 、A s 。 基本公式：
单筋矩形截面计算框图
精选ppt
3
第4章 受弯构件正截面承载力
3 截面复核
已知：b 、h 、A s 、f y 、f c 、M u、 s 求： M u 未知数： x 、M u
基本公式： 1fcbxfyA s MM u1fcbx(h02 x)fyA s(h02 x)
（1）当 x bh0且 As mibn h时，用基本公式直接计算 M u ；
精选ppt
7
精选ppt
8
精选ppt
9
第4章 受弯构件正截面承载力（选讲）
应用（选讲）
精选ppt
10
4.4 单筋矩形截面受弯承载力计算
（1） s
M = 1 fcbh0梁，改用双筋梁或增大截面尺寸重新计算；
（3）当 b时，用基本公式直接计算 A s；
（4）如果 As minbh，说明是少筋梁， 取 As minbh。
精选ppt
5
4.4 单筋矩形截面受弯承载力计算
精选ppt
6