专题11小题提分限时训练10(原卷版)-2021年新高考数学小题限时提分训练(45分钟)
高考数学专题03:临考强化2021年数学(理)小题综合限时提分专练(原卷版)
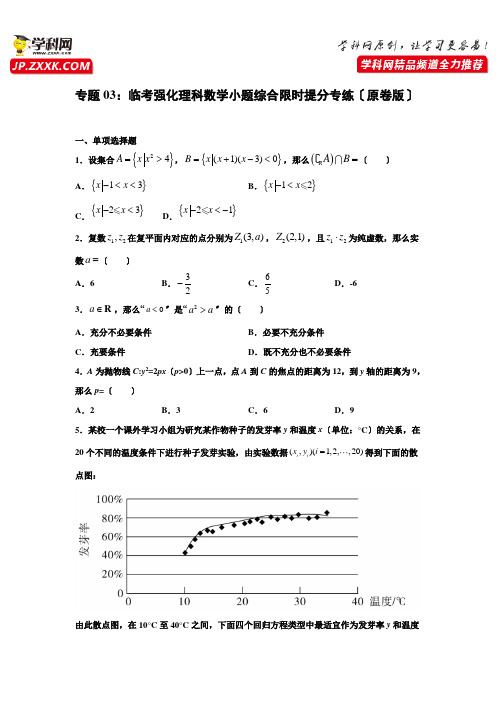
专题03:临考强化理科数学小题综合限时提分专练〔原卷版〕一、单项选择题1.设集合{}24A x x =>,{}(1)(3)0B x x x =+-<,那么()R A B =〔 〕 A .{}13x x -<<B .{}12x x -<C .{}23x x -<D .{}21x x -<-2.复数12,z z 在复平面内对应的点分别为1(3,)Z a ,2(2,1)Z ,且12z z ⋅为纯虚数,那么实数a =〔 〕A .6B .32-C .65D .-6 3.a ∈R ,那么“0a <〞是“2a a >〞的〔 〕A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件4.A 为抛物线C :y 2=2px 〔p >0〕上一点,点A 到C 的焦点的距离为12,到y 轴的距离为9,那么p =〔 〕A .2B .3C .6D .95.某校一个课外学习小组为研究某作物种子的发芽率y 和温度x 〔单位:°C 〕的关系,在20个不同的温度条件下进行种子发芽实验,由实验数据(,)(1,2,,20)i i x y i =得到下面的散点图:由此散点图,在10°C 至40°C 之间,下面四个回归方程类型中最适宜作为发芽率y 和温度x 的回归方程类型的是〔 〕A .y a bx =+B .2y a bx =+C .e x y a b =+D .ln y a b x =+6.函数43()2f x x x =-的图像在点(1(1))f ,处的切线方程为〔 〕 A .21y x =--B .21y x =-+C .23y x =-D .21y x =+ 7.设函数()cos π()6f x x ω=+在[π,π]-的图像大致如下列图,那么f (x )的最小正周期为〔 〕 A .10π9B .7π6 C .4π3 D .3π2 8.25()()x x y xy ++的展开式中x 3y 3的系数为〔 〕 A .5B .10C .15D .209. π()0,α∈,且3cos28cos 5αα-=,那么sin α=〔 〕 A 5B .23C .13D .510.,,A B C 为球O 的球面上的三个点,⊙1O 为ABC 的外接圆,假设⊙1O 的面积为4π,1AB BC AC OO ===,那么球O 的外表积为〔 〕A .64πB .48πC .36πD .32π11.⊙M :222220x y x y +---=,直线l :220x y ++=,P 为l 上的动点,过点P 作⊙M 的切线,PA PB ,切点为,A B ,当||||PM AB ⋅最小时,直线AB 的方程为〔 〕 A .210x y --=B .210x y +-=C .210x y -+=D .210x y ++= 12.假设242log 42log a b a b +=+,那么〔 〕A .2a b >B .2a b <C .2a b >D .2a b <二、填空题13.2sin ()4πα+ =23,那么sin 2α的值是____. 14.如图,六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的.螺帽的底面正六边形边长为2 cm ,高为2 cm ,内孔半径为0.5 cm ,那么此六角螺帽毛坯的体积是____cm.15.在△ABC 中,43=90AB AC BAC ==︒,,∠,D 在边BC 上,延长AD 到P ,使得AP =9,假设3()2PA mPB m PC =+-〔m 为常数〕,那么CD 的长度是________.16.在平面直角坐标系xOy 中,3(0)P ,A ,B 是圆C :221()362x y +-=上的两个动点,满足PA PB =,那么△PAB 面积的最大值是__________.。
专题8小题提分限时训练7(原卷版)-2021年新高考数学小题限时提分训练(45分钟)

专题8新高考数学小题提分限时训练7(原卷版)一、单选题1.已知集合{}13A x x =-<<,{}1,0,1,2,3B =-,则AB =( ) A .{}0,1,2 B .{}1,0,1,2,3-C .{}13x x -≤≤D .{}0,1,2,3 2.若23z z i +=-,则||z =( )A .1B .2C .3D .23.设函数)(),(x g x f 的定义域为R ,且)(x f 是奇函数,)(x g 是偶函数,则下列结论中正确的是( )A .)()(x g x f 是偶函数B .)(|)(|x g x f 是奇函数C ..|)(|)(x g x f 是奇函数D .|)()(|x g x f 是奇函数4.已知为双曲线:的一个焦点,则点到的一条渐近线的距离为( )A .B .3C .D .6.如图,图O 的半径为1,A 是圆上的定点,P 是圆上的动点,角x 的始边为射线OA ,终边为射线OP ,过点P 作直线OA 的垂线,垂足为M ,将点M 到直线OP 的距离表示成x 的函数,则的图像大致为( )A .B .C .D .7.将函数3sin(2)3y x π=+的图象向右平移2π个单位长度,所得图象对应的函数( ) A .在区间7[,]1212ππ上单调递减 B .在区间7[,]1212ππ上单调递增 C .在区间[,]63ππ-上单调递减 D .在区间[,]63ππ-上单调递增 8.已知定义在[0,1]上的函数()f x 满足:①(0)(1)0f f ==;②对所有,[0,1]x y ∈,且x y ≠,有1()()2f x f y x y -<-. 若对所有,[0,1]x y ∈,()()f x f y k -<,则k 的最小值为( )A .12 B .14 C .12π D .18二、多选题9.下列命题中,正确的有( )A .若0a b <<,则22a ab b <<B .若a b >,c d >,则a d b c ->-C .若0b a <<,0c <,则c c a b <D .若0a >,0b c >>,则c c a b b a +<+ A .从匀速传递的产品生产流水线上,质检员每20分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样B .已知变量x 与y 正相关,且由观测数据算得样本平均数x =3,y =3.5,则由该观测数据算得的回归方程可能是y =0.4x +2.3C .将某选手的9个得分(不完全相同)去掉1个最高分,去掉1个最低分,则平均数一定会发生变化D .方差描述了一组数据围绕平均数波动的大小,方差越大,数据的离散程度越大,方差越小,数据的离散程度越小11.如图,在直三棱柱111ABC A B C -中,160,2ABC AB BC BB ∠====,,M N 分别是111,A B AC 的中点,则下列说法正确的是( )A .直线//MN 平面11BCC BB .1ABC 的面积为27 C .四棱锥111C ABB A -的表面积为238+D .四棱锥111C ABB A -的表面积为738++12.已知数列{}n a 的前4项为2,0,2,0,则该数列的通项公式可能为( )A .0,2,n n a n ⎧=⎨⎩为奇数为偶数 B .1(1)1n n a -=-+ C .2sin2n n a π= D .cos(1)1n a n π=-+三、填空题 13.利用计算机产生~之间的均匀随机数,则事件‘’的概率为_________14.二项式(x+y )5的展开式中,含x 2y 3的项的系数是___(用数字作答). 15.如图,在棱长为2的正方体ABCD-A 1B 1C 1D 1中,E 为BC 的中点,点P 在线段D 1E 上,点P 到直线CC 1的距离的最小值为 .16.等差数列{a n}的前n项和为S n,已知S10=0,S15=25,则nS n的最小值为________.【答案】-49。
2021年新高考数学小题习题(附答案)

选填训练1一、选择题(共8小题;共40分)1. 已知集合 A ={x∣ x 2−x −6≤0},B ={x∣ x −1<0},则 ( )A. (−∞,3]B. (−∞,2]C. (−∞,1)D. [−2,1) 2. 若复数 z 满足 z (1+i )=−2i (其中 i 为虚数单位),则 z 的共轭复数是 ( ) A. 1−iB. 1+iC. −1−iD. −1+i3. 设 x ∈R ,则“2x >4”是“lg (∣x ∣−1)>0”的 ( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件4. 考古发现,在埃及金字塔内有一组神秘的数字 142857,因为 142857×2=285714,142857×3=428571,⋯,所以这组数字又叫走马灯数.该组数字还有如下规律:142+857=999,571+428=999,⋯.若从 1,4,2,8,5,7 这 6 个数字中任意取出 3 个数字构成一个三位数 x ,则 999−x 的结果恰好是剩下 3 个数字构成的一个三位数的概率为 ( )A. 45B. 35C. 25D.3105. 已知函数 f (x )={xlnx,x >0x ex ,x ≤0,则函数 y =f (1−x ) 的图象大致是 ( ) A. B.C. D.6. 若抛物线 y 2=2px (p >0) 的焦点到准线的距离为 2,过焦点的直线与抛物线交于 A ,B 两点,且 ∣AB ∣=8,则弦 AB 的中点到 y 轴的距离为 ( ) A. 2B. 3C. 4D. 67. 已知函数 f (x )=lg(√x 2+1+x)+12,则 f (ln5)+f (ln 15)= ( )A. 0B. 12C. 1D. 28. 若 F 为双曲线 C : x 24−y 25=1 的左焦点,过原点的直线 l 与双曲线 C 的左、右两支分别交于 A ,B 两点,则 1∣FA∣−4∣FB∣ 的取值范围是 ( )A. [14,15] B. [−15,15] C. (−14,0] D. [−14,15]二、选择题(共4小题;共20分)9. 习总书记讲到:“广大人民群众坚持爱国奉献,无怨无悔,让我感到千千万万普通人最伟大,同时让我感到幸福都是奋斗出来的”.某企业2019年12个月的收入与支出数据的折线图如下:已知利润=收入−支出,根据该折线图,下列说法正确的是( )A. 该企业2019年1月至6月的总利润低于2019年7月至12月的总利润B. 该企业2019年第一季度的利润约是60万元C. 该企业2019年4月至7月的月利润持续增长D. 该企业2019年11月份的月利润最大10. 声音是由物体振动产生的声波,其中包含着正弦函数.纯音的数学模型是函数y=Asinωt,我们听到的声音是由纯音合成的,称之为复合音.若一个复合音的数学模型是函数f(x)=sinx+ 12sin2x,则下列结论正确的是( )A. 2π是f(x)的一个周期B. f(x)在[0,2π]上有3个零点C. f(x)的最大值为3√34D. f(x)在[0,π2]上是增函数11. 给定两个不共线的空间向量a⃗与b⃗⃗,定义叉乘运算:a⃗×b⃗⃗.规定:①a⃗×b⃗⃗为同时与a⃗,b⃗⃗垂直的向量;②a⃗,b⃗⃗,a⃗×b⃗⃗三个向量构成右手系(如图1);③∣∣a⃗×b⃗⃗∣∣=∣a⃗∣∣∣b⃗⃗∣∣sin⟨a⃗,b⃗⃗⟩.如图2,在长方体ABCD−A1B1C1D1中,AB=AD=2,AA1=4,则下列结论正确的是( )A. AB ⃗⃗⃗⃗⃗⃗×AD ⃗⃗⃗⃗⃗⃗=AA 1⃗⃗⃗⃗⃗⃗⃗⃗B. AB ⃗⃗⃗⃗⃗⃗×AD ⃗⃗⃗⃗⃗⃗=AD ⃗⃗⃗⃗⃗⃗×AB⃗⃗⃗⃗⃗⃗ C. (AB ⃗⃗⃗⃗⃗⃗+AD ⃗⃗)×AA 1⃗⃗⃗⃗⃗⃗⃗⃗=AB ⃗⃗⃗⃗⃗⃗×AA 1⃗⃗⃗⃗⃗⃗⃗⃗+AD ⃗⃗⃗⃗⃗⃗×AA 1⃗⃗⃗⃗⃗⃗⃗⃗D. 长方体 ABCD −A 1B 1C 1D 1 的体积 V =(AB ⃗⃗⃗⃗⃗⃗×AD ⃗⃗⃗⃗⃗⃗)⋅CC 1⃗⃗⃗⃗⃗⃗⃗⃗12. 若实数 a ,b 满足 2a +3a =3b +2b ,则下列关系式中可能成立的是 ( )A. 0<a <b <1B. b <a <0C. 1<a <bD. a =b三、填空题(共4小题;共20分) 13. 已知 sin (α−π3)=−3cos (α−π6),则 tan2α 的值为 .14. (2x −y )5 的展开式中,含 x 3y 2 项的系数为 (用数字作答).15. 平行四边形 ABCD 中,M 为 CD 的中点,点 N 满足 BN⃗⃗⃗⃗⃗⃗⃗=2NC ⃗⃗⃗⃗⃗⃗,若 AB ⃗⃗⃗⃗⃗⃗=λAM ⃗⃗⃗⃗⃗⃗⃗+μAN ⃗⃗⃗⃗⃗⃗⃗,则 λ+μ 的值为 .16. 如图,矩形 ABCD 中,AB =2√3,AD =2,Q 为 BC 的中点,点 M ,N 分别在线段 AB ,CD 上运动(其中 M 不与 A ,B 重合,N 不与 C ,D 重合),且 MN ∥AD ,沿 MN 将 △DMN 折起,得到三棱锥 D −MNQ ,则三棱锥 D −MNQ 体积的最大值为 ;当三棱锥 D −MNQ 体积最大时,其外接球的表面积的值为 .选填训练2一、选择题(共8小题;共40分)1. 已知集合M={x∣ f(x)=log2(x2−2x)},集合N={x∣ 3x>1},则M∩N=( )A. (2,+∞)B. (0,2)C. [2,+∞)D. (3,+∞)2. 已知复数z=1+i1−i+3i,则复数z的虚部是( )A. 4iB. 2iC. 2D. 43. 已知向量a⃗,b⃗⃗均为非零向量(a⃗−2b⃗⃗)⊥a⃗,∣a⃗∣=∣∣b⃗⃗∣∣,则a⃗,b⃗⃗的夹角为( )A. π6B. π3C. 2π3D. 5π64. 中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初行健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔细算相还.”其意思为:有一个人走378里路,第一天健步行走,从第二天起脚痛每天走的路程为前一天的一半,走了6天后到达目的地,请问第二天走了( )A. 24里B. 48里C. 96里D. 192里5. 在△ABC中,内角A,B,C所对的边分别是a,b,c,若asinBcosC+csinBcosA=√32b,且a>b,则∠B=( )A. π3B. π6C. 2π3D. 5π66. 过抛物线y2=2px(p>0)的焦点F作倾斜角为60∘的直线l交抛物线于A,B两点,且∣AF∣>∣BF∣,则∣AF∣∣BF∣=( )A. 2B. 3C. 43D. 327. 考古发现,在埃及金字塔内有一组神秘的数字142857,因为142857×2=285714,142857×3=428571,⋯,所以这组数字又叫走马灯数.该组数字还有如下规律:142+857=999,571+428=999,⋯,若从1,4,2,8,5,7这6个数字中任意取出3个数字构成一个三位数x,则999−x的结果恰好是剩下3个数字构成的一个三位数的概率为( )A. 45B. 35C. 25D. 3108. 如图所示的三棱柱ABC−A1B1C1,其中AC⊥BC,若AA1=AB=2,当四棱锥B−A1ACC1体积最大时,三棱柱ABC−A1B1C1外接球的体积为( )A. 163π B. 4√23π C. 8√23π D. 43π二、选择题(共4小题;共20分)9. 习总书记讲到:“广大人民群众坚持爱国奉献,无怨无悔,让我感到千千万万普通人最伟大,同时让我感到幸福都是奋斗出来的”.某企业2019年12个月的收入与支出数据的折线图如下:已知:利润=收入−支出,根据该折线图,下列说法正确的是( )A. 该企业2019年1月至6月的总利润低于2019年7月至12月的总利润B. 该企业2019年第一季度的利润约是60万元C. 该企业2019年4月至7月的月利润持续增长D. 该企业2019年11月份的月利润最大10. 声音是由物体振动产生的声波,其中包含着正弦函数.纯音的数学模型是函数y=Asinωt,我们听到的声音是由纯音合成的,称之为复合音.若一个复合音的数学模型是函数f(x)=sinx+ 12sin2x,则下列结论正确的是( )A. 2π是f(x)的一个周期B. f(x)在[0,2π]上有3个零点C. f(x)的最大值为3√34D. f(x)在[0,π2]上是增函数11. 在平面直角坐标系xOy中,如图放置的边长为2的正方形ABCD沿x轴滚动(无滑动滚动),点D恰好经过坐标原点.设顶点B(x,y)的轨迹方程是y=f(x),则对函数y=f(x)的判断正确的是( )A. 函数 y =f (x ) 是奇函数B. 对任意的 x ∈R ,都有 f (x +4)=f (x −4)C. 函数 y =f (x ) 的值域为 [0,2√2]D. 函数 y =f (x ) 在区间 [6,8] 上单调递增12. 如图,正方形 ABCD 中,E ,F 分别是 AB ,BC 的中点,将 △ADE ,△CDF ,△BEF 分别沿 DE ,DF ,EF 折起,使 A ,B ,C 重合于点 P .则下列结论正确的是 ( )A. PD ⊥EFB. 平面PDE ⊥平面PDFC. 二面角 P −EF −D 的余弦值为 13D. 点 P 在平面 DEF 上的投影是 △DEF 的外心三、填空题(共4小题;共20分) 13. 设 f (x ) 是定义在 R 上的奇函数,且满足 f (x +2)=−f (x ),则 f (−2)= . 14. 已知 (2x −1)(x +a )6 的展开式中 x 5 的系数为 24,则 a = .15. 双曲线 x 2a2−y 2b 2=1(a >0,b >0) 的左焦点为 F 1,过点 F 1 作斜率为 √2 的直线与 y 轴及双曲线的右支分别交于 A ,B 两点,若 F 1A ⃗⃗⃗⃗⃗⃗⃗⃗=AB ⃗⃗⃗⃗⃗⃗,则双曲线的离心率为 .16. 已知函数 f (x )=x 2cosπx 2,数列 {a n } 中,a n =f (n )+f (n +1)(n ∈N ∗),则数列 {a n } 的前 100项之和 S 100= .选填训练3一、选择题(共8小题;共40分)1. 已知复数 z 1,z 2 在复平面内对应的点分别为 z 1(1,1),z 2(0,1),则 z1z 2= ( )A. 1+iB. −1+iC. −1−iD. 1−i2. 设 a ∈R ,则“sinα=cosα”是“sin2α=1”的 ( )A. 充分而不必要条件B. 必要而不充分条件C. 充分必要条件D. 既不充分也不必要条件3. 向量 b ⃗⃗,a ⃗ 满足 ∣a ⃗∣=1,∣∣b ⃗⃗∣∣=√2,(a⃗+b ⃗⃗)⊥(2a ⃗−b ⃗⃗),则向量 a ⃗ 与 b ⃗⃗ 的夹角为 ( ) A. 45∘ B. 60∘ C. 90∘ D. 120∘ 4. 已知点 M (2,4) 在抛物线 C:y 2=2px (p >0) 上,点 M 到抛物线 C 的焦点的距离是 ( ) A. 4B. 3C. 2D. 15. 在 △ABC 中,AB ⃗⃗⃗⃗⃗⃗+AC ⃗⃗⃗⃗⃗⃗=2AD ⃗⃗⃗⃗⃗⃗,AE ⃗⃗⃗⃗⃗⃗+2DE ⃗⃗⃗⃗⃗⃗=0⃗⃗,若 EB⃗⃗⃗⃗⃗⃗=xAB ⃗⃗⃗⃗⃗⃗+yAC ⃗⃗⃗⃗⃗⃗,则 ( ) A. y =2xB. y =−2xC. x =2yD. x =−2y6. 已知数列 {a n } 中,a 3=2,a 7=1.若 {1a n} 为等差数列,则 a 5= ( )A. 23B. 32C. 43D. 347. 已知双曲线 C:x 2a 2−y 2b 2=1(a >0,b >0) 的左、右焦点分别为 F 1,F 2,O 为坐标原点,P 是双曲线在第一象限上的点,∣∣PF 1⃗⃗⃗⃗⃗⃗⃗⃗∣∣=2∣∣PF 2⃗⃗⃗⃗⃗⃗⃗⃗∣∣=2m (m >0),PF 1⃗⃗⃗⃗⃗⃗⃗⃗⋅PF 2⃗⃗⃗⃗⃗⃗⃗⃗=m 2,则双曲线 C 的渐近线方程为( )A. y =±12xB. y =±√22x C. y =±x D. y =±√2x8. 已知奇函数 f (x ) 是 R 上增函数,g (x )=xf (x ),则 ( )A. g (log 314)>g (2−32)>g (2−23) B. g (log 314)>g (2−23)>g (2−32)C. g (2−32)>g (2−23)>g (log 314)D. g (2−23)>g (2−32)>g (log 314)二、选择题(共4小题;共20分)9. 要得到函数 y =cos2x 的图象 C 1,只要将 y =sin (2x +π3) 图象 C 2 怎样变化得到?( )A. 将 y =sin (2x +π3) 的图象 C 2 沿 x 轴方向向左平移 π12 个单位 B. 将 y =sin (2x +π3) 的图象 C 2 沿 x 轴方向向右平移 11π12 个单位C. 先作 C 2 关于 x 轴对称图象 C 3,再将图象 C 3 沿 x 轴方向向右平移 5π12 个单位D. 先作 C 2 关于 x 轴对称图象 C 3,再将图象 C 3 沿 x 轴方向向左平移 π12 个单位10. 如图,正方体 ABCD −A 1B 1C 1D 1 的棱长为 1,则下列四个命题正确的是:( )A. 直线 BC 与平面 ABC 1D 1 所成的角等于 π4B. 点 C 到面 ABC 1D 1 的距离为 √22 C. 两条异面直线 D 1C 和 BC 1 所成的角为 π4 D. 三棱柱 AA 1D 1−BB 1C 1 外接球半径为 √3211. 已知集合 M ={(x,y )∣y =f (x )},若对于 ∀(x 1,y 1)∈M ,∃(x 2,y 2)∈M ,使得 x 1x 2+y 1y 2=0成立,则称集合 M 是“互垂点集”.给出下列四个集合:M 1={(x,y )∣y =x 2+1};M 2={(x,y )∣∣y =√x +1};M 3={(x,y )∣y =e x};M 4={(x,y )∣y =sinx +1}.其中是“互垂点集”集合的为 ( ) A. M 1B. M 2C. M 3D. M 412. 德国著名数学家狄利克雷(Dirichlet ,1805∼1859)在数学领域成就显著.19 世纪,狄利克雷定义了一个“奇怪的函数”y =f (x )={1,x ∈Q0,x ∈∁R Q,其中 R 为实数集,Q 为有理数集.则关于函数 f (x ) 有如下四个命题其中真命题是:( ) A. 函数 f (x ) 是偶函数B. ∀x 1,x 2∈∁R Q ,f (x 1+x 2)=f (x 1)+f (x 2) 恒成立C. 任取一个不为零的有理数 T ,f (x +T )=f (x ) 对任意的 x ∈R 恒成立D. 不存在三个点 A(x 1,f (x 1)),B(x 2,f (x 2)),C(x 3,f (x 3)),使得 △ABC 为等腰直角三角形三、填空题(共4小题;共20分)13. 已知直线 x −y +a =0 与圆 O:x 2+y 2=2 相交于 A ,B 两点(O 为坐标原点),且 △AOB 为等腰直角三角形,则实数 a 的值为 .14. 已知直线 y =x +2 与曲线 y =ln (x +a ) 相切,则 a 的值为 .15. 2019 年 7 月,中国良渚古城遗址获准列入世界遗产名录,标志着中华五千年文明史得到国际社会认可.良渚古城遗址是人类早期城市文明的范例,实证了中华五千年文明史.考古科学家在测定遗址年龄的过程中利用了“放射性物质因衰变而减少”这一规律.已知样本中碳 14 的质量 N 随时间 t (单位:年)的衰变规律满足 N =N 0⋅2−r5730(N 0 表示碳 14 原有的质量),则经过 5730 年后,碳 14 的质量变为原来的 ;经过测定,良渚古城遗址文物样本中碳 14 的质量是原来的 37 至 12,据此推测良渚古城存在的时期距今约在 5730 年到 年之间.(参考数据:lg2≈0.3,lg7≈0.84,lg3≈0.48)16. 已知 △ABC 的顶点 A ∈平面α,点 B ,C 在平面 α 异侧,且 AB =2,AC =√3,若 AB ,AC 与α 所成的角分别为 π3,π6,则线段 BC 长度的取值范围为 .选填训练4一、选择题(共8小题;共40分)1. 集合 A ={x ∈R ∣x 2−x −2<0},集合 B ={x ∈R∣e x ≥e },则 A ∩B = ( ) A. (1,2)B. (1,2]C. [1,2]D. [1,2)2. 已知 i 是虚数单位,复数a+i 1+i(a ∈R ) 为纯虚数的充要条件是 ( )A. a =2B. a =1C. a =−1D. a =−23. 某校高三年级的学生参加了一次数学测试,学生的成绩全部介于 60 分到 140 分之间(满分 150 分),为统计学生的这次考试情况,从中随机抽取 100 名学生的考试成绩作为样本进行统计.将这 100 名学生的测试成绩的统计结果按如下方式分成八组:第一组 [60,70),第二组 [70,80),第三组 [80,90),⋯⋯ 如图是按上述分组方法得到的频率分布直方图的一部分.则第七组的频数为 ( )A. 8B. 10C. 12D. 164. 设函数 f (x ) 的定义域为 R ,满足 f (x +2)=2f (x ),且 f (x )={2x+1,x ∈(0,1)ln (x +2),x ∈[1,2].则 f (e )=( )A. 2e+1B. 2eC. 2e−1D. ln (e +2)5. 在直角梯形 ABCD 中,AB =4,CD =2,AB ∥CD ,AB ⊥AD ,E 为 BC 的中点,则 AB ⃗⃗⃗⃗⃗⃗⋅(AC ⃗⃗⃗⃗⃗⃗+AE ⃗⃗⃗⃗⃗⃗)= ( ) A. 20B. 16C. 12D. 86. 已知函数 f (x )=x 1+∣x∣,则不等式 f (x −3)+f (2x )>0 的解集为 ( )A. (−∞,−3)B. (−∞,1)C. (−3,+∞)D. (1,+∞)7. 三棱锥 P −ABC 的底面 △ABC 是边长为 √3 的等边三角形,该三棱锥的所有顶点均在半径为 2 的球上,则三棱锥 P −ABC 的体积最大值为 ( ) A.2√3−34B. 3√34C. 3+2√34D.9+6√348. 已知定义在 R 上函数 f (x ) 的图象是连续不断的,满足 f (1−x )=f (1+x ),f (−x )=−f (x ),且 f (x ) 在 [0,1] 上单调递增,若 a =f (log 23),b =f(√10),c =f (2020),则 ( )A. a <b <cB. a <c <bC. c <b <aD. b <c <a二、选择题(共4小题;共20分)9. 已知点 F (1,0) 为曲线 C 的焦点,则曲线 C 的方程可能为 ( )A. y 2=4xB. x 2=4yC.x 2cos 2θ+y 2sin 2θ=1(0<θ<π2) D.x 2cos 2θ−y 2sin 2θ=1(0<θ<π2)10. 在棱长为 1 的正方体 ABCD −A 1B 1C 1D 1 中,点 M 在棱 CC 1 上,则下列结论正确的是 ( )A. 直线 BM 与平面 ADD 1A 1 平行B. 平面 BMD 1 截正方体所得的截面为三角形C. 异面直线 AD 1 与 A 1C 1 所成的角为 π3D. ∣MB ∣+∣MD 1∣ 的最小值为 √511. 对于函数 f (x )=√3sin (ωx −π3)+1(其中 ω>0),下列结论正确的是 ( )A. 若 ω=2,x ∈[0,π2],则 y =f (x ) 的最小值为 −12B. 若 ω=2,则函数 y =√3sin2x +1 的图象向右平移 π3个单位可以得到函数 y =f (x ) 的图象C. 若 ω=2,则函数 y =f (x ) 在 (0,π2) 上单调递增D. 若函数 y =f (x ) 的一个对称中心到与它最近一条对称轴的距离为 π4,则 ω=212. 如图 A (2,0),B (1,1),C (−1,1),D (−2,0),CD⏜ 是以 OD为直径的圆上一段圆弧,CB⏜ 是以 BC 为直径的圆上一段圆弧,BA⏜ 是以 OA 为直径的圆上一段圆弧,三段弧构成曲线 W .则下述正确的是 ( )A. 曲线 W 与 x 轴围成的面积等于 2π;B. 曲线 W 上有 5 个整点(横纵坐标均为整数的点);C. CB⏜ 所在圆的方程为:x 2+(y −1)2=1;D. CB⏜ 与 BA ⏜ 的公切线方程为:x +y =√2+1.三、填空题(共4小题;共20分) 13. 若命题“∃x 0∈R ,x 02−2x 0−a =0”为假命题,则实数 a 的取值范围是 .14. 已知等比数列 {a n } 的前 n 项和为 S n ,若 S 3−3S 2+2S 1=0,则 a2a 1= .15. 若二项式 (1−3x )n (n ∈N ∗) 的展开式中所有项的系数和为 −32,则 n = ;该二项式展开式中含有 x 3 项的系数为 .16. 黄金分割比 ω=√5−12≈0.618 被誉为“人间最巧的比例”.离心率 e =√5−12的椭圆被称为“优美椭圆”,“优美椭圆”C:x 2a2+y 2b 2=1(a >b >0) 的左右顶点分别为 A ,B ,“优美椭圆”C 上动点 P (异于椭圆的左右顶点),设直线 PA ,PB 的斜率分别为 k 1,k 2,则 k 1k 2= .选填训练5一、选择题(共9小题;共45分)1. 命题:“∀x ∈(−∞,0),3x ≥4x ”的否定为 ( ) A. ∃x 0∈[0,+∞),3x 0<4x 0 B. ∃x 0∈[0,+∞),3x 0≤4x 0 C. ∃x 0∈(−∞,0),3x 0<4x 0 D. ∃x 0∈(−∞,0),3x 0≤4x 02. i 是虚数单位,若复数 z =2i−1,则 z 的虚部为 ( )A. −1B. 0C. −iD. 13. 设 A ={x∣ x 2−8x +15=0},B ={x∣ ax −1=0},若 A ∩B =B ,求实数 a 组成的集合的子集个数有 ( ) A. 2 个B. 3 个C. 4 个D. 8 个4. 在 △ABC 中,若 AB =√13,BC =3,∠C =120∘,则 AC = ( )A. 1B. 2C. 3D. 45. 若 a ,b 是任意实数,且 a >b ,则 ( )A. a 2>b 2B. ba <1C. lg (a −b )>0D. (12)a<(12)b6. 古代数学著作《九章算术》有如下的问题:“今有女子善织,日自倍,五日织五尺,问日织几何?”意思是:“一女子善于织布,每天织的布都是前一天的 2 倍,已知她 5 天共织布 5 尺,问这女子每天分别织布多少?”根据上述已知条件,若要使织布的总尺数不少于 30 尺,则至少需要 ( )A. 6 天B. 7 天C. 8 天D. 9 天7. 已知 cos (π2−α)=2cos (π+α),且 tan (α+β)=13,则 tanβ 的值为 ( )A. −7B. 7C. 1D. −18. 已知函数 f (x )=asin2x −√3cos2x 的图象关于直线 x =−π12 对称,若 f (x 1)⋅f (x 2)=−4,则 a∣∣x 1−x 2∣ 的最小值为 ( )A. π4B. π2C. πD. 2π9. 已知函数 f (x )={(x +1)2,x ≤0∣log 2x ∣,x >0,若方程 f (x )=a 有四个不同的解 x 1,x 2,x 3,x 4,且 x 1<x 2<x 3<x 4,则 (x 1+x 2)⋅x 3+1x 32⋅x 4的取值范围是 ( )A. [−1,1]B. (−1,1]C. [−1,1)D. (−1,1)二、选择题(共3小题;共15分)10. 对于任意的平面向量 a ⃗,b ⃗⃗,c ⃗,下列说法错误的是 ( ) A. 若 a ⃗∥b ⃗⃗ 且 b ⃗⃗∥c ⃗,则 a ⃗∥c ⃗ B. (a ⃗+b ⃗⃗)⋅c ⃗=a ⃗⋅c ⃗+b ⃗⃗⋅c ⃗C. 若 a ⃗⋅b ⃗⃗=a ⃗⋅c ⃗,且 a ⃗≠0⃗⃗,则 b ⃗⃗=c ⃗D. (a⃗⋅b⃗⃗)⋅c⃗=a⃗⋅(b⃗⃗⋅c⃗)11. 已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<π2),−π3为f(x)的一个零点,x=π6为f(x)图象的一条对称轴,且f(x)在(0,π)上有且仅有7个零点,下述结论正确的是( )A. φ=π6B. ω=5C. f(x)在(0,π)上有且仅有4个极大值点D. f(x)在(0,π42)上单调递增12. 设定义在R上的函数f(x)满足f(−x)+f(x)=x2,且当x≤0时,fʹ(x)<x.已知存在x0∈{x∣ f(x)−12x2≥f(1−x)−12(1−x)2},且x0为函数g(x)=e x−√ex−a(a∈R,e为自然对数的底数)的一个零点,则实数a的取值可能是( )A. 12B. √e2C. e2D. √e三、填空题(共4小题;共20分)13. 已知向量a⃗,b⃗⃗满足:∣a⃗∣=3,∣∣b⃗⃗∣∣=2,∣∣a⃗+b⃗⃗∣∣=4,则∣∣a⃗−b⃗⃗∣∣=.14. 设命题p:2x−1x−1<0,命题q:x2−(2a+1)x+a(a+1)≤0,若p是q的充分不必要条,则实数a的取值范围是.15. 在△ABC中,a,b,c分别为内角A,B,C的对边,若2sinB=sinA+sinC,cosB=35,且S△ABC=6,则b=.16. 现有橡皮泥制作的底面半径为5,高为9的圆锥和底面半径为√3,高为8的圆柱各一个.若将它们重新制作成总体积与各自的高均保持不变,但底面半径相同的新的圆锥与圆柱各一个,则新的底面半径为,若新圆锥的内接正三棱柱表面积取到最大值,则此正三棱柱的底面边长为.选填训练6一、选择题(共9小题;共45分)1. 已知集合 A ={x∣ x 2−2x −3<0},B ={x∣ −2<x <2},若 A ∩B = ( ) A. (−2,2)B. (−2,1)C. (−1,3)D. (−1,2)2. 已知命题 p :∃x ∈R ,e x −x −1≤0,则命题 ¬p ( )A. ∀x ∈R ,e x −x −1>0B. ∀x ∉R ,e x −x −1>0C. ∀x ∈R ,e x −x −1≥0D. ∃x ∈R ,e x −x −1>03. 要得到函数 y =sin (2x +π3) 的图象,只要将函数 y =sin2x 的图象 ( )A. 向左平移 π3 个单位 B. 向右平移 π3 个单位 C. 向左平移 π6 个单位D. 向右平移 π6 个单位4. 函数 f (x )=log a x (a >0,a ≠1) 是增函数的一个充分不必要条件是 ( )A. 0<a <12B. 0<a <1C. a >1D. 2<a <45. 函数 f (x )=x 3−(12)x的零点所在区间为 ( )A. (−1,0)B. (0,12)C. (12,1)D. (1,2)6. 已知数列 {a n } 满足 a n+1=a n +2 且 a 2+a 4+a 6=9,则 log 3(a 5+a 7+a 9)= ( )A. −3B. 3C. −13D. 137. 若 a >0,b >0,lga +lgb =lg (a +2b ),则 2a +b 的最小值为 ( )A. 9B. 8C. 7D. 68. 泉城广场上矗立着的“泉标”成为泉城济南的标志和象征.为了测量“泉标”高度,某同学在“泉标”的正西方向的点 A 处测得“泉标”顶端的仰角为 45∘,沿点 A 向北偏东 30∘ 前进 100 m 到达点 B ,在点 B 处测得“泉标”顶端的仰角为 30∘,则“泉标”的高度为 ( )A. 50 mB. 100 mC. 120 mD. 150 m9. 已知偶函数 f (x ) 的定义域为 (−π2,π2),其导函数为 fʹ(x ),当 0<x <π2时,有 fʹ(x )cosx +f (x )sinx <0 成立,则关于 x 的不等式 f (x )<√2f (π4)⋅cosx 的解集为 ( ) A. (π4,π2)B. (−π2,−π4)∪(π4,π2)C. (−π4,0)∪(0,π4)D. (−π4,0)∪(π4,π2)二、选择题(共3小题;共15分)10. 下列函数中,既是偶函数,又在 (0,+∞) 上单调递增的是 ( ) A. y =x 2 B. y =x −2 C. y =e ∣x∣ D. y =lgx 211. 在平面直角坐标系 xOy 中,角 α 以 Ox 为始终,终边经过点 P (1,m )(m <0),则下列各式一定为正的是 ( )A. sinα+cosαB. cosα−sinαC. sinαcosαD. sinαtanα12. 已知函数 f (x )=xlnx +x 2,x 0 是函数 f (x ) 的极值点,以下几个结论中正确的是 ( )A. 0<x 0<1e B. x 0>1eC. f (x 0)+2x 0<0D. f (x 0)+2x 0>0三、填空题(共4小题;共20分) 13. 已知 tanα=13,则sin2α−sin 2α1+cos2α的值为 .14. 已知函数 f (x ) 是定义在 R 上的奇函数,当 x 1≠x 2 时,有 [f (x 1)−f (x 2)](x 1−x 2)<0 恒成立,若 f (3x +1)+f (2)>0,则 x 的取值范围是 .15. 设等差数列 {a n } 前 n 项和为 S n ,若 a 2=10,S 5=40,则 a 5= ,S n 的最大值为 .16. 已知函数 f (x )={2√x,0<x ≤12x,x >1,若方程 f (x )=−x +a 有三个不同的实根,则实数 a 的取值范围是 .训练1答案第一部分1. A2. D3. A4. C5. B6. B7. C8. D第二部分9. A, C10. A, B, C11. A, C, D12. A, B, D第三部分13. −4√314. 8015. 1216. 1,25π3训练2答案第一部分1. A2. D3. B4. C5. A6. B7. C8. C 第二部分9. A, C10. A,B, C【解析】A选项:f(x+2π)=sin(x+2π)+12sin(x+2π)⋅2=sinx+12sin2x=f(x),故A正确.B选项:fʹ(x)=cosx+12cos2x⋅2=2cos2x−1+cosx.令cosx=t∈[−1,1],所以fʹ(t)=(2t−1)(t+1),cosx=−1时,x=π,当t∈[−1,12]时,fʹ(t)<0,f(t)在[−1,12]上单减,cosx=12时,x=π3或5π3,当t∈[12,1]时,f(t)>0,f(t)在[12,1]上单增,则f(x)在[0,π3]上单增,[π3,5π3]上单减,[5π3,2π]上单增,f(0)=sin0+12sin2×0=0,f(5π3)=sin5π3+12sin10π3=−√32+1−√32⋅2=−3√34<0,f(2π)=sin2π+12sin4π=0,所以f(x)在[0,2π]上有个零点.C选项,由A,B可得:f(x)的最大值为f(π3)=sinπ3+12sin2⋅π3=3√34,故C正确.D选项:由A,B可得:f(x)在[0,π3]上单增,在[π3,π2]上单减,故D错误.故选A,B,C.11. B, C, D【解析】当−4≤x<−2时,B的轨迹是以A为圆心,半径为2的14圆;当−2≤x<2时,B的轨迹是以D为圆心,半径为2√2的14圆;当2≤x<4时,B的轨迹是以C为圆心,半径为1的14圆;当4≤x<6时,B的轨迹是以A为圆心,半径为2的14圆.所以函数的周期是8,因此最终形成的图象如下:由图象的对称性,可知函数f(x)是偶函数,故A选项错误;由图象即分析可知函数的周期是8,即f(x+8)=f(x),所以f(x+4)=f(x−4).故B选项正确;由图象可得f(x)的值域为[0,2√2].故C选项正确;由图象可得:f(x)在区间[6,8]上单调递增.故D选项正确.故正确的选项有B,C,D.12. A, B, C【解析】如图,由已知可得PE,PF,PD三条侧棱两两互相垂直,则PD⊥平面PEF,所以PD⊥EF,故A正确;PE ⊥平面PDF ,而 PE ⊂平面PDE , 所以 平面PDE ⊥平面PDF , 故B 正确;取 EF 最低 G ,连接 PG ,DG ,可得 PG ⊥EF ,DG ⊥EF , 得 ∠PGD 为二面角 P −EF −D 的平面角,设正方形 ABCD 的边长为 2,则 PD =2,PG =12EF =√22,DG =3√22, 所以 cos∠PGD =√223√22=13,即二面角 P −EF −D 的余弦值为 13,故C 正确;过 P 作 PO ⊥DG ,则 O 为 P 在底面 DEF 上的射影, 因为 PE <PD , 所以 OE <OD ,则 O 不是 △DEF 的外心, 故D 错误. 第三部分 13. 0【解析】因为 f (x ) 是定义在 R 上的奇函数,所以 f (0)=0,在等式 f (x +2)=−f (x ) 中令 x =−2,得 f (−2)=0. 14. 1 或 −45【解析】因为 (2x −1)(x +a )6=2x (x +a )6−(x +a )6,所以 (2x −1)(x +a )6 的展开式中 x 5 的系数为 2⋅C 62⋅a 2−C 61a 1=30a 2−6a ,所以 30a 2−6a =24,解得 a =1 或 a =−45, 则 a =1 或 a =−45, 故答案为:1 或 −45.15. √2+√3【解析】F 1A ⃗⃗⃗⃗⃗⃗⃗⃗=AB ⃗⃗⃗⃗⃗⃗=y B =2y A ,即 A 为 F 1B 中点, 则 AO 为中位线,所以 BF 2⊥F 1F 2, 所以tan∠BF 1F 2=BF 2F 1F 2=b 22ac=√2⇒c 2−a 2−2√2ac =0⇒e =√2+√3.16. 10200【解析】因为 f (x )=x 2cosπx 2,所以a n=f(n)+f(n+1)=n2cos nπ2+(n+1)2cos(n+1)π2,a4n−3=(4n−3)2cos4n−32π+(4n−2)2cos4n−22π=−(4n−2)2,同理可得:a4n−2=−(4n−2)2,a4n−1=(4n)2,a4n=(4n)2.所以a4n−3+a4n−2+a4n−1+a4n=−2(4n−2)2+2(4n)2=8(4n−1).所以数列{a n}的前100项之和S100=8×(3+7+⋯+99)=10200.第一部分1. D2. C3. A4. B5. A6. D7. C8. D第二部分9. A, D10. A, C, D11. A, D12. B, C, D第三部分13. a<−114. 215. 5,−27016. 1−√52第一部分1. D2. C3. C4. A5. D6. C7. D8. B第二部分9. A, B, C10. A, B, D11. B, D12. C, D第三部分13. ±√214. 315. 1,6876216. [√7,√13]训练5答案第一部分1. C【解析】命题的否定,把 ∀ 改成 ∃,≤ 改为 <. 2. A【解析】由题意可得: z =2i−1=2(i+1)(i−1)(i+1)=2i+2i 2−1=2i+2−2=−1−i .故虚部为:−1.3. D 【解析】A ={x∣ x 2−8x +15=0}={3,5},因为 A ∩B =B , 所以 B ⊂A ,且 B 中最多只有一个元素,因此 B =∅,{3},{5},对应实数 a 的值为 0,13,15,其组成的集合的子集个数有 23=8.4. A 【解析】设 AC =x ,由余弦定理得:cos120∘=x 2+9−132⋅x⋅3=−12, x 2−4=−3x ⇒x 2+3x −4=0,x =1或−4(舍),所以 AC =1.5. D6. C 【解析】由题意知,这是一个等比数列问题,已知等比数列 {a n } 的公比 9=2,S 5=5,求 S n ≥30 的最小正整数, 因为 a 1(1−25)1−2=5, 所以 a 1=531, 所以 531⋅1−2n 1−2≥30, 2n ≥187,所以 n ≥8.故选C .7. B 【解析】因为 cos (π2−α)=sinα,cos (π+α)=cosα, 所以 cos (π2−α)=2cos (π+α) 即 sinα=−2cosα,所以 tanα=−2,又因为 tan (α+β)=tanα+tanβ1−tanα⋅tanβ=−2+tanβ1+2tanβ=13,解得 tanβ=7. 故选B .8. B 【解析】由辅助角公式知 f (x )=√a 2+3sin (2x +φ),φ∈[0,2π),f (x ) 图象类似于 sinx ,可判断 x =−π12时取最值, sin (2⋅(−π12)+φ)=±1,φ−π6=π2或32π,φ=23π或53π,而 sinφ=√3√a 2+3,于是 φ=53π, cosφ=√a 2+3=cos 53π, 解得 a =1, f (x )=2sin (2x +53π),f (x 1)⋅f (x 2)=−4 只有一个取 2,一个取 −2,最大值点与最小值点 ∣x 1−x 2∣min =T 2=2π2ω=π2,于是 a∣∣x 1−x 2∣min ≥π2. 综上,选B .9. B 【解析】由图象可得 x 1+x 2=−2,x 3x 4=1,x 3∈[12,1), 因此 x 3⋅(x 1+x 2)+1x 32⋅x 4=−2x 3+1x 3, y =−2x +1x 在 [12,1) 上单调递减,从而 x 3⋅(x 1+x 2)+1x 32⋅x 4∈(−1,1].故选B .第二部分10. A , C , D 11. C , D【解析】① −π3ω+φ=k 1π,k ∈Z ,② π6ω+φ=π2+k 2π,k ∈Z , ② − ①得 π2ω=π2+k 3π,k 3∈Z , ω=2k 3+1,k 3∈Z ,因为 f (x ) 在 (0,π) 上有且仅有 7 个零点,所以 6π<ωπ<8π,6<ω<8,所以 ω=7,代入①得 −73π+φ=k 1π, φ=73π+k 1π,k 1∈Z ,因为 0<φ<π2, 所以 φ=π3,所以 f (x )=sin (7x +π3),所以 f (0)=sin π3,f (π)=sin 223π, 易知,对于 y =sinx ,从 π3 到 223π 会出现 4 个极大值点,f (π42)=sin π2, 易知,对于 y =sinx ,从 π3 到 π2 是单调递增的, 所以AB 错,CD 对.12. B , C , D【解析】因为令函数 T (x )=f (x )−12x 2, 因为 f (−x )+f (x )=x 2,所以 T (x )+T (−x )=f (x )−12x 2+f (−x )−12(−x )2=f (x )+f (−x )−x 2=0,所以 T (x ) 为奇函数,当 x ≤0 时,Tʹ(x )=fʹ(x )−x <0,所以 T (x ) 在 (−∞,0] 上单调递减,所以 T (x ) 在 R 上单调递减,因为存在 x 0∈{x∣ T (x )≥T (1−x )},所以得 T (x 0)≥T (1−x 0),x 0≤1−x 0,即 x 0≤12,因为 g (x )=e x −√ex −a (x ≤12),因为 x 0 为函数 y =g (x ) 的一个零点,因为当 x ≤12 时,gʹ(x )=e x −√ex ≤0,所以函数 g (x ) 在 x ≤12 时单调递减,由选项知 a >0,取 x =√e <12, 又因为 g √e )=e √e>0, 所以要使 g (x ) 在 x ≤12 时有一个零点,只需 g (12)=√e −12√e −a ≤0, 解得 a ≥√e 2, 所以 a 的取值范围为 [√e 2,+∞). 故选:BCD .第三部分13. √10【解析】因为∣∣a⃗+b⃗⃗∣∣=4,所以(a⃗+b⃗⃗)2=16,∣a⃗∣2+2a⃗⋅b⃗⃗+∣∣b⃗⃗∣∣2=16.所以2a⃗⋅b⃗⃗+13=16,所以2a⃗⋅b⃗⃗=3,所以(a⃗−b⃗⃗)2=∣a⃗∣2−2a⃗⋅b⃗⃗+∣∣b⃗⃗∣∣2=9+4−3=10.所以∣∣a⃗−b⃗⃗∣∣=√10.14. [0,12]【解析】由题意得,p:2x−1x−1<0,解得12<x<1,所以p:12<x<1,由q:x2−(2a+1)x+a(a+1)≤0,解得a≤a≤a+1,即q:a≤a≤a+1,要使得p是q充分不必要条件,则{a+1≥1,a≤12,解得0≤a≤12,所以实数a的取值范围是[0,12].15. 4【解析】已知等式2sinB=sinA+sinC,利用正弦定理可化简得:2b=a+c,因为2b=a+c,所以cosB=35,所以sinB=√1−cosB2=45,所以S△ABC=12ac⋅sinB=12ac×45=6,解得:ac=15,由余弦定理得:b2=a2+c2=−2accosB=(a+c)2−2ac(1+cosB)=4b2−2×15×(1+35).解得b=4.16. 3,9√35【解析】设新的底面半径为r,由V旧圆锥+V旧圆柱=V新圆锥+V新圆柱,1 3×9×π×52+8×π×(√3)2=13×9⋅πr2+8πr2,解得r2=9,r=3,如图正三棱柱ABC−A1B1C1内接于该圆锥,设 △A 1B 1C 1 边长为 a ,外接圆半径 R =a 2sin60∘=√33a , 由比例知上半个圆锥高 ℎ1 满足ℎ19=R 3, ℎ1=3R =√3a ,AA 1=9−ℎ1=9−√3a ,正三棱柱 ABC −A 1B 1C 1 的,S 表=2S △A 1B 1C 1+3S A 1ABB 1,=2⋅√34a 2+3⋅a(9−√3a),=−√52√3a 2+27a, 在 a =−2⋅(−52√3) 时取到最大值, 即 a =9√35.训练6答案第一部分1. D 【解析】集合 A ={x∣ x 2−2x −3<0}={x∣ −1<x <3},集合 B ={x∣ −2<x <2},所以 A ∩B ={x∣ −1<x <3}∩{x∣ −2<x <2}={x∣ −1<x <2}.2. A 【解析】因为命题 p :∃x ∈R ,e x −x −1≤0,所以 ¬p :∀x ∈R ,e x −x −1>0. 3. C 【解析】y =sin (2x +π3)=sin2(x +π6), 故要得到 y =sin (2x +π3) 的图象, 只需将函数 y =sin2x 的图象向左平移 π6 个单位.故选C .4. D5. C【解析】因为函数 f (x )=x 3−(12)x , 所以 f (−1)=(−1)3−(12)−1=−1−2=−3<0,f (0)=0−1=−1<0,f (12)=(12)3−(12)12<0,f (1)=13−(12)1=12>0,因为 f (12)⋅f (1)<0, 故函数 f (x ) 的零点所在区间为 (12,1).6. B 【解析】因为数列 a n+1=a n +2,所以数列为等差数列且 d =2,又因为 a 2+a 4+a 6=9,即 3a 1+9d =3a 1+18=9,所以 a 1=−3,所以 a 5+a 7+a 9=3a 1+18d =−9+36=27,所以 log 3(a 5+a 7+a 9)=log 327=3.7. A 【解析】因为 lga +lgb =lgab =lg (a +2b ),所以 ab =a +2b , 所以 1=1b +2a ,所以 2a +b =(2a +b )(1b +2a )=2a b +1+4+2b a =5+2(b a +a b ), 因为 a >0,b <0,所以 b a >0,a b <0,所以2a+b≥5+4√ba ⋅ab=9,当且仅当ba =ab时,即a=b时等号成立,所以2a+b的最小值为9,故答案选A.8. A 【解析】如图所示,AO⊥平面OCD,CD=100,∠ACO=30∘,∠ADO=45∘,∠ODC=60∘,设OA=ℎ上,在R△OAD,则OD=ℎ,同理可得:OC=√3ℎ,在△OCD,OC2=OD2+CD2−2OD⋅CD⋅cos60∘,所以(√3ℎ)2=ℎ2+1002−2×ℎ×100×12,化简得:ℎ2+50ℎ−5000=0,解得ℎ=50,因此“泉标”的高度为50m.故选:A.9. B 【解析】根据题意,设g(x)=f(x)cosx,其导函数为gʹ(x)=fʹ(x)cosx+f(x)sinxcos2x,又当0<x<π2时,fʹ(x)cosx+f(x)sinx<0,则有gʹ(x)<0,则函数g(x)在(0,π2)上为减函数,又f(x)在(−π2,π2)上是偶函数,所以g(−x)=f(−x)cos(−x)=f(x)cosx=g(x),则函数g(x)为偶函数,所以f(x)<√2f(π4)cosx⇒f(x)cosx<√2f(π4)⇒f(x)cosx<f(π4)cosπ4⇒g(x)<g(π4),又由 g (x ) 为偶函数且在 (0,π2) 上为减函数, 且其定义域为 (−π2,π2), 则有 ∣x ∣>π4,解得 −π2<x <−π4 或 π4<x <π2, 即不等式的解集为 (−π2,−π4)∪(π4,π2).第二部分10. C , D11. B , D【解析】由已知得 r =∣OP ∣=√1+m 2,则 sinα=√1+m 2,cosα=√1+m 2,tanα=1m , 所以A 选项,sinα+cosα=√1+m 2, 因为 m <0,所以 1+m 正负不确定,故A 错误.B 选项,cosα−sinα=√1+m 2, 因为 m <0,所以 1−m >0,所以 cosα+sinα>0,故B 正确.C 选项,sinα−cosα=√1+m √1+m 2=m 1+m 2, 因为 m <0,所以 sinα⋅cosα<0,故C 错误.D 选项,sinαtanα=√1+m 2⋅m =2√1+m 2>0,故D 正确, 综上,答案为BD .12. A , D 【解析】因为函数 f (x )=xlnx +x 2(x >0),所以 f ′(x )=lnx +1+2x ,易得 f ′(x )=lnx +1+2x 在 (0,+∞) 上递增,所以 f ′(1e )=ln 1e +1+2⋅1e =2e>0, 因为当 x 趋近于 0 时,f ′(x )=lnx +1+2x 趋近于 −∞,即 f ′(0)<0,所以 0<x 0<1e ,故A 正确,B 错误;因为 lnx 0+1+2x 0=0,所以f(x0)+2x0=x0lnx0+x02+2x0=x0(lnx0+x0+2)=x0(−1−x0+2)=x0(1−x0),由A得0<x0<1e,所以1−x0>0,所以x0(1−x0)>0,即f(x0)+2x0>0,故C错误,D正确;综上,答案为AD.第三部分13. 518【解析】因为sin2α−sin2α1+cos2α=2sinα⋅cosα−sin2α2cos2α=2sinα−cosα2cos2α−sin2α2cos2α=tanα−12tan2α,又因为tanα=13,所以sin2α−sin2α1+cos2α=tanα−12tan2α=13−12×19=518,故答案为518.14. (−∞,−1)【解析】因为函数f(x)满足x1≠x2时,[f(x1)−f(x2)](x1−x2)<0,所以f(x)为R上的单调递减,不等式f(3x+1)+f(2)>0等价于f(3x+1)>−f(2),又因为函数f(x)为奇函数,所以−f(2)=f(−2),即不等式满足f(3x+1)>f(−2),由f(x)的单调性可得:3x+1<−2,解得:x<−1,故x的取值范围为:(−∞,−1).15. 4,42【解析】设等差数列首次为a,公差为d,则 {a 2=a 1+d =10,S 5=5a 1+10d =40,解得 {a 1=12,d =−2,所以 a n =12+(n −1)×(−2)=14−2n ,所以 a 5=14−2×5=4,所以S n=ℎa 1+n (n−1)2d =12n −n 2+n =−n 2+13n =−(n −132)2+1694,因为 n 为整数,所以 S nmax =S 6=S 7=42.16. (2√2,3)【解析】因为函数 f (x )={2√x,0<x ≤12x,x >1,其函数图象如图所示:若方程 f (x )=−x +a 有三个不同实根,则 f (x ) 和 y =−x +a 在图象上有 3 个交点,当 a 最小时,即 y =−x +a 截距最小时应在 y =−x +a 和 f (x )=2x 相切时,令 fʹ(x )=2−x 2=−1,解得 x =√2,所以切点坐标为 (√2,√2),所以 a min =x +y =2√2,当 a 最大时,即 y =−x +a 截距最大时应在 (1,2) 处,所以 a min =x +y =3,所以 a 的范围为 (2√2,3).故答案为:(2√2,3).。
专题7小题提分限时训练6(解析版)-2021年新高考数学小题限时提分训练(45分钟)

专题7新高考数学小题提分限时训练6(解析版)一、单选题1.已知集合{12}A x x =-≤<∣,{13}B x x =<≤∣,则A B =( )A .{12}xx ≤≤∣ B .{12}xx <<∣ C .{13}xx -<<∣ D .{13}xx -≤≤∣ 【答案】D 【分析】由题中条件,根据并集的概念,可直接得出结果. 【详解】因为集合{12}A xx =-≤<∣,{13}B x x =<≤∣, 所以{13}A B xx ⋃=-≤≤∣. 故选:D.2.设i 是虚数单位,若复数1iz i=+,则|z |=( )A .12B C .1D【答案】B 【分析】 直接根据|||1|i z i =+进行计算,即可得答案; 【详解】|||1|2i z i ===+, 故选:B. 【点睛】本题考查复数模的计算,考查运算求解能力,属于基础题.3.在一组样本数据(x 1,y 1),(x 2,y 2),…,(x n ,y n )(n≥2,x 1,x 2,…,x n 不全相等)的散点图中,若所有样本点(x i ,y i )(i=1,2,…,n)都在直线y=12x+1上,则这组样本数据的样本相关系数为( )A .-1B .0C .12D .1【答案】D 【分析】所有样本点(x i ,y i )(i=1,2,…,n )都在直线112y x =+上,故这组样本数据完全正相关,故其相关系数为1. 【详解】由题设知,所有样本点(x i ,y i )(i=1,2,…,n )都在直线112y x =+上, ∴这组样本数据完全正相关,故其相关系数为1,故选D.根据样本相关系数的定义可知,当所有样本点都在直线上时,相关系数为1.4.设1F 、2F 是椭圆E :22221(0)x y a b a b+=>>的左、右焦点,P 为直线32a x =上一点,21F PF ∆是底角为30的等腰三角形,则E 的离心率为( ) A .12B .23C .34D .45【答案】C 【解析】试题分析:如下图所示,21F PF ∆是底角为30的等腰三角形,则有1221221,30F F PF PF F F PF =∠=∠=所以2260,30PF A F PA ∠=∠=,所以22322322PF AF a c a c ⎛⎫==-=- ⎪⎝⎭又因为122F F c =,所以,232c a c =-,所以34c e a == 所以答案选C.考点:椭圆的简单几何性质.5.ABC ∆中,AB 边的高为CD ,若CB a =,CA b =,0a b ⋅=,1a =,2b =,则AD =( ) A .1133a b - B .2233a b - C .3355a b - D .4455a b - 【答案】D 【详解】试题分析:由0a b ⋅=,1a =,2b =可知5BD =()144555BD BA AD AB a b ∴=∴==- 6.在ABC ∆中,内角A ,B ,C 所对的边分别是c b a ,,,已知8b=5c ,C=2B ,则cosC=(A )257 (B )257- (C )257± (D )2524【答案】A【解析】在ABC ∆中,由正弦定理可知:2sin 2847,cos ,cos cos 22cos 1.sin 5525B c BC B B B b ==∴=∴==-= 【考点定位】本题考查解三角形,考查学生灵活应用正弦定理和二倍角公式的解题能力 7.设R n m ∈,,若直线02)1()1(=-+++y n x m 与圆1)1()1(22=-+-y x 相切,则m + n 的取值范围是(A )]31,31[+- (B )),31[]31,(+∞+⋃--∞ (C )]222,222[+- (D )),222[]222,(+∞+⋃--∞ 【答案】D【解析】直线与圆相切,则有221, 1.,(),24m n t mn m n m n t mn +=∴=+++=≤=设221,440,4t t t t t ∴+≤∴--≥∴∈),222[]222,(+∞+⋃--∞【考点定位】本题考查直线与圆的位置关系和均值不等式,考查学生的转化能力和换元法的应用8.设点P 在曲线12xy e =上,点Q 在曲线ln(2)yx =上,则PQ 最小值为( ) A .1ln2- B ln 2)-C .1ln2+D ln 2)+【答案】B 【详解】由题意知函数y =12e x与y =ln(2x )互为反函数,其图象关于直线y =x 对称,两曲线上点之间的最小距离就是y =x 与y =12e x 上点的最小距离的2倍.设y =12e x 上点(x 0,y 0)处的切线与直线y =x平行.则1=12x e ,∴x 0=ln 2,y 0=1, ∴点(x 0,y 0)到y =x(1-ln 2), 则|PQ |的最小值为2(1-ln 2)×2(1-ln 2).二、多选题9.《几何原本》中的几何代数法(以几何方法研究代数问题)成为了后世数学家处理问题的重要依据.通过这一原理,很多代数的公理或定理都能够通过图形实现证明.如图,在AB 上取一点C ,使得,AC a BC b ==,过点C 作CD AB ⊥交以AB 为直径,O 为圆心的半圆周于点D ,连接OD .下面不能由OD CD ≥直接证明的不等式为( )A .(00)2a bab a b +≤>>, B .2(00)abab a b a b≥>>+, C .222(00)a b ab a b +≥>>, D .22(00)22a b a b a b ++≤>>,【答案】BCD 【分析】由,AC a BC b ==,得到()12OD a b =+,然后利用射影定理得到2CD ab =判断. 【详解】因为,AC a BC b ==, 所以()12OD a b =+, 因为90ADB ∠=,所以由射影定理得2CD ab =, 因为OD CD ≥, 所以2a bab +≤,当且仅当a b =时取等号, 故选:BCD10.已知函数()y f x =的图象关于点(,)P a b 成中心对称图形的充要条件是函数()y f x a b =+-为奇函数,函数()y f x =图象关于直线x c =成轴对称图形的充要条件是函数()y f x c =+为偶函数,则( ) A .函数32()3f x x x =+的对称中心是(1,2)P - B .函数32()3f x x x =+的对称中心是(1,4)PC .函数222()22x xf x x x -=-+有对称轴D .函数222()22x xf x x x -=-+无对称轴【答案】AC【分析】A 选项,判断函数(1)2y f x =--是否为奇函数,即可得出其正误;B 选项,判断函数(1)4y f x =+-是否为奇函数,即可得出其正误; CD 选项,判断(1)y f x =+是否为偶函数,即得出这两项的正误. 【详解】A 选项,因为32()3f x x x =+,所以()()323(1)213123f x x x x x --=-+--=-, 令3()3g x x x =-,x ∈R ,其定义域关于原点对称,且3()3()g x x x g x -=-+=-,所以3()3g x x x =-是奇函数,即函数(1)2y f x =--是奇函数,根据题中条件,可得函数32()3f x x x =+的对称中心是(1,2)P -,即A 正确; B 选项,因为32()3f x x x =+,所以()()3232(1)4131469f x x x x x x +-=+++-=++,令32()69g x x x x =++,x ∈R ,其定义域关于原点对称,但32()69()g x x x x g x -=-+-≠-,所以32()69g x x x x =++不是奇函数,所以函数32()3f x x x =+的对称中心不是(1,4)P ;即B 错;CD 选项,因为()()2222112()2211x x x f x x x x ---==-+-+,所以221(1)1x f x x -+=+,令221()1x g x x -=+,x ∈R ,其定义域关于原点对称,且2222()11()()()11x x g x g x x x ----===-++,所以221()1x g x x -=+是偶函数,因此函数222()22x xf x x x -=-+关于直线1x =对称,即C 选项正确;所以D 错;故选:AC. 【点睛】 关键点点睛:求解本题的关键在于理解题中条件,由题中条件可知,要判断函数的对称中心和对称轴,只需验证对应函数的奇偶性,进而即可求解.11.如果12,e e 是平面α内两个不共线的向量,那么下列说法中不正确的是( ) A .λ1e +μ2e (λ,μ∈R)可以表示平面α内的所有向量B .对于平面α内任一向量a ,使a =λ1e +μ2e 的实数对(λ,μ)有无穷多个C .若向量λ11e +μ12e 与λ21e +μ22e 共线,则有且只有一个实数λ,使得λ11e +μ12e =λ(λ21e +μ22e )D .若实数λ,μ使得12λμ+=0e e ,则λ=μ=0 【答案】BC 【分析】根据平面向量基本定理可以判定ABD ,取向量λ1e +μ2e 与λ21e +μ22e 均为零向量或者λ21e +μ22e 为零向量的特殊情况,可以判定C. 【详解】由平面向量基本定理可知,A ,D 是正确的.对于B ,由平面向量基本定理可知,若一个平面的基底确定,那么该平面内的任意一个向量在此基底下的实数对是唯一的.对于C ,当两个向量均为零向量时,即λ1=λ2=μ1=μ2=0时,这样的λ有无数个,或当λ11e +μ12e 为非零向量,而λ21e +μ22e 为零向量(λ2=μ2=0),此时λ不存在. 故选:BC . 【点睛】本题考查平面向量基本定理,属基础题,要准确全面掌握平面向量的基本定理的内容和意义.判定C 时要注意考虑问题要周密.12.在平面直角坐标系xOy 中,动点P 与两个定点()1F 和)2F 连线的斜率之积等于13,记点P 的轨迹为曲线E ,直线l :()2y k x =-与E 交于A ,B 两点,则( )A .E 的方程为2213x y -=B .EC .E 的渐近线与圆2221x y 相切 D .满足AB =l 有2条【答案】CD【分析】13=,即可得E的方程为221,3xy x-=≠E的离心率,利用圆心到E的渐近线距离判断圆与E 的渐近线的位置关系,联立直线l与曲线E,结合12|AB x x=-求k值的个数,由此即可判断各选项的正误.【详解】令(,)P x y13=,即得221,3xy x-=≠∴A错误,又2a c==,即3e=,故B错误,由E的渐近线为3y x=±,而2221x y圆心为(2,0),半径为1,∴(2,0)到y x=距离为1d==,故E的渐近线与圆2221x y相切,故C正确,联立曲线E与直线l的方程,整理得:2222(13)123(41)0k x k x k-+-+=,210k∆=+>,∴22121222123(41),3131k kx x x xk k++==--,而12|AB x x=-=代入整理:22)|||31|kABk+==-21k=或20k=(由0y=与221,3xy x-=≠),故1k=±,∴D正确.故选:CD【点睛】易错点睛:(1)两点式表示斜率时要保证分母不为0,从而确定曲线E 的轨迹要去掉3x ≠±. (2)由2121||23AB k x x =+-=求得k 值要考虑曲线E 的轨迹不包含3x ≠±的情况舍掉增根.三、填空题13.设,x y 满足约束条件:,0{13x y x y x y ≥-≥-+≤,则2z x y =-的取值范围为__________.【答案】【解析】解析:画出不等式1{30,0x y x y x y -≥-+≤>>表示的区域如图,结合图形可以看出当动直线1122y x z =-分别经过点(3,0),(1,2)A B 时z 取最大值和最小值分别为3,3-,所以 [3,3]z ∈-,应填答案[3,3]-.点睛:本题在求解时,先画出不等式组1{30,0x y x y x y -≥-+≤>>表示的平面区域,然后巧妙地运用数形结合思想平行移动动直线1122y x z =-,从而将问题进行转化与化归为求目标函数1122y x z =-的最大值和最小值问题.最后结合图形求出目标函数经过点(3,0),(1,2)A B 时z 取最大值和最小值分别为3,3-,进而使得问题获解.求解的过程体现了转化与化归的数学思想、数形结合的数学思想与方法的灵活运用14.某个部件由三个元件按图方式连接而成,元件1或元件2正常工作,且元件3正常工作,则部件正常工作,设三个电子元件的使用寿命(单位:小时)均服从正态分布2(1000,50)N ,且各个元件能否正常相互独立,那么该部件的使用寿命超过1000小时的概率为 _____【答案】【解析】设元件1,2,3的使用寿命超过1000小时的事件分别记为A ,B ,C ,显然P(A)=P(B)=P(C)=12, ∴该部件的使用寿命超过1000的事件为(A B +A B +AB)C. ∴该部件的使用寿命超过1000小时的概率为P =111111222222⎛⎫⨯+⨯+⨯ ⎪⎝⎭×12=38.15.已知()(2)(3),()22=-++=-x f x m x m x m g x ,若同时满足条件:①,()0∀∈<x R f x 或()0<g x ;②(,4),()()0∃∈-∞-<x f x g x .则m 的取值范围是________________. 【答案】()4,2∈--m 【解析】根据()220xg x =-<可解得x<1,由于题目中第一个条件的限制,导致f(x)在1x ≥是必须是()0f x <,当m=0时,()0f x =不能做到f(x)在1x ≥时()0f x <,所以舍掉,因此,f(x)作为二次函数开口只能向下,故m<0,且此时2个根为122,3x m x m ==--,为保证条件成立,只需1221{31x m x m =<=--<1{24m m <⇒>-,和大前提m<0取交集结果为40m -<<;又由于条件2的限制,可分析得出在(,4),()x f x ∃∈-∞-恒负,因此就需要在这个范围内g(x)有得正数的可能,即-4应该比12x x 两个根中较小的来的大,当(1,0)m ∈-时,34m --<-,解得交集为空,舍.当m=-1时,两个根同为24->-,舍.当(4,1)m ∈--时,24m <-,解得2m <-,综上所述,(4,2)m ∈--. 【考点定位】本题考查学生函数的综合能力,涉及到二次函数的图像开口,根大小,涉试卷第11页,总11页 及到指数函数的单调性,还涉及到简易逻辑中的“或”,还考查了分类讨论思想.16.数列{}n a 满足1(1)21n n n a a n ++-=-,则{}n a 的前60项和为____【答案】1830【解析】试题分析:()()11121211n nn n n n a a n a n a +++--∴---=,=,令1414243444143434242412n n n n n n n n n n n b a a a a a a a a a a +++++++++++=++++=+--=,()(),424444434342168n n n n n n a a a a a a n +++++++=-++=+()(),则14142434443424141616n n n n n n n n n n b a a a a a a a a b +++++---=+++=++++=+,即数列{}n b 是以16为公差的等差数列,{}n a 的前60项和为即为数列{b n }的前15项和1123415141010151618302b a a a a S ⨯=+++=∴⨯+⨯== 考点:数列递推式,数列求和【名师点睛】本题主要考查了由数列的递推公式求解数列的和,属难题.解题时要注意等差数列的求和公式的应用,解题的关键是有已知条件的特征构造等差数列,利用等差数列求和.。
专题2小题提分限时训练1(原卷版)-2021年新高考数学小题限时提分训练(45分钟)

专题2新高考数学小题限时训练1(原卷版)一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合{}32M m m =∈-<<Z ,{}13N n n =∈-≤≤Z ,则MN =( ) A .{}0,1B .{}1,0,1-C .{}0,1,2D .1,0,1,2 2.若复数151i z i -+=+,其中i 为虚数单位,则z 的虚部是( ) A .3 B .3- C .2 D .2- 3.设一组样本数据x 1,x 2,…,x n 的方差为0.01,则数据10x 1,10x 2,…,10x n 的方差为( ) A .0.01 B .0.1 C .1 D .10 4.函数y =x cos x +sin x 在区间[–π,π]的图象大致为( )A .B .C .D .5.43(1)(1)x x --的展开式中2x 的系数为(A )6- (B )3- (C )0 (D )36.若0<α<,﹣<β<0,cos (+α)=,cos (﹣)=,则cos (α+)=( )A .B .﹣C .D .﹣ 6.设圆锥曲线τ的两个焦点分别为12,F F ,若曲线τ上存在点P 满足1122::PF F F PF 4:3:2=,则曲线τ的离心率等于A .12或32B .23或2C .12或2D .23或32 7.(3分)(2011•重庆)在圆x 2+y 2﹣2x ﹣6y=0内,过点E (0,1)的最长弦和最短弦分别为AC 和BD ,则四边形ABCD 的面积为( )A .B .C .D .8.由曲线y x =,直线2y x =-及y 轴所围成的图形的面积为( ) A .103 B .4 C .163 D .6二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9.下列各题中,p 是q 的充要条件的有( )A .p :四边形是正方形;q :四边形的对角线互相垂直且平分B .p :两个三角形相似;q :两个三角形三边成比例C .p :0xy >;q :0x >,0y >;D .p :1x =是一元二次方程20ax bx c ++=的一个根;q :()00a b c a ++=≠ 10.如图,正方体1111ABCD A B C D -的棱长为1,E ,F 是线段11B D 上的两个动点,且12EF =,则下列结论中正确的是( )A .AC BE ⊥B .//EF 平面ABCDC .AEF 的面积与BEF 的面积相等D .三棱锥E ABF -的体积为定值 11.已知曲线22:1(,)C mx ny m n +=∈R ,则下列说法正确的是( ).A .若0m >,0n >,则曲线C 是椭圆B .若0m n >>,则曲线C 是焦点在y 轴上的椭圆C .若0m n >>,则曲线C 是焦点在x 轴上的双曲线D .曲线C 可以是抛物线12.已知()ln x f x x=,下列说法正确的是( ) A .()f x 在1x =处的切线方程为1y x =- B .单调递增区间为(),e -∞C .()f x 的极大值为1eD .方程()1f x =-有两个不同的解三、填空题:本题共4小题,每小题5分,共20分.13.已知,2παπ⎛⎫∈ ⎪⎝⎭,5sin α=,则tan2α=_________. 14.的二项展开式中,的系数是____________(用数字作答). 15.已知ABC ∆的一个内角为120,并且三边长构成公差为4的等差数列,则ABC ∆的面积为_______________.16.已知点E F 、分别在正方体1111ABCD A B C D -的棱1BB 、1CC 上,且12B E EB =,12CF FC =,侧面AEF 与面ABC 所成的二面角的正切值等于_______.。
专题4小题提分限时训练3(解析版)-2021年新高考数学小题限时提分训练(45分钟)

专题4新高考数学小题提分限时训练3(解析版)一、单选题1.已知集合{}{}11,21M x x N x x =-≤=-<≤,则M N =( )A .{}20x x -≤≤ B .{}01x x ≤≤C .{}21x x -≤≤D .{}22x x -≤≤【答案】B 【分析】先求得集合M ,根据交集运算的定义,即可求得答案. 【详解】因为11x -≤,所以02x ≤≤,所以{}02M x x =≤≤, 所以{}01M N x x ⋂=≤≤, 故选:B2.已知复数z 满足(2)z i i -=(i 为虚数单位),则z =( ) A .125i-+ B .125i-- C .125i- D .125i+ 【答案】A 【分析】 由已知可得2iz i=-,再根据复数的除法运算可得答案. 【详解】因为(2)z i i -=,所以()()()2122225i i i i z i i i +-+===--+. 故选:A.3.下面四个条件中,使a b >成立的充分而不必要的条件是 A .1a b +> B .1a b ->C .22a b >D .33a b >【答案】A 【解析】 试题分析:由,但无法得出,A 满足;由、均无法得出,不满足“充分”;由,不满足“不必要”.考点:不等式性质、充分必要性.4.已知角θ的顶点与原点重合,始边与x轴的正半轴重合,终边在直线y=2x上,则cos2θ=()A.-45B.-35C.35D.45【答案】B【分析】根据直线的斜率等于倾斜角的正切值,由已知直线的斜率得到tanθ的值,然后根据同角三角函数间的基本关系求出cosθ的平方,然后根据二倍角的余弦函数公式把所求的式子化简后,把cosθ的平方代入即可求出值.【详解】解:根据题意可知:tanθ=2,所以cos2θ22221115cossin cos tanθθθθ===++,则cos2θ=2cos2θ﹣1=215⨯-135=-.故选B.【点睛】此题考查学生掌握直线的斜率与倾斜角之间的关系,灵活运用同角三角函数间的基本关系化简求值,是一道中档题.5.设实数x、y满足不等式组,若x、y为整数,则3x+4y的最小值是()A.14 B.16 C.17 D.19【答案】B【解析】依题意作出可行性区域如图,目标函数z=3x+4y在点(4,1)处取到最小值z=16.故选B.6.(2011•湖北)已知定义在R 上的奇函数f (x )和偶函数g (x )满足f (x )+g (x )=a x ﹣a ﹣x +2(a >0,且a≠0).若g (a )=a ,则f (a )=( ) A .2 B . C . D .a 2【答案】B【解析】∵f (x )是定义在R 上的奇函数,g (x )是定义在R 上的偶函数 由f (x )+g (x )=a x ﹣a ﹣x +2 ①得f (﹣x )+g (﹣x )=a ﹣x ﹣a x +2=﹣f (x )+g (x ) ② ①②联立解得f (x )=a x ﹣a ﹣x ,g (x )=2 由已知g (a )=a ∴a=2∴f (a )=f (2)=22﹣2﹣2=故选B7.(1+2x)5的展开式中,x 2的系数等于 A .80 B .40C .20D .10【答案】B 【详解】()512x + 的展开式的通项515(2)r r r T C x -+= ,令52r解得3r =∴(1+2x)5的展开式中,x 2的系数为325C 240=8.设圆锥曲线τ的两个焦点分别为12,F F ,若曲线τ上存在点P 满足1122::PF F F PF 4:3:2=,则曲线τ的离心率等于A .12或32B .23或2 C .12或2 D .23或32【答案】A 【分析】设1122432PF t F F t PF t ===,,,讨论两种情况,分别利用椭圆与双曲线的定义求出,a c 的值,再利用离心率公式可得结果.【详解】因为1122::PF F F PF 4:3:2=,所以可设1122432PF t F F t PF t ===,,, 若曲线为椭圆则123262a PF PF t c t =+==,,则12c e a ==; 若曲线为双曲线则,324222a t t t a t c t ,,=-===,∴32c e a ==,故选A .【点睛】本题主要考查椭圆的定义及离心率以及双曲线的定义及离心率,属于中档题. 离心率的求解在圆锥曲线的考查中是一个重点也是难点,一般求离心率有以下几种情况:①直接求出,a c ,从而求出e ;②构造,a c 的齐次式,求出e ;③采用离心率的定义以及圆锥曲线的定义来求解;④根据圆锥曲线的统一定义求解.二、多选题 9.下列各式中值为12的是( ). A .2sin 75cos75B .2π12sin12- C .cos 45cos15sin 45sin15- D .()tan 77tan 3221tan 77tan 32-+⋅【答案】ACD 【分析】利用二倍角正弦公式即可判断选项A ;利用二倍角余弦公式即可判断选项B ; 利用两角和的余弦公式可判断选项C ;利用两角差的正切公式可判断选项D ; 【详解】对于选项A :由二倍角正弦公式可得12sin 75cos75sin1502==,故选项A 正确;对于选项B :由二倍角余弦公式2ππ312sin cos 1262-==,故选项B 不正确; 对于选项C :由两角和的余弦公式()cos 45cos15sin 45sin15cos 4515-=+1cos602==;故选项C 正确; 对于选项D :由两角差的正切公式可得:()()tan 77tan 32111tan 7732tan 4522221tan 77tan 32-=-==+⋅故选项D 正确. 故选:ACD10.已知{}n a 为等比数列,下面结论中错误的是( ) A .1322a a a +B .2221322a a a + C .若13a a =,则12a a = D .若31a a >,则42a a >【答案】ACD 【分析】根据等比数列的通项公式对各选项一一分析即可判断; 【详解】解:设等比数列的公比为q ,则2132a a a a q q+=+, 当20a >,0q <时,1322a a a +<,故A 不正确;2222221322()()2a a a a q a q+=+,∴2221322a a a +当且仅当13a a =时取等号,故B 正确; 若13a a =,则211a a q =,21q ∴=,1q ∴=±,12a a ∴=或12a a =-,故C 不正确;若31a a >,则211a q a >,2421(1)a a a q q ∴-=-,其正负由q 的符号确定,故D 不正确 故选:ACD .11.若直线0ax by +=与圆22420x y x +-+=有公共点,则( ) A .ln ln a b B .||||a bC .()()0a b a b +-D .a b【答案】BC【分析】根据题意可得圆心到直线的距离小于等于半径,可得22a b ≤,即可判断.【详解】解析:圆的标准方程为()2222x y -+=,圆心为(2,0),半径为2, 因为直线0ax by +=与圆22420x y x +-+=有公共点,所以222a b≤+,解得22a b ≤,即()()0a b a b +-≤,等价于||||a b ≤,所以BC正确,AD 错误. 故选:BC.12.已知四边形ABCD 是等腰梯形(如图1),3AB =,1DC =,45BAD ∠=︒,DE AB ⊥.将ADE 沿DE 折起,使得AE EB ⊥(如图2),连结AC ,AB ,设M 是AB 的中点.下列结论中正确的是( )A .BC AD ⊥B .点E 到平面AMC 6C .//EM 平面ACD D .四面体ABCE 的外接球表面积为5π【答案】BD 【分析】过C 做CF AB ⊥,交AB 于F ,根据题意,可求得各个边长,根据线面垂直的判定定理,可证AE ⊥平面BCDE ,即AE BC ⊥,假设BC AD ⊥,根据线面垂直的判定及性质定理,可得BC ⊥DE ,与已知矛盾,可得A 错误,利用等体积法,可求得点E 到平面AMC 的距离,即可判断B 的正误;由题意可证//EB 平面ADC ,假设//EM 平面ACD ,则平面ACD //平面AEB ,与已知矛盾,可得C 错误;根据四棱锥的几何性质,可确定球心的位置,代入公式,即可判断D 的正误,即可得答案. 【详解】因为DE AB ⊥,45BAD ∠=︒,所以ADE 为等腰直角三角形,过C 做CF AB ⊥,交AB 于F ,如图所示:所以ADE BCF ≌,即AE=BF ,又3AB =,1DC =, 所以1AE EF FB DE CF =====,则=2AD BC =, 对于A :因为AE EB ⊥,AE DE ⊥,,BE DE ⊂平面BCDE , 所以AE ⊥平面BCDE ,BC ⊂平面BCDE , 所以AE BC ⊥,若BC AD ⊥,且,AE AD ⊂平面ADE , 则BC ⊥平面ADE , 所以BC ⊥DE与已知矛盾,所以BC 与AD 不垂直,故A 错误; 对于B :连接MC ,如图所示,在DEC Rt △中,DE=DC =1,所以2EC ==2BC ,EB =2,所以222EC BC EB +=,所以EC BC ⊥, 又因为AE BC ⊥,,AE EC ⊂平面AEC , 所以BC ⊥平面AEC ,AC ⊂平面AEC , 所以BC AC ⊥,即ABC 为直角三角形, 在Rt AEC 中,1,2AE EC ==3AC =因为M 是AB 的中点,所以AMC 的面积为Rt ABC 面积的一半,所以1163222AMCS =⨯=因为,DE AE DE EB ⊥⊥,所以DE 即为两平行线CD 、EB 间的距离,因为E AMC C AEM V V --=,设点E 到平面AMC 的距离为h ,则1133AMEAMCSDE S h ⨯⨯=⨯⨯,即1111113234h ⨯⨯⨯⨯=⨯,所以h =,所以点E 到平面AMC ,故B 正确; 对于C :因为//EB DC ,EB ⊄平面ADC ,DC ⊂平面ADC , 所以//EB 平面ADC ,若//EM 平面ACD ,且,,EB EM E EB EM ⋂=⊂平面AEB , 所以平面ACD //平面AEB ,与已知矛盾,故C 错误.对于D :因为EC BC ⊥,所以BCE 的外接圆圆心为EB 的中点, 又因为AE EB ⊥,所以ABE △的外接圆圆心为AB 的中点M , 根据球的几何性质可得:四面体ABCE 的外接球心为M ,又E 为球上一点,在ABE △中,12EM AB ==所以外接球半径2R ME ==, 所以四面体ABCE 的外接球表面积254454S R ,故D 正确. 故选:BD 【点睛】解题的关键是熟练掌握线面平行的判定定理,线面垂直的判定和性质定理等知识,并灵活应用,求点到平面距离时,常用等体积法将点到面的距离转化为椎体的高,再求解,考查逻辑推理,分析理解的能力,综合性较强,属中档题.三、填空题13.已知向量(1,2)a =-,(,1)b m =.若向量a 与b 平行,则m =_______. 【答案】12- 【分析】根据向量a 与b 平行,由21m =-求解. 【详解】向量(1,2)a =-,(,1)b m =,因为向量a 与b 平行, 所以21m =-,解得12m =-, 故答案为:12-14.曲线ln 1y x x =++的一条切线的斜率为2,则该切线的方程为______________. 【答案】2y x = 【分析】设切线的切点坐标为00(,)x y ,对函数求导,利用0|2x y '=,求出0x ,代入曲线方程求出0y ,得到切线的点斜式方程,化简即可. 【详解】设切线的切点坐标为001(,),ln 1,1x y y x x y x=++'=+, 00001|12,1,2x x y x y x ='=+===,所以切点坐标为(1,2), 所求的切线方程为22(1)y x -=-,即2y x =. 故答案为:2y x =. 【点睛】本题考查导数的几何意义,属于基础题.15.设{a n }是公差为d 的等差数列,{b n }是公比为q 的等比数列.已知数列{a n +b n }的前n 项和221()n n S n n n +=-+-∈N ,则d +q 的值是_______. 【答案】4 【分析】结合等差数列和等比数列前n 项和公式的特点,分别求得{}{},n n a b 的公差和公比,由此求得d q +. 【详解】设等差数列{}n a 的公差为d ,等比数列{}n b 的公比为q ,根据题意1q ≠. 等差数列{}n a 的前n 项和公式为()2111222n n n d d P na d n a n -⎛⎫=+=+- ⎪⎝⎭,等比数列{}n b的前n项和公式为()111 1111nnnb q b bQ qq q q-==-+---,依题意n n nS P Q=+,即22111212211n nb bd dn n n a n qq q⎛⎫-+-=+--+⎪--⎝⎭,通过对比系数可知111212211ddaqbq⎧=⎪⎪⎪-=-⎪⎨⎪=⎪⎪=-⎪-⎩⇒11221daqb=⎧⎪=⎪⎨=⎪⎪=⎩,故4d q+=.故答案为:4【点睛】本小题主要考查等差数列和等比数列的前n项和公式,属于中档题.16.某中学开展劳动实习,学生加工制作零件,零件的截面如图所示.O为圆孔及轮廓圆弧AB所在圆的圆心,A是圆弧AB与直线AG的切点,B是圆弧AB与直线BC的切点,四边形DEFG为矩形,BC⊥DG,垂足为C,tan∠ODC=35,//BH DG,EF=12 cm,DE=2 cm,A到直线DE和EF的距离均为7 cm,圆孔半径为1 cm,则图中阴影部分的面积为________cm2.【答案】542π+【分析】利用3tan5ODC∠=求出圆弧AB所在圆的半径,结合扇形的面积公式求出扇形AOB 的面积,求出直角OAH△的面积,阴影部分的面积可通过两者的面积之和减去半个单位圆的面积求得.试卷第11页,总11页 【详解】设==OB OA r ,由题意7AM AN ==,12EF =,所以5NF =,因为5AP =,所以45AGP ︒∠=,因为//BH DG ,所以45AHO ︒∠=,因为AG 与圆弧AB 相切于A 点,所以OA AG ⊥,即OAH △为等腰直角三角形;在直角OQD △中,252OQ r =-,272DQ r =-, 因为3tan 5OQ ODC DQ ∠==,所以3252212522r r -=-, 解得22r =等腰直角OAH △的面积为11222242S =⨯=; 扇形AOB 的面积(221322324S ππ=⨯⨯=, 所以阴影部分的面积为1215422S S ππ+-=+. 故答案为:542π+. 【点睛】 本题主要考查三角函数在实际中应用,把阴影部分合理分割是求解的关键,以劳动实习为背景,体现了五育并举的育人方针.。
2021高考数学提分专项练习及答案
2021高考数学提分专项练习及答案(1)一、选择题1.现采用随机模拟的方法估计某运动员射击4次,至少击中3次的概率:先由计算器给出0到9之间取整数值的随机数,指定0,1表示没有击中目标,2,3,4,5,6,7,8,9表示击中目标,以4个随机数为一组,代表射击4次的结果,经随机模拟产生了20组随机数:7527 0293 7140 9857 0347 4373 8636 69471417 4698 0371 6233 2616 8045 6011 36619597 7424 7610 4281根据以上数据估计该射击运动员射击4次至少击中3次的概率为( )A.0.852B.0.819 2C.0.8D.0.75答案:D 命题立意:本题主要考查随机模拟法,考查考生的逻辑思维能力.解题思路:因为射击4次至多击中2次对应的随机数组为7140,1417,0371,6011,7610,共5组,所以射击4次至少击中3次的概率为1-=0.75,故选D.2.在菱形ABCD中,ABC=30°,BC=4,若在菱形ABCD内任取一点,则该点到四个顶点的距离均不小于1的概率是( )A. 1/2B.2C. -1D.1答案:D 命题立意:本题主要考查几何概型,意在考查考生的运算求解能力.解题思路:如图,以菱形的四个顶点为圆心作半径为1的圆,图中阴影部分即为到四个顶点的距离均不小于1的区域,由几何概型的概率计算公式可知,所求概率P==.3.设集合A={1,2},B={1,2,3},分别从集合A和B中随机取一个数a和b,确定平面上的一个点P(a,b),记“点P(a,b)落在直线x+y=n上”为事件Cn(2≤n≤5,nN) ,若事件Cn的概率,则n 的所有可能值为( )A.3B.4C.2和5D.3和4答案:D 解题思路:分别从集合A和B中随机取出一个数,确定平面上的一个点P(a,b),则有(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),共6种情况,a+b=2的有1种情况,a+b=3的有2种情况,a+b=4的有2种情况,a+b=5的有1种情况,所以可知若事件Cn的概率,则n的所有可能值为3和4,故选D.4.记a,b分别是投掷两次骰子所得的数字,则方程x2-ax+2b=0有两个不同实根的概率为( )A. 3/4B.1/2C. 1/3D.1/4答案:B 解题思路:由题意知投掷两次骰子所得的数字分别为a,b,则基本事件有:(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),…,(6,1),(6,2),(6,3),(6,4),(6,5),(6,6),共有36个.而方程x2-ax+2b=0有两个不同实根的条件是a2-8b>0,因此满足此条件的基本事件有:(3,1),(4,1),(5,1),(5,2),(5,3),(6,1),(6,2),(6,3),(6,4),共有9个,故所求的概率为=.5.在区间内随机取两个数分别为a,b,则使得函数f(x)=x2+2ax-b2+π2有零点的概率为( )A.1-B.1-C.1-D.1-答案:B 解题思路:函数f(x)=x2+2ax-b2+π2有零点,需Δ=4a2-4(-b2+π2)≥0,即a2+b2≥π2成立.而a,b[-π,π],建立平面直角坐标系,满足a2+b2≥π2的点(a,b)如图阴影部分所示,所求事件的概率为P===1-,故选B.6.袋中共有6个除了颜色外完全相同的球,其中有1个红球、2个白球和3个黑球.从袋中任取两球,两球颜色为一白一黑的概率等于( )A.5/6B.11/12C. 1/2D.3/4答案:B 解题思路:将同色小球编号,从袋中任取两球,所有基本事件为:(红,白1),(红,白2),(红,黑1),(红,黑2),(红,黑3),(白1,白2),(白1,黑1),(白1,黑2),(白1,黑3),(白2,黑1),(白2,黑2),(白2,黑3),(黑1,黑2),(黑1,黑3),(黑2,黑3),共有15个基本事件,而为一白一黑的共有6个基本事件,所以所求概率P==.故选B.二、填空题7.已知集合表示的平面区域为Ω,若在区域Ω内任取一点P(x,y),则点P的坐标满足不等式x2+y2≤2的概率为________.答案:命题立意:本题考查线性规划知识以及几何概型的概率求解,正确作出点对应的平面区域是解答本题的关键,难度中等.解题思路:如图阴影部分为不等式组表示的平面区域,满足条件x2+y2≤2的点分布在以为半径的四分之一圆面内,以面积作为事件的几何度量,由几何概型可得所求概率为=.8.从5名学生中选2名学生参加周六、周日社会实践活动,学生甲被选中而学生乙未被选中的概率是________.答案:命题立意:本题主要考查古典概型,意在考查考生分析问题的能力.解题思路:设5名学生分别为a1,a2,a3,a4,a5(其中甲是a1,乙是a2),从5名学生中选2名的选法有(a1,a2),(a1,a3) ,(a1,a4),(a1,a5),(a2,a3),(a2,a4),(a2,a5),(a3,a4),(a3,a5),(a4,a5),共10种,学生甲被选中而学生乙未被选中的选法有(a1,a3),(a1,a4),(a1,a5),共3种,故所求概率为.2021高考数学提分专项练习及答案(2)一、选择题1.若点P是两条异面直线l,m外的任意一点,则( )A.过点P有且仅有一条直线与l,m都平行B.过点P有且仅有一条直线与l,m都垂直C.过点P有且仅有一条直线与l,m都相交D.过点P有且仅有一条直线与l,m都异面答案:B 命题立意:本题考查异面直线的几何性质,难度较小.解题思路:因为点P是两条异面直线l,m外的任意一点,则过点P有且仅有一条直线与l,m都垂直,故选B.2.如图,P是正方形ABCD外一点,且PA平面ABCD,则平面PAB与平面PBC、平面PAD的位置关系是( )A.平面PAB与平面PBC、平面PAD都垂直B.它们两两垂直C.平面PAB与平面PBC垂直,与平面PAD不垂直D.平面PAB与平面PBC、平面PAD都不垂直答案:A 解题思路: DA⊥AB,DAPA,AB∩PA=A,DA⊥平面PAB,又DA平面PAD,平面PAD平面PAB.同理可证平面PAB平面PBC.把四棱锥P-ABCD放在长方体中,并把平面PBC 补全为平面PBCD1,把平面PAD补全为平面PADD1,易知CD1D即为两个平面所成二面角的平面角,CD1D=APB,CD1D<90°,故平面PAD与平面PBC不垂直.3.设α,β分别为两个不同的平面,直线lα,则“lβ”是“αβ”成立的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件答案:A 命题立意:本题主要考查空间线面、面面位置关系的判定与充分必要条件的判断,意在考查考生的逻辑推理能力.解题思路:依题意,由lβ,lα可以推出αβ;反过来,由αβ,lα不能推出lβ.因此“lβ”是“αβ”成立的充分不必要条件,故选A.4.若m,n为两条不重合的直线,α,β为两个不重合的平面,则下列结论正确的是( )A.若m,n都平行于平面α,则m,n一定不是相交直线B.若m,n都垂直于平面α,则m,n一定是平行直线C.已知α,β互相垂直,m,n互相垂直,若mα,则nβD.m,n在平面α内的射影互相垂直,则m,n互相垂直答案:B 解题思路:本题考查了空间中线面的平行及垂直关系.在A中:因为平行于同一平面的两直线可以平行,相交,异面,故A为假命题;在B中:因为垂直于同一平面的两直线平行,故B为真命题;在C中:n可以平行于β,也可以在β内,也可以与β相交,故C为假命题;在D中:m,n也可以不互相垂直,故D为假命题.故选B.5.如图所示,已知正方体ABCD-A1B1C1D1的棱长为2,长为2的线段MN的一个端点M在棱DD1上运动,另一端点N在正方形ABCD内运动,则MN的中点的轨迹的面积为( )A.4πB.2πC.πD.-π答案:D 解题思路:本题考查了立体几何中的点、线、面之间的关系.如图可知,端点N在正方形ABCD内运动,连接ND,由ND,DM,MN构成一个直角三角形,设P为NM的中点,根据直角三角形斜边上的中线长度为斜边的一半可得,不论MDN如何变化,点P到点D 的距离始终等于1.故点P的轨迹是一个以D为中心,半径为1的球的球面,其面积为.技巧点拨:探求以空间图形为背景的轨迹问题,要善于把立体几何问题转化到平面上,再联合运用平面几何、立体几何、空间向量、解析几何等知识去求解,实现立体几何到解析几何的过渡.6.如图是一几何体的平面展开图,其中四边形ABCD为正方形,E,F分别为PA,PD的中点,在此几何体中,给出下面四个结论:直线BE与直线CF是异面直线;直线BE与直线AF是异面直线;直线EF平面PBC;平面BCE平面PAD.其中正确结论的序号是( )A.1B.1C. 3D.4答案:B 解题思路:本题考查了立体几何中的点、线、面之间的关系.画出几何体的图形,如图,由题意可知,直线BE与直线CF是异面直线,不正确,因为E,F分别是PA与PD的中点,可知EFAD,所以EFBC,直线BE与直线CF是共面直线;直线BE与直线AF是异面直线,满足异面直线的定义,正确;直线EF平面PBC,由E,F是PA与PD的中点,可知EFAD,所以EFBC,因为EF平面PBC,BC平面PBC,所以判断是正确的;由题中条件不能判定平面BCE平面PAD,故不正确.故选B.技巧点拨:翻折问题常见的是把三角形、四边形等平面图形翻折起来,然后考查立体几何的常见问题:垂直、角度、距离、应用等问题.此类问题考查学生从二维到三维的升维能力,考查学生空间想象能力.解决该问题时,不仅要知道空间立体几何的有关概念,还要注意到在翻折的过程中哪些量是不变的,哪些量是变化的.二、填空题7.如图,四边形ABCD为菱形,四边形CEFB为正方形,平面ABCD平面CEFB,CE=1,AED=30°,则异面直线BC与AE所成角的大小为________.答案:45°解题思路:因为BCAD,所以EAD就是异面直线BC 与AE所成的角.因为平面ABCD平面CEFB,且ECCB,所以EC平面ABCD.在RtECD中,EC=1,CD=1,故ED==.在AED中,AED=30°,AD=1,由正弦定理可得=,即sinEAD===.又因为EAD∈(0°,90°),所以EAD=45°.故异面直线BC与AE所成的角为45°.8.给出命题:异面直线是指空间中既不平行又不相交的直线;两异面直线a,b,如果a平行于平面α,那么b不平行于平面α;两异面直线a,b,如果a平面α,那么b不垂直于平面α;两异面直线在同一平面内的射影不可能是两条平行直线.上述命题中,真命题的序号是________.答案:解题思路:本题考查了空间几何体中的点、线、面之间的关系.根据异面直线的定义知:异面直线是指空间中既不平行又不相交的直线,故命题为真命题;两条异面直线可以平行于同一个平面,故命题为假命题;若bα,则ab,即a,b共面,这与a,b为异面直线矛盾,故命题为真命题;两条异面直线在同一个平面内的射影可以是:两条平行直线、两条相交直线、一点一直线,故命题为假命题.9.如果一个棱锥的底面是正多边形,并且顶点在底面的射影是底面的中心,这样的棱锥叫做正棱锥.已知一个正六棱锥的各个顶点都在半径为3的球面上,则该正六棱锥的体积的值为________.答案:16 命题立意:本题以球的内接组合体问题引出,综合考查了棱锥体积公式、利用导数工具处理函数最值的方法,同时也有效地考查了考生的运算求解能力和数学建模能力.解题思路:设球心到底面的距离为x,则底面边长为,高为x+3,正六棱锥的体积V=×(9-x2)×6(x+3)=(-x3-3x2+9x+27),其中0≤x10.已知三棱锥P-ABC的各顶点均在一个半径为R的球面上,球心O在AB上,PO平面ABC,=,则三棱锥与球的体积之比为________.答案:命题立意:本题主要考查线面垂直、三棱锥与球的体积计算方法,意在考查考生的空间想象能力与基本运算能力.解题思路:依题意,AB=2R,又=,ACB=90°,因此AC=R,BC=R,三棱锥P-ABC的体积VP-ABC=PO·SABC=×R××R×R=R3.而球的体积V球=R3,因此VP-ABCV球=R3R3=.2021高考数学提分专项练习及答案(3)一、选择题1.已知等比数列{an},且a4+a8=dx,则a6(a2+2a6+a10)的值为( )A.π2B.4C.πD.-9π答案:A 命题立意:本题考查等比数列的性质及定积分的运算,正确地利用定积分的几何意义求解积分值是解答本题的关键,难度中等.解题思路:由于dx表示圆x2+y2=4在第一象限内部分的面积,故dx=×π×22=π,即a4+a8=π,又由等比数列的性质,得a6(a2+2a6+a10)=a6a2+2a+a6a10=a+2a4a8+a=(a4+a8)2=π2,故选A.2.(东北三校二次联考)已知{an}是等差数列,Sn为其前n项和,若S21=S4 000,O为坐标原点,点P(1,an),点Q(2 011,a2 011),则·=( )A.2 011B.-2 011C.0D.1答案:A 命题立意:本题考查等差数列前n项和公式与性质及平面向量的坐标运算,难度中等.解题思路:由已知S21=S4 000a22+a23+…+a4 000==3 979a2 011=0,故有a2 011=0,因此·=2 011+ana2 011=2 011,故选A.3.以双曲线-=1的离心率为首项,以函数f(x)=4x-2的零点为公比的等比数列的前n项的和Sn=( )A.3×(2n-1)B.3-(2n-1)C.- 3×(2n-1)D.-3+(2n-1)答案:B 命题立意:本题考查双曲线的离心率及函数的零点与等比数列前n项和公式的应用,难度较小.解题思路:由双曲线方程易得e==,函数零点为,故由公式可得Sn==3=3-,故选B.4.等差数列{an}的前n项和为Sn,若a4=15,S5=55,则过点P(3,a3),Q(4,a4)的直线的斜率为( )A.4B.1C.-4D.-14答案:A 命题立意:本题考查等差数列的性质、前n项和及直线斜率的坐标计算形式,难度较小.解题思路:由题S5==55,故a1+a5=22,根据等差数列的性质可知a1+a5=2a3=22,故a3=11,因为a4=15,则过点P(3,a3),Q(4,a4)的直线的斜率为kPQ===4,故选A.5.在等比数列{an}中,对于n∈N*都有an+1·a2n=3n,则a1·a2·…·a6=( )A.±()11B.()13C.±35D.36答案:D 命题立意:本题考查数列的递推公式、等比数列的性质及整体代换思想,考查考生的运算能力,难度中等.解题思路:由等比数列的性质可知,a1·a2·a3·a4·a5·a6=(a2·a6)·a4·(a1·a5)·a3=(a3)3(a4) 3=(a3·a4)3,令n=2,得a3·a4=32,故选D.6.等差数列{an}的前n项和为Sn,公差为d,已知(a8+1)3+2 013(a8+1)=1,(a2 006+1)3+2 013(a2 006+1)=-1,则下列结论正确的是( )A.d0,S2 013=2 013C.d0,S2 013=-2 013答案:C 命题立意:本题考查函数的性质——单调性与奇偶性、等差数列的性质与前n项和公式,难度中等.解题思路:记f(x)=x3+2 013x,则函数f(x)是在R上的奇函数与增函数;依题意有f(a8+1)=-f(a2 006+1)=1>f(0)=0,即f(a8+1)=f[-(a2 006+1)]=1,a8+1=-(a2 006+1),a8+1>0>a2 006+1即a8>a2 006,d=二、填空题7.在等差数列{an}中,a2=5,a1+a4=12,则an=________;设bn=(nN*),则数列{bn}的前n项和Sn=________.答案:2n+1 命题立意:本题考查等差数列的通项公式与裂项相消法,难度中等.解题思路:设等差数列{an}的公差为d,则有a2+a3=5+a3=12,a3=7,d=a3-a2=2,an=a2+(n-2)d=2n+1,bn==,因此数列{bn}的前n项和Sn=×==.8.设Sn为数列{an}的前n项和,若(nN*)是非零常数,则称该数列为“和等比数列”,若数列{cn}是首项为2,公差为d(d≠0)的等差数列,且数列{cn}是“和等比数列”,则d=________.答案:4 解题思路:由题意可知,数列{cn}的前n项和为Sn=,前2n项和为S2n=,所以==2+=2+,所以当d=4时,=4.9.已知定义在R上的函数f(x)是奇函数且满足f=f(x),f(-2)=-3,数列{an}满足a1=-1,且Sn=2an+n(其中Sn为{an}的前n项和),则f(a5)+f(a6)=______.答案:3 解题思路:因为Sn=2an+n,则Sn-1=2an-1+n-1,两式相减得an=2an-1-1,通过拼凑整理得an-1=2(an-1-1),所以{an-1}是等比数列,则an-1=-2n,因此an=1-2n,所以a5=-31,a6=-63.由f=f(x)且函数f(x)是奇函数,用-x代替x得到f=f(-x)=-f(x),用+x代替x得到f(3+x)=f(x),所以函数f(x)为周期为3,则f(a5)+f(a6)=f(-31)+f(-63)=f(-1)+f(0)=f(2)+0=-f(-2)=3.10.已知ABC的内角A,B,C的对边分别为a,b,c,且a,b,c成递减的等差数列.若A=2C,则的值为________.答案:命题立意:本题主要考查等差数列、正弦定理、余弦定理与三角函数基本公式.解题思路是依据题意得出a,b,c之间的关系,再结合正弦定理、余弦定理及A=2C,从而得出a,c之间的关系.解题思路:依题意知b=,===2cos C=2×,即====,所以a2=c,即(2a-3c)(a-c)=0,又由a>c,因此有2a=3c,故=.2021高考数学提分专项练习及答案(4)一、选择题1.已知{an}为等差数列,其前n项和为Sn,若a3=6,S3=12,则公差d等于( )A.1B.C.2D.3答案:C 命题立意:本题主要考查等差数列的通项公式、求和公式,考查运算求解能力.解题思路:根据已知,a1+2d=6,3a1+3d=12,解得d=2,故选C.2.已知数列{an}的前n项和Sn=an-1(a≠0),则{an}( )A.一定是等差数列B.一定是等比数列C.或者是等差数列,或者是等比数列D.既不可能是等差数列,也不可能是等比数列答案:C 命题立意:等差数列和等比数列的基本运算是高考经常考查的重点,本题根据数列的前n项和求解通项公式,渗透等差数列和等比数列的定义,体现了基本知识的应用,同时也体现了分类讨论的思想,对能力要求较高,应予以重视.解题思路: Sn=an-1(a≠0), an=即an=当a=1时,an=0,数列{an}是一个常数列,也是等差数列;当a≠1时,数列{an}是一个等比数列,故选C.3.在数列{an}中,若对任意的n均有an+an+1+an+2为定值(nN*),且a7=2,a9=3,a98=4,则数列{an}的前100项的和S100等于( )A.132B.299C.68D.99答案:B 解题思路:设an+an+1+an+2=x,则an+1+an+2+an+3=x,两式作差得an=an+3,所以数列{an}为周期数列并且周期T=3,a98=a3×32+2=a2,a9=a3×2+3=a3,a7=a1,所以S100=33×S3+a1=299,故选B.4.已知等比数列{an}的各项均为不等于1的正数,数列{bn}满足bn=lg an,b3=18,b6=12,则数列{bn}的前n项和的值等于( )A.126B.130C.132D.134答案:C 解题思路:bn+1-bn=lg an+1-lg an=lg =lg q(常数),{bn}为等差数列.设公差为d,∴由bn=-2n+24≥0,得n≤12, {bn}的前11项为正,第12项为零,从第13项起为负, S11,S12且S11=S12=132.5.在数列{an}中,a1=1,a2=2,若an+2=2an+1-an+2,则an等于( )A.n3-n+B.n3-5n2+9n-4C.n2-2n+2D.2n2-5n+4答案:C 命题立意:本题考查等差数列的定义与通项公式、累加法求数列的通项公式,难度中等.解题思路:依题意得(an+2-an+1)-(an+1-an)=2,因此数列{an+1-an}是以1为首项,2为公差的等差数列,an+1-an=1+2(n-1)=2n-1.当n≥2时,an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)=1+1+3+…+(2n-3)=1+=(n-1)2+1=n2-2n+2.又a1=1=12-2×1+2,因此an=n2-2n+2,故选C.6.(天津模拟)已知数列{an}满足a1=0,an+1=(nN*),则a20=( )A.0B.-1 C1. D.2答案:B 命题立意:本题主要考查数列的周期性,难度中等.解题思路:因为数列{an}满足a1=0,an+1=(nN*),a2=-,a3=,a4=0, T=3,则a20=a2=-,故选B.二、填空题7.已知数列{an}中,a1=1,an+1=(-1)n(an+1),记Sn为{an}前n项的和,则S2 013=________.答案:-1 005 命题立意:本题主要考查递推数列的有关知识,要求考生掌握常见的几类求递推数列的通项与前n项和,首先是与等差(等比)数列相关的递推数列,其次是一阶线性递推数列,还有具有周期性的数列.本题就是一种具有周期性的递推数列.解题思路:由a1=1,an+1=(-1)n(an+1)可得该数列是周期为4的数列,且a1=1,a2=-2,a3=-1,a4=0.所以S2013=503(a1+a2+a3+a4)+a2 013=503×(-2)+1=-1 005.8.在各项均为正数的等比数列{an}中,已知a3+a4=11a2a4,且它的前2n项的和等于它的前2n项中偶数项之和的11倍,则数列{an}的通项公式an=________.答案:102-n 命题立意:本题考查等比数列的通项公式及其前n项和公式等知识,考查考生的运算能力.解题思路:设等比数列{an}的公比为q,前2n项和为S2n,前2n项中偶数项之和为Tn,由题意知q≠1,则S2n=,Tn=.由题意可知S2n=11Tn,即=.解得q=(或令n=1,则S2=11T1,即a1+a2=11a2,化简得a1=10a2,故q=).又a3+a4=11a2a4,所以a1q2+a1q3=11aq4,化简得1+q=11a1q2,将q=代入可得a1=10,故an=a1qn-1==102-n.9.已知各项都为正数的数列{an},其前n项的和为Sn,且Sn=(+)2(n≥2),若bn=+,且数列{bn}的前n项的和为Tn,则Tn=________.答案:解题思路:-=,则=n,Sn=n2a1,an=Sn-Sn-1=(2n-1)a1,bn=+=2+-,Tn=++…+=2n+2-=.10.数列{an}满足a1=3,an-anan+1=1,An表示{an}的前n项之积,则A2 013=________.答案:-1 命题立意:本题与常考的求等差、等比数列的通项公式或前n项和不同,本题考查给定数列的前n项之积,这就要求考生能根据已知数列,得到数列的性质.求解本题的关键是得到{an}的周期.解题思路:由a1=3,an-anan+1=1,得an+1=,所以a2==,a3=-,a4=3,所以{an}是以3为周期的数列,且a1a2a3=-1,又2 013=3×671,所以A2 013=(-1)671=-1.2021高考数学提分专项练习及答案(5)一、选择题1.已知等差数列{an}的公差和等比数列{bn}的公比都是d(d≠1),且a1=b1,a4=b4,a10=b10,则a1和d的值分别为( )A.1B.-2C.2D.-1答案:D 解题思路:由得由两式得a1=,代入式中,+3d=·d3,化简得d9-3d3+2=0,即(d3-1)(d6+d3-2)=0,d≠1,由d6+d3-2=0,得d=-,a1=-d=.2.已知数列{an}满足an+2-an+1=an+1-an,nN*,且a5=.若函数f(x)=sin 2x+2cos2,记yn=f(an),则数列{yn}的前9项和为( )A.0B.-9C.9D.1答案:C 命题立意:本题考查等差数列的定义与性质及诱导公式的应用,考查综合分析能力,难度中等.解题思路:据已知得2an+1=an+an+2,即数列{an}为等差数列,又f(x)=sin 2x+2×=sin 2x+1+cos x,因为a1+a9=a2+a8=…=2a5=π,故cos a1+cos a9=cos a2+cos a8=…=cos a5=0,又2a1+2a9=2a2+2a8=…=4a5=2π,故sin 2a1+sin 2a9=sin 2a2+sin 2a8=…=sin 2a5=0,故数列{yn}的前9项之和为9,故选C.3.已知数列{an}满足an+1=an-an-1(n≥2),a1=1,a2=3,记Sn=a1+a2+…+an,则下列结论正确的是( )A.a100=-1,S100=5B.a100=-3,S100=5C.a100=-3,S100=2D.a100=-1,S100=2答案:A 命题立意:本题考查数列的性质与求和,难度中等.解题思路:依题意,得an+2=an+1-an=-an-1,即an+3=-an,an+6=-an+3=an,数列{an}的项是以6为周期重复性地出现,且a1+a2+a3+a4+a5+a6=(a1+a4)+(a2+a5)+(a3+a6)=0;注意到100=6×16+4,因此S100=16×0+a1+a2+a3+a4=(a1+a4)+a2+a3=a2+(a2-a1)=2a2-a1=5,a100=a4=-a1=-1,故选A.4.已知等差数列{an}的公差d≠0,且a1,a3,a13成等比数列,若a1=1,Sn是数列{an}前n项的和,则(nN*)的最小值为( )A.4B.3C.2-2D.答案:A 命题立意:本题考查等差数列的通项公式与求和公式以及均值不等式的应用,难度中等.解题思路:据题意由a1,a3,a13成等比数列可得(1+2d)2=1+12d,解得d=2,故an=2n-1,Sn=n2,因此====(n+1)+-2,根据均值不等式,知=(n+1)+-2≥2-2=4,当n=2时取得最小值4,故选A.5.设等差数列{an}的前n项和为Sn,若-amA.Sm>0,且Sm+10C.Sm>0,且Sm+1>0D.Sm<0,且Sm+1<0答案:A 命题立意:本题考查等差数列的性质及前n项和公式的应用,难度中等.解题思路:据已知可得a1+am>0,a1+am+10,Sm+1=<0,故选A.6.在数列{an}中,an+1=can(c为非零常数),前n项和为Sn=3n+k,则实数k为( )A.-1B.0C.1D.2和公式与通项间的关系,难度中等.解题思路:依题意得,数列{an}是等比数列,a1=3+k,a2=S2-S1=6,a3=S3-S2=18,62=18(3+k),解得k=-1,故选A.二、填空题7.已知数列{an}的首项为2,数列{bn}为等差数列且bn=an+1-an(nN*).若b2=-2,b7=8,则a8=________.答案:16 解题思路: {bn}为等差数列,且b2=-2,b7=8,设其公差为d,b7-b2=5d,即8+2=5d. d=2.bn=-2+(n-2)×2=2n-6.an+1-an=2n-6.由a2-a1=2×1-6,a3-a2=2×2-6,…,an-an-1=2×(n-1)-6,累加得:an-a1=2×(1+2+…+n-1)-6(n-1)=n2-7n+6,an=n2-7n+8. a8=16.8.公差不为0的等差数列{an}的部分项ak1,ak2,ak3,…构成等比数列,且k1=1,k2=2,k3=6,则k4=________.公式的应用,难度中等.解题思路:据题意知等差数列的a1,a2,a6成等比数列,设等差数列的公差为d,则有(a1+d)2=a1(a1+5d),解得d=3a1,故a2=4a1,a6=16a1ak4=64a1=a1+(k4-1)(3a1),解得k4=22.9.已知数列{an}满足a1=33,an+1-an=2n,则的最小值为________.答案:命题立意:本题主要考查累加法,难度中等.解题思路:因为a1=33,an+1-an=2n,故利用累加法表示.an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1,那么可知==n+-1,借助于函数的性质可知当n=6时,取得最小值为.10.已知数列{an}满足a1=1,an=(n≥2),则数列{an}的通项公式为an=________.答案:命题立意:本题主要考查等差数列的定义与通项公式等知识,意在考查考生的观察能力、化归与转化能力、运算能力.解题思路:依题意,得-=(n≥2),因此数列是以1为首项、为公差的等差数列,于是有=1+(n-1),an=.三、解答题11.已知Sn是正数数列{an}的前n项和,S,S,…,S,…是以3为首项,以1为公差的等差数列;数列{bn}为无穷等比数列,其前四项之和为120,第二项与第四项之和为90.(1)求an,bn;(2)从数列中能否挑出的无穷等比数列,使它的各项和等于?若能的话,请写出这个数列的第一项和公比;若不能的话,请说明理由.解析:(1){S}是以3为首项,以1为公差的等差数列,所以S=3+(n-1)=n+2.因为an>0,所以Sn=(nN*).当n≥2时,an=Sn-Sn-1=-,又a1=S1=,所以an=(nN*).设{bn}的首项为b1,公比为q,则有所以即bn=3n(nN*).(2)=n,设可以挑出一个无穷等比数列{cn},首项为c1=p,公比为k(p,kN*),它的各项和等于=,则有=,所以p=.当p≥k时,3p-3p-k=8,即3p-k(3k-1)=8,因为p,kN*,所以只有当p-k=0,k=2,即p=k=2时,数列{cn}的各项和为.当pp,右边含有3的因数,而左边非3的倍数,故不存在p,kN*,所以存在的等比数列{cn},首项为,公比为,使它的各项和等于.12.已知数列{an}是公比大于1的等比数列,对任意的nN*,有an+1=a1+a2+…+an-1+an+.(1)求数列{an}的通项公式;(2)设数列{bn}满足:bn=(log3 a1+log3 a2+…+log3 an+log3 t)(nN*),若{bn}为等差数列,求实数t的值及数列{bn}的通项公式.解析:(1)解法一:设{an}的公比为q,则由题设,得即由-,得a1q2-a1q=-a1+a1q,即2a1q2-7a1q+3a1=0.a1≠0, 2q2-7q+3=0,解得q=(舍去)或q=3.将q=3代入,得a1=1,an=3n-1.解法二:设{an}的公比为q,则由已知,得a1qn=+a1qn-1+,即a1qn=qn-+,比较系数得解得(舍去)或 an=3n-1.(2)由(1),得bn=(log3 30+log3 31+…+log3 3n-1+log3 t) =[1+2+…+(n-1)+log3 t]==+log3 t.{bn}为等差数列,bn+1-bn等于一个与n无关的常数,而bn+1-bn=-+log3 t=-log3 t,log3 t=0, t=1,此时bn=.13.已知数列{an}的前n项和Sn=-an-n-1+2(nN*),数列{bn}满足bn=2n·an.(1)求证数列{bn}是等差数列,并求数列{an}的通项公式;(2)设cn=log2,数列的前n项和为Tn,求满足Tn<(nN*)的n 的值.解析:(1)证明:在Sn=-an-n-1+2中,令n=1,可得S1=-a1-1+2=a1,得a1=.当n≥2时,Sn-1=-an-1-n-2+2,an=Sn-Sn-1=-an+an-1+n-1,即2an=an-1+n-1.2n·an=2n-1·an-1+1.bn=2n·an, bn=bn-1+1.又b1=2a1=1, {bn}是以1为首项,1为公差的等差数列.于是bn=1+(n-1)·1=n, an=.(2) cn=log2=log22n=n,==-.Tn=++…+=1+--.由Tn<,得1+--,f(n)=+单调递减,f(3)=,f(4)=,f(5)=,n的值为4.2021高考数学提分专项练习及答案(6)一、选择题1.已知=,则tan α+=( )A.-8B.8C.1D.-1答案:A 解题思路:==cos α-sin α=,1-2sin αcos α=,即sin αcos α=-.则tan α+=+===-8.故选A.2.在ABC中,若tan Atan B=tan A+tan B+1,则cos C的值为( )A.-1/2B.1/3C. 1/2D.-1答案:B 解题思路:由tan Atan B=tan A+tan B+1,可得=-1,即tan(A+B)=-1,又因为A+B(0,π),所以A+B=,则C=,cos C=.3.已知曲线y=2sincos与直线y=相交,若在y轴右侧的交点自左向右依次记为P1,P2,P3,…,则||等于( )A.πB.2πC.3πD.4π答案:B 命题立意:本题考查三角恒等变换及向量的坐标运算,难度较小.解题思路:由于f(x)=2sin2=2×=1+sin 2x,据题意,令1+sin 2x=,解得2x=2kπ-或2x=2kπ-(kZ),即x=kπ-或x=kπ-(kZ),故P1,P5,因此||==2π.4.在ABC中,角A,B,C所对的边分别为a,b,c,S表示ABC 的面积,若acos B+bcos A=csin C,S=(b2+c2-a2),则B等于( )A.90°B.60°C.45°D.30°答案:C 解题思路:由正弦定理和已知条件知sin AcosB+sin Bcos A=sin2C,即sin(A+B)=sin2C, sin C=1,C=,从而S=ab=(b2+c2-a2)=(b2+b2),解得a=b,因此B=45°.5.已知=k,0<θA.随着k的增大而增大B.有时随着k的增大而增大,有时随着k的增大而减小C.随着k的增大而减小D.是一个与k无关的常数答案:A 解题思路:k===2sin θcos θ=sin 2θ,因为0<θ6.在ABC中,角A,B,C的对边分别为a,b,c,已知4sin2-cos 2C=,且a+b=5,c=,则ABC的面积为( )A.3B.3C.-1/2D.1/2答案:A 命题立意:本题主要考查余弦定理及三角形面积的求解,意在考查考生对余弦定理的理解和应用能力.解题思路: 4sin2-cos 2C=,2[1-cos(A+B)]-2cos2C+1=,2+2cos C-2cos2C+1=,cos2C-cos C+=0,解得cos C=,故sin C=.根据余弦定理有cos C==,ab=a2+b2-7,3ab=a2+b2+2ab-7=(a+b)2-7=25-7=18,ab=6,S=absin C=×6×=.二、填空题7.若sin=,则sin 2α=__________.答案:- 解题思路:sin 2α=-cos=-cos=2sin2-1=2×2-1=-.8.在锐角三角形ABC中,a,b,c分别为角A,B,C的对边且a=2csin A,c=,ABC的面积为,则a+b=________.答案:5 命题立意:本题考查解三角形的基本知识,包括三角形面积公式、正弦定理、余弦定理等,考查考生对知识的整合能力.解题思路:由a=2csin A及正弦定理得==, sin A≠0, sin C=.ABC是锐角三角形, C=,S△ABC=ab·sin =,即ab=6, c=,由余弦定理得a2+b2-2abcos =7,即a2+b2-ab=7,解得(a+b)2=25,故a+b=5.9.有这样一道题:“在ABC中,已知a=,________,2cos2=(-1)cos B,求角A.”已知该题的答案是A=60°,若横线处的条件为三角形中某一边的长度,则此条件应为________.答案:c= 解题思路:由2cos2=(-1)cos B得1-cos B=(-1)cos B,即cos B=,所以B=45°,则C=180°-45°-60°=75°,由正弦定理,得=,所以c=.10.已知ABC中,角A,B,C所对边分别为a,b,c,若1+=,则的最小值为________.答案:1 解题思路:因为A,B,C为ABC中的角,角A,B,C 所对边分别为a,b,c,又1+===,由正弦定理得=,所以1+=,而1+=,所以cos A=,又A为ABC 中的内角,所以A=.由余弦定理得a2=b2+c2-2bccos A=b2+c2-2bc×≥2bc-bc=bc.(当且仅当b=c时取“=”)所以的最小值为1.三、解答题11.如图,在海岸A处发现北偏东45°方向,距A处(-1)海里的B处有一艘走私船,在A处北偏西75°方向,距A处2海里的C 处的我方缉私船奉命以10海里/小时的速度追截走私船,此时走私船正以10海里/小时的速度,从B处向北偏东30°方向逃窜.问:缉私船沿什么方向行驶才能最快截获走私船?并求出所需时间.解析:设缉私船应沿CD方向行驶t小时,才能最快截获走私船(在D点),则CD=10t海里,BD=10t海里.在ABC中,由余弦定理,得BC2=AB2+AC2-2AB·ACcos A=(-1)2+22-2(-1)·2·cos 120°=6,BC=(海里).由正弦定理知=,sin ∠ABC===,ABC=45°, B点在C点的正东方向上,CBD=90°+30°=120°.在BCD中,由正弦定理,得=,sin ∠BCD===,BCD=30°,缉私船沿北偏东60°的方向行驶. 又在BCD中,CBD=120°,BCD=30°,D=30°,BD=BC,即10t=,t=小时≈15分钟.故缉私船应沿北偏东60°的方向行驶,才能最快截获走私船,大约需要15分钟.12.已知向量m=sin(A-B),sin,n=(1,2sin B),m·n=sin2C,其中A,B,C分别为ABC的三边a,b,c所对的角.(1)求角C的大小;(2)若sin A+sin B=2sin C,且SABC=,求边c的长.解析:(1) m·n=sin(A-B)+2cos Asin B=sin Acos B+cos Acos B=sin(A+B),在ABC中,A+B=π-C且0sin(A+B)=sin C,又 m·n=sin 2C,sin C=sin 2C=2cos Csin C,cos C=, C=.(2) sin A+sin B=2sin C,由正弦定理得a+b=2c,。
小题专练10-2021届高考数学二轮复习新高考版(含解析)
小题专练10解析几何(B)一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(考点:两条直线的位置关系,★)已知直线l :x+m 2y=0与直线n :x+y+m=0,则“l ∥n ”是“m=1”的( ). A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分也不必要条件2.(考点:双曲线性质的应用,★★)已知双曲线x 24-y 2m=1(m>0)的离心率为2,则双曲线x 2m-y 2=1的焦距是( ).A .2√3B .√13C .4√3D .2√133.(考点:椭圆性质的应用,★★)已知椭圆x 2+my 2=1的焦点在y 轴上,长轴长是短轴长的两倍,则实数m 的值为( ). A .14 B .12 C .2 D .44.(考点:直线与圆的位置关系,★★)过圆C :(x-2)2+(y-1)2=25上一点P (-1,-3)作切线l ,直线m :3x+ay=0与切线l平行,则实数a 的值为( ). A .35B .2C .125D .45.(考点:求双曲线的渐近线方程,★★)设F 1和F 2为双曲线x 2a 2-y 2b 2=1(a >0,b >0)的两个焦点,若点P (0,2b ),F 1,F 2是等腰直角三角形的三个顶点,则该双曲线的渐近线方程是( ). A .y=±√3x B .y=±√217x C .y=±√33xD .y=±√213x 6.(考点:求双曲线的离心率,★★)若双曲线C :x 2a 2-y 2b 2=1(a>0,b>0)的一条渐近线被曲线x 2+y 2-4x+2=0所截得的弦长为2,则该双曲线C 的离心率为( ). A .√3B .2√33C .√5D .2√557.(考点:求双曲线的方程,★★)已知双曲线C :x 2a 2-y 2b 2=1(a>0,b>0)的右焦点为F ,O 为坐标原点,以OF 为直径的圆与双曲线C 的一条渐近线交于点O 及点A (4√55,2√55),则双曲线C 的方程为( ).A .x 2-y24=1 B .x 24-y 2=1C .x 26-y 22=1D .x 22-y 26=18.(考点:直线与抛物线的位置关系,★★)已知焦点为F 的抛物线C :y 2=4x 的准线与x 轴交于点A ,点M 在抛物线C 上,则当|MA ||MF |取得最大值时,直线MA 的方程为( ). A .y=x+1或y=-x-1 B .y=12x+12或y=-12x-12 C .y=2x+2或y=-2x-2 D .y=-2x+2二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分. 9.(考点:点到直线的距离,★★)下列说法正确的是( ). A .“c=5”是“点(2,1)到直线3x+4y+c=0的距离为3”的充要条件 B .直线x sin α-y+1=0的倾斜角的取值范围为[0,π4]∪[3π4,π)C .直线y=-2x+5与直线2x+y+1=0平行,且与圆x 2+y 2=5相切D .离心率为√3的双曲线的渐近线方程为y=±√2x10.(考点:抛物线性质的应用,★★)过抛物线y 2=4x 的焦点F 作直线交抛物线于A ,B 两点,M 为线段AB 的中点,则下列说法正确的是( ). A .以线段AB 为直径的圆与直线x=-32相离 B .以线段BM 为直径的圆与y 轴相切 C .当AF⃗⃗⃗⃗⃗ =2FB ⃗⃗⃗⃗⃗ 时,|AB|=92D .|AB|的最小值为411.(考点:椭圆性质的应用,★★)设椭圆C :x 22+y 2=1的左、右焦点分别为F 1,F 2,P 是椭圆C 上的动点,则下列结论正确的是( ). A .|PF 1|+|PF 2|=2√2 B .离心率e=12C .△PF 1F 2面积的最大值为√2D .以线段F 1F 2为直径的圆与直线x+y-√2=0相切12.(考点:双曲线的性质综合,★★★)已知点P 是双曲线E :x 216-y 29=1右支上的一点,F 1,F 2为双曲线E 的左、右焦点,△PF 1F 2的面积为20,则下列说法正确的是( ).A.点P的横坐标为203B.△PF1F2的周长为803C.∠F1PF2小于π3D.△PF1F2的内切圆半径为34三、填空题:本题共4小题,每小题5分,共20分.13.(考点:求双曲线的方程,★★)已知双曲线C1与双曲线C2:x22-y26=1的渐近线相同,且双曲线C1的焦距为8,则双曲线C1的方程为.14.(考点:椭圆定义的应用,★★)已知P为椭圆x2100+y291=1上的一个动点,M,N分别为圆C:(x-3)2+y2=1与圆D:(x+3)2+y2=r2(0<r<3)上的动点,若|PM|+|PN|的最小值为17,则r= .15.(考点:直线与双曲线的位置关系,★★)已知直线l与双曲线y2-2x2=1交于A,B两点,当A,B两点的对称中心的坐标为(1,1)时,直线l的方程为.16.(考点:双曲线的几何性质的应用,★★★)已知A,B分别是双曲线C:x2-y22=1的左、右顶点,P为C上一点,且点P在第一象限.记直线PA,PB的斜率分别为k1,k2,当2k1+k2取得最小值时,k1的值为,△PAB的重心坐标为.答案解析:1.(考点:两条直线的位置关系,★)已知直线l:x+m2y=0与直线n:x+y+m=0,则“l∥n”是“m=1”的().A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【解析】若l∥n,则1×1=m2×1,故m=1或m=-1.故“l∥n”是“m=1”的必要不充分条件.【答案】B2.(考点:双曲线性质的应用,★★)已知双曲线x24-y2m=1(m>0)的离心率为2,则双曲线x2m-y2=1的焦距是().A .2√3B .√13C .4√3D .2√13【解析】由题意可得√4+m2=2,解得m=12,则双曲线x 2m-y 2=1的焦距为2√m +1=2√12+1=2√13. 【答案】D3.(考点:椭圆性质的应用,★★)已知椭圆x 2+my 2=1的焦点在y 轴上,长轴长是短轴长的两倍,则实数m 的值为( ). A .14 B .12 C .2 D .4【解析】将椭圆方程化为标准方程得x 2+y 21m=1,由题意可得1m >1,且1m =4,解得m=14.故选A .【答案】A4.(考点:直线与圆的位置关系,★★)过圆C :(x-2)2+(y-1)2=25上一点P (-1,-3)作切线l ,直线m :3x+ay=0与切线l平行,则实数a 的值为( ). A .35 B .2 C .125 D .4【解析】由题意得k PC =1-(-3)2-(-1)=43, 所以切线的斜率为-34. 所以-3a=-34,解得a=4.【答案】D5.(考点:求双曲线的渐近线方程,★★)设F 1和F 2为双曲线x 2a 2-y 2b 2=1(a >0,b >0)的两个焦点,若点P (0,2b ),F 1,F 2是等腰直角三角形的三个顶点,则该双曲线的渐近线方程是( ). A .y=±√3x B .y=±√217x C .y=±√33xD .y=±√213x 【解析】设F 1(-c ,0),F 2(c ,0).∵F 1,F 2,P 是等腰直角三角形的三个顶点,∴c=2b ,∴c 2=a 2+b 2=4b 2,即a 2=3b 2,∴b a =√33,∴该双曲线的渐近线方程为y=±√33x. 【答案】C6.(考点:求双曲线的离心率,★★)若双曲线C :x 2a -y 2b =1(a>0,b>0)的一条渐近线被曲线x 2+y 2-4x+2=0所截得的弦长为2,则该双曲线C 的离心率为( ).A .√3B .2√33C .√5D .2√55【解析】双曲线C :x 2a 2-y 2b2=1(a>0,b>0)的渐近线方程为y=±bax ,依据对称性,不妨取y=bax ,即bx-ay=0.又曲线方程x 2+y 2-4x+2=0可化为(x-2)2+y 2=2, 则其是圆心坐标为(2,0),半径为√2的圆. 由题意得,圆心到该渐近线的距离d=√(√2)2-12=1,又由点到直线的距离公式可得d=√b 2+a 2=1,解得b 2a2=13,所以e=√c 2a2=√a 2+b 2a 2=√1+b 2a 2=2√33. 【答案】B7.(考点:求双曲线的方程,★★)已知双曲线C :x 2a 2-y 2b 2=1(a>0,b>0)的右焦点为F ,O 为坐标原点,以OF 为直径的圆与双曲线C 的一条渐近线交于点O 及点A (4√55,2√55),则双曲线C 的方程为( ).A .x 2-y 24=1 B .x 24-y 2=1C .x 26-y 22=1 D .x 22-y 26=1【解析】因为双曲线的渐近线方程为y=±ba x ,所以由点到直线的距离公式可得出右焦点F 到渐近线的距离为b. 由题意可得|OA|2=c 2-b 2=a 2=4,且b a =12, 所以b 2=1,即双曲线C 的方程为x 24-y 2=1.【答案】B8.(考点:直线与抛物线的位置关系,★★)已知焦点为F 的抛物线C :y 2=4x 的准线与x 轴交于点A ,点M 在抛物线C 上,则当|MA ||MF |取得最大值时,直线MA 的方程为( ).A .y=x+1或y=-x-1B .y=12x+12或y=-12x-12C .y=2x+2或y=-2x-2D .y=-2x+2【解析】过点M 作MP 与准线垂直,垂足为P ,则|MA ||MF |=|MA ||MP |=1cos∠AMP =1cos∠MAF ,则当|MA ||MF |取得最大值时,∠MAF 最大,此时AM 与抛物线C 相切, 易知此时直线AM 的斜率存在,设切线方程为y=k (x+1),联立{y =k (x +1),y 2=4x ,得k 2x 2+(2k 2-4)x+k 2=0,由Δ=16-16k 2=0,解得k=±1,则直线AM 的方程为y=±(x+1). 【答案】A二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分. 9.(考点:点到直线的距离,★★)下列说法正确的是( ). A .“c=5”是“点(2,1)到直线3x+4y+c=0的距离为3”的充要条件 B .直线x sin α-y+1=0的倾斜角的取值范围为[0,π4]∪[3π4,π) C .直线y=-2x+5与直线2x+y+1=0平行,且与圆x 2+y 2=5相切 D .离心率为√3的双曲线的渐近线方程为y=±√2x【解析】对于选项A,由点(2,1)到直线3x+4y+c=0的距离为3,可得|6+4+c |5=3,解得c=5或-25,所以“c=5”是“点(2,1)到直线3x+4y+c=0的距离为3”的充分不必要条件,故选项A 错误;对于选项B,直线x sin α-y+1=0的斜率k=sin α∈[-1,1],设直线的倾斜角为θ,则0≤tan θ<1或-1≤tan θ<0,所以θ∈[0,π4]∪[3π4,π),故选项B 正确;对于选项C,直线y=-2x+5可化为2x+y-5=0,其与直线2x+y+1=0平行,圆x 2+y 2=5的圆心O (0,0)到直线2x+y-5=0的距离d=√1+4=√5,则直线2x+y-5=0与圆x 2+y 2=5相切,故选项C 正确;对于选项D,离心率e=ca =√3,则ba=√2,若焦点在x 轴,则双曲线的渐近线方程为y=±√2x ,若焦点在y 轴,则双曲线的渐近线方程为y=±√22x ,故选项D错误. 【答案】BC10.(考点:抛物线性质的应用,★★)过抛物线y 2=4x 的焦点F 作直线交抛物线于A ,B 两点,M 为线段AB 的中点,则下列说法正确的是( ). A .以线段AB 为直径的圆与直线x=-32相离B .以线段BM 为直径的圆与y 轴相切C .当AF⃗⃗⃗⃗⃗ =2FB ⃗⃗⃗⃗⃗ 时,|AB|=92D .|AB|的最小值为4【解析】对于选项A,点M 到准线x=-1的距离为12(|AF|+|BF|)=12|AB|,于是以线段AB 为直径的圆与直线x=-1一定相切,与直线x=-32一定相离,故A 正确.对于选项B,显然线段BM 中点的横坐标与12|BM|不一定相等,故B 错误.对于选项C,D,设A (x 1,y 1),B (x 2,y 2),直线AB 方程为x=my+1,联立直线与抛物线方程可得y 2-4my-4=0,y 1y 2=-4,x 1x 2=1,若设A (4a 2,4a ),则B (14a 2,-1a ),于是|AB|=x 1+x 2+p=4a 2+14a2+2,所以|AB|的最小值为4,故D 正确;由AF⃗⃗⃗⃗⃗ =2FB ⃗⃗⃗⃗⃗ 可得y 1=-2y 2,即4a=-2(-1a),所以a 2=12,|AB|=92,故C 正确. 【答案】ACD11.(考点:椭圆性质的应用,★★)设椭圆C :x 22+y 2=1的左、右焦点分别为F 1,F 2,P 是椭圆C 上的动点,则下列结论正确的是( ). A .|PF 1|+|PF 2|=2√2 B .离心率e=12C .△PF 1F 2面积的最大值为√2D .以线段F 1F 2为直径的圆与直线x+y-√2=0相切【解析】对于A 选项,由椭圆的定义可知|PF 1|+|PF 2|=2a=2√2,所以A 选项正确; 对于B 选项,依题意a=√2,b=1,c=1,所以e=ca =2=√22,所以B 选项错误;对于C 选项,|F 1F 2|=2c=2,当P 为椭圆短轴端点时,△PF 1F 2的面积取得最大值,最大值为12·2c ·b=c ·b=1,所以C 选项错误;对于D 选项,以线段F 1F 2为直径的圆,其圆心为(0,0),半径c=1,圆心到直线x+y-√2=0的距离为√2√2=1,即圆心到直线的距离等于半径,所以以线段F 1F 2为直径的圆与直线x+y-√2=0相切,所以D 选项正确. 【答案】AD12.(考点:双曲线的性质综合,★★★)已知点P 是双曲线E :x 216-y 29=1右支上的一点,F 1,F 2为双曲线E 的左、右焦点,△PF 1F 2的面积为20,则下列说法正确的是( ). A .点P 的横坐标为203B .△PF 1F 2的周长为803C .∠F 1PF 2小于π3D .△PF 1F 2的内切圆半径为34【解析】双曲线E :x 216-y 29=1中的a=4,b=3,c=5,不妨设P (m ,n )(m>0,n>0),由△PF 1F 2的面积为20,可得12|F 1F 2|n=cn=5n=20,即n=4, 由m 216-169=1,可得m=203,故A 正确;由P (203,4),且F 1(-5,0),F 2(5,0),可得k PF 1=1235,k PF 2=125,则tan ∠F 1PF 2=125-12351+125×1235=360319∈(0,√3),则∠F 1PF 2<π3,故C 正确;由|PF 1|+|PF 2|=√16+(353)2+√16+(53)2=373+133=503,则△PF 1F 2的周长为503+10=803,故B 正确;设△PF 1F 2的内切圆半径为r ,可得12r (|PF 1|+|PF 2|+|F 1F 2|)=20,解得r=32,故D 错误. 【答案】ABC三、填空题:本题共4小题,每小题5分,共20分.13.(考点:求双曲线的方程,★★)已知双曲线C 1与双曲线C 2:x 22-y 26=1的渐近线相同,且双曲线C 1的焦距为8,则双曲线C 1的方程为 .【解析】设双曲线C 1的方程为x 22-y 26=λ(λ≠0),故x 22λ-y 26λ=1(λ≠0), 则2λ+6λ=16或-2λ-6λ=16,解得λ=2或λ=-2, 故双曲线C 1的方程为x 24-y 212=1或y 212-x 24=1.【答案】x 24-y 212=1或y 212-x 24=114.(考点:椭圆定义的应用,★★)已知P 为椭圆x 2100+y 291=1上的一个动点,M ,N 分别为圆C :(x-3)2+y 2=1与圆D :(x+3)2+y 2=r 2(0<r<3)上的动点,若|PM|+|PN|的最小值为17,则r= .【解析】由题意可得,C (3,0),D (-3,0)恰好为椭圆的两个焦点,且|PM|≥|PC|-1,|PN|≥|PD|-r , 所以|PM|+|PN|≥|PC|+|PD|-1-r=2a-1-r. 因为a 2=100,解得a=10,所以20-1-r=17,解得r=2. 【答案】215.(考点:直线与双曲线的位置关系,★★)已知直线l 与双曲线y 2-2x 2=1交于A ,B 两点,当A ,B 两点的对称中心的坐标为(1,1)时,直线l 的方程为 . 【解析】设A (x 1,y 1),B (x 2,y 2),直线l 的斜率为k ,则{y 12-2x 12=1,y 22-2x 22=1,两式相减得到(y 1+y 2)(y 1-y 2)-2(x 1+x 2)(x 1-x 2)=0,将x 1+x 2=2,y 1+y 2=2代入上式,化简得k=2. 故直线l 的方程为y=2x-1,即2x-y-1=0. 【答案】2x-y-1=016.(考点:双曲线的几何性质的应用,★★★)已知A ,B 分别是双曲线C :x 2-y 22=1的左、右顶点,P 为C 上一点,且点P 在第一象限.记直线PA ,PB 的斜率分别为k 1,k 2,当2k 1+k 2取得最小值时,k 1的值为 ,△PAB 的重心坐标为 .【解析】由题意知A (-1,0),B (1,0),设P (x ,y ),则k 1=yx+1,k 2=yx -1,∴k 1k 2=y 2x 2-1=2,2k 1+k 2≥2√2k 1k 2=4,当且仅当2k 1=k 2时取等号,此时k 1=1,直线PA 的方程为y=x+1;k 2=2,直线PB 的方程为y=2(x-1). 联立{y =x +1,y =2(x -1),解得{x =3,y =4,∴P (3,4),∴△PAB 的重心坐标为(-1+1+33,0+0+43),即(1,43).【答案】1 (1,43)。
2023新高考数学押题卷第10题 三角函数(新高考)(原卷)
押第10题 三角函数从近几年的高考考察的方向来看.这部分的高考题以选择.解答题出现的机会较多.有时候也以填空题的形式出现.它们经常与三角函数的性质.解三角形及向量联合考察.主要题型有三角函数求值.通过三角式的变换研究三角函数的性质. 本讲内容是高考复习的重点之一.三角函数的化简.求值及三角恒等式的证明是三角变换的基本问题.历年高考中.在考察三角公式的掌握和运用的同时.还注重考察思维的灵活性和发散性.以及观察能力.运算及观察能力.运算推理能力和综合分析能力.(1)解答此类题目,一般考虑如下三层:第一层次:通过诱导公式和倍角公式的简单运用,解决有关三角函数基本性质的问题。
如判断符号、求值、求周期、判断奇偶性等。
第二层次:三角函数公式变形中的某些常用技巧的运用。
如辅助角公式、平方公式逆用、切弦互化等。
第三层次:充分利用三角函数作为一种特殊函数的图象及周期性、奇偶性、单调性、有界性等特殊性质,解决较复杂的函数问题。
如分段函数值,求复合函数值域等。
(2)方法总结 (1)常值代换:特(2)项的分拆与角的配凑。
(3)降次与升次。
(4)化弦(切)法。
(5)引入辅助角。
1.(2021·新高考全国卷Ⅰ数学·高考真题)下列区间中,函数()7sin 6f x x π⎛⎫=- ⎪⎝⎭单调递增的区间是( ) A .0,2π⎛⎫⎪⎝⎭B .,2ππ⎛⎫ ⎪⎝⎭C .3,2ππ⎛⎫ ⎪⎝⎭D .3,22ππ⎛⎫⎪⎝⎭2.(2021·新高考全国卷Ⅰ数学·高考真题)若tan 2θ=-,则()sin 1sin 2sin cos θθθθ+=+( )A .65-B .25-C .25D .653.(2021·新高考全国卷Ⅰ数学·高考真题)已知O 为坐标原点,点()1cos ,sin P αα,()2cos ,sin P ββ-,()()()3cos ,sin P αβαβ++,1,0A ,则( ) A .12OP OP = B .12AP AP = C .312OA OP OP OP ⋅=⋅ D .123OA OP OP OP ⋅=⋅ 4.(2021·全国高考甲卷数学真题(理))已知12,F F 是双曲线C 的两个焦点,P 为C 上一点,且121260,3F PF PF PF ∠=︒=,则C 的离心率为( ) A .72B .132C .7D .135.(2021·全国高考甲卷数学真题(理))2020年12月8日,中国和尼泊尔联合公布珠穆朗玛峰最新高程为8848.86(单位:m ),三角高程测量法是珠峰高程测量方法之一.如图是三角高程测量法的一个示意图,现有A ,B ,C 三点,且A ,B ,C 在同一水平面上的投影,,A B C '''满足45AC B ∠'''=︒,60A B C ''∠'=︒.由C 点测得B 点的仰角为15︒,BB '与CC '的差为100;由B 点测得A 点的仰角为45︒,则A ,C 两点到水平面A B C '''的高度差AA CC ''-约为(3 1.732≈)( )A .346B .373C .446D .4731.(多选)(2022·山东聊城·一模)已知函数()()2sin ,0f x x a ωϕω=++>,则下列结论正确的是( )A .若对于任意的x ∈R ,都有()1f x 成立,则1a -B .若对于任意的x ∈R ,都有()()f x f x π+=成立,则2ω=C .当3πϕ=时,若()f x 在0,2π⎡⎤⎢⎥⎣⎦上单调递增,则ω的取值范围为10,3⎛⎤⎥⎝⎦D .当3a =-时,若对于任意的ϕ∈R ,函数()f x 在0,2π⎡⎤⎢⎥⎣⎦上至少有两个零点,则ω的取值范围为[)4,+∞2.(2022·河北石家庄·模拟预测)已知双曲线()2222:10,0x y C a b a b-=>>的一条渐近线的倾斜角为θ(其中θ为钝角),则双曲线C 的离心率为( ) A .1sin θB .1cos θC .1sin θ-D .1cos θ-3.(2022·广东·模拟预测)小说《三体》中的“水滴”是三体文明派往太阳系的探测器,由强相互作用力材料制成,被形容为“像一滴圣母的眼泪”.小刘是《三体》的忠实读者,他利用几何作图软件画出了他心目中的水滴(如图),由线段AB ,AC 和优弧BC 围成,其中BC 连线竖直,AB ,AC 与圆弧相切,已知“水滴”的水平宽度与竖直高度之比为74,则cos BAC ∠=( ).A .1725B .437C .45D .574.(2022·山东聊城·一模)若()()2sin cos f x x x ϕ=+-为奇函数,则ϕ=___________.(填写符合要求的一个值)5.(2022·山东潍坊·一模)已知π0,2α⎛⎫∈ ⎪⎝⎭,且3cos2sin 1αα+=,则( ).A .()2sin π3α-=B .()2cos π3α-=-C .π5sin 23α⎛⎫+=- ⎪⎝⎭D .π5cos 23α⎛⎫+=- ⎪⎝⎭(限时:30分钟)1.已知tan 3α=,则2sin 2sin αα=( )A .32B .23C .16D .62.已知22sin(2)43512cos ()26πααπ-=--,则sin 3πα⎛⎫-= ⎪⎝⎭( )A .25B .35C .25-D .453.已知tan 3α=,则sin 2cos 2sin cos αααα+-的值为( )A .1B .32C .2D .54.已知sin 4πα⎛⎫+= ⎪⎝⎭,则sin 2α的值为( )A .12B .12-CD. 5.设1F ,2F 分别是双曲线221445x y -=的左、右焦点,P 是该双曲线上的一点,且1235PF PF =,则12PF F △的面积等于( )A.B.C.D.6.已知在三角形ABC 中,4BC =,2AB AC =,则AB AC ⋅的取值范围是( ) A .32,329⎛⎫- ⎪⎝⎭B .32,329⎡-⎢⎥⎣⎦C .()0,32D .[)0,327.已知tan 3α=-,则3sin sin sin 2ααπα-=⎛⎫+ ⎪⎝⎭( ) A .34-B .34C .310D .310-8.函数()2sin 23f x x π⎛⎫=- ⎪⎝⎭的一个单调递减区间是( )A .511,66ππ⎡⎤⎢⎥⎣⎦B .5,1212ππ⎡⎤⎢⎥⎣⎦C .511,1212ππ⎡⎤⎢⎥⎣⎦D .5,66ππ⎡⎤⎢⎥⎣⎦9.已知函数()()sin 2cos2101f x x x ωωω=-+<<,将()f x 的图象先向左平移π4个单位长度,然后再向下平移1个单位长度,得到函数()g x 的图象,若()g x 图象关于π,04⎛⎫⎪⎝⎭对称,则ω为( ) A .14B .12C .23D .3410.对于函数()()2sin cos 2f x x x x =+,有下列结论:①最小正周期为π;②最大值为3;③减区间为()7,1212k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦;④对称中心为,06k k Z ππ⎛⎫-+∈ ⎪⎝⎭.则上述结论正确的个数是( ) A .1B .2C .3D .411.时钟花是原产于南美热带雨林的藤蔓植物,从开放到闭合与体内的一种时钟酶有关.研究表明,当气温上升到20°C 时,时钟酶活跃起来,花朵开始开放;当气温上升到28°C 时,时钟酶的活性减弱,花朵开始闭合,且每天开闭一次.已知某景区一天内5~17时的气温T (单位:°C )与时间t (单位:h )近似满足关系式2010sin 88T t ππ⎛⎫=-- ⎪⎝⎭,则该景区这天时钟花从开始开放到开始闭合约经历( )3sin 0.810π⎛⎫≈ ⎪⎝⎭A .1.4hB .2.4hC .3.2hD .5.6h12.已知函数()πcos (0)6f x x ωω⎛⎫=+> ⎪⎝⎭在区间0,6π⎛⎫⎪⎝⎭上无极值,则ω的取值范围是( )A .(0,5]B .(0,5)C .(0,52) D .(0,52] 13.已知函数()sin cos f x x x ωω=+(0>ω)在ππ,48⎡⎤-⎢⎥⎣⎦上单调递增,则ω的一个取值为________.14.七巧板是一种古老的中国传统智力玩具.如图,边长为4的七巧板左下角为坐标原点,其中各点的横、纵坐标均为整数.当函数sin()y A x b ωϕ=++ (0,||2)b ωπ≤≤≤经过的顶点数最多时,Ab的值为( )A .1B .2C .1或12D .1或215.设sin7a =,则( )A .222log aa a << B .22log 2a a a << C .22log 2aa a <<D .22log 2aa a <<。
专题13小题提分限时训练12(解析版)-2021年新高考数学小题限时提分训练(45分钟)
专题13新高考数学小题提分限时训练12(解析版)一、单选题1.若集合A ={x |–2<x <1},B={x |x <–1或x >3},则A B = A .{x |–2<x <–1} B .{x |–2<x <3} C .{x |–1<x <1} D .{x |1<x <3}【答案】A 【解析】试题分析:利用数轴可知{}21A B x x ⋂=-<<-,故选A. 【考点】集合的运算【名师点睛】集合分为有限集合和无限集合,若集合个数比较少时可以用列举法表示;若集合是无限集合就用描述法表示,并注意代表元素是什么.集合的交、并、补运算问题,应先把集合化简再计算,常常借助数轴或韦恩图进行处理.2.若复数(1–i )(a +i )在复平面内对应的点在第二象限,则实数a 的取值范围是 A .(–∞,1) B .(–∞,–1) C .(1,+∞) D .(–1,+∞) 【答案】B 【解析】试题分析:设()()()()1i i 11i z a a a =-+=++-,因为复数对应的点在第二象限,所以1010a a +<⎧⎨->⎩,解得:1a <-,故选B.【考点】复数的运算【名师点睛】复数的分类及对应点的位置问题都可以转化为复数的实部与虚部应该满足的条件问题,只需把复数化为代数形式,列出实部和虚部满足的方程(不等式)组即可.复数z =a +b i 复平面内的点Z (a ,b )(a ,b ∈R).复数z =a +b i(a ,b ∈R) 平面向量OZ .3.已知函数1()3()3x xf x =-,则()f xA .是奇函数,且在R 上是增函数B .是偶函数,且在R 上是增函数C .是奇函数,且在R 上是减函数D .是偶函数,且在R 上是减函数【答案】A【解析】分析:讨论函数()133xx f x ⎛⎫=- ⎪⎝⎭的性质,可得答案. 详解:函数()133xxf x ⎛⎫=- ⎪⎝⎭的定义域为R ,且()()111333,333xxx xxx f x f x --⎡⎤⎛⎫⎛⎫⎛⎫-=-=-+=--=-⎢⎥ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦即函数()f x 是奇函数,又1y 3,3xxy ⎛⎫==- ⎪⎝⎭在R 都是单调递增函数,故函数()f x 在R 上是增函数.故选A.点睛:本题考查函数的奇偶性单调性,属基础题.4.设m,n 为非零向量,则“存在负数λ,使得λ=m n ”是“0<⋅m n ”的 A .充分而不必要条件 B .必要而不充分条件 C .充分必要条件 D .既不充分也不必要条件【答案】A 【解析】试题分析:若0λ∃<,使λ=m n ,则两向量,m n 反向,夹角是180︒,那么cos1800⋅=︒=-<m n m n m n ;若0m n ⋅<,那么两向量的夹角为(]90,180︒︒,并不一定反向,即不一定存在负数λ,使得λ=m n ,所以是充分而不必要条件,故选A.【名师点睛】判断充分必要条件的的方法:(1)根据定义,若,p q q p ⇒≠>,那么p 是q 的充分不必要条件,同时q 是p 的必要不充分条件;若p q ⇔,那么p ,q 互为充要条件;若,p q q p ≠>≠>,那么就是既不充分也不必要条件.(2)当命题是以集合形式给出时,那就看包含关系,已知2222222040/2/22300B A AB v v a m s m s S --===-⨯ :q x B ∈,若A B ≠⊂,那么p 是q 的充分不必要条件,同时q 是p 的必要不充分条件;若A B =,那么p ,q 互为充要条件;若没有包含关系,那么就是既不充分也不必要条件.(3)命题的等价性,根据互为逆否命题的两个命题等价,将p 是q 条件的判断,转化为q ⌝是p ⌝条件的判断.5.已知双曲线22221(0,0)x y a b a b-=>>的左焦点为F ,2.若经过F 和(0,4)P 两点的直线平行于双曲线的一条渐近线,则双曲线的方程为A .22144x y -=B .22188x y -=C .22148x y -=D .22184x y -=【答案】B 【解析】由题意得224,14,22188x y a b c a b c ==-⇒===-=- ,选B.【考点】 双曲线的标准方程【名师点睛】利用待定系数法求圆锥曲线方程是高考常见题型,求双曲线方程最基础的方法就是依据题目的条件列出关于,,a b c 的方程,解方程组求出,a b ,另外求双曲线方程要注意巧设双曲线(1)双曲线过两点可设为221(0)mx ny mn -=>,(2)与22221x y a b-=共渐近线的双曲线可设为2222(0)x y a bλλ-=≠,(3)等轴双曲线可设为22(0)x y λλ-=≠等,均为待定系数法求标准方程.6.设函数()2sin()f x x ωϕ=+,x ∈R ,其中0>ω,||ϕπ<.若5()28f π=,()08f 11π=,且()f x 的最小正周期大于2π,则A .23ω=,12πϕ=B .23ω=,12ϕ11π=-C .13ω=,24ϕ11π=-D .13ω=,724πϕ=【答案】A 【解析】由题意125282118k k ωππϕπωπϕπ⎧+=+⎪⎪⎨⎪+=⎪⎩,其中12,k k Z ∈,所以2142(2)33k k ω=--,又22T ππω=>,所以01ω<<,所以23ω=,11212k ϕ=π+π,由ϕπ<得12πϕ=,故选A .【考点】求三角函数的解析式【名师点睛】有关sin()y A x ωϕ=+问题,一种为提供函数图象求解析式或某参数的范围,一般先根据图象的最高点或最低点确定A ,再根据周期或12周期或14周期求出ω,最后再利用最高点或最低点坐标满足解析式,求出满足条件的ϕ值,另一种时根据题目用文字形容的函数图象特点,如对称轴或曲线经过的点的坐标,根据题意自己画出图象,再寻求待定的参变量,题型很活,求ω或ϕ的值或最值或范围等.7.已知奇函数()f x ,且()()g x xf x =在[0,)+∞上是增函数.若2(log 5.1)a g =-,0.8(2)b g =,(3)c g =,则a ,b ,c 的大小关系为A .a b c <<B .c b a <<C .b a c <<D .b c a <<【答案】C 【详解】因为()f x 是奇函数,从而()()g x xf x =是R 上的偶函数,且在[0,)+∞上是增函数,22(log 5.1)(log 5.1)a g g =-=,0.822<,又4 5.18<<,则22log 5.13<<,所以即0.8202log 5.13<<<,0.82(2)(log 5.1)(3)g g g <<,所以b a c <<,故选C . 【考点】指数、对数、函数的单调性 【名师点睛】比较大小是高考常见题,指数式、对数式的比较大小要结合指数函数、对数函数,借助指数函数和对数函数的图象,利用函数的单调性进行比较大小,特别是灵活利用函数的奇偶性和单调性数形结合不仅能比较大小,还可以解不等式.8.已知函数23,1,()2, 1.x x x f x x x x ⎧-+≤⎪=⎨+>⎪⎩设a R ∈,若关于x 的不等式()||2x f x a ≥+在R 上恒成立,则a 的取值范围是 A .47[,2]16-B .4739[,]1616-C.[- D.39[]16- 【答案】A【解析】不等式()2x f x a ≥+为()()2xf x a f x -≤+≤(*), 当1x ≤时,(*)式即为22332xx x a x x -+-≤+≤-+,2233322x x a x x -+-≤≤-+, 又22147473()241616x x x -+-=---≤-(14x =时取等号), 223339393()241616x x x -+=-+≥(34x =时取等号),所以47391616a -≤≤, 当1x >时,(*)式为222x x a x x x --≤+≤+,32222x x a x x --≤≤+, 又3232()2322x x x x --=-+≤-23x =,22222x x x x+≥⨯=(当2x =时取等号), 所以232a -≤≤, 综上47216a -≤≤.故选A . 【考点】不等式、恒成立问题 【名师点睛】首先满足()2x f x a ≥+转化为()()22x xf x a f x --≤≤-去解决,由于涉及分段函数问题要遵循分段处理原则,分别对x 的两种不同情况进行讨论,针对每种情况根据x 的范围,利用极端原理,求出对应的a 的范围.二、多选题9.如图,某池塘里浮萍的面积y (单位:2m )与时间t (单位:月)的关系为t y a =.关于下列说法正确的是( )A .浮萍面积每月的增长率为2;B .浮萍每月增加的面积都相等;C .第4个月时,浮萍面积就会超过280m ;D .若浮萍蔓延到22m 、24m 、28m 所经过的时间分别是1t 、2t 、3t ,则2132t t t =+. 【答案】ACD 【分析】将点()1,3的坐标代入函数ty a =的解析式,求出底数a 的值,然后利用指数函数的基本性质以及指数运算逐个分析各选项的正误,可得出结论. 【详解】将点()1,3的坐标代入函数t y a =的解析式,得13a =,函数的解析式为3ty =.对于A 选项,由13323n nn+-=可得浮萍每月的增长率为2,A 选项正确;对于B 选项,浮萍第1个月增加的面积为()12332m-=,第2个月增加的面积为()212336m -=,26≠,B 选项错误;对于C 选项,第4个月时,浮萍的面积为438180=>,C 选项正确; 对于D 选项,由题意可得132t =,234t =,338t =,2428=⨯,()2122333t t t ∴=⨯,即132233t t t +=,所以2132t t t =+,D 选项正确. 故选:ACD.10.已知向量(,3)a x =,(3,)b x =-,则下列叙述中,不正确是( ) A .存在实数x ,使a bB .存在实数x ,使()a b a +C .存在实数x ,m ,使()ma b a +D .存在实数x ,m ,使()ma b b +【答案】ABC 【分析】对选项逐一利用向量平行的坐标表示进行验证,由此确定正确选项. 【详解】由a b ,得29x =-,无实数解,故A 中叙述错误;(3,3)a b x x +=-+,由()a b a +∥,得3(3)(3)0x x x --+=,即29x =-,无实数解,故B 中叙述错误;(3,3)ma b mx m x +=-+,由()ma b a +∥,得(3)3(3)0m x x mx +--=,即29x =-,无实数解,故心中叙述错误;由()ma b b +∥,得3(3)(3)0m x x mx -+--=,即()290m x +=,所以0m =,x ∈R ,故D 中叙述正确. 故选:ABC【点睛】本小题主要考查两个向量平行的坐标表示,考查方程的思想,属于基础题.11.已知12,F F 分别是双曲线22:1C x y -=的左右焦点,点P 是双曲线上异于双曲线顶点的一点,且向量120PF PF ⋅=,则下列结论正确的是( ) A .双曲线C 的渐近线方程为y x =±B .以12F F 为直径的圆的方程为221x y +=C .1F 到双曲线的一条渐近线的距离为1D .12PF F ∆的面积为1【答案】ACD 【分析】求出双曲线C 渐近线方程,焦点12,F F ,12PF F ∆的面积即可判断. 【详解】A .代入双曲线渐近线方程得y x =±,正确.B .由题意得12(2,0),(2,0)F F -,则以12F F 为直径的圆的方程不是221x y +=,错误.C .1(2,0)F ,渐近线方程为y x =,距离为1,正确. D . 由题意得12(2,0),(2,0)F F -,设00(,)P x y ,根据120PF PF ⋅=,解得02x =±02y =± 12PF F ∆的面积为1.正确.故选:ACD. 【点睛】考查双曲线的渐近线方程,焦点,以及双曲线上的几何性质.题目涉及知识点较为广泛. 12.已知函数()32f x x ax x c =+-+(x ∈R ),则下列结论正确的是( ).A .函数()f x 一定存在极大值和极小值B .若函数()f x 在1()x -∞,、2()x ,+∞上是增函数,则21x x -≥ C .函数()f x 的图像是中心对称图形D .函数()f x 的图像在点00())(x f x ,(0x R ∈)处的切线与()f x 的图像必有两个不同的公共点 【答案】ABC 【分析】首先求函数的导数2()3210f x x ax =+-=',再根据极值点与导数的关系,判断AB 选项;证明()()2()333a a af x f x f -++--=-,判断选项C ;令0a c ==,求切线与()f x 的交点个数,判断D 选项.【详解】A 选项,2()3210f x x ax =+-='的24120a ∆=+>恒成立,故()0f x '=必有两个不等实根,不妨设为1x 、2x ,且12x x <,令()0f x '>,得1x x <或2x x >,令()0f x '<,得12x x x <<,∴函数()f x 在12()x x ,上单调递减,在1()x -∞,和2()x ,+∞上单调递增, ∴当1x x =时,函数()f x 取得极大值,当2x x =时,函数()f x 取得极小值,A 对, B 选项,令2()3210f x x ax =+-=',则1223ax x +=-,1213x x ⋅=-,易知12x x <,∴213x x -==≥,B对,C 选项,易知两极值点的中点坐标为(())33a a f --,,又23()(1)()333a a a f x x x f -+=-+++-,∴()()2()333a a af x f x f -++--=-, ∴函数()f x 的图像关于点(())33a af --,成中心对称,C 对,D 选项,令0a c ==得3()f x x x =-,()f x 在(0)0,处切线方程为y x =-, 且3y xy x x =-⎧⎨=-⎩有唯一实数解, 即()f x 在(0)0,处切线与()f x 图像有唯一公共点,D 错, 故选:ABC . 【点睛】方法点睛:解决函数极值、最值综合问题的策略:1、求极值、最值时,要求步骤规范,含参数时,要讨论参数的大小;2、求函数最值时,不可想当然地认为极值点就是最值点,要通过比较才能下结论;3、函数在给定闭区间上存在极值,一般要将极值与端点值进行比较才能确定最值.三、填空题13.已知实数,x y 满足0200x y x y y -≥⎧⎪+-≤⎨⎪≥⎩,则34z x y =-最小值为________.【答案】1- 【解析】由34z x y =-,得344zy x =-,作出不等式对应的可行域(阴影部分), 平移直线344z y x =-,由平移可知当直344zy x =-,经过点B (1,1)时,直线344zy x =-的截距最大,此时z 取得最小值, 将B 的坐标代入34341z x y =-=-=-, 即目标函数34z x y =-y 的最小值为−1. 故答案为−1.14.设等比数列{}n a 满足a 1 + a 2 = –1, a 1 – a 3 = –3,则a 4 = ___________. 【答案】-8 【解析】设等比数列{}n a 的公比为q ,很明显1q ≠-,结合等比数列的通项公式和题意可得方程组:()()12121311113a a a q a a a q ⎧+=+=-⎪⎨-=-=-⎪⎩,①,②,由②①可得:2q =-,代入①可得11a =, 由等比数列的通项公式可得3418a a q ==-.【名师点睛】等比数列基本量的求解是等比数列中的一类基本问题,解决这类问题的关键在于熟练掌握等比数列的有关公式并能灵活运用,尤其需要注意的是,在使用等比数列的前n 项和公式时,应该要分类讨论,有时还应善于运用整体代换思想简化运算过程.15.设函数10()20xx x f x x +≤⎧=⎨>⎩,,,,则满足1()()12f x f x +->的x 的取值范围是____________. 【答案】1(,)4-+∞ 【解析】由题意得: 当12x >时,12221x x -+>恒成立,即12x >;当102x <≤时,12112x x +-+> 恒成立,即102x <≤;当0x ≤时,1111124x x x ++-+>⇒>-,即014x -<≤.综上,x 的取值范围是1(,)4-+∞.【名师点睛】分段函数的考查方向注重对应性,即必须明确不同的自变量所对应的函数解析式是什么,然后代入该段的解析式求值.解决此类问题时,要注意区间端点是否取到及其所对应的函数值,尤其是分段函数结合点处的函数值.16.a ,b 为空间中两条互相垂直的直线,等腰直角三角形ABC 的直角边AC 所在直线原创精品资源学科网独家享有版权,侵权必究!与a ,b 都垂直,斜边AB 以直线AC 为旋转轴旋转,有下列结论:①当直线AB 与a 成60°角时,AB 与b 成30°角;②当直线AB 与a 成60°角时,AB 与b 成60°角;③直线AB 与a 所成角的最小值为45°;④直线AB 与a 所成角的最大值为60°.其中正确的是________.(填写所有正确结论的编号)【答案】②③【分析】由题意知,a 、b 、AC 三条直线两两相互垂直,构建如图所示的边长为1的正方体,|AC |=1,|AB |2=AB 以直线AC 为旋转轴,则A 点保持不变,B 点的运动轨迹是以C 为圆心,1为半径的圆,以C 坐标原点,以CD 为x 轴,CB 为y 轴,CA 为z 轴,建立空间直角坐标系,利用向量法能求出结果.【详解】解:由题意知,a 、b 、AC 三条直线两两相互垂直,画出图形如图,不妨设图中所示正方体边长为1,故|AC |=1,|AB |2=斜边AB 以直线AC 为旋转轴,则A 点保持不变,B 点的运动轨迹是以C 为圆心,1为半径的圆,以C 坐标原点,以CD 为x 轴,CB 为y 轴,CA 为z 轴,建立空间直角坐标系, 则D (1,0,0),A (0,0,1),直线a 的方向单位向量a =(0,1,0),|a |=1, 直线b 的方向单位向量b =(1,0,0),|b |=1,设B 点在运动过程中的坐标中的坐标B ′(cosθ,sinθ,0),其中θ为B ′C 与CD 的夹角,θ∈[0,2π),∴AB ′在运动过程中的向量,'AB =(cosθ,sinθ,﹣1),|'AB |2=设'AB 与a 所成夹角为α∈[0,2π], 则cosα()()10102'cos sin a AB θθ--⋅==⋅,,,,∈[0,22], ∴α∈[4π,2π],∴③正确,④错误. 设'AB 与b 所成夹角为β∈[0,2π],试卷第12页,总12页 cosβ()()'11002''AB bcos sin AB b b AB θθ⋅-⋅===⋅⋅,,,,|co sθ|, 当'AB 与a 夹角为60°时,即α3π=, |sinθ|22232cos cos πα===, ∵cos 2θ+sin 2θ=1,∴cosβ22=|cosθ|12=, ∵β∈[0,2π],∴β3π=,此时'AB 与b 的夹角为60°, ∴②正确,①错误.故答案为②③.【名师点睛】(1)平移直线法是求异面直线所成角的常用方法,其基本思路是通过平移直线,把异面问题化归为共面问题来解决,具体步骤如下:①平移:平移异面直线中的一条或两条,作出异面直线所成的角;②认定:证明作出的角就是所求异面直线所成的角;③计算:求该角的值,常利用解三角形;④取舍:由异面直线所成的角的取值范围是π0,2⎛⎤ ⎥⎝⎦,可知当求出的角为钝角时,应取它的补角作为两条异面直线所成的角.(2)求异面直线所成的角要特别注意异面直线之间所成角的范围.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
原创精品资源学科网独家享有版权,侵权必究!
专题11新高考数学小题提分限时训练10(原卷版)
一、单选题
1.设集合,,则( )
A .
B .
C .
D . 2.设
,其中x ,y 是实数,则i =x y + A .1 B .2 C .3 D .2 3.已知向量()()1,3,2a m b ==-,,且()a b b +⊥,则m =( )
A .−8
B .−6
C .6
D .8 4.圆的圆心到直线的距离为1,则( )
A .
B .
C .
D .2
5.已知直线a ,b 分别在两个不同的平面α,β内.则“直线a 和直线b 相交”是“平面α和平面β相交”的
(A )充分不必要条件 (B )必要不充分条件
(C )充要条件 (D )既不充分也不必要条件
6.函数f (x )=3sin x+cos x )3–sin x )的最小正周期是
(A )2π (B )π (C )2
3π (D )2π 7.已知函数f(x)的定义域为R.当x<0时,3()1f x x =- ;当11x -≤≤ 时,
()()f x f x -=-;当12x > 时,11()()22
f x f x +=- .则f(6)= (A )−2 (B )−1 (C )0 (D )2
8.若函数y=f(x)的图象上存在两点,使得函数的图象在这两点处的切线互相垂直,则称y=f(x)具有T 性质.下列函数中具有T 性质的是
(A )y=sin x (B )y=ln x (C )y=e x (D )y=x 3
二、多选题
试卷第2页,总3页
9.下列结论中正确的有( )
A .“x ∃∈R ,sin 10x +<”是真命题
B .“3log 2x <”是“29100x x --<”的充分不必要条件
C .命题“0x ∀>,231x x +>”的否定为“0x ∃>,231x x +≤”
D .“0x >”是“21x >”的必要不充分条件
10.某人退休前后各类支出情况如下,已知退休前工资收入为8000元月,退休后每月储蓄的金额比退休前每月储蓄的金额少1500元,则下面结论中正确的是( )
A .该教师退休前每月储蓄支出2400元
B .该教师退休后的旅行支出是退休前旅行支出的3倍
C .该教师退休工资收入为6000元月
D .该教师退休后的其他支出比退休前的其他支出少
11.已知变量,x y 之间的线性回归方程为ˆ0.710.3y
x =-+,且变量,x y 之间的一组相关数据如表所示,则下列说法正确的是( ) x 6 8
10 12 y 6 m
3 2
A .变量,x y 之间呈现负相关关系
B .4m =
C .可以预测,当11x =时,y 约为2.6
D .由表格数据知,该回归直线必过点()9,4
12.已知函数()||
sin 1x f x e x =⋅+,则( ) A .()f x 的周期为2π B .()f x 的图象关于点()0,1对称
原创精品资源学科网独家享有版权,侵权必究! C .()f x 在30,4π
⎡⎤⎢⎥⎣⎦
上为增函数 D .()f x 在区间[]5,5ππ-上所有的极值之和为10
三、填空题
13.已知a >b >1.若log a b+log b a=52
,a b =b a ,则a= ,b= . 14. 设数列{a n }的前n 项和为S n .若S 2=4,a n +1=2S n +1,n ∈N *,则a 1=________,S 5=________.
15.如图,在ABC 中,AB=BC=2,∠ABC=120°.若平面ABC 外的点P 和线段AC 上的点D ,满足PD=DA ,PB=BA ,则四面体PBCD 的体积的最大值是 .
16.已知向量a ,b ,|a | =1,|b |=2,若对任意单位向量e ,均有 |a·e |+|b·e |
≤6,则a·
b 的最大值是 .。
