逻辑推理常见关系
数学的逻辑关系

数学的逻辑关系数学作为一门学科,是研究数量、结构、变化以及空间等概念与符号之间的关系的科学。
而数学的逻辑关系则是指数学中所运用的逻辑思维和推理方式,用于描述和解释数学概念、定理和证明的关系。
一、基本逻辑关系在数学中,最基本的逻辑关系是命题之间的关系。
命题是可以判断真假的陈述句,在数学中通常用字母表示。
命题之间存在三种基本的逻辑关系:合取、析取和否定。
1.合取关系合取关系是指将两个命题连接起来形成一个新的命题。
用逻辑符号“∧”表示。
当且仅当两个命题同时为真时,合取关系才为真。
例如,命题p为“2是偶数”,命题q为“3是奇数”,则合取关系p∧q 表示“2是偶数且3是奇数”。
2.析取关系析取关系是指将两个命题连接起来形成一个新的命题。
用逻辑符号“∨”表示。
当至少有一个命题为真时,析取关系就为真。
例如,命题p为“2是偶数”,命题q为“3是奇数”,则析取关系p∨q 表示“2是偶数或3是奇数”。
3.否定关系否定关系是指将一个命题的真值取反,形成一个新的命题。
用逻辑符号“¬”表示。
例如,命题p为“2是偶数”,则否定关系¬p表示“2不是偶数”。
二、推理和证明中的逻辑关系数学中的推理和证明是建立在逻辑关系的基础上的。
推理是指从已知的命题出发,根据逻辑关系得出新的命题的过程。
而证明则是通过推理过程来验证或证实一个命题是否成立。
1.演绎推理演绎推理是基于已知命题和逻辑关系,通过一系列逻辑推理,得出结论的过程。
它包括三个部分:前提、推理规则和结论。
例如,已知命题p为“所有A都是B”,命题q为“a是A”,则根据演绎推理的规则,可以得出结论“a是B”。
2.归纳推理归纳推理是从具体事例中归结出一般结论的推理方式。
它通过整体的观察,找出事物之间的规律,从而得出结论。
例如,通过观察一系列自然数的奇偶性可发现,所有的偶数都能被2整除。
因此,可以归纳得出结论“所有偶数都能被2整除”。
3.直接证明直接证明是一种以已知命题为前提,通过逻辑推理得出结论的证明方法。
逻辑判断公式

逻辑判断公式大全一、有真有假型
解题思路:矛盾→包容→反对
1、矛盾关系
〔1〕矛盾关系必然是一真一假
〔2〕常见矛盾关系
2、包容关系
一真前假,一假后真
〔1〕若A→B,则A真B真,B假A假
①只有一真,一真前假
②只有一假,一假后真
〔2〕常见包容关系
①所有→某人→有的
②A且B→A〔B〕→A或B
3、反对关系
〔1〕两个"有的〞,必有一真
〔2〕两个"所有〞,必有一假
二、翻译推理型
1、全真判断型
〔1〕翻译:
〔2〕三段论:
A→B,B→C,退出A→C〔3〕判断:
〔4〕推理
2、全真推理型
〔1〕
〔2〕已知P→Q,则
①肯定P,也就是肯定Q
②否定Q,也就是否定P
③否定P和肯定Q,什么也推理不出来
〔3〕A且B→C 等价于A→〔B→C〕等价于A且B→C A→B 等价于–A或B
三、排列组合题型
题干充分用图表法→信息最大优先原则
选项充分用排除法→特殊信息优先原则
四、日常推理型
1、主体一致原则
2、无关概念排除原则
3、优选"可能〞论断→慎选宏观论断
4、因果关系看清
五、加强型
六、削弱型。
逻辑推理公式整理

逻辑推理公式整理逻辑推理是一种基于事实和前提的推导过程,通过推理规则和逻辑公式来得出新的结论。
在逻辑推理中,公式扮演着重要的角色,可以帮助我们理解和描述逻辑关系。
以下是一些常见的逻辑推理公式。
1.求取命题的否定:公式:¬P说明:这个公式表示命题P的否定,即P不成立。
2.条件推理:公式:P→Q说明:这个公式表示如果P成立,则Q也成立。
这是一种常见的逻辑推理形式。
3.充分必要条件:公式:P↔Q说明:这个公式表示P与Q是充分必要条件,即当P成立时Q成立,且当Q成立时P也成立。
4.假言推理:公式:P,Q/P→Q说明:这个公式表示如果同时有P和Q成立,则可以得出P推出Q。
5.排中律:公式:P∨¬P说明:这个公式表示一个命题P或它的否定¬P一定成立。
这是一种基本的逻辑定律。
6.矛盾律:公式:P∧¬P说明:这个公式表示一个命题P与它的否定¬P是矛盾的,不可能同时成立。
7.分配律:公式:P∧(Q∨R)≡(P∧Q)∨(P∧R)说明:这个公式表示逻辑中的分配律,可以帮助我们简化复杂命题的形式。
8.合取范式:公式:(P∨Q)∧(¬P∨Q)∨(P∨¬Q)∧(¬P∨¬Q)说明:这个公式表示合取范式,可以将命题写成一组合取式的多个命题的析取。
9.析取范式:公式:(P∧Q)∨(¬P∧Q)∨(P∧¬Q)∨(¬P∧¬Q)说明:这个公式表示析取范式,可以将命题写成一组析取式的多个命题的合取。
10.假言三段论:公式:P→Q,Q→R/P→R说明:这个公式表示如果P推出Q,且Q推出R,则可以得出P推出R。
这些是一些常见的逻辑推理公式,可以应用于不同的逻辑推理问题中。
逻辑公式的运用能够帮助我们进行准确有效的推理和论证,提高逻辑思维能力。
在实际应用中,还有更多的逻辑推理公式可以用于解决复杂的问题。
小学数学逻辑知识点总结

小学数学逻辑知识点总结一、逻辑运算在小学数学中,逻辑运算作为数学推理的基础,通过对命题的真假进行判断和推理,帮助我们解决问题。
常见的逻辑运算有与、或、非三种。
1. 与运算:当且仅当两个命题同时为真时,与运算的结果为真。
2. 或运算:当至少有一个命题为真时,或运算的结果为真。
3. 非运算:非运算是对一个命题的否定,即真变为假,假变为真。
二、数学逻辑关系在小学数学中,逻辑关系是指事物之间的联系和联系的规律。
常见的数学逻辑关系有包含关系、等价关系和推理关系。
1. 包含关系:包含关系是指一个集合包含另一个集合的关系。
比如,集合A包含在集合B中,可以表示为A ⊆ B。
2. 等价关系:等价关系是指在某种条件下,两个命题同时为真或同时为假。
比如,两个相等的数是等价的。
3. 推理关系:推理关系是指根据已知的条件,从而得出结论的过程。
常见的推理方式有归纳法和演绎法。
三、数学逻辑问题在小学数学中,逻辑问题是指需要通过逻辑思维进行分析和解决的问题。
常见的数学逻辑问题有“观察与推理”和“填空与推理”两类。
1. 观察与推理:这类问题通过观察一组数学图形、图表或者数列的规律,进行推理和分析,得出结果。
例如,给出一组数字,要求找出其中的规律并预测下一个数字是多少。
2. 填空与推理:这类问题通过给出部分信息,要求根据已知条件进行推理和填空,完成全面的解题过程。
例如,给出一个数学方程,要求求出元素的值。
四、运用逻辑知识解决数学问题的技巧1. 分析问题:当遇到一个数学问题时,首先要仔细分析问题的要求和条件,明确问题的目标。
2. 使用逻辑运算:根据问题的要求和条件,通过逻辑运算的方式进行推理和判断。
3. 观察和推理:对于观察与推理类的问题,可以通过观察和推理的方式来找出规律和解决问题。
4. 转化为数学表达式:对于填空与推理类的问题,要将问题所给的条件和要求转化为数学表达式,然后运用逻辑思维进行推导和计算。
5. 反复验证:在解决数学问题时,要反复验证结果,确保得到的答案符合问题的要求和条件。
命题之间的逻辑关系

命题之间的逻辑关系是指不同命题之间的相互关系,包括推理关系、对比关系、并列关系等。
这些关系是构成逻辑推理的基本要素,能够帮助我们更加准确地理解语言表达和进行合理的推理。
一、推理关系推理关系是指从一个或多个前提出发,根据某种逻辑规则得出结论的关系。
具体包括三种类型:假言推理、演绎推理和归纳推理。
1. 假言推理假言推理又称条件推理,是从条件命题中推出结论的推理方式。
其中条件命题由两个部分组成:前件和后件。
例如:“如果今天下雨,那么路上会很滑。
”在这个命题中,“今天下雨”就是前件,“路上会很滑”就是后件。
假言推理的形式如下:如果 A,则 BA因此,B例如:如果今天下雨,那么路上会很滑。
今天下雨。
因此,路上很滑。
2. 演绎推理演绎推理又称直接推理,是从普遍命题和特殊命题中推出结论的推理方式。
这种推理方式常被用于证明定理等数学科学领域。
演绎推理的形式如下:所有 A 都是 BC 是 A因此,C 是 B例如:所有狗都会叫。
小华的宠物狗也会叫。
因此,小华的宠物狗是狗。
3. 归纳推理归纳推理是从个别命题中推出普遍命题的推理方式。
这种推理方式常被用于实证科学领域。
归纳推理的形式如下:B 出现在 A 的许多实例中。
因此,B 是 A 的属性。
例如:我见过的所有猫都会爬树。
因此,猫是会爬树的动物。
二、对比关系对比关系是指不同命题之间相互对比、相互区别的关系。
具体包括两种类型:反义对比和比较对比。
1. 反义对比反义对比是通过命题之间的矛盾来表达相互对比的关系。
例如:“他是一个好人,而他是一个坏人。
”这个命题中,“好人”与“坏人”就是反义对比的两个概念。
2. 比较对比比较对比是通过对两个或多个命题进行比较来表达相互对比的关系。
例如:“这家餐馆的菜比那家餐馆的菜好吃。
”在这个命题中,“这家餐馆的菜”和“那家餐馆的菜”就是比较对比的两个概念。
三、并列关系并列关系是指具有同等重要性的命题之间的关系。
具体包括两种类型:交叉并列和并列递进。
行测逻辑推理题型

行测逻辑推理题型
在行测中,逻辑推理题型主要包括以下几种:
1. 强化型推理:根据提供的前提条件和规则,推断出结论。
例如:A是B的兄弟,而B是C的兄弟,那么A和C是兄弟关系。
2. 弱化型推理:根据提供的前提条件和规则,推断出不符合条件的结论。
例如:所有A都是B,但B没有C,因此A也不
会有C。
3. 假设型推理:根据提供的假设条件,推断出符合条件的结论。
例如:如果假设A是真的,那么B也必然是真的。
4. 排除型推理:根据提供的选项,通过排除法找出符合条件的结论。
例如:A、B、C、D四个选项中,只有A和C符合条件,那么可以得出结论选择A或C。
5. 综合推理:将多个前提条件和规则进行综合分析,得出最终的结论。
例如:A在早上7点到10点之间去超市购物,B在
早上8点到11点之间购物,那么A和B有可能在早上8点到10点之间碰面。
以上只是行测中比较常见的逻辑推理题型,具体的题目形式和难度还会根据不同考试的要求而有所变化。
在解答这类题型时,要注意理解题目的要求,运用逻辑思维和推理能力,进行推断和分析,选出最符合条件的选项。
十二个必须的逻辑关系

十二个必须的逻辑关系1. 因果关系,指一个事件或行为导致另一个事件或行为发生的关系。
例如,雨水导致道路湿滑。
2. 充分必要关系,指一个条件是发生某事的充分条件,同时也是必要条件。
例如,一个人是学生的充分必要条件是他/她在学校注册并且参加了课程。
3. 对立关系,指两个概念或事物之间的相互排斥或矛盾的关系。
例如,黑与白、好与坏。
4. 整体与部分关系,指整体和部分之间的关系。
例如,一辆汽车包括引擎、车轮、座位等部分。
5. 类比关系,指两个对象或概念之间的相似性关系。
例如,心脏对于人体就像引擎对于汽车。
6. 包容关系,指一个概念包含另一个概念的关系。
例如,动物包含狗、猫、鸟等。
7. 程度关系,指两个事物之间的程度上的关系。
例如,热与冷、大与小。
8. 条件关系,指某种情况下,某种结果会发生的关系。
例如,如果下雨,那么地面就会潮湿。
9. 比较关系,指两个事物之间的相对关系。
例如,A比B更大、更快。
10. 同一关系,指两个或多个概念指代同一对象的关系。
例如,太阳和日光是同一物体的不同表现。
11. 时间顺序关系,指事件发生的先后顺序关系。
例如,早晨起床→吃早饭→上班。
12. 递进关系,指事物发展或变化的逐步推进关系。
例如,学习越多,知识就会越丰富。
以上是十二个必须的逻辑关系,它们在日常生活和学术研究中都起着重要的作用。
希望这些解释能够帮助你理解逻辑关系的多样性和复杂性。
判断推理——逻辑判断
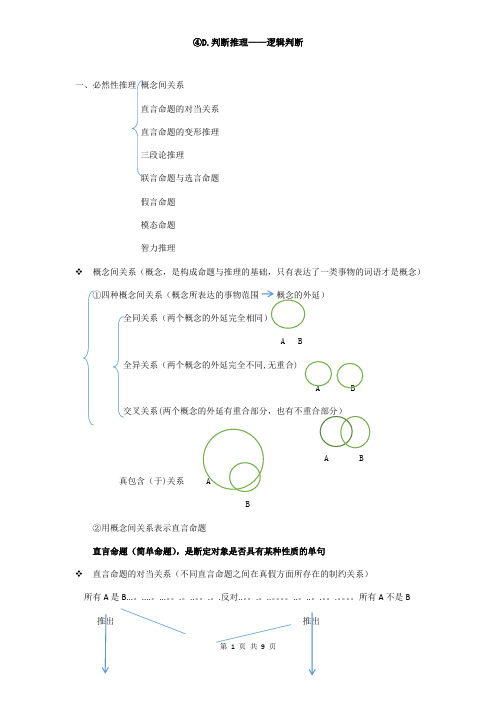
一、必然性推理概念间关系直言命题的对当关系直言命题的变形推理三段论推理联言命题与选言命题假言命题模态命题智力推理❖概念间关系(概念,是构成命题与推理的基础,只有表达了一类事物的词语才是概念)①四种概念间关系(概念所表达的事物范围概念的外延)全同关系(两个概念的外延完全相同)A B全异关系(两个概念的外延完全不同,无重合)A B交叉关系(两个概念的外延有重合部分,也有不重合部分)A B真包含(于)关系 AB②用概念间关系表示直言命题直言命题(简单命题),是断定对象是否具有某种性质的单句❖直言命题的对当关系(不同直言命题之间在真假方面所存在的制约关系)所有A是B...。
....。
...。
.。
..。
.。
.反对..。
.。
..。
..。
..。
.。
.。
所有A不是B 推出推出矛盾有的A是B..。
.。
..。
....。
..。
..。
下反对。
.....。
...。
.。
.。
.。
..。
有的A不是B“所有A是B"与“有的A不是B”、“.所有A不是B”与“有的A是B”必有一真一假“所有A是B”与“.所有A不是B”必有一假(可以同假)“有的A不是B”与“有的A是B”必有一真(可以同真)一个命题前面+“并非"=这个命题的矛盾命题所有与有的互换,有“不”的去掉,没“不"的加上❖直言命题的变形推理(通过改变前提中直言命题的联项或主项与谓项的关系结论)①换质推理(换一种说法)双重否定表示肯定将“不是”改为“是”或将“是”改为“不是”②换位推理(倒过来说)所有A是B 有些B是A所有A不是B 所有B不是A有些A是B 有些B是A有些A不是B特殊词量(少数,大部分,一半)作为量项引导命题,不能换位❖三段论推理(两个直言命题作为前提/一个直言命题作为结论)(两个前提包含三个概念/前提和结论中,每个概念都出现两次)两条常用规则一特得特:两个前提不能都是特称命题(含有“有的"命题)只有一个前提是特称,结论也是特称一否得否:两个前提不能都是否定命题只有一个前提是否定,结论也是否定❖联言命题与选言命题复言命题(有两个或多个单句通过联结词联结的命题)联言命题选言命题假言命题一、定义及真假关系①联言命题(多做做情况同时存在/P并且Q)联结词:表并列、递进、转折、顺承等关系(虽然…但是/既…又)②选言命题a。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
类比推理的题干和选项都由词语组成,着重考查考生对词语概念的理解和对事物关系的分析能力,因此了解词项间关系是十分必要的。
通过对多年考试题目的研究和总结,华图教育专家将类比推理词项间关系归纳为概念间关系、近反义关系、描述关系、条件关系和语法关系及常识问题。
我们将分三个专题对这部分知识进行深度剖析,帮助大家在最后冲刺阶段抓住重点针对备考。
本篇主要针对概念间关系、近反义关系进行深入解读。
一、概念间关系
概念间关系主要有全同关系、包含关系、交叉关系、并列关系和全异关系五种。
(一)全同关系
1.同一事物的全称、简称、别称、美称、谦称、敬称等。
如:鄙人:自己、美国:USA。
2.音译名与中文名、口语和书面语等。
如:麦克风:话筒、罗曼蒂克:浪漫。
例题1家父:父亲
A.老媪:老伴
B.鼻祖:祖宗
C.作者:自己
D.鄙人:自己
解析:家父是父亲的谦称,鄙人是自己的谦称。
老媪是老妇人的意思;鼻祖指创始人,与祖宗含义不同;作者指写作的人,而不是自己。
故答案选D。
(二)包含关系
1.种与属。
如:苹果:水果、杂志:期刊。
2.整体与部分。
如:阳光:紫外线、书包:背带。
例题2电脑:鼠标
A.水壶:茶杯
B.手机:短信
C.船:锚
D.录音机:磁带
解析:鼠标是电脑的一部分;锚是船的一部分。
且鼠标和锚都能起定位作用。
故答案选C。
词语所表示的集合之间存在交集,即有些A是B且有些A不是B。
如:体育明星:江苏人、大学生:愤青。
例题3影星:江西人
A.蔬菜:种植
B.专家:军人
C.鼓手:乐队
D.社会:自然
解析:题干中的词项是交叉关系:影星可能是江西人,也可能不是江西人。
专家可能是军人,也可能不是军人,故答案选B
(四)并列关系
1.同属于一类事物。
如:咖啡:绿茶、铅笔:钢笔。
2.具有相同属性或相同功能。
如:手机:电话、手表:闹钟。
例题4比喻:拟人
A.报纸:课本
B.冰箱:洗衣机
C.金丝猴:香蕉
D.月球:月亮
解析:比喻和拟人都属于修辞方法,冰箱和洗衣机都属于家用电器。
故答案选B。
(五)全异关系
所有A都不是B,且A和B之间并不是并列关系。
如:实数:木耳、蝙蝠:鸟类。
例题5伞:雨衣
A.现金:支票
B.空调:暖气
C.钢笔:铅笔
D.蚊香:蚊帐
解析:伞和雨衣都可以遮雨,伞还有遮阳的功能;空调和暖气都可以取暖,空调还有降温的功能。
故答案选B。
二、近反义关系
近反义关系包括近义或反义关系两种,并不局限于近义词或反义词。
1.同义词或近义词。
如:安居乐业:丰衣足食、谨慎:慎重。
2.其他具有相近含义或属性相近的词语。
如:鼓舞:煽动、微笑:大笑。
例题1休克:晕厥
A.同一:统一
B.口误:误口
C.分类:划分
D.再见:再会
解析:休克和晕厥是同义词;再会和再见是同义词。
故答案选D。
(二)反义关系:
1.反义词。
如:节约:浪费、早晨:傍晚。
2.其他具有相反含义或属性相反的词语。
如:粗心大意:细心、雨水:干旱。
例题2灯光:黑暗
A.财富:贫困
B.墨镜:光明
C.笤帚:卫生
D.小草:绿化
解析:灯光可以消除黑暗,财富可以消除贫困。
故答案选A。
