六年级奥数——蝴蝶模型 燕尾定理练习题 教案
六年级数学奥数培优教案(下册)图形问题之蝴蝶模型

蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径。
通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系。
类型 1:任意四边形中的蝴蝶模型① S 1 ⨯ S 3 = S 2 ⨯ S 4 (上、下两部分面积的积等于左、右两部分面积的积);② S 1 : S 4 = S 2 : S 3 = (S 1 + S 2 ): (S 4 + S 3 )= AO : OC (左:右 = 左和:右和)类型 2:梯形中的蝴蝶模型① S 2 = S 4 ;② S 1 ⨯ S 3 = S 2 ⨯ S 4 ;③OC AO s s s s s s s s :)(:)(::34213241=++==④)(::::::224231ab ab ab b a s s s s 上下平方,左右=⑤梯形 S 的对应份数为 (a + b )2【例1】如图,某公园的外轮廓是四边形 ABCD ,被对角线 AC 、BD 分成四个部分,△ AOB面积为 1 平方千米,△BOC 面积为 2 平方千米,△COD 的面积为 3 平方千米,公园由陆地面积是 6.92 平方千米和人工湖组成,求人工湖的面积是多少平方千米?【例2】如图,边长为 1 的正方形 ABCD 中,BE=2EC ,CF=FD ,求△AEG 的面积.【例3】梯形 ABCD 的对角线 AC 与 BD 交于点 O ,已知梯形上底为 2,且△ABO 的面积等于△BOC 面积的32 ,求△AOD 与△BOC 的面积之比. 专题:图形问题之蝴蝶模型【例4】正方形 ABCD 的面积是 120 平方厘米, BE =31AB , BF = 21BC ,四边形 BGHF 的面积是多少平方厘米?1、如图,四边形被两条对角线分成4个三角形,则△BGC 的面积为 ;AG:GC=2、如图,四边形ABCD 的对角线AC 与BD 交于点O 若△ABD的面积等于△BCD 的面积的31,且AO=2,DO=3,那么CO 的 长度是DO 的 倍。
小学奥数平面几何

所以
S△ ADN
1 3
S△
ABN
1 3
1 7
S△
ABC
1 21
S△
ABC
同理
S△BEQ
1 21 S△ABC
在∆ABC中,根据燕尾定理,S△ABP : S△ACP BF : CF 1: 2 S△ABP : S△CBP AI : CI 1: 2
所以 S△ABP
1 5 S△ABC
所以 S五边形DNPQE
A
A
CD E B
FG
CD E
F
G
B
【解析】连接AF,BD, 根据题意可知CF=5+7+15=27,DG=7+15+6;
所以,SBEF
15 27
SCBF
SBEC
12 27
SCBF
SAEG
21 28 SADG
SAED
7 28 SADG
于是:
21 28
SADG
15 27 SCBF
65
7
12
28 SADG 27 SCBF 38
A
B
CD
④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的 平行四边形);
⑤三角形面积等于与它等底等高的平行四边形面积的一半;
⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底 相等,面积比等于它们的高之比.
3
.
二、鸟头定理
两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形. 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比. 如图在∆ABC中,D,E分别AB,AC是上的点如图 ⑴(或D在BA的延长线上,E在
最新六年级奥数——蝴蝶模型-燕尾定理练习题-教案
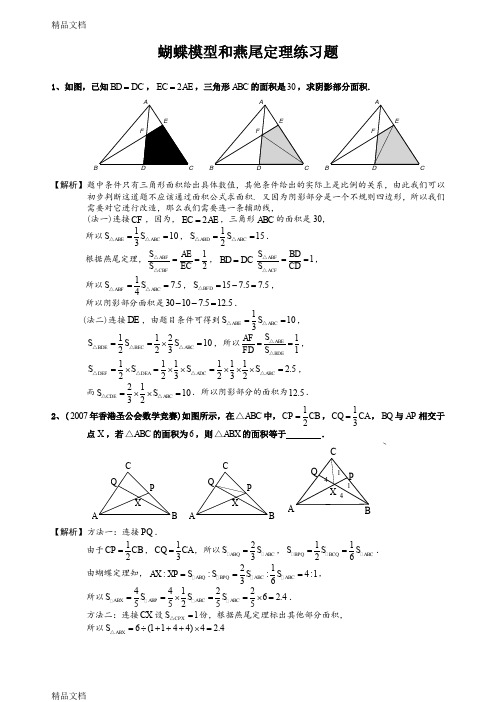
蝴蝶模型和燕尾定理练习题1、如图,已知BD DC =,2EC AE =,三角形ABC 的面积是30,求阴影部分面积.D EFC B AD EF C B AD EF CB A【解析】 题中条件只有三角形面积给出具体数值,其他条件给出的实际上是比例的关系,由此我们可以初步判断这道题不应该通过面积公式求面积. 又因为阴影部分是一个不规则四边形,所以我们需要对它进行改造,那么我们需要连一条辅助线,(法一)连接CF ,因为,2EC AE =,三角形ABC 的面积是30,所以1103ABE ABC S S ==△△,1152ABD ABC S S ==△△.根据燕尾定理,12ABF CBF S AE S EC ==△△,BD DC =1ABF ACF S BDS CD==△△,所以17.54ABF ABC S S ==△△,157.57.5BFD S =-=△,所以阴影部分面积是30107.512.5--=.(法二)连接DE ,由题目条件可得到1103ABE ABC S S ==△△,11210223BDE BEC ABC S S S ==⨯=△△△,所以11ABE BDE S AF FD S ==△△, 1111112.5223232DEF DEA ADC ABC S S S S =⨯=⨯⨯=⨯⨯⨯=△△△△,而211032CDE ABC S S =⨯⨯=△△.所以阴影部分的面积为12.5.2、(2007年香港圣公会数学竞赛)如图所示,在ABC △中,12CP CB =,13CQ CA =,BQ 与AP 相交于点X ,若ABC △的面积为6,则ABX △的面积等于 .XQPABC XQPAB C4411XQPCBA【解析】 方法一:连接PQ .由于12CP CB =,13CQ CA =,所以23ABQ ABC SS =,1126BPQ BCQABCS S S ==.由蝴蝶定理知,21:::4:136ABQ BPQ ABC ABC AX XP S S S S ===,所以441226 2.455255ABX ABP ABC ABC S S S S ==⨯==⨯=.方法二:连接CX 设1CPX S =△份,根据燕尾定理标出其他部分面积, 所以6(1144)4 2.4ABX S =÷+++⨯=△3、如图所示,在四边形ABCD 中,3AB BE =,3AD AF =,四边形AEOF 的面积是12,那么平行四边形BODC 的面积为________.OFEDCBA684621O F EDCBA【解析】 连接,AO BD ,根据燕尾定理::1:2ABO BDO S S AF FD ==△△,::2:1AOD BOD S S AE BE ==△△,设1BEO S =△,则其他图形面积,如图所标,所以221224BODC AEOF S S ==⨯=.4、ABCD 是边长为12厘米的正方形,E 、F 分别是AB 、BC 边的中点,AF 与CE 交于G ,则四边形AGCD 的面积是_________平方厘米.GFE DCBAGFE D CBA【解析】 连接AC 、GB ,设1A G C S =△份,根据燕尾定理得1AGB S =△份,1B G C S =△份,则11126S =++⨯=正方形()份,314ADCG S =+=份,所以22126496(cm )ADCG S =÷⨯=5、(2009年清华附中入学测试题)如图,四边形ABCD 是矩形,E 、F 分别是AB 、BC 上的点,且13AE AB =,14CF BC =,AF 与CE 相交于G ,若矩形ABCD 的面积为120,则AEG ∆与CGF ∆的面积之和为 .A BC DEFGH A BCDE FGA BCDEF G【解析】 (法1)如图,过F 做CE 的平行线交AB 于H ,则::1:3EH HB CF FB ==,所以122AE EB EH ==,::2AG GF AE EH ==,即2AG GF =,所以122311033942AEG ABF ABCD S S S ∆∆=⨯⨯=⨯⨯=.且22313342EG HF EC EC ==⨯=,故CG GE =,则1152CGF AEG S S ∆∆=⨯⨯=.所以两三角形面积之和为10515+=. (法2)如上右图,连接AC 、BG .根据燕尾定理,::3:1ABG ACG S S BF CF ∆∆==,::2:1BCG ACG S S BE AE ∆∆==,而1602ABC ABCD S S ∆==,所以3321ABG S ∆=++,160302ABC S ∆=⨯=,2321BCG S ∆=++,160203ABC S ∆=⨯=,则1103AEG ABG S S ∆∆==,154CFG BCG S S ∆∆==,所以两个三角形的面积之和为15.6、两条线段把三角形分为三个三角形和一个四边形,如图所示, 三个三角形的面积 分别是3,7,7,则阴影四边形的面积是多少?773773FEDCBAx+3x 773FED CBA【解析】 方法一:遇到没有标注字母的图形,我们第一步要做的就是给图形各点标注字母,方便后面的计算.再看这道题,出现两个面积相等且共底的三角形.设三角形为ABC ,BE 和CD 交于F ,则BF FE =,再连结DE . 所以三角形DEF 的面积为3.设三角形ADE 的面积为x ,则()():33:10:10x AD DB x +==+,所以15x =,四边形的面积为18.方法二:设ADF S x =△,根据燕尾定理::ABF BFC AFE EFC S S S S =△△△△,得到3AEF S x =+△,再根据向右下飞的燕子,有(37):7:3x x ++=,解得7.5x =四边形的面积为7.57.5318++=7、如下图,正方形 ABCD 的面积是a ,正三角形BPC 的面积是 b ,求阴影三角形BPD 的面积.【分析】 连接 AC 交 BD 于O 点,并连接PO .如图所示,可得P O / / DC ,所以三角形DPO 与三角形 CPO 面积相等(同底等高),所以有:8、已知四边形ABCD 和CEFG 都是正方形,且正方形ABCD 的边长为10厘米,那么图中阴影三角形BFD 的面积为多少平方厘米?【分析】 连接FC ,有FC 平行BD ,设BF 与DC 连接于O ,那么在梯形蝴蝶中有1===502DFO BCODCB ABCD S S S S S ∆∆∆=阴影9、如图,已知在平行四边形ABCD 中,AB=16,AD=10,BE=4,那么FC 的F GED CBA长度是多少?【分析】图中有一个沙漏,也有金字塔,但我们用沙漏就能解决问题,因为AB 平行于CD ,所以::4:16B F F C B E C D ===,所以410814FC =⨯=+. 10、四边形ABCD 和四边形CEFG 是两个正方形,BF 与CD 相交于H ,已知CH:DH=1:2, 6BCH S ∆=,求五边形ABEFD 的面积。
小学六年级奥数 五大模型——蝴蝶模型、燕尾模型
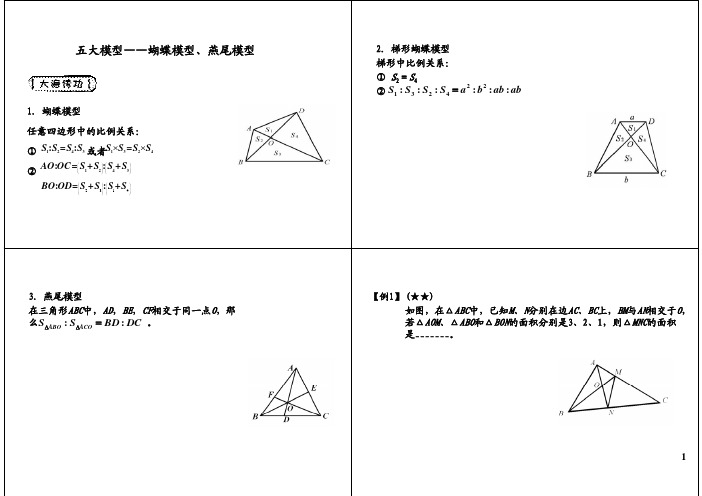
1
【例2】(★★★)
如图,长方形ABCD被CE、DF分成四块,已知其中3块的面积分别 为2、5、8平方厘米,那么余下的四边形OFBC的面积为 ___________平方厘米。
【例3】 (★★★)
如图,ABCD长方形中,阴影部分是直角三角形且面积为54,OD 的长是16,OB的长是9。那么四边形OECD的面积是多少?
五大模型——蝴蝶模型、燕尾模型
1.蝴蝶模型
任意四边形中的比例关系:
①
S :S =S :S
12
43
或者S1
S 3
=
S 2
S 4
② AO:OC = S +S : S +S
1
2
4
3
BO:OD= S +S : S +S
ቤተ መጻሕፍቲ ባይዱ
2
3
Aa D S1
S2 O S4
S3
B
C
b
二、本讲经典例题 例1,例4,例6,例7,例8
3.燕尾模型 在三角形ABC中,AD,BE,CF相交于同一点O,那么 SABO : SACO BD : DC 。
4
1
4
3.燕尾模型
在三角形ABC中,AD,BE,CF相交于同一点O,那 么SABO : SACO BD : DC 。
2.梯形蝴蝶模型 梯形中比例关系: ① S2=S4 ② S1 : S3 : S2 : S4 a2 : b2 : ab : ab
小学奥数几何六大模型及例题整理

SABO : SACO SOBD : SOCD SABD : SACD BD : CD
金字塔、沙漏模型 所谓的金字塔、沙漏模型,就是指形状相同,大小不同
的两个三角形,一切对应线段的长度成比例的模型,如图 所示:
勾股定理 我国最早发现在直角三角形中两条直角边的平方和等于
例题5 如图,已知三角形ABC面积为1,延长AB至D,使BD=AB, 延长BC至E,使CE=2BC,延长CA至F,使AF=3AC,求三 角形DEF的面积。
例题6 如图1,正六边形的面积为6,那么阴影部分的面积是多少?
例题7 如图1,△ABC中,BD=2DA,CE=2EB,AF=2FC,那么 △ABC的面积是阴影三角形面积的 倍。
例题8 正六边形 分别是正六边形各边的中点,那么图中阴影六边 形的面积是 平方厘米。
斜边的平方,把这一特性叫做勾股定理或勾股弦定理,外 国称为毕达哥拉斯定理。如右图 在直角三角形 ABC中有c2 a2 b2
例题1 (2008年第一届“陈省身杯”六年级2试) 如图,BC=45,AC=21,△ABC被分成9个面积相等的小三 角形,那么DI+FK为多少?
例题2 如图1,并排放有三个正方形,其中正方形GBEF的边长为 10厘米,连接GK,交EF于O,连接DE,交BG于Q,连接 DG,求阴影部分的面积。
等积变形
等积变形这里的积指的是面积,因为任何直线型图形都可分解成
若干个三角形,所以三角形是最基本图形,等积变形里主要研究的 是三角形面积变换。
三角形面积=底×高÷2 决定三角形面积的大小,取决于底和高这两个量。 等底等高:如果两个三角形等底等高,则这两个三角形面积相同 (如图1);(典型的夹在一组平行线间的,两个三角形若同底,则 面积相同) 同底看高:如果两个三角形等底,但高不等,则面积比等于高的 比(如图2); 同高看底:如果两个三角形等高,但底不等,则面积比等于底的 比(如图3)。
小学奥数几何篇五大模型蝴蝶定理(附答案)

小学奥数几何篇五大模型蝴蝶定理一、蝴蝶定理的定义与公式蝴蝶定理是小学奥数几何篇中的一个重要模型,它描述了在等腰三角形中,一条平行于底边的线段将底边平分,并且这条线段与等腰三角形的两腰相交于同一点时,该线段的中点与等腰三角形的顶点、底边的中点以及两腰上的交点形成一个等腰三角形。
蝴蝶定理的公式如下:设等腰三角形ABC中,AB=AC,底边BC的长度为2a,点D在BC上,且BD=DC=a,点E在AB上,点F在AC上,DE平行于BC,交AB于点E,交AC于点F,点G为DE的中点,连接AG、BG、CG,则AG=BG=CG。
二、蝴蝶定理的应用1. 在等腰三角形中求边长:通过蝴蝶定理,可以快速求出等腰三角形中未知边的长度。
例如,已知等腰三角形ABC中,AB=AC,底边BC 的长度为2a,点D在BC上,且BD=DC=a,点E在AB上,点F在AC上,DE平行于BC,交AB于点E,交AC于点F,点G为DE的中点,连接AG、BG、CG,求AG的长度。
解答:根据蝴蝶定理,AG=BG=CG,又因为AB=AC,所以AG=AB/2=a。
2. 在等腰三角形中求角度:通过蝴蝶定理,可以求出等腰三角形中未知角的度数。
例如,已知等腰三角形ABC中,AB=AC,底边BC的长度为2a,点D在BC上,且BD=DC=a,点E在AB上,点F在AC上,DE平行于BC,交AB于点E,交AC于点F,点G为DE的中点,连接AG、BG、CG,求∠AGB的度数。
解答:由于AG=BG=CG,所以△AGB是等边三角形,∠AGB=60°。
3. 在等腰三角形中求面积:通过蝴蝶定理,可以求出等腰三角形中未知部分的面积。
例如,已知等腰三角形ABC中,AB=AC,底边BC的长度为2a,点D在BC上,且BD=DC=a,点E在AB上,点F在AC上,DE平行于BC,交AB于点E,交AC于点F,点G为DE的中点,连接AG、BG、CG,求△AGB的面积。
解答:由于△AGB是等边三角形,所以△AGB的面积=(a^2 √3)/ 4。
小学奥数之燕尾定理(完整版)
小学奥数之燕尾定理燕尾定理:在三角形ABC 中,AD ,BE ,CF 相交于同一点O ,那么::ABO ACO S S BD DC ∆∆=.上述定理给出了一个新的转化面积比与线段比的手段,因为ABO ∆和ACO ∆的形状很象燕子的尾巴,所以这个定理被称为燕尾定理.该定理在许多几何题目中都有着广泛的运用,它的特殊性在于,它可以存在于任何一个三角形之中,为三角形中的三角形面积对应底边之间提供互相联系的途径.通过一道例题证明一下燕尾定理:如右图,D 是BC 上任意一点,请你说明:1423:::S S S S BD DC ==【解析】 三角形BED 与三角形CED 同高,分别以BD 、DC 为底,所以有14::S S BD DC =;三角形ABE 与三角形EBD 同高,12::S S ED EA =;三角形ACE 与三角形CED 同高,43::S S ED EA =,所以1423::S S S S =;综上可得1423:::S S S S BD DC ==.【例 1】 如右图,三角形ABC 中,:4:9BD DC =,:4:3CE EA =,求:AF FB .【考点】燕尾定理 【难度】3星 【题型】解答 【解析】 根据燕尾定理得::4:912:27AOB AOC S S BD CD ===△△::3:412:16AOB BOC S S AE CE ===△△(都有AOB △的面积要统一,所以找最小公倍数) 所以:27:16:AOC BOC S S AF FB ==△△【点评】本题关键是把AOB △的面积统一,这种找最小公倍数的方法,在我们用比例解题中屡见不鲜,如果能掌握它的转化本质,我们就能达到解奥数题四两拨千斤的巨大力量!OFE DCBAS 3S 1S 4S 2EDCBA O F EDCBA燕尾定理例题精讲【答案】27:16【巩固】如右图,三角形ABC 中,:3:4BD DC =,:5:6AE CE =,求:AF FB .【考点】燕尾定理 【难度】3星 【题型】解答 【解析】 根据燕尾定理得::3:415:20AOB AOC S S BD CD ===△△ ::5:615:18AOB BOC S S AE CE ===△△(都有AOB △的面积要统一,所以找最小公倍数) 所以:20:1810:9:AOC BOC S S AF FB ===△△【答案】10:9【巩固】如图,:2:3BD DC =,:5:3AE CE =,则:AF BF =【考点】燕尾定理 【难度】3星 【题型】填空 【解析】 根据燕尾定理有:2:310:15ABG ACG S S ==△△,:5:310:6ABG BCG S S ==△△,所以:15:65:2:ACG BCG S S AF BF ===△△ 【答案】5:2【巩固】如右图,三角形ABC 中,:2:3BD DC =,:5:4EA CE =,求:AF FB .【考点】燕尾定理 【难度】3星 【题型】解答 【解析】 根据燕尾定理得::2:310:15AOB AOC S S BD CD ===△△::5:410:8AOB BOC S S AE CE ===△△(都有AOB △的面积要统一,所以找最小公倍数) 所以:15:8:AOC BOC S S AF FB ==△△【点评】本题关键是把AOB △的面积统一,这种找最小公倍数的方法,在我们用比例解题中屡见不鲜,如果能掌握它的转化本质,我们就能达到解奥数题四两拨千斤的巨大力量!【答案】15:8【例 2】 如图,三角形ABC 被分成6个三角形,已知其中4个三角形的面积,问三角形ABC 的面积是多少?O F EDCBAGF EDCBAO F EDCBA【考点】燕尾定理 【难度】3星 【题型】解答 【解析】 设BOF S x =△,由题意知:4:3BD DC =根据燕尾定理,得::4:3ABO ACO BDO CDO S S S S ==△△△△,所以33(84)6344ACO S x x =⨯+=+△,再根据::ABO BCO AOE COE S S S S =△△△△,列方程3(84):(4030)(6335):354x x ++=+-解得56x =:35(5684):(4030)AOE S =++△,所以70AOE S =△所以三角形ABC 的面积是844030355670315+++++=【答案】315【例 3】 如图,三角形ABC 的面积是1,E 是AC 的中点,点D 在BC 上,且:1:2BD DC =,AD 与BE交于点F .则四边形DFEC 的面积等于 .【考点】燕尾定理 【难度】3星 【题型】填空【关键词】希望杯,五年级,初赛 【解析】 方法一:连接CF ,根据燕尾定理,12ABF ACF S BD S DC ==△△,1ABF CBF S AES EC==△△,设1BDF S =△份,则2DCF S =△份,3ABF S =△份,3AEF EFC S S ==△△份,如图所标所以551212DCEF ABC S S ==△方法二:连接DE ,由题目条件可得到1133ABD ABC S S ==△△,11212233ADE ADC ABC S S S ==⨯=△△△,所以11ABD ADES BF FE S ==△△, 111111122323212DEF DEB BEC ABC S S S S =⨯=⨯⨯=⨯⨯⨯=△△△△,而211323CDE ABC S S =⨯⨯=△△.所以则四边形DFEC 的面积等于512.【答案】512【巩固】如图,已知BD DC =,2EC AE =,三角形ABC 的面积是30,求阴影部分面积.35304084O FED CBAFED CBA33321F E DC BAABCDEF【考点】燕尾定理 【难度】3星 【题型】解答 【解析】 题中条件只有三角形面积给出具体数值,其他条件给出的实际上是比例的关系,由此我们可以初步判断这道题不应该通过面积公式求面积. 又因为阴影部分是一个不规则四边形,所以我们需要对它进行改造,那么我们需要连一条辅助线,(法一)连接CF ,因为BD DC =,2EC AE =,三角形ABC 的面积是30,所以1103ABE ABC S S ==△△,1152ABD ABC S S ==△△.根据燕尾定理,12ABF CBF S AE S EC ==△△,1ABF ACF S BDS CD==△△,所以17.54ABF ABC S S ==△△,157.57.5BFD S =-=△,所以阴影部分面积是30107.512.5--=.(法二)连接DE ,由题目条件可得到1103ABE ABC S S ==△△,11210223BDE BEC ABC S S S ==⨯=△△△,所以11ABE BDES AF FD S ==△△, 1111112.5223232DEF DEA ADC ABC S S S S =⨯=⨯⨯=⨯⨯⨯=△△△△,而211032CDE ABC S S =⨯⨯=△△.所以阴影部分的面积为12.5.【答案】12.5【巩固】如图,三角形ABC 的面积是2200cm ,E 在AC 上,点D 在BC 上,且:3:5AE EC =,:2:3BD DC =,AD 与BE 交于点F .则四边形DFEC 的面积等于 .【考点】燕尾定理 【难度】3星 【题型】填空 【解析】 连接CF ,根据燕尾定理,2639ABF ACF S BD S DC ===△△,36510ABF CBF S AE S EC ===△△,设6ABF S =△份,则9ACF S =△份,10BCF S =△份,5459358EFC S =⨯=+△份,310623CDF S =⨯=+△份,所以24545200(6910)(6)8(6)93(cm )88DCFE S =÷++⨯+=⨯+= 【答案】93【巩固】如图,已知3BD DC =,2EC AE =,BE 与CD 相交于点O ,则ABC △被分成的4部分面积各占ABC △ 面积的几分之几?FED CBAABC DEF FEDCBA【考点】燕尾定理 【难度】3星 【题型】解答 【解析】 连接CO ,设1AEO S =△份,则其他部分的面积如图所示,所以1291830ABC S =+++=△份,所以四部分按从小到大各占ABC △面积的12 4.5139313.59,,,30306030103020+===【答案】920【巩固】如图所示,在ABC △中,12CP CB =,13CQ CA =,BQ 与AP 相交于点X ,若ABC △的面积为6,则ABX △的面积等于 .【考点】燕尾定理 【难度】3星 【题型】填空 【关键词】香港圣公会数学竞赛 【解析】 方法一:连接PQ .由于12CP CB =,13CQ CA =,所以23ABQ ABC S S =,1126BPQ BCQ ABCS S S==.由蝴蝶定理知,21:::4:136ABQ BPQ ABC ABC AX XP S S S S ===,所以441226 2.455255ABX ABP ABC ABC S S S S ==⨯==⨯=.方法二:连接CX 设1CPX S =△份,根据燕尾定理标出其他部分面积,所以6(1144)4 2.4ABX S =÷+++⨯=△【答案】2.4【巩固】 两条线段把三角形分为三个三角形和一个四边形,如图所示, 三个三角形的面积 分别是3,7,7,则阴影四边形的面积是多少?【考点】燕尾定理 【难度】3星 【题型】解答 【解析】 方法一:遇到没有标注字母的图形,我们第一步要做的就是给图形各点标注字母,方便后面的计算.再看这道题,出现两个面积相等且共底的三角形.OE DCBA 13.54.59211213O E D CBA XQPABC XQPABC4411XQPCBA设三角形为ABC ,BE 和CD 交于F ,则BF FE =,再连结DE . 所以三角形DEF 的面积为3.设三角形ADE 的面积为x ,则()():33:10:10x AD DB x +==+,所以15x =,四边形的面积为18.方法二:设ADF S x =△,根据燕尾定理::ABF BFC AFE EFC S S S S =△△△△,得到3AEF S x =+△,再根据向右下飞的燕子,有(37):7:3x x ++=,解得7.5x =四边形的面积为7.57.5318++=【答案】18【巩固】如图,三角形ABC 的面积是1,2BD DC =,2CE AE =,AD 与BE 相交于点F ,请写出这4部分的面积各是多少?【考点】燕尾定理 【难度】3星 【题型】解答【解析】 连接CF ,设1AEF S =△份,则其他几部分面积可以有燕尾定理标出如图所示,所以121AEF S =△,62217ABF S ==△,821BDF S =△,242217FDCE S +== 【答案】27【巩固】如图,E 在AC 上,D 在BC 上,且:2:3AE EC =,:1:2BD DC =,AD 与BE 交于点F .四边形DFEC 的面积等于222cm ,则三角形ABC 的面积 .【考点】燕尾定理 【难度】3星 【题型】填空【解析】 连接CF ,根据燕尾定理,12ABF ACF S BD S DC ==△△,23ABF CBF S AE S EC ==△△,设1BDF S =△份,则2DCF S =△份,2ABF S =△份,4AFC S =△份,24 1.623AEF S =⨯=+△ 份,34 2.423EFC S =⨯=+△份,如图所标,所以2 2.4 4.4EFDC S =+=份,2349ABC S =++=△份 所以222 4.4945(cm )ABCS =÷⨯=△【答案】45【巩固】三角形ABC 中,C 是直角,已知2AC =,2CD =,3CB =,AM BM =,那么三角形AMN (阴影部分)的面积为多少?ABCDE F48621ABCDEFA BCDE FA BCDEF 2.41.62A BC DE F 12【考点】燕尾定理 【难度】3星 【题型】解答 【解析】 连接BN .ABC △的面积为3223⨯÷=根据燕尾定理,::2:1ACN ABN CD BD ==△△; 同理::1:1CBN CAN BM AM ==△△设AMN △面积为1份,则MNB △的面积也是1份,所以ANB △的面积是112+=份,而ACN △的面积就是224⨯=份,CBN △也是4份,这样ABC △的面积为441110+++=份,所以AMN △的面积为31010.3÷⨯=.【答案】0.3【例 4】 如图所示,在ABC △中,:3:1BE EC =,D 是AE 的中点,那么:AF FC = .【考点】燕尾定理 【难度】3星 【题型】填空 【解析】 连接CD .由于:1:1ABD BED S S =△△,:3:4BED BCD S S =△△,所以:3:4ABD BCD S S =△△, 根据燕尾定理,::3:4ABD BCD AF FC S S ==△△.【答案】3:4【巩固】在ABC ∆中,:3:2BD DC =, :3:1AE EC =,求:OB OE =?【考点】燕尾定理 【难度】3星 【题型】解答 【解析】 连接OC .因为:3:2BD DC =,根据燕尾定理,::3:2AOB AOC S S BD BC ∆∆==,即32AOB AOC S S ∆∆=; 又:3:1AE EC =,所以43AOC AOE S S ∆∆=.则3342223AOB AOC AOE AOE S S S S ∆∆∆∆==⨯=, 所以::2:1AOB AOEOB OE S S ∆∆==.【答案】2:1【巩固】在ABC ∆中,:2:1BD DC =, :1:3AE EC =,求:OB OE =?FE D C B AFE DCB AA BCDE OABCDE O【考点】燕尾定理 【难度】3星 【题型】解答 【解析】 题目求的是边的比值,一般来说可以通过分别求出每条边的值再作比值,也可以通过三角形的面积比来做桥梁,但题目没告诉我们边的长度,所以应该通过面积比而得到边长的比.本题的图形一看就联想到燕尾定理,但两个燕尾似乎少了一个,因此应该补全,所以第一步要连接OC . 连接OC .因为:2:1BD DC =,根据燕尾定理,::2:1AOB AOC S S BD BC ∆∆==,即2AOB AOC S S ∆∆=;又:1:3AE EC =,所以4AOC AOE S S ∆∆=.则2248AOB AOC AOE AOE S S S S ∆∆∆∆==⨯=, 所以::8:1AOB AOE OB OE S S ∆∆==.【答案】8:1【例 5】 如图9,三角形BAC 的面积是1,E 是AC 的中点,点D 在BC 上,且BD:DC=1:2,AD 与BE交于点F ,则四边形DEFC 的面积等于 。
小学奥数几何六大模型及例题
可以简记为 左边:右边=左和:右和
梯形中蝴蝶模型 梯形 的对应份数为 可以简记为: 上下平方,左右相乘。
燕尾模型 从三角形一个顶点向对边上任意一点的画线段,在线段 上任取一点组成的图形面积也会有如下关系:
Hale Waihona Puke 例题1 (2008年第一届“陈省身杯”六年级2试) 如图,BC=45,AC=21,△ABC被分成9个面积相等的小三 角形,那么DI+FK为多少?
例题2 如图1,并排放有三个正方形,其中正方形GBEF的边长为 10厘米,连接GK,交EF于O,连接DE,交BG于Q,连接 DG,求阴影部分的面积。
例题3 如图1,梯形ABCD,下底BC上有一点E,梯形空白处的面 积比阴影△ADE得到面积多200平方厘米,又知梯形下底 BC比上底AD长20厘米。求这个梯形的高是多少?
等积变形
等积变形这里的积指的是面积,因为任何直线型图形都可分解成 若干个三角形,所以三角形是最基本图形,等积变形里主要研究的 是三角形面积变换。 三角形面积=底×高÷2 决定三角形面积的大小,取决于底和高这两个量。 等底等高:如果两个三角形等底等高,则这两个三角形面积相同 (如图1);(典型的夹在一组平行线间的,两个三角形若同底,则 面积相同) 同底看高:如果两个三角形等底,但高不等,则面积比等于高的 比(如图2); 同高看底:如果两个三角形等高,但底不等,则面积比等于底的 比(如图3)。
例题7 如图1,△ABC中,BD=2DA,CE=2EB,AF=2FC,那么 △ABC的面积是阴影三角形面积的 倍。
例题8 正六边形 分别是正六边形各边的中点,那么图中阴影六边 形的面积是 平方厘米。
蝴蝶定理与燕尾定理(纯奥数类)
两条线段把三角形分为三个三角形和一个四边形,如图所示,三个三角形的面积分别是3,7,7,则阴影四边形的面积是多少?
【例3】★★★(06年西城某名校试验班选拔真题)
如图,已知长方形ADEF的面积是16,三角形ADB的面积是3,三角形ACF的面积是4,那么三角形ABC的面积是____.
【例2】★★★如图,有四个长方形的面积分别是1平方厘米、2平方厘米、
3平方厘米和4平方厘米,组合成一个大的长方形,求图中阴影部分的面积。
模型三:燕尾定理
S△AGB:S△AGC=S△BGE:S△CGE=BE:EC;
S△BGA:S△BGC=S△AGF:S△CGF=AF:FC;
S△CGA:S△CGB=S△AGD:S△BGD=AD:DB;
S1-S2=7平方厘米,线段AB是圆的直径,AB=20cm,求BC长?
课后练习:
考点及考试要求
求面积的比例,求面积的大小
教学内容:
模型一:同一三角形中,相应面积与底的正比关系:
即:两个三角形高相等,面积之比等于对应底边之比。
模型一的拓展:等分点结论(“鸟头定理”)
如图,三角形AED占三角形ABC面积的 × =
1.(北京市第八届“迎春杯”数学竞赛决赛第一题第4题)
如右图BE= BC,CD= AC,那么三角形AED的面积是三角形ABC面积的______.
模型二:任意四边形中的比例关系(“蝴蝶定理”)
①S1︰S2=S4︰S3或者S1×S3=S2×S4
②AO︰OC=(S1+S2)︰(S4+S3)
【例1】★★★
任意四边形ABCD各边都延长一倍,如果四边形ABCD的面积为1,求新四边形的面积?
小学奥数必学几何五大模型及例题解析
小学奥数必学几何五大模型及例题解析一、等积变换模型——很重要,小学常考⑴等底等高的两个三角形面积相等;⑵两个三角形高相等,面积比等于它们的底之比;两个三角形底相等,面积比等于它们的高之比。
如下图右图12::S S a b =⑶夹在一组平行线之间的等积变形,如下图ACDBCD S S =△△;反之,如果ACDBCD S S =△△,则可知直线AB 平行于CD 。
⑷正方形的面积等于对角线长度平方的一半;⑸三角形面积等于与它等底等高的平行四边形面积的一半;经典例题:1S 2S 解析:连接CE ,如图。
AE=3AB,所以S △AEC =3S △ABC=3 所以 S △BCE =2又因为:BD=2BC,所以S △BDE =2 S △BCE =4点评:此题就是三角形等积变换模型的直接应用二、鸟头定理(共角定理)模型两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形。
共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比。
如图,在ABC △中,,D E 分别是,AB AC 上的点(如图1)或D 在BA 的延长线上,E 在AC 上(如图2),则:():()ABC ADE S S AB AC AD AE =⨯⨯△△图1 图2此模型的结论可以用将来初中学到的正弦定理进行证明!因为S △ABC =AB ×ACsinA ,S △ADE =AD ×AEsinA所以:S △ABC :S △ADE= (AB ×ACsinA ):(AD ×AEsinA )=(AB ×AC ):(AD ×AE )经典例题:S △ADF :S △ABC=(AD ×AF ):(AB ×AC )=(2BD ×AF ):(3BD ×4AF )=1:6 S △BDE :S △ABC=(BD ×BE ):(AB ×BC )=(BD ×BE ):(3BD ×2BE )=1:6 S △CEF :S △ABC=(CE ×CF ):(CB ×CA )=(CE ×3AF ):(2CE ×4AF )=3:8 1-1/6-1/6-3/8=7/24 S △ABC =7÷7/24=24(平方厘米).点评:本题直接用到鸟头模型,先分别求出三个角上的三个三角形占S △ABC 的比例,再求出S △DEF 占S △ABC 的比例,就能直接求出S △ABC 的面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
蝴蝶模型和燕尾定理练习题1、如图,已知BD DC =,2EC AE =,三角形ABC 的面积是30,求阴影部分面积.BB【解析】 题中条件只有三角形面积给出具体数值,其他条件给出的实际上是比例的关系,由此我们可以初步判断这道题不应该通过面积公式求面积. 又因为阴影部分是一个不规则四边形,所以我们需要对它进行改造,那么我们需要连一条辅助线,(法一)连接CF ,因为,2EC AE =,三角形ABC 的面积是30,所以1103ABE ABC S S ==△△,1152ABD ABC S S ==△△.根据燕尾定理,12ABF CBF S AE S EC ==△△,BD DC =1ABF ACF S BDS CD==△△,所以17.54ABF ABC S S ==△△,157.57.5BFD S =-=△,所以阴影部分面积是30107.512.5--=.(法二)连接DE ,由题目条件可得到1103ABE ABC S S ==△△,11210223BDE BEC ABC S S S ==⨯=△△△,所以11ABE BDE S AF FD S ==△△, 1111112.5223232DEF DEA ADC ABC S S S S =⨯=⨯⨯=⨯⨯⨯=△△△△,而211032CDE ABC S S =⨯⨯=△△.所以阴影部分的面积为12.5.2、(2007年香港圣公会数学竞赛)如图所示,在ABC △中,12CP CB =,13CQ CA =,BQ 与AP 相交于点X ,若ABC △的面积为6,则ABX △的面积等于 .XQPABC XQPAB C4411XQPCBA【解析】 方法一:连接PQ .由于12CP CB =,13CQ CA =,所以23ABQ ABC SS =,1126BPQ BCQABCS S S ==.由蝴蝶定理知,21:::4:136ABQ BPQ ABC ABC AX XP S S S S ===,所以441226 2.455255ABX ABP ABC ABC S S S S ==⨯==⨯=.方法二:连接CX 设1CPX S =△份,根据燕尾定理标出其他部分面积, 所以6(1144)4 2.4ABX S =÷+++⨯=△3、如图所示,在四边形ABCD 中,3AB BE =,3AD AF =,四边形AEOF 的面积是12,那么平行四边形BODC 的面积为________.OFEDCBA684621O F EDCBA【解析】 连接,AO BD ,根据燕尾定理::1:2ABO BDO S S AF FD ==△△,::2:1AOD BOD S S AE BE ==△△,设1BEO S =△,则其他图形面积,如图所标,所以221224BODC AEOF S S ==⨯=.4、ABCD 是边长为12厘米的正方形,E 、F 分别是AB 、BC 边的中点,AF 与CE 交于G ,则四边形AGCD 的面积是_________平方厘米.GFE DCBAGFED CBA【解析】 连接AC 、GB ,设1AGCS =△份,根据燕尾定理得1AGB S =△份,1BGC S =△份,则11126S =++⨯=正方形()份,314ADCG S =+=份,所以22126496(cm )ADCG S =÷⨯=5、(2009年清华附中入学测试题)如图,四边形ABCD 是矩形,E 、F 分别是AB 、BC 上的点,且13AE AB =,14CF BC =,AF 与CE 相交于G ,若矩形ABCD 的面积为120,则AEG ∆与CGF ∆的面积之和为 .EEE【解析】 (法1)如图,过F 做CE 的平行线交AB 于H ,则::1:3EH HB CF FB ==,所以122AE EB EH ==,::2AG GF AE EH ==,即2AG GF =,所以122311033942AEG ABF ABCD S S S ∆∆=⨯⨯=⨯⨯=.且22313342EG HF EC EC ==⨯=,故CG GE =,则1152CGF AEG S S ∆∆=⨯⨯=.所以两三角形面积之和为10515+=. (法2)如上右图,连接AC 、BG .根据燕尾定理,::3:1ABG ACG S S BF CF ∆∆==,::2:1BCG ACG S S BE AE ∆∆==,而1602ABC ABCD S S ∆==,所以3321ABG S ∆=++,160302ABC S ∆=⨯=,2321BCG S ∆=++,160203ABC S ∆=⨯=,则1103AEG ABG S S ∆∆==,154CFG BCG S S ∆∆==,所以两个三角形的面积之和为15.6、两条线段把三角形分为三个三角形和一个四边形,如图所示, 三个三角形的面积 分别是3,7,7,则阴影四边形的面积是多少?773773FEDCBAx+3x773FED CBA【解析】 方法一:遇到没有标注字母的图形,我们第一步要做的就是给图形各点标注字母,方便后面的计算.再看这道题,出现两个面积相等且共底的三角形.设三角形为ABC ,BE 和CD 交于F ,则BF FE =,再连结DE . 所以三角形DEF 的面积为3.设三角形ADE 的面积为x ,则()():33:10:10x AD DB x +==+,所以15x =,四边形的面积为18.方法二:设ADF S x =△,根据燕尾定理::ABF BFC AFE EFC S S S S =△△△△,得到3AEF S x =+△,再根据向右下飞的燕子,有(37):7:3x x ++=,解得7.5x =四边形的面积为7.57.5318++=7、如下图,正方形 ABCD 的面积是a ,正三角形BPC 的面积是 b ,求阴影三角形BPD 的面积.【分析】 连接 AC 交 BD 于O 点,并连接PO .如图所示,可得P O / / DC ,所以三角形DPO 与三角形 CPO 面积相等(同底等高),所以有:8、已知四边形ABCD 和CEFG 都是正方形,且正方形ABCD 的边长为10厘米,那么图中阴影三角形BFD 的面积为多少平方厘米?【分析】 连接FC ,有FC 平行BD ,设BF 与DC 连接于O ,那么在梯形蝴蝶中有1===502DFO BCODCB ABCD S S S S S ∆∆∆=阴影9、如图,已知在平行四边形ABCD 中,AB=16,AD=10,BE=4,那么FC 的F GED CBA长度是多少?【分析】图中有一个沙漏,也有金字塔,但我们用沙漏就能解决问题,因为AB 平行于CD ,所以::4:161:4BF FC BE CD ===,所以410814FC =⨯=+. 10、四边形ABCD 和四边形CEFG 是两个正方形,BF 与CD 相交于H ,已知CH:DH=1:2, 6BCH S ∆=,求五边形ABEFD 的面积。
【分析】因为CH:DH=1:2,所以:1:2BCH BHD S S ∆∆=,即BHD S ∆=2×6=12 18BCD S ∆=,所以正方形ABCD 面积为36,BC=6 又6BCH S ∆=,所以CH=2连接CF,由蝴蝶定理得:6DFH BCH S S ∆∆==设小正方形边长为a ,则26a =得3a = ABCD CEFD DFG S S S S ∆=++=6×6+3×3+(6-3)×3÷2=49.511、如图,已知正方形ABCD 的边长为10厘米,E 为AD 中点,F 为CE 中点,G 为BF 中点,求三角形BDG 的面积.【分析】 设BD 与CE 的交点为O ,连接BE 、DF .由蝴蝶定理可知::BEDBCDEO OC SS=,而14BEDABCDSS =,12BCDABCDSS =,所以::1:2BED BCDEO OC SS==,故13EO EC =. 由于F 为CE 中点,所以12EF EC =,故:2:3EO EF =,:1:2FO EO =.由蝴蝶定理可知::1:2BFD BED S S FO EO ==,所以1128BFD BED ABCD S S S ==,那么1111010 6.2521616BGDBFDABCDS S S ===⨯⨯=(平方厘米).FEF EDCBA12、点E 、M 分别为直角梯形ABCD 两边上的点,且DQ 、CP 、ME 彼此平行,若5AD =,7BC =,5AE =,3EB =.求阴影部分的面积.B CEQ B CE【分析】 连接CE 、DE .由于DQ 、CP 、ME 彼此平行,所以四边形CDQP 是梯形,且ME 与该梯形的两个底平行,那么三角形QME 与DEM 、三角形PME 与CEM 的面积分别相等,所以三角形PQM 的面积与三角形CDE 的面积相等.而三角形CDE 的面积根据已知条件很容易求出来.由于ABCD 为直角梯形,且5AD =,7BC =,5AE =,3EB =,所以三角形CDE 的面积的面积为:()()1115753553725222+⨯+⨯-⨯⨯-⨯⨯=.所以三角形PQM 的面积为25.。
