聚类分析作业
sas聚类作业
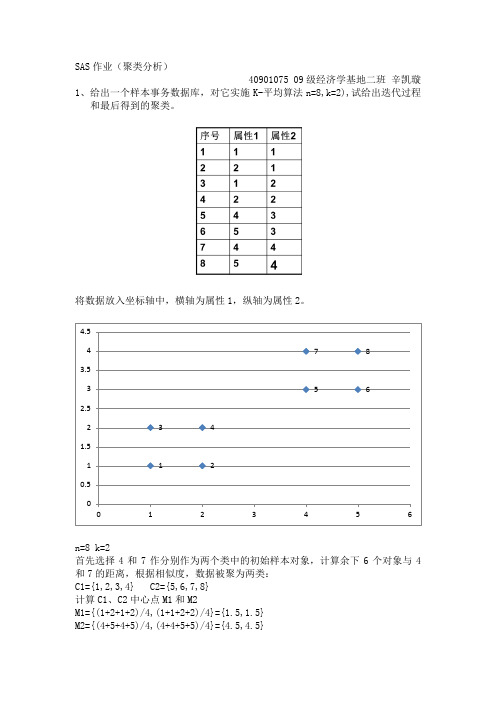
SAS作业(聚类分析)40901075 09级经济学基地二班辛凯璇1、给出一个样本事务数据库,对它实施K-平均算法n=8,k=2),试给出迭代过程和最后得到的聚类。
将数据放入坐标轴中,横轴为属性1,纵轴为属性2。
n=8 k=2首先选择4和7作分别作为两个类中的初始样本对象,计算余下6个对象与4和7的距离,根据相似度,数据被聚为两类:C1={1,2,3,4} C2={5,6,7,8}计算C1、C2中心点M1和M2M1={(1+2+1+2)/4,(1+1+2+2)/4}={1.5,1.5}M2={(4+5+4+5)/4,(4+4+5+5)/4}={4.5,4.5}此时,E2=e12+e22=2+2=4重新计算1-8与M1,M2的距离,数据的聚类仍然保持不变,C1={1,2,3,4} C2={5,6,7,8}此时,算法停止,因为如果继续分析新中心和样本之间的距离,样本会全部分配给同样的类。
因此,数据被分为两类,第一类中心点为{1.5,1.5},C1={1,2,3,4},第二类中心点为{4.5,4.5},C2={5,6,7,8}。
2、给出一个样本事务数据库,采用凝聚层次聚类(n=8,k=2),利用最小距离方法,试给出聚类过程和最后形成的聚类。
将数据放入坐标轴中,横轴为属性1,纵轴为属性2。
n=8 k=2将每个对象看成一个新类。
首先计算两两对象之间的距离,根据最小距离法,分别由1,2和5,6形成一个新类,1,2与3,5,6与7可以分别再形成一个新类,1,2,3与4,5,6,7与8分别可以再形成一个新类。
此时,形成的两个聚类是:C1={1,2,3,4},C2={5,6,7,8}。
甚至还可以将1,2,3,4,5,6,7,8形成一个聚类。
凝聚层次聚类法需要设定阀值,因此最终的聚类结果和设定的距离阀值有关。
聚类分析大作业

全国各地区农民家庭收支的聚类与判别分析摘要本文引用某年全国各地区农民家庭收支的抽样调查资料,运用SPSS统计软件中的聚类分析与判别分析对这些原始数据进行分类处理,旨在研究全国各地区农民家庭收支的分布规律,并对此进行简要讨论。
关键词:农民家庭收支,聚类分析,判别分析1引言随着中国经济的发展和社会的进步,人民的生活水平日益提高,特别是在我国广大农村,农民的生活水平更是上了一个大台阶,这主要有以下三个原因:第一是中国城镇化水平的提高和农村剩余劳动力的大量转移,许多农民也像城镇人口一样取得了固定性的工资收入;第二是农民不再单纯地依靠种植收入,而是进行家庭经营取得经营收入;第三也是最重要的是政府意识到“三农”问题的重要性,加大了对农业、农村、农民的投入力度。
正因为如此,近年来各地农民家庭收入逐年递增,正朝着小康水平迈进。
农民家庭的收入增加,必然会导致家庭消费支出总额的增加和家庭消费支出结构的变化。
从最近几年的统计数据可以看出农村地区对吃穿等基本生活资料的消费呈下降趋势,而对于文化教育及医疗保健的支出消费逐年递增。
从农村家庭收支的变化情况可以看出整个国家的经济增长状况,以小见大,为政府决策提供一定的依据。
为了研究我国各地的农民家庭收支情况,现抽取了28个省、市、自治区的样品,每个样本有6个指标,即食品、衣着、燃料、住房、生活用品及其他和文化生活服务支出6个指标,对其进行分析。
原始数据如表1所示:经济研究过去常常采用定性分析,根据经验进行经济决策,这种方法有很多的弊端,因而人们越来越多地采用定性与定量分析相结合,以事实说话,更客观地反映经济变化的规律。
这里我们利用已有的统计数据,运用SPSS统计软件对其进行分析,主要进行的是聚类和判别分析。
2聚类分析聚类分析是在不知道类别数目的情况下对样本数据进行分类。
它是根据“物以类聚”的道理,对样品和指标进行分类的一种多元统计分析方法。
聚类分析要讨论的对象是一大堆样品,要求能合理地按它们各自的特性来进行合理的分类。
第二章作业聚类分析

第二章作业1.画出给定迭代次数为n的系统聚类法的算法流程框图. 答:算法流程图如下:2.对如下5个6维模式样本,用最小距离准则进行系统聚类分析: x 1: 0, 1, 3, 1, 3, 4 x 2: 3, 3, 3, 1, 2, 1 x 3: 1, 0, 0, 0, 1, 1 x 4: 2, 1, 0, 2, 2, 1x 5: 0, 0, 1, 0, 1, 0解:将每一样本看成单独一类,得(0)11{}G x =, (0)22{}G x =,(0)33{}G x = (0)44{}G x =, (0)55{}G x =计算各类之间的欧式距离,可得距离矩阵(0)D (表1-1)。
表1-1① 矩阵(0)D,它是(0)3G 和(0)5G 之间的距离,将它们合并为一类,得到新的分类为(1)(0)11{}G G =,(1)(0)22{}G G =,(1)(0)(0)335{,}G G G = (1)(0)44{}G G =计算聚类后的距离矩阵(1)D 。
按最小距离准则,分别计算(0)3G 与(1)1G 、(1)2G 、(1)4G ,(0)5G 与(1)1G 、(1)2G 、 (1)4G 之间的两种距离,并选用最小距离。
如(1)(0)(1)(0)(1)133151min{D G G G G =与的距离,与的距离}}=5 由此可求得距离矩阵(1)D (表1-2)② 距离矩阵(1)D ,它是(1)3G 和(1)4G 之间的距离,于是合并(1)3G 和(1)4G ,得到新的分类为(2)(1)11{}G G =,(2)(1)22{}G G =,(2)(1)(1)334{,}G G G =按最小距离准则计算距离矩阵(2)D ,得表1-3表1-3选择距离阈值(2)D 则算法停止,得到聚类结果G 1(2)={X1} G 2(2) ={X2} G 3(2)={X3,X5, X4}。
3. 模式样本如下:{X1(0,0),X2(1,0),X3(0,1),X4(1,1),X5(2,1),X6(1,2),X7(2,2),X8(3,2),X9(6,6),X10(7,6),X11(8,6), X12(6,7), X13(7,7), X14(8,7), X15(9,7), X16(7,8), X17(8,8), X18(9,8), X19(8,9), X20(9,9). 选K=2,11210(1)=(00),(1)(76)ttz x z x ===,用K —均值算法进行分类。
聚类分析实验报告例题

一、实验目的1. 理解聚类分析的基本原理和方法。
2. 掌握K-means、层次聚类等常用聚类算法。
3. 学习如何使用Python进行聚类分析,并理解算法的运行机制。
4. 分析实验结果,并评估聚类效果。
二、实验环境1. 操作系统:Windows 102. 编程语言:Python3.83. 库:NumPy、Matplotlib、Scikit-learn三、实验数据本次实验使用的数据集为Iris数据集,包含150个样本,每个样本有4个特征(花萼长度、花萼宽度、花瓣长度、花瓣宽度),属于3个不同的类别。
四、实验步骤1. 导入Iris数据集,并进行数据预处理。
2. 使用K-means算法进行聚类分析,选择合适的K值。
3. 使用层次聚类算法进行聚类分析,观察聚类结果。
4. 分析两种算法的聚类效果,并进行比较。
5. 使用Matplotlib绘制聚类结果的可视化图形。
五、实验过程1. 数据预处理```pythonfrom sklearn import datasetsimport numpy as np# 加载Iris数据集iris = datasets.load_iris()X = iris.datay = iris.target# 数据标准化X = (X - np.mean(X, axis=0)) / np.std(X, axis=0) ```2. K-means聚类分析```pythonfrom sklearn.cluster import KMeans# 选择K值k_values = range(2, 10)inertia_values = []for k in k_values:kmeans = KMeans(n_clusters=k, random_state=42) kmeans.fit(X)inertia_values.append(kmeans.inertia_)# 绘制肘部图import matplotlib.pyplot as pltplt.plot(k_values, inertia_values, marker='o') plt.xlabel('Number of clusters')plt.ylabel('Inertia')plt.title('Elbow Method')plt.show()```3. 层次聚类分析```pythonfrom sklearn.cluster import AgglomerativeClustering# 选择层次聚类方法agglo = AgglomerativeClustering(n_clusters=3)y_agglo = agglo.fit_predict(X)```4. 聚类效果分析通过观察肘部图,可以发现当K=3时,K-means算法的聚类效果最好。
统计学作业聚类分析

聚类分析采用欧式距离,分别运用类平均法、最短距离法、最长距离法,对31个省、直辖市、自治区分类。
1、类平均法* * * * * * * * * * * * * * * * * * * H I E R A R C H I C A L C L U S T E R A N A L Y S I S * * * * * * * * * * * * * * * * * * *Dendrogram using Average Linkage (Between Groups)Rescaled Distance Cluster CombineC A S E 0 5 10 15 20 25Label Num +---------+---------+---------+---------+---------+甘肃 28 -+宁夏 30 -+青海 29 -+-+河南 16 -+ |新疆 31 -+ +-+黑龙江 8 -+ | |陕西 4 -+-+ +-+内蒙古 5 -+ | |陕西 27 -----+ +-+山东 15 ---+-+ | |湖南 18 ---+ | | |河北 3 -+-+ +-+ |吉林 7 -+ +-+ |湖北 17 ---+ | +---+四川 23 -+-+ | | |云南 25 -+ +-+ | |辽宁 6 ---+ | +-----+江西 14 -+-+ | | |贵州 24 -+ +-----+ | |安徽 12 ---+ | |广西 20 -------+-----+ +-----------------------------+海南 21 -------+ | |江苏 10 -+-------+ | |重庆 22 -+ +---+ | |天津 2 ---------+ +---+ | |福建 13 -------------+ +-+ |西藏 26 -----------------+ |北京 1 ---------+ |上海 9 ---------+---+ |浙江 11 ---------+ +-----------------------------------+广东 19 -------------+2、最短距离法* * * * * * * * * * * * * * * * * * * H I E R A R C H I C A L C L U S T E R A N A L Y S I S * * * * * * * * * * * * * * * * * * *Dendrogram using Single LinkageRescaled Distance Cluster CombineC A S E 0 5 10 15 20 25Label Num +---------+---------+---------+---------+---------+甘肃 28 -+宁夏 30 -+青海 29 -+---+河南 16 -+ |新疆 31 -+ |黑龙江 8 -+ |陕西 4 -+---+-+内蒙古 5 -+ | |陕西 27 -----+ |四川 23 -----+-+云南 25 -----+ |河北 3 -+---+ |吉林 7 -+ | |湖北 17 -----+-+山东 15 -----+ |辽宁 6 -------+-+湖南 18 -------+ |江西 14 ---+-+ | +---+贵州 24 ---+ +-+ | |安徽 12 -----+ | +-+广西 20 ---------+ | |江苏 10 -+-----------+ +---+重庆 22 -+ | +---+海南 21 ---------------+ | +-+天津 2 -------------------+ | +-----------------------+福建 13 -----------------------+ | |西藏 26 -------------------------+ |北京 1 -------------------+-+ |上海 9 -------------------+ +-+ |浙江 11 ---------------------+ +-------------------------+广东 19 -----------------------+3、最长距离法* * * * * * * * * * * * * * * * * * * H I E R A R C H I C A L C L U S T E R A N A L Y S I S * * * * * * * * * * * * * * * * * * *Dendrogram using Complete LinkageRescaled Distance Cluster CombineC A S E 0 5 10 15 20 25Label Num +---------+---------+---------+---------+---------+甘肃 28 -+宁夏 30 -+青海 29 -+---+河南 16 -+ |新疆 31 -+ +---+黑龙江 8 -+ | |陕西 4 -+-+ | |内蒙古 5 -+ +-+ +-----+陕西 27 ---+ | |山东 15 ---+---+ | |湖南 18 ---+ | | |河北 3 -+-+ +-+ |吉林 7 -+ +-+ | |湖北 17 ---+ +-+ +---------+四川 23 -+-+ | | |云南 25 -+ +-+ | |辽宁 6 ---+ | |江西 14 -+ | |贵州 24 -+-------+ | +-----------------------+安徽 12 -+ +-----+ | |广西 20 -----+---+ | |海南 21 -----+ | |江苏 10 -+-----+ | |重庆 22 -+ +---------+ | |天津 2 -------+ +-------+ |福建 13 -----------+-----+ |西藏 26 -----------+ |北京 1 -------+ |上海 9 -------+-----+ |浙江 11 -------+ +-----------------------------------+广东 19 -------------+由上述图表可知,类平均法分为三类:{1,9,11,19}为第一类,{13,22,2,10,26}为第二类,其他为第三类;最短距离分为两类,{1,9,11,19}为第一类,其余的归为第二类;最长距离法归为三类:{1,9,11,19}为第一类,{13,22,2,10,26}为第二类,其他为第三类。
高级统计学作业-聚类分析

全国各地区消费价格增长水平的聚类分析摘要:针对我国各省(直辖)市的2009年度消费价格增长水平数据,选取9个经济指标进行系统聚类分析,得到我国3类不同的地区消费价格增长水平类型。
聚类结果为制订有针对性的地区消费市场战略提供依据。
关键词:SPSS;聚类分析;消费水平。
1.引言由于传统的经济发展起点不同,加上地域、资源、技术和政策等条件的差异,各个地区的经济发展水平高低不齐,导致各地区的工资水平和消费价格增长水平的不同。
因此,对各地区消费价格增长水平进行分类、比较和研究,总结出有助于市场调节和商业发展的对策,有针对性地制订地区经济发展战略,对促进国民经济协调发展有重要意义。
聚类分析和判别分析是是进行以上分析的两个重要的方法。
1.1聚类分析[1]定义:聚类分析又称群分析、点群分析。
根据研究对象特征对研究对象进行分类的一种多元分析技术,把性质相近的个体归为一类,使得同一类中的个体都具有高度的同质性,不同类之间的个体具有高度的异质性。
聚类分析的基本思想:我们所研究的样品或指标(变量)之间存在程度不同的相似性(亲疏关系),于是根据一批样品的多个观测指标,具体找出一些能够度量样品或指标之间相似程度的统计量,以这些统计量作为划分类型的依据,把一些相似程度较大的样品(或指标)聚合为一类,把另外一些相似程度较大的样品(或指标)又聚合为另一类;关系密切的聚合到一个小的分类单位,关系疏远的聚合到一个大的分类单位,直到把所有的样品(或指标)聚合完毕。
1.1.1 系统聚类法系统聚类法的基本原理:首先将一定数量的样本或指标各自看成一类,然后根据样本(或指标)的亲疏程度,将亲疏程度最高的两类进行合并,然后考虑合并后的类与其他类之间的亲疏程度,再进行合并。
重复这一过程,直到将所有的样本(或指标)合并为一类。
系统聚类分为Q型聚类和R型聚类两种:Q型聚类是对样本进行聚类,它使具有相似特征的样本聚集在一起,使差异性大的样本分离开来;R型聚类是对变量进行聚类,它使差异性大的变量分离开来,相似的变量聚集在一起,这样就可以在相似变量中选择少数具有代表性的变量参与其他分析,实现减少变量个数、降低变量维度的目的。
聚类分析作业
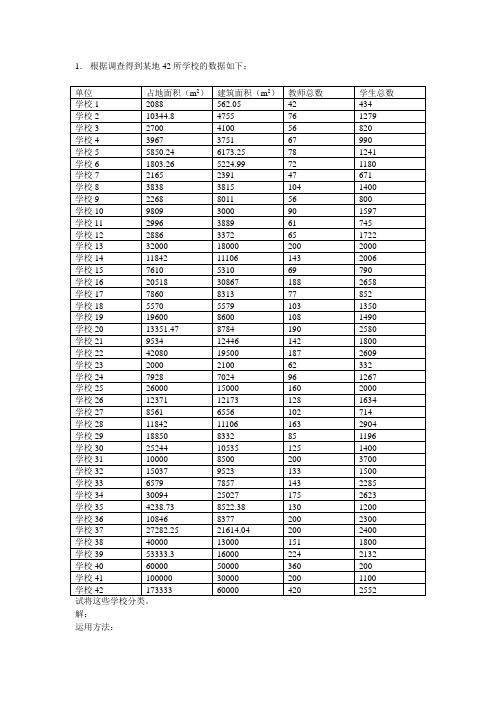
1.根据调查得到某地42所学校的数据如下:试将这些学校分类。
解:运用方法:将所有学校分为3类:第一类:(3,11,15,4,9,17,27,1,23,7,19,30,32,21,26,14,10,12,5,6,2,8,18,24,29,36,33,20,34,37,22,16,25,38, 13,39,31)第二类:(40,41)第三类:(42)2.16种饮料的热量、咖啡因、钠及价格四种变量数据如下表:饮料编号热量咖啡因钠价格1 207.20 3.30 15.50 2.802 36.80 5.90 12.90 3.303 72.20 7.30 8.20 2.404 36.70 .40 10.50 4.005 121.70 4.10 9.20 3.506 89.10 4.00 10.20 3.307 146.70 4.30 9.70 1.808 57.60 2.20 13.60 2.109 95.90 .00 8.50 1.3010 199.0 .00 10.60 3.5011 49.80 8.00 6.30 3.7012 16.60 4.70 6.30 1.5013 38.50 3.70 7.70 2.0014 .00 4.20 13.10 2.2015 118.80 4.70 7.20 4.1016 107.00 .00 8.30 4.20试将这些饮料分类。
解:所有饮料分为4类:(5,6,7,3,2,4,11)(8,14,12,13,9)(1)(15,16,10)3.20种啤酒的成分和价格数据如下表:beername calorie sodium alcohol cost Budweiser 144.00 19.00 4.70 .43 Schlitz 181.00 19.00 4.90 .43 Ionenbrau 157.00 15.00 4.90 .48 Kronensourc 170.00 7.00 5.20 .73 Heineken 152.00 11.00 5.00 .77 Old-milnaukee 145.00 23.00 4.60 .26 Aucsberger 175.00 24.00 5.50 .40Strchs-bohemi 149.00 27.00 4.70 .42 Miller-lite 99.00 10.00 4.30 .43 Sudeiser-lich 113.00 6.00 3.70 .44 Coors 140.00 16.00 4.60 .44 Coorslicht 102.00 15.00 4.10 .46 Michelos-lich 135.00 11.00 4.20 .50 Secrs 150.00 19.00 4.70 .76 Kkirin 149.00 6.00 5.00 .79 Pabst-extra-l 68.00 15.00 2.30 .36 Hamms 136.00 19.00 4.40 .43 Heilemans-old 144.00 24.00 4.90 .43 Olympia-gold- 72.00 6.00 2.90 .46 Schlite-light 97.00 7.00 4.20 .47 试将这些啤酒分类。
聚类分析大作业

应用数理统计大作业(二)部分省市经济类型的聚类和判别分析学院:学号:姓名:班级:部分省市经济类型的聚类和判别分析摘要一个省市的经济类型和众多因素比如地理位置、国民生产总值、人口素质等息息相关,本文利用统计软件SPSS,对北京市等10省市2008年的地区生产总值(亿元)、职工人均工资(元)、第一、二、三产业各自在国民生产总值中占的比重作为判别经济类型的五个因素,进行聚类分析,得出了分类结果,分类结果和我们的直观判断相吻合。
本文所进行的分析结果在一定程度上反映了这些省市的经济类型和经济特点。
关键词:经济类型,聚类分析,判别分析,SPSS符号说明符号说明X1 地区生产总值X2职工人均工资X3第一产业在国民生产总值中占的比重X4第二产业在国民生产总值中占的比重X5第三产业在国民生产总值中占的比重0 引言随着中国经济迅速发展,各个省市自治区的经济呈现出各自不同的发展态势。
通过研究各省市的经济发展状况和经济类型对于正确认识我国的经济发展情况具有重要意义。
一个省自治区直辖市的经济类型和众多因素比如地理位置、国民生产总值、人口素质等因素息息相关,本文利用功能强大的统计软件SPSS,对北京市、天津市、河北省、辽宁省、江苏省、浙江省、安徽省、湖北省、湖南省、河南省、广东省、四川省和山东省2008年的地区生产总值(亿元)、职工人均工资(元)、第一、二、三产业各自在国民生产总值中占的比重作为判别经济类型的五个因素,进行聚类分析,结果北京市和天津市属于一类,河北省、浙江省和河南省属于一类,辽宁省、安徽省、湖南省、湖北省、四川省属于一类,江苏省、山东省、广东省属于一类,这个结果和我们的直观判断一致。
这个结果也充分说明了本文进行的分析是合理的,具有一定的科学性。
1 源数据的提取本文所用的数据全来自2009年出版的《中国统计年鉴》,从中提取了有关北京市、天津市、河北省、辽宁省、江苏省、浙江省、安徽省、湖北省、湖南省、河南省、广东省、四川省和山东省总计13省2008年的五种数据。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.根据调查得到某地42所学校的数据如下:
试将这些学校分类。
2.16种饮料的热量、咖啡因、钠及价格四种变量数据如下表:
试将这些饮料分类。
3.20种啤酒的成分和价格数据如下表:
试将这些啤酒分类。
4.50名学生参加10个测验项目的测试数据如下表:
试将学生分类。
5.下表列出了2007年我国31个省、市、自治区和直辖市的城镇居民家庭平均每人全年消费性支出的8个主要变量数据。
利用系统聚类法,对各地区进行聚类分析:
试将这些地区分类
6.在全国服装标准制定中,对某地区成年女子的14个部位尺寸(体型尺寸)进行了测量,根据测量数据计算得到14个部位尺寸之间的相关系数矩阵,如下表所示,:试对14个变量进行聚类分析:
7.下表列出了2006年我国31个省、市、自治区和直辖市的12个月的月平均气温数据。
数据来源:中华人民共和国国家统计局网站,现利用聚类法,对各地区进行聚类分析。
