第二章作业聚类分析
模式识别聚类分析

x1 ,
(
( x1
x2旳值。可用下列递推
k ) xi ) /( N1(k ) 1)
x(k 1) 2
(k)
x2
(k)
(x2
xi
)
/(
N
(k 2
)
1)
x1 (k ) , x2 (k )是第k步对分时两类均值,
x1(k 1) , x2(k 1)是下一次对分时把xi从G1(k )
划到G2(k)时的两类均值
所以x1 Z1(1)
再继续进行第二,第三次迭代… 计算出 E(2) , E(3) , …
次数 1 2 3 4 5 6 7 8 9
10 11
G1 G2
x21 x20 x18 x14 x15 x19
x11 x13 x12 x17 x16
E值 56.6 79.16 90.90 102.61 120.11 137.15 154.10 176.15 195.26 213.07 212.01
Ni为第i类的样本数.
离差平方和增量:设样本已提成ωp,ωq两类, 若把ωp,ωq合为ωr类,则定义离差平方:
Dp2q Sr (S p Sq )
其中S p , Sq分别为 p类于q类的离差平方和, S r为 r 类的离差平方和
增量愈小,合并愈合理。
聚类准则
Jw Min
类内距离越小越好 类间距离越大越好
体积与长,宽,高有关;比重与材料,纹理,颜 色有关。这里低、中、高三层特征都有了。
措施旳有效性
特征选用不当 特征过少 特征过多 量纲问题
主要聚类分析技术
谱系法(系统聚类,层次聚类法) 基于目旳函数旳聚类法(动态聚类) 图论聚类法 模糊聚类分析法
2.2模式相同度度量
应用多元分析聚类分析作业

应用多元分析——聚类分析5.1解:判别分析是根据一定的判别准则,判定一个样本归属于哪一类,用具体的数学语言来表达就是,设有n 个样本,对每个样本测得p 项指标(变量)的数据,已知每个样本属于k 个类别(或总体)G 1,G 2,……,G k 中的某一类,且它们的分布函数分别为F 1(x ),F 2(x ),……,F k (x )通过找出一个最优的划分,使得不同类别的样本尽可能地区别开,并对测得同样p 项指标(变量)数据的一个新样本,能判别该样本属于哪个总体。
聚类分析是分析如何对样品(或变量)进行量化分类的问题。
而聚类分析是指,在聚类之前,我们并不知道判别标准,而是通过一次次的聚类,使相近的样品(或变量)聚合形成总体,即进行量化分类。
通俗来讲,判别分析是在已知有多少类及是什么类的情况下进行分类,而聚类分析是在不知道类的情况下进行分类。
5.3解:对样品进行聚类分析时,用距离来测定样品之间的相似程度。
因为我们把n 个样本看作p 维空间的n 个点,点之间的距离即可代表样品间的相似度,将距离近的归为一类,距离较远的点归为不同类。
常用的距离为: (一)闵可夫斯基距离:1/1()()p qq ij ik jk k d q X Xq 取不同值,分为 (1)绝对距离(1q ) 1(1)p ij ikjkk d X X(2)欧氏距离(2q )21/21(2)()p ij ikjk k d X X(3)切比雪夫距离(q)1()max ij ikjkk pd X X(二)马氏距离(三)兰氏距离对变量的相似性进行度量的时候,因为多元数据中的变量表现为向量的形式,在几何上可以用多维空间的一个有向线段表示,相对于数量的大小,我们更多地要了解变量的变化趋势或变化方向,因此用相关性进行衡量。
将变量看作p 维空间的向量,一般用:(一) 夹角余弦(二)相关系数5.5解:11()p ik jkijk ik jk X X d L p X X21()()()ij i j i j d M X X ΣX X12cos pik jkk ij p pX X 12211()()()()pik i jk j k ij p p ik i jk j k k X X X X r X X X X相同点:K—均值法和系统聚类法一样,都是以距离的远近亲疏为标准进行聚类的。
北航数理统计大作业2-聚类与判别分析讲解

应用数理统计作业二学号:姓名:电话:二〇一四年十二月对NBA球队的聚类分析和判别分析摘要:NBA联盟作为篮球的最高殿堂深受广大球迷的喜爱,联盟的30支球队大家也耳熟能详,本文选取NBA联盟30支球队2013-2014常规赛赛季场均数据。
利用spss软件通过聚类分析对27个地区进行实力类型分类,并利用判断分析对其余3支球队对分类结果进行验证。
可以看出各球队实力类型与赛季实际结果相吻合。
关键词:聚类分析,判别分析,NBA目录1. 引言 (4)2、相关统计基础理论 (5)2.1、聚类分析 (5)2.2,判别分析 (6)3.聚类分析 (7)3.1数据文件 (7)3.2聚类分析过程 (9)3.3 聚类结果分析 (11)4、判别分析 (12)4.1 判别分析过程 (12)4.2判别检验 (17)5、结论 (20)参考文献 (21)致谢 (22)1. 引言1896年,美国第一个篮球组织"全国篮球联盟(简称NBL)"成立,但当时篮球规则还不完善,组织机构也不健全,经过几个赛季后,该组织就名存实亡了。
1946年4月6日,由美国波士顿花园老板沃尔特.阿.布朗发起成立了“美国篮球协会”(简称BAA)。
1949年在布朗的努力下,美国两大篮球组织BAA和NBL合并为“全国篮球协会”(简称NBA)。
NBA季前赛是 NBA各支队伍的热身赛,因为在每个赛季结束后,每支球队在阵容上都有相当大的变化,为了让各队磨合阵容,熟悉各自球队的打法,确定各队新赛季的比赛阵容、同时也能增进队员、教练员之间的沟通,所以在每个赛季开始之前,NBA就举办若干场季前赛,使他们能以比较好的状态投入到漫长的常规赛的比赛当中。
为了扩大NBA在全球的影响,季前赛有约三分之一的球队在美国以外的国家举办。
从总体上看,NBA的赛程安排分为常规赛、季后赛和总决赛。
常规赛采用主客场制,季后赛和总决赛采用七场四胜制的淘汰制。
[31]NBA常规赛从每年的11月的第一个星期二开罗,到次年的4月20日左右结束。
聚类分析方法

聚类分析方法聚类分析是一种常用的数据分析方法,它可以将数据集中的对象按照其相似性进行分组,形成若干个簇。
通过聚类分析,我们可以发现数据中的内在结构,帮助我们更好地理解数据集的特点和规律。
在实际应用中,聚类分析被广泛应用于市场分割、社交网络分析、图像处理等领域。
本文将介绍聚类分析的基本原理、常用方法和应用场景,希望能够帮助读者更好地理解和应用聚类分析。
聚类分析的基本原理是将数据集中的对象划分为若干个簇,使得同一簇内的对象相似度较高,不同簇之间的对象相似度较低。
在进行聚类分析时,我们需要选择合适的相似性度量方法和聚类算法。
常用的相似性度量方法包括欧氏距离、曼哈顿距离、余弦相似度等,而常用的聚类算法包括K均值聚类、层次聚类、DBSCAN等。
不同的相似性度量方法和聚类算法适用于不同的数据类型和应用场景,选择合适的方法对于聚类分析的效果至关重要。
K均值聚类是一种常用的聚类算法,它通过不断迭代更新簇中心的方式,将数据集中的对象划分为K个簇。
K均值聚类的优点是简单、易于理解和实现,但是它对初始簇中心的选择较为敏感,容易收敛到局部最优解。
层次聚类是另一种常用的聚类算法,它通过逐步合并或分裂簇的方式,构建一棵层次化的聚类树。
层次聚类的优点是不需要事先确定簇的个数,但是它对大数据集的处理效率较低。
DBSCAN是一种基于密度的聚类算法,它能够发现任意形状的簇,并且对噪声数据具有较强的鲁棒性。
不同的聚类算法适用于不同的数据特点和应用场景,我们需要根据具体情况选择合适的算法进行聚类分析。
聚类分析在实际应用中有着广泛的应用场景。
在市场分割中,我们可以利用聚类分析将顾客分为不同的群体,从而制定针对性的营销策略。
在社交网络分析中,我们可以利用聚类分析发现社交网络中的社区结构,从而发现潜在的影响力人物。
在图像处理中,我们可以利用聚类分析对图像进行分割和特征提取,从而实现图像内容的理解和识别。
聚类分析在各个领域都有着重要的应用,它为我们理解和利用数据提供了有力的工具。
聚类分析_精品文档

1聚类分析内涵1.1聚类分析定义聚类分析(Cluste.Analysis)是一组将研究对象分为相对同质的群组(clusters)的统计分析技术.也叫分类分析(classificatio.analysis)或数值分类(numerica.taxonomy), 它是研究(样品或指标)分类问题的一种多元统计方法, 所谓类, 通俗地说, 就是指相似元素的集合。
聚类分析有关变量类型:定类变量,定量(离散和连续)变量聚类分析的原则是同一类中的个体有较大的相似性, 不同类中的个体差异很大。
1.2聚类分析分类聚类分析的功能是建立一种分类方法, 它将一批样品或变量, 按照它们在性质上的亲疏、相似程度进行分类.聚类分析的内容十分丰富, 按其聚类的方法可分为以下几种:(1)系统聚类法: 开始每个对象自成一类, 然后每次将最相似的两类合并, 合并后重新计算新类与其他类的距离或相近性测度. 这一过程一直继续直到所有对象归为一类为止. 并类的过程可用一张谱系聚类图描述.(2)调优法(动态聚类法): 首先对n个对象初步分类, 然后根据分类的损失函数尽可能小的原则对其进行调整, 直到分类合理为止.(3)最优分割法(有序样品聚类法): 开始将所有样品看成一类, 然后根据某种最优准则将它们分割为二类、三类, 一直分割到所需的K类为止. 这种方法适用于有序样品的分类问题, 也称为有序样品的聚类法.(4)模糊聚类法: 利用模糊集理论来处理分类问题, 它对经济领域中具有模糊特征的两态数据或多态数据具有明显的分类效果.(5)图论聚类法: 利用图论中最小支撑树的概念来处理分类问题, 创造了独具风格的方法.(6)聚类预报法:利用聚类方法处理预报问题, 在多元统计分析中, 可用来作预报的方法很多, 如回归分析和判别分析. 但对一些异常数据, 如气象中的灾害性天气的预报, 使用回归分析或判别分析处理的效果都不好, 而聚类预报弥补了这一不足, 这是一个值得重视的方法。
实验二聚类分析
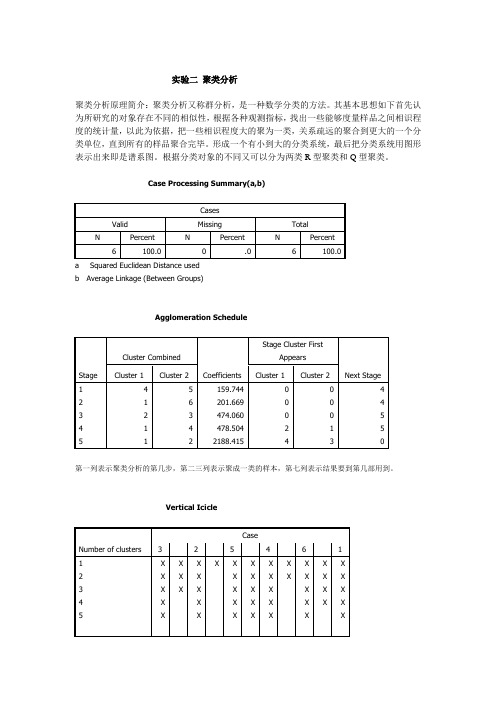
实验二聚类分析
聚类分析原理简介:聚类分析又称群分析,是一种数学分类的方法。
其基本思想如下首先认为所研究的对象存在不同的相似性,根据各种观测指标,找出一些能够度量样品之间相识程度的统计量,以此为依据,把一些相识程度大的聚为一类,关系疏远的聚合到更大的一个分类单位,直到所有的样品聚合完毕。
形成一个有小到大的分类系统,最后把分类系统用图形表示出来即是谱系图。
根据分类对象的不同又可以分为两类R型聚类和Q型聚类。
Case Processing Summary(a,b)
a Squared Euclidean Distance used
b Average Linkage (Between Groups)
Agglomeration Schedule
第一列表示聚类分析的第几步,第二三列表示聚成一类的样本,第七列表示结果要到第几部用到。
Vertical Icicle
样品分类冰柱图
Dendrogram
样品分类谱系图
可知样品分为三类,3、4为第一类,1、2为第二大类,5为孤立元素。
聚类分析

第五章 聚类分析聚类分析是研究多个样品或指标的分类问题的一种多元统计分析方法。
聚类分析起源于分类学,在古老的分类学中,人们主要依靠经验和专业知识,它很少利用数学,带有一定的主观性和任意性。
随着生产技术和科学的发展,对分类的准确性和精确度要求越来越高,单凭经验和专业知识已经不能满足这个要求,于是数学被逐渐引入分类学中,形成了数值分类学。
随着数理统计中多元分析方法的发展,多元分析的技术自然被引用到分类学中,于是聚类分析逐渐从数值分类学中分离出来,形成一个新的分支。
在经济、社会、人口研究中,存在着大量的多个样品、多个指标的分类问题。
例如,根据经济发展水平对我国各省、市、自治区进行分类,可以选择人均GDP 、人均能源消费、农村人口比重、人口预期寿命、新生婴儿死亡率、识字率等指标,根据这些指标值来把所有不同的地区划分为若干类。
在自然科学中,也存在分类的问题,例如为区分多种动物群体而建立的生物分类学。
和多元分析的其他方法相比,聚类分析的方法是很粗糙的,理论上也不够完善。
但是作为一种实用性很强的数学工具,聚类分析可以解决许多实际问题,因此受到人们的重视。
将它与判别分析、主成分分析、回归分析等方法结合使用时,往往能得到很好的效果。
§5.1 聚类分析的一般问题一、聚类分析及其目的聚类分析就是对样品或指标(变量)进行分类,目的在于使同一类中的对象的同质性最大化、类与类之间的异质性最大化,从而更好的揭示事物的内在联系和本质差别。
聚类分析的一般提法如下:设有n 个样品,每个样品测得p 个指标,第i 个样品的第j 个指标的观测结果记为ij x ,则n p ⨯个观测结果构成如下数据矩阵:11121(1)21222(2)1212()(,,,)p p p n n np n x x x X x x x X X X X X x x x X '⎡⎤⎡⎤⎢⎥⎢⎥'⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥⎢⎥'⎢⎥⎢⎥⎣⎦⎣⎦(5.1) 其中,(1)(2)(),,,n X X X 表示p 维空间pR 中的n 个样品,第i 个样品用向量()12(,,,),1,2,i i i ip X x x x i n '== (5.2)表示;12,,,p X X X 表示n 维空间nR 中的p 个指标,第j 个指标用向量12,1,2,,j j j nj x x X j p x ⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎣⎦(5.2)表示。
模式识别第二章ppt课件

• 试探方法
凭直观感觉或经验,针对实际问题定义一种 相似性测度的阈值,然后按最近邻规则指定 某些模式样本属于某一个聚类类别。
– 例如对欧氏距离,它反映了样本间的近邻性,但 将一个样本分到不同类别中的哪一个时,还必须 规定一个距离测度的阈值作为聚类的判别准则。
精选ppt课件2021
• 特征选择的维数
在特征选择中往往会选择一些多余的特征,它增加了 维数,从而增加了聚类分析的复杂度,但对模式分类 却没有提供多少有用的信息。在这种情况下,需要去 掉相关程度过高的特征(进行降维处理)。
• 降维方法
– 结论:若rij->1,则表明第i维特征与第j维特征所反 映的特征规律接近,因此可以略去其中的一个特
– 距离阈值T对聚类结果的影响
精选ppt课件2021
17
2.3 基于试探的聚类搜索算法
2.3.2 最大最小距离算法
• 基本思想:以试探类间欧氏距离为最大 作为预选出聚类中心的条件。
• 病人的病程
– 名义尺度:指定性的指标,即特征度量时没有数量
关系,也没有明显的次序关系,如黑色和白色的关
系,男性和女性的关系等,都可将它们分别用“0”
和“1”来表示。
• 超过2个状态时,可精选用pp多t课个件2数021值表示。
8
2.2 模式相似性的测度和
聚类准则
2.2.1 相似Βιβλιοθήκη 测度• 目的:为了能将模式集划分成不同的类别,必须定义 一种相似性的测度,来度量同一类样本间的类似性和 不属于同一类样本间的差异性。
12
2.2 模式相似性的测度和
聚类准则
2.2.2 聚类准则
• 聚类准则函数法
– 依据:由于聚类是将样本进行分类以使类别间可 分离性为最大,因此聚类准则应是反映类别间相 似性或分离性的函数;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章作业1.画出给定迭代次数为n的系统聚类法的算法流程框图. 答:算法流程图如下:2.对如下5个6维模式样本,用最小距离准则进行系统聚类分析: x 1: 0, 1, 3, 1, 3, 4 x 2: 3, 3, 3, 1, 2, 1 x 3: 1, 0, 0, 0, 1, 1 x 4: 2, 1, 0, 2, 2, 1x 5: 0, 0, 1, 0, 1, 0解:将每一样本看成单独一类,得(0)11{}G x =, (0)22{}G x =,(0)33{}G x = (0)44{}G x =, (0)55{}G x =计算各类之间的欧式距离,可得距离矩阵(0)D (表1-1)。
表1-1① 矩阵(0)D,它是(0)3G 和(0)5G 之间的距离,将它们合并为一类,得到新的分类为(1)(0)11{}G G =,(1)(0)22{}G G =,(1)(0)(0)335{,}G G G = (1)(0)44{}G G =计算聚类后的距离矩阵(1)D 。
按最小距离准则,分别计算(0)3G 与(1)1G 、(1)2G 、(1)4G ,(0)5G 与(1)1G 、(1)2G 、 (1)4G 之间的两种距离,并选用最小距离。
如(1)(0)(1)(0)(1)133151min{D G G G G =与的距离,与的距离}}=5 由此可求得距离矩阵(1)D (表1-2)② 距离矩阵(1)D ,它是(1)3G 和(1)4G 之间的距离,于是合并(1)3G 和(1)4G ,得到新的分类为(2)(1)11{}G G =,(2)(1)22{}G G =,(2)(1)(1)334{,}G G G =按最小距离准则计算距离矩阵(2)D ,得表1-3表1-3选择距离阈值(2)D 则算法停止,得到聚类结果G 1(2)={X1} G 2(2) ={X2} G 3(2)={X3,X5, X4}。
3. 模式样本如下:{X1(0,0),X2(1,0),X3(0,1),X4(1,1),X5(2,1),X6(1,2),X7(2,2),X8(3,2),X9(6,6),X10(7,6),X11(8,6), X12(6,7), X13(7,7), X14(8,7), X15(9,7), X16(7,8), X17(8,8), X18(9,8), X19(8,9), X20(9,9). 选K=2,11210(1)=(00),(1)(76)ttz x z x ===,用K —均值算法进行分类。
解:第一步:选K=2,并选11(1)=(00)tz x =,210(1)(76)t z x ==第二步:因12(1)(1)i i x z x z -<-P P P P ,i=1,2, …,8,故1(1),1,2,,8i x S i ∈=K 又12(1)(1)i i x z x z ->-P P P P ,i=9,10, …,20,故2(1),9,10,,20i x S i ∈=K 得 },...,{)1(8211x x x S =,},...,{)1(201092x x x S = 第三步:计算新的聚类中心181(1)1111(2)(1.25 1.13)8t i x S i z x x N ∈====∑∑ 2202(1)9211(2)(7.677.33)12t i x S i z x x N ∈====∑∑ 第四步:(2)(1),1,2,j j z z j ≠=故回到第二步。
第二步:从新的聚类中心,得12(2)(2)i i x z x z -<-P P P P i=1,2, …,8,故1(1),1,2,,8i x S i ∈=K 12(1)(1)i i x z x z ->-P P P P i=9,10, …,20,故2(1),9,10,,20i x S i ∈=K得 1128(2){,,...}S x x x =,291020(2){,,...}S x x x =第三步:计算聚类中心181(2)1111(3)(1.25 1.13)8t i x S i z x x N ∈====∑∑ 2202(2)9211(3)(7.677.33)12t i x S i z x x N ∈====∑∑ 第四步:(3)(2),1,2,j j z z j ==所以聚类算法收敛,得聚类中心为1(1.25 1.13)tz =, 2(7.677.33)t z =最终聚类结果为:},...,{8211x x x S =,},...,{201092x x x S = 4.编写K-均值聚类算法程序,对下图所示数据进行聚类分析(选k=2)。
clear all ; close all ;Data=[0 0 1 1 1 2 2 3 6 6 7 7 7 8 8 8 8 9 9 9 0 1 0 1 2 1 2 2 6 7 6 7 8 6 7 8 9 7 8 9;]; [DataRow,DataColumn]=size(Data); Step=10;NumKind=2;Center=Data(:,1:NumKind);[KindData,KindNum]=Clustering(Center,Data);NewCenter=CaculateCenter(KindData,KindNum,DataRow);while (sum(sum(NewCenter~=Center))) & StepCenter=NewCenter;[KindData,KindNum]=Clustering(Center,Data);NewCenter=CaculateCenter(KindData,KindNum,DataRow);Step=Step-1;endfor i=1:NumKindKindData(:,1:KindNum(i),i)end%计算聚类中心function NewCenter=CaculateCenter(KindData,KindNum,DataRow) TotalKindNum=length(KindNum);NewCenter=zeros(DataRow,TotalKindNum);for i=1:TotalKindNumTemp=KindData(:,1:KindNum(i),i);NewCenter(:,i)=sum(Temp')'/KindNum(i);end%聚类function [KindData,KindNum]=Clustering(Center,Data)[DataRow,DataColumn]=size(Data);[CenterRow,CenterColumn]=size(Center);KindData=zeros(DataRow,DataColumn,CenterColumn);KindNum=linspace(0,0,CenterColumn);for i=1:DataColumnDistance=linspace(0,0,CenterColumn);for j=1:CenterColumnfor k=1:DataRowDistance(j)=Distance(j)+(Data(k,i)-Center(k,j)).^2;endendDistance=sqrt(Distance);[X,Y]=min(Distance);KindData(:,KindNum(Y)+1,Y)=Data(:,i);KindNum(Y)=KindNum(Y)+1;endans =0 0 1 1 1 2 2 30 1 0 1 2 1 2 2ans =6 67 7 78 8 8 89 9 96 7 6 7 8 6 7 8 9 7 8 9 5.画出ISODATA的的流程图。
第八步分裂运算具体算法:第十一步合并处理具体算法:6.试用ISODATA 对如下模式进行聚类分析:{x1(0,0), x2(3,8),x3(2,2), x4(1,1), x5(5,3), x6(4,8), x7(6,3), x8(5,4), x9(6,4), x10(7,5)} 解:第一步:已知N=10,n=2;取参数K=3, c N =1,1(00)t z =N θ=1,S θ=1,c θ=1,L=1,I=6。
第二步:因只有一个聚类中心,故11210{,,,}S x x x =K 和1N =10。
第三步:因1N >N θ,所以无子集可抛弃。
第四步:修改聚类中心 1111(3.93.8)t x S z x N ∈==∑第五步:计算j D 11111 3.0749x S D x zN ∈=-=∑P P第六步:计算D D =1D =3.0749第七步:因为还不是最后一次迭代,且c N <K/2,故进入第八步。
第八步:求1S 中的标准差向量 t 1(2.21132.5219)σ=第九步:1σ中的最大分量是2.5219,因此1max 2.5219σ=。
第十步:因为1max σ>S θ,且c N <K/2,可将1z 分裂成两个新的聚类。
设1max 0.5 1.2610j r σ=≈,则1(3.9 5.1)tz +=, 1(3.9 1.5)t z -=分别记为1z 和2z ,且c N =2,跳回到第二步。
第二步:新的样本集为1268910{,,,,.}S x x x x x =,213457{,,,,}S x x x x x = 则1N =5,2N =5 第三步:因为1N 和2N 都大于N θ,无子集可抛弃。
第四步:修改聚类中心 1(55.8)t z =,2(2.8 1.8)t z =第五步:计算j D ,j=1,2 111112.2806x S D x zN ∈=-=∑P P ,22221 2.4093x S D x zN ∈=-=∑P P第六步:计算D21111 2.34510c N j j j j j j D N D N D N =====∑∑ 第七步:因为这是偶次迭代,进入第十一步。
第十一步:计算聚类中心之间的距离 1212 4.5651D z z =-=P P 第十二步:比较12D 与c θ,12D >c θ.第十三步:聚类中心不能合并。
第十四步:因聚类之间的分离度大于类内样本分离的标准差,且每一子集的样本数目都具有样本总数中的足够大的百分比,所以不需修改给定的参数。
回到第二步。
第二步:新的样本集为12678910{,,,,,}S x x x x x x =,21345{,,,}S x x x x =且1N =6,2N =4。
因为1N 和2N 都大于N θ,无子集可抛弃。
第四步:修改聚类中心1(5.175.33)t z =,2(2 1.5)t z =第五步:计算j D ,j=1,2 11111 2.2673x S D x z N ∈=-=∑P P ,22221 1.868x S D x zN ∈=-=∑P P第六步:计算D21111 2.107610c N j j j j j j D N D N D N =====∑∑ 第七步:因不满足任何一个条件,直接进入第八步。
