ANSYS实例分析75道(含结果)
ansys结果误差分析

有限元法分析结果的误差影响2009年12月23日安世亚太一、引言有限元法分析起源于50年代初杆系结构矩阵的分析。
随后,Clough于1960年第一次提出了“有限元法”的概念。
其基本思想是利用结构离散化的概念,将连续介质体或复杂结构体划分成许多有限大小的子区域的集合体,每一个子区域称为单元(或元素),单元的集合称为网格,实际的连续介质体(或结构体)可以看成是这些单元在它们的节点上相互连接而组成的等效集合体;通过对每个单元力学特性的分析,再将各个单元的特性矩阵组集成可以建立整体结构的力学方程式,即力学计算模型;按照所选用计算程序的要求,输入所需的数据和信息,运用计算机进行求解。
当前,有限元方法/理论已经发展的相当成熟和完善,而计算机技术的不断革新,又在很大程度上推进了有限元法分析在工程技术领域的应用。
然而,如此快速地推广和应用使得人们很容易忽视一个前提,即有限元分析软件提供的计算结果是否可靠、满足使用精度的前提,是合理地使用软件和专业的工程分析。
只有这两者很好地结合,我们才能得到工程上切实可信的计算结果,否则只会在工程上造成极大的浪费,甚至带来严重的工程事故。
二、误差分析有限元法分析一般包括四个步骤:物理模型的简化、数学模型的程序化、计算模型的数值化和计算结果的分析。
每一个步骤在操作过程中都或多或少地引入了误差,这些误差的累积最终可能会对计算结果造成灾难性的影响,进而蒙蔽我们的认识和判断。
第一步,物理模型的简化,主要有几何实体、连接/装配关系、环境边界条件和材料特性的简化,进而构建数学模型。
这些简化或者说假设,是必要的,也是必须的,但是也由此在模型中引入了理想化误差(idealization error)。
有些理想化误差是非良性奇异的,比如几何实体简化时细节部位上忽略小的圆/倒角,连接/装配关系简化时忽略焊缝和螺栓连接等,往往导致模型发生结构方面(诸如L形截面的角点)的奇异,即结构奇异(奇异的数学定义是在某一点处导数无穷);有些理想化误差是良性奇异的,比如边界条件简化时添加集中载荷和孤立点约束,导致模型发生边界条件的奇异,即边界奇异;其它理想化误差,比如几何实体简化时三维壳/面体简化为二维壳/面、三维梁简化为一维梁,边界条件简化时非均匀温度场和压力场简化为均匀温度场和压力场等,只会影响计算结果的准确度,不会引发计算结果方面的数值奇异,即应力奇异和位移奇异等。
最新ANSYS子弹碰撞问题实例

非线性静态实例分析(GUI 方法)在这个实例分析中,你将进行一个子弹冲击刚性壁的非线性分析。
问题描述一个子弹以给定的速度射向壁面。
壁面假定是刚性的和无摩擦的。
将研究子弹和壁面接触后达80 微秒长的现象。
目的是确定子弹的整个变形,速度历程,以及最大等效V on Mises 应变。
求解使用SI 单位。
用轴对称单元模拟棒。
求解最好能通过单一载荷步实现。
在这个载荷步中,将同时施加初始速度和约束。
将圆柱体末端的节点Y 方向约束住以模拟一固壁面。
打开自动时间分步来允许ANSYS 确定时间步长。
定义分析结束的时间为8E-5 秒,以确保有足够长的时间来扑捉整个变形过程。
问题详细说明下列材料性质应用于这个问题:EX=117.0E09(杨氏模量)DENS=8930.0 (密度)NUXY=0.35(泊松比)Yield Strength=400.0OE06(屈服强度)Tangent Modulus (剪切模量)下列尺寸应用于这个问题:长=32.4E-3m 直径=6.4E-3m 对于这个问题的初始速度是227.0。
图1─10 铜圆柱体图解求解步骤:步骤一:设置分析标题1、选择菜单路径:Utility Menn>File>ChangeTitle。
2、键入文字“Coppery Cylinder Impacting a Rigid Wall”3、单击OK。
步骤二:定义单元类型1、选择菜单路径Mail Menu>Preprocessor>Element Type>All/Edit/Delete。
2、单击Add。
Library of Element Types(单元类型库)对话框出现。
3、在靠近左边的列表中,单击“V isio Solid”仅一次。
4、选靠近右边的列表中,单击“4node Plas 106”仅一次。
5、单击OK。
Library of Element Types 对话框关闭。
6、单击Options (选项)。
ANSYS弹性及塑性分析非常经典

目录什么是塑性 (1)路径相关性 (1)率相关性 (1)工程应力、应变与真实应力、应变 (1)什么是激活塑性 (2)塑性理论介绍 (2)屈服准则 (2)流动准则 (3)强化准则 (3)塑性选项 (5)怎样使用塑性 (6)ANSYS输入 (7)输出量 (7)程序使用中的一些基本原则 (8)加强收敛性的方法 (8)查看结果 (9)塑性分析实例(GUI方法) (9)塑性分析实例(命令流方法) (14)弹塑性分析在这一册中,我们将详细地介绍由于塑性变性引起的非线性问题--弹塑性分析,我们的介绍人为以下几个方面:∙什么是塑性∙塑性理论简介∙ANSYS程序中所用的性选项∙怎样使用塑性∙塑性分析练习题什么是塑性塑性是一种在某种给定载荷下,材料产生永久变形的材料特性,对大多的工程材料来说,当其应力低于比例极限时,应力一应变关系是线性的。
另外,大多数材料在其应力低于屈服点时,表现为弹性行为,也就是说,当移走载荷时,其应变也完全消失。
由于屈服点和比例极限相差很小,因此在ANSYS程序中,假定它们相同。
在应力一应变的曲线中,低于屈服点的叫作弹性部分,超过屈服点的叫作塑性部分,也叫作应变强化部分。
塑性分析中考虑了塑性区域的材料特性。
路径相关性:即然塑性是不可恢复的,那么这种问题的就与加载历史有关,这类非线性问题叫作与路径相关的或非保守的非线性。
路径相关性是指对一种给定的边界条件,可能有多个正确的解—内部的应力,应变分布—存在,为了得到真正正确的结果,我们必须按照系统真正经历的加载过程加载。
率相关性:塑性应变的大小可能是加载速度快慢的函数,如果塑性应变的大小与时间有关,这种塑性叫作率无关性塑性,相反,与应变率有关的性叫作率相关的塑性。
大多的材料都有某种程度上的率相关性,但在大多数静力分析所经历的应变率范围,两者的应力-应变曲线差别不大,所以在一般的分析中,我们变为是与率无关的。
工程应力,应变与真实的应力、应变:塑性材料的数据一般以拉伸的应力—应变曲线形式给出。
ansysworkbench瞬态动力学实例

在本文中,我将为您撰写一篇关于ANSYS Workbench瞬态动力学实例的文章。
我们将深入探讨ANSYS Workbench在瞬态动力学仿真方面的应用,从简单到复杂、由浅入深地讨论其原理和实践操作,并共享个人观点和理解。
第一部分:介绍ANSYS Workbench瞬态动力学仿真ANSYS Workbench是一种用于工程仿真的全面评台,包含了结构、流体、热传递、多物理场等多种仿真工具。
瞬态动力学仿真是ANSYS Workbench的重要应用之一,它能够模拟在时间和空间上随机变化的动力学过程,并对结构在外部力作用下的动力响应进行分析。
在瞬态动力学仿真中,ANSYS Workbench可以模拟诸如碰撞、冲击、振动等动态载荷下的结构响应,用于评估零部件的耐久性、振动特性、动态稳定性等重要工程问题。
通过对这些现象的模拟和分析,工程师可以更好地了解结构在实际工况下的性能,进而进行有效的设计优化和改进。
第二部分:实例分析为了更直观地展示ANSYS Workbench瞬态动力学仿真的应用,我们以汽车碰撞仿真为例进行分析。
假设我们需要评估汽车前部结构在碰撞事故中的动态响应,我们可以通过ANSYS Workbench建立汽车前部结构的有限元模型,并对其进行碰撞载荷下的瞬态动力学仿真。
我们需要构建汽车前部结构的有限元模型,包括车身、前保险杠、引擎盖等部件,并设定材料属性、连接方式等。
接下来,我们可以在仿真中引入具体的碰撞载荷,如40km/h车速下的正面碰撞载荷,并进行瞬态动力学仿真分析。
通过仿真结果,我们可以获取汽车前部结构在碰撞中的应力、应变分布,以及变形情况,从而评估其在碰撞事故中的性能表现。
第三部分:个人观点与总结通过以上实例分析,我们可以看到ANSYS Workbench瞬态动力学仿真在工程实践中的重要应用价值。
瞬态动力学仿真不仅能够帮助工程师分析结构在动态载荷下的响应,还可以为设计优化、安全评估等工程问题提供重要参考。
ANSYS计算结果与分析

ANSYS 计算结果与分析一、 有限元原理:有限元的解题思路可简述为:从结构的位移出发,通过寻找位移和应变, 应变与应力,应力与内力,内力与外力的关系,建立相应的方程组,从而由已知的外力求出结构的内应力和位移。
有限元分析过程由其基本代数方程组成:[K] {V}={Q},[K]为整个结构的刚变矩阵,{V}为未知位移量,{Q}为载荷向量。
这些量是不确定的,依靠所需解决的问题进行定量描述。
上述结构方程是通过应用边界条件,将结构离散化成小单元,从综合平衡方程中获得。
有限元是通过单元划分, 在某种程度上模拟真实结构,并由数字对结构诸方面进行描述。
其描述的准确性依赖于单元细划的程度,载荷的真实性,材料力学参数的可信度,边界条件处理的正确程度。
本算例采用三角形六结点来划分单元。
二、 有限元解题步骤:有限元的解题步骤为: ①连续体的离散化;②选择单元位移函数;③建立单元刚度矩阵;④求解代数方程组,得到所有节点位移分量;⑤由节点位移求出内力或应力。
三、工程实例分析现已知一混凝土截面梁,长为L=2.4m ,梁高为m h 3.0=,梁宽设为单位宽度。
混凝土材料的各项属性为:容重3/25m KN =γ,E=2.4E10Pa ,2.0=λ。
若该混凝土梁分别受到以下两种不同约束和不同受力的作用:(1)两端受固定约束作用,中间作用一个集中荷载P=10KN 作用,如图A 所示。
(2)一端受固定约束作用悬臂梁,梁上作用一均布荷载q=5KN/m作用,如图B所示。
现要求使用有限元中的三角形六节点单元来计算两种情况下梁的位移与应力,并与力学计算结果进行比较和分析ANSYS分析过程(1)两端固定有限元模型Y方向位移图X方向应力图具体节点位移如下表:Y方向挠度(单位:m)节点挠度节点挠度节点挠度节点挠度1 0 82 -1.25E-05 163 -5.75E-06 244 -2.89E-052 0 83 -5.84E-06 164 -5.76E-06 245 -2.88E-053 -1.16E-06 84 -1.11E-06 165 -5.81E-06 246 -2.74E-054 -3.19E-06 85 -1.02E-06 166 -9.02E-06 247 -2.74E-055 -5.87E-06 86 -5.78E-06 167 -9.00E-06 248 -2.75E-056 -9.05E-06 87 -1.25E-05 168 -8.99E-06 249 -2.75E-057 -1.25E-05 88 -1.94E-05 169 -8.98E-06 250 -2.75E-058 -1.60E-05 89 -2.53E-05 170 -8.97E-06 251 -2.75E-059 -1.94E-05 90 -2.89E-05 171 -8.97E-06 252 -2.75E-0510 -2.25E-05 91 -2.89E-05 172 -8.97E-06 253 -2.75E-0511 -2.52E-05 92 -2.53E-05 173 -8.97E-06 254 -2.75E-0512 -2.74E-05 93 -1.94E-05 174 -8.98E-06 255 -2.74E-0513 -2.87E-05 94 -1.25E-05 175 -9.00E-06 256 -2.74E-0514 -2.92E-05 95 -5.78E-06 176 -9.01E-06 257 -2.53E-0515 -2.87E-05 96 -1.03E-06 177 -1.25E-05 258 -2.53E-0516 -2.73E-05 97 -9.93E-07 178 -1.25E-05 259 -2.53E-0517 -2.52E-05 98 -5.75E-06 179 -1.25E-05 260 -2.53E-0518 -2.25E-05 99 -1.25E-05 180 -1.25E-05 261 -2.53E-05应力表(单位:pa)xNODE SX SY SZ SXY SYZ SXZ1 -0.47117E+06 -94234. 0.0000 -71939. 0.0000 0.00002 -0.44824E+06 -43524. 0.0000 36804. 0.0000 0.0000 4 -0.26659E+06 24017. 0.0000 11756. 0.0000 0.00006 -0.11092E+06 -1675.1 0.0000 -1416.0 0.0000 0.00008 26454. -287.29 0.0000 -529.21 0.0000 0.000010 0.14396E+06 -296.19 0.0000 -428.64 0.0000 0.000012 0.24665E+06 -154.80 0.0000 -931.20 0.0000 0.0000 14 0.31294E+06 -651.06 0.0000 1868.1 0.0000 0.000016 0.25514E+06 777.86 0.0000 2607.3 0.0000 0.0000 18 0.15259E+06 421.23 0.0000 955.79 0.0000 0.0000 20 36815. 350.40 0.0000 1367.3 0.0000 0.0000 22 -99169. 406.51 0.0000 1539.1 0.0000 0.0000 24 -0.25029E+06 709.47 0.0000 469.07 0.0000 0.0000 26 0.47021E+06 94043. 0.0000 71822. 0.0000 0.0000 28 -0.26849E+06 -41899. 0.0000 46711. 0.0000 0.0000 30 -0.12480E+06 -20589. 0.0000 44463. 0.0000 0.0000 32 2346.1 1441.3 0.0000 44301. 0.0000 0.0000 34 0.13084E+06 23544. 0.0000 46007. 0.0000 0.0000 36 0.27890E+06 44622. 0.0000 49721. 0.0000 0.0000 38 0.44740E+06 43435. 0.0000 -36738. 0.0000 0.000040 0.26576E+06 -23958. 0.0000 -11724. 0.0000 0.0000 42 0.11006E+06 1672.9 0.0000 1413.1 0.0000 0.0000 44 -27364. 285.26 0.0000 538.86 0.0000 0.0000 46 -0.14505E+06 297.97 0.0000 455.70 0.0000 0.0000 48 -0.23089E+06 828.18 0.0000 -2277.4 0.0000 0.0000 50 -0.35045E+06 -94932. 0.0000 4506.0 0.0000 0.0000 52 -0.23867E+06 40010. 0.0000 13774. 0.0000 0.0000 54 -0.15354E+06 -1579.2 0.0000 -2170.7 0.0000 0.0000 56 -37694. -287.51 0.0000 -1318.8 0.0000 0.0000 58 98366. -412.70 0.0000 -1539.9 0.0000 0.0000 60 0.24952E+06 -708.11 0.0000 -474.61 0.0000 0.0000 63 0.26768E+06 41770. 0.0000 -46653. 0.0000 0.0000 65 0.12400E+06 20454. 0.0000 -44435. 0.0000 0.0000 67 -3155.0 -1579.4 0.0000 -44304. 0.0000 0.0000 69 -0.13167E+06 -23682. 0.0000 -46041. 0.0000 0.0000 71 -0.27977E+06 -44758. 0.0000 -49784. 0.0000 0.0000 151 0.18243E+06 -5692.4 0.0000 37694. 0.0000 0.0000 153 93763. -895.44 0.0000 60650. 0.0000 0.0000155 2906.0 1964.2 0.0000 67290. 0.0000 0.0000157 -87037. 5292.4 0.0000 58490. 0.0000 0.0000159 -0.17211E+06 11178. 0.0000 31663. 0.0000 0.0000167 73372. -851.10 0.0000 31158. 0.0000 0.0000169 39292. -840.75 0.0000 49441. 0.0000 0.0000171 3787.8 -337.99 0.0000 55813. 0.0000 0.0000173 -32101. 100.68 0.0000 50074. 0.0000 0.0000175 -67944. 717.92 0.0000 32029. 0.0000 0.0000183 -17938. -922.76 0.0000 27092. 0.0000 0.0000185 -6795.5 -612.85 0.0000 42946. 0.0000 0.0000187 3071.2 18.206 0.0000 48306. 0.0000 0.0000189 12803. 565.23 0.0000 43126. 0.0000 0.0000191 22747. 538.90 0.0000 27571. 0.0000 0.0000199 -96298. -717.39 0.0000 22710. 0.0000 0.0000201 -46228. -1019.6 0.0000 36320. 0.0000 0.0000203 2626.4 121.91 0.0000 40665. 0.0000 0.0000205 51239. 880.36 0.0000 36356. 0.0000 0.0000207 0.10012E+06 736.28 0.0000 23263. 0.0000 0.0000215 -0.15923E+06 18494. 0.0000 11061. 0.0000 0.0000217 -83947. 9075.8 0.0000 29103. 0.0000 0.0000219 -2385.6 4224.8 0.0000 35294. 0.0000 0.0000221 80991. 2496.3 0.0000 32516. 0.0000 0.0000223 0.16576E+06 1612.2 0.0000 21754. 0.0000 0.0000231 -0.20646E+06 -75438. 0.0000 -1738.1 0.0000 0.0000 233 -93006. -51133. 0.0000 -1579.6 0.0000 0.0000235 6530.2 -30687. 0.0000 -666.93 0.0000 0.0000237 0.10345E+06 -14749. 0.0000 125.67 0.0000 0.0000 239 0.20441E+06 -4119.4 0.0000 970.85 0.0000 0.0000 247 -0.16755E+06 9862.5 0.0000 -17509. 0.0000 0.0000 249 -87809. 3440.9 0.0000 -31319. 0.0000 0.0000 251 -5584.0 978.66 0.0000 -35737. 0.0000 0.0000 253 77562. 806.61 0.0000 -31968. 0.0000 0.0000 255 0.16243E+06 1086.9 0.0000 -20148. 0.0000 0.0000 263 -0.10061E+06 -689.88 0.0000 -23108. 0.0000 0.0000 265 -51874. -100.28 0.0000 -35992. 0.0000 0.0000 267 -3478.2 629.38 0.0000 -40521. 0.0000 0.0000 269 45225. 1049.3 0.0000 -36167. 0.0000 0.0000 271 95246. 1060.4 0.0000 -22892. 0.0000 0.0000 279 -23597. -576.87 0.0000 -27627. 0.0000 0.0000 281 -13606. -652.21 0.0000 -43170. 0.0000 0.0000 283 -3857.7 -89.957 0.0000 -48308. 0.0000 0.0000 285 5980.8 542.38 0.0000 -42912. 0.0000 0.0000 287 17073. 893.21 0.0000 -27066. 0.0000 0.0000 295 67130. -714.95 0.0000 -32028. 0.0000 0.0000 297 31274. -97.707 0.0000 -50075. 0.0000 0.0000 299 -4624.8 340.23 0.0000 -55817. 0.0000 0.0000 301 -40137. 841.32 0.0000 -49444. 0.0000 0.0000 303 -74225. 850.89 0.0000 -31160. 0.0000 0.0000 311 0.17131E+06 -11152. 0.0000 -31681. 0.0000 0.0000 313 86204. -5274.6 0.0000 -58500. 0.0000 0.0000 315 -3755.8 -1950.0 0.0000 -67295. 0.0000 0.0000 317 -94623. 911.23 0.0000 -60649. 0.0000 0.0000 319 -0.18330E+06 5714.3 0.0000 -37686. 0.0000 0.0000由以上分析结果可以得出:跨中最大挠度为:2.95E-05m 梁端上截面应力为:-0.35Mpa 跨中上截面应力: 0.47Mpa 跨中下截面应力为:-0.471Mpa 用材料力学进行校核:62bh W z =, 左右杆端弯矩为:122ql , 跨中弯矩为:242ql左右杆端截面正应力为:MPa bh ql bh ql 32.026122222===σ 跨中截面正应力为:MPa bhql bh ql 47.046242222===σ 由图乘法求跨中截面的挠度,具体的计算公式如下:mE EIql ql EI l ql l l l ql l l ql EI W 0595.23741)384157611441(1)212321232312224121322212121(144222-==--=⨯⨯⨯⨯-⨯⨯⨯⨯-⨯⨯⨯⨯=ANSYS 分析结果 结构力学结果误差跨中挠度(m ) 2.95E-05 2.53E-05 16.60% 梁端上截面应力(Mpa ) -0.35 -0.32 9.38% 梁端下截面应力(Mpa ) 0.313 0.32 2.19% 跨中上截面应力(Mpa ) 0.47 0.44 6.82% 跨中下截面应力(Mpa ) -0.471 -0.447.05%(2)一端固定一端自由Y 方向位移图X方向应力图具体节点位移如下表:节点挠度节点挠度节点挠度节点挠度1 0 82 -7.74E-05 163 -8.12E-04 244 -3.03E-042 -9.72E-04 83 -3.10E-05 164 -8.12E-04 245 -3.03E-043 -5.05E-06 84 -4.71E-06 165 -8.12E-04 246 -2.59E-044 -1.55E-05 85 -9.19E-04 166 -7.59E-04 247 -2.59E-045 -3.13E-05 86 -8.12E-04 167 -7.59E-04 248 -2.59E-046 -5.22E-05 87 -7.06E-04 168 -7.59E-04 249 -2.59E-047 -7.77E-05 88 -6.00E-04 169 -7.59E-04 250 -2.58E-048 -1.07E-04 89 -4.97E-04 170 -7.59E-04 251 -2.58E-049 -1.41E-04 90 -3.97E-04 171 -7.59E-04 252 -2.58E-0410 -1.77E-04 91 -3.03E-04 172 -7.59E-04 253 -2.58E-0411 -2.17E-04 92 -2.16E-04 173 -7.59E-04 254 -2.59E-0412 -2.59E-04 93 -1.40E-04 174 -7.59E-04 255 -2.59E-0413 -3.03E-04 94 -7.70E-05 175 -7.59E-04 256 -2.59E-0414 -3.50E-04 95 -3.05E-05 176 -7.59E-04 257 -2.17E-0415 -3.97E-04 96 -4.15E-06 177 -7.06E-04 258 -2.16E-0416 -4.47E-04 97 -9.19E-04 178 -7.06E-04 259 -2.16E-0417 -4.97E-04 98 -8.12E-04 179 -7.06E-04 260 -2.16E-04应力表(单位:pa)xNODE SX SY SZ SXY SYZ SXZ1 -0.25013E+07-0.50026E+06 0.0000 -0.23536E+06 0.0000 0.00002 2344.3 55.551 0.0000 1381.4 0.0000 0.0000 4 -0.20145E+07 0.13137E+06 0.0000 42962. 0.0000 0.0000 6 -0.16765E+07 -5697.0 0.0000 -4238.2 0.0000 0.0000 8 -0.13587E+07 -602.67 0.0000 -1529.1 0.0000 0.0000 10 -0.10740E+07 -762.28 0.0000 -1374.8 0.0000 0.0000 12 -0.82262E+06 -655.05 0.0000 -1117.5 0.0000 0.0000 14 -0.60460E+06 -562.14 0.0000 -863.89 0.0000 0.0000 16 -0.41991E+06 -468.62 0.0000 -610.04 0.0000 0.0000 18 -0.26856E+06 -375.13 0.0000 -356.22 0.0000 0.0000 20 -0.15053E+06 -281.65 0.0000 -102.36 0.0000 0.0000 22 -65843. -187.66 0.0000 150.44 0.0000 0.0000 24 -14504. -102.05 0.0000 417.31 0.0000 0.0000 26 -3100.4 -5193.8 0.0000 775.10 0.0000 0.0000 28 742.77 684.07 0.0000 633.96 0.0000 0.0000 30 -17.938 -317.56 0.0000 -285.27 0.0000 0.000032 -477.64 -2424.3 0.0000 -770.67 0.0000 0.000034 -781.28 -4602.3 0.0000 -570.42 0.0000 0.0000 36 -1125.5 -5696.4 0.0000 -174.96 0.0000 0.0000 38 0.24391E+07 0.24437E+06 0.0000 -0.11805E+06 0.0000 0.0000 40 11812. -4996.7 0.0000 -1071.1 0.0000 0.0000 42 60425. -5175.6 0.0000 -1154.9 0.0000 0.0000 44 0.14240E+06 -5280.4 0.0000 -1421.3 0.0000 0.0000 46 0.25771E+06 -5372.8 0.0000 -1674.3 0.0000 0.0000 48 0.40636E+06 -5466.3 0.0000 -1928.2 0.0000 0.0000 50 0.58834E+06 -5559.8 0.0000 -2182.0 0.0000 0.0000 52 0.80365E+06 -5653.3 0.0000 -2435.9 0.0000 0.0000 54 0.10523E+07 -5746.8 0.0000 -2689.9 0.0000 0.0000 56 0.13342E+07 -5842.7 0.0000 -2932.1 0.0000 0.0000 58 0.16503E+07 -5879.4 0.0000 -3376.0 0.0000 0.0000 60 0.19778E+07 -7803.0 0.0000 2914.3 0.0000 0.0000 63 0.15354E+07 0.22889E+06 0.0000 -0.10713E+06 0.0000 0.0000 65 0.73975E+06 0.11355E+06 0.0000 -70967. 0.0000 0.0000 67 -7600.7 -6004.9 0.0000 -61499. 0.0000 0.0000 69 -0.75765E+06-0.12447E+06 0.0000 -78773. 0.0000 0.0000 71 -0.15608E+07-0.23582E+06 0.0000 -0.12284E+06 0.0000 0.0000 151 9798.9 -5221.2 0.0000 -7608.6 0.0000 0.0000 153 4996.1 -4256.1 0.0000 -11467. 0.0000 0.0000 155 -911.85 -2609.3 0.0000 -12699. 0.0000 0.0000 157 -6764.9 -887.12 0.0000 -11142. 0.0000 0.0000 159 -11230. 312.08 0.0000 -6755.7 0.0000 0.0000 167 42347. -5311.7 0.0000 -14833. 0.0000 0.0000 169 20742. -4334.3 0.0000 -22836. 0.0000 0.0000 171 -1834.5 -2501.8 0.0000 -25426. 0.0000 0.0000 173 -24341. -653.58 0.0000 -22464. 0.0000 0.0000 175 -45318. 505.18 0.0000 -13939. 0.0000 0.0000 183 97163. -5261.6 0.0000 -22022. 0.0000 0.0000 185 47621. -4327.6 0.0000 -34159. 0.0000 0.0000 187 -2750.4 -2507.1 0.0000 -38140. 0.0000 0.0000 189 -53018. -662.65 0.0000 -33786. 0.0000 0.0000 191 -0.10162E+06 539.25 0.0000 -21132. 0.0000 0.0000 199 0.17420E+06 -5215.6 0.0000 -29214. 0.0000 0.0000 201 85610. -4326.4 0.0000 -45483. 0.0000 0.0000 203 -3667.2 -2509.3 0.0000 -50853. 0.0000 0.0000 205 -92806. -660.75 0.0000 -45110. 0.0000 0.0000 207 -0.18014E+06 586.11 0.0000 -28324. 0.0000 0.0000 215 0.27346E+06 -5169.3 0.0000 -36406. 0.0000 0.0000 217 0.13471E+06 -4324.8 0.0000 -56807. 0.0000 0.0000 219 -4584.1 -2511.7 0.0000 -63566. 0.0000 0.0000 221 -0.14371E+06 -659.14 0.0000 -56434. 0.0000 0.0000 223 -0.28088E+06 632.39 0.0000 -35517. 0.0000 0.0000231 0.39494E+06 -5123.0 0.0000 -43599. 0.0000 0.0000 233 0.19492E+06 -4323.2 0.0000 -68131. 0.0000 0.0000 235 -5500.9 -2514.0 0.0000 -76279. 0.0000 0.0000 237 -0.20572E+06 -657.53 0.0000 -67758. 0.0000 0.0000 239 -0.40384E+06 678.71 0.0000 -42709. 0.0000 0.0000 247 0.53864E+06 -5076.5 0.0000 -50791. 0.0000 0.0000 249 0.26624E+06 -4321.2 0.0000 -79456. 0.0000 0.0000 251 -6417.7 -2516.1 0.0000 -88993. 0.0000 0.0000 253 -0.27884E+06 -655.95 0.0000 -79083. 0.0000 0.0000 255 -0.54903E+06 724.90 0.0000 -49901. 0.0000 0.0000 263 0.70456E+06 -5031.3 0.0000 -57983. 0.0000 0.0000 265 0.34868E+06 -4322.8 0.0000 -90782. 0.0000 0.0000 267 -7336.1 -2519.0 0.0000 -0.10171E+06 0.0000 0.0000 269 -0.36307E+06 -649.67 0.0000 -90406. 0.0000 0.0000 271 -0.71644E+06 772.81 0.0000 -57090. 0.0000 0.0000 279 0.89269E+06 -5018.3 0.0000 -65150. 0.0000 0.0000 281 0.44225E+06 -4346.5 0.0000 -0.10206E+06 0.0000 0.0000 283 -8193.7 -2657.9 0.0000 -0.11441E+06 0.0000 0.0000 285 -0.45838E+06 -751.50 0.0000 -0.10180E+06 0.0000 0.0000 287 -0.90611E+06 819.40 0.0000 -64358. 0.0000 0.0000 295 0.11033E+07 -4700.3 0.0000 -72715. 0.0000 0.0000 297 0.54631E+06 -1332.2 0.0000 -0.11431E+06 0.0000 0.0000 299 -10032. -610.15 0.0000 -0.12657E+06 0.0000 0.0000 301 -0.56488E+06 156.41 0.0000 -0.11184E+06 0.0000 0.0000由以上分析结果可一得出:梁端最大挠度为:9.72E-04m 梁端截面最大应力为:-2.5Mpa 用材料力学进行校核:62bh W z =, 杆端弯矩为:FL左右杆端截面正应力为:MPa bh ql bh ql 32.026122222===σ固端截面正应力为:MPa bhFLbh FL 4.226622===σ 左右杆端截面正应力为:MPa bhql bh ql 32.026122222===σ 由图乘法可知自由端的挠度为:m EIFL L L FL EI W 04-9.60E 31)3221(13==⨯⨯⨯=结论在对本工程进行ANSYS有限元数值分析过程中,作者采用的单元形式为三角形六节点单元PLANE2单元,因其为平面单元,ANSYS计算过程中没有输入梁的宽度,其计算默认的梁宽为一个单位。
ANSYS实例分析-飞机机翼
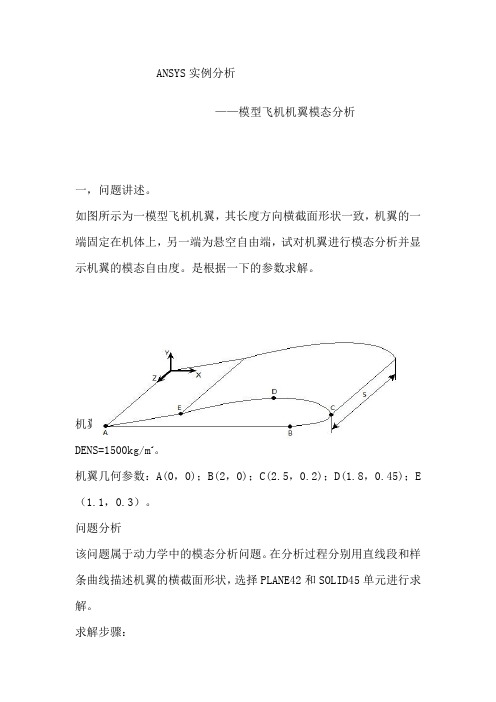
ANSYS实例分析——模型飞机机翼模态分析一,问题讲述。
如图所示为一模型飞机机翼,其长度方向横截面形状一致,机翼的一端固定在机体上,另一端为悬空自由端,试对机翼进行模态分析并显示机翼的模态自由度。
是根据一下的参数求解。
机翼材料参数:弹性模量EX=7GPa;泊松比PRXY=0.26;密度DENS=1500kg/m3。
机翼几何参数:A(0,0);B(2,0);C(2.5,0.2);D(1.8,0.45);E (1.1,0.3)。
问题分析该问题属于动力学中的模态分析问题。
在分析过程分别用直线段和样条曲线描述机翼的横截面形状,选择PLANE42和SOLID45单元进行求解。
求解步骤:第1 步:指定分析标题并设置分析范畴1.选取菜单途径Utility Menu>File>Change Title2.输入文字“Modal analysis of a model airplane wing”,然后单击OK。
3.选取菜单途径Main Menu>Preferences.4.单击Structure选项使之为ON,单击OK。
主要为其命名的作用。
第2 步:定义单元类型1.选取菜单途径:MainMenu>Preprocessor>Element Type>Add/Edit/Delete。
2.Element Types对话框将出现。
3.单击Add。
Library ofElement Types对话框将出现。
4.在左边的滚动框中单击“Structural Solid”。
5.在右边的滚动框中单击“Quad 4node 42”。
6.单击Apply。
7.在右边的滚动框中单击“Brick 8node 45”。
8.单击OK。
9.单击Element Types对话框中的Close按钮。
第3 步:指定材料性能1.选取菜单途径Main Menu>Preprocessor>MaterialProps>-Constant-Isot ropic。
ANSYS接触实例分析参考
ANSYS接触实例分析参考1.实例描述一个钢销插在一个钢块中的光滑销孔中。
已知钢销的半径是0.5 units, 长是2.5 units,而钢块的宽是 4 Units, 长4 Units,高为1 Units,方块中的销孔半径为0.49 units,是一个通孔。
钢块与钢销的弹性模量均为36e6,泊松比为0.3.由于钢销的直径比销孔的直径要大,所以它们之间是过盈配合。
现在要对该问题进行两个载荷步的仿真。
(1)要得到过盈配合的应力。
(2)要求当把钢销从方块中拔出时,应力,接触压力及约束力。
2.问题分析由于该问题关于两个坐标面对称,因此只需要取出四分之一进行分析即可。
进行该分析,需要两个载荷步:第一个载荷步,过盈配合。
求解没有附加位移约束的问题,钢销由于它的几何尺寸被销孔所约束,由于有过盈配合,因而产生了应力。
第二个载荷步,拔出分析。
往外拉动钢销1.7 units,对于耦合节点上使用位移条件。
打开自动时间步长以保证求解收敛。
在后处理中每10个载荷子步读一个结果。
本篇先谈第一个载荷步的计算。
下篇再谈第二个载荷步的计算。
3.读入几何体首先打开ANSYS APDL然后读入已经做好的几何体。
从【工具菜单】-->【File】-->【Read Input From】打开导入文件对话框找到ANSYS自带的文件(每个ansys都自带的)\Program Files\Ansys Inc\V145\ANSYS\data\models\block.inp【OK】后,四分之一几何模型被导入。
4.定义单元类型只定义实体单元的类型SOLID185。
至于接触单元,将在下面使用接触向导来定义。
5.定义材料属性只有线弹性材料属性:弹性模量36E6和泊松比0.36.划分网格打开MESH TOOL,先设定关键地方的网格划分份数然后在MESH TOOL中设定对两个体均进行扫略划分,在volumeSweeping中选择pick all,按下【Sweep】按钮,在主窗口中选择两个体,进行网格划分。
ANSYS弹性及塑性分析非常经典
什么是塑性 (1)路径相关性 (1)率相关性 (1)工程应力.应变与真实应力.应变 (1)什么是激活塑性 (2)塑性理论介绍 (2)屈服准则 (2)流动准则 (3)强化准则 (3)塑性选项 (5)怎样使用塑性 (6)ANSYS 输入 (7)输出量 (7)程序使用中的一些基本原则 (8)加强收敛性的方法 (8)査看结果 (9)塑性分析实例(GUI方法) (9)塑性分析实例(命令流方法) (14)弹塑性分析在这一册中,我们将详细地介绍由于塑性变性引起的非线性问题一弹塑性分析,我们的介绍人为以下几个方而:•什么是塑性•塑性理论简介•ANSYS程序中所用的性选项•怎样使用塑性•塑性分析练习题什么是塑性塑性是一种在某种给定载荷下,材料产生永久变形的材料特性,对大多的工程材料来说, 当其应力低于比例极限时,应力一应变关系是线性盹另外,大多数材料在其应力低于屈服点时,表现为弹性行为,也就是说•当移走载荷时,其应变也完全消失。
由于屈服点和比例极限相差很小,因此在ANSYS程序中,假左它们相同。
在应力一应变的曲线中.低于屈服点的叫作弹性部分,超过屈服点的叫作塑性部分,也叫作应变强化部分。
塑性分析中考虑了塑性区域的材料特性。
路径相关性:即然塑性是不可恢复的,那么这种问题的就与加载历史有关,这类非线性问题叫作与路径相关的或非保守的非线性。
路径相关性是指对一种给左的边界条件,可能有多个正确的解一内部的应力,应变分布一存在,为了得到真正正确的结果.我们必须按照系统真正经历的加载过程加载。
率相关性:塑性应变的大小可能是加载速度快慢的函数,如果塑性应变的大小与时间有关,这种塑性叫作率无关性塑性,相反,与应变率有关的性叫作率相关的塑性。
大多的材料都有某种程度上的率相关性,但在大多数静力分析所经历的应变率范围,两者的应力一应变曲线差别不大,所以在一般的分析中.我们变为是与率无关的• 工程应力,应变与真实的应力.应变:塑性材料的数据一般以拉伸的应力一应变曲线形式给出。
ANSYS 整体式钢筋混凝土建模算例
ANSYS整体式钢筋混凝土模型算例分析在土木工程结构中,最为常用的一种结构形式就是钢筋混凝土结构,在各类房屋、水坝、桥梁、道路中都有广泛应用。
ANSYS软件提供了专门的钢筋混凝土单元和材料模型。
本算例将介绍ANSYS软件分析混凝土一些基本应用。
(1) 首先建立有限元模型,这里我们选用ANSYS软件自带的专门针对混凝土的单元类型Solid 65,进入ANSYS主菜单Preprocessor->Element Type->Add/Edit/Delete,选择添加Solid 65号混凝土单元。
(2) 点击Element types窗口中的Options,设定Stress relax after cracking为Include,即考虑混凝土开裂后的应力软化行为,这样在很多时候都可以提高计算的收敛效率。
(3) 下面我们要通过实参数来设置Solid 65单元中的配筋情况。
进入ANSYS主菜单Preprocessor-> Real Constants->Add/Edit/Delete,添加实参数类型1与Solid 65单元相关,输入钢筋的材料属性为2号材料,但不输入钢筋面积,即这类实参数是素混凝土的配筋情况。
(4) 再添加第二个实参数,输入X方向配筋为0.05,即X方向的体积配筋率为5%。
(5) 下面输入混凝土的材料属性。
混凝土的材料属性比较复杂,其力学属性部分一般由以下3部分组成:基本属性,包括弹性模量和泊松比;本构关系,定义等效应力应变行为;破坏准则,定义开裂强度和压碎强度。
下面分别介绍如下。
(6) 首先进入ANSYS主菜单Preprocessor-> Material Props-> Material Models,在Define Material Model Behavior 窗口中选择Structural-> Linear -> Elastic-> Isotropic,输入弹性模量和泊松比分别为30e9和0.2(7) 下面输入混凝土的等效应力应变关系,这里我们选择von Mises屈服面,该屈服面对于二维受力的混凝土而言精度还是可以接受的。
ANSYS实例分析(三角桁架受力分析 )
三角桁架受力分析1 问题描述图1所示为一三角析架受力简图。
图中各杆件通过铰链连接,杆件材料参数及几何参数见表1和表2,析架受集中力F1=5000N, F2=3000N 的作用,求析架各点位移及反作用力。
图1 三角桁架受力分析简图表1 杆件材料参数表2 杆件几何参数2 问题分析该问题属于析架结构分析问题。
对于一般的析架结构,可通过选择杆单元,并将析架中各杆件的几何信息以杆单元实常数的形式体现出来,从而将分析模型简化为平面模型。
在本例分析过程中选择LINK l 杆单元进行分析求解。
3 求解步骤3.1 前处理(建立模型及网格划分) 1.定义单元类型及输入实常量选择Structural Link 2D spar 1单元,步骤如下:选择Main Menu|Preprocessor|Element Type|Add Edit/Delete 命令,出现Element Types 对话框,单击Add 按钮,出现Library of Element Types 对话框。
在Library of Element Types 列表框中选择Structural Link 2D spar 1,在Element type reference number 文本框中输入1,单击OK 按钮关闭该对话框。
如图2所示。
E 1/Pa E 2/Pa E 3/Pa ν1 ν2 ν3 2.2E11 6.8E102.0E110.30.260.26L1/m L 1/m L 1/m A 1/m 2 A 2/m 2 A 3/m 2 0.4 0.50.36E-49E-44E-4图2 单元类型的选择输入三杆的实常量(横截面积),步骤如下:选择Main Menu|Preprocessor|Real Constants|Add/Edit/Delete命令,出现Real Constants 对话框,单击Add按钮,出现Element Type for Real Constants对话框,单击OK按钮,出现Real Constant Set Number 1, for LINK1对话框,在Real Constant Set No.文本框中输入1,在Cross-sectional area文本框中输入6E-4,在Initial strain文本框中输入0。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ANSYS实例分析75道(含结果)【【ANSYS算例算例】】3.4.2(1)基于图形界面的桁架桥梁结构分析基于图形界面的桁架桥梁结构分析(stepbystep)下面以一个简单桁架桥梁为例,以展示有限元分析的全过程。
背景素材选自位于密执安的“OldNorthParkBridge“(1904-1988),见图3-22。
该桁架桥由型钢组成,顶梁及侧梁,桥身弦杆,底梁分别采用3种不同型号的型钢,结构参数见表3-6。
桥长L=32m,桥高H=5.5m。
桥身由8段桁架组成,每段长4m。
该桥梁可以通行卡车,若这里仅考虑卡车位于桥梁中间位置,假设卡车的质量为4000kg,若取一半的模型,可以将卡车对桥梁的作用力简化为P1,P2和P3,其中P1=P3=5000N,P2=10000N,见图3-23。
图3-22位于密执安的“OldNorthParkBridge“(1904-1988)图3-23桥梁的简化平面模型(取桥梁的一半)表3-6桥梁结构中各种构件的几何性能参数构件惯性矩m4横截面积m2顶梁及侧梁桥身弦梁底梁解答解答以下为基于ANSYS 图形界面(GraphicUserInterface,GUI)的菜单操作流程。
(1)进入进入ANSYS(设定工作目录和工作文件)(设定工作目录和工作文件)程序程序→→ANSYS→→ANSYSInteractive→→Workingdirectory(设置工作目录)→Initialjobname(设置工作文件名):TrussBridge→→Run→→OK(2)设置计算类型设置计算类型:Preferences…→→Structural→→OK(3)定义单元类型定义单元类型ANSYSMainMenu:Preprocessor→→ElementType→→Add/Edit/Delete.→→Add…→→Beam:2delastic3→→OK(返回到ElementTypes窗口)→→Close(4)定义实常数以确定梁单元的截面参数定义实常数以确定梁单元的截面参数ANSYSMainMenu:Preprocessor→→RealConstants…→→Add/Edit /Delete→→Add…→→selectType1Beam3→→OK→→RealConsta ntsSetNo.:1,AREA:2.19E-3,,Izz:3.83e-6(1号实常数用于顶梁和侧梁)→→Apply→→RealConstantsSetNo.:2,AREA:1.185E-3,,Izz:1.87E-6(2号实常数用于弦杆)→→Apply→→RealConstantsSetNo.:3,AREA:3.031E-3,,Izz:8.47E-6(3号实常数用于底梁)→→OK(backtoRealConstantswindow)→Close(theRealConstant swindow)(5)定义材料参数定义材料参数ANSYSMainMenu:Preprocessor→→MaterialProps→→MaterialMo dels→→Structural→→Linear→→Elastic→→Isotropic→→EX:2.1e11,PRXY:0.3(定义泊松比及弹性模量)→→OK→→Density(定义材料密度)→DENS:7800,→→OK→→Close(关闭材料定义窗口)(6)构造桁架桥模型构造桁架桥模型生成桥体几何模型ANSYSMainMenu:Preprocessor→→Modeling→→Create→→Keypoints→→InActive CS→→NPTKeypointnumber::1,,X,,Y,,ZLocationinactiveCS::0,,0→→Apply→→同样输入其余15个特征点坐标(最左端为起始点,坐标分别为(4,0),(8,0),(12,0),(16,0),(20,0),(24,0),(28,0),(32,0),(4,5.5),(8,5.5),(12 ,5.5),(16.5.5),(20,5.5),(24,5.5),(28,5.5))→Lines→Lines→→StraightLine→→依次分别连接特征点→→OK网格划分ANSYSMainMenu:Preprocessor→→Meshing→→MeshAttributes→→PickedLines→→选择桥顶梁及侧梁→→OK→→selectREAL:1,TYPE:1→→Apply→→选择桥体弦杆→→OK→→selectREAL:2,TYPE:1→→Apply→→选择桥底梁→→OK→→selectREAL:3,TYPE:1→→OK→→ANSYSMainMen u:Preprocessor→→Meshing→→MeshTool→→位于SizeControls 下的Lines::Set→→ElementSizeonPicked→→Pickall→→Apply→→NDIV::1→→OK→→Mesh→→Lines→→Pickall→→OK(划分网格)(7)模型加约束模型加约束ANSYSMainMenu:Solution→→DefineLoads→→Apply→→Struct ural→→Displacement→→OnNodes→→选取桥身左端节点→→OK→→selectLab2:AllDOF(施加全部约束)→→Apply→→选取桥身右端节点→→OK→→selectLab2:UY(施加Y方向约束)→→OK(8)施加载荷施加载荷ANSYSMainMenu:Solution→→DefineLoads→→Apply→→Struct ural→→Force/Moment→→OnKeypoints→→选取底梁上卡车两侧关键点(X坐标为12及20)→→OK→→selectLab:FY,,Value:-5000→→Apply→→选取底梁上卡车中部关键点(X坐标为16)→→OK→→selectLab:FY,,Value:-10000→→OK→→ANSYSUtilityMenu:→→Select→→Everything(9)计算分析计算分析ANSYSMainMenu:Solution→→Solve→→CurrentLS→→OK(10)结果显示结果显示ANSYSMainMenu:GeneralPostproc→→PlotResults→→Deedshape→→Defshapeonly →→OK(返回到PlotResults)→→ContourPlot→→NodalSolu→→DOFSolution,Y-Componentof Displacement→→OK(显示Y方向位移UY)(见图3-24(a))定义线性单元I节点的轴力ANSYSMainMenu→GeneralPostproc→→ElementTable→→Define Table→→Add→→Lab:[bar_I],Bysequencenum:[SMISC,1]→→OK →→Close定义线性单元J节点的轴力ANSYSMainMenu→→GeneralPostproc→→ElementTable→→Def ineTable→→Add→→Lab:[bar_J],Bysequencenum:[SMISC,1]→→OK→→Close画出线性单元的受力图(见图3-24(b))ANSYSMainMenu→→GeneralPostproc→→PlotResults→→ContourPlot→→LineElemRes→→LabI:[bar_I],LabJ:[bar_J],Fact :[1]→→OK(11)退出系统退出系统ANSYSUtilityMenu:File→→Exit→→SaveEverything→→OK(a)桥梁中部最大挠度值为0.003374m(b)桥梁中部轴力最大值为25380N图3.24桁架桥挠度UY以及单元轴力计算结果【【ANSYS算例算例】】3.4.2(2)基于命令流方式的桁架桥梁结构分析基于命令流方式的桁架桥梁结构分析!%%%%%[ANSYS 算例]3.4.2(2)%%%%%begin%%%%%%!------注:命令流中的符号$,可将多行命令流写成一行------/prep7!进入前处理/PLOPTS,DATE,0!设置不显示日期和时间!=====设置单元和材料ET,1,BEAM3!定义单元类型R,1,2.19E-3,3.83e-6,,,,,!定义1号实常数用于顶梁侧梁R,2,1.185E-3,1.87e-6,0,0,0,0,!定义2号实常数用于弦杆R,3,3.031E-3,8.47E-6,0,0,0,0,!定义3号实常数用于底梁MP,EX,1,2.1E11!定义材料弹性模量MP,PRXY,1,0.30!定义材料泊松比MP,DENS,1,,7800!定义材料密度!-----定义几何关键点K,1,0,0,,$K,2,4,0,,$K,3,8,0,,$K,4,12,0,,$K,5,16,0,,$K,6,20,0,,$K,7,2 4,0,,$K,8,28,0,,$K,9,32,0,,$K,10,4,5.5,,$K,11,8,5.5,,$K,12,12,5.5,,$K,13,16,5.5,,$K,14,20,5.5,,$K,15,24,5.5,,$K,16,28,5.5,,!-----通过几何点生成桥底梁的线L,1,2$L,2,3$L,3,4$L,4,5$L,5,6$L,6,7$L,7,8$L,8,9!------生成桥顶梁和侧梁的线L,9,16$L,15,16$L,14,15$L,13,14$L,12,13$L,11,12$L,10,11$L,1,10! ------生成桥身弦杆的线L,2,10$L,3,10$L,3,11$L,4,11$L,4,12$L,4,13$L,5,13$L,6,13$L,6,14 $L,6,15$L,7,15$L,7,16$L,8,16!------选择桥顶梁和侧梁指定单元属性LSEL,S,,,9,16,1,LATT,1,1,1,,,,!-----选择桥身弦杆指定单元属性LSEL,S,,,17,29,1,LATT,1,2,1,,,,!-----选择桥底梁指定单元属性LSEL,S,,,1,8,1,LATT,1,3,1,,,,!------划分网格AllSEL,all!再恢复选择所有对象LESIZE,all,,,1,,,,,1!对所有对象进行单元划分前的分段设置LMESH,all!对所有几何线进行单元划分!=====在求解模块中,施加位移约束、外力,进行求解/soluNSEL,S,LOC,X,0!根据几何位置选择节点D,all,,,,,,ALL,,,,,!对所选择的节点施加位移约束AllSEL,all!再恢复选择所有对象NSEL,S,LOC,X,32!根据几何位置选择节点D,all,,,,,,,UY,,,,!对所选择的节点施加位移约束ALLSEL,all!再恢复选择所有对象!------基于几何关键点施加载荷FK,4,FY,-5000$FK,6,FY,-5000$FK,5,FY,-10000/replot!重画图形Allsel,all!选择所有信息(包括所有节点、单元和载荷等)solve!求解!=====进入一般的后处理模块/post1!后处理PLNSOL,U,Y,0,1.0!显示Y方向位移PLNSOL,U,X,0,1.0!显示X方向位移!------显示线单元轴力------ETABLE,bar_I,SMISC,1ETABLE,bar_J,SMISC,1PLLS,BAR_ I,BAR_J,0.5,1!画出轴力图finish!结束!%%%%%[ANSYS算例]3.4.2(2)%%%%%end%%%%%%【【ANSYS算例算例】】3.2.5(3)四杆桁架结构的有限元分析四杆桁架结构的有限元分析下面针对【典型例题】3.2.5(1)的问题,在ANSYS平台上,完成相应的力学分析。
