SPSS方差分析案例实例

合集下载

spss应用案例一方差分析

（二）模型选择与数据来源
单因变量多因素方差分析
本文选择山东省17地市养猪（场）户作为调查对象，本次调查共发放720份问卷，最终获得有效问卷660份，有效率为91.67%，达到了预期的要求。
（三）结果分析与研究结论
1、样本的描述统计分析是用来分析样本的分布特征。
2、主效应分析是用来检验养猪规模、兼业程度、养猪年限和仔猪来源渠道四个因素是否对养猪场（户）的市场风险预控能力有显著性影响。 3、多重比较分析是为了进一步研究探讨不同养殖规模、养殖年限和仔猪来源渠道之间的养猪场（户）市场风险预控能力的差异程度。
1、样本的描述统计分析
——受访养猪场（户）经营特征
表 3 受访养猪场（户）的经营特征情况指标值样本数散养：50头以下 275 小规模：50～499头 297 中规模：500～2999头 74 大规模：3000及以上 14 高兼业程度：50％以下 206 中兼业程度：50～80％ 276 低兼业程度：80％以上 178 1～3年 121 4～6年 320 7年及以上 219 自繁自养 360 外部采购 300
表6 基于生猪养殖年限的多重比较分析 95% 置信区间 (I) 养殖年限 1~3年 4~6年 7年及以上 (J) 养殖年限 4~6年 7年及以上 1~3年 7年及以上 1~3年 4~6年平均差异 (I-J) -0.09 -0.35 0.09 -0.27 0.35 0.27 标准误差 0.092 0.102 0.092 0.080 0.102 0.080 显著度 0.732 0.732 下限 -0.31 -0.14 上限 0.14 -0.11 0.31 -0.08 0.60 0.46
表 4 主效应分析检验结果因素校正模型截距养殖规模养殖年限猪来源渠道兼业程度误差总和校正总和偏差平方和 34.509 1146.329 11.581 8.366 7.084 1.719 497.467 4788.000 531.976 自由度df 8 1 3 2 1 2 651 660 659 均方 4.314 1146.329 3.860 4.183 7.084 0.860 0.764 F值 5.645 1500.120 5.052 5.474 9.271 1.125 显著度P 0.000** 0.000** 0.002** 0.004** 0.002** 0.325

管理统计SPSS方差齐性分析实例

请分析一个班三组不同性别的同学（分别接受了三种不同的教学方法）在数学成绩上是否有显著差异？根据题意，数学成绩分数的高低可能受到不同的教学方法跟性别的的影响，因此考虑两个因素水平下成绩的差异问。

在对其进行方差齐性分析前，首先对数据进行独立性，正态性，方差齐性检验。

1独立性检验用游程检验，检验其独立性，检验结果如下：图1-1游程检验数学成绩检验值a76.83案例 < 检验值8案例 >= 检验值10案例总数18Runs 数7Z -1.176渐近显著性(双侧) .240a. 均值根据图1-1数学成绩关于游程检验的结果可以看到，游程检验的P值为0.089 大于显著性水平 =0.05，故接受原假设，即认为各位同学的数学成绩不具有相关性，所以各变量之间是独立的。

2 正态性检验图1-2单样本 Kolmogorov-Smirnov 检验数学成绩N 18正态参数a,b均值76.83标准差17.041最极端差别绝对值.244正.167负-.244Kolmogorov-Smirnov Z 1.035渐近显著性(双侧) .235a. 检验分布为正态分布。

b. 根据数据计算得到。

根据图1-2可以看到数学成绩的K-S正太分布检验显著性水平位0.235，大于0.05，故接受原假设，既数学成绩服从正太分布。

3方差齐性检验图1-3根据图1-3可以看到，sig值为0.477，明显大于显著性水平0.05，故接受原假设，即认为各样本的数学成绩具方差齐性。

主体间因子N组别0 61 62 6性别 f 7m 11从上表可以看出，组别的SIG值为0，既拒绝原假设，可以认为，在95%的置信水平下，组别既不同的教学方法对成绩的影响存在显著的差异。

性别跟组别跟性别之间的叫互影响均对数学成绩没有显著地影响。

并且也可以看到2R=0.849，调整后的2R=0.849可见方程的拟合度非常好。

问题：已知一个班三组同学的入学成绩和分别接受了三种不同的教学方法后的数学成绩如下表所示，试研究这三组同学在接受了不同的教学方法后在数学成绩上是否有显著性差异？本案例中，主要研究不同的教学方法对数学成绩的影响，但是入学成绩可能可能对数学成绩有一定的影响，但又不是我们主要关心的因素，应尽量排除入学成绩对成绩的影响，因此将入学成绩做为协变量。

用SPSS作方差分析

平方和 SS 516 430 946
方差分析表自由度 df r-1 nT-r nT-1
自由度 df 2 15 17
均方 MS MSTR MSE
F值 MSTTR/MSE
均方
F值
MS
258.00
9.00
28.67
总平方和 = 处理平方和 + 误差平方和
SST = SSA + SSE
r nj
j1 i1
组内估计不受原假设影响，H0为真或为假，组内估计总是σ2的无偏估计。
___
x 1 1
___
2 x 2
___
x 3 3
___
x 4 4
2的组间估计量 F 2的组内估计量服从分子自由度为 r 1 ，分母自由度为 nT r 的 F 分布。
(25.25)自由度
(5.5)自由度 (2.1)自由度
20个地块的小麦产量（公斤）
化肥地块
1 2 3 4 5
鸿福
27.9 25.1 28.5 24.2 26.5
祥丰
26.5 28.7 25.1 29.1 27.2
云天
31.2 28.3 30.8 27.9 29.6
可富
30.8 29.6 32.4 31.7 32.8
样本均值样本方差总样本均值
x1 =26.44 s12 =3.298
nT r
nT r
18 3 15
F MSA MSE
F 统计量服从 F 分布，其分子自由度为r 1，分母自由度为 nT r。
F MSA 258 9.00 MSE 28.67
MSA
0
F
MSE
方差来源组间组内总差异
方差来源组间组内总差异

多元方差分析spss实例

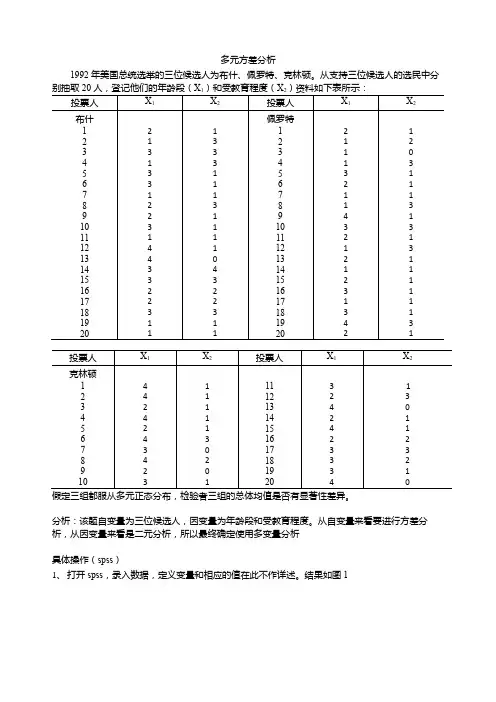
多元方差分析1992年美国总统选举的三位候选人为布什、佩罗特、克林顿。

从支持三位候选人的选民中分别分析：该题自变量为三位候选人，因变量为年龄段和受教育程度。

从自变量来看要进行方差分析，从因变量来看是二元分析，所以最终确定使用多变量分析具体操作（spss）1、打开spss，录入数据，定义变量和相应的值在此不作详述。

结果如图1图1 被投票人：1、布什2、佩罗特3、克林顿2、在spss窗口中选择分析——一般线性模型——多变量，调出多变量分析主界面，将年龄段和受教育程度移入因变量框中，被投票人移入固定因子框中。

如图2图2 多变量分析主界面3、点击选项按钮在输出框中选择方差齐性分析（既包括协方差矩阵等同性分析也包括误差方差齐性分析），其它使用默认即可，点击继续返回主界面。

如图3图3 选项子对话框4、点击确定，运行多变量分析过程。

结果解释1、协方差矩阵等同性的Box检验结果，如图4图4 协方差矩阵检验结果说明：此Box检验的协方差矩阵为三位候选人每个人的支持者的年龄段和受教育程度的协方差矩阵。

因为sig>0.05，所以差异不显著，即各个因变量的协方差矩阵在所有三个候选人组中是相等的。

可以对其进行多元方差分析。

2、多变量检验结果，如图5图5 多变量检验结果说明：被投票人在四种统计方法中的sig均小于0.05，所以差异显著，即三组的总体均值有显著性差异3、误差方差等同性的Levene检验结果，如图6图6 Levene检验结果说明：只考虑单个变量，年龄段或者受教育程度，每位候选人的20名支持者的随机误差是否有显著性差异。

因为sig>0.05，差异不显著，所以三位候选人的20名支持者的随机误差相等。

可以进行单因素方差分析。

4、主体间效应的检验结果，如图7图7 主体间效应的检验结果说明：被投票人一行中，年龄段的sig<0.05，差异显著，即支持三位候选人的选民中，年龄段之间存在显著差异；而受教育程度的sig>0.05，差异不显著，即支持三位候选人的选民中，受教育程度差异不显著。

方差分析spss操作2(共72张PPT)

1 5.9290
0.017
42 14.7865
(132) (25.1241) 3 21.9763 3 1.2701
126 1.8777
11.70 0.68
P
<0.001
<0.001 0.568
软件操作步骤：1、变量设置
3、方差分析： analyze—general linear
model—repeated measures
• m——正交表纵列数(最多能安排的因数个数)
Spss操作
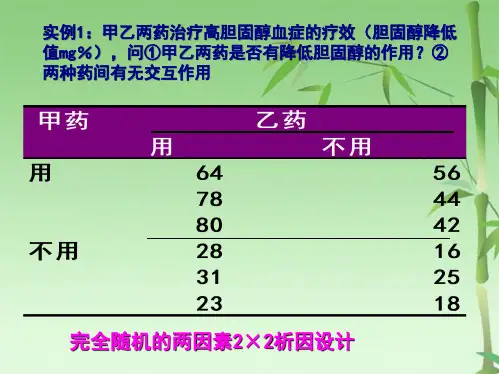
正交设计方差分析 • 见50页例1：观察3各因素对细胞色素b5的
影响 • 因素A:诱导剂，2水平（生理盐水、戊己比
妥） • 因素B：正氟醚，2水平（用、不用） • 因素C：性别，2水平（雄性、雌性）
• P均大于0.05，各因素均无统计学意义。
互效应的各组均数不呈任何趋势。
三、交叉设计
（cross-over design）
按纳入标准
阶段 I
确定病人
A 处理(测量)
间
歇
B 处理(测量)
期
阶段 II
B 处理(测量)
A 处理(测量)
交叉设计的方差分析
• 两阶段效应无差别；AB两种处理间有差别；受试者（白鼠）间有差别。
可以把受试者编号放入随机因素栏
Within-subject factor-受试者内因素，用于定义重复测量变量及重复次数
Options对话框
先输出了重复测量的变量名
因变量的描述性统计
球对称检验：p=0.003，拒绝H0，不满足球对称性，应对自由度进行校正
Mauchly’s test of sphericity
• 如果满足球对称，则看下面的一元分析结果（tests of within-subjects effects）中 sphericity assumed所在行的统计量及p值。

(完整word版)SPSS方差分析案例实例

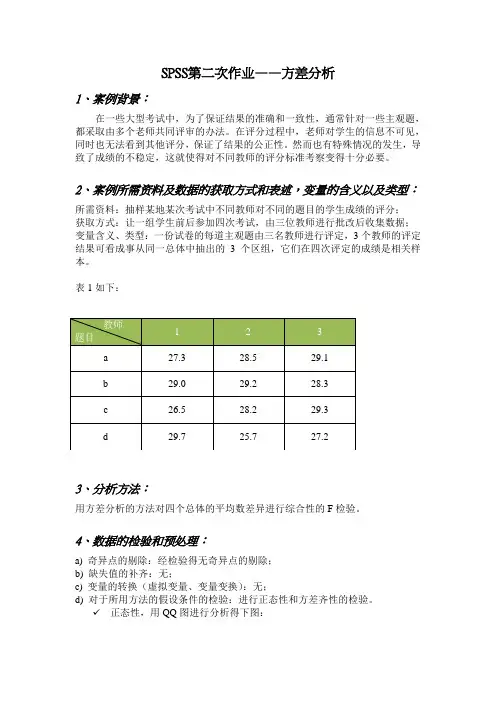
SPSS第二次作业——方差分析1、案例背景：在一些大型考试中，为了保证结果的准确和一致性，通常针对一些主观题，都采取由多个老师共同评审的办法。

在评分过程中，老师对学生的信息不可见，同时也无法看到其他评分，保证了结果的公正性。

然而也有特殊情况的发生，导致了成绩的不稳定，这就使得对不同教师的评分标准考察变得十分必要。

2、案例所需资料及数据的获取方式和表述，变量的含义以及类型：所需资料：抽样某地某次考试中不同教师对不同的题目的学生成绩的评分；获取方式：让一组学生前后参加四次考试，由三位教师进行批改后收集数据；变量含义、类型：一份试卷的每道主观题由三名教师进行评定，3个教师的评定结果可看成事从同一总体中抽出的3个区组，它们在四次评定的成绩是相关样本。

表1如下：3、分析方法：用方差分析的方法对四个总体的平均数差异进行综合性的F检验。

4、数据的检验和预处理：a) 奇异点的剔除：经检验得无奇异点的剔除；b) 缺失值的补齐：无；c) 变量的转换（虚拟变量、变量变换）：无；d) 对于所用方法的假设条件的检验：进行正态性和方差齐性的检验。

✓正态性，用QQ图进行分析得下图：得到近似满足正态性。

✓对方差齐性的检验：用SPSS对方差齐性的分析得下表：Test of Homogeneity of Variances分数Levene Statistic df1 df2 Sig..732 2 9 .508易知P〉0.05，接受方差齐性的假设。

5、分析过程：a) 所用方法：单因素方差分析；方差分析中的多重比较。

b) 方法细节：●单因素方差分析第一步，提出假设：H0：μ1=μ2=μ3；（教师的评定基本合理，即均值相同）H1：μi(i=1,2,3)不全相等；（教师的评定不够合理，均值有差异）第二步，为检验H0是否成立，首先计算以下统计量：1,计算水平均值及总体均值：表2 三位教师评选结果的均值2-计算平方和和自由度：总离差平方和：SST=211)-(∑∑==ki n j iij x x =16.947，自由度为n-1=11组内离差平方和：SSE=211)x -(i ∑∑==ki n j iij x =16.275，自由度为n-k=9组间平方和：SSA=211)-(∑∑==ki n j ii x x =0.672,自由度为k-1=23-计算均方：MSA=1SSA -k =0.336MSE=kn -SSE =1.8084-计算检验的统计量F ： F=MSEMSA ~F(k-1,n-k) 计算F=0.186将结果汇集到表中：第三步，统计决断:查F 值表得F 0.01(2,11)=7.21>0.186。

spss 单因素方差分析例子

第一题：data0706-nutrition为地衣(lichen)、树叶成叶和嫩叶的蛋白质和可溶性碳水化合物(water soluble carbohydrate)的含量，先分析三者之间蛋白质的含量有无差异？如果有差异，具体是怎么差异的？再可溶性碳水化合物的含量有无差异？如果有差异，具体怎么差异？（1）地衣(lichen)、树叶成叶和嫩叶的蛋白质的含量差异分析；第一步：导出变量items和protein，以便删除protein中缺失数据。

第二步：打开导出数据data0706-nutrition1，先排序，然后删除缺失数据。

第三步：对data0706-nutrition1数据的正态性、异常值和极值、方差齐性进行检验，对数据做一个检查，Analyze->Descriptive Statistics->Explore；首先：如上图，把要检验的变量protein送入Dependent List，把分组变量（因素变量）items送入Factor List。

其次：如下图，点击Plots打开：选择Factor Levels together、Stem-and-leaf、Histogram、Normality plots with tests，下方Spread vs Level with Levene Test可以提供方差齐性的检验，选择Untransformed（不对数据进行转换）。

输出结果：第一组是尽管sig=0.935，但由于样本数太小，正态一般；第二组正态性不好。

第三组中，p较小，也只是近似正态。

基于平均数的计算(Based on Mean)，各组方差有差异(p=0.044)。

由直方图可以看出，在第二组和第三组存在一些极值，数据分布不均匀，连续性不好。

由茎叶图可知，第二组和第三组分别存在4个，3个极值。

由qq图和QQ图不能得到一些较有用的信息，因为正态性之前已经判断。

箱图并与茎叶图一致，在第二组标识了4个异常值，第三组标识了3个异常值。

spss相关分析案例多因素方差分析

本次实验采用2005年东部、中部和西部各地区省份城镇居民月平均消费类型划分的数据（课本139页），将东部、中部和西部看作三个不同总体，31个数据分别来自于这三个总体。

本人对这三个不同地区的城镇居民月平均消费水平进行比较，并选取人均粮食支出、副食支出、烟酒及饮料支出、其他副食支出、衣着支出、日用杂品支出、水电燃料支出和其他非商品支出八个指标来衡量城镇居民月平均消费情况。

在进行比较分析之前，首先对个数据是否服从多元正态分布进行检验，输出结果为：表一如表一，因为该例中样本数n=31<2000,所以此处选用Shapiro-Wilk统计量。

由正态性检验结果的sig.值可以看到，人均粮食支出、烟酒及饮料支出、其他副食支出、水电燃料支出和其他非商品支出均明显不遵从正态分布（Sig.值小于,拒绝服从正态分布的原假设），因此，在下面分析中，只对人均副食支出、衣着支出和日用杂品支出三项指标进行比较，并认为这三个变量组成的向量都遵从正态分布，并对城镇居民月平均消费状况做出近似的度量。

另外，正态性的检验还可以通过Q-Q图来实现，此时应判别数据点是否与已知直线拟合得好。

如果数据点均落在直线附近，说明拟合得好，服从正态分布，反之，不服从。

具体情况这里不再赘述。

下面进行多因素方差分析：一、多变量检验表二由地区一栏的（即第二栏）所列几个统计量的Sig.值可以看到，无论从那个统计量来看，三个地区的城镇居民月平均消费水平都是有显著差别的（Sig.值小于，拒绝地区取值不同，对Y，即城镇居民月平均消费水平的取值没有显著影响的原假设）。

二、主体间效应检验表三如表三，可以看到三个指标地区一栏的（即第三栏）Sig.值分别为、、，说明三个地区在人均衣着支出指标上没有明显的差别（Sig.值大于，不拒绝地区取值不同，对指标的取值没有显著影响的原假设），反之，而在人均副食支出和日用杂品支出指标上有显著差别。

三、多重比较表四Contrast Results (K Matrix)地区 Simple Contrast aDependent Variable 人均副食支出(元/人)人均日用杂品支出(元/人)人均衣着支出(元/人)Level 1 vs. Level 3 Contrast EstimateHypothesized Value0 0 0 Difference (Estimate - Hypothesized) Std. Error Sig..001.036.51795% Confidence Interval for DifferenceLower Bound.173Upper BoundLevel 2 vs. Level 3 Contrast EstimateHypothesized Value0 0 0 Difference (Estimate - Hypothesized) Std. Error Sig..668.343.63895% Confidence Interval for DifferenceLower BoundUpper Bound表四Contrast Results (K Matrix)地区 Simple Contrast aDependent Variable 人均副食支出(元/人)人均日用杂品支出(元/人)人均衣着支出(元/人)Level 1 vs. Level 3 Contrast EstimateHypothesized Value0 0 0 Difference (Estimate - Hypothesized) Std. Error Sig..001.036.51795% Confidence Interval for DifferenceLower Bound.173Upper BoundLevel 2 vs. Level 3 Contrast EstimateHypothesized Value0 0 0 Difference (Estimate - Hypothesized) Std. Error Sig..668.343.63895% Confidence Interval for DifferenceLower BoundUpper Bounda. Reference category = 3如表四，在显著水平下，东部和西部的人均副食支出（Sig.值为）和日用杂品支出（Sig.值为）指标有明显差别(小于，拒绝原假设)，而在人均衣着支出（Sig.值为）指标上没有明显的差别。

48单因素方差分析的SPSS实现

5
43014..267.6
40.7 31.5
394.80.7
42.9
373.91.5
45.4
384.82.9
44.3
53164..385.4
54.2 46.0
414.24.3
45.9
42.合2 计(Ti )
514.311.2
4355.04.2
494.9 4
)
合计 1 1 1 1
1 1 1 1
2023/12/28
2
表1 三组战士的第一秒用力肺活量(L)
对照组锻炼组药物组合计
3.25
3.66
3.44
3.32
3.64
3.62
3.29
3.48
3.48
3.343.48
3.52
3.64
3.20
3.60
3.60
3.62
3.32
3.28
3.56
3.44
3.52
3.44
3.16
3.26
3.82
3.28
3
2.随机区组（或单位组、配伍组）设计的方差分析
例4-2 下表是11名战士在不同海拔高度的血氨
值( mol L )。试作方差分析
表 4-6 不同海拔高表度4-的6 血不氨同值海(拔m高o度l 的L血氨)值( mol L
平原战士编号
1
32.7 2
3500平m原
32.7
33.735.4
3450500m0m
33.7
353.49.2
4500m
39.2 57.2
35.4 3
33.3
4 5
44.8 6
32.3 7

SPSS双因素方差分析

SPSS双因素方差分析例1 对小白鼠喂以三种不同的营养素，目的是了解不同营养素增重的效果。

采用随机区组设计方法，以窝别作为划分区组的特征，以消除遗传因素对体重增长的影响。

现将同品系同体重的24只小白鼠分为8个区组，每个区组3只小白鼠。

三周后体重增量结果(克)列于下表，问小白鼠经三种不同营养素喂养后所增体重有无差别？区组号营养素1 营养素2 营养素31 50.10 58.20 64.502 47.80 48.50 62.403 53.10 53.80 58.604 63.50 64.20 72.505 71.20 68.40 79.306 41.40 45.70 38.407 61.90 53.00 51.208 42.20 39.80 46.20这可以认为是无重复实验的双因素方差分析，SPSS软件版本：18.0中文版。

1、建立数据文件变量视图：建立3个变量，如下图1数据视图：如下图：区组号用1-8表示，营养素号用1-3表示。

数据文件见“小白鼠喂3种不同的营养素增重数量.sav”，可以直接使用。

2、统计分析菜单选择：分析-> 一般线性模型-> 单变量1点击进入“单变量”对话框1旗开得胜将“体重”选入“因变量”框，“区组”、“营养素”选入固定因子框点击右边“模型”按钮，进入“单变量：模型对话框”1点击“设定”单选按钮（无重复双因素方差分析不能选全因子！），在“构建项”下拉菜单中选择“主效应”（只能选主效应）1把左边的因子与协变量框中区组和营养素均选入右边的模型框中其余选项取默认值就行，点击“继续”按钮，回到“单变量”界面1点击“两两比较”按钮，进入下面对话框1将左边框中“区组”、“营养素”均选入右边框中再选择两两比较的方法，LSD、S-N-K，Duncan为常用的三种方法，点击“继续”按钮回到“单变量”主界面。

1点击“选项”按钮1勾选“统计描述”及“方差齐性检验”，设置显著性水平，点击“继续”按钮，回到“单变量”主界面1点击下方“确定”按钮，开始分析。

SPSS单因素方差分析案例

百度文库
1 单因素方差分析
步骤：
1.如图，进入单因素方差分析。

2.将“销售额”选入，“广告形式”选入。

3.将中的“广告形式”换成“地区”。

结果呈现：
表一广告形式对销售额的单因素方差分析结果
表二地区对销售额的单因素方差分析结果
分析：
1.如果仅仅考虑广告形式单个因素对销售额的影响，从“广告形式对销售额的单因素方差
分析结果”可以看出，统计量F对应的概率P-值为0.000，小于显著性水平a=0.05（a=0.01），所以，拒绝原假设，即，认为不同广告形式对销售额产生了显著的影响。

2.如果仅仅考虑地区单个因素对销售额的影响，从“地区对销售额的单因素方差分析结果”
可以看出，统计量F对应的概率P-值为0.000，小于显著性水平a=0.05(a=0.01),所以，拒绝原假设，即，认为不同地区对销售额产生了显著的影响。

3. 从上述两表可以看出，“广告形式对销售额的单因素方差分析结果”中的F值为13.483，“地区对销售额的单因素方差分析结果”中的F值为
4.062，而13.483>4.062，所以，如果从单因素考虑，广告形式对销售额的影响较地区有更明显的作用。

spss单因素方差分析例子

第二步：打开导出数据data0706-nutrition1，先排序，然后删除缺失数据。

输出结果：第一组是尽管sig=0.935，但由于样本数太小，正态一般；第二组正态性不好。

第三组中，p较小，也只是近似正态。

基于平均数的计算(Based on Mean)，各组方差有差异(p=0.044)。

由直方图可以看出，在第二组和第三组存在一些极值，数据分布不均匀，连续性不好。

由茎叶图可知，第二组和第三组分别存在4个，3个极值。

由qq图和QQ图不能得到一些较有用的信息，因为正态性之前已经判断。

箱图并与茎叶图一致，在第二组标识了4个异常值，第三组标识了3个异常值。

spss方差分析实例

SPSS——单因素方差分析实例单因素方差分析也称作一维方差分析。

它检验由单一因素影响的一个(或几个相互独立的)因变量由因素各水平分组的均值之间的差异是否具有统计意义。

还可以对该因素的若干水平分组中哪一组与其他各组均值间具有显著性差异进行分析，即进行均值的多重比较。

One-Way ANOV A过程要求因变量属于正态分布总体。

如果因变量的分布明显的是非正态，不能使用该过程，而应该使用非参数分析过程。

如果几个因变量之间彼此不独立，应该用Repeated Measure过程。

[例子]调查不同水稻品种百丛中稻纵卷叶螟幼虫的数量，数据如表1-1所示。

表1-1不同水稻品种百丛中稻纵卷叶螟幼虫数数据保存在“data1.sav”文件中，变量格式如图1-1。

分析水稻品种对稻纵卷叶螟幼虫抗虫性是否存在显著性差异。

2）启动分析过程点击主菜单“Analyze”项，在下拉菜单中点击“Compare Means”项，在右拉式菜单中点击“0ne-Way ANOV A”项，系统打开单因素方差分析设置窗口如图1-2。

3）设置分析变量因变量: 选择一个或多个因子变量进入“Dependent List”框中。

本例选择“幼虫”。

因素变量: 选择一个因素变量进入“Factor”框中。

本例选择“品种”。

4）设置多项式比较单击“Contrasts”按钮，将打开如图1-3所示的对话框。

该对话框用于设置均值的多项式比较。

定义多项式的步骤为：均值的多项式比较是包括两个或更多个均值的比较。

例如图1-3中显示的是要求计算“1.1×mean1-1×mean2”的值，检验的假设H0：第一组均值的1.1倍与第二组的均值相等。

单因素方差分析的“0ne-Way ANOV A”过程允许进行高达5次的均值多项式比较。

多项式的系数需要由读者自己根据研究的需要输入。

具体的操作步骤如下：①选中“Polynomial”复选项，该操作激活其右面的“Degree”参数框。

SPSS单因素方差分析案例

SPSS单因素方差分析案例
一、案例简介
本案例主要探讨不同年龄组对对不同种类游戏的不同评价。

采用
SPSS软件进行单因素方差分析，研究对象为50名参与游戏评测的受试者，其中25名为年龄段20-30，25名为年龄段30-40。

每位受试者都被分配3
种不同类型的游戏来评价，评价方式为3分制，值得1，2，3分，分别表
示很差，一般，不错。

二、SPSS分析
1.数据的输入
①打开SPSS软件，点击“文件”-“打开”，选择需要进行分析的数据；
②若原始数据是excel格式，选择“所有的excel文件”，点击“打开”；
③若原始数据是文本格式，选择“所有文本文件”，点击“打开”；
④若原始数据是spss格式，选择“spss 调查”，点击“打开”；
⑤若原始数据是SAS格式，选择“所有SAS文件”，点击“打开”。

2.数据分析
①点击“统计”菜单，在下拉菜单中选择“多元统计分析”；
②在多元统计分析对话框中，在“因变量”栏中选择需要分析的评测
结果；
③在“自变量”栏中选择“受试者的年龄”；
④点击“确定”按钮，开始进行单因素方差分析；
⑤点击“分析”按钮，在下拉菜单中选择“单因素方差分析”；
⑥点击“分析”按钮。

spss 多因素方差分析例子

作业8：多因素方差分析1，data0806-height是从三个样方中测量的八种草的高度，问高度在三个取样地点,以及八种草之间有无差异？具体怎么差异的？打开spss软件，打开data0806-height数据，点击Analyze—〉General Linear Model —>Univariate打开：把plot和species送入Fixed Factor（s)，把height送入Dependent Variable，点击Model 打开:选择Full factorial，Type III Sum of squares,Include intercept in model（即全部默认选项)，点击Continue回到Univariate主对话框，对其他选项卡不做任何选择,结果输出：因无法计算MM e rror,即无法分开MM intercept和MM error，无法检测interaction的影响，无法进行方差分析，重新Analyze—〉General Linear Model-〉Univariate打开：选择好Dependent Variable和Fixed Factor（s)，点击Model打开：点击Custom，把主效应变量species和plot送入Model框，点击Continue回到Univariate主对话框，点击Plots：把date送入Horizontal Axis，把depth送入Separate Lines，点击Add，点击Continue回到Univariate对话框，点击Options：把OVERALL,species, plot送入Display Means for框,选择Compare main effects,Bonferroni，点击Continue回到Univariate对话框，输出结果:可以看到:SS species=33.165，df species=7，MS species=4.738；SS plot=33.165，df plot=7，MS plot=4.738；SS error=21。

《方差分析》spss实例操作

方差分析方差分析的应用条件⏹各样本是相互独立的随机样本；⏹各组样本均来自正态总体；⏹各组的总体方差相等⏹各单元格样本含量比较大(>30)且各单元格样本含量相同的情况下，方差是否相等对结果影响几乎没有方差分析的基本思想⏹全部数据的总变异分成多个部分（离均差平方和SS）⏹均方MS=SS/df⏹各部分变异的MS与随机误差的MS做比，形成F统计量⏹注意：H0为各组总体均数不全相等⏹完全随机设计方差分析⏹多组样本均数两两比较⏹随机区组设计方差分析⏹析因设计方差分析⏹例题：⏹某人研究北京机关工作人员血脂水平，随机抽取不同年龄组男性受试者各10名，检测他们的总胆固醇（TC）的含量(mmol/L)，其结果如下：⏹青年组5.00 4.85 4.93 5.18 4.95 4.78 5.18 4.895.07 5.21⏹中年组5.12 5.13 4.89 5.20 4.99 5.14 5.16 4.985.16 5.25⏹老年组5.24 5.26 5.23 5.10 5.31 5.23 5.21 4.985.15 5.19⏹请问：三个年龄组的总胆固醇平均含量之间的差别是否具有统计学意义？完全随机设计方差分析⏹库结构⏹分组检验正态性⏹Analyze-Compare Means-One-Way ANOVA-Dependent List选入指标-Factor选入组别-(Post Hoc两两比较-勾选两两比较方法-continue-Option-勾选Homogeneity of variance test-continue)-OK可以认为各组TC均符合正态分布可以认为三组总体方差相等经检验，F=5.897，P=0.008，在检验水准为0.05的水平下，差异有统计学意义，拒绝H0，接受H1，可以认为三组的TC水平不全相等多组均数的两两比较⏹SNK法/LSD法：事后分析，所有组之间都比较⏹Dunnet-t检验：计划好的两两比较，和同一组比较⏹Bonferroni法: 调整检验水准；除以使用次数方差齐性不满足方差齐性同一列，无差别；不同列，有差别练习1⏹例题：⏹研究者欲比较生物蛋白粉饲料、血浆蛋白粉饲料和普通饲料喂养断奶仔猪的增重效果。

spss相关分析案例多因素方差分析及SPSS检验车辆运行速度案例分析

由正态性检验结果的sig.值可以看到，人均粮食支出、烟酒及饮料支出、其他副食支出、水电燃料支出和其他非商品支出均明显不遵从正态分布（Sig.值小于0.05,拒绝服从正态分布的原假设），因此，在下面分析中，只对人均副食支出、衣着支出和日用杂品支出三项指标进行比较，并认为这三个变量组成的向量都遵从正态分布，并对城镇居民月平均消费状况做出近似的度量。

另外，正态性的检验还可以通过Q-Q图来实现，此时应判别数据点是否与已知直线拟合得好。

如果数据点均落在直线附近，说明拟合得好，服从正态分布，反之，不服从。

具体情况这里不再赘述。

下面进行多因素方差分析：一、多变量检验表二由地区一栏的（即第二栏）所列几个统计量的Sig.值可以看到，无论从那个统计量来看，三个地区的城镇居民月平均消费水平都是有显著差别的（Sig.值小于0.05，拒绝地区取值不同，对Y，即城镇居民月平均消费水平的取值没有显著影响的原假设）。

二、主体间效应检验表三如表三，可以看到三个指标地区一栏的（即第三栏）Sig.值分别为0.001、0.017、0.790，说明三个地区在人均衣着支出指标上没有明显的差别（Sig.值大于0.05，不拒绝地区取值不同，对指标的取值没有显著影响的原假设），反之，而在人均副食支出和日用杂品支出指标上有显著差别。

SPSS-习题(方差分析)

大鼠烫伤后肝脏atp的测量结果mg7761114108577111608588431142719847138593610301353959667141688111736948225781301995661141811266971772868将18名原发性血小板减少症患者按年龄相近的原则配为6个区组每个区组3名患者随机分配到abc三个治疗组中治疗后血小板升高情况见下表问三种治疗方法的疗TP)的影响，将30只雄性大鼠随机分成3组，每组10只：A组为烫伤对照组，B组烫伤后24h （休克期）切痂组，C组为烫伤后96h（非休克期）切痂组。全部动物统一在烫伤168h处死并测量其肝脏ATP含量，结果见下表。
大鼠烫伤后肝脏ATP的测量结果(mg) A组 B组 C组 7.76 11.14 10.85 7.71 11.60 8.58 8.43 11.42 7.19 8.47 13.85 9.36 10.30 13.53 9.59 6.67 14.16 8.81 11.73 6.94 8.22 5.78 13.01 9.95 6.61 14.18 11.26 6.97 17.72 8.68
习题2
用简便法与常规法分别对12份人尿进行尿铅含量测定，所得结果如下表。问根据现有资料能否说明两种方法检测结果不同？
两法测定12份尿铅含量的结果样品号简便法 1 2 3 4 5 6 7 8 9 10 11 12 3.05 3.76 2.75 3.23 3.67 4.49 5.16 5.45 2.06 1.64 2.55 1.23 尿铅含量/(umol.L-1) 常规法 2.80 3.04 1.88 3.43 3.81 4.00 4.44 5.41 1.24 1.83 1.45 0.92
习题4
将18名原发性血小板减少症患者按年龄相近的原则配为6个区组，每个区组3名患者随机分配到A、B、C三个治疗组中，治疗后血小板升高情况见下表，问三种治疗方法的疗效有无差别？

spss方差分析操作示范-步骤-例子

第五节方差分析的SPSS操作一、完全随机设计的单因素方差分析1．数据采用本章第二节所用的例1中的数据，在数据中定义一个group变量来表示五个不同的组，变量math表示学生的数学成绩。

数据输入格式如图6－3（为了节省空间，只显示部分数据的输入）：图 6-3 单因素方差分析数据输入将上述数据文件保存为“6-6-1.sav”。

2．理论分析要比较不同组学生成绩平均值之间是否存在显著性差异，从上面数据来看，总共分了5个组，也就是说要解决比较多个组（两组以上）的平均数是否有显著的问题。

从要分析的数据来看，不同组学生成绩之间可看作相互独立，学生的成绩可以假设从总体上服从正态分布，在各组方差满足齐性的条件下，可以用单因素的方差分析来解决这一问题。

单因素方差分析不仅可以检验多组均值之间是否存在差异，同时还可进一步采取多种方法进行多重比较，发现存在差异的究竟是哪些均值。

3．单因素方差分析过程（1）主效应的检验假如我们现在想检验五组被试的数学成绩（math）的均值差异是否显著性，可依下列操作进行。

①单击主菜单Analyze/Compare Means/One-Way Anova…，进入主对话框，请把math选入到因变量表列（Dependent list）中去，把group选入到因素（factor）中去，如图6-4所示：图6-4：One-Way Anova主对话框②对于方差分析，要求数据服从正态分布和不同组数据方差齐性，对于正态性的假设在后面非参数检验一章再具体介绍；One-Way Anova可以对数据进行方差齐性的检验，单击铵钮Options，进入它的主对话框，在Homogeneity-of-variance项上选中即可。

设置如下图6-5所示：图6-5：One-Way Anova的Options对话框点击Continue，返回主对话框。

③在主对话框中点击OK，得到单因素方差分析结果4．结果及解释（1）输出方差齐性检验结果Test of Homogeneity of VariancesMATHLevene Statistic df1 df2 Sig.1.238 4 35 .313上表结果显示，Levene方差齐性检验统计量的值为1.238，Sig=0.313>0.05，所以五个组的方差满足方差齐性的前提条件，如果不满足方差齐性的前提条件，后面方差分析计算F统计量的方法要稍微复杂，本章我们只考虑方差齐性条件满足的情况。

SPSS_单因素方差分析(ANOVA)案例解析

SPSS-单因素方差分析（ANOVA) 案例解析2011-08-30 11:10这几天一直在忙电信网上营业厅用户体验优化改版事情，今天将我最近学习SPSS单因素方差分析（ANOVA)分析，今天希望跟大家交流和分享一下：继续以上一期的样本为例，雌性老鼠和雄性老鼠，在注射毒素后，经过一段时间，观察老鼠死亡和存活情况。

研究的问题是：老鼠在注射毒液后，死亡和存活情况，会不会跟性别有关？样本数据如下所示：（a代表雄性老鼠 b代表雌性老鼠 0代表死亡 1 代表活着 tim 代表注射毒液后，经过多长时间，观察结果）点击“分析”——比较均值———单因素AVOVA, 如下所示：从上图可以看出，只有“两个变量”可选, 对于“组别（性别）”变量不可选，这里可能需要进行“转换”对数据重新进行编码，点击“转换”—“重新编码为不同变量” 将a,b"分别用8,9进行替换，得到如下结果”此时的8 代表a(雄性老鼠） 9代表b雌性老鼠，我们将“生存结局”变量移入“因变量列表”框，将“性别”移入“因子”框，点击“两两比较”按钮，如下所示：“ 勾选“将定方差齐性”下面的 LSD 选项，和“未假定方差齐性”下面的Tamhane's T2选项点击继续点击“选项”按钮，如下所示：勾选“描述性”和“方差同质检验” 以及均值图等选项，得到如下结果：结果分析：方差齐性检验结果，“显著性”为0，由于显著性0<0.05 所以，方差齐性不相等，在一般情况下，不能够进行方差分析但是对于SPSS来说，即使方差齐性不相等，还是可以进行方差分析的，由于此样本组少于三组，不能够进行多重样本对比从结果来看“单因素ANOVA” 分析结果，显著性0.098，由于0.098>0.05 所以可以得出结论：生存结局受性别的影响不显著很多人，对这个结果可能存在疑虑，下面我们来进一步进行论证，由于“方差齐性不相等”下面我们来进行“非参数检验”检验结果如下所示：（此处采用的是“Kruskal-Wallis "检验方法）通过“Kruskal-Wallis ”检验方法，我们得出“sig=0.098"跟我们先前分析的结果一样，都是0.098，事实得到论证。