三角形有关的角知识点总结与随堂练(基础篇)
三角形角度问题知识点总结

三角形角度问题知识点总结一、三角形内角的性质1. 三角形内角和三角形的内角和是180度。
对于任意一个三角形ABC,我们可以通过以下公式来计算三角形的内角和:∠A + ∠B + ∠C = 180°这个性质是三角形内角计算的基础,我们可以根据这个公式来解决一些与三角形内角相关的问题。
2. 等腰三角形内角在等腰三角形中,两个底边的角相等,即∠A = ∠B。
由于我们知道三角形的内角和是180度,在等腰三角形中,我们可以根据这个性质来计算另外一个角的度数。
3. 直角三角形内角在直角三角形中,有一个角是直角,即90度,其他两个角的内角和是90度。
我们可以利用这个性质来计算和证明直角三角形的相关问题。
4. 三角形内角之间的关系在三角形中,三个内角之间有一些特殊的关系。
例如,其中一角大于其他两角的和。
我们可以利用这些关系来解决一些与三角形内角之间的大小关系相关的问题。
二、三角形外角的性质1. 三角形外角和三角形的外角和等于360度。
对于任意一个三角形ABC,我们可以通过以下公式来计算三角形的外角和:∠A' + ∠B' + ∠C' = 360°这个性质是三角形外角的计算的基础,我们可以根据这个公式来解决一些与三角形外角相关的问题。
2. 三角形外角与对应内角的关系在三角形中,一个外角的度数等于与之相对的两个内角的和,即∠A' = ∠B + ∠C。
这个性质是三角形外角与内角之间的重要关系。
三、三角形角度计算和证明1. 三角形内角计算在计算三角形的内角时,一般可以通过已知的内角和性质来进行计算。
例如,根据等腰三角形的性质来计算等腰三角形的内角,或者利用直角三角形的性质来计算直角三角形的内角。
2. 三角形内角大小比较在比较三角形的内角大小时,可以利用三角形内角之间的关系来进行比较。
例如,我们可以通过比较三角形内角之间的关系来判断一个角是否大于另外一个角。
3. 三角形外角计算和证明在计算三角形的外角时,一般可以通过已知的外角和性质来进行计算。
初中数学知识点总结:与三角形有关的线段、角

初中数学知识点总结:与三角形有关的线段、角知识点总结一、三角形的有关概念1.三角形:由不在同一直线上的三条线段首尾顺次相接组成的图形叫三角形。
三角形的特征:①不在同一直线上;②三条线段;③首尾顺次相接;④三角形具有稳定性。
2.三角形中的三条重要线段:角平分线、中线、高(1)角平分线:三角形的一个内角的平分线与这个角的对边相交,这个角的顶点和交点之间的线段叫做三角形的角平分线。
(2)中线:在三角形中,连接一个顶点和它的对边中点的线段叫做三角形的中线。
(3)高:从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足间的线段叫做三角形的高。
说明:①三角形的角平分线、中线、高都是线段;②三角形的角平分线、中线都在三角形内部且都交于一点;三角形的高可能在三角形的内部(锐角三角形)、外部(钝角三角形),也可能在边上(直角三角形),它们(或延长线)相交于一点。
二、三角形的边和角三边关系:三角形中任意两边之和大于第三边。
由三边关系可以推出:三角形任意两边之差小于第三边。
三、三角形内、外角的关系1.三角形的内角和等于180°。
2.直角三角形的两个锐角互余。
3.三角形的一外角等于和它不相邻的两个内角之和,三角形的一个外角大于任何一个和它不相邻的内角。
4.三角形的外角和为360°。
四、等腰三角形与直角三角形:1.等腰三角形:有两条边相等的三角形称为等腰三角形,相等的两边叫做等腰三角形的腰,三条边都相等的三角形叫做等边三角形(或正三角形)。
说明:等边三角形是等腰三角形的特殊情况。
2.直角三角形:有一个角是直角的三角形是直角三角形,它的两个锐角互余。
五、三角形的分类:六、三角形的面积:1.一般计算公式2.性质:等底等高的三角形面积相等。
常见考法(1)考查三角形的性质和概念;(2)根据三角形内角和以及内、外角关系,给出已知两角,来求第三个角;(3)根据三角形内、外角的关系,比较两角大小的;(4)利用三边关系判断三条线段能否组成三角形或给出三角形的两边长,来确定第三边长的取值范围,亦或证明线段之间的不等关系。
三角形中边角关系,命题与证明专项复习(附带知识点练习)

第十三章:三角形中的边角关系,命题与证明第一节:三角形三边关系知识点:1、三角形定义:由不在同一条直线上的三条线段首尾依次相接所组成的封闭图形叫做三角形;组成三角形的线段叫做三角形的边;相邻两边的公共断点叫做顶点;相邻两边组成的角叫做三角形的内角。
如图三角形可记做,读作“三角形ABC”2、角形的分类:,有两条边相等的三角形叫做等腰三角形,的三角形叫做等边三角形又叫做正三角形.边,两腰的夹角叫做顶角,腰与底边的夹角叫做低角.3、三角形角的关系:三个角都是锐角的三角形叫做锐角三角形,有一个角是直角的三角形叫做直角三角形,有一个角是钝角的三角形叫做钝角三角形考点:(一)、会用符号表示三角形,了解什么是三角形的边、角、顶点,并且能用符号来表示;(二)、了解等腰三角形的腰,顶角,低角的概;(三)、运用两边之和大于第三边,两边之差小于第三边求范围和判断是否能围成三角形;(四)、运用三角形的内角和和直角三角形求角的度数例题:3、已知一个等腰三角形的一边长是5,一边长是12,求这个三角形的周长4、已知三角形的三边长分别是a、b、c,化简│a+b-c│-│b-a-c│的结果为————5、已知等腰∆ABC的周长为10,若设腰长为x,则x的取值范围————6、三角形中最大角α的范围是——————,最小角β的范围是——————7、在下列空白出,分别填上“锐角”、“直角”、“钝角”(一)∆ABC中,∠A=∠B+∠C,则∆ABC是——————三角形(二)∆ABC中,∠A+∠B=20°,则∆ABC是——————三角形(三)∆ABC中,∠A=40°,∠B=∠C,则∆ABC是——————三角形8、在∆ABC中,∠A是∠B的2倍,∠C比∠A与∠B的和还要大30°,求∆ABC各角的度数。
9、四条线段的长度分别为4、6、8、10,可以组成三角形的组数为()A.4B.3C.2D.1第二课时:三角形的角平分线、中线、高知识点:(一)、三角形中,一个角的平分线与这个角对边相交,顶点与交点之间的线段叫做三角形的角平分线(二)、三角形中,连接一个顶点与它对边中点的线段叫做三角形的中线三角形的任意一条中线把三角形分成面积相等的两个三角形(三)、从三角形的一个顶点到它对边所在直线的垂线段叫做三角形的高线,也叫三角形的高。
三角形知识点总结

三角形知识点总结八年级上册数学三角形知识点总结(通用7篇)我们在学习数学的过程中,会学习各种各样的图形,其中在八年级的时候我们重点学习了三角形的定理知识。
下面是店铺为大家整理的八年级上册数学三角形知识点总结,希望对大家有用!三角形知识点总结篇11. 三角形的边角关系:(1)三角形的任意两边之和大于第三边,任意两边之差小于第三边。
(2)三角形内角和等于180°。
(3)三角形的任一个外角等于与它不相邻的两个内角的和。
2. 证明线段相等的方法:(1)可证明它们所在的两个三角形全等。
(2)角平分线性质:角平分线上的点到角的两边距离相等。
(3)等角对等边。
(4)等腰三角形的三线合一的性质。
(5)垂直平分线的性质:线段垂直平分线上的点到线段两端点的距离相等。
(6)等式的性质。
(7)中点的定义。
3. 证明角相等的方法:(1)同角(等角)的余角相等。
(2)同角(等角)的补角相等。
(3)平行线的性质:①两直线平行,同位角相等。
②两直线平行,内错角相等。
(4)全等三角形的对应角相等。
(5)等边对等角。
(6)角平分线的定义。
(7)等式的性质。
(8)对顶角相等。
4. 证明垂直的方法(1)证邻补角相等。
(2)证和已知直角三角形全等。
(3)勾股定理的逆定理。
三角形知识点总结篇2轴对称1.如果一个图形沿某条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形;这条直线叫做对称轴。
对称轴所在直线经过对称点所连线段的中点,并且垂直于这条线段.2.轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线。
3.角平分线上的点到角两边距离相等。
4.对称轴所在直线经过对称点所连线段的中点,并且垂直于这条线段.我们把经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线.5.线段垂直平分线的性质,即:线段垂直平分线上的点与这条线段两个端点的距离相等;这条线段两个端点距离相等的点都在它的垂直平分线上.6.轴对称图形上对应线段相等、对应角相等。
解直角三角形基础知识
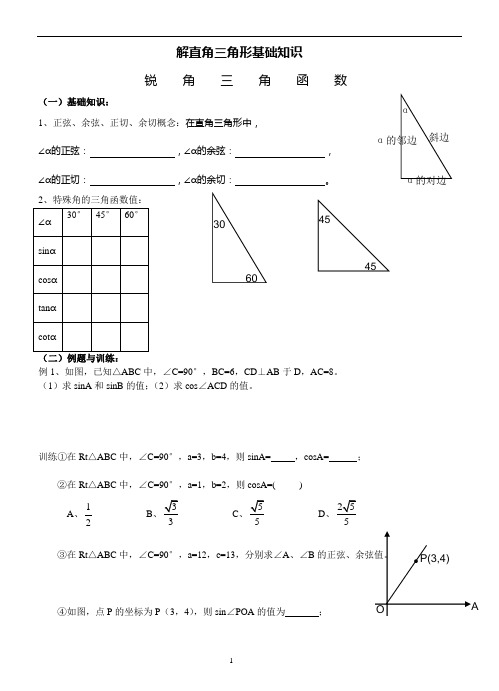
α α的对边α的邻边 斜边解直角三角形基础知识 锐 角 三 角 函 数(一)基础知识:1、正弦、余弦、正切、余切概念:在直角三角形中,∠α的正弦: ,∠α的余弦: , ∠α的正切: ,∠α的余切:例1、如图,已知△ABC 中,∠C=90°,BC=6,CD ⊥AB 于D ,AC=8。
(1)求sinA 和sinB 的值;(2)求cos ∠ACD 的值。
训练①在Rt △ABC 中,∠C=90°,a=3,b=4,则sinA= ,cosA= ;②在Rt △ABC 中,∠C=90°,a=1,b=2,则cosA=( )A 、12B 、3C 、5D 、5③在Rt △ABC 中,∠C=90°,a=12,c=13,分别求∠A 、∠B④如图,点P 的坐标为P (3,4),则sin ∠POA 的值为 ;解 直 角 三 角 形(一)基础知识:解直角三角形: ; 解直角三角形运用的知识:边的关系: ; 角的关系: ; 边角关系: 。
(二)例题与训练:例1、已知Rt △ABC 中,∠C=90°,根据下列条件解直角三角形:(1)∠A=60°,b=4(2)a=19,c=训练①在Rt △ABC 中,∠C=90°,,,则sinA= ,cosA= ;②Rt △ABC 中,∠C=90°,AC ∶BC=1AB=6,则∠B= ,AC= ;③Rt △ABC 中,∠C=90°,a=b=,则c= ,∠A= ;④在Rt △ABC 中,∠C=90°,已知a 及∠A ,则c 应为( ) A 、asinA B 、sin a A C 、acosA D 、cos a A例2、等边三角形的边长为8,它的面积为 。
训练①已知等腰△ABC 的顶角∠A=120°,底边BC=24,那么腰上的高BD 及腰AB 的长分别为( )A 、9和15B 、12和C 、5和13D 、②等腰三角形的底边长为10,周长为36,那么底角的余弦为( ) A 、513 B 、1213 C 、1013 D 、512③等腰梯形的底角为60°,上底长为2,下底长为6,则梯形面积为( )A 、B 、C 、D 、AC E AC例3、如图,甲、乙两建筑物的水平距离为30米,以A 点测得C 点的仰角为60°,测得D 点的俯角为30°,求建筑物甲的高CD 。
有关三角形知识点(大全)

有关三角形知识点(大全)有关三角形知识点 (大全)三角形是一种基本的几何形状,由三条线段组成,形成一个封闭的平面图形。
在数学中,三角形有许多重要的性质和知识点。
本文将为您介绍有关三角形的知识点,如下所示:一、三角形的分类1.按照角度分类:- 锐角三角形:三个内角都是锐角的三角形。
- 钝角三角形:至少有一个内角是钝角的三角形。
- 直角三角形:其中一个内角是直角的三角形。
2.按照边长分类:- 等边三角形:三条边的边长完全相等的三角形。
- 等腰三角形:两条边的边长相等的三角形。
- 普通三角形:三条边的边长都不相等的三角形。
二、三角形的性质1.内角和定理:三角形的三个内角和等于180度。
证明:设三角形的三个内角分别为A、B、C,则角A、角B和角C的补角分别为180°-A,180°-B和180°-C。
由于角的补角互补,所以有(180°-A)+(180°-B)+(180°-C)=540°。
而三角形的三个内角之和和为180°,所以有A+B+C=180°。
2.外角和定理:三角形的一个内角的外角等于其他两个内角的和。
证明:设三角形的一个内角为A,则该内角的外角为180°-A。
另外两个内角的外角分别为180°-B和180°-C。
根据外角和定理,有(180°-A)+(180°-B)+(180°-C)=360°,即180°-A=180°-B+180°-C。
3.等腰三角形的性质:等腰三角形的底边上的两个角是相等的。
证明:设等腰三角形的两边边长相等,底边的两个角分别为A和B。
由于等腰三角形的两条腰相等,所以角A和角B的对边也相等。
根据对应角相等的性质,可以得出角A=角B。
4.直角三角形的性质:直角三角形的两条直角边的平方和等于斜边的平方。
高中数学-解三角形知识点汇总及典型例题

a
b
c
2R ( R为外接圆半径)
sin A sin B sin C
( 3)余弦定理:三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积
的两倍
a2= b2+ c2-2bccos A;
b2= c2+a2- 2cacos B;
c2=a2+ b2- 2abcosC。
3 .三角形的面积公式:
AB 在△ ABC中, sin BCA
AC sin AB C , 即
ACsin60 AB= sin 15
3 2 6, 20
32 6 因此, BD= 20
0.33km。
故 B, D 的距离约为 0.33km 。 点评:解三角形等内容提到高中来学习,又近年加强数形结合思想的考查和对三角变换要求的降低, 对三角的综合考查将向三角形中问题伸展,但也不可太难,只要掌握基本知识、概念,深刻理解其中 基本的数量关系即可过关。 三、思维总结
另解:角化边
点评:本题考查了三角形的基本性质,要求通过观察、分析、判断明确解题思路和变形方向,通
畅解题途径
题型 5:三角形中求值问题
例 5. ABC 的三个内角为
出这个最大值。
A、 B、 C ,求当 A 为何值时, cos A
2cos B
C
取得最大值,并求
2
解析:由
A+B+C=π,得
B+C π 2 =2
.
5.三角形中的三角变换
三角形中的三角变换,除了应用上述公式和上述变换方法外,还要注意三角形自身的特点。
( 1)角的变换
因为在△ ABC 中, A+B+C=π ,所以 sin(A+B)=sinC ; cos(A+B)= -cosC; tan(A+B)= - tanC 。
三角形知识点总结完

三角形知识点全面总结1、三角形全等的性质及判定全等三角形的对应边相等,对应角也相等判定:SSS、SAS、ASA、AAS、HL (RtA^RtA)2、等腰三角形的判定及性质性质:①两腰相等②等边对等角(即“等腰三角形的两个底角相等”)③三线合一(即“等腰三角形顶角的平分线、底边上的中线、底边上的高互相重合”)判定:①有两边相等的三角形是等腰三角形②有两个角相等的三角形是等腰三角形(等角对等边)结论总结:等腰三角形底边上的任意一点到两腰的距离之和等于一腰【即:DE+DF=CP,(D为BC上的任意一点)】3、等边三角形的性质及判定定理性质:①三条边都相等②三个角都相等,并且每个角都等于60度③三线合一(即“等腰三角形顶角的平分线、底边上的中线、底边上的高互相重合”)④等边三角形是轴对称图形,有3条对称轴。
判定:①三条边都相等的三角形是等边三角形②三个角都相等的三角形是等边三角 形。
③有一个角是60度的等腰三角形是等边三角形。
结论总结:①高二亘边【即: AD =巨AB 】 2 2②面积二三3边2【即:S=三3AB 2】4 A ABC 4 4、直角三角形的性质及判定 性质:①两锐角互余②勾股定理③30°角所对的直角边等于斜边的一半。
④斜边中 线等于斜边一半判定:①有一个内角是直角的三角形是直角三角形②勾股定理的逆定理(即“如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形。
”)5、线段的垂直平分线性质:线段垂直平分线上的点到这条线段两个端点的距离相等。
判定:①定义法②到一条线段两个端点距离相等的点在这条线段的垂直平分线上。
(2)三角形三边的垂直平分线的性质③一边中线等于这边一半的三角形是直角三角形结论总结:直角三角形斜边上的高二 直角边的乘积 斜边(1)线段垂直平分线的性质及判定【即:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等。
(3)如何用尺规作图法作线段的垂直平分线:分别以线段的两个端点人、B 为圆心, 以大于AB 的一半长为半径作弧,两弧交于点乂、N ;作直线MN ,则直线MN 就是线段 AB 的垂直平分线。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角形有关的角知识点总结与随堂练(基础篇)知识点一:三角形内角和定理?
定理:三角形三个内角的和等于180°.?
注意:①在三角形中,已知两个内角可以求出第三个内角.?
②在三角形中,已知三个内角的比或它们之间的关系,求各内角.?
③三角形最多只有一个直角或者钝角,最少有两个锐角.?
知识点二:直角三角形的性质与判定
性质:直角三角形的两个锐角互余。
?
判定:有两个角互余的三角形是直角三角形。
知识点三:三角形的外角?
定义:三角形的一边与另一边的延长线组成的角,叫做三角形的外角.? 性质:?①三角形的一个外角等于与它不相邻的两个内角的和.?
②三角形的一个外角大于与它不相邻的任何一个内角.?
三角形的外角和为360度.?三角形的外角最少两个钝角
随堂练
一、选择题:
1.如果三角形的三个内角的度数比是2:3:4,则它是( )毛
A.锐角三角形
B.钝角三角形;
C.直角三角形
D.钝角或直角三角形
2.下列说法正确的是( )
A.三角形的内角中最多有一个锐角;
B.三角形的内角中最多有两个锐角
C.三角形的内角中最多有一个直角;
D.三角形的内角都大于60°
3.已知三角形的一个内角是另一个内角的
,是第三个内角的
,则这个三角形各内角的度数分别为( )
A.60°,90°,75°
B.48°,72°,60°
C.48°,32°,38° D .40°,50°,90°
4.已知△ABC中,∠A=2(∠B+∠C),则∠A的度数为( )
A.100°
B.120°
C.140°
D.160°
5.已知三角形两个内角的差等于第三个内角,则它是( )
A.锐角三角形
B.钝角三角形
C.直角三角形
D.等边三角形
6.设α,β,γ是某三角形的三个内角,则α+β,β+γ,α+γ 中 ( )
A.有两个锐角、一个钝角
B.有两个钝角、一个锐角
C.至少有两个钝角
D.三个都可能是锐角
7.在△ABC中,∠A=
∠B=
∠C,则此三角形是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等腰三角形
8.如果三角形的一个外角和与它不相邻的两个内角的和为180°,那么与这个外角相邻的内角的度数为( )
A.30°
B.60°
C.90°
D.120°
9.已知三角形的三个外角的度数比为2:3:4,则它的最大内角的度数为( )
A.90°
B.110°
C.100°
D.120°
10.已知等腰三角形的一个外角是120°,则它是( )
A.等腰直角三角形;
B.一般的等腰三角形;
C.等边三角形;
D.等腰钝角三角形
11.如图1所示,若∠A=32°,∠B=45°,∠C=38°,则∠DFE等于( )
A.120°
B.115°
C.110°
D.105°
12.如图2所示,在△ABC中,E,F分别在AB,AC上,则下列各式不能成立的是( )
A.∠BOC=∠2+∠6+∠A;
B.∠2=∠5-
∠A; C.∠5=∠1+∠4; D.∠1=∠ABC+∠4
二、填空题:
1.三角形中,若最大内角等于最小内角的2倍,最大内角又比另一个内角大20°,则此三角形的最小内角的度数是________.
2.在△ABC中,若∠A+∠B=∠C,则此三角形为_______三角形;若∠A+∠B<∠C,则此三角形是_____三角形.
3.已知等腰三角形的两个内角的度数之比为1: 2, 则这个等腰三角形的顶角为_______.
5.三角形的三个外角中,最多有_______个锐角.
6.如图所示,∠1=_______.
7.如果一个三角形的各内角与一个外角的和是225°,则与这个外角相邻的内角是____度.
8.已知等腰三角形的一个外角为150°,则它的底角为_____.
三、解答题
1.在△ABC中,已知∠B-∠A=5°,∠C-∠B=20°,求三角形各内角的度数.
2.如图所示,在△ABC中,∠A=70°,BO,CO分别平分∠ABC和∠ACB,求∠BOC的度数.。
