1998年全国统一高考数学试卷(理科)
1989年全国统一高考数学试卷(理科)
1989年全国统一高考数学试卷（理科）一、选择题（共12小题，每小题3分，满分36分） 1．（3分）（2000•北京）如果I={a ，b ，c ，d ，e}，M={a ，c ，d}，N={b ，d ，e}，其中I 是全集，那么（C I M ）∩（C I N ）等于（ ） A ． φ B ． {d} C ． {a ，c} D ． {b ，e} 2．（3分）与函数y=x 有相同图象的一个函数是（ ） A ． B ． C ． y =a log a x ．其中a ＞0，a≠1 D ． y =log a a x ．其中a ＞0，a≠1 3．（3分）如果圆锥的底面半径为，高为2，那么它的侧面积是（ ） A ． B ． C ． D ． 4．（3分）的值等于（ ） A ． ﹣1 B ．C ．D ．5．（3分）已知{an}是等比数列，如果a 1+a 2+a 3=18，a 2+a 3+a 4=﹣9，S n =a 1+a 2+…+an ，那么S n 的值等于（ ） A ． 8 B ． 16 C ． 32 D ． 486．（3分）如果的值等于（ ） A ．B ．C ．D ．7．（3分）（2010•宁波模拟）设复数z 满足关系：z+||=2+i ，那么z 等于（ ） A ． ﹣+i B ． +i C ． ﹣﹣iD ． ﹣i 8．（3分）已知球的两个平行截面的面积分别为5π和8π，它们位于球心的同一侧，且相距为1，那么这个球的半径是（ ） A ． 4 B ． 3 C ． 2 D ． 59．（3分）已知椭圆的极坐标方程是，那么它的短轴长是（ ） A ． B ．C ．D ．10．（3分）如果双曲线上一点P 到它的右焦点的距离是8，那么点P 到它的右准线的距离是（ ）A ． 10B ．C ．D ．11．（3分）已知f （x ）=8+2x ﹣x 2，如果g （x ）=f （2﹣x 2），那么g （x ）（ ） A ． 在区间（﹣1，0）上是减函数 B ． 在区间（0，1）上是减函数 C ． 在区间（﹣2，0）上是增函数 D ． 在区间（0，2）上是增函数 12．（3分）由数字1，2，3，4，5组成没有重复数字的五位数，其中小于50000的偶数共有（ ） A ． 60个 B ． 48个 C ． 36个 D ． 24个二、填空题（共6小题，每小4分，满24分） 13．（4分）方程的解集是_________ 14．（4分）（2010•焦作二模）不等式|x 2﹣3x|＞4的解集是 _________ ．15．（4分）函数的反函数的定义域是 _________ ．16．（4分）（2010•佛山模拟）若（1+x ）6=a 0+a 1x+a 2x 2+…+a 6x 6，则a 1+a 2+…+a 6= _________ ． 17．（4分）已知A 和B 是两个命题，如果A 是B 的充分条件，那么B 是A 的 _________ 条件 18．（4分）如图，已知圆柱的底面半径是3，高是4，A 、B 两点分别在两底面的圆周上，并且AB=5，那么直线AB 与轴OO'之间的距离等于 _________ ．三、解答题（共6小题，满分60分） 19．（8分）证明：．20．（10分）如图，在平行六面体ABCD ﹣A 1B 1C 1D 1中，已知AB=5，AD=4，AA 1=3，AB ⊥AD ，∠A 1AB=∠A 1AD=．（Ⅰ）求证：顶点A 1在底面ABCD 的射影O 在∠BAD 的平分线上； （Ⅱ）求这个平行六面体的体积．21．（10分）自点A（﹣3，3）发出的光线L射到x轴上，被x轴反射，其反射光线所在直线与圆x2+y2﹣4x﹣4y+7=0相切，求光线L所在直线的方程．22．（12分）已知a＞0，a≠1，试求使方程有解的k的取值范围．23．（10分）是否存在常数a，b，c使得等式1•22+2•32+…+n（n+1）2=（an2+bn+c）对于一切正整数n都成立？并证明你的结论．24．（10分）设f（x）是定义在区间（﹣∞，+∞）上以2为周期的函数，对k∈Z，用I k表示区间（2k ﹣1，2k+1]，已知当x∈I0时，f（x）=x2．（1）求f（x）在I k上的解析表达式；（2）对自然数k，求集合M k={a|使方程f（x）=ax在I k上有两个不等的实根}1989年全国统一高考数学试卷（理科）参考答案与试题解析一、选择题（共12小题，每小题3分，满分36分） 1．（3分）（2000•北京）如果I={a ，b ，c ，d ，e}，M={a ，c ，d}，N={b ，d ，e}，其中I 是全集，那么（C I M ）∩（C I N ）等于（ ） A ． φ B ． {d} C ． {a ，c} D ． {b ，e}考点： 交、并、补集的混合运算． 分析： 根据交集、补集的意义直接求解．或者根据（C I M ）∩（C I N ）=C I （M ∪N ）求解． 解答： 解：C I M={b ，e}，C I N={a ，c}，∴（C I M ）∩（C I N ）=∅，故选A点评： 本题考查集合的基本运算，较容易． 2．（3分）与函数y=x 有相同图象的一个函数是（ ） A ． B ． C ． y =a log a x ．其中a ＞0，a≠1 D ． y =log a a x ．其中a ＞0，a≠1考点： 反函数． 分析： 欲寻找与函数y=x 有相同图象的一个函数，只须考虑它们与y=x 是不是定义域与解析式都相同即可．解答： 解：对于A ，它的定义域为R ，但是它的解析式为y=|x|与y=x 不同，故错；对于B ，它的定义域为x≠0，与y=x 不同，故错； 对于C ，它的定义域为x ＞0，与y=x 不同，故错；对于D ，它的定义域为R ，解析式可化为y=x 与y=x 同，故正确； 故选D ．点评： 本题主要考查了函数的概念、函数的定义域等，属于基础题． 3．（3分）如果圆锥的底面半径为，高为2，那么它的侧面积是（ ） A ． B ． C ． D ．考点： 棱柱、棱锥、棱台的侧面积和表面积． 专题： 计算题． 分析： 根据圆锥的侧面积公式直接解答即可． 解答： 解：圆锥的底面半径为，高为2，母线长为：，那么它的侧面积：故选C ．点评： 本题考查圆锥的侧面积和表面积，是基础题、必会题．4．（3分）的值等于（ ）A ． ﹣1B ．C ．D ．考点：反三角函数的运用．专题：计算题．分析：利用反函数的运算法则，以及两角和的余弦公式求解即可．解答：解：===﹣[cos（arcsin）cos（arccos）+sin（arcsin）sin（arccos）]=﹣[]=﹣1故选A．点评：本题考查反函数的运算，两角和的正弦公式，是基础题．5．（3分）已知{an}是等比数列，如果a1+a2+a3=18，a2+a3+a4=﹣9，S n=a1+a2+…+an，那么S n的值等于（）A．8B．16 C．32 D．48考点：极限及其运算；等比数列的前n项和；等比数列的性质．专题：计算题．分析：由题意知，所以，S n=．解答：解：∵a1+a1q+a1q2=18，a1q+a1q2+a1q3=﹣9，∴．∴，∴S n=．故选B．点评：本题考查等比数列的计算和极限，解题时要正确选取公式，注意公式的灵活运用．6．（3分）如果的值等于（）A．B．C．D．考点：二倍角的余弦．分析：由题目中给出的角θ的范围，确定余弦值，用余弦表示sin，求出结果，容易出错的地方是，要求结果的正负，要用角的范围帮助分析解答：解：∵，∴，∵∴或，∵，∴，故选C点评：已知一个角的某个三角函数式的值，求这个角的其他三角函数式的值，一般需用三个基本关系式及其变式，通过恒等变形或解方程求解．已知一个角的某个三角函数式的值，求这个角的半角或二倍角的三角函数值，要用到二倍角公式．7．（3分）（2010•宁波模拟）设复数z满足关系：z+||=2+i，那么z等于（）A．﹣+i B．+i C．﹣﹣i D．﹣i考点：复数的基本概念；复数代数形式的乘除运算．专题：计算题；综合题．分析：解法1：设出复数，利用复数相等的条件求解即可；解法2：利用复数模的性质，移项平方，然后解方程即可；解法3：考虑选择题的特点，考查选项复数的模，结合题干推出复数z的实部、虚部的符号即可．解答：解：法1：设z=a+bi（a，b∈R）由已知a+bi+=2+i由复数相等可得∴故z=+i故选B．法2：由已知可得z=﹣||+i ①取模后平方可得|z|2=（2﹣|z|）2+1=4﹣4|z|+|z|2+1，所以，代入①得，故选B．法3：选择支中的复数的模均为，又，而方程右边为2+i，它的实部，虚部均为正数，因此复数z的实部，虚部也必须为正，故选B．点评：本题考查复数的基本概念，复数代数形式的乘除运算，复数的模，考查计算能力，判断能力，是基础题．8．（3分）已知球的两个平行截面的面积分别为5π和8π，它们位于球心的同一侧，且相距为1，那么这个球的半径是（）A．4B．3C．2D．5考点：球面距离及相关计算．专题：计算题．分析：画出图形，求出两个截面圆的半径，即可解答本题．解答：解：由题意画轴截面图，截面的面积为5π，半径为，截面的面积为8π的圆的半径是，设球心到大截面圆的距离为d，球的半径为r，则5+（d+1）2=8+d2，∴d=1，∴r=3故选B．点评：本题考查球的截面圆的半径，球的半径，球心到截面圆心的距离的关系，是基础题．9．（3分）已知椭圆的极坐标方程是，那么它的短轴长是（）A．B．C．D．考点：简单曲线的极坐标方程．专题：计算题．分析：利用圆锥曲线统一的极坐标方程，求出圆锥曲线的短轴长即可．解答：解：将原极坐标方程为，化成：极坐标方程为ρ=．，对照圆锥曲线统一的极坐标方程得：e=，a=3，b=，c=2．∴它的短轴长2故选C点评：本题主要考查了圆锥曲线的极坐标方程，属于基础题．10．（3分）如果双曲线上一点P到它的右焦点的距离是8，那么点P到它的右准线的距离是（）A．10 B．C．D．考点：双曲线的简单性质．专题：计算题．分析：由双曲线的第二定义可知点P到双曲线右焦点的距离和点P到它的右准线的距离之比等于离心率，由此可以求出点P到它的右准线的距离．解答：解：设点P 到它的右准线的距离是x ，∵， ∴，解得．故点P 到它的右准线的距离是．故选D ．点评： 本题考查双曲线的第二定义，解题时注意认真审题． 11．（3分）已知f （x ）=8+2x ﹣x 2，如果g （x ）=f （2﹣x 2），那么g （x ）（ ） A ． 在区间（﹣1，0）上是减函数 B ． 在区间（0，1）上是减函数 C ． 在区间（﹣2，0）上是增函数 D ． 在区间（0，2）上是增函数考点： 复合函数的单调性． 专题： 计算题；综合题；压轴题． 分析： 先求出g （x ）的表达式，然后确定它的区间的单调性，即可确定选项． 解答： 解：因为 f （x ）=8+2x ﹣x 2，则 g （x ）=f （2﹣x 2）=8+2x 2﹣x 4 =﹣（x 2﹣1）2+9，因为g′（x ）=﹣4x 3+4x ，x ∈（﹣1，0），g′（x ）＜0，g （x ）在区间（﹣1，0）上是减函数． 故选A ．点评： 本题考查复合函数的单调性，考查学生发现问题解决问题的能力，是基础题． 12．（3分）由数字1，2，3，4，5组成没有重复数字的五位数，其中小于50000的偶数共有（ ） A ． 60个 B ． 48个 C ． 36个 D ． 24个考点： 排列及排列数公式． 专题： 压轴题． 分析： 由题意本题的要求是个位数字是偶数，最高位不是5．可先安排个位，方法有2种，再安排最高位，方法有3种，其他位置安排方法有A 33=6种，求乘积即可．解答： 解：由题意，符合要求的数字共有2×3A 33=36种故选C点评： 本题考查有特殊要求的排列问题，属基本题．有特殊要求的排列问题，一般采用特殊位置优先或特殊元素优先考虑．二、填空题（共6小题，每小4分，满24分） 13．（4分）方程的解集是 {x|x=2kπ+或x=2kπ+}（k ∈Z ）考点： 正弦函数的图象；三角函数的积化和差公式． 专题： 计算题．分析： 先利用两角和公式对化简整理，进而根据正弦函数的性质可求得x 的解集． 解答：解：=2（sinx ﹣cosx ）=2sin （x ﹣）=∴sin（x﹣）=∴x﹣=2kπ+或2kπ+∴x=2kπ+或2kπ+故答案为{x|x=2kπ+或x=2kπ+}（k∈Z）点评：本题主要考查了正弦函数的基本性质．考查了学生对正弦函数基础知识的理解和运用．14．（4分）（2010•焦作二模）不等式|x2﹣3x|＞4的解集是{x|x＜﹣1，或x＞4}．考点：绝对值不等式的解法．专题：计算题．分析：用绝对值的意义将绝对值不等式转化为一般不等式求解．解答：解：∵|x2﹣3x|＞4∴x2﹣3x＞4 或x2﹣3x＜﹣4由x2﹣3x＞4解得x＜﹣1或x＞4，x2﹣3x＜﹣4无解∴不等式|x2﹣3x|＞4的解集是{x|x＜﹣1或x＞4}故应填{x|x＜﹣1或x＞4}点评：考查绝对值不等式的解法，用绝对值的几何意义来进行转化．15．（4分）函数的反函数的定义域是（﹣1，1）．考点：反函数．专题：计算题．分析：欲求反函数的定义域，可以通过求在函数的值域获得，所以只要求出函数的值域即可．解答：解：由得，e x=．∵ex＞0，∴．＞0，∴﹣1＜y＜1，∴反函数的定义域是（﹣1，1）．故填：（﹣1，1）点评：本题主要考查反函数的性质，考查了互为反函数的两个函数的定义域和值域正好相反．属于基础题．16．（4分）（2010•佛山模拟）若（1+x）6=a0+a1x+a2x2+…+a6x6，则a1+a2+…+a6=63．考点：二项式系数的性质．专题：计算题．分析：本题为求二项式系数的和，注意到等式右边当x=1时即为a0+a1+a2+…+a6，故可采用赋值法，只要再求出a0即可．解答：解：在原式中，令x=1得26=a0+a1+a2+…+a6=64，又因为a0=1，所以a1+a2+…+a6=63；故答案为：63点评：本题考查二项式系数求和：赋值法的应用，准确理解二项式定理是解决本题的关键．17．（4分）已知A和B是两个命题，如果A是B的充分条件，那么B是A的必要条件考点：必要条件、充分条件与充要条件的判断．专题：压轴题；阅读型．分析：本题考查的知识点是充要条件的定义，如果A是B的充分条件，那么B是A的必要条件．解答：解：由充要条件的定义，如果A是B的充分条件，那么B是A的必要条件．故答案为：必要点评：判断充要条件的方法是：①若p⇒q为真命题且q⇒p为假命题，则命题p是命题q的充分不必要条件；②若p⇒q为假命题且q⇒p为真命题，则命题p是命题q的必要不充分条件；③若p⇒q为真命题且q⇒p为真命题，则命题p是命题q的充要条件；④若p⇒q为假命题且q⇒p为假命题，则命题p是命题q的即不充分也不必要条件．⑤判断命题p与命题q所表示的范围，再根据“谁大谁必要，谁小谁充分”的原则，判断命题p与命题q的关系．18．（4分）如图，已知圆柱的底面半径是3，高是4，A、B两点分别在两底面的圆周上，并且AB=5，那么直线AB与轴OO'之间的距离等于．考点：棱柱的结构特征；点、线、面间的距离计算．专题：计算题；压轴题．分析：画出几何图形，直线AB与轴OO'之间的距离，等于直线轴OO'与平面ABC的距离，求解即可．解答：解：如图直线AB与轴OO'之间的距离，等于直线轴OO'与平面ABC的距离，由图形可知直线AB与轴OO'之间的距离等于O到BC 的距离，AB=5，AC=4，所以BC=3所以所求距离为：故答案为：点评：本题考查棱柱的结构特征，点、线、面间的距离计算，考查空间想象能力，考查计算能力，是中档题．三、解答题（共6小题，满分60分）19．（8分）证明：．考点：两角和与差的正弦函数；三角函数恒等式的证明；弦切互化．分析：等式左边是两个正切值，右边是余弦、正弦的分式，左边是半角与，右边是单角x和倍角2x．若从右向左证，需进行单角变半角，而分母可进行和化积，关键是分子的变化，仍从角入手，将x写成﹣，再用两角差公式，而从左向右证，需进行切变弦，同时还要考虑变半角为单角．解答：证明：=点评：本题主要考查同角三角函数的基本关系和两角差的正弦公式．属中档题．三角函数部分公式比较多要强化记忆．20．（10分）如图，在平行六面体ABCD﹣A1B1C1D1中，已知AB=5，AD=4，AA1=3，AB⊥AD，∠A1AB=∠A1AD=．（Ⅰ）求证：顶点A1在底面ABCD的射影O在∠BAD的平分线上；（Ⅱ）求这个平行六面体的体积．考点：棱柱、棱锥、棱台的体积．专题：计算题；证明题；综合题．分析：（Ⅰ）如图利用Rt△A1NA≌Rt△A1MA证明A1M=A1N，OM=ON，即证明顶点A1在底面ABCD 的射影O在∠BAD的平分线上；（Ⅱ）求出底面ABCD的面积，和高A1O，然后可求几何体的体积．解答：解：（Ⅰ）证：连接A1O，则A1O⊥底面ABCD．作OM⊥AB交AB于M，作ON⊥AD交AD于N，连接A1M，A1N由三垂线定理得A1M⊥AB，A1N⊥AD∵∠A1AM=∠A1AN，∴Rt△A1NA≌Rt△A1MA∴A1M=A1N∴OM=ON．∴点O在∠BAD的平分线上（Ⅱ）∵AM=AA1，∴AO=AM．又在职Rt△AOA1中，A1O2=AA12﹣AO2=，∴A1O=．∴平行六面体的体积V=．点评：本题考查棱柱的体积，以及射影问题，考查学生逻辑思维能力，是基础题．21．（10分）自点A（﹣3，3）发出的光线L射到x轴上，被x轴反射，其反射光线所在直线与圆x2+y2﹣4x﹣4y+7=0相切，求光线L所在直线的方程．考点：直线和圆的方程的应用；关于点、直线对称的圆的方程．分析：化简圆的方程为标准方程，求出关于x轴对称的圆的方程，设l的斜率为k，利用相切求出k的值即可得到l的方程．解答：解：已知圆的标准方程是（x﹣2）2+（y﹣2）2=1，它关于x轴的对称圆的方程是（x﹣2）2+（y+2）2=1，设光线L所在直线的方程是y﹣3=k（x+3）（其中斜率k待定）由题设知对称圆的圆心C'（2，﹣2）到这条直线的距离等于1，即．整理得：12k2+25k+12=0，解得：，或．故所求的直线方程是，或，即3x+4y﹣3=0，或4x+3y+3=0．点评：本题考查点、直线和圆的对称问题，直线与圆的关系，是基础题，解答简洁值得借鉴．22．（12分）已知a＞0，a≠1，试求使方程有解的k的取值范围．考点：对数函数图象与性质的综合应用．专题：计算题；压轴题．分析：由题设条件可知，原方程的解x应满足，当（1），（2）同时成立时，（3）显然成立，因此只需解，再根据这个不等式组的解集并结合对数函数的性质可以求出k的取值范围．解答：解：由对数函数的性质可知，原方程的解x应满足当（1），（2）同时成立时，（3）显然成立，因此只需解由（1）得2kx=a（1+k2）（4）当k=0时，由a＞0知（4）无解，因而原方程无解．当k≠0时，（4）的解是把（5）代入（2），得．解得：﹣∞＜k＜﹣1或0＜k＜1．综合得，当k在集合（﹣∞，﹣1）∪（0，1）内取值时，原方程有解．点评：解题时要注意分类讨论思想的灵活运用．23．（10分）是否存在常数a，b，c使得等式1•22+2•32+…+n（n+1）2=（an2+bn+c）对于一切正整数n都成立？并证明你的结论．考点：数学归纳法；数列的极限．专题：证明题；压轴题．分析：先假设存在符合题意的常数a，b，c，再令n=1，n=2，n=3构造三个方程求出a，b，c，再用用数学归纳法证明成立，证明时先证：（1）当n=1时成立．（2）再假设n=k（k≥1）时，成立，即1•22+2•32+…+k（k+1）2=（3k2+11k+10），再递推到n=k+1时，成立即可．解答：证明：假设存在符合题意的常数a，b，c，在等式1•22+2•32+…+n（n+1）2=（an2+bn+c）中，令n=1，得4=（a+b+c）①令n=2，得22=（4a+2b+c）②令n=3，得70=9a+3b+c③由①②③解得a=3，b=11，c=10，于是，对于n=1，2，3都有1•22+2•32+…+n（n+1）2=（3n2+11n+10）（*）成立．下面用数学归纳法证明：对于一切正整数n，（*）式都成立．（1）当n=1时，由上述知，（*）成立．（2）假设n=k（k≥1）时，（*）成立，即1•22+2•32+…+k（k+1）2=（3k2+11k+10），那么当n=k+1时，1•22+2•32+…+k（k+1）2+（k+1）（k+2）2=（3k2+11k+10）+（k+1）（k+2）2=（3k2+5k+12k+24）=[3（k+1）2+11（k+1）+10]，由此可知，当n=k+1时，（*）式也成立．综上所述，当a=3，b=11，c=10时题设的等式对于一切正整数n都成立．点评：本题主要考查研究存在性问题和数学归纳法，对存在性问题先假设存在，再证明是否符合条件，数学归纳法的关键是递推环节，要符合假设的模型才能成立．24．（10分）设f（x）是定义在区间（﹣∞，+∞）上以2为周期的函数，对k∈Z，用I k表示区间（2k﹣1，2k+1]，已知当x∈I0时，f（x）=x2．（1）求f（x）在I k上的解析表达式；（2）对自然数k，求集合M k={a|使方程f（x）=ax在I k上有两个不等的实根}考点：根的存在性及根的个数判断；函数解析式的求解及常用方法．专题：计算题；压轴题．分析：（1）利用2为周期2k也是周期可得f（x）=f（x﹣2k）=（x﹣2k）2即为所求．（2）转化为x2﹣（4k+a）+4k2=0在区间I k上恰有两个不相等的实根，再求有两个不相等的实根成立的条件即可．解答：解：（1）∵f（x）是以2为周期的函数，∴当k∈Z时，2k也是f（x）的周期．又∵当x∈I k时，（x﹣2k）∈I0，∴f（x）=f（x﹣2k）=（x﹣2k）2．即对k∈Z，当x∈I k时，f（x）=（x﹣2k）2．（2）当k∈Z且x∈I k时，利用（1）的结论可得方程（x﹣2k）2=ax，整理得：x2﹣（4k+a）+4k2=0．它的判别式是△=（4k+a）2﹣16k2=a（a+8k）．上述方程在区间I k上恰有两个不相等的实根的充要条件是a满足化简得由（1）知a＞0，或a＜﹣8k．当a＞0时：因2+a＞2﹣a，故从（2），（3）可得，即当a＜﹣8k时：2+a＜2﹣8k＜0，易知无解，综上所述，a应满足故所求集合点评：本题借助于函数的周期性对函数解析式的求法和根的存在性'根的个数的判断的综合考查，是道中档题．。
1999年全国统一高考数学试卷(理科)及其参考考答案
1999年全国统一高考数学试卷（理科）及其参考考答案本试卷分第I 卷（选择题）和第II 卷（非选择题）两部分。
第I 卷1至2页。
第II 卷3至8。
共150分。
考试时间120分钟。
第I 卷（选择题 共60分）注意事项：l ．答第I 卷前，考生务必将自己的姓名、准考证号、考试科目、试卷类型（A 或B ）用铅笔涂写在答题卡上。
2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后。
再选涂其它答案，不能答在试题卷上。
3．考试结束。
监考人将本试卷和答题卡一并收回。
参考公式：三角函数的积化和差公式[]1sin cos sin()sin()2αβαβαβ=++- []1cos sin sin()sin()2αβαβαβ=+--[]1cos cos cos()cos()2αβαβαβ=++-正棱台、圆台的侧面积公式：1()2S c c l ='+台侧 其中c '、c 分别表示上、下底面周长，l 表示斜高或母线长．球的体积公式：343V r π=球，其中R 表示球的半径．台体的体积公式：h S S S S V )31'++=‘台体（，其中'S ，S 分别表示上下底面积，h表示高。
一、选择题：本大题共14小题；第1—10题每小题4分，第11—14题每小题5分，共60分在每小题给出的四个选顶中，只有一顶是符合题目要求的。
（1）如图,I 是全集,M 、P 、S 、是I 的3个子集，由阴影部分所表示的集合是 ( )（A ）)(N M ⋂S ⋂ （B ）S P M ⋃⋂)(（C ）S P M ⋂⋂)( （D ）S P M ⋃⋂)(（2）已知映射f:A 中中的元素都是集合其中，集合A B A B },,3,2,1,1,2,3{,---=→ 元素在映射f 下的象，且对任意的a ∈A 中则集合中和它对应的元素是在B {a},B ,元 素的个数是 ( )（A ）4 （B ）5 （C ）6 （D ）7（3）若函数y=f(x)的反函数是y=g(x),f(a)=b,ab 等于则)(,0b g ≠ ( ) （A ）a（B ）1a -（C ）b （D ）1b -（4）函数f(x)=Msin(在区间)0)(>+ωϕωx [a,b]上是增函数，且f(a)=-M,f(b)=M,则函数g(x)=Mcos(上在],[)b a x φω+ ( )(A)是增函数 （B ）是减函数 （C ）可以取得最大值M （D ）可以取得最小值－M （5）若f(x)sinx 是周期为π的奇函数，则f(x)可以是（A ）sinx (B)cosx (C)sin2x (D)cos2x （6）在极坐标系中，曲线关于)3sin(4πθρ-= ( )(A)直线3πθ=对称（B ）直线πθ65=轴对称 （C ）点(2,)3π中心对称 （D ）极点中心对称（７）若干毫升水倒入底面半径为２cm 的圆柱形器皿中，量得水面的高度为６cm ，若将这些水倒入轴截面是正三角形的倒圆锥形器皿中，则水面的高度是 （ ）(A)cm 36 （B ）cm 6 （C ）2（D ）3（8）2312420443322104)(),)32(a a a a a x a x a x a x a a x +-++++++=+则（若 的值为 （ ）(A)1 (B)-1 (C)0 (D)2(9)直线为得的劣弧所对的圆心角截圆4032322=+=-+y x y x （ ）（A ）6π (B)4π (C)3π (D)2π(10) 如图，在多面体ＡＢＣＤＥＦ中 , 已知面ＡＢＣＤ是边长为３的正方形ＥＦ∥ＡＢＥＦ＝EF ,23与面ＡＣ的距离为２，则该多面体的体积 （ ） （A ）29 (B)5 (C)6 (D)215（11）若sin (αααctg tg >>∈<<-απαπ则),22（ ）(A))4,2(ππ--(B) )0,4(π- (C) )4,0(π (D) )2,4(ππ （12）如果圆台的上底面半径为5，下底面半径为R ，中截面把圆台分为上、下两个圆台，它们的侧面积的比为1∶2，那么R ＝（ ）（A ）10 （B ）15 （C ）20 （D ）25（13）已知丙点M （1，),45,4()45--N 、给出下列曲线方程：4x+2y-1=0 ②322=+y x ③1222=+y x ④1222=-y x 在曲线上存在点P 满足MP P N =的所有曲线方程是 （A ）①③ （B ）②④ （C ）①②③ （D ）②③④（14）某电脑用户计划使用不超过500元的资金购买单价分别为60元、70元的单片软件和盒装磁盘。
1998年高考数学试题及答案(全国理)-推荐下载
对全部高中资料试卷电气设备，在安装过程中以及安装结束后进行高中资料试卷调整试验；通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术通关，1系电过，力管根保线据护敷生高设产中技工资术艺料0不高试仅中卷可资配以料置解试技决卷术吊要是顶求指层，机配对组置电在不气进规设行范备继高进电中行保资空护料载高试与中卷带资问负料题荷试2下卷2，高总而中体且资配可料置保试时障卷，各调需类控要管试在路验最习；大题对限到设度位备内。进来在行确管调保路整机敷使组设其高过在中程正资1常料中工试，况卷要下安加与全强过，看度并22工且22作尽22下可22都能22可地护以缩1关正小于常故管工障路作高高；中中对资资于料料继试试电卷卷保破连护坏接进范管行围口整，处核或理对者高定对中值某资，些料审异试核常卷与高弯校中扁对资度图料固纸试定，卷盒编工位写况置复进.杂行保设自护备动层与处防装理腐置，跨高尤接中其地资要线料避弯试免曲卷错半调误径试高标方中高案资等，料，编试要5写、卷求重电保技要气护术设设装交备备置底4高调、动。中试电作管资高气，线料中课并敷3试资件且、设卷料中拒管技试试调绝路术验卷试动敷中方技作设包案术，技含以来术线及避槽系免、统不管启必架动要等方高多案中项；资方对料式整试，套卷为启突解动然决过停高程机中中。语高因文中此电资，气料电课试力件卷高中电中管气资壁设料薄备试、进卷接行保口调护不试装严工置等作调问并试题且技，进术合行，理过要利关求用运电管行力线高保敷中护设资装技料置术试做。卷到线技准缆术确敷指灵设导活原。。则对对：于于在调差分试动线过保盒程护处中装，高置当中高不资中同料资电试料压卷试回技卷路术调交问试叉题技时，术，作是应为指采调发用试电金人机属员一隔，变板需压进要器行在组隔事在开前发处掌生理握内；图部同纸故一资障线料时槽、，内设需，备要强制进电造行回厂外路家部须出电同具源时高高切中中断资资习料料题试试电卷卷源试切，验除线报从缆告而敷与采设相用完关高毕技中，术资要资料进料试行，卷检并主查且要和了保检解护测现装处场置理设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况，然后根据规范与规程规定，制定设备调试高中资料试卷方案。
1998年试题全国高考数学试题及参考答案
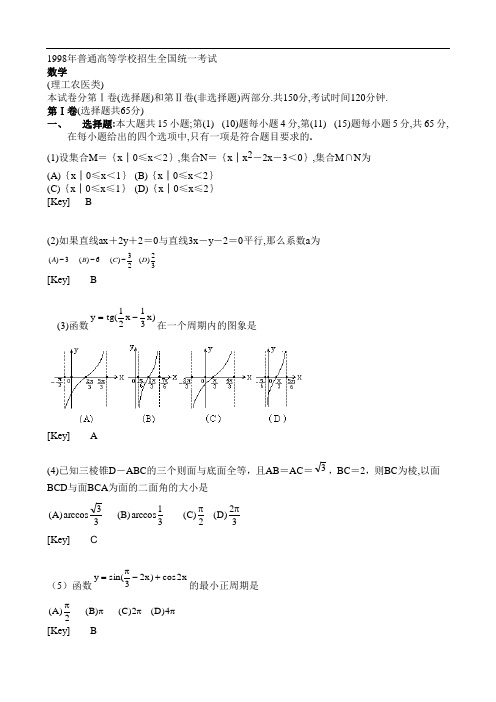
1998年普通高等学校招生全国统一考试 数学(理工农医类)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分,考试时间120分钟. 第Ⅰ卷(选择题共65分)一、 选择题:本大题共15小题;第(1) (10)题每小题4分,第(11) (15)题每小题5分,共65分,在每小题给出的四个选项中,只有一项是符合题目要求的. (1)设集合M ＝｛x │0≤x ＜2｝,集合N ＝｛x │x 2－2x －3＜0｝,集合M ∩N 为 (A)｛x │0≤x ＜1｝ (B)｛x │0≤x ＜2｝ (C)｛x │0≤x ≤1｝ (D)｛x │0≤x ≤2｝ [Key] B(2)如果直线ax ＋2y ＋2＝0与直线3x －y －2＝0平行,那么系数a 为32)(23)(6)(3)(D C B A ---[Key] B(3)函数)x 31x 21(tg y -=在一个周期内的图象是[Key] A(4)已知三棱锥D －ABC 的三个则面与底面全等，且AB ＝AC ＝3，BC ＝2，则BC 为棱,以面BCD 与面BCA 为面的二面角的大小是32)D (2)C (31arccos)B (33arccos)A (ππ[Key] C（5）函数x2cos )x 23sin(y +-π=的最小正周期是 ππππ4)D (2)C ()B (2)A ([Key] B(6)满足arccos(1－x)≥arccosx 的x 的取值范围是]1,21)[(]21,0)[(]0,21)[(]21,1)[(D C B A --[Key] D(7)将y ＝2x 的图象(A)先向左平行移动1个单位 (B)先向右平行移动1个单位 (C)先向上平行移动1个单位 (D)先向下平行移动1个单位 再作关于直线y ＝x 对称的图象,可得到函数y ＝log 2(x ＋1)的图象.[Key] D(8)长方体一个顶点上三条棱的长分别是3,4,5,且它的八个顶点都在同一个球面上,这个球的表面积是ππππ200)(50)(225)(220)(D C B A[Key] C(9)曲线的参数方程⎪⎩⎪⎨⎧-=-=2111t y tx （t 是参数，t ≠0）,它的普通方程是 11)(1)1(1)()1()2()(1)1()1)((2222+-=--=--==--x xy D x y C x x x y B y x A[Key] B(10)函数y ＝cos 2x －3cosx ＋2的最小值为6)(41)(0)(2)(D C B A -[Key] B(11)椭圆C 与14)2(9)3(22=-+-y x 椭圆关于直线x ＋y ＝0对称，椭圆C 的方程是 (A) 19)3(4)2(22=+++y x (B) 14)3(9)2(22=-+-y x(C) 14)3(9)2(22=+++y x (D) 19)3(4)2(22=-+-y x[Key] A(12)圆台上、下底面积分别为π、4π,侧面积为6π,这个圆台的体积是337)(637)(32)(332)(ππππD C B A[Key] D(13)定义在区间(－∞,＋∞)的奇函数f(x)为增函数；偶函数g(x)在区间［0,＋∞)的图象与f(x)的图象重合.设a>b>0,给出下列不等式 ①f(b)－f(－a)>g(a)－g(－b); ②f(b)－f(－a)＜g(a)－g(－b); ③f(a)－f(－b)>g(b)－g(－a); ④f(a)－f(－b)＜g(b)－g(－a), 其中成立的是(A)①与④ (B)②与③ (C)①与③ (D)②与④ [Key] C（14）不等式组⎪⎩⎪⎨⎧+->+->x x x x x 22330的解集是 (){}20<<x x A (){}5.20<<x x B (){}60<<x x C (){}30<<x x D[Key] C(15)四面体的顶点和各棱中点共10个点,在其中取4个不共面的点,不同的取法共有 (A)150种 (B)147种 (C)144种 (D)141种[Key] D(16)已知92⎪⎪⎭⎫⎝⎛-x x a 的展开式中x 3的系数为49，常数a 的值为_________. [Key] 4(17)已知直线的极坐标方程22)4sin(=+πθρ则极点到该直线的距离是_______。
1998年全国高考理科数学试题及其解析
1998年普通高等学校招生全国统一考试数学（理工农医类）本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分，满分150分，考试120分钟．第Ⅰ卷(选择题共65分)一．选择题：本大题共15小题；第1—10题每小题4分，第11— 15题每小题5分，共65分．在每小题给出的四个选项中，只有一项是符合题目要求的(1) sin600º( )(A)21 (B) －21(C) 23 (D) －23(2) 函数y =a |x |(a ＞1)的图像是( )(3) 曲线的极坐标方程ρ=4sin θ化成直角坐标方程为( )(A) x 2＋(y ＋2)2=4 (B) x 2＋(y －2)2=4 (C) (x －2)2＋y 2=4 (D) (x ＋2)2＋y 2=4 (4) 两条直线A 1x ＋B 1y ＋C 1=0，A 2x ＋B 2y ＋C 2=0垂直的充要条件是( )(A) A 1A 2＋B 1B 2=0 (B) A 1A 2－B 1B 2=0 (C)12121-=B B A A (D) 12121=A A B B(5) 函数f (x )=x1( x ≠0)的反函数f －1(x )= ( ) (A) x (x ≠0) (B) x 1(x ≠0) (C) －x (x ≠0) (D) －x1(x ≠0)(6) 已知点P (sin α－cos α，tg α)在第一象限，则在)20[π，内α的取值是 ( )(A) (432ππ，)∪(45ππ，) (B) (24ππ，)∪(45ππ，) (C) (432ππ，)∪(2345ππ，) (D) (24ππ，)∪(ππ，43) (7) 已知圆锥的全面积是底面积的3倍，那么该圆锥的侧面展开图扇形的圆心角为 ( )(A) 120º (B) 150º (C) 180º (D) 240º (8) 复数－i 的一个立方根是i ，它的另外两个立方根是( )(A)2123± i (B) －2123± i (C) ±2123+ i (D) ±2123-i (9) 如果棱台的两底面积分别是S ，S ′，中截面的面积是S 0，那么( )(A) 2S S S '+=0 (B) S 0=S S '(C) 2 S 0=S ＋S ′ (D) S S S '=22(10) 向高为H 的水瓶中注水，注满为止，如果注水量V 与水深h 的函数关系的图像如下图所示，那么水瓶的形状是( )(11) 3名医生和6名护士被分配到3所学校为学生体检，每校分配1名医生和2名护士．不同的分配方法共有( )(A) 90种 (B) 180种 (C) 270种 (D) 540种(12) 椭圆31222y x +=1的焦点为F 1和F 2，点P 在椭圆上，如果线段PF 1的中点在y 轴上，那么|P F 1|是|P F 2|的( )(A) 7倍 (B) 5倍 (C) 4倍 (D) 3倍 (13) 球面上有3个点，其中任意两点的球面距离都等于大圆周长的61，经过这3个点的小圆的周长为4π，那么这个球的半径为( )(A) 43 (B)23 (C) 2 (D) 3(14) 一个直角三角形三内角的正弦值成等比数列，其最小内角为( )(A) arccos215- (B) arcsin215- (C) arccos251- (D) arcsin 251-(15) 在等比数列{a n }中，a 1>1，且前n 项和S n 满足∞→n lim S n =11a ，那么a 1的取值范围是( ) (A)(1，＋∞) (B)(1，4) (C) (1，2) (D)(1，2)第Ⅱ卷(非选择题共85分)二、填空题：本大题共4小题；每小题4分，共16分．把答案填在题中横线上．16．设圆过双曲线116922=-y x 的一个顶点和一个焦点，圆心在此双曲线上，则圆心到双曲线中心的距离是_________17．(x ＋2)10(x 2－1)的展开式中x 10的系数为____________（用数字作答）18．如图，在直四棱柱A 1B 1C 1 D 1－ABCD 中，当底面四边形ABCD 满足条件____________时，有A 1 C ⊥B 1 D 1．(注：填上你认为正确的一种条件即可，不必考虑所有可能的情形)19．关于函数f (x )=4sin(2x ＋3π)(x ∈R )，有下列命题: ①由f (x 1)= f (x 2)=0可得x 1－x 2必是π的整数倍； ②y =f (x )的表达式可改写为y =4cos(2x －6π)； ③y =f (x )的图像关于点(－6π，0)对称； ④y =f (x )的图像关于直线x =－6π对称．其中正确的命题的序号是_______ (注：把你认为正确的命题的序号都．填上．) 三、解答题：本大题共6小题；共69分．解答应写出文字说明，证明过程或演算步骤． (20)(本小题满分10分)在△ABC 中，a ，b ，c 分别是角A ，B ，C 的对边，设a ＋c =2b ，A －C=3π．求sin B 的值． 以下公式供解题时参考： sin θ＋sin ϕ =2sin2ϕθ+cos2ϕθ-， sin θ－sin ϕ=2cos2ϕθ+sin2ϕθ-，cos θ＋cos ϕ=2cos 2ϕθ+cos 2ϕθ-， cos θ－cos ϕ=－2sin 2ϕθ+sin 2ϕθ-.(21)(本小题满分11分)如图，直线l1和l2相交于点M，l1⊥l2，点N∈l1．以A，B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等．若△AMN为锐角三角形，|AM|=17，|AN|=3，且|BN|=6．建立适当的坐标系，求曲线段C的方程．(22)(本小题满分12分)如图，为处理含有某种杂质的污水，要制造一底宽为2米的无盖长方体沉淀箱，污水从A孔流入，经沉淀后从B孔流出．设箱体的长度为a米，高度为b米．已知流出的水中该杂质的质量分数与a，b的乘积ab成反比．现有制箱材料60平方米．问当a，b各为多少米时，经沉淀后流出的水中该杂质的质量分数最小(A、B孔的面积忽略不计)．(23)(本小题满分12分)已知斜三棱柱ABC －A 1 B 1 C 1的侧面A 1 ACC 1与底面ABC 垂直，∠ABC =90º，BC =2，AC=23，且AA 1 ⊥A 1C ，AA 1= A 1 C ．Ⅰ．求侧棱A 1A 与底面ABC 所成角的大小；Ⅱ．求侧面A 1 ABB 1 与底面ABC 所成二面角的大小； Ⅲ．求顶点C 到侧面A 1 ABB 1的距离．(24)(本小题满分12分)设曲线C 的方程是y =x 3－x ，将C 沿x 轴、y 轴正向分别平行移动t 、s 单位长度后得曲线C 1．Ⅰ．写出曲线C 1的方程； Ⅱ．证明曲线C 与C 1关于点A (3t ，2s)对称； Ⅲ．如果曲线C 与C 1有且仅有一个公共点，证明s =43t －t 且t ≠0．(25)(本小题满分12分)已知数列{b n }是等差数列，b 1=1，b 1＋b 2＋…＋b 10=145． Ⅰ．求数列{b n }的通项b n ； Ⅱ．设数列{a n }的通项a n =log a (1＋nb 1)(其中a ＞0，且a ≠1)，记S n 是数列{a n }的前n 项和．试比较S n 与31log a b n +1的大小，并证明你的结论．1998年普通高等学校招生全国统一考试数学试题（理工农医类）参考答案一、选择题（本题考查基本知识和基本运算．）1．D 2．B 3．B 4．A 5．B 6．B 7．C 8．D 9．A 10．B 11．D 12．A 13．B 14．B 15．D 二、填空题（本题考查基本知识和基本运算．）16．31617．179 18．AC ⊥BD ，或任何能推导出这个条件的其他条件．例如ABCD 是正方形，菱形等 19．②，③ 三、解答题20．本小题考查正弦定理，同角三角函数基本公式，诱导公式等基础知识，考查利用三角公式进行恒等变形的技能及运算能力．解：由正弦定理和已知条件a +c =2b 得 sin A +sin C =2sin B .由和差化积公式得2sin 2C A +cos 2CA -=2sinB . 由A +B +C =π 得 sin 2C A +=cos 2B，又A －C =3π 得 23cos 2B=sin B ，所以23cos 2B =2sin 2B cos 2B. 因为0<2B <2π，cos 2B≠0， 所以sin2B =43， 从而cos2B =4132sin 12=-B 所以sinB=83941323=⨯.21．本小题主要考查根据所给条件选择适当的坐标系，求曲线方程的解析几何的基本思想．考查抛物线的概念和性质，曲线与方程的关系以及综合运用知识的能力．解法一：如图建立坐标系，以l 1为x 轴，MN 的垂直平分线为y 轴，点O 为坐标原点．依题意知：曲线段C 是以点N 为焦点，以l 2为准线的抛物线的一段，其中A ，B 分别为C 的端点．设曲线段C 的方程为y 2=2px （p >0），（x A ≤x ≤x B ，y >0），其中x A ，x B 分别为A ，B 的横坐标，p =|MN |. 所以 M （2p -，0），N （2p，0）. 由|AM |= 17 ，|AN |=3 得（x A +2p ）2+2px A =17， ① （x A －2p）2+2px A =9. ②由①，②两式联立解得x A =p4.再将其代入①式并由p >0解得 ⎩⎨⎧==⎩⎨⎧==.2,2;1,4AA x p x p 或 因为ΔAMN 是锐角三角形，所以2p> x A ，故舍去⎩⎨⎧==22A x p 所以p =4，x A =1.由点B 在曲线段C 上，得x B =|BN |－2p=4. 综上得曲线段C 的方程为y 2=8x （1≤x ≤4，y >0）.解法二：如图建立坐标系，分别以l 1、l 2为x 、y 轴，M 为坐标原点． 作AE ⊥ l 1，AD ⊥ l 2，BF ⊥ l 2，垂足分别为E 、D 、F . 设A （x A ，y A ）、B （x B ，y B ）、N （x N ，0）.依题意有x A =|ME |=|DA |=|AN |=3， y A =|DM |=2222=-DAAM，由于ΔAMN 为锐角三角形，故有 x N =|ME |+|EN | =|ME |+22AE AN -=4x B =|BF |=|BN |=6.设点P （x ，y ）是曲线段C 上任一点，则由题意知P 属于集合｛（x ，y ）|（x －x N ）2+y 2=x 2，x A ≤x ≤x B ，y >0｝.故曲线段C 的方程为y 2=8（x －2）（3≤x ≤6，y >0）.22．本小题主要考查综合应用所学数学知识、思想和方法解决实际问题的能力，考查建立函数关系、不等式性质、最大值、最小值等基础知识．解法一：设y 为流出的水中杂质的质量分数，则y =abk，其中k >0为比例系数.依题意，即所求的a ，b 值使y 值最小.根据题设，有4b +2ab +2a =60（a >0，b >0）， 得 b =aa+-230（0<a <30）. ① 于是 y =ab k =aaa k+-230226432+-+-=a a k ⎪⎭⎫ ⎝⎛+++-=264234a a k≥()2642234+⋅+-a a k18k =， 当a +2=264+a 时取等号，y 达到最小值. 这时a =6，a =－10（舍去）. 将a =6代入①式得b =3.故当a 为6米，b 为3米时，经沉淀后流出的水中该杂质的质量分数最小. 解法二：依题意，即所求的a ，b 的值使ab 最大. 由题设知 4b +2ab +2a =60（a >0，b >0），即 a +2b +ab =30（a >0，b >0）. 因为 a +2b ≥2ab 2， 所以 ab 22+ab ≤30， 当且仅当a =2b 时，上式取等号. 由a >0，b >0，解得0<ab ≤18.即当a =2b 时，ab 取得最大值，其最大值为18. 所以2b 2=18.解得b =3，a =6.故当a 为6米，b 为3米时，经沉淀后流出的水中该杂质的质量分数最小．23．本小题主要考查直线与直线、直线与平面、平面与平面的位置关系，棱柱的性质，空间的角和距离的概念，逻辑思维能力、空间想象能力及运算能力．Ⅰ．解：作A 1D ⊥AC ，垂足为D ，由面A 1ACC 1⊥面ABC ，得A 1D ⊥面ABC ， 所以∠A 1AD 为A 1A 与面ABC 所成的角. 因为AA 1⊥A 1C ，AA 1=A 1C ， 所以∠A 1AD =45º为所求.Ⅱ．解：作DE ⊥AB ，垂足为E ，连A 1E ，则由A 1D ⊥面ABC ，得A 1E ⊥AB . 所以∠A 1ED 是面A 1ABB 1与面ABC 所成二面角的平面角. 由已知，AB ⊥BC ，得ED ∥BC . 又D 是AC 的中点，BC =2，AC =23， 所以DE =1，AD =A 1D =3， tg ∠A 1ED =DEDA 1=3. 故∠A 1ED =60º为所求.Ⅲ．解法一：由点C 作平面A 1ABB 1的垂线，垂足为H ，则CH 的长是C 到平面A 1ABB 1的距离.连结HB ，由于AB ⊥BC ，得AB ⊥HB . 又A 1E ⊥AB ，知HB ∥A 1E ，且BC ∥ED ， 所以∠HBC =∠A 1ED =60º 所以CH =BC sin60º=3为所求. 解法二：连结A 1B .根据定义，点C 到面A 1ABB 1的距离，即为三棱锥C －A 1AB 的高h . 由ABC A AB A C V V --=11锥锥得D A S h S ABC B AA 131311∆∆=， 即 322312231⨯⨯=⨯h 所以3=h 为所求.24．本小题主要考查函数图像、方程与曲线，曲线的平移、对称和相交等基础知识，考查运动、变换等数学思想方法以及综合运用数学知识解决问题的能力.Ⅰ．解：曲线C 1的方程为y =（x －t ）3－（x －t ）+s .Ⅱ．证明：在曲线C 上任取一点B 1（x 1，y 1）.设B 2（x 2，y 2）是B 1关于点A 的对称点，则有2221t x x =+， 2221sy y =+. 所以 x 1=t －x 2， y 1=s －y 2.代入曲线C 的方程，得x 2和y 2满足方程：s －y 2=（t －x 2）3－（t －x 2），即 y 2=（x 2－t ）3－（x 2－t ）+ s ， 可知点B 2（x 2，y 2）在曲线C 1上.反过来，同样可以证明，在曲线C 1上的点关于点A 的对称点在曲线C 上. 因此，曲线C 与C 1关于点A 对称.Ⅲ．证明：因为曲线C 与C 1有且仅有一个公共点，所以，方程组⎪⎩⎪⎨⎧+---=-=st x t x y xx y )()(33有且仅有一组解.消去y ，整理得3tx 2－3t 2x +（t 3－t －s ）=0， 这个关于x 的一元二次方程有且仅有一个根. 所以t ≠0并且其根的判别式Δ=9t 4－12t （t 3－t －s ）=0.即 ⎩⎨⎧=--≠.0)44(,03s t t t t所以 t t s -=43且 t ≠0. 25．本小题主要考查等差数列基本概念及其通项求法，考查对数函数性质，考查归纳、推理能力以及用数学归纳法进行论证的能力.解：Ⅰ．设数列{b n }的公差为d ，由题意得⎪⎩⎪⎨⎧=-+=.1452)110(1010,111d b b 解得⎩⎨⎧==.3,11d b 所以 b n =3n －2.Ⅱ．由b n =3n －2，知S n =log a （1+1）+ log a （1+41）+…+ log a （1+231-n ） = log a [（1+1）（1+41）……（1+231-n ）]， 31log a b n +1= log a 313+n . 因此要比较S n 与31log a b n +1的大小，可先比较（1+1）（1+41）……（1+231-n ）与313+n 的大小.取n =1有（1+1）>3113+⋅，取n =2有（1+1）（1+41）>3123+⋅， ……由此推测（1+1）（1+41）……（1+231-n ）>313+n . ① 若①式成立，则由对数函数性质可断定：当a >1时，S n >31log a b n +1. 当0<a <1时，S n <31log a b n +1. 下面用数学归纳法证明①式.（ⅰ）当n =1时已验证①式成立.（ⅱ）假设当n =k （k ≥1）时，①式成立，即（1+1）（1+41）……（1+231-k ）>313+k . 那么，当n =k +1时，（1+1）（1+41）……（1+231-k ）（1+()2131-+k ）>313+k （1+131+k ） =13133++k k （3k +2）. 因为()[]333343231313+-⎥⎦⎤⎢⎣⎡+++k k k k ()()()()22313134323+++-+=k k k k ()013492>++=k k ， 所以13133++k k （3k +2）>().1134333++=+k k 因而（1+1）（1+41）……（1+231-k ）（1+131+k ）>().1133++k 这就是说①式当n=k +1时也成立.由（ⅰ），（ⅱ）知①式对任何正整数n 都成立.由此证得：当a >1时，S n >31log a b n +1. 当0<a <1时，S n <31log a b n +1.。
1998年全国高考数学试题及答案解析
第 1 页 共 10 页 1998年普通高等学校招生全国统一考试
数学
(理工农医类)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分,考试时间120分钟.
第Ⅰ卷(选择题共65分)
一、 选择题:本大题共15小题;第(1) (10)题每小题4分,第(11) (15)题每小题5分,共65分,
在每小题给出的四个选项中,只有一项是符合题目要求的.
(1)设集合M=｛x │0≤x<2｝,集合N=｛x │x 2-2x-3<0｝,集合M ∩N 为
(A)｛x │0≤x<1｝ (B)｛x │0≤x<2｝
(C)｛x │0≤x ≤1｝ (D)｛x │0≤x ≤2｝
[Key] B
(2)如果直线ax+2y+2=0与直线3x-y-2=0平行,那么系数a 为
32
)(23
)(6)(3)(D C B A ---
[Key] B
(3)函数
)x 31x 21(tg y -=在一个周期内的图象是
[Key] A
(4)已知三棱锥D-ABC 的三个则面与底面全等，且AB=AC=3，BC=2，则BC 为棱,以面BCD 与面BCA 为面的二面角的大小是
32)D (2)C (31
arccos )B (33
arccos )A (ππ
[Key] C
（5）函数x 2cos )x 23sin(y +-π=的最小正周期是
ππππ
4)D (2)C ()B (2)A (
[Key] B。
1998年高考数学试题及答案(全国理)
1998年普通高等学校招生全国统一考试数学（理工农医类）本试卷分第Ⅰ卷(选择题）和第Ⅱ卷（非选择题)两部分。
共150分,考试时间120分钟。
第Ⅰ卷(选择题共65分)一、选择题:本大题共15小题;第(1） （10）题每小题4分，第(11) （15）题每小题5分，共65分，在每小题给出的四个选项中，只有一项是符合题目要求的.1、sin600°的值是23.D 23.C 21.B 21.A --［Key] D2、函数)1a (a y |x |>=的图象是［Key ］ B3、曲线的极坐标方程θ=ρsin 4化成直角坐标方程为A ． 4)2y (x 22=++B ．4)2y (x 22=-+ C ． 4y )2x (22=+- D ．4y )2x (22=++[Key ］ B4、两条直线0C y B x A ,0C y B x A 222111=++=++垂直的充要条件是A ． 0B B A A 2121=+B ． 0B B A A 2121=-C ． 1B B A A 2121-=D ． 1B B A A 2121=[Key ］ A5、函数)0x (x 1)x (f ≠=的反函数=-)x (f 1A ． x （x ≠0）B ． )0x (x 1≠C ． —x(x ≠0)D ．)0x (x 1≠- ［Key ］ B6、已知点)tg ,cos (sin P αα-α在第一象限,则在)2,0(π内α的取值范围是A ． )45,()43,2(ππ⋃ππ B ． )45,()2,4(ππ⋃ππ C ． )23,45()43,2(ππ⋃ππ D ． ),43()2,4(ππ⋃ππ［Key] B °7、已知圆锥的全面积是底面积的3倍,那么该圆锥的侧面展开图扇形的圆心角为A ．120°B ．150°C ．180°D ．240°［Key ］ C8、复数-i 的一个立方根是i ，它的另外两个立方根是A ． i 2123±B ．i 2123±-C ． i 2123+±D ．i 2123-± ［Key ］ D9、如果棱台的两底面积分别是S ， S’，中截面的面积是S 0,那么A ． 'S S +=22B ． S 'S S =0C ． 'S S S +=02D ． S 'S S 220=[Key ］ A10、向高为H 的水瓶中注水,注满为止，如果注水量V 与水深h 的函数关系的图象如右图所示,那么水瓶的形状是［Key ］ B11、3名医生和6名护士被分配到3所学校为学生体检，每校分配1名医生和2名护士，不同的分配方法共有A ．90种B ．180种C ．270种D ．540种[Key] D12、椭圆131222=+y x 的焦点为F 1和F 2，点P 在椭圆上，如果线段PF 1的中点在y 轴上，那么｜PF 1｜是|PF 2|的A ．7倍B ．5倍C ．4倍D ．3倍[Key ］ A13、球面上有3个点,其中任意两点的球面距离都等于大圆周长的1/6，经过这3个点的小圆的周长为4π，那么这个球的半径为A ． 34B ．32C ．2D ．3[Key ］ B14、一个直角三角形三内角的正弦值成等比数列，其最小内角为A ． 215arccos -B ． 215arcsin -C ． 251arccos- D ． 251arcsin - [Key ］ B15、在等比数列{a n ｝中，a 1〉1，且前n 项和S n 满足11lim a S n n =∞→，那么a 1的取值范围是 A ．（1,+∞) B ．（1，4） C ．（1，2） D ．(1，2)[Key ］ D16、设圆过双曲线116922=+y x 的一个顶点和一个焦点，圆心在此双曲线上，则圆心到双曲线中心的距离是 _______.［Key ］ 31617、)1()2(210-+x x 的展开式中x 10的系数为____ （用数字作答）. ［Key] 17918、如图，在直四棱柱A 1B 1C 1D 1 ABCD 中,当底面四边形ABCD 满足条件_____时,有A 1C ⊥B 1D 1。
1988-1998年高考理科数学试题参考答案
S FAC ED 1988年普通高等学校招生全国统一考试理科数学参考答案 满分120分，120分钟一、（本题满分45分）BCBAD ACDCD CBDBA 二、（本题满分20分）1.2;116π 2. 2x =- 3.-3 4.555. 1．三、（本题满分10分） 解：3sin sin 33cos cos3x xx x ++2sin sin sin 32cos cos cos3x x x x x x ++=++ 2sin 2sin 2cos 2cos 2cos 2cos x x x x x x +=+ 22sin 4sin cos 2cos (1cos 2)x x xx x +=+ 22tan (12cos )2cos x x x+=2tan (sec 2)2x x =+ 22tan (tan 3)(3)22x a x a =+=+．四、（本题满分10分）解：连接AE ，SE ．∵△SBC 和△ABC 都是边长为a 的正三 角形，E 是BC 的中 点，∴SE 和AE 分别是它们的中线，且SE =AE ，∴△SAE 为等腰三角形．∵D 是SA 的中点，∴DE ⊥SA ．由已知条件及上述解析得：在正△SBC 中有，cos302SE SB a =︒=； 在等腰△SAE 中有，2DE a ==． 作DF ⊥SE ，交SE 于点F ，则1122SDE S SE DF SD DE ∆=⋅=⋅，∴6a SD DE DF SE ⋅===． 所求的旋转体的体积是以DF 为底面半径，分别以SF 和EF 为高的两个圆锥的体积的和，即2211))33V SF EF ππ=⋅⋅+⋅⋅旋转体22311()3636236a SE a ππ=⋅⋅=⋅=． 五、（本题满分11分） 解：∵0t >，∴12t +≥当且仅当1t =时“=”成立．1log log 2a a t = ∵当01a <<时，函数log a y x =是减函数，∴1log log 2aa t +≤ 11log log 22a a t t +≤；∵当1a >时，函数log a y x =是增函数，∴1log log 2aa t +≥ 11log log 22a a t t +≥．综上可得：当01a <<时，11log log 22a a t t +≤；当1a >时，11log log 22aa t t +≥． 六、（本题满分12分）本题共2小题，第（1）小题满分4分，第（2）小题满分8分. 解：（1）设11122212(,),(,)()M x y M x y x x ≠函数图象上任意两个不同的点，则l DA y xO 2121211111x x y y ax ax ---=--- 12211211211(1)(1)(1)ax x x ax ax x x ax ax ax --+---+=-- 2121212121()()()(1)(1)(1)(1)(1)a x x x x x x a ax ax ax ax -----==----， ∴1a ≠，且12x x ≠，∴210y y -≠．∴直线12M M 的斜率21210y y k x x -=≠-，∴直线12M M 不平行于x 轴．（2）设点(,)P x y ''是函数图象上任意一点，则1x a '≠，且11x y ax '-'='-，点(,)P x y ''关于直线y x =的对称点为(,)P y x '''，11111111x y x ax ax x ay a a ax '--'''--'-'===''---'-，∴点(,)P y x '''在已知函数图象上，即函数的图象关于直线y x =成轴对称图形． 七、（本题满分12分）解：由已知条件知椭圆方程为22[(2)]214px y -++=； 以l 为准线、点A为焦点的抛物线方程为22y px =． 椭圆上有四点符 合题意的充要条 件是下面的方程组有四个不同的实数解：222[(2)]21,(1)42.(2)p x y y px ⎧-+⎪⎪+=⎨⎪=⎪⎩ 将（2）式代入（1）式，得2[(2)]842px px -++=，即22(74)204p x p x p +-++=．（3）∴原方程组有4个不同的实数解，当且仅当方程（3）有两个不相等的正根，∴2220,(74)4(2)0,420,4740.P p p p p p p >⎧⎪⎪∆=--+>⎪⎨⎪+>⎪⎪-<⎩ ∴103p <<∴p 的取值范围为.31p 0<<．B 1D 1C 1N A C MD OA 11989年普通高等学校招生全国统一考试理科数学参考答案 满分120分，120分钟一、选择题（本题满分36分，共12个小题）ADCAB CDDCD AC 二、填空题（本题满分24分，共6个小题，每一个小题满分4分） 13．7{|2,(21),}1212x x k x k k Z ππππ=+=++∈或 或{|(1),}43kx x k k Z πππ=+-+∈14．(,1)(4,)-∞-+∞ 15．(1,1)-16． -2 17．必要，必要（注：仅答对一个结果的，只给2分） 18．233 三、解答题（本题满分60分，共6个小题.） 19．（本小题满分8分）证明：3sinsin322322cos cos 22x xx x tg tg x x-=- 33sin cos cos sin22223cos cos22x x x x x x -=sin 3cos cos22xx x =2sin cos cos 2x x x =+. 20．（本小题满分10分）解：（Ⅰ）连接1AO ，则1AO ⊥底面ABCD .作OM ⊥AB 交AB 于M ，作ON ⊥AD 交AD 于N ．连接1A M ，1A N ，则由三垂线定理得1A M ⊥AB ，1A N ⊥AD . ∵∠1A AM =∠1A AN ， ∴Rt △1A NA ≌Rt △1A MA ，∴1A M =1A N ，∴OM ON =∴点O 在∠BAD 的平分线上. （Ⅱ）∵AM =1AA ,232133cos =⋅=π ∴AO =AM .2234csc=π 又在Rt △1AOA 中，2221199922AO AA AO =-=-=.∴1A O =∴平行六面体的体积54V =⋅ 21．（本小题满分10分） 解(一)：圆的标准方程为：1)2()2(22=-+-y x ，它关于x 轴对称的圆的方程为： 1)2()2(22=++-y x ． 设光线l 所在的直线方程为： )3(3+=-x k y ．由题意知，l 是圆1)2()2(22=++-y x 的切线， ∴11552=++kk ， 解得34k =-， 或43k =-∴l 的方程为：3430x y +-=或4330x y ++=． 解(二)：圆的标准方程为：1)2()2(22=-+-y x ．设光线l 所在的直线方程为： )3(3+=-x k y ．由题意知0≠k ，于是l 与x 轴的交点为)0,)1(3(kk +-．由于入射角等于反射角，所以反射光线l '的斜率为k -，∴直线l '的方程为：))1(3(kk x k y ++-=，即 0)1(3=+++k y kx ． 由于l '与已知圆相切，所以11552=++kk ，解得3443-=-=k k 或. ∴l 的方程为：3430x y +-=或4330x y ++=． 点评 本题难度不大，但涉及的知识面较广，属跨学科问题. 22．（本小题满分12分） 解：由对数函数的性质可知，原方程的解x 应满足22222(),(1)0,(2)0.(3)x ak x a x ak x a ⎧-=-⎪->⎨⎪->⎩当（1），（2）同时成立时，（3）显然成立，因此只需解222(),(1)0,(2)x ak x a x ak ⎧-=-⎨->⎩ 由（1）得22(1).(4)k x a k =+ 当0k =时，由0a >知（4）无解，因而原方程无解.当0k ≠时，（4）的解是2(1).(5)2a k x k+=把（5）代入（2），得212k k k+>， 解得10 1.k k -∞<<-<<或综合得，当k 在集合(,1)(0,1)-∞-内取值时，原方程有解. 23．（本小题满分10分） 解：假设存在,,a b c 使题设的等式成立，则当n =1,2,3时有24,4344,9310.a b c a b c a b c ++=⎧⎪++=⎨⎪++=⎩解得3,11,10a b c ===.①由上可知，当n =1,2,3时，下面等式成立：2221223(1)n n ⋅+⋅+++2(1)(31110)12n n n n +=++.②记2221223(1)n S n n =⋅+⋅+++. 假设当n k =时上式成立，即2(1)(31110)12k k k S k k +=++.∴21(1)(2)k k S S k k +=+++ 22(1)(31110)(1)(2)12k k k k k k +=+++++2(1)(2)(35)(1)(2)12k k k k k k +=+++++2(1)(2)(351224)12k k k k k ++=+++2(1)(2)[3(1)11(1)10]12k k k k ++=++++.也就是说，当1n k =+时等式成立.综上所述，当3,11,10a b c ===时，题设的等式对一切自然数n 成立. 24．（本小题满分10分） 解：（1）∵()f x 是以2为周期的函数， ∴当k Z ∈时，2k 也是()f x 的周期又∵当k x I ∈时，02(1,1]x k I -∈=-， ∴2()(2)(2)f x f x k x k =-=-. ∴对k Z ∈，当k x I ∈时，2()(2)f x x k =-. （2）对自然数k ，且k x I ∈时，由（1）的结论可得方程2(2)x k ax -=，即22(4)40x k a x k -++=.上述方程在区间k I 上恰有两个不相等的实根的充要条件是a 满足22(4)16(8)0,121[42121[42k a k a a k k k a k k a ⎧⎪∆=+-=+>⎪⎪-<+⎨⎪⎪+≥+⎪⎩，即(8)0,(1)2,(2)2,(3)a a k a a +>⎧+≤- 由（1）知0a >，或8a k <-. 当0a >时，22a a +>-， ∴由（2），（32a ≤-，即2(8)(2),20,a a k a a ⎧+≤-⎨->⎩ 解得1021a k <≤+.当8a k <-时，2280a k +<-<，2a <+无解，综上所述，a 应满足1021a k <≤+.∴故所求集合1|021k M a a k ⎧⎫=<≤⎨⎬+⎩⎭.1990年普通高等学校招生全国统一考试数学（理工农医类）参考答案 满分120分，120分钟 一、选择题: 共45分．1-5 ABDCC 6-10 BADBD 10-15 CBBCD 二、填空题: 共15分． 16．165y =± 17．20- 18．2 19．12+ 20．75 三、解答题. 21．（本小题满分8分）小题考查等差数列、等比数列的概念和运用方程（组）解决问题的能力.解法一:设四个数依次为,,a d a a d -+，2()a d a +，则由已知条件得 2()16,12.a d a d a a a d ⎧+-+=⎪⎨⎪++=⎩消去d ，整理得213360a a -+=， 解得 124,9a a ==.代入③式得 124,6d d ==-.从而得所求四个数为0,4,8,16或15,9,3,1. 解法二:设四个数依次为,,12,16x y y x --，则由已知条件得2122,(1)(16)(12).(2)x y y y x y +-=⎧⎨-=-⎩ 由（1）式得 312x y =-. （3）将（3）式代入（2）式得2(16312)(12)y y y -+=-,整理得 213360y y -+=. 解得 124,9y y ==.代入（3）式得120,15x x == .从而得所求四个数为0,4,8,16或15,9,3,1. 22．（本小题满分10分）本小题考查三角公式以及三角函数式的恒等变形和运算能力. 解：由已知得sin sin 3cos cos 4αβαβ+=+，即2sincos32242cos cos22αβαβαβαβ+-=+-， ∴3tan 24αβ+=， ∴22tan2tan()1tan 2αβαβαβ++=+- 2322447314⨯==⎛⎫- ⎪⎝⎭． 23．（本小题满分10分）本小题考查直线和平面,直线和直线的位置关系,二面角等基本知识,以及逻辑推理能力和空间想象能力.解: ∵SB ＝BC,且E 是SC 的中点,∴BE 是等腰三角形SBC 的边SC 的中线, ∴SC ⊥BE ． 又已知SC ⊥DE, BE ∩DE ＝E, ∴SC ⊥面BDE, ∴SC ⊥BD.又∵SA ⊥底面ABC, BD 在底面ABC 上, ∴SA ⊥BD.而SC ∩SA ＝S,∴BD ⊥面SAC. ∵DE ＝面SAC ∩面BDE, DC ＝面SAC ∩面BDC, ∴BD ⊥DE,BD ⊥DC.∴∠EDC 是所求的二面角的平面角. ∵SA ⊥底面ABC,∴SA ⊥AB,SA ⊥AC ． 设SA ＝a ，则AB= a ，． 又∵AB ⊥BC，∴AC =．在R t SAC ∆中SA tg ACS AC ∠== ∴∠ACS ＝30°.又已知DE ⊥SC,所以∠EDC ＝60°， 即所求的二面角等于60°． 24．（本小题满分10分）本小题考查复数与解方程等基本知识以及综合分析能力. 解法一：设(,R)z x yi x y =+∈,代入原方程得222x y xyi a -+=，即22,(1)0. (2)x y a xy ⎧-+=⎪⎨=⎪⎩由（2）式得0x =或0y =. ①若0x =，则方程（1）为2y a -+=，即220(0)y y a y ++=<， ……（3） 或220(0)y y a y -+=≥．……（4） 由（3）得2(1)1(0)y a y +=-<，当01a ≤≤时，1y =-1y =-， 当1a >时无解．由（4）得2(1)1(0)y a y -=-≥，当01a ≤≤时，1y =，或1y = 当1a >时无解．综上可得，当01a ≤≤时，(1z i =±+，或(1z i =±-当1a >时无解．②若0y =，则方程（1）为2x a +=，即2(1)1(0)x a x +=+≥， ……（5） 或2(1)1(0)x a x -=+<．………（6） ∵0a ≥，∴解（5）得1x =- 解（6）得1x =综上可得，1z =±．③若0x =且0y =，则方程（1）为0a =，当0a =时，0x =，0y =是其解；当0a ≠时无解．当0a =时，0z =是其解；当0a ≠时无解．显然，当0a =时，0z =包含在上述两种情况之中．综上可得，实数解为(1z =±； 当01a ≤≤时，(1z i =±，或(1z i =±，当1a >时无纯虚数解． 25．（本小题满分10分）本小题考查椭圆的性质,距离公式,最大值知识以及分析问题的能力.解：设所求椭圆的直角坐标方程是22221(0)x y a b a b+=>>，则 222222314c a b b e a a a -⎛⎫⎛⎫===-= ⎪ ⎪⎝⎭⎝⎭，即 2a b =，∴椭圆的方程可变形为222214x y b b+=,设椭圆上的点(,)x y 到点P 的距离为d ，则22232d x y ⎛⎫=+- ⎪⎝⎭22234()2b y y ⎛⎫=-+- ⎪⎝⎭2213432y b ⎛⎫=-+++ ⎪⎝⎭，其中b y b -≤≤.若102b <<，则当y b =-时，2d 有最大值，且2372b ⎛⎫--= ⎪⎝⎭，解之得3122b =>，与102b <<相矛盾，舍去若12b ≥，则当12y =-时，2d 有最大值，且2437b +=，解之得1b =， ∴2,1a b ==,∴所求椭圆的直角坐标方程是2214x y +=． 当12y =-时，x =∴所求的点的坐标是12⎛⎫- ⎪⎝⎭．26．（本小题满分12分）本题考查对数函数,指数函数,数学归纳法,不等式的知识以及综合运用有关知识解决问题的能力.(Ⅰ)解: ∵()f x 当(,1]x ∈-∞时有意义， ∴12(1)0x x x n n a +++-+>，即121x x xn a n n n ⎡⎤-⎛⎫⎛⎫⎛⎫>-+++⎢⎥ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦，(,1]x ∈-∞．∵(1,2,,1)xk k n n ⎛⎫-=- ⎪⎝⎭在(,1]-∞上都是增函数，∴121()x x xn g x n n n ⎡⎤-⎛⎫⎛⎫⎛⎫=-+++⎢⎥ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦在(,1]-∞上是增函数，∴max 121()(1)n g x g n n n -⎛⎫==-+++ ⎪⎝⎭1(1)2n =--,∴1(1)2a n >--，即a 的取值范围为1(1),2n ⎛⎫--+∞ ⎪⎝⎭． (Ⅱ) 要证2()(2)f x f x <，即12(1)2lg x x x n n an+++-+22212(1)lg x x x n n a n+++-+<.，只需证明212(1)xx x n n a ⎡⎤+++-+⎣⎦22212(1)x x x n n n a ⎡⎤<+++-+⎣⎦．当01a <<时，2a a <．∴当01a <<，0x ≠时，由柯西不等式得22212(1)xx x n n n a ⎡⎤+++-+⎣⎦ 222212(1)x x x n n n a ⎡⎤>+++-+⎣⎦()()222222(111)12x x n a ⎡⎤=++++++⎢⎥⎣⎦ 212(1)xx x n n a ⎡⎤≥+++-+⎣⎦， ∴当01a <<，0x ≠时，22212(1)xx x n n n a ⎡⎤+++-+⎣⎦212(1)x x x n n a ⎡⎤>+++-+⎣⎦．当1a =，0x ≠时，1(1,2,,)x k k n ≠=，22212(1)x x x n n n a ⎡⎤+++-+⎣⎦ 22212(1)x x x n n n ⎡⎤>+++-+⎣⎦212(1)xx x n n ⎡⎤>+++-+⎣⎦． 综上可得，当01a <≤，0x ≠时，有22212(1)xx x n n n a ⎡⎤+++-+⎣⎦212(1)xx xn n a ⎡⎤>+++-+⎣⎦，即22212(1)x x x n n an+++-+212(1)x x x n n a n ⎡⎤+++-+>⎢⎥⎣⎦，12(1)2lg x x x n n a n+++-+22212(1)lg x x x n n a n+++-+<，∴2()(2)f x f x <，(0,1]a ∈，0x ≠．注：可用数学归纳法证明．1991年普通高等学校招生全国统一考试数学(理工农医类)参考解答本试卷共120分．考试时间120分钟． 一、选择题．本题考查基本知识和基本运算．每小题3分，满分45分．1-15 ADBBA DADCC ACBCD二、填空题．本题考查基本知识和基本运算．每小题3分，满分15分．16.4π17.()2,0- 18.31419.1+510 20.23a π三、解答题21. （本小题满分8分）本小题考查三角函数式的恒等变形及三角函数的性质． 解：22sin 2sin cos 3cos y x x x x =++212sin cos 2cos x x x =++sin 2cos 22x x =++224x π⎛⎫=++ ⎪⎝⎭．当22()42x k k Z πππ+=-∈，即3()8x k k Z ππ=-∈时y 取得最小值2使取最小值的x 的集合为3()8x x k k Z ππ⎧⎫=-∈⎨⎬⎩⎭． 22. （本小题满分8分）本小题考查复数基本概念和运算能力． 解：∵ 1z i =+，∴ 2361z z z -++2(1)3(1)631112i i i i i i+-++-===-+++，∴1i -的模为22)1(1-+=2，辐角的主值74π， ∴所给复数的模为2，辐角的主值74π． 23. （本小题满分10分）本小题考查直线与直线，直线与平面，平面与平面的位置关系，以及逻辑推理和空间想象能力．满分10分．解：如图，连接,,,,EG FG EF BD AC ，,EF BD 分别交AC 于H ，O ．∵ABCD 是正方形，,E F 分别为AB 和AD 的中点，∴EF ∥BD ，H 为AO 的中点． BD 不在平面EFG 上．否则，平面EFG 和平面A B C D 重合，从而点G 在平面的ABCD 上，与题设矛盾． ∴BD ∥平面EFG ，∴BD 到平面EFG 的距离就是点B 到平面EFG 的距离．∵BD ⊥AC ，∴EF ⊥HC ．∵CG ⊥平面ABCD ，∴EF ⊥CG ， ∴EF ⊥平面HCG ．∴ 平面EFG ⊥平面HCG ，HG 是这两个垂直平面的交线．作OK ⊥HG 交HG 于点K ，则OK ⊥平面EFG ，∴线段OK 的长就是点B 到平面EFG 的距离．∵ 正方形ABCD 的边长为4，CG =2， ∴AC =42，HO =2，HC =32． ∴ 在Rt △HCG 中，HG=由于Rt △HOK 和Rt △HCG 有一个锐角是公共的，∴ Rt △HOK ∽△HCG ．∴ OK =111122222=⨯=⋅HG GC HO ，即 点B 到平面EFG 的距离为11112．注：未证明“BD 不在平面EFG 上”不扣分． 24. （本小题满分10分）本小题考查函数单调性的概念，不等式的证明，以及逻辑推理能力．证法一：在(),-∞+∞上任取12,x x 且12x x <，则332112()()f x f x x x -=- 22121122()()x x x x x x =-++21212213())24x x x x x ⎡⎤⎛⎫=-++ ⎪⎢⎥⎝⎭⎣⎦．∵12x x <，∴120x x -<，且212213)024x x x ⎛⎫++> ⎪⎝⎭（否则，120x x ==，与题设不符）．∴21()()0f x f x -<，即21()()f x f x <． ∴函数3()1f x x =-+在(),-∞+∞上是减函数．证法二：在(),-∞+∞上任取12,x x ，且12x x <，则332112()()f x f x x x -=-= 22121122()()x x x x x x -++． ∵12x x <，∴120x x -<．∵12,x x 不同时为零，∴ x 21＋x 22>0．又 ∵2222121212121()2x x x x x x x x +>+≥≥-， ∴ 2211220x x x x ++>，∴21()()0f x f x -<，即21()()f x f x <． ∴函数3()1f x x =-+在(),-∞+∞上是减函数．25. （本小题满分12分）本小题考查对数、数列、解不等式等基本知识，以及分析问题的能力．满分12分．解：利用对数换底公式，原不等式左端化为∵231log 4log 12log (2)log n n a a a a x x x n x --+++-1log 2log 4log (2)log n a a a a x x x x -=-+++- 112(2)log n a x -⎡⎤=-++-⎣⎦1(2)log 3n a x --=，∴原不等式可化为21(2)1(2)log log ()33n na a x x a ---->-．①（1）当n 为奇数时，1(2)03n-->， 不等式①等价于2l o g l o g ()a a x x a >-． ② ∵1a >，∴②式等价于220,0,x x a x x a >⎧⎪->⎨⎪>-⎩20,0x x x x a >⎧⎪⇔>⎨⎪--<⎩⇔x x ⎧><<∵102<， 2411a ++>24a=a ，∴，不等式②的解集为12⎭． （2）当n 为偶数时，1(2)03n--<， 不等式①等价于2log log ()a a x x a <-． ③∵a >1，∴③式等价于220,0,,x x a x x a >⎧⎪->⎨⎪<-⎩20,0,x x x x a >⎧⎪⇔>⎨⎪-->⎩x x ⎧>⎪⇔⎨<⎪⎩ 或x x ⎧>⎪⎨>⎪⎩∵，，a a a a =>++<+-24241102411∴不等式③的解集为⎫+∞⎪⎪⎝⎭． 综合得：当n 为奇数时，原不等式的解集是12⎫+⎪⎪⎭； 当n 为偶数时，原不等式的解集是⎫+∞⎪⎪⎝⎭． 26. （本小题满分12分）本小题考查双曲线性质，两点距离公式，两直线垂直条件，代数二次方程等基本知识，以及综合分析能力．解：设双曲线的方程为22221x y a b-=，焦点为12(,0),(,0)F c F c -．由题意知，直线PQ 的方程为)y x c =-． 将直线方程代入双曲线方程得()2222315x x c a b --=，即 22222222(53)6(53)0b a x a cx a b a c -+-+=．① ∵,P Q 是右焦点的直线与双曲线的两个交点，∴22530b a -≠．设1122(,),(,)P x y Q x y ，则12,x x 方程①的两个根，且21222222212226,5353.53a c x x b a a b a c x x b a ⎧+=-⎪⎪-⎨+⎪=-⎪-⎩∵OP OQ ⊥，∴1212OP OQ y yk k x x ⋅=⋅121==-，即2121283()30x x x x c c -++=，∴2222222222253683305353a b a c a c c b a b a+-⋅+⋅+=--，即2222(3)(3)0a b a b +-=．∵230a +≠，∴223b a =，∴2c a =，且12212,9.4x x a a x x +=-⎧⎪⎨=-⎪⎩∵4PQ =，∴221212()()x x y y -+-2212123()()5x x x x =-+-2212128()416165x x x x a ⎡⎤=+-==⎣⎦． ∴21a =，23b =．∴所求双曲线方程为x 2－2213y x -=．1992年普通高等学校招生全国统一考试数学(理工农医类)参考答案本试卷共120分．考试时间120分钟． 一、选择题：本题考查基本知识和基本运算．共54分．1-18 ADDBD BBCDD BBADD CAC 二、填空题：本题考查基本知识和基本运算．共15分． 19.1x =- 20.41 21.1281522.()1124222=--y x 23.1613三、解答题24. （本小题满分9分）本小题考查复数相等的条件及解方程的知识．满分9分． 解：设(,R)z x yi x y =+∈，则已知方程可变形为．()()3()13x yi x yi i x yi i +---=+，即223313x y y ix i +--=+．根据复数相等的定义，得⎩⎨⎧=-+=-.13,3322y y x x 解得1,0x y =-=或3y =． ∴1z =-或13z i =-+．25. （本小题满分10分）本小题主要考查三角函数和角公式等基础知识及运算能力．满分10分． 解：∵432παβπ<<<， ∴30,42ππαβπαβ<-<<+<，又∵ 123cos(),sin()135αβαβ-=+=-，∴ ()sin αβ-=513==，()cos αβ+=45=-，∴]sin 2sin ()()ααβαβ=-++ sin()cos()cos()sin()αβαβαβαβ=-++-+ =655653131254135-=⎪⎭⎫ ⎝⎛-⨯+⎪⎭⎫ ⎝⎛-⨯． 26. （本小题满分10分）本小题考查空间图形的线面关系，空间想象能力和逻辑思维能力．满分10分．解：设经过b 与a 平行的平面为α，经过a 和1AA 的平面为β，c αβ=，则c ∥a ．∴b ，c 所成的角等于θ，且1AA ⊥c ． ∵1AA ⊥b ，1AA ⊥c ， ∴1AA ⊥α．∴β⊥α．在平面β内作EG c ⊥，垂足为G ，则1EG AA =．且EG α⊥． 连结FG ，则EG FG ⊥．在Rt △EFG 中，222EF EG FG =+． ∴1AG A E m ==，1EG AA d ==， ∴ 在△AFG 中，2222cos FG m n mn θ=+-．∴22222cos EF d m n mn θ=++-． 如果点F (或E )在点A (或1A )的另一侧，则22222cos EF d m n mn θ=+++．∴EF 27. （本小题满分10分）本小题考查数列、不等式及综合运用有关知识解决问题的能力．满分12分．解：(Ⅰ)由已知条件得()()31121131212,12121120,213131130,2a a d S a d S a d ⎧=+=⎪⎪⨯-⎪=+⋅>⎨⎪⎪⨯-=+⋅<⎪⎩即 111122,2110,60,a d a d a d =-⎧⎪+>⎨⎪+<⎩ ∴ 2470,30,d d +>⎧⎨+<⎩解得 2437d -<<-． (Ⅱ)解法一：由(Ⅰ)知0d <， ∴{}n a 单调递减．由已知条件得11313713()1302a a S a +==<，即70a <；112126712()6()02a a S a a +==+>，即670a a +>，∴60a >． ∴在1212,,,S S S 中6S 的值最大．(Ⅱ)解法二：()d n n na S n 211-+= ()()d n n d n 121212-+-=22124124=552222d d n d d ⎡⎤⎡⎤⎛⎫⎛⎫---- ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎣⎦⎣⎦． ∵0d <，∴ 224521⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛--d n 最小时，n S 最大．当2437d -<<-时， 124136522d ⎛⎫<-< ⎪⎝⎭，∵ 正整数6n =时224521⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛--d n 最小，∴6S 最大．解法三：由(Ⅰ)知0d <， ∴{}n a 单调递减．∵ 12130,0,S S >⎧⎨<⎩∴111211120,21312130.2a d a d ⨯⎧+>⎪⎪⎨⨯⎪+<⎪⎩∴1150,260,d a d a d ⎧+>->⎪⎨⎪+<⎩即670,0.a a >⎧⎨<⎩ ∴在1212,,,S S S 中6S 的值最大．28. （本小题满分12分）本小题考查椭圆性质、直线方程等知识，以及综合分析能力．证法一：设,A B 的坐标分别为11(,)x y 和22(,)x y ．∵线段AB 的垂直平分线与x 轴相交， ∴ AB 不平行于y 轴，即12x x ≠． 又交点为0(,0)P x ，∴ PA PB =，即2222101202()()x x y x x y -+=-+． ① ∵ ,A B 在椭圆上，∴ 2122221x a b b y -=，2222222x ab b y -=．将上式代入①，得()22222102122()a b x x x x x a--=- ． ② ∵12x x ≠，∴2212022x x a b x a+-=⋅． ③ ∵12,a x a a x a -≤≤-≤≤，且12x x ≠，∴1222a x x a -≤+≤，∴22220a b a b x a a---<<． 证法二：设,A B 的坐标分别为11(,)x y 和22(,)x y ．0(,0)P x 在AB 的垂直平分线上，以点P为圆心，PA r =为半径的圆P 过,A B 两点，∴圆P 的方程为2220()x x y r -+= ，与椭圆方程联立，消去y 得2222202()b x x x r b a--=-，∴02222002222=+-+--b r x x x x ab a ．① ∵,A B 是椭圆与圆P 的交点， ∴12,x x 为方程①的两个根，且2120222a x x x a b+=-．∵12,a x a a x a -≤≤-≤≤，且12x x ≠，∴1222a x x a -≤+≤，即2022222a a x a a b -<<-a ，∴ 22220a b a b x a a---<<．1993年普通高等学校招生全国统一考试数学试题(理工农医类)参考解答 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．共150分．考试时间120分钟． 一、选择题：本题考查基本知识和基本运算．每小题4分，满分68分．1-17 ACBBA DCABD CADDA CB 二、填空题：本题考查基本知识和基本运算．每小题4分，满分24分．18.6322+ 19.{k ||k |>31} 20.100 21)1 22.1760 23. 30 三、解答题 24. （本小题满分10分）本小题考查函数的奇偶性、对数函数的性质、不等式的性质和解法等基本知识及运算能力．解 (Ⅰ)由已知函数知011>-+x x ， 解得－1<x <1； ∴()f x 的定义域为(1,1)-． (Ⅱ) ∵ ()1log 1a xf x x--=+ ()1log 1a x f x x +=-=--，∴ f (x )为奇函数． (Ⅲ)由(Ⅰ)知，()f x 的定义域为(1,1)-，∴当1a >时，由1log 01axx+>-得 111>-+xx，解得01x <<； 当01a <<时，由1log 01axx+>-得 1011x x+<<-，解得10x -<<．综上所述，当1a >时，()0f x >的x 取值范围(0,1)；当01a <<时，()0f x >的x 取值范围(1,0)-．25. （本小题满分12分）本小题考查观察、分析、归纳的能力和数学归纳法． 解：由123482448809254981S S S S ====，，，， … ，猜想()()()N n n n S n ∈+-+=2212112． 下面用数学归纳法证明如下：①当1n =时，98313221=-=S ，等式成立．②设当n k =时等式成立，即()()2221121k k S k +-=+． ()()()221321218++++=+k k k S S k k ()()()()()222232121812112+++++-+=k k k k k ()()()()()222232121832]112[+++++-+=k k k k k ()()()()()()22222321218323212+++++-++=k k k k k k ()()()()()222223212123212+++-++=k k k k k ()()2232132+-+=k k ()()22]112[1]112[++-++=k k 由此可知，当1n k =+时等式也成立． 根据①②可知，等式对任何n N ∈都成立． 26. （本小题满分12分）本小题考查直线与平面的平行、垂直和两平面垂直的基础知识，及空间想象能力和逻辑思维能力．证法一：(Ⅰ)设α∩γ=AB ，β∩γ=AC ． 在γ内任取一点P ，并在γ内作直线PM ⊥AB ，PN ⊥AC 交AB ，AC 于点,M N ．∵γ⊥α，∴PM ⊥α． 而 a ⊂α，∴PM ⊥a ． 同理PN ⊥a ．又 PM ⊂γ，PN ⊂γ， ∴ a ⊥γ．(Ⅱ)在直线a 上任取点Q ，过b 与Q 作一平面交α于直线1a ，交β于直线2a ． ∵b ∥α，∴b ∥1a ． 同理b ∥2a ． ∴ 1a ∥2a ． ∵12a a Q =，∴1a 与2a 重合．又 1a ⊂α，2a ⊂β，∴1a ，2a 都是α、β的交线，即都重合于a ． ∵b ∥1a ，∴ b ∥a ． 而a ⊥γ，∴b ⊥γ．证法二：(Ⅰ)在a 上任取一点P ，过P 作直线a '⊥γ．∵α⊥γ，P ∈α，∴a '⊂α． 同理a '⊂β．∴ a '是α，β的交线，即a '重合于a ． 又a '⊥γ，∴ a ⊥γ．(Ⅱ)于α内任取不在a 上的一点，过b 和该点作平面与α交于直线c ．同理过b 作平面与β交于直线d ．∵b ∥α，b ∥β．∴b ∥c ，b ∥d ． 又 c ⊄β，d ⊂β，∴c 与d 不重合，且c ∥d ．∴c ∥β．∵c ∥β，c ⊂α，α∩β=a ，∴c ∥a ．∵b ∥c ，a ∥c ，b 与a 不重合(b ⊄α，a ⊂α)，∴b ∥a ． 而a ⊥γ，∴b ⊥γ．27. （本小题满分12分）解法一：如图，以MN 所在直线为x 轴，MN 的垂直平分线为y 轴建立直角坐标系，设以,M N 为焦点且过点P 的椭圆方程为12222=+by a x ，且焦点为(,0),(,0)(0)M c N c c ->．由tan ,tan 22PMN MNP ∠=∠=-知，直线PM 和直线PN 的斜率分别为1,22，直线方程分别为1(),2()2y x c y x c =+=-． 由1(),22()y x c y x c ⎧=+⎪⎨⎪=-⎩解得54,33x c y c ==，即 54,33P c c ⎛⎫⎪⎝⎭． 在PMN ∆中，|MN |=2c ，MN 上的高为点P 的纵坐标，∴214421233MNP S c c c ∆=⋅⋅==，∴ c =P 点坐标为⎪⎪⎭⎫ ⎝⎛332635，． 由椭圆过点P 得2a PM PN =+==， ∴a =．∴222153344b a c =-=-=， ∴所求椭圆方程为1315422=+y x ． 解法二：同解法一得23=c ，P 点的坐标为⎪⎪⎭⎫⎝⎛332635，．∵ 点P 在椭圆上，且222a b c =+，∴ 13322363522222=⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛b b ，即 423830b b --=，解得23b =，或213b =- (舍去)．∴222154a b c =+=，∴所求椭圆方程为1315422=+y x ． 说明：本小题主要考查坐标系、椭圆的概念和性质、直线方程以及综合应用能力．本题也可用正弦定理求解．28. （本小题满分12分）本小题考查复数的基本概念和运算，三角函数式的恒等变形及综合解题能力． 解法一：()()[][]44sin cos 1sin cos 1θθθθωi i ++-+--=()()θθθθ4sin 4cos 14sin 4cos 1i i ++----= θθθθθθ2cos 2sin 22cos 22cos 2sin 22sin 222i i ++=()θθθ4cos 4sin 2tg i +=．∴tg2sin 4cos4i ωθθθ=⋅+tg2θ==332tg ±=θ．∵ πθ<<0，∴57112,,,6666ππππθ=，即 511,,,121212πππ． ∴当12πθ=时，cos sin 333i ππω⎫=+⎪⎝⎭，得 arg 32ππω=<，适合题意．当712πθ=时，77cos sin cos sin 333333i i ππππω⎫⎫=+=+⎪⎪⎝⎭⎝⎭，得arg 32ππω=<，适合题意．当512πθ=时，55cos sin 333i ππω⎫=-+⎪⎝⎭22cos sin 333i ππ⎫=+⎪⎝⎭， 2arg 32ππω=>，不适合题意，舍去．当1112πθ=时，1111cos sin 333i ππω⎫=-+⎪⎝⎭22cos sin 366i ππ⎫=+⎪⎝⎭， 2arg 32ππω=>，不适合题意，舍去．综上可得12πθ=或127πθ=．解法二：θθ4sin 4cos 4i z +=． 记θϕ4=，得()()ϕϕsin cos 44i z z -==．ϕϕϕϕωsin cos 1sin cos 1i i +++-=()ϕϕϕϕcos sin cos 1sin i ++=()ϕϕϕcos sin 2tg i +=．∵ 33=ω，2arg πω<，∴t g ,(1)2tg sin 0,(2)2tg cos 0.(3)2ϕϕϕϕϕ⎧=⎪⎪⎪⋅>⎨⎪⎪⋅≥⎪⎩当（1）成立时，（2）恒成立，所以θ应满足(ⅰ) ⎪⎪⎩⎪⎪⎨⎧≥=<<04cos 332tg 0θθπθ，或(ⅱ) ⎪⎪⎩⎪⎪⎨⎧≤-=<<04cos 332tg 0θθπθ，解(ⅰ)得12πθ=或127πθ=．(ⅱ)无解．综合(ⅰ)、(ⅱ) 12πθ=或127πθ=．1994年普通高等学校招生全国统一考试数学试题(理工农医类)参考解答本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．共150分，考试时间120分钟． 一、选择题(本题考查基本知识和基本运算) 1-15 CDDAB DBAAC CBDBC 二、填空题(本题考查基本知识和基本运算) 16．－189 17．223,(2)1x x y =-+= 18．43- 19． π322 20．()121n a a a n+++三、解答题 21．（本小题满分11分）本小题考查共轭复数、复数的三角形式等基础知识及运算能力．解：(1)∵1z i =+，∴()223413(1)4z z i i ω=+-=+++-23(1)41i i i =+--=--，∴ω的三角形式是⎪⎭⎫ ⎝⎛+ππ45sin 45cos 2i ．(2) ∵1z i =+，∴()()()()1111112222++-+++++=+-++i i b i a i z z b az z()()()()221a b a i a a b i i i+++==+-+=-，∴21,()1,a a b +=⎧⎨-+=-⎩解得⎩⎨⎧=-=.2,1b a 22．（本小题满分12分）本小题考查三角函数基础知识、三角函数性质及推理能力． 证明：121212sin sin tan tan cos cos x x x x x x +=+121212sin cos cos sin cos cos x x x x x x +=()2121cos cos sin x x x x +=()()()1212122sin cos cos x x x x x x +=++-， ∵12,0,2x x π⎛⎫∈ ⎪⎝⎭，且12x x ≠， ∴()122sin 0x x +>，12cos cos 0x x >，且()120cos 1x x <-<， ∴()()12120cos cos x x x x <++-()121cos x x <++，∴()()1212122sin tan tan 1cos x x x x x x ++>++12122124sin cos 222cos 2x x x x x x ++⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭=+⎛⎫ ⎪⎝⎭122tan 2x x +⎛⎫= ⎪⎝⎭，∴12121(tan tan )tan 22x x x x ++>，即 []12121()()()22x x f x f x f ++>． 23．（本小题满分12分）本小题考查空间线面关系、正棱柱的性质、空间想象能力和逻辑推理能力．(1)证明：∵A 1B 1C 1－ABC 是正三棱柱， ∴四边形B 1BCC 1是矩形．连接B 1C 交BC 1于E ，则B 1E =EC ． 连接DE ．在△AB 1C 中，∵AD =DC ，∴DE ∥AB 1． 又AB 1⊄平面DBC 1，DE ⊂平面DBC 1，∴AB 1∥平面DBC 1．(2)解：作DF ⊥BC ，垂足为F ，则DF ⊥面B 1BCC 1，连结EF ，则EF 是ED 在平面B 1BCC 1上的射影． ∵AB 1⊥BC 1，由(1)知AB 1∥DE ，∴DE ⊥BC 1，则BC 1⊥EF ，∴∠DEF 是二面角的平面角α． 设AC =1，则DC =21．∵△ABC 是正三角形，∴在Rt △DCF 中， DF =DC ·sin C =43，CF =DC ·cos C =41．取BC 中点G ．∵EB =EC ，∴EG ⊥BC ．在Rt △BEF 中，EF 2=BF ·GF ，又BF =BC －FC =43，GF =41， ∴EF 2=43·41，即EF =43． ∴tg ∠DEF =14343==EF DF． ∴∠DEF =45°． ∴二面角α为45°． 24．（本小题满分12分）本小题考查直线与抛物线的基本概念和性质，解析几何的基本思想方法以及综合运用知识解决问题的能力．解法一：依题设抛物线C 的方程可写为22(0)y px p =>，且x 轴和y 轴不是所求直线，又l 过原点，因而可设l 的方程为 (0)y kx k =≠)． ① 设A '，B '分别是A ， B 关于l 的对称点， 因而A 'A ⊥l ，直线 A 'A 的方程为()11+-=x ky ② 由①，②联立解得AA '与l 的交点M 的坐标为⎪⎭⎫ ⎝⎛+-+-11122k k k ，．又M 为AA '的中点，从而点A '的坐标为222112111A k x k k '-⎛⎫=-+= ⎪++⎝⎭， 2222011A k k y k k '-⎛⎫=+=- ⎪++⎝⎭．③ 同理得点B '的坐标为2161B kx k '=+， ()22811B k y k '-=+．④又A '，B '均在抛物线22(0)y px p =>上，由③得112122222+-⋅=⎪⎭⎫ ⎝⎛+-k k p k k ， 由此知k ≠±1，即1242-=k kp ． ⑤ 同理由④得()11621182222+⋅=⎪⎪⎭⎫ ⎝⎛+-k k p k k ， 即 ()()kk k p 112222+-=． 从而 1242-k k=()()kk k 112222+-，整理得210k k --=，解得.25125121-=+=k k ， 但当251-=k 时，由③知055<-='A x ，这与A '在抛物线y 2=2px (p >0)上矛盾，故舍去2512-=k ．设251+=k ，则直线l 的方程为x y 251+=．将251+=k 代入⑤，求得552=p ．所以直线方程为x y 251+=．抛物线方程为x y 5542=．解法二：设点A 、B 关于l 的对称点分别为A '(x 1、y 1)、B '(x 2，y 2)，则 |OA '|=|OA |=1，|OB '|=|OB |=8．设由x 轴正向到OB '的转角为α，则 228cos ,8sin x y αα==． ① 因为A '，B '为A ，B 关于直线l 的对称点，而∠BOA 为直角，故∠B 'OA '为直角，因此1cos sin 2x παα⎛⎫=-= ⎪⎝⎭，1sin cos 2y παα⎛⎫=-=- ⎪⎝⎭ ②由题意知x 1>0，x 2>0，故α为第一象限角．因为A '，B '都在抛物线y 2=2px 上，将①、②代入得22cos 2sin ,64sin 16cos p p αααα==，∴338sin cos αα=，即2sin cos αα=，解得52cos 51sin ==αα，． 将52cos 51sin ==αα，代入 2cos 2sin p αα=得552sin 2cos 2==ααp ， ∴抛物线C 的方程为x y 5542=． 因为直线l 平分∠B 'OB ，故l 的斜率1tan tan 2224k παπαα⎡⎤⎛⎫⎛⎫=+-=+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦251sin 1cos 2cos 12sin +=-=⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=ααπαπα，∴直线l 的方程为x y 215+=．25．（本小题满分14分）本小题考查等差数列、等比数列、数列极限等基础知识考查逻辑推理能力和分析问题与解决问题的能力．解：(1)由题意，当n =1时有122a +==12a =． 当n =2时有222a +==，整理得(a 2－2)2=16．由20a >，解得26a =． 当n =3时有322a +，整理得()23264a -=．由30a >，解得310a =． ∴该数列的前3项为2，6，10． (2)解法一：由(1)猜想数列{}n a 有通项公式42n a n =-．下面用数学归纳法证明数列{}n a 的通项公式是42()n a n n N =-∈ ．①当n =1时，因为4×1－2=2，又在(1)中已求出12a =，所以上述结论成立． ②假设n =k 时结论成立，即有42k a k =-． 222k a k +==，即22k S k =．又由题意有=122k a ++==，整理得221144160k k a a k ++-+-=．由10k a +>，解得142k a k +=+，即14(1)2k a k +=+-．这就是说，当n =k +1时，上述结论成立． 根据①、②，上述结论对所有的自然数n 成立．解法二：由已知条件得()N n S a n n ∈=+222， 整理得21(2)8n n S a =+，由此得2111(2)8n n S a ++=+，∴2211111(2)(2)88n n n n n a S S a a +++=-=+-+，即11()(4)0n n n n a a a a +++--=．由题意知 10n n a a ++>， ∴14n n a a +-=．∴数列{}n a 为等差数列，其中a 1=2，公差d =4，且a n =a 1+(n －1)d =2+4(n －1)， ∴{}n a 通项公式为42n a n =-． (3)解：令1n n c b =-，则 ⎪⎪⎭⎫ ⎝⎛-+=++22111n n n n n a a a ac⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+-+⎪⎭⎫ ⎝⎛--+=112121121221n n n n 121121+--=n n ， 1212n n b b b n c c c +++-=+++ 11111=13352121n n ⎛⎫⎛⎫⎛⎫-+-++- ⎪ ⎪ ⎪-+⎝⎭⎝⎭⎝⎭1211+-=n ．∴()12lim n n b b b n →∞+++-1lim 1121n n →∞⎛⎫=-= ⎪+⎝⎭．1995年普通高等学校招生全国统一考试数学试题(理工农医类)参考解答本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．共150分，考试时间120分钟． 一、选择题(本题考查基本知识和基本运算) 1-15 CBCBD DBCAD BCADA 二、填空题(本题考查基本知识和基本运算) 16．{x |－2<x <4} 17．3237 18． 43-19．4 20．144 三、解答题 21．（本小题满分7分）本小题主要考查复数基本概念和几何意义，以及运算能力． 解：设Z 1，Z 3对应的复数分别为z 1，z 3，依题设得]4sin 4[cos 2121⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-=ππi z z ()⎪⎪⎭⎫ ⎝⎛-+=i i 22223121i 213213-++=． ⎪⎭⎫ ⎝⎛+=4sin 4cos 2123ππi z z=()⎪⎪⎭⎫⎝⎛++i i 22223121i 231231++-=． 22．（本小题满分10分）本小题主要考查三角恒等式和运算能力． 解：原式1cos 401cos100=22-︒+︒+cos 20sin 50+︒︒cos100cos 40sin70sin 30=1+22︒-︒︒-︒+︒+︒︒-=70sin 2130sin 70sin 4343=．23．（本小题满分12分）本小题主要考查空间线面关系、圆柱性质、空间想象能力和逻辑推理能力．解：(1)根据圆柱性质，DA ⊥平面ABE ． ∵EB ⊂平面ABE ，∴DA ⊥EB ．∵AB 是圆柱底面的直径，点E 在圆周上， ∴AE ⊥EB ． 又AE ∩AD =A ， ∴EB ⊥平面DAE ． ∵AF ⊂平面DAE ， ∴EB ⊥AF ． 又AF ⊥DE ，且 EB ∩DE =E ，∴AF ⊥平面DEB ． ∵DB ⊂平面DEB ， ∴AF ⊥DB ．(2)解：过点E 作EH ⊥AB ，H 是垂足，连接DH ．根据圆柱性质，平面ABCD ⊥平面ABE ，AB 是交线．且EH 平面ABE ， ∴EH ⊥平面ABCD ． 又DH 平面ABCD ，∴DH 是ED 在平面ABCD 上的射影，从而∠EDH 是DE 与平面ABCD 所成的角． 设圆柱的底面半径为R ，则DA =AB =2R ， ∴32R V π=圆柱,.32312EH R S AD V ABE ABE D ⋅=⋅=∆-由π3=-ABE D V V ：圆柱，得R EH =，可知H 是圆柱底面的圆心，且R AH =，R AH DA DH 522=+=，∴5arctg EHDHarcctg EDH ==∠， 24．（本小题满分12分）本小题主要考查运用所学数学知识和方法解决实际问题的能力，以及函数的概念、方程和不等式的解法等基础知识和方法． 解：(1)由 Q P =有()2840500)8(1000--=-+x t x ，即0)280644)808(522=+-+-+t t x t x （．当判别式0168002≥-=∆t ，即0t ≤≤时，。
98年高考数学试卷
98年高考数学试卷
98年高考数学试卷指的是中国教育部于1998年为评估和选拔当年高中毕业生而制定的数学学科考试试卷。
该试卷主要测试学生在数学基础知识、数学思维方法、实际应用等方面的能力和水平。
以下是 98年高考数学试卷题目：
1、已知函数 f(x) = x^2 + ax + 3 在区间 [-1, 2] 上的最小值为 -1，则 a 的值为：
A. -2
B. -4
C. 2
D. 4
2、下列数列中，是等差数列的是：
A. 1, 2, 3, 4, 5
B. 1, 3, 5, 7, 9
C. -1, -3, -5, -7, -9
D. 1/2, 1/4, 1/6, 1/8, 1/10
3、下列二次函数中，其图像与 x 轴有交点的是：
A. y = x^2 - 3x + 2
B. y = x^2 + 2x + 3
C. y = x^2 - x - 2
D. y = x^2 + x - 2
4、下列四个命题中，真命题是：
A. 若 a > b，则 a^2 > b^2
B. 若 a > b，则 a^3 > b^3
C. 若 a > b，则 a^4 > b^4
D. 若 a > b，则 a^5 > b^5
5、若方程 x^2 - mx + m = 0 有两个不等的实根，则实数 m 的取值范围是：
A. m < -2
B. m < -1
C. m > -2
D. m > -1。
(详细解析)1998年全国高考理科数学试题及其解析(可打印修改)
1998年普通高等学校招生全国统一考试数学（理工农医类）本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，满分150分，考试120分钟．第Ⅰ卷（选择题共65分）一．选择题：本大题共15小题；第1—10题每小题4分，第11— 15题每小题5分，共65分．在每小题给出的四个选项中，只有一项是符合题目要求的1．的值是sin 600︒A ．B ．C ．D ．2112-23【答案】D【解析】sin 600sin(720120)sin(120)sin120sin(18060)︒=︒-︒=-︒=-︒=-︒-︒sin 60=-︒=2．函数的图像是(1)xy a a =>【答案】B【解析】函数为偶函数，当时，为增函数，且过点，B 正确．0x ≥xy a =(0,1)3．曲线的极坐标方程化成直角坐标方程为4sin ρθ=A ． B ．22(2)4x y ++=22(2)4x y +-=C ．D ．22(2)4x y -+=22(2)4x y ++=【答案】B【解析】由已知得，即，化为标准方程为．4yρρ=⨯224x y y +=22(2)4x y +-=4．两条直线垂直的充要条件是1112220,0A x B y C A x B y C ++=++=A ．B ．C ．D ．12120A A B B +=12120A A B B -=12121-=B B A A 12121=A A B B 【答案】A【解析】①若一条直线的斜率不存在，则另一条直线一定与轴垂直，满足x ；12120A A B B +=②若两条直线斜率均存在，则，有，即，121212,A A k k B B =-=-121k k =-1212(1A AB B --=-所以．12120A A B B +=5．函数的反函数1()(0)f x x x=≠1()f x -=A ． B ． C ．D ．(0)x x ≠1(0)x x≠(0)x x -≠1(0)x x-≠【答案】B 【解析】为反比例函数，所以反函数．1()f x x =11()(0)f x x x-=≠6．已知点在第一象限，则在内的取值是(sin cos ,tan )P ααα-)20[π，αA ．B ．35()()244ππππU ，，5()()424ππππU ，，C ．D ．353(,)()2442ππππU ,3((,)424ππππU ，【答案】B【解析】点在第一象限，则，即，P sin cos 0,tan 0ααα->>sin cos ,tan 0ααα>>为第一象限或第三象限的角，若为第一象限的角，则由得，ααsin cos αα>tan 1α>所以；若为第三象限的角，则，结合正切函数图象可得(42ππα∈，α0tan 1α<<．5()4παπ∈，7．已知圆锥的全面积是底面积的3倍，那么该圆锥的侧面展开图扇形的圆心角为A ．120ºB ．150ºC ．180ºD ．240º【答案】C【解析】由题设得，得，扇形的圆心角为．22S rl S rππ==侧底2l r =22rr ππ=8．复数的一个立方根是，它的另外两个立方根是i -iA B ． C ． D ．12i ±12i 12i +12i -【答案】D【解析】设，则，解方程得33x i i =-=3322()()0x i x i x xi i -=-++=220x xi i ++=．12x i =9．如果棱台的两底面积分别是，中截面的面积是，那么,S S '0SA ．B ．C ．D ．=+0S =02S S S '=+SS S '=220【答案】A【解析】设两底和中截面的半径分别为和，则，所以,r r '0r 22200,,S r S r S r πππ''===，则0r r r '===02r r r '=+=+=10．向高为的水瓶中注水，注满为止，如果注水量与水深的函数关系的图像如下图H V h 所示，那么水瓶的形状是【答案】B【解析】在函数图象中，取水深时，注水量，即水深至一半时，实际2Hh =02V V V '=>注水量大于水瓶总水量的一半，只有B 正确．【难度】较难．11．3名医生和6名护士被分配到3所学校为学生体检，每校分配1名医生和2名护士，不同的分配方法共有A ．90种 B ．180种 C ．270种 D ．540种【答案】D【解析】先分配医生有种分法；再分配护士有种分法，不同的分配方336A =22264290C C C =法有540种．12．椭圆的焦点为和，点在椭圆上．如果线段的中点在轴上，221123x y +=1F 2F P 1PF y 那么是的1PF 2PF A ．7倍 B ．5倍 C ． 4倍 D ．3倍【答案】A【解析】线段的中点在轴上，则轴，有，，1PF y 2PF x ⊥221123By c +=2y PF P ==所以，是的7倍．122PF a PF =-=1PF 2PF 13．球面上有3个点，其中任意两点的球面距离都等于大圆周长的，经过这3个点的小61圆的周长为，那么这个球的半径为4πA ．B ．C ．2D ．3【答案】B【解析】设球的半径为，球面上3个点为，则为等边三角形，小圆的半R ,,A B C ABC ∆径为，所以2r=AB =R ==14．一个直角三角形三内角的正弦值成等比数列，其最小内角为A ．B ．C ．D ．arcsin arcsin【解析】不妨设，则，且，所以A B C <<2C π=sin sin sin 1A B C <<=，2sin sin A B =，化简得，解得（负值舍去），2sin sin ()2A A π=-2sin sin 10A A +-=sin A =则．A =15．在等比数列中，，且前项和满足，那么的取值范围是{}n a 11a >n n S 11lim n x S a →∞=1a A ． B ． C ．D ．(1,)+∞(1,4)(1,2)【答案】D【解析】显然公比，由题设得，可知，而01q <<111lim 11n x a S q a →∞==<-10q -<<，所以．211(1,2)a q =-∈1a ∈第Ⅱ卷（非选择题共85分）二、填空题：本大题共4小题；每小题4分，共16分．把答案填在题中横线上．16．设圆过双曲线的一个顶点和一个焦点，圆心在此双曲线上，则圆心到双116922=-y x 曲线中心的距离是 ．【答案】316【解析】根据题设，顶点、焦点和圆心在此双曲线的同一支上，设，则00(,)P x y ，故．200531674,29x y +⨯===163OP ==17．的展开式中的系数为（用数字作答）．102(2)(1)x x +-10x【解析】的通项公式为，故的系数10(2)x +101102r rr r T C x -+=⋅⋅10x 为．2210102179C C ⋅-=18．如图，在直四棱柱中，当底面四边形满足条件 时，1111A B C D ABCD -ABCD有．（注：填上你认为正确的一种条件即可，不必111A C B D ⊥考虑所有可能的情形．）【答案】，或任何能推导出这个条件的其他条件．例如AC BD ⊥是正方形，菱形等ABCD 【解析】连接，则，由于，所以要,AC BD 11//BD B D 1AA BD ⊥使，只需，只需平面，也即111A C B D ⊥1A C BD ⊥BD ⊥1A AC ．BD AC ⊥19．关于函数，有下列命题：()4sin(2)()3f x x x R π=+∈①由可得必是的整数倍；12()()0f x f x ==12x x -π②的表达式可改写为；()y f x =()4cos(26f x x π=-③的图像关于点对称；()y f x =(,0)6π-④的图像关于直线对称．()y f x =6x π=-其中正确的命题的序号是 ．（注：把你认为正确的命题的序号都填上．）【答案】②③【解析】必是的整数倍，①错误；12x x -2π()4sin(24cos[(2323f x x x πππ=+=-+；的图像的对称点的横坐标满足，即4cos(26x π=-()y f x =2()3x k k Z ππ+=∈，当时，对称点为，③正确，④不正确．26x k ππ=⋅-0k =(,0)6π-三、解答题：本大题共6小题；共69分．解答应写出文字说明，证明过程或演算步骤．20．（本小题满分10分）在中，分别是角的对边，设．求的ABC ∆,,a b c ,,A B C 2,3a cb A C π+=-=sin B 值．以下公式供解题时参考：，sin sin 2sincos,sin sin 2cossin2222θϕθϕθϕθϕθϕθϕ+-+-+=-=cos cos 2cos cos ,cos cos 2sin sin2222θϕθϕθϕθϕθϕθϕ+-+-+=-=-．【解】本小题考查正弦定理，同角三角函数基本公式，诱导公式等基础知识，考查利用三角公式进行恒等变形的技能及运算能力．由正弦定理和已知条件得．2a c b +=sin sin 2sin A C B +=由和差化积公式得．2sin cos sin 22A C A CB +-=由得，A BC π++=sin cos 22A C B+=又．3A C π-=sin 2B B =2sin cos 222B B B =因为，所以，从而0,cos 0222B B πθ<<≠sin 2B =cos 2B ==所以．sin B ==21．（本小题满分11分）如图，直线和相交于点，，点．以为端点的曲线段上的任1l 2l M 12l l ⊥1N l ∈,A B C一点到的距离与到点的距离相等．若为锐角三角形，2l N AMN ∆，且．建立适当的坐标系，求曲线段3AM =6BN =的方程．C 【解】本小题主要考查根据所给条件选择适当的坐标系，求曲线方程的解析几何的基本思想．考查抛物线的概念和性质，曲线与方程的关系以及综合运用知识的能力．解法一：如图建立坐标系，以为轴，的垂直平分线为轴，点为坐标原点．1l x MN y O依题意知：曲线段是以点为焦点，以为准线的抛C N 2l 物线的一段，其中分别为的端点．,A B C 设曲线段的方程为C ，22(0),(,0)A B y px p x x x y =>≤≤>其中分别为的横坐标，．所以．,A B x x ,A B p MN =(,0),(,0)22p pM N -由得， ①3AM =2(2172A A p x px ++=．②2(292A A px px -+=由①，②两式联立解得，再将其代入①式并由解得4A x p =0p >⎩⎨⎧==⎩⎨⎧==.2,2;1,4A A x p x p 或因为是锐角三角形，所以，故舍去AMN ∆2A px >2,2.A p x =⎧⎨=⎩所以．4,1A p x ==由点在曲线段上，得．B C 42B px BN =-=综上得曲线段的方程为．C 28(14,0)y x x y =≤≤>解法二：如图建立坐标系，分别以为轴，为坐标原点．12,l l ,x y M 作，垂足分别为．122,,AE l AD l BF l ⊥⊥⊥,,E D F 设．(,),(,),(,0)A A B B N A x y B x y N x 依题意有，3A x ME DA AN ====A y DM ==由于为锐角三角形，故有AMN∆4N x ．6B x BF BN ===设点是曲线段上任一点，则由题意知属于集合(,)P x y C P ．{}222(,)(),,0NA B x y x xy xx x x y -+=≤≤>|故曲线段的方程为．C 28(2)(36,0)y x x y =-≤≤>22．（本小题满分12分）如图，为处理含有某种杂质的污水，要制造一底宽为2米的无盖长方体沉淀箱．污水从孔流入，经沉淀后从孔流出．设箱体的长度为米，高度为米．已知流出的水中A B a b 该杂质的质量分数与的乘积成反比．现有制箱材料60平方米．问当各为多少,a b ab ,a b 米时，经沉淀后流出的水中该杂质的质量分数最小（孔的面,A B 积忽略不计）．【解】本小题主要考查综合应用所学数学知识、思想和方法解决实际问题的能力，考查建立函数关系、不等式性质、最大值、最小值等基础知识．解法一：设为流出的水中杂质的质量分数，则，其中为比例系数．依题意，y ky ab=0k >即所求的值使值最小．,a b y 根据题设，有，42260(0,0)b ab a a b ++=>>得． ①30(030)2ab a a-=<<+于是26464303234(2)222k k k k y a a ab a a a a a====--+--+++++，18k ≥=当时取等号，达到最小值．这时，（舍去）．6422a a +=+y 6a =10a =-将代入①式得．6a =3b =故当为6米，为3米时，经沉淀后流出的水中该杂质的质量分数最小．a b 解法二：依题意，即所求的的值使最大．,a b ab 由题设知，即．42260(0,0)b ab a a b ++=>>230(0,0)a b ab a b ++=>>因为2，当且仅当时，上式取等2a b +≥30ab +≤2a b =号．由，解得．0,0a b >>018ab <≤即当时，取得最大值，其最大值为18．2a b =ab 所以．解得．2218b =3,6b a ==故当为6米，为3米时，经沉淀后流出的水中该杂质的质量分数最小．a b 23．（本小题满分12分）已知斜三棱柱的侧面与底面垂直，111ABC A B C -11A ACC ABC 90,ABC BC ∠=︒=，且．2,AC =1111,AA A C AA A C ⊥=（Ⅰ）求侧棱与底面所成角的大小；1A A ABC（Ⅱ）求侧面与底面所成二面角的大小；11A ABB ABC （Ⅲ）求顶点到侧面的距离．C 11A ABB 【解】本小题主要考查直线与直线、直线与平面、平面与平面的位置关系，棱柱的性质，空间的角和距离的概念，逻辑思维能力、空间想象能力及运算能力．（Ⅰ）作，垂足为，由面面，得面，1A D AC ⊥D 11A ACC ⊥ABC 1A D ⊥ABC 所以为与面所成的角．1A AD ∠1A A ABC 因为，1111,AA A C AA A C ⊥=所以为所求．145A AD ∠=︒（Ⅱ）作，垂足为，连，则由面，得．DE AB ⊥E 1A E 1A D ⊥ABC 1A E AB ⊥所以是面与面所成二面角的平面角．1A ED ∠11A ABB ABC 由已知，，得．AB BC ⊥//ED BC又是的中点，D AC 2,BC AC ==所以．11,DE AD A D ===11tan A DA ED DE∠==故为所求．160A ED ∠=︒（Ⅲ）解法一：由点作平面的垂线，垂足为，则的长是到平面C 11A ABB H CH C 的距离．11A ABB连结，由于，得．HB AB BC ⊥AB HB ⊥又，知，且，1A E AB ⊥1//HB A E //BC ED 所以．160HBC A ED ∠=∠=︒所以sin 60CH BC =︒=解法二：连结．1A B 根据定义，点到面的距离，即为三棱锥的高．C 11A ABB 1C A AB -h 由得，即．ABC A AB A C V V --=11锥锥D A S h S ABC B AA 131311∆∆=322312231⨯⨯=⨯h 所以为所求．3=h 24．（本小题满分12分）设曲线的方程是，将沿轴、轴正向分别平行移动单位长度后C 3y x x =-C x y ,t s 得曲线．1C （Ⅰ）写出曲线的方程；1C （Ⅱ）证明曲线与关于点对称；C 1C (,)22t sA （Ⅲ）如果曲线与有且仅有一个公共点，证明且．C 1C 34t s t =-0t ≠【解】本小题主要考查函数图像、方程与曲线，曲线的平移、对称和相交等基础知识，考查运动、变换等数学思想方法以及综合运用数学知识解决问题的能力．（Ⅰ）曲线的方程为．1C 3()()y x t x t s =---+（Ⅱ）证明：在曲线上任取一点．设是关于点的对称点，则C 111(,)B x y 222(,)B x y 1B A 有，．2221t x x =+2221sy y =+所以．1212,x t x y s y =-=-代入曲线的方程，得和满足方程：，C 2x 2y 3222()()s y t x t x -=---即，可知点在曲线上．3222()()y x t x t s =---+222(,)B x y 1C 反过来，同样可以证明，在曲线上的点关于点A 的对称点在曲线上．1C C 因此，曲线与关于点A 对称．C 1C （Ⅲ）证明：因为曲线与有且仅有一个公共点，所以，方程组C 1C 33,()().y x x y x t x t s ⎧=-⎪⎨=---+⎪⎩有且仅有一组解．消去，整理得，y 22333()0tx t x t t s -+--=这个关于的一元二次方程有且仅有一个根．x 所以并且其根的判别式．即0t ≠43912()0t t t t s ∆=---=⎩⎨⎧=--≠.0)44(,03s t t t t 所以且．t t s -=430t ≠25．（本小题满分12分）已知数列是等差数列，．{}n b 112101,145b b b b =++⋅⋅⋅+=（Ⅰ）求数列的通项；{}n b n b （Ⅱ）设数列的通项（其中，且），记是数列{}n a 1log (1)n a na b =+0a >1a ≠n S 的前项和．试比较与的大小，并证明你的结论．{}n a n nS 11log 3a nb +【解】本小题主要考查等差数列基本概念及其通项求法，考查对数函数性质，考查归纳、推理能力以及用数学归纳法进行论证的能力．（Ⅰ）设数列的公差为，由题意得解得{}n b d ⎪⎩⎪⎨⎧=-+=.1452)110(1010,111d b b ⎩⎨⎧==.3,11d b 所以．32n b n =-（Ⅱ）由，知32n b n =-11log (11)log (1log (1432n a a a S n =++++⋅⋅⋅++- ，11log [(11)(1)(1432a n =++⋅⋅⋅+-．11log log 3a n ab +=因此要比较与的大小，n S 11log 3a n b +可先比较与的大小．11(11)(1(1)432n ++⋅⋅⋅+-313+n 取有1n =11+>取有2n =1(11)(1)4++>……由此推测 ①11(11)(1(1)432n ++⋅⋅⋅+>-若①式成立，则由对数函数性质可断定：当时，．1a >11log 3n a n S b +>当时，．01a <<11log 3n a n S b +<下面用数学归纳法证明①式．（ⅰ）当时已验证①式成立．1n =（ⅱ）假设当时，①式成立，即．(1)nk k =≥11(11)(1(1)432k ++⋅⋅⋅+>-那么，当时，1n k=+1111(11)(1)(1)(1)4323(1)231k k k ++⋅⋅⋅++>+-+-+．2)k=+因为)()()()()332323234313231k k k k k ⎤+-+++-=⎥+⎦，()013492>++=k k．2)k +>=因而111(11)(1)(1)43231k k ++⋅⋅⋅++>-+这就是说①式当时也成立．1n k =+由（ⅰ），（ⅱ）知①式对任何正整数都成立．n 由此证得：当时，．1a >11log 3n a n S b +>当时，．01a <<11log 3n a n S b +<。
1998年高考数学试题及答案(全国文)
98年全国高校招生数学统考试题（文史类）一、选择题：本大题共15小题；第（1）－（10）题每小题4分，第（11）－（15）题每小题5分，共65分。
在每小题给出的四项选项中，只有一项是符合题目要求的。
（1）sin600°的值是（A）1/2 （B）-1/2 （C）/2 （D）-/2 （2）函数y=a|x|(a>1)的图象是（3）已知直线x=a(a>0)和圆(x-1)2+y2=4相切，那么a的值是（A）5 （B）4 （C）3 （D）2（4）两条直线A1x+B1y+C1=0，A2x+B2y+C2=0垂直的充要条件是（A）A1A2+B1B2=0 （B）A1A2-B1B2=0（C）A1A2/B1B2=-1 （D）B1B2/A1A2=1（5）函数f(x)=1/x(x≠0)的反函数f-1(x)=（A）x(x≠0) （B）1/x(x≠0)（C）-x(x≠0) （D）-1/x(x≠0)（6）已知点P（sinα-cosα,tgα）在第一象限，则[0,2π)内α的取值范围是（A）(π/2,3π/4)∪(π,5π/4) （B）(π/4,π/2)∪(π,5π/4)（C）(π/2,3π/4)∪(5π/2,3π/2) （D）(π/4,π/2)∪(3π/4,π)（7）已知圆锥的全面积是底面积的3倍，那么该圆锥的侧面积展开图扇形的圆心角为（A）120°（B）150°（C）180°（D）240°（8）复数-i的一个立方根是i，它的另外两个立方根是（A）/2±1/2 （B）-/2±1/2i（C）±/2+1/2i （D）±/2-1/2i（9）如果棱台的两底面积分别是S，S'，中截面的面积是S0，那么（A）2=+（B）S0＝（C）2S O＝S＋S'（D）S02＝2S'S（10）2名医生和4名护士被分配到2所学校为学生体检，每校分配1名医生和2 名护士。
1998年全国Ⅱ高考数学试题(理)
1998年普通高等数学招生全国统一考试（全国Ⅱ）理科数学参考公式：三角函数的积化和差公式：[]1sin cos sin()sin()2αβαβαβ=++- []1cos sin sin()sin()2αβαβαβ=+--[]1cos cos cos()cos()2αβαβαβ=++-[]1sin sin cos()cos()2αβαβαβ=-+--正棱台、圆台的侧面积公式1()2S c c l ='+台侧 其中c '、c 分别表示上、下底面周长，l 表示斜高或母线长．球的体积公式：343V r π=球，其中R 表示球的半径．第Ⅰ卷（选择题共60分）一、选择题：本大题共15小题，第1－10题第小题4分，第11－15题每小题5分，共65分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．sin 600的值是A ．12B ．12-CD．2．函数||(1)x y a a =>的图像是D3．曲线的极坐标方程4sin ρθ=化成直角坐标方程为A ．22(2)4x y ++= B ．22(2)4x y +-=C ．22(2)4x y -+=D ．22(2)4x y ++=4．两条直线1110A x B y C ++=，2220A x B y C ++=垂直的充要条件是A ．12120A AB B +=B ．12120A A B B -=C ．12121A A B B =- D ．12121A A B B =5．函数1()(0)f x x x=≠的反函数1()f x -＝ A ．(0)x x ≠ B ．1(0)x x≠ C ．(0)x x -≠D ．1(0)x x-≠ 6．已知点(sin cos ,tan )P ααα-在第一象限，则在()0,2π内α的取值范围是A ．35,,244ππππ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭B ．5,,424ππππ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭C ．353,,2442ππππ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭ D ．3,,424ππππ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭7．已知圆锥的全面积是底面积的3倍，那么该圆锥的侧面展开图扇形的圆心角为A ．120°B ．150°C ．180°D ．240°8．复数i -的一个立方根是i，它的另外两个立方根是A 12iB ．12i ±C ．12i ±+ D ．12i9．如果棱台的两底面积分别是S ，S '，中截面的面积是0S ，那么A．=B ．0S =C ．02S S S '=+D ．202S SS '=10．向高为H 的水瓶中注水，注满为止，如果注水量V 与水深h 的函数关系的图像如右图所示，A ．B ．C ． D．11．3名医生和6名护士被分配到3所学校为学生体检，每校分配1名医生和2名护士，不同的分配方法共有A ．90种B ．180种C ．270种D ．540种12．椭圆221123x y +=的焦点为1F 和2F ，点P 在椭圆上，如果线段1PF 的中点在y 轴上，那么1||PF 是2||PF 的A ．7倍B ．5倍C ．4倍D ．3倍13．球面上有3个点，其中任意两点的球面距离都等于大圆周长的16，经过这3个点的小圆的周长为4π，那么这个球的半径为A．B．C ．2D14．一个直角三角形三内角的正弦值成等比数列，其最小内角为A．1arccos2 B．1arcsin 2 C．1arccos 2D．1arcsin 2-15．在等比数列{}n a 中，11a >，且前n 项和n S 满足11lim n n S a →∞=，那么1a 的取值范围是 A ．()1,+∞ B ．()1,4 C ．()1,2D．(第Ⅱ卷（非选择题共90分）注意事项：用钢笔或圆珠笔直接答在答题卡上．二、填空题：本大题共4小题，每小题4分，共16分，把答案填在题中横线上．16．设圆过双曲线221916x y -=的一个顶点和一个焦点，圆心在此双曲线上，则圆心到双曲线中心的距离是 ．17．102(2)(1)x x +-的展开式中10x 的系数为 （用数字作答）．18．如图，在直四棱柱1111ABCD A B C D -中，当底面四边形ABCD满足条件 时，有111AC B D ⊥．（注：填上你认为正确的一种条件即可，不必考虑所有可能的情形．） 19关于函数()4sin(2)()3f x x x R π=+∈，有下列命题：①由12()()0f x f x ==可得12x x -必是π的整数倍；②()y f x =的表达式可改写为4cos(2)3y x π=-；③()y f x =的图像关于点(,0)6π-对称；④()y f x =的图像关于直线6x π=-对称．其中正确的命题的序号是 ．（注：把你认为正确的命题的序号都填上．）A BCDA 1D 1B 1C 1三、解答题：本大题共6小题，共69分，解答应写出文字说明，证明过程或演算步骤．20．（本小题满分10分）在△ABC 中，a 、b 、c 分别是角A 、B 、C 的对边，设2a c b +=，3A C π-=．求sin B 的值．以下公式供解题时参考：sin sin 2sincos22θϕθϕθϕ+-+=，sin sin 2cossin22θϕθϕθϕ+--=，cos cos 2cos cos 22θϕθϕθϕ+-+=，cos cos 2sin sin22θϕθϕθϕ+--=- 21．（本小题满分11分）如图，直线1l 和2l 相交于点M ，1l ⊥2l ，点1N l ∈．以A 、B 为端点的曲线段C 上的任一点到2l 的距离与到点N 的距离相等，若△AMN为锐角三角形，||AM =||3AN =且||6BN =．建立适当的坐标系，求曲线段C 的方程． 22．（本小题满分12分）如图，为处理含有某种杂质的污水，要制造一底宽为2米的无盖长方体沉淀箱，污水从A 孔流入，经沉淀后从B 孔流出．设箱体的长度为a 米，高度为b 米．已知流出的水中该杂质的质量分数与a ，b 的乘积ab 成反比．现有制箱材料60平方米．问当a ，b 各为多少米时，经常常后流出的水中该杂质的质量分数最小（A 、B 孔的面积忽略不计）． 23．（本小题满分12分）已知斜三棱柱111ABC A B C -的侧面11A ACC 与底面ABC 垂直，90ABC ∠=，2BC =，AC =11AA A C ⊥，11AA A C =．（1）求侧棱1AA 与底面ABC 所成角的大小； （2）求侧面11A ABB 与底面ABC 所成二面角的大小； （3）求顶点C 到侧面11A ABB 的距离．24．（本小题满分12分）设曲线C 的方程是3y x x =-，将C 沿x 轴、y 轴正向分别平行移动t 、s 单位长度后得到曲线1C ．lABCA 1B 1C 1（1）写出曲线1C 的方程；（2）证明曲线C 与1C 关于点(,)22t s A 对称；（3）如果曲线C 与1C 有且仅有一个公共点，证明34t s t =-且0t ≠．25．（本小题满分12分）已知数列{}n b 是等差数列，11b =，1210145b b b +++=．（1）求数列{}n b 的通项n b ； （2）设数列{}n a 的通项1log (1)n a na b =+（其中0a >，且1a ≠），记n S 是数列{}n a 的前n 项和．试比较n S 与11log 3a nb +的大小，并证明你的结论．数学试题参考答案一、选择题，本题考查基础知识，基本概念和基本运算能力二、填空题．本题考查基础知识,基本概念和基本运算技巧 13． 14． 15． 16．三、解答题 17．1998年普通高等学校招生全国统一考试数学试题（理工农医类）参考答案一、选择题（本题考查基本知识和基本运算．）1．D 2．B 3．B 4．A 5．B 6．B 7．C 8．D 9．A 10．B 11．D 12．A 13．B 14．B 15．D 二、填空题（本题考查基本知识和基本运算．）16．31617．179 18．AC ⊥BD ，或任何能推导出这个条件的其他条件．例如ABCD 是正方形，菱形等 19．②，③ 三、解答题20．本小题考查正弦定理，同角三角函数基本公式，诱导公式等基础知识，考查利用三角公式进行恒等变形的技能及运算能力．解：由正弦定理和已知条件a +c =2b 得 sin A +sin C =2sin B .由和差化积公式得2sin 2C A +cos 2CA -=2sinB . 由A +B +C =π 得 sin 2C A +=cos 2B，又A －C =3π 得 23cos 2B =sin B ，所以23cos 2B =2sin 2B cos 2B.因为0<2B <2π，cos 2B ≠0，所以sin 2B =43，从而cos 2B =4132sin 12=-B所以sinB=83941323=⨯. 21．本小题主要考查根据所给条件选择适当的坐标系，求曲线方程的解析几何的基本思想．考查抛物线的概念和性质，曲线与方程的关系以及综合运用知识的能力．解法一：如图建立坐标系，以l 1为x 轴，MN 的垂直平分线为y 轴，点O 为坐标原点． 依题意知：曲线段C 是以点N 为焦点，以l 2为准线的抛物线的一段，其中A ，B 分别为C 的端点．设曲线段C 的方程为y 2=2px （p >0），（x A ≤x ≤x B ，y >0），其中x A ，x B 分别为A ，B 的横坐标，p =|MN |. 所以 M （2p -，0），N （2p，0）. 由|AM |= 17 ，|AN |=3 得（x A +2p ）2+2px A =17， ① （x A －2p）2+2px A =9. ②由①，②两式联立解得x A =p 4.再将其代入①式并由p >0解得⎩⎨⎧==⎩⎨⎧==.2,2;1,4AA x p x p 或 因为ΔAMN 是锐角三角形，所以2p> x A ，故舍去⎩⎨⎧==22A x p 所以p =4，x A =1. 由点B 在曲线段C 上，得x B =|BN |－2p=4. 综上得曲线段C 的方程为y 2=8x （1≤x ≤4，y >0）.解法二：如图建立坐标系，分别以l 1、l 2为x 、y 轴，M 为坐标原点． 作AE ⊥ l 1，AD ⊥ l 2，BF ⊥ l 2，垂足分别为E 、D 、F . 设A （x A ，y A ）、B （x B ，y B ）、N （x N ，0）. 依题意有x A =|ME |=|DA |=|AN |=3，y A =|DM |=2222=-DAAM，由于ΔAMN 为锐角三角形，故有x N =|ME |+|EN |=|ME |+22AE AN -=4x B =|BF |=|BN |=6.设点P （x ，y ）是曲线段C 上任一点，则由题意知P 属于集合｛（x ，y ）|（x －x N ）2+y 2=x 2，x A ≤x ≤x B ，y >0｝.故曲线段C 的方程为y 2=8（x －2）（3≤x ≤6，y >0）.22．本小题主要考查综合应用所学数学知识、思想和方法解决实际问题的能力，考查建立函数关系、不等式性质、最大值、最小值等基础知识．解法一：设y 为流出的水中杂质的质量分数，则y =abk，其中k >0为比例系数.依题意，即所求的a ，b 值使y 值最小.根据题设，有4b +2ab +2a =60（a >0，b >0），得b =a a+-230（0<a <30）. ① 于是 y =abk=aa a k +-230226432+-+-=a a k⎪⎭⎫ ⎝⎛+++-=264234a a k≥()2642234+⋅+-a a k18k =， 当a +2=264+a 时取等号，y 达到最小值.这时a =6，a =－10（舍去）. 将a =6代入①式得b =3.故当a 为6米，b 为3米时，经沉淀后流出的水中该杂质的质量分数最小.解法二：依题意，即所求的a ，b 的值使ab 最大.由题设知 4b +2ab +2a =60（a >0，b >0），即 a +2b +ab =30（a >0，b >0）.因为 a +2b ≥2ab 2，所以 ab 22+ab ≤30，当且仅当a =2b 时，上式取等号. 由a >0，b >0，解得0<ab ≤18.即当a =2b 时，ab 取得最大值，其最大值为18. 所以2b 2=18.解得b =3，a =6.故当a 为6米，b 为3米时，经沉淀后流出的水中该杂质的质量分数最小．23．本小题主要考查直线与直线、直线与平面、平面与平面的位置关系，棱柱的性质，空间的角和距离的概念，逻辑思维能力、空间想象能力及运算能力．Ⅰ．解：作A 1D ⊥AC ，垂足为D ，由面A 1ACC 1⊥面ABC ，得A 1D ⊥面ABC ， 所以∠A 1AD 为A 1A 与面ABC 所成的角. 因为AA 1⊥A 1C ，AA 1=A 1C ， 所以∠A 1AD =45º为所求.Ⅱ．解：作DE ⊥AB ，垂足为E ，连A 1E ，则由A 1D ⊥面ABC ，得A 1E ⊥AB . 所以∠A 1ED 是面A 1ABB 1与面ABC 所成二面角的平面角. 由已知，AB ⊥BC ，得ED ∥BC .又D 是AC 的中点，BC =2，AC =23，所以DE =1，AD =A 1D =3， tg ∠A 1ED =DEDA 1=3. 故∠A 1ED =60º为所求.Ⅲ．解法一：由点C 作平面A 1ABB 1的垂线，垂足为H ，则CH 的长是C 到平面A 1ABB 1的距离.连结HB ，由于AB ⊥BC ，得AB ⊥HB .又A 1E ⊥AB ，知HB ∥A 1E ，且BC ∥ED ，所以∠HBC =∠A 1ED =60º 所以CH =BC sin60º=3为所求. 解法二：连结A 1B .根据定义，点C 到面A 1ABB 1的距离，即为三棱锥C －A 1AB 的高h . 由ABC A AB A C V V --=11锥锥得D A S h S ABC B AA 131311∆∆=，即322312231⨯⨯=⨯h所以3=h 为所求.24．本小题主要考查函数图像、方程与曲线，曲线的平移、对称和相交等基础知识，考查运动、变换等数学思想方法以及综合运用数学知识解决问题的能力.Ⅰ．解：曲线C 1的方程为y =（x －t ）3－（x －t ）+s .Ⅱ．证明：在曲线C 上任取一点B 1（x 1，y 1）.设B 2（x 2，y 2）是B 1关于点A 的对称点， 则有2221t x x =+， 2221sy y =+.所以 x 1=t －x 2， y 1=s －y 2. 代入曲线C 的方程，得x 2和y 2满足方程：s －y 2=（t －x 2）3－（t －x 2）， 即y 2=（x 2－t ）3－（x 2－t ）+ s ，可知点B 2（x 2，y 2）在曲线C 1上. 反过来，同样可以证明，在曲线C 1上的点关于点A 的对称点在曲线C 上. 因此，曲线C 与C 1关于点A 对称.Ⅲ．证明：因为曲线C 与C 1有且仅有一个公共点，所以，方程组⎪⎩⎪⎨⎧+---=-=st x t x y xx y )()(33有且仅有一组解.消去y ，整理得3tx 2－3t 2x +（t 3－t －s ）=0，这个关于x 的一元二次方程有且仅有一个根.所以t ≠0并且其根的判别式Δ=9t 4－12t （t 3－t －s ）=0.⎩⎨⎧=--≠.0)44(,03s t t t t 所以 t t s -=43且 t ≠0.25．本小题主要考查等差数列基本概念及其通项求法，考查对数函数性质，考查归纳、推理能力以及用数学归纳法进行论证的能力.解：Ⅰ．设数列{b n }的公差为d ，由题意得⎪⎩⎪⎨⎧=-+=.1452)110(1010,111d b b 解得⎩⎨⎧==.3,11d b 所以 b n =3n －2.Ⅱ．由b n =3n －2，知S n =log a （1+1）+ log a （1+41）+…+ log a （1+231-n ）= log a [（1+1）（1+41） (1)231-n ）]，31log a b n +1= log a 313+n . 因此要比较S n 与31log a b n +1的大小，可先比较（1+1）（1+41）……（1+231-n ）与313+n 的大小.取n =1有（1+1）>3113+⋅， 取n =2有（1+1）（1+41）>3123+⋅， ……由此推测（1+1）（1+41）……（1+231-n ）>313+n . ① 若①式成立，则由对数函数性质可断定：当a >1时，S n >31log a b n +1. 当0<a <1时，S n <31log a b n +1.下面用数学归纳法证明①式. （ⅰ）当n =1时已验证①式成立.（ⅱ）假设当n =k （k ≥1）时，①式成立，即（1+1）（1+41）……（1+231-k ）>313+k . 那么，当n =k +1时，（1+1）（1+41）……（1+231-k ）（1+()2131-+k ）>313+k （1+131+k ）=13133++k k （3k +2）.第 11 页 (共 11 页)110988818.doc 因为()[]333343231313+-⎥⎦⎤⎢⎣⎡+++k k k k ()()()()22313134323+++-+=k k k k ()013492>++=k k ， 所以13133++k k （3k +2）>().1134333++=+k k 因而（1+1）（1+41）……（1+231-k ）（1+131+k ）>().1133++k 这就是说①式当n=k +1时也成立. 由（ⅰ），（ⅱ）知①式对任何正整数n 都成立. 由此证得：当a >1时，S n >31log a b n +1. 当0<a <1时，S n <31log a b n +1.。
1988-1998年高考理科数学试题
D /C /B/A /D CB A 1988年普通高等学校招生全国统一考试理科数学试题 满分120分，120分钟一、（本题满分45分）本题共有15个小题，每小题都给出代号为A ，B ，C ，D 的四个结论，其中只有一个结论是正确的，把你认为正确结论的代号写在题后的圆括号内.1.211i i -⎛⎫ ⎪+⎝⎭的值等于 A.1 B.-1 C.i D.i -2.设圆M 的方程为22(3)(2)2x y -+-=,直线l 的方程为30x y +-=,点P 的坐标为(2,1)，那么A.点P 在直线l 上，但不在圆M 上B.点P 在圆M 上，但不在直线l 上C.点P 既在圆M 上，又在直线l 上D.点P 既不在直线l 上，也不在圆M 上3.集合{}1,2,3的子集共有A.7个B.8个C.6个D.5个 4.已知双曲线方程15y 20x 22=-，那么它的焦距是A.10B.5C.15D.1525.在10(x 的展开式中，6x 的系数是 A.610C 27- B.410C 27 C.610C 9- D.410C 9 6.函数44cos sin y x x =-的最小正周期是A.πB.π2C.2πD.π47.方程24cos 30x x -+=的解集是A.{|(1),}6kx x k k Z ππ=+-⋅∈B.{|(1),}3k x x k k Z ππ=+-⋅∈C.{|2,}6x x k k Z ππ=±∈D.{|2,}3x x k k Z ππ=±∈8.极坐标方程432cos ρθ=-所表示的曲线是A.圆B.双曲线右支C.抛物线D.椭圆 9.如图，正四棱台中，A D ''所在的直线与BB '所在的直线是 A.相交直线 B.平行直线C.不互相垂直的异面直线D.互相垂直的异面直线10.1tan(arctan arctan 3)5+的值等于 A.4 B.21 C.81D.811.设命题甲：△ABC 的一个内角为600命题乙：△ABC 的三内角的度数成等差数列数列那么A.甲是乙的充分条件，但不是必要条件B.甲是乙的必要条件，但不是充分条件C.甲是乙的充要条件D.甲不是乙的充分条件，也不是乙的必要条件12.在复平面内，若复数z 满足|1||z z i +=-，则z 所对应的点Z 的集合构成的图形是A.圆B.直线C.椭圆D.双曲线 13.如果曲线222210x y x y ----=经过平移坐标轴后的新方程为221x y ''-=，那么新坐标系的原点在原坐标系中的坐标为 A.(1,1) B.(1,1)-- C.(1,1)- D.(1,1)- 14.假设在200件产品中有3件次品，现在从中任意抽取5件，其中至少有2件次品的抽法有A.233197C C 种 B.233231973197C C C C +种 C.55200197C C -种 D.5142003197C C C -种15.已知二面角AB αβ--的平面角是锐角，C 是平面α内一 点（它不在棱AB 上）， 点D 是点C 在面βl D A y xO S A B C D SF A C ED 上的射影，点E 是棱 AB 上满足CEB ∠为锐角的任一点，那么 A.CEB DEB ∠>∠ B.CEB DEB ∠=∠ C.CEB DEB ∠<∠D.CEB ∠与DEB ∠的大小关系不能确定 二．（本题满分20分）本题共5小题，每一个小题满分4分只要求直接写出结果1.i 的模和辐角的主值．2.解方程192327.xx---⋅=3.已知37sin ,352πθπθ=-<<，求tan2θ的值． 4.如图，四棱锥S ABCD -的底面是边长为1的正方形，侧棱SB 垂直于底面，并且SB =α 表示∠ASD ，求sin α的值．5.已知等比数列{}n a 的公比1q >，并且1(0)a b b =≠，求．123678lim nn n a a a a a a a a →∞++++++． 三、（本题满分10分） 已知tan x a =，求3sin sin 33cos cos3x xx x++的值．四、（本题满分10分）如图，正三棱锥S ABC -的侧面是边长为a 的正三角形，D 是SA 的中点，E 是BC 的中点，求△SDE 绕直线SE 旋转一周所得的旋转体的体积．五、（本题满分11分） 设0,1,0a a t >≠>，比较1l o g 2a t 与1log 2at +的大小，并证明你的结论． 六、本题满分12分）本题共2小题，第（1）小题满分4分，第（2）小题满分8分.给定实数,0a a ≠，且1a ≠，设函数1(1x y x R ax -=∈-且1x a≠） 证明：（1）经过这个函数图象上任意两个不同的点的直线不平行 于x 轴；（2）这个函数的图象关于直线y x =成轴对称图形．七、本题满分12分） 如图，直线l 的方程为2px =-，其中0P >，椭圆的中心为(2,0)2pD +，焦点在x 轴上，长半轴长为2，短半轴长为1，它的一个顶点为(2pA 问p 在哪个范围内取值时，椭圆上有四个不同的点，它们中每一个点到点A 的距离等于该点到直线l 的距离．1989年普通高等学校招生全国统一考试理科数学试题 满分120分，120分钟一、选择题（本题满分36分，共12个小题，每小题3分） 1．1.如果{,,,,},{,,}I a b c d e M a c d ==,{,,}N b d e =，其中I 是全集，那么M N等于A.φB.{d }C.{,a c }D.{,b e } 2．与函数y x =有相同图象的一个函数是A.y =2xy x=C.log (0,1)a xy aa a =>≠D.log (0,1)x a y a a a =>≠3．如果圆锥的底面半径为2，高为2，那么它的侧面积是A.π34B.π22C.π32D.π24 4．43cos[sin()cos()]55arc arc ---的值等于A.-1B.257-C.257D.510- 5．已知{}n a 是等比数列，如果12318a a a ++=，2349a a a ++=-，且12n n S a a a =+++，那么lim n n S →∞的值等于 A.8 B.16 C.32 D.486．如果15|cos |,352θπθπ=<<，那么sin 2θ的值等于A.510-B.510C.515-D.5157．设复数z 满足关系式||2z z i +=+，那么z 等于A.34i -+B.34i - C.34i -- D.34i +8．已知球的两个平行截面的面积分别为5π和8π，它们位于球心的同一侧，且相距为1，那么这个球的半径是 A.4 B.3 C.2 D.59．已知椭圆的极坐标方程是532cos ρθ=-，那么它的短轴长是A.310 B.5 C.52 D.32 10．如果双曲线2216436x y -=上一点P 到它的右焦点的距离是8，那么点P 到它的右准线的距离是A.10B.7732 C.72 D.53211．已知2()82f x x x =+-，如果2()(2)g x f x =-，那么()g x A.在区间(1,0)-上是减函数 B.在区间(0,1)上是减函数 C.在区间(2,0)-上是增函数 D.在区间(0,2)上是增函数12．由数字1，2，3，4，5组成没有重复数字的五位数，其中小于50000的偶数共有A.60个B.48个C.36个D.24个 二、填空题（本题满分24分，共6个小题，每一个小题满分4分）13．方程sin x x = _________________14．不等式2|3|4x x ->的解集是_____15．函数11x x e y e -=+的反函数的定义域是_____________16．已知7270127(12)x a a x a x a x -=++++，那么127a a a +++=____17．已知A 和B 是两个命题，如果A 是B 的充分条件，那么B 是A 的_______条件;A 是B 的______条件 18．如图，已知圆柱的底面 半径是3，高是4，A ，B 两点分别在两底面的圆周上， 并且AB =5，那么直线AB 与轴OO '之间的距离等于 ________________三、解答题（本题满分60分，共6个小题.） 19．（本小题满分8分）证明：32sin 22cos cos 2x x xtg tg x x-=+. 20、（本小题满分10分）如图，在平行六面体1111ABCD A BC D -中，已知15,4,3AB AD AA ===，AB ⊥AD ，∠1AA B =∠1A AD =.3π（Ⅰ）求证：顶点1A 在底面ABCD 上的射影O 在∠BAD 的平分线上;（Ⅱ）求这个平行六面体的体积. 21、（本小题满分10分）自点)3,3(-A 出发的光线l 射到x 轴上，被x 轴反射，其反射光线所在直线与圆074422=+--+y x y x 相切，求入射光线l 所在的直线方程．22、（本小题满分12分）已知0,1a a >≠，试求使方程222log ()log ()a a x ak x a -=-有解的k 的取值范围. 23、（本小题满分10分）是否存在常数,,a b c 使得等式2221223(1)n n ⋅+⋅+++ 2(1)()12n n an bn c +=++对一切自然数n都成立？并证明你的结论. 24、（本小题满分10分）设()f x 是定义在区间(,)-∞+∞上以2为周期的函数，对k Z ∈,用k I 表示区间(21,21]k k -+，已知当0x I ∈时，2()f x x =.（1）求()f x 在k I 上的解析表达式;（2）对自然数k ,求集合{|k M a =使方程()f x ax =在k I 上有两个不相等的实根}.1990年普通高等学校招生全国统一考试数学（理工农医类） 满分120分，120分钟一、选择题:（共45分）在每小题给出的四个选项中,只有一项是符合题目要求的,把所选项前的字母填在题后括号内. 1.方程3log 124x=的解是A.19x = B.x = CD .9x =2.把复数1i +对应的向量按顺时针方向旋转23π，所得到的向量对应的复数是A.1122-+ B .1122-+--+C.1122-++D.1122--+3.如果轴截面为正方形的圆柱的侧面积是S ,那么圆柱的体积等于CD4.方程sin 2sin x x =在区间()0,2π内的解的个数是A.1 B .2 C .3 D .4.已知上图是函数2s i n (y x ωϕ=+ 2πϕ⎛⎫< ⎪⎝⎭的图象，那么A.10,116πωϕ== B .10,116πωϕ==- C .2,6πωϕ==D .2,6πωϕ==-6.函数c o s c ot s i n t a n s i n c o s t a n c o tx x x x y x x x x =+++的值域是A.{2,4}- B . {2,0,4}- C .{2,0,2,4}- D .{4,2,0,4}--7．如果直线2y ax =+与直线3y x b =-关于直线y x =称,那么 A.1,63a b == B .1,63a b ==- C . 3,6a b ==- D . 3,6a b == 8．极坐标方程24sin 52θρ=表示的曲线是A.圆 B .椭圆 C .双曲线的一支 D .抛物线9．设全集{}I=(,),R x y x y ∈，集合3(,)12y M x y x ⎧-⎫==⎨⎬-⎩⎭，{}(,)1N x y y x =≠+，那么M N 等于A.12 B .{(2,3)} C . (2,3) D .{}(,)1x y y x =+ 10．如果实数满足等式22(2)3x y -+=，那么yx的最大值是 A.12 BCD11．如图,正三棱锥S ABC -的侧棱与底面边长相 等,如果,E F 分别为,SC AB 的中点,那么 异面直线EF 与SA所成的角等于A.90° B .60° C .45° D .30°12．已知0h >.设命题甲为:两个实数,a b 满足2a b h -<;命题乙为:两个实数,a b 满足1a h -<且1b h -<.那么A.甲是乙的充分条件,但不是乙的必要条件B .甲是乙的必要条件,但不是乙的充分条件C .甲是乙的充分条件D .甲不是乙的充分条件,也不是乙的必要条件13．,,,,A B C D E 五人并排站成一排,如果B 必须站在A 的右边（,A B 可以不相邻）,那么不同的排法共有A.24种 B .60种 C .90种 D .120种 14．以一个正方体的顶点为顶点的四面体共有A.70个 B .64个 C .58个 D .52个 15．设函数arctan y x =的图象沿x 轴正方向平移2个单位所得到的图象为C .又设图象C '与C 关于原点对称,那么C '所对应的函数是A.arctan(2)y x =-- B .arctan(2)y x =-C .arctan(2)y x =-+D .arctan(2)y x =+二、填空题: （本题满分15分，共5个小题，每一个小题满分3分）把答案填在题中横线上. 16．双曲线221169x y-=的准线方程是 17．234(1)(1)(1)(1)x x x x ---+---5(1)x +-的展开式中, 2x 的系数等于 ．18．已知{}n a 是公差不为零的等差数列,如果n S 是{}n a 的前n 项的和,那么l i m n n nn aS →+∞= ． 19．函数sin cos sin cosy x x x x =++的最大值是 ．20．如图,三棱柱111ABC A B C -中,若,E F 分别为,AB AC 的中点,平面11EB C F 将三棱柱分成体积为12,V V 的两部分,那么V :2V ＝ ．三、解答题（本题满分60分，共6个小题.） 21．（本小题满分8分）有四个数,其中前三个数成等差数列,后三个数成等比数列,并且第一个数与第四个数的和是16,第二个数与第三个数的和是12.求这四个数. 22．（本小题满分10分） 已知11sin sin ,cos cos 43αβαβ+=+=，求t an()αβ+的值23．（本小题满分10分）如图,在三棱锥S ABC -中， SA ⊥底面ABC ，AB BC ⊥，DE 垂直平分SC ，且分别交AC ，SC 于,D E ，又SA AB =，SB BC =，求以BD 为棱,以BDE 与BDC 为面的二面角的度数.24．（本小题满分10分）设0a ≥，在复数集C 中解方程22z z a +=.25．（本小题满分10分）设椭圆的中心是坐标原点，长轴在x轴上，离心率e =已知点30,2P ⎛⎫⎪⎝⎭到这个椭圆上的点的最远求这个椭圆的方程，并求椭圆上到点P.26．（本小题满分12分）12(1)()lg x x x n n af x n+++-+=，其中a 是实数，n 是任意自然数，且2n ≥ (Ⅰ)如果()f x 当(,1]x ∈-∞时有意义,求a 的取值范围;(Ⅱ)如果(0,1]a ∈,证明2()(2)f x f x <当0x ≠时成立.1991年普通高等学校招生全国统一考试数学(理工农医类)本试卷共120分．考试时间120分钟． 一、选择题：本大题共15小题；每小题3分，共45分. 1.已知4sin 5α=，并且α是第二象限的角，那么tan α的值等于A .34-B .43- C .43 D .342.焦点在(1,0)-，顶点在(1,0)的抛物线方程是A .28(1)y x =+B .28(1)y x =-+C .28(1)y x =-D .28(1)y x =-- 3．函数44cos sin y x x =-的最小正周期是 A .2πB .πC .2πD .4π 4.如果把两条异面直线看成“一对”，那么六棱锥的棱所在的12条直线中，异面直线共有( )A .12对B .24对C .36对D .48对 5.函数5sin 22y x π⎛⎫=+ ⎪⎝⎭)的图像的一条对称轴的方程是 A .2x π=-B .4x π=-C . 8π=x D .45π=x6.如果三棱锥S ABC -的底面是不等边三角形，侧面与底面所成的二面角都相等，且顶点S 在底面的射影O 在△ABC 内，那么O 是△ABC 的A . 垂心B .重心C .外心D .内心 7.已知{}n a 是等比数列，且0n a >，243546225a a a a a a ++=，那么35a a +的值等于A .5B . 10C .15D .208.如果圆锥曲线的极坐标方程为1653cos ρθ=-，那么它的焦点的极坐标为A . (0,0),(6,)πB .(3,0),(3,0)-C .(0,0),(3,0)D .(0,0),(6,0)9.从4台甲型和5台乙型电视机中任意取出3台，其中至少要有甲型与乙型电视机各1台，则不同的取法共有A . 140种B .84种C .70种D .35种 10.如果0AC <，且0BC <，那么直线0Ax By C ++=不通过A . 第一象限B .第二象限C .第三象限D . 第四象限 11.设甲、乙、丙是三个命题．如果甲是乙的必要条件；丙是乙的充分条件但不是乙的必要条件，那么A .丙是甲的充分条件，但不是甲的必要条件B .丙是甲的必要条件，但不是甲的充分条件C .丙是甲的充要条件D .丙不是甲的充分条件，也不是甲的必要条件12.111lim[(1)(1)(1)345n n →∞--- (1)21+n )]的值等于 A . 0 B . 1 C .2 D .313.如果奇函数()f x 在区间[3,7]上是增函数且最小值为5，那么()f x 在区间[7,3]--上是A .增函数且最小值为－5B .增函数且最大值为－5C .减函数且最小值为－5D .减函数且最大值为－514.圆222430x x y y +++-=上到直线10x y ++=的距离为2的点共有A .1个B .2个C .3个D .4个15.设全集为R ，()sin f x x =，()cos g x x =，{()0},{()0}M x f x N x g x =≠=≠，那么集合{()()0}x f x g x =等于 A .N M ⋂ B .N MC .N MD .N M二、填空题：本大题共5小题；每小题3分，共15分．把答案填在题中横线上.16.11arctanarctan 32+的值是________. 17.不等式2261x x +-<的解集是________.18.已知正三棱台上底面边长为2，下底面边长为4，且侧棱与底面所成的角是45°，那么这个正三棱台的体积等于 . 19.7(1)ax +的展开式中，3x 的系数是2x的系数与4x 的系数的等差中项．若实数1a >，那么a = .20.在球面上有四个点,,,P A B C ，如果,,PA PB PC 两两互相垂直，且PA PB PC a ===．那么这个球面的面积是 .三、解答题：本大题共6小题；共60分． 21. (本小题满分8分)求函数22sin 2sin cos 3cos y x x x x =++的最小值，并写出使函数y 取最小值的x 的集合．22. (本小题满分8分)已知复数1z i =+, 求复数1632++-z z z 的模和辐角的主值． 23. (本小题满分10分)已知ABCD 是边长为4的正方形，,E F 分别是,AB AD 的中点，CG 垂直于ABCD 所在的平面，且2CG =．求点B 到平面EFG 的距离．24. (本小题满分10分)根据函数单调性的定义，证明函数3()1f x x =-+在(),-∞+∞上是减函数．25. (本小题满分12分)已知n 为自然数，实数1a >，解关于x 的不等式23log 4log 12log a a a x x x -++121(2)(2)log log ()3n nn a a n x x a ---+->-26. (本小题满分12分)双曲线的中心在坐标原点O ，焦点在x 轴上，过双曲线右焦点且斜率为53的直线交双曲线于,P Q 两点．若OP OQ ⊥，4PQ =，求双曲线的方程．NABCD 1C 1B 1A 1MD1992年普通高等学校招生全国统一考试数学(理工农医类)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．共120分．考试时间120分钟． 一、选择题：本大题共18小题；每小题3分，共54分．1.3log 9log 28的值是 A .32 B .1 C .23D .22.如果函数sin cos y x x ωω=的最小正周期是4π，那么常数ω为A . 4B .2C .21D .413.极坐标方程分别是cos ρθ=和sin ρθ=的两个圆的圆心距是A . 2B .2C .1D .224.方程s i n 4c o s 5c o s 4s i n xx x x =-的一个解是A . 10°B .20°C . 50°D .70° 5.已知轴截面是正方形的圆柱的高与球的直径相等，则圆柱的全面积与球的表面积的比是A . 6：5B .5：4C .4：3D .3：2 6.图中曲线是幂函数ny x =在第一象限的图像．已知n 取±2，±21四个值，则相应于曲线1234,,,c c c c 的n 依次为A .112222--，，， B .112222--，，， C .112222--，，， D .112222--，，， 7.若log 2log 20a b <<，则A .01a b <<<B . 01b a <<<C .1b a <<D .1a b << ( )8.直线 ⎪⎩⎪⎨⎧⋅-=+⋅=20cos 320sin t y t x (t 为参数)的倾斜角是A . 20°B .)70°C .110°D .160° 9.在四棱锥的四个侧面中，直角三角形最多可有A . 1个B .2个C .3个D .4个 10.圆心在抛物线22y x =上，且与x 轴和该抛物线的准线都相切的一个圆的方程是A . 221202x y x y +---= B .22210x y x y ++-+=C .22210x y x y +--+=D . 221204x y x y +--+= 11.在25(32)x x ++的展开式中x 的系数为A . 160B .240C .360D .800 12.若01a <<，在[]0,2π上满足sin x a ≥的x 的范围是A . []0,arcsin aB . []arcsin ,arcsin a a π-C .[]arcsin ,a ππ-D .arcsin ,arcsin 2a a π⎡⎤+⎢⎥⎣⎦13.已知直线1l 和2l 夹角的平分线为y x =，如果1l 的方程是0ax by c ++=(0)ab >，那么2l 的方程是A . 0bx ay c ++=B . 0ax by c -+=C .0bx ay c +-=D .0bx ay c -+=14.在棱长为1的正方体1111ABCD A BC D - 中，M 和N 分别为 11A B 和1BB 的中点， 那么直线AM 与CN 所成角的余弦值是A . 23B .1010C .53D . 5215.已知复数z 的模为2，则|z i -|的最大值为A . 1B .2C .5D . 316.函数2x xe e y --=的反函数( ) A .是奇函数，它在(0,)+∞上是减函数 B .是偶函数，它在(0,)+∞上是减函数 C .是奇函数，它在(0,)+∞上是增函数 D .是偶函数，它在(0,)+∞上是增函数17.如果函数2()f x x bx c =++对任意实数t 都有(2)(2)f t f t +=-，那么 A . (2)(1)(4)f f f << B .(1)(2)(4)f f f << C .(2)(4)(1)f f f <<D .(4)(2)(1)f f f << 18.长方体的全面积为11，十二条棱长度之和为24，则这个长方体的一条对角线长为 A . 32 B .14 C .5 D .6二、填空题：本大题共5小题；每小题3分，共15分．把答案填在题中横线上．19.方程33131=++-xx的解是________. 20.sin15sin 75︒︒的值是 .21.设含有10个元素的集合的全部子集数为S ，其中由3个元素组成的子集数为T ，则ST的值为___________________. 22.焦点为1(2,0)F -和2(6,0)F ，离心率为2的双曲线的方程是__________. 23.已知等差数列{}n a 的公差0d ≠，且139,,a a a 成等比数列，则1042931a a a a a a ++++的值是____________________.三、解答题：本大题共5小题；共51分.解答应写出文字说明、演算步骤.24. (本小题满分9分)已知z ∈C ，解方程z z －3i z =1+3i ．25. (本小题满分10分) 已知432παβπ<<<，12cos()13αβ-=，3sin()5αβ+=-．求sin 2α的值．26. (本小题满分10分)已知：两条异面直线,a b 所成的角为θ，它们的公垂线段1AA 的长度为d ．在直线,a b 上分别取点,E F ，设1A E m =，AF n =．求证：EF =27. (本小题满分10分)设等差数列{}n a 的前n 项和为n S ．已知3121312,0,0a S S =><． (Ⅰ)求公差d 的取值范围．(Ⅱ)指出1212,,,S S S 中哪一个值最大，并说明理由．28. (本小题满分12分)已知椭圆22221(0)x y a b a b+=>> ， ,A B是椭圆上的两点，线段AB 的垂直平分线与x 轴相交于点0(,0)P x ．证明ab a x a b a 22022-<<--．1993年普通高等学校招生全国统一考试数学(理工农医类)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．共150分，考试时间120分钟．第Ⅰ卷(选择题共68分)一、选择题：本大题共17小题；每小题4分，共68分．在每小题给出的四个选项中，只有一项是符合题目要求的1.函数()sin cos f x x x =+的最小正周期是( ) A .2π B .π22 C .π D .4π 2．如果双曲线的焦距为6，两条准线间的距离为4，那么该双曲线的离心率为 ( )A .23 B .23 C . 26 D .2 3．和直线3x －4y +5=0关于x 轴对称的直线的方程为( )A .3x +4y －5=0B . 3x +4y +5=0C .－3x +4y －5=0D .－3x +4y +5=0 4．极坐标方程435cos ρθ=-所表示的曲线是( ) A . 焦点到准线距离为54的椭圆 B .焦点到准线距离为54的双曲线右支 C .焦点到准线距离为34的椭圆D .焦点到准线距离为34的双曲线右支5．53x y =在[－1，1]上是 ( ) A .增函数且是奇函数 B .增函数且是偶函数 C .减函数且是奇函数 D .减函数且是偶函数6．5215lim22+--∞→n n n n 的值为( )A .51-B . 25- C .51 D .257．集合{|}24k M x x k Z ππ==+∈，， {|}42k N x x k Z ππ==+∈，，则 A . M =N B .N M ⊃ C .N M ⊂ D .=⋂N M Ø 8．sin20ºcos70º+sin10ºsin50º的值是A .41 B .23 C . 21 D .43 9．参数方程()⎪⎪⎩⎪⎪⎨⎧+=+=θθθsin 1212sin 2cos y x()πθ20<<表示A . 双曲线的一支，这支过点⎪⎭⎫⎝⎛211，B .抛物线的一部分，这部分过⎪⎭⎫⎝⎛211， C .双曲线的一支，这支过点⎪⎭⎫ ⎝⎛-211，D .抛物线的一部分，这部分过⎪⎭⎫ ⎝⎛-211， 10．若,a b 是任意实数，且a b >，则A .22a b > B .1<abC .lg()0a b ->D .ba ⎪⎭⎫⎝⎛<⎪⎭⎫ ⎝⎛212111．一动圆与两圆221x y +=和228120x y x +-+=都外切，则动圆圆心轨迹为 A .圆 B .椭圆 C .双曲线的一支 D .抛物线12．圆柱轴截面的周长l 为定值，那么圆柱体积的最大值是A . π36⎪⎭⎫⎝⎛l B .π3291⎪⎭⎫ ⎝⎛l C .π34⎪⎭⎫ ⎝⎛l D .π342⎪⎭⎫⎝⎛l 13．(x +1)4(x －1)5展开式中x 4的系数为A . －40B .10C . 40D .45 14．直角梯形的一个内角为45º，下底长为上底长的23，这个梯形绕下底所在的直线旋转一周所成的旋转体的全面积为(5π+，则旋转体的体积为( ) A . 2π B .π324+ C .π325+ D .π3715．已知a 1，a 2，…，a 8为各项都大于零的等比数列，公式q ≠1，则( ) A .a 1+ a 8> a 4+ a 5 B . a 1+ a 8< a 4+ a 5 C .a 1+ a 8= a 4+ a 5 D .a 1+ a 8和a 4+ a 5的大小关系不能由已知条件确定 16．设有如下三个命题：甲：相交两直线l ，m 都在平面α内，并且都不在平面β内． 乙：l ，m 之中至少有一条与β相交．丙：α与β相交．当甲成立时A . 乙是丙的充分而不必要的条件B .乙是丙的必要而不充分的条件C .乙是丙的充分且必要的条件D .乙既不是丙的充分条件又不是丙的必要条件17．将数字1，2，3，4填入标号为1，2，3，4的四个方格里，每格填一个数字，则每个方格的标号与所填的数字均不相同的填法有( ) A . 6种 B . 9种C .11种 D .23种第Ⅱ卷(非选择题共82分)二、填空题：本大题共6小题；每小题4分，共24分．把答案填在题中横线上．18．⎪⎭⎫ ⎝⎛+31arccos 21arccos sin = _______.19．若双曲线222249k y k x -=1与圆221x y +=没有公共点，则实数k 的取值范围为_________________.20．从1，2，…，10这十个数中取出四个数，使它们的和为奇数，共有______________种取法(用数字作答)．21．设1()42x x f x +=-，则1(0)f -=__. 22．建造一个容积为8m 3 ，深为2m 的长方体无盖水池．如果池底和池壁的造价每平方米分别为120元和80元，那么水池的最低总造价为________________元. 23．如图，ABCD 是正方形，E 是AB 的中点，如将△DAE 和△CBE 分别沿虚线DE 和CE 折起，使AE 与BE 重合，记A 与B 重合后的点为P ，则面PCD 与面ECD 所成的二面角为__________度.三、解答题：本大题共5小题；共58分．解题应写出文字说明、演算步骤． 24．(本小题满分10分)已知1()log (0,1)1axf x a a x+=>≠-．(Ⅰ)求()f x 的定义域；(Ⅱ)判断()f x 的奇偶性并予以证明；(Ⅲ)求使()0f x >的x 取值范围．25．(本小题满分12分)已知数列()()2222228182813352121nn n ⋅⋅⋅⋅-+，，，，. n S 为其前n 项和．计算得123482448809254981S S S S ====，，，，….观察上述结果，推测出计算n S 的公式，并用数学归纳法加以证明． 26．(本小题满分12分) 已知：平面α∩平面β=直线a ．α，β同垂直于平面γ，又同平行于直线b ． 求证：(Ⅰ) a ⊥γ；(Ⅱ)b ⊥γ．PM b a βα27．(本小题满分12分)在面积为1的PMN ∆中，1tan 2PMN ∠=，tan 2MNP ∠=-．建立适当的坐标系，求以M ，N 为焦点且过点P 的椭圆方程．28．(本小题满分12分) 设复数()πθθθ<<+=0si n c o s i z ，()4411zz+-=ω，并且33=ω，2arg πω<，求θ．1994年普通高等学校招生全国统一考试数学(理工农医类)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．共150分，考试时间120分钟．第Ⅰ卷(选择题共65分)一、选择题：本大题共15小题；第(1)—(10)题每小题4分，第(11)—(15)题每小题5分，共65分，在每小题给出的四个选项中，只有一项是符合题目要求的1.设全集{0,1,2I =，集合{0,1,2A =，集合{2,3,4}B =，则A BA .{0}B .{0,1}C .{0,1,4}D .{0,1,2,3,4}2.如果方程222x ky +=表示焦点在y 轴上的椭圆，那么实数k 的取值范围是A .()0,+∞B .()0,2C .()1,+∞D .()0,1 3.极坐标方程cos 4πρθ⎛⎫=-⎪⎝⎭所表示的曲线是A .双曲线B .椭圆C .抛物线D .圆 4.设θ是第二象限的角，则必有 A .tgctg22θθ> B . 2ctg2tg θθ<C .2cos2sinθθ> D .2cos2sinθθ<5.某种细菌在培养过程中，每20分钟分裂一次(一个分裂为两个)．经过3小时，这种细菌由1个可繁殖成A .511个B . 512个C .1023个D .1024个6.在下列函数中，以2π为周期的函数是 ( )A .sin 2cos 4y x x =+B .sin 2cos 4y x =C .sin 2cos 2y x x =+D .sin 2cos 2y x x =7.已知正六棱台的上、下底面边长分别为2和4，高为2，则其体积为A .323B . 283C .243D . 2038.设F 1和F 2为双曲线2214x y -=的两个焦点，点P 在双曲线上且满足1290F PF ∠=︒，则△12F PF 的面积是A .1B .25C .2D .5 9.如果复数z 满足2z i z i ++-=，那么1z i ++的最小值是A .1B . 2C .2D . 510.有甲、乙、丙三项任务，甲需2人承担，乙、丙各需1人承担．从10人中选派4人承担这三项任务，不同的选法共有 A .1260种 B . 2025种 C . 2520种 D . 5040种 11.对于直线m ，n 和平面,αβ，αβ⊥的一个充分条件是 A .m ⊥n ，m ∥α，n ∥β B . m ⊥n ，α∩β=m ，n ⊂α C . m ∥n ，n ⊥β，m ⊂α D .m ∥n ，m ⊥α，n ⊥β12.设函数()110)f x x =-≤≤，则函数1()y f x -=的图像是A .B .C .D . 13.已知过球面上A ，B ，C 三点的截面和球心的距离等于球半径的一半，且2AB BC CA ===，则球面面积是A .169π B . 83π C .4π D .649π14.函数2r c c o s (s i n )33y a x x ππ⎛⎫=-<< ⎪⎝⎭的值域是 A .⎪⎭⎫⎝⎛656ππ， B .⎪⎭⎫⎢⎣⎡650π，C .⎪⎭⎫⎝⎛323ππ， D .⎪⎭⎫⎢⎣⎡326ππ， 15.定义在(),-∞+∞上的任意函数()f x 都可以表示成一个奇函数()g x 和一个偶函数()h x 之和，如果()()lg(101)(,)x f x x =+∈-∞+∞，那么A .(),()lg(10102)x x g x x h x -==++B .1()lg(101)2x g x x ⎡⎤=++⎣⎦, 1()lg(101)2x h x x ⎡⎤=+-⎣⎦ C .(),()lg(101)22xx x g x h x ==+-D .(),()lg(101)22xx x g x h x =-=++第Ⅱ卷(非选择题共85分)二、填空题 (本大题共5小题，共6个空格；每空格4分，共24分．把答案填在题中横线上)16.在()73x -的展开式中，5x 的系数是(用数字作答) .17.抛物线284y x =-的准线方程是 ，圆心在该抛物线的顶点且与其准线相切的圆的方程是_____. 18.已知1sin cos ((0,))5θθθπ+=∈，则ctg θ的值是_____________.19.设圆锥底面圆周上两点A ，B 间的距离为2，圆锥顶点到直线AB 的距离为3，AB 和圆锥的轴的距离为1，则该圆锥的体积为_________.20.在测量某物理量的过程中，因仪器和观察的误差，使得n 次测量分别得到a 1，a 2，…，a n 共n 个数据，我们规定所测量物理量的“最佳近似值” a 是这样一个量：与其他近似值比较，a 与各数据的差的平方和最小．依此规定，从a 1，a 2，…，a n 推出的a = ____.三、解答题(本大题共5小题，共61分；解答应写出文字说明、证明过程或推演步骤) 21. (本小题满分11分)已知1z i =+．(1)设234z z ω=+-，求ω的三角形式； (2)如果2211z az bi z z ++=--+，求实数,a b 的值．22. (本小题满分12分) 已知函数()tan ,0,2f x x x π⎛⎫=∈ ⎪⎝⎭．若 12,0,2x x π⎛⎫∈ ⎪⎝⎭，且12x x ≠，证明[]12121()()()22x x f x f x f ++>23. (本小题满分12分)如图，已知A 1B 1C 1－ABC 是正三棱柱，D 是AC 中点．(1)证明AB 1∥平面DBC 1； (2)假设AB 1⊥BC 1，求以BC 1为棱，DBC 1与CBC 1为面的二面角α的度数．24. (本小题满分12分)已知直线l 过坐标原点，抛物线C 顶点在原点，焦点在x 轴正半轴上．若点)0,1(-A 和点B (0，8)关于l 的对称点都在C 上，求直线l 和抛物线C 的方程．25. (本小题满分14分)设{}n a 是正数组成的数列，其前n 项和为n S ，并且对于所有的自然数n ，n a 与2的等差中项等于n S 与2的等比中项．(1)写出数列{}n a 的前3项；(2)求数列{}n a 的通项公式(写出推证过程)； (3)令()1112n n n n n a a b n a a ++⎛⎫=+∈ ⎪⎝⎭N ，求()12lim .n n b b b n →∞+++-1995年普通高等学校招生全国统一考试数学(理工农医类)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．满分150分，考试时间120分． 第Ⅰ卷(选择题共65分)一、选择题(本大题共15小题,第1—10题每小题4分，第11—15题每小题5分，共65分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．已知I 为全集，集合M ，N ⊂I ，若 M ∩N =N ，则A .N M ⊇B .N M ⊆C .N M ⊆D .N M ⊇ 2．函数11y x =-+的图像是A ．B ．C ．D ． 3．函数4sin(3)3cos(3)44y x x ππ=+++的最小正周期是 A .π6 B .π2 C .32π D .3π 4．正方体的全面积是2a ，它的顶点都在球面上，这个球的表面积是 A .23a π B .22a π C .22aπD .23a π5．若图中的直线1l ，2l ，3l 的斜率分别为1k ，2k ，3k ，则A .321k k k <<B .213k k k <<C .123k k k <<D .231k k k <<6．在）（31x -10)1(x +的展开式中，5x 的系数是A ．－297B ．－252C .297D ．207 7．使arcsin arccos x x >成立的x 的取值范围是A .⎥⎦⎤⎝⎛220，B .⎥⎦⎤ ⎝⎛122， C .⎪⎪⎭⎫⎢⎣⎡-221， D .[)01，-8．双曲线3322=-y x 的渐近线方程是A .x y 3±=B .x y 31±=C .x y 3±=D .x y 33±=9．已知θ是第三象限角，且95cos sin 44=+θθ，那么sin 2θ等于 A .322 B .322- C .32 D .32-10．已知直线l ⊥平面α，直线m ⊂平面β，有下面四个命题：①α∥β⇒l ⊥m ②α⊥β⇒l ∥m ③l ∥m ⇒α⊥β ④l ⊥m ⇒α∥β 其中正确的两个命题是A .①与②B .③与④C .②与④D .①与③ 11．已知)2(log ax y a -=在[0，1]上是x 的减函数，则a 的取值范围是 A ．(0，1) B . (1，2) C . (0，2) D .[)∞+，2 12．等差数列}{n a ，{}n b 的前n 项和分别为n S 与n T ，若132+=n nT S n n ，则nn n b a ∞→lim 等于 A .1 B .36C .32D .9413．用1，2，3，4，5这五个数字，组成没有重复数字的三位数，其中偶数共 A .24个 B .30个 C .40个 D .60个 14．在极坐标系中，椭圆的二焦点分别在极点和点)0,2(c ，离心率为e ，则它的极坐标方程是A .()θρcos 11e e c --=B ．()θρcos 112e e c --=C .()θρcos 11e e c --=D .()()θρcos 112e e e c --=15．如图，A 1B 1C 1－ABC 是直三棱柱，∠BCA =90°，点D 1，F 1分别是A 1B 1，A 1C 1的中点，若BC =CA =CC 1，则BD 1与AF 1所成的角的余弦值是 A .1030B .21C .1530 D .1015第Ⅱ卷(非选择题，共85分)二、填空题(本大题共5小题，每小题4分，共20分，把答案填在题中横线上) 16．不等式x x 283312-->⎪⎭⎫ ⎝⎛的解集是_____17．已知圆台上、下底面圆周都在球面上，且下底面过球心，母线与底面所成的角为3π，则圆台的体积与球体积之比为_____ 18．函数x x y cos )6sin(π-=的最小值是____________19．直线l 过抛物线)0)(1(2>+=a x a y 的焦点，并且与x 轴垂直，若l 被抛物线截得的线段长为4，则a20．四个不同的小球放入编号为1，2，3，4的四个盒中，则恰有一个空盒的放法共有 __________种(用数字作答)三、解答题(本大题共6小题，共65分．解答应写出文字说明、证明过程或推演步骤) 21．(本小题满分7分)在复平面上，一个正方形的四个顶点按照逆时针方向依次为Z 1，Z 2，Z 3，O (其中O是原点)，已知Z 2对应复数i Z 312+=．求Z 1和Z 3对应的复数． 22．(本小题满分10分)求50cos 20sin 50cos 20sin 22++的值．23．(本小题满分12分) 如图，圆柱的轴截面ABCD 是正方形，点E 在底面的圆周上，AF ⊥DE ，F 是垂足．(1)求证：AF ⊥DB ；(2)如果圆柱与三棱锥D －ABE 的体积的比等于π3，求直线DE 与平面ABCD 所成的角．24．(本小题满分12分)某地为促进淡水鱼养殖业的发展，将价格控制在适当范围内，决定对淡水鱼养殖提供政府补贴．设淡水鱼的市场价格为x 元/千克，政府补贴为t 元/千克．根据市场调查，当148≤≤x 时，淡水鱼的市场日供应量P 千克与市场日需求量Q 千克近似地满足关系： )08)(8(1000≥≥-+=t x t x P ，，)148()8(405002≤≤--=x x Q ． 当Q P =时市场价格称为市场平衡价格．(1)将市场平衡价格表示为政府补贴的函数，并求出函数的定义域；(2)为使市场平衡价格不高于每千克10元，政府补贴至少为每千克多少元?25．(本小题满分12分)设}{n a 是由正数组成的等比数列，n S 是其前n 项和．(1)证明12lg 2lg lg ++<+n n n S S S ；(2)是否存在常数0>c ，使得 ()()()c S c S c S n n n -=-+-++12lg 2lg lg 成立?并证明你的结论．26．(本小题满分12分)已知椭圆1162422=+y x ，直线1812:=+y x l ．P 是l上点，射线OP 交椭圆于点R ，又点Q 在OP 上且满足|OQ |·|OP |=|OR |2，当点P 在l 上移动时，求点Q 的轨迹方程，并说明轨迹是什么曲线．1996年普通高等学校招生全国统一考试数学(理工农医类)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．共150分，考试时间120分钟．第Ⅰ卷(选择题共65分)一、选择题：本大题共15小题，第1—10题每小题4分，第11—15题每小题5分，共65分．1．已知全集N I =，集合 },2|{N n n x x A ∈==，{|4,}B x x n n N ==∈，则A ．B A I =B ．B A I =C ．B A I =D ．B A I =2． 当1>a 时，在同一坐标系中，函数x y a -=与log a y x =的图像A ．B ．C ．D ． 3．若x x 22cos sin >，则x 的取值范围是A ．⎭⎬⎫⎩⎨⎧∈+<<-Z k k x k x ,412432ππππ B ．⎭⎬⎫⎩⎨⎧∈+<<+Z k k x k x ,452412ππππ C ．⎭⎬⎫⎩⎨⎧∈+<<-Z k k x k x ,4141ππππ D ．⎭⎬⎫⎩⎨⎧∈+<<+Z k k x k x ,4341ππππ 4．复数54)31()22(i i -+等于A ．i 31+B ．i 31+-C ．i 31-D ．i 31--5．如果直线l ，m 与平面α，β，γ满足：,//l l βγα=,m α⊂和γ⊥m ，那么必有A ．αγ⊥且m l ⊥B ．αγ⊥且β//mC ．β//m 且m l ⊥D ．//αβ且αγ⊥ 6．当22ππ≤≤-x 时，函数x x x f cos 3sin )(+=的A ．最大值是1，最小值是－1B ．最大值是1，最小值是－21 C ．最大值是2，最小值是－2 D ．最大值是2，最小值是－1 7．椭圆⎩⎨⎧+-=+=ϕϕsin 51,cos 33y x 的两个焦点坐标是A ．(3,5),(3,3)---B ．(3,3),(3,5)-C ．(1,1),(7,1)-D ．(1,1),(7,1)--- 8．若02πα<<，则ar c s i n [c o s ()]2πα++arccos[sin()]πα+=A ．2πB ．2π-C ．απ22-D ．απ22--9．将边长为a 的正方形ABCD 沿对角线AC 折起，使得a BD =，则三棱锥D －ABC的体积为A ．63aB ．123aC ．3123a D ．3122a 10．等比数列{}n a 的首项11-=a ，前n 项和为n S ，若3231510=S S 则n n S ∞→lim 等于 A ．32 B ．－32C ．2D ．－211．椭圆的极坐标方程为θρcos 23-=，则它在短轴上的两个顶点的极坐标是 A ．(3，0)，(1，π) B ． (3，2π)，(3，23π)。
1998年高考数学试题
1998年普通高等学校招生全国统一考试 数学(理工农医类)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分,考试时间120分钟. 第Ⅰ卷(选择题共65分)一、 选择题:本大题共15小题;第(1) (10)题每小题4分,第(11) (15)题每小题5分,共65分,在每小题给出的四个选项中,只有一项是符合题目要求的. (1)设集合M=｛x │0≤x<2｝,集合N=｛x │x 2-2x-3<0｝,集合M ∩N 为 (A)｛x │0≤x<1｝ (B)｛x │0≤x<2｝ (C)｛x │0≤x ≤1｝ (D)｛x │0≤x ≤2｝ [Key] B(2)如果直线ax+2y+2=0与直线3x-y-2=0平行,那么系数a 为32)(23)(6)(3)(D C B A ---[Key] B(3)函数)x 31x 21(tg y -=在一个周期内的图象是[Key] A(4)已知三棱锥D-ABC 的三个则面与底面全等，且AB=AC=3，BC=2，则BC 为棱,以面BCD 与面BCA 为面的二面角的大小是32)D (2)C (31arccos)B (33arccos)A (ππ[Key] C（5）函数x2cos )x 23sin(y +-π=的最小正周期是 ππππ4)D (2)C ()B (2)A ([Key] B(6)满足arccos(1-x)≥arccosx 的x 的取值范围是]1,21)[(]21,0)[(]0,21)[(]21,1)[(D C B A --[Key] D(7)将y=2x 的图象(A)先向左平行移动1个单位 (B)先向右平行移动1个单位 (C)先向上平行移动1个单位 (D)先向下平行移动1个单位 再作关于直线y=x 对称的图象,可得到函数y=log 2(x+1)的图象.[Key] D(8)长方体一个顶点上三条棱的长分别是3,4,5,且它的八个顶点都在同一个球面上,这个球的表面积是ππππ200)(50)(225)(220)(D C B A[Key] C(9)曲线的参数方程⎪⎩⎪⎨⎧-=-=2111t y tx （t 是参数，t ≠0）,它的普通方程是 11)(1)1(1)()1()2()(1)1()1)((2222+-=--=--==--x xy D x y C x x x y B y x A[Key] B(10)函数y=cos 2x-3cosx+2的最小值为6)(41)(0)(2)(D C B A -[Key] B(11)椭圆C 与14)2(9)3(22=-+-y x 椭圆关于直线x+y=0对称，椭圆C 的方程是 (A) 19)3(4)2(22=+++y x (B) 14)3(9)2(22=-+-y x(C) 14)3(9)2(22=+++y x (D) 19)3(4)2(22=-+-y x[Key] A(12)圆台上、下底面积分别为π、4π,侧面积为6π,这个圆台的体积是337)(637)(32)(332)(ππππD C B A[Key] D(13)定义在区间(-∞,+∞)的奇函数f(x)为增函数；偶函数g(x)在区间［0,+∞)的图象与f(x)的图象重合.设a>b>0,给出下列不等式①f(b)-f(-a)>g(a)-g(-b); ②f(b)-f(-a)<g(a)-g(-b); ③f(a)-f(-b)>g(b)-g(-a); ④f(a)-f(-b)<g(b)-g(-a), 其中成立的是(A)①与④ (B)②与③ (C)①与③ (D)②与④ [Key] C（14）不等式组⎪⎩⎪⎨⎧+->+->x x x x x 22330的解集是(){}20<<x x A (){}5.20<<x x B (){}60<<x x C (){}30<<x x D[Key] C(15)四面体的顶点和各棱中点共10个点,在其中取4个不共面的点,不同的取法共有 (A)150种 (B)147种 (C)144种 (D)141种[Key] D(16)已知92⎪⎪⎭⎫⎝⎛-x x a的展开式中x 3的系数为49，常数a 的值为_________. [Key] 4(17)已知直线的极坐标方程22)4sin(=+πθρ则极点到该直线的距离是_______。
高考理科数学试卷普通高等学校招生全国统一考试1998
高考理科数学试卷普通高等学校招生全国统一考试注意事项： 1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷1至3页，第Ⅱ卷3至5页. 2.答题前，考生务必将自己的姓名、准考证号填写在本试题相应的位置. 3.全部答案在答题卡上完成，答在本试题上无效. 4.考试结束后，将本试题和答题卡一并交回.第Ⅰ卷一. 选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的.（1）已知集合{1,}A =2,3，{|(1)(2)0,}B x x x x =+-<∈Z ，则AB =（A ）{1}（B ）{12}，（C ）{0123}，，，（D ）{10123}-，，，， （2）已知(3)(1)i z m m =++-在复平面内对应的点在第四象限，则实数m 的取值范围是（A ）(31)-，（B ）(13)-，（C ）(1,)∞+（D ）(3)∞--，（3）已知向量(1,)(3,2)m =-，=a b ，且()⊥a +b b ，则m= （A ）－8（B ）－6 （C ）6 （D ）8（4）圆2228130x y x y +--+=的圆心到直线10ax y +-=的距离为1，则a= （A ）43-（B ）34-（C ）3（D ）2（5）如图，小明从街道的E 处出发，先到F 处与小红会合，再一起到位于G 处的老年公寓参加志愿者活动，则小明到老年公寓可以选择的最短路径条数为（A ）24 （B ）18 （C ）12 （D ）9（6）右图是由圆柱与圆锥组合而成的几何体的三视图，则该几何体的表面积为（A ）20π（B ）24π（C ）28π（D ）32π（7）若将函数y=2sin 2x 的图像向左平移π12个单位长度，则评议后图象的对称轴为（A ）x=kπ2–π6 (k ∈Z) （B ）x=kπ2+π6 (k ∈Z) （C ）x=kπ2–π12 (k ∈Z) （D ）x=kπ2+π12 (k ∈Z)（8）中国古代有计算多项式值的秦九韶算法，右图是实现该算法的程序框图.执行该程序框图，若输入的x=2，n=2，依次输入的a 为2，2，5，则输出的s=（A ）7 （B ）12 （C ）17 （D ）34 （9）若cos(π4–α)=35，则sin 2α=（A ）725（B ）15（C ）–15（D ）–725（10）从区间[]0,1随机抽取2n 个数1x ,2x ，…，nx ，1y ，2y ，…，ny ，构成n 个数对()11,x y ，()22,x y ，…，(),n n x y ，其中两数的平方和小于1的数对共有m 个，则用随机模拟的方法得到的圆周率π的近似值为（A ）4n m （B ）2n m （C ）4m n （D ）2m n（11）已知F1，F2是双曲线E 22221x y a b-=的左，右焦点，点M 在E 上，M F1与x 轴垂直，sin 2113MF F ∠=,则E 的离心率为（AB ）32（CD ）2 （12）已知函数学.科网()()f x x ∈R 满足()2()f x f x -=-，若函数1x y x+=与()y f x =图像的交点为1122(,),(,),,(,),m m x y x y x y ⋅⋅⋅则1()mi i i x y =+=∑（A ）0 （B ）m （C ）2m （D ）4m第II 卷本卷包括必考题和选考题两部分.第(13)题~第(21)题为必考题，每个试题考生都必须作答.第(22)题~第(24)题为选考题，考生根据要求作答.二、填空题：本大题共3小题，每小题5分(13)△ABC 的内角A 、B 、C 的对边分别为a 、b 、c ，若cos A=45，cos C=513，a=1，则b=. (14)α、β是两个平面，m 、n 是两条直线，有下列四个命题：（1）如果m ⊥n ，m ⊥α，n ∥β，那么α⊥β. （2）如果m ⊥α，n ∥α，那么m ⊥n.（3）如果α∥β，m ⊂α，那么m ∥β. （4）如果m ∥n ，α∥β，那么m 与α所成的角和n 与β所成的角相等.其中正确的命题有.(填写所有正确命题的编号）（15）有三张卡片，分别写有1和2，1和3，2和3。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1998年全国统一高考数学试卷（理科）一、选择题（共15小题，每小题4分，满分60分）1．（4分）（2008•陕西）sin330°等于（）A ．B．C．D．2．（4分）函数y=a|x|（a＞1）的图象是（）A ．B．C．D．3．（4分）曲线的极坐标方程ρ=4cosθ化为直角坐标方程为（）A ．（x+2）2+y2=4B．（x﹣2）2+y2=4C．（x+4）2+y2=16D．（x﹣4）2+y2=164．（4分）两条直线A1x+B1y+C1=0，A2x+B2y+C2=0垂直的充要条件是（）A ．A1A2+B1B2=0B．A1A2﹣B1B2=0C．D．5．（4分）函数f（x）=（x≠0）的反函数f﹣1（x）=（）A ．x（x≠0）B．（x≠0）C．﹣x（x≠0）D．﹣（x≠0）6．（4分）若点P（sinα﹣cosα，tanα）在第一象限，则在[0，2π）内α的取值范围是（）A．* B．C．D．7．（4分）已知圆锥的全面积是底面积的3倍，那么该圆锥的侧面展开图扇形的圆心角为（）A ．120°B．150°C．180°D．240°8．（4分）复数﹣i的一个立方根是i，它的另外两个立方根是（）A ．i B．﹣iC．±i D．±i9．（4分）如果棱台的两底面积分别是S，S′，中截面的面积是S0，那么（）A ．2B．S0=C．2S0=S+S′D．S02=2S'S10．（4分）向高为H的水瓶中注水，注满为止．如果注水量V与水深h的函数关系如图，那么水瓶的形状是图中的（）A ．B．C．D．11．（4分）3名医生和6名护士被分配到3所学校为学生体检，每校分配1名医生和2名护士．不同的分配方法共有（）A ．90种B．180种C．270种D．540种12．（4分）（2014•邯郸一模）椭圆=1的焦点为F1和F2，点P在椭圆上，如果线段PF1的中点在y轴上，那么|PF1|是|PF2|的（）A ．7倍B．5倍C．4倍D．3倍13．（4分）（2007•崇文区二模）球面上有3个点，其中任意两点的球面距离都等于大圆周长的，经过这3个点的小圆的周长为4π，那么这个球的半径为（）A ．4B．2C．2 D．14．（4分）一个直角三角形三内角的正弦值成等比数列，其最小内角是（）A ．arccos B．arcsin C．arccos D．arcsin15．（4分）在等比数列{a n}中，a1＞1，且前n 项和S n 满足S n=，那么a1的取值范围是（）A ．（1，+∞）B．（1，4）C．（1，2）D．（1，）二、填空题（共4小题，每小题5分，满分20分）16．（5分）（2014•云南一模）已知圆C过双曲线﹣=1的一个顶点和一个焦点，且圆心在此双曲线上，则圆心到双曲线中心的距离是_________．17．（5分）（x+2）10（x2﹣1）的展开式中x10的系数为_________（用数字作答）．18．（5分）如图，在直四棱柱A1B1C1D1﹣ABCD中，当底面四边形ABCD满足条件_________时，有A1C⊥B1D1．（注：填上你认为正确的一种条件即可，不必考虑所有可能的情形．）19．（5分）（2010•江西模拟）关于函数f（x）=4sin（x∈R），有下列命题：①由f（x1）=f（x2）=0可得x1﹣x2必是π的整数倍；②y=f（x）的表达式可改写为y=4cos；③y=f（x）的图象关于点对称；④y=f（x）的图象关于直线x=﹣对称．其中正确的命题的序号是_________．（把你认为正确的命题序号都填上）三、解答题（共6小题，满分70分）20．（10分）在△ABC中，a，b，c分别是角A，B，C的对边，设a+c=2b，A﹣C=．求sinB的值．以下公式供解题时参考：sinθ+sin∅=2sin cos，sinθ﹣sin∅=2cos sin，cosθ+cos∅=2cos cos，cosθ﹣cos∅=﹣2sin sin．21．（12分）如图，直线l1和l2相交于点M，l1⊥l2，点N∈l1．以A，B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等．若△AMN为锐角三角形，|AM|=，|AN|=3，且|BN|=6．建立适当的坐标系，求曲线段C的方程．22．（12分）如图，为处理含有某种杂质的污水，要制造一底宽为2米的无盖长方体沉淀箱，污水从A孔流入，经沉淀后从B孔流出．设箱体的长度为a米，高度为b米．已知流出的水中该杂质的质量分数与a，b的乘积ab成反比．现有制箱材料60平方米．问当a，b各为多少米时，经沉淀后流出的水中该杂质的质量分数最小（A、B孔的面积忽略不计）．23．（12分）已知如图，斜三棱柱ABC﹣A1B1C1的侧面A1ACC1与底面ABC垂直，∠ABC=90°，BC=2，AC=2，且AA1⊥A1C，AA1=A1C．（1）求侧棱A1A与底面ABC所成角的大小；（2）求侧面A1ABB1与底面ABC所成二面角的大小；（3）求顶点C到侧面A1ABB1的距离．24．（12分）设曲线C的方程是y=x3﹣x，将C沿x轴、y轴正向分别平行移动t、s单位长度后得曲线C1．（1）写出曲线C1的方程；（2）证明曲线C与C1关于点A（，）对称；（3）如果曲线C与C1有且仅有一个公共点，证明s=﹣t且t≠0．25．（12分）已知数列{b n}是等差数列，b1=1，b1+b2+…+b10=145．（1）求数列{b n}的通项b n；（2）设数列{a n}的通项a n=log a（1+）（其中a＞0，且a≠1），记S n是数列{a n}的前n项和．试比较S n与log a b n+1的大小，并证明你的结论．1998年全国统一高考数学试卷（理科）参考答案与试题解析一、选择题（共15小题，每小题4分，满分60分）1．（4分）（2008•陕西）sin330°等于（）A ．B．C．D．考点：运用诱导公式化简求值．分析：根据330°=360°﹣30°，由诱导公式一可得答案．解答：解：∵故选B．点评：本题主要考查根据三角函数的诱导公式进行化简求值的问题．属基础题．对于三角函数的诱导公式一定要强化记忆．2．（4分）函数y=a|x|（a＞1）的图象是（）A ．B．C．D．考点：指数函数的图像与性质．专题：数形结合．分析：可以先由函数的解析式判断函数是偶函数，图象关于y 轴对称，再考虑x≥0时，函数是指数函数，据它的图象特征，从而选出正确的答案．解答：解：法一：由题设知y=，又a＞1．由指数函数图象易知答案为B．法二：因y=a|x|是偶函数，又a＞1．所以a|x|≥1，排除AC．当x≥0，y=a x，由指数函数图象知选B点评：本题考查指数函数的图象特征．3．（4分）曲线的极坐标方程ρ=4cosθ化为直角坐标方程为（）A ．（x+2）2+y2=4B．（x﹣2）2+y2=4C．（x+4）2+y2=16D．（x﹣4）2+y2=16考点：简单曲线的极坐标方程．专题：计算题．分析：先将原极坐标方程ρ=4cosθ两边同乘以ρ后化成直角坐标方程，再利用直角坐标方程进行判断．解答：解：将原极坐标方程ρ=4cosθ，化为：ρ2=4ρcosθ，化成直角坐标方程为：x2+y2﹣4x=0，即y2+（x﹣2）2=4．故选B ．点评：本题考查点的极坐标和直角坐标的互化，利用直角坐标与极坐标间的关系，即利用ρcosθ=x，ρsinθ=y，ρ2=x2+y2，进行代换即得．4．（4分）两条直线A1x+B1y+C1=0，A2x+B2y+C2=0垂直的充要条件是（）A ．A1A2+B1B2=0B．A1A2﹣B1B2=0C．D．考点：两条直线垂直的判定．专题：常规题型；计算题．分析：两条直线A1x+B1y+C1=0，A2x+B2y+C2=0垂直，就是两条直线的方向向量的数量积为0，求解即可得到选项．解答：解：直线A1x+B1y+C1=0的方向向量为（﹣B1，A1），直线A2x+B2y+C2=0的方向向量为（﹣B2，A2），两条直线A1x+B1y+C1=0，A2x+B2y+C 2=0垂直，就是两条直线的方向向量的数量积为0，即：（﹣B1，A1）（﹣B2，A2）=0 可得A1A2+B1B2=0故选A．点评：本题考查两条直线垂直的判定，考查逻辑思维能力，是基础题．5．（4分）函数f（x）=（x≠0）的反函数f﹣1（x）=（）A ．x（x≠0）B．（x≠0）C．﹣x（x≠0）D．﹣（x≠0）考点：反函数．专题：计算题．分析：先求出函数f（x ）=的值域y≠0，再由函数y=解出x后，将x与y互换位置即可得到答案．解答：由y=得x=且y≠0，所以反函数f﹣1（x）=且x≠0 故选则B点评：本题主要考查反函数的求法，属于基础题．6．（4分）若点P（sinα﹣cosα，tanα）在第一象限，则在[0，2π）内α的取值范围是（）A．* B．C．D．考点：正弦函数的单调性；象限角、轴线角；正切函数的单调性．专题：计算题．分析：先根据点P（sinα﹣cosα，tanα）在第一象限，得到sinα﹣cosα＞0，tanα＞0，进而可解出α的范围，确定答案．解答：解：∵故选B．点评：本题主要考查正弦、正切函数值的求法．考查基础知识的简单应用．7．（4分）已知圆锥的全面积是底面积的3倍，那么该圆锥的侧面展开图扇形的圆心角为（）A ．120°B．150°C．180°D．240°考点：扇形面积公式；旋转体（圆柱、圆锥、圆台）．专题：计算题．分析：圆锥的全面积是底面积的3倍，那么母线和底面半径的比为2，求出侧面展开图扇形的弧长，可求其圆心角．解答：解：圆锥的全面积是底面积的3倍，那么母线和底面半径的比为2，设圆锥底面半径为1，则圆锥母线长为2，圆锥的侧面展开图扇形的弧长是圆锥底面周长为2π，该圆锥的侧面展开图扇形的圆心角：π，即180°故选C．点评：本题考查圆锥的侧面展开图，及其面积等知识，考查空间想象能力，是基础题．8．（4分）复数﹣i的一个立方根是i，它的另外两个立方根是（）A ．i B．﹣iC．±i D．±i考点：复数乘法的棣莫弗公式；复数代数形式的混合运算．专题：计算题．分析：先把复数化简成标准的三角形式，再利用棣莫弗定理，求其立方根．解答：解：∵﹣i=cos+isin，其立方根是cos+isin ，k∈0，1，2，即i，﹣﹣i，﹣i，故选D．点评：本题考查复数的三角形式，棣莫弗定理得应用．9．（4分）如果棱台的两底面积分别是S，S′，中截面的面积是S0，那么（）A ．2B．S0=C．2S0=S+S′D．S02=2S'S考点：棱台的结构特征．专题：计算题；综合题．分析：棱台不妨看做三棱台，利用相似的性质，面积之比是相似比的平方，化简即可．解答：解：不妨设棱台为三棱台，设棱台的高为2r，上部三棱锥的高为a，根据相似比的性质可得：消去r，然后代入一个方程，可得2故选A．点评：本题考查棱台的结构特征，结论可作公式应用，是基础题．10．（4分）向高为H的水瓶中注水，注满为止．如果注水量V与水深h的函数关系如图，那么水瓶的形状是图中的（）A ．B．C．D．考点：函数的图象；旋转体（圆柱、圆锥、圆台）．专题：数形结合．分析：本题利用排除法解．从所给函数的图象看出，V不是h的正比例函数，由体积公式可排除一些选项；从函数图象的单调性及切线的斜率的变化情况看，又可排除一些选项，从而得出正确选项．解答：解：如果水瓶形状是圆柱，V=πr2h，r不变，V是h的正比例函数，其图象应该是过原点的直线，与已知图象不符．故D错；由已知函数图可以看出，随着高度h的增加V也增加，但随h变大，每单位高度的增加，体积V的增加量变小，图象上升趋势变缓，其原因只能是瓶子平行底的截面的半径由底到顶逐渐变小．故A、C错．故选：B．点评：本题主要考查知识点：旋转体（圆柱、圆锥、圆台）等简单几何体和函数的图象，属于基础题．本题还可从注水一半时的状况进行分析求解．11．（4分）3名医生和6名护士被分配到3所学校为学生体检，每校分配1名医生和2名护士．不同的分配方法共有（）A ．90种B．180种C．270种D．540种考点：组合及组合数公式．专题：计算题；综合题．分析：三所学校依次选1名医生、2名护士，同一个学校没有顺序，可得不同的分配方法数．解答：解：三所学校依次选医生、护士，不同的分配方法共有：C31C62C21C42=540种．故选D．点评：不同考查组合及组合数公式，考查计算能力，是基础题．12．（4分）（2014•邯郸一模）椭圆=1的焦点为F1和F2，点P在椭圆上，如果线段PF1的中点在y轴上，那么|PF1|是|PF2|的（）A ．7倍B．5倍C．4倍D．3倍考点：椭圆的简单性质．专题：计算题．分析：由题设知F1（﹣3，0），F2（3，0），由线段PF1的中点在y轴上，设P（3，b），把P（3，b）代入椭圆=1，得．再由两点间距离公式分别求出|P F1|和|P F2|，由此得到|P F1|是|P F2|的倍数．解答：解：由题设知F1（﹣3，0），F2（3，0），如图，∵线段PF1的中点M在y轴上，∴可设P（3，b），把P（3，b）代入椭圆=1，得．∴|PF1|=，|PF2|=．．故选A．点评：本题考查椭圆的基本性质和应用，解题时要注意两点间距离公式的合理运用．13．（4分）（2007•崇文区二模）球面上有3个点，其中任意两点的球面距离都等于大圆周长的，经过这3个点的小圆的周长为4π，那么这个球的半径为（）A ．4B．2C．2 D．考点：球面距离及相关计算．专题：计算题．分析：解法一：利用大小排除，解法二：这三个点满足等边三角形，即可求解角的大小，进而求解R，解法三：因为正三角形ABC的外径r=2，故可以得到高，D是BC的中点．在△OBC中，又可以得到角以及边与R的关系，在Rt△ABD中，再利用直角三角形的勾股定理，即可解出R．解答：解法一：过O作OO′⊥平面ABC，O′是垂足，则O′是△ABC的中心，则O′A=r=2，又因为∠AOC=θ=，OA=OC知OA=AC＜2O′A．其次，OA是Rt△OO′A的斜边，故OA＞O′A．所以O′A＜OA＜2O′A．因为OA=R，所以2＜R＜4．因此，排除A、C、D，得B．解法二：在正三角形ABC中，应用正弦定理，得AB=2rsin60°=2．因为∠AOB=θ=，所以侧面AOB是正三角形，得球半径R=OA=AB=2．解法三：因为正三角形ABC的外径r=2，故高AD=r=3，D是BC的中点．在△OBC中，BO=CO=R，∠BOC=，所以BC=BO=R，BD=BC=R．在Rt△ABD中，AB=BC=R，所以由AB2=BD2+AD2，得R2=R2+9，所以R=2．故选B．点评：本题考查学生的空间想象能力，以及对球的性质认识及利用，是基础题．14．（4分）一个直角三角形三内角的正弦值成等比数列，其最小内角是（）A ．arccos B．arcsin C．arccos D．arcsin考点：等比数列的性质；同角三角函数基本关系的运用．专题：计算题；压轴题．分析：设Rt△ABC中，C=，则A与B互余且A为最小内角．根据等比数列的性质得sin2B=sinA，求的sinA，进而求的A ．解答：解：设Rt△ABC中，C=，则A与B互余且A为最小内角．又由已知得sin2B=sinA，即cos2A=sinA，1﹣sin 2A=sinA，解得sinA=或sinA=（舍）．故选B点评：本题主要考查了等比数列的性质和同角三角函数基本关系的应用．属基础题．15．（4分）在等比数列{a n}中，a 1＞1，且前n项和S n满足S n=，那么a1的取值范围是（）A（1，+∞）B（1，4）C（1，2）D（1，）．．．．考点：极限及其运算．专题：计算题；压轴题．分析：在等比数列{a n}中，S n=，由题意可知，=，再由a1＞1，|q|＜1能够推导出a1的取值范围．解答：解：由题意知S n==，∴a12=1﹣q，∵a1＞1，|q|＜1，∴1＜a12＜2，∴．故选D．点评：本题考查数列的极限及其应用，解题时要注意掌握极限的逆运算．二、填空题（共4小题，每小题5分，满分20分）16．（5分）（2014•云南一模）已知圆C过双曲线﹣=1的一个顶点和一个焦点，且圆心在此双曲线上，则圆心到双曲线中心的距离是．考点：双曲线的简单性质．专题：计算题．分析：由双曲线的几何性质易知圆C过双曲线同一支上的顶点和焦点，所以圆C的圆心的横坐标为4．故圆心坐标为（4，±）．由此可求出它到双曲线中心的距离．解答：解：由双曲线的几何性质易知圆C过双曲线同一支上的顶点和焦点，所以圆C的圆心的横坐标为4．故圆心坐标为（4，±）．∴它到中心（0，0）的距离为d==．故答案为：．点评：本题考查双曲线的性质和应用，解题时注意圆的性质的应用．17．（5分）（x+2）10（x2﹣1）的展开式中x10的系数为179（用数字作答）．考点：二项式系数的性质．专题：计算题．分析：利用二项展开式的通项公式求出第r+1项，令r=0，2得展开式系数．解答：解：（x+2）10（x2﹣1）=x2（x+2）10﹣（x+2）10∴（x+2）10（x2﹣1）的展开式中x10的系数是（x+2）10展开式的x8的系数﹣x10的系数∵（x+2）10展开式的通项为T r+1=C10r x10﹣r2r=2r C10r x10﹣r∴令r=0，2分别得x10，x8的系数为1，180故展开式中x10的系数为180﹣1=179，故答案为179点评：二项展开式的通项公式是解决二项展开式的特定项问题的工具．18．（5分）如图，在直四棱柱A1B1C1D1﹣ABCD中，当底面四边形ABCD满足条件AC⊥BD时，有A1C⊥B1D1．（注：填上你认为正确的一种条件即可，不必考虑所有可能的情形．）考点：空间中直线与直线之间的位置关系．专题：压轴题；开放型．分析：根据题意，由A1C⊥B1D1，结合直棱柱的性质，分析底面四边形ABCD得到BD⊥AC，进而验证即可得答案．解答：解：∵四棱柱A1B1C1D1﹣ABCD是直棱柱，∴B1D1⊥A1A，若A1C⊥B1D1则B1D1⊥平面A1AC1C∴B1D1⊥AC，又由B1D1∥BD，则有BD⊥AC，反之，由BD⊥AC亦可得到A1C⊥B1D1故答案为：BD⊥AC．点评：本题主要通过开放的形式来考查线线，线面，面面垂直关系的转化与应用．19．（5分）（2010•江西模拟）关于函数f（x）=4sin（x∈R），有下列命题：①由f（x1）=f（x2）=0可得x1﹣x2必是π的整数倍；②y=f（x）的表达式可改写为y=4cos；③y=f（x）的图象关于点对称；④y=f（x）的图象关于直线x=﹣对称．其中正确的命题的序号是②．（把你认为正确的命题序号都填上）考点：三角函数的周期性及其求法；命题的真假判断与应用；运用诱导公式化简求值；正弦函数的对称性．专题：计算题；压轴题．分析：首先根据函数求出最小正周期，然后根据诱导公式求出对称中心，然后根据图象分别求出最大值和最小值，最后综合判断选项．解答：解：函数f（x）=4sin的最小正周期T=π，由相邻两个零点的横坐标间的距离是=知①错．利用诱导公式得f（x）=4cos=4cos=4cos，知②正确．由于曲线f（x）与x轴的每个交点都是它的对称中心，将x=代入得f（x）=4sin≠0，因此点（，0）不是f（x）图象的一个对称中心，故命题③错误．曲线f（x）的对称轴必经过图象的最高点或最低点，且与y轴平行，而x=﹣时y=0，点（﹣，0）不是最高点也不是最低点，故直线x=﹣不是图象的对称轴，因此命题④不正确．故答案为：②点评：本题考查三角函数的周期性及其求法，诱导公式的利用，以及正弦函数的对称性问题，属于基础题．三、解答题（共6小题，满分70分）20．（10分）在△ABC中，a，b，c分别是角A，B，C的对边，设a+c=2b，A﹣C=．求sinB的值．以下公式供解题时参考：sinθ+sin∅=2sin cos，sinθ﹣sin∅=2cos sin，cosθ+cos∅=2cos cos，cosθ﹣cos∅=﹣2sin sin．考点：正弦定理的应用；三角函数中的恒等变换应用．分析：先根据正弦定理将边的关系转化为角的正弦的关系，再经过和差化积和诱导公式转化即可求出的余弦和正弦值，再由正弦的二倍角公式可得答案．解答：解：由正弦定理和已知条件a+c=2b得sinA+sinC=2sinB．由和差化积公式得2sin cos=2sinB．由A+B+C=π得sin=cos，又A﹣C=得cos=sinB，所以cos=2sin cos．因为0＜＜，cos≠0，所以sin=，从而cos=所以sinB=．点评：本小题考查正弦定理，同角三角函数基本公式，诱导公式等基础知识，考查利用三角公式进行恒等变形的技能及运算能力．21．（12分）如图，直线l1和l2相交于点M，l1⊥l2，点N∈l1．以A，B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等．若△AMN为锐角三角形，|AM|=，|AN|=3，且|BN|=6．建立适当的坐标系，求曲线段C的方程．考点：轨迹方程．专题：应用题．分析：方法一：由抛物线的定义知该曲线段是一段抛物线，建立适当的坐标系，依据题意求参数值．用定义法写出抛物线的方程．方法二：建立相应的坐标系，设出曲线段C上的任意一点的坐标（x，y），依据题意曲线段C上的任一点到l2的距离与到点N的距离相等得出方程整理即得抛物线的方程．解答：解：法一：如图建立坐标系，以l1为x轴，MN的垂直平分线为y轴，点O为坐标原点．依题意知：曲线段C是以点N为焦点，以l2为准线的抛物线的一段，其中A，B分别为C的端点．设曲线段C的方程为y2=2px（p＞0），（x A≤x≤x B，y＞0），其中x A，x B分别为A，B的横坐标，p=|MN|．所以M（，0），N（，0）．由|AM|=，|AN|=3得（x A+）2+2px A=17，①（x A﹣）2+2px A=9．②由①，②两式联立解得x A=．再将其代入①式并由p＞0解得因为△AMN是锐角三角形，所以＞x A，故舍去所以p=4，x A=1．由点B在曲线段C上，得x B=|BN|﹣=4．综上得曲线段C的方程为y2=8x（1≤x≤4，y＞0）．解法二：如图建立坐标系，分别以l1、l2为x、y轴，M为坐标原点．作AE⊥l1，AD⊥l2，BF⊥l2，垂足分别为E、D、F．设A（x A，y A）、B（x B，y B）、N（x N，0）．依题意有x A=|ME|=|DA|=|AN|=3，y A=|DM|=，由于△AMN为锐角三角形，故有x N=|ME|+|EN|=|ME|+=4x B=|BF|=|BN|=6．设点P（x，y）是曲线段C上任一点，则由题意知P属于集合{（x，y）|（x﹣x N）2+y2=x2，x A≤x≤x B，y＞0}．故曲线段C的方程为y2=8（x﹣2）（3≤x≤6，y＞0）．点评：考查利用坐标法求轨迹方程，以及抛物线的定义，本题主要是训练利用符号语言进行运算的能力．22．（12分）如图，为处理含有某种杂质的污水，要制造一底宽为2米的无盖长方体沉淀箱，污水从A孔流入，经沉淀后从B孔流出．设箱体的长度为a米，高度为b米．已知流出的水中该杂质的质量分数与a，b的乘积ab成反比．现有制箱材料60平方米．问当a，b各为多少米时，经沉淀后流出的水中该杂质的质量分数最小（A、B孔的面积忽略不计）．考点：基本不等式在最值问题中的应用．专题：压轴题．分析：先将实际问题转化成数学中的函数的最值问题，再利用基本不等式求．解答：解法一：设y为流出的水中杂质的质量分数，则y=，其中k＞0为比例系数．依题意，即所求的a，b值使y值最小．根据题设，有4b+2ab+2a=60（a＞0，b＞0），得b=（0＜a＜30）．①于是y====≥=，当a+2=时取等号，y达到最小值．这时a=6，a=﹣10（舍去）．将a=6代入①式得b=3．故当a为6米，b为3米时，经沉淀后流出的水中该杂质的质量分数最小．解法二：依题意，即所求的a，b的值使ab最大．由题设知4b+2ab+2a=60（a＞0，b＞0），即a+2b+ab=30（a＞0，b＞0）．因为a+2b≥2，所以+ab≤30，当且仅当a=2b时，上式取等号．由a＞0，b＞0，解得0＜ab≤18．即当a=2b时，ab取得最大值，其最大值为18．所以2b2=18．解得b=3，a=6．故当a为6米，b为3米时，经沉淀后流出的水中该杂质的质量分数最小．点评：本小题主要考查综合应用所学数学知识、思想和方法解决实际问题的能力，考查建立函数关系、不等式性质、最大值、最小值等基础知识．23．（12分）已知如图，斜三棱柱ABC﹣A1B1C1的侧面A1ACC1与底面ABC垂直，∠ABC=90°，BC=2，AC=2，且AA1⊥A1C，AA1=A1C．（1）求侧棱A1A与底面ABC所成角的大小；（2）求侧面A1ABB1与底面ABC所成二面角的大小；（3）求顶点C到侧面A1ABB1的距离．考点：棱柱的结构特征．专题：计算题；证明题；综合题；转化思想．分析：（1）要求侧棱A1A与底面ABC所成角的大小；必须先找出线面角，就是∠A1AC；（2）要求侧面A1ABB1与底面ABC所成二面角的大小；利用三垂线定理作出角，即作DE⊥AB，垂足为E，连A1E，则由A1D⊥面ABC，得A1E⊥AB．所以∠A1ED是面A1ABB1与面ABC所成二面角的平面角．求解即可；（3）求顶点C到侧面A1ABB1的距离，可以应用等体积法求解，也可以直接作出距离解三角形即可．解答：（1）解：如图作A1D⊥AC，垂足为D，由面A1ACC1⊥面ABC，得A1D⊥面ABC，所以∠A1AD为A1A与面ABC所成的角．因为AA1⊥A1C，AA1=A1C，所以∠A1AD=45°为所求．（2）解：作DE⊥AB，垂足为E，连A1E，则由A1D⊥面ABC，得A1E⊥AB．所以∠A1ED是面A1ABB1与面ABC所成二面角的平面角．由已知，AB⊥BC，得ED∥BC．又D是AC的中点，BC=2，AC=2，所以DE=1，AD=A1D=，tan∠A1ED==．故∠A1ED=60°为所求．（3）解法一：由点C作平面A1ABB1的垂线，垂足为H，则CH的长是C到平面A1ABB1的距离．连接HB，由于AB⊥BC，得AB⊥HB．又A1E⊥AB，知HB∥A1E，且BC∥ED，所以∠HBC=∠A1ED=60°所以CH=BCsin60°=为所求．解法二：连接A1B．根据定义，点C到面A1ABB1的距离，即为三棱锥C﹣A1AB的高h．由得，即所以为所求．点评：本小题主要考查直线与直线、直线与平面、平面与平面的位置关系，棱柱的性质，空间的角和距离的概念，逻辑思维能力、空间想象能力及运算能力．24．（12分）设曲线C的方程是y=x3﹣x，将C沿x轴、y轴正向分别平行移动t、s单位长度后得曲线C1．（1）写出曲线C1的方程；（2）证明曲线C与C1关于点A（，）对称；（3）如果曲线C与C1有且仅有一个公共点，证明s=﹣t且t≠0．考点：曲线与方程；函数的图象．专题：压轴题；函数的性质及应用．分析：（1）将C沿x轴、y轴正向分别平行移动t、s单位长度后，x变为x﹣t，y变为y﹣s，（2）在曲线C上任取一点B1（x1，y1），利用中点公式求出它关于点A的对称点B2，证明点B2在曲线C1上，同样证明，在曲线C1上的点关于点A的对称点在曲线C上．（3）曲线C与C1有且仅有一个公共点，即方程组有唯一解，对应的一元二次方程的判别式等于0，解答：（1）解：曲线C1的方程为y=（x﹣t）3﹣（x﹣t）+s．（2）证明：在曲线C上任取一点B1（x1，y1）．设B2（x2，y2）是B1关于点A的对称点，则有，，所以x1=t﹣x2，y1=s﹣y2．代入曲线C的方程，得x2和y2满足方程：s﹣y2=（t﹣x2）3﹣（t﹣x2），即y2=（x2﹣t）3﹣（x2﹣t）+s，可知点B2（x2，y2）在曲线C1上．反过来，同样可以证明，在曲线C1上的点关于点A的对称点在曲线C上．因此，曲线C与C1关于点A对称．（3）证明：因为曲线C与C1有且仅有一个公共点，所以，方程组有且仅有一组解．消去y，整理得3tx2﹣3t2x+（t3﹣t﹣s）=0，这个关于x的一元二次方程有且仅有一个根．所以t≠0并且其根的判别式△=9t4﹣12t（t3﹣t﹣s）=0，即所以且t≠0．点评：本小题主要考查函数图象、方程与曲线，曲线的平移、对称和相交等基础知识，考查运动、变换等数学思想方法以及综合运用数学知识解决问题的能力．25．（12分）已知数列{b n}是等差数列，b1=1，b1+b2+…+b10=145．（1）求数列{b n}的通项b n；（2）设数列{a n}的通项a n=log a（1+）（其中a＞0，且a≠1），记S n是数列{a n}的前n项和．试比较S n与log a b n+1的大小，并证明你的结论．考点：等差数列的通项公式；数列的求和；数学归纳法．专题：计算题；证明题；压轴题．分析：（1）根据数列{b n}是等差数列，建立b1与d的方程组，解之即可；（2）因此要比较S n与log a b n+1的大小，可先比较（1+1）（1+）（1+）与的大小，利用用数学归纳法证明此式，当a＞1时，S n＞log a b n+1，当0＜a＜1时，S n＜log a b n+1．解答：解：（1）设数列{b n}的公差为d，由题意得解得所以b n=3n﹣2．（2）由b n=3n﹣2，知S n=log a（1+1）+log a（1+）++log a（1+）=log a[（1+1）（1+）（1+）]，log a b n+1=log a．因此要比较S n与log a b n+1的大小，可先比较（1+1）（1+）（1+）与的大小．取n=1有（1+1）＞，取n=2有（1+1）（1+）＞，由此推测（1+1）（1+）（1+）＞．①若①式成立，则由对数函数性质可断定：当a＞1时，S n＞log a b n+1．当0＜a＜1时，S n＜log a b n+1．下面用数学归纳法证明①式．（ⅰ）当n=1时已验证①式成立．（ⅱ）假设当n=k（k≥1）时，①式成立，即（1+1）（1+）（1+）＞．那么，当n=k+1时，（1+1）（1+）（1+）（1+）＞（1+）=（3k+2）．因为==，所以（3k+2）＞．因而（1+1）（1+）（1+）（1+）＞．这就是说①式当n=k+1时也成立．由（ⅰ），（ⅱ）知①式对任何正整数n都成立．由此证得：当a＞1时，S n＞log a b n+1．当0＜a＜1时，S n＜log a b n+1．点评：本小题主要考查等差数列基本概念及其通项求法，考查对数函数性质，考查归纳、推理能力以及用数学归纳法进行论证的能力．。