非对称加密实验

合集下载

实验三、不对称加密算法RSA (1)

实验三、实验报告
姓名：学号：实验日期：
一、实验名称: 不对称加密算法RSA
二、实验目的
1、掌握RSA算法的工作原理。

2、熟悉利用素性检测找素数的工作原理。

三、实验基本方法
1、用C或C++语言编写找素数的算法，并编写RSA参数的计算程序，并将结果显示显示在屏幕上。

2、用C或C++语言编写一个RSA算法；
3、编程实现对32位二进数(4个字符)的加、解密；
4、手工验证加、解密的结果。

说明：
1、RSA算法可以自编，也可以网上下载现成算法。

四、实验步骤
1、编程实现找素数的算法。

2、编程实现找RSA参数的计算程序。

3、编写一个RSA算法；
4、对4个字符加、解密，改变最低1位明文观察并记录RSA的输出。

5、对4个字符加、解密，改变最高1位明文观察并记录RSA的输出。

五、实验结果
1、程序设计的思想，及程序关键原代码。

2、说明素性检测的原理。

3、说明RSA参数的e、d计算的原理。

4、报告对4个字符加、解密，改变最高低和最低1位明文RSA的输出结果。

5、分析上述输出的原因，手工验证输出的正确性。

实验2 非对称加密实验

实验2 非对称加密实验一、实验目的了解非对称密码的加密和解密特点，理解加密解密与数字签名的基本原理，掌握PGP加密的原理，使用PGP加密软件加密信息。

二、实验原理1. PGP (Preety Good Privacy) 是基于一种公钥原理 (Public Key)——RSA 的软件,使得人们可以通过公用信道安全地传输机密信息。

2.加密电子邮件我们一般的Email是明码传送的，在经过Internet上多个主机转发后，我们无法保证它不曾被他人截获过。

使用PGP则可以非常安全地发送机密信件。

首先用明码传送或查数据库服务器得到收件人的"publickey"，然后用这个"public key"先加密要发他的信件，再发送出去。

由于这封信只有与这个"publickey"对应的"private key"能解，而" private key"只掌握在收件人手中，即使别人截获这封信也不可能解得开，从而保证了信件的安全。

3.电子签名当您往INTERNET上发送一篇文章或一个文件时，别人怎么保证这是您发的而不是冒名顶替的呢,用电子签名就可以解决这个问题。

您先用您的"privatekey"加密您的签名，然后发出去。

别人收到以后就用您的"public key"去解，如果解开了，那您就是货真价实的了。

解不开的话，肯定是冒名顶替的。

因为您的"privatekey"只有您个人才拥有，谁都不可能伪造。

4.见“PGP加密/解密技术”文档三、实验步骤1、安装PGP软件用PGP加密解密文件2、发送PGP加密和签名后的电子邮件并解密邮件四(回答问题:1) 简要阐述加密解密与数字签名的原理和异同。

数字签名主要经过以下几个过程:a.信息发送者使用一单向散列函数(HASH函数)对信息生成信息摘要; b.信息发送者使用自己的私钥签名信息摘要; c.信息发送者把信息本身和已签名的信息摘要一起发送出去; d.信息接收者通过使用与信息发送者使用的同一个单向散列函数(HASH函数)对接收的信息本身生成新的信息摘要，再使用信息发送者的公钥对信息摘要进行验证，以确认信息发送者的身份和信息是否被修改过。

实验4 非对称密码算法RSA

实验4 非对称密码算法RSA（验证型）一、实验目的通过实际编程了解非对称密码算法RSA的加密和解密过程，加深对非对称密码算法的认识。

二、实验原理对称密码算法要求通信双方通过交换密钥实现使用同一个密钥，这在密钥的管理、发布和安全性方面存在很多问题，而非对称密码算法解决了这个问题。

加密密钥和解密密钥是不同的，其中加密密钥是可以公开的，解密密钥是要求保密的，并且不能用其中的一个推导出另一个。

它的安全性是建立在“大数分解和素性检测”这个数论难题的基础上，即将两个大素数相乘在计算上容易实现，而将该乘积分解为两个大素数因子的计算量相当大。

虽然它的安全性还未能得到理论证明，但经过30年的密码分析和攻击，迄今仍然被实践证明是安全的。

三、实验环境运行Windows或者Linux操作系统的PC机，具有gcc（Linux）、VC（Windows）等C语言编译环境。

四、实验内容和步骤1、为了加深对RSA算法的了解，根据已知参数：2qp，手工=M11,,3==计算公私钥，并对明文进行加密，然后对密文进行解密。

2、编写RSA程序，加密一段文字，了解RSA算法原理。

尝试加密一大段文字，记录程序的运行时间。

使用DES算法加密相同的文字，比较两种算法加密的速度。

x e mod，记录程3、编写一个程序，随机选择3个较大的数nx,,，计算ne序运行时间。

查阅资料给出简单说明大数在计算机上是如何表示，如何进行运算。

4、查阅资料，找出目前实际可行的素数判定法则，并比较各自的优缺点。

五、实验步骤1、p=3，q=11 则n=pq=33,f(n)=20，选择e=7,则d=3那么加密得c=29 解密得m=22、打开VC++，编写程序如下：#include<stdio.h>#include <iostream.h>#include <stdlib.h>#include <time.h>//using namespace std;typedef struct RSA_PARAM_Tag{ //64 位数unsigned __int64 p, q; //两个素数，不参与加密解密运算unsigned __int64 f; //f=(p-1)*(q-1)，不参与加密解密运算unsigned __int64 n, e; //公匙，n=p*q，gcd(e,f)=1unsigned __int64 d; //私匙，e*d=1 (mod f)，gcd(n,d)=1unsigned __int64 s; //块长，满足2^s<=n的最大的s，即log2(n) } RSA_PARAM;//小素数表,用于素性测试前,用小素数来初步筛选素数.const static unsigned __int64 g_PrimeTable[]={3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97};const static long g_PrimeCount=sizeof(g_PrimeTable) / sizeof(long); //乘数const unsigned __int64 multiplier=12747293821;// 加数const unsigned __int64 adder=1343545677842234541;//随机数类class RandNumber{private:unsigned __int64 randSeed;/* */public:RandNumber(unsigned __int64 s=0);unsigned __int64 Random(unsigned __int64 n);};/* */RandNumber::RandNumber(unsigned __int64 s){if(!s){randSeed= (unsigned __int64)time(NULL);}else{randSeed=s;}}/* 一个简单的随机数产生算法*/unsigned __int64 RandNumber::Random(unsigned __int64 n){randSeed=multiplier*randSeed+adder;return randSeed%n;}//定义了一个静态的类对象static RandNumber g_Rnd;/*模乘运算，返回值x=a*b mod n*/inline unsigned __int64 MulMod(unsigned __int64 a, unsigned __int64 b, unsigned __int64 n){return a * b % n;}/*模幂运算，返回值x=base^pow mod n*/unsigned __int64 PowMod(unsigned __int64 base, unsigned __int64 pow, unsigned __int64 n){ unsigned __int64 r=1;pow=pow+1;while(pow!=1) //循环结果为pow(a,b)%c{r=r*base;r=r%n;pow--;}return r;}/*{ unsigned __int64 a=base, b=pow, c=1;while(b){while(!(b & 1)){b>>=1; //a=a * a % n; //函数看起来可以处理64位的整数，但由于这里a*a在a>=2^32时已经造成了溢出，因此实际处理范围没有64位a=MulMod(a, a, n);}b--; //c=a * c % n; //这里也会溢出，若把64位整数拆为两个32位整数不知是否可以解决这个问题。

实验二数据加密标准DES及非对称RSA算法实现

实验四数据加密标准DES及非对称RSA算法实现
一、实验目的
1、了解密码学传统对称及非对称加密方法。

2、掌握对称的数据加密标准DES算法及非对称RSA算法原理。

二、实验内容
1、在VC++环境下编程并实现DES及RSA算法。

2、通过自主设定密钥及输入明文，观察每次循环加密过程。

三、实验仪器或环境
1、微型计算机
2、WindowsXP/2003操作系统
3、Visual C++可视化编程软件
四、实验原理
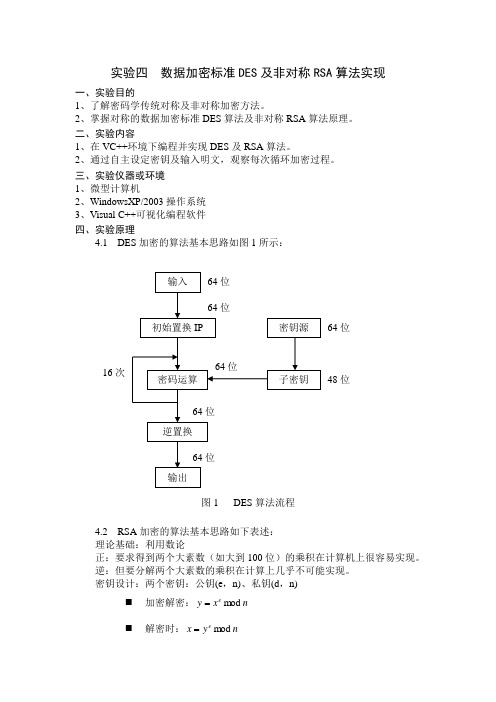
4.1 DES加密的算法基本思路如图1所示：
图1 DES算法流程
4.2 RSA加密的算法基本思路如下表述：
理论基础：利用数论
正：要求得到两个大素数（如大到100位）的乘积在计算机上很容易实现。

逆：但要分解两个大素数的乘积在计算上几乎不可能实现。

密钥设计：两个密钥：公钥(e，n)、私钥(d，n)
⏹加密解密：n
x
y e mod
=
⏹解密时：n
y
x e mod
=
实现步骤：
(1) 选取两个很大的素数p和q，令模数
(2) 求n的欧拉函数)1
Φq
=
n，并从2至[1
-
p
)
)(
(-
1
(
Φn]中任选一个数
(-
)
作为加密指数e；
(3) 解同余方程：1
⨯n
d
e，求得解密指数d；
Φ
)
(
mod=
(4) (e，n)即为公开密钥，(d，n)即为秘密密钥。

五、主要程序代码
请把主要实现的程序代码写入此栏
六、实验结果。

非对称密码算法实验原理

任务一 RSA算法一．非对称密钥加密概述前面讲述了对称密钥加密体制。

使用对称密钥加密体制进行保密通信时，任意不同的两个用户之间都应该使用互不相同的密钥。

这样，如果一个网络中有n个用户，他们之间彼此可能需要进行秘密通信，这时网络中将共需要n(n-1)/2个密钥（其中，每个用户都需要保存n-1个密钥），这样巨大的密钥量给密钥分配和管理带来了极大的困难。

另外，随着计算机网络，特别是因特网的发展，网络上互不相识的用户可能需要进行保密的会话（例如，如果用户在进行电子商务活动时，需要保密的连接，这时的客户对象可能根本不是固定的对象）。

最后，对称密钥加密机制难以解决签名验证问题。

非对称密钥加密也称为公开密钥加密，或者叫做公钥加密算法。

使用公开密钥密码的每一个用户都分别拥有两个密钥：加密密钥和解密密钥，它们两者并不相同，并且由加密密钥得到解密密钥在计算机上是不可行的。

每一个用户的加密密钥都是公开的（因此，加密密钥也称为公开密钥）。

所有用户的公开密钥都将记录在作用类似于电话号码薄的密钥本上，而它可以被所有用户访问，这样每一个用户都可以得到其他所有用户的公开密钥。

同时，每一个用户的解密密钥将由用户保存并严格保密（因此，解密密钥也称为私有密钥）。

非对称密码算法解决了对称密码体制中密钥管理的难题，并提供了对信息发送人的身份进行验证的手段，是现代密码学最重要的发明。

公钥加密算法一般是将对密钥的求解转化为对数学上的困难问题的求解，例如RSA算法的安全性是建立在“大数分解和素性检测”这个数论难题的基础上，已知两个大素数a、b，求出a*b是容易计算的，而已知a*b，想知道其是哪两个大素数的乘积目前还没有好的计算方法，另外也有一些非对称加密算法（如ELGamal算法）的安全性是基于求“离散对数”这个数学难题上的。

在公钥密码系统中每个实体都有自己的公钥和相应的私钥。

公钥密码系统的加密变换和解密变换分别用E和D表示。

任何实体B要向实体A发送信息m的步骤如下：实体B首先获得实体A的真实公钥的拷贝（eA），实体B使用eA计算密文 c=E（m）并发送给实体A ，实体A使用自己的私钥dA，计算m=D（c）解密密文，恢复出明文m。

现代密码算法实验报告(3篇)

第1篇一、实验目的1. 了解现代密码学的基本原理和数论基础知识；2. 掌握非对称密码体制的著名代表RSA加密算法的工作原理和流程；3. 设计实现一个简单的密钥系统；4. 掌握常用加密算法AES和DES的原理及实现。

二、实验内容1. RSA加密算法实验2. AES加密算法实验3. DES加密算法实验三、实验原理1. RSA加密算法RSA算法是一种非对称加密算法，由罗纳德·李维斯特、阿迪·沙米尔和伦纳德·阿德曼三位密码学家于1977年提出。

其基本原理是选择两个大质数p和q，计算它们的乘积n=pq，并计算欧拉函数φ(n)=(p-1)(q-1)。

选择一个整数e，满足1<e<φ(n)且e与φ(n)互质。

计算e关于φ(n)的模逆元d。

公开密钥为(e,n)，私有密钥为(d,n)。

加密过程为C=Me mod n，解密过程为M=Cd mod n。

2. AES加密算法AES（Advanced Encryption Standard）是一种分组加密算法，采用128位分组大小和128、192或256位密钥长度。

AES算法主要分为四个阶段：初始轮、密钥扩展、中间轮和最终轮。

每个轮包括字节替换、行移位、列混淆和轮密钥加。

3. DES加密算法DES（Data Encryption Standard）是一种分组加密算法，采用64位分组大小和56位密钥长度。

DES算法主要分为16轮，每轮包括置换、置换-置换、S盒替换和密钥加。

四、实验步骤及内容1. RSA加密算法实验（1）选择两个大质数p和q，计算n=pq和φ(n)=(p-1)(q-1)；（2）选择一个整数e，满足1<e<φ(n)且e与φ(n)互质，计算e关于φ(n)的模逆元d；（3）生成公开密钥(e,n)和私有密钥(d,n)；（4）用公钥对明文进行加密，用私钥对密文进行解密。

2. AES加密算法实验（1）选择一个128、192或256位密钥；（2）初始化初始轮密钥；（3）进行16轮加密操作，包括字节替换、行移位、列混淆和轮密钥加；（4）输出加密后的密文。

pgp加密实验报告

pgp加密实验报告PGP加密实验报告引言：在当今数字化时代，保护个人隐私和数据安全变得尤为重要。

随着互联网的普及，我们的个人信息和敏感数据越来越容易暴露在网络威胁之下。

为了解决这个问题，加密技术成为了一种重要的手段。

本实验旨在探究PGP（Pretty Good Privacy）加密技术，并通过实际操作来了解其原理和应用。

一、PGP加密的背景和原理PGP加密技术最早由菲尔·齐默曼（Phil Zimmermann）在1991年开发，它是一种非对称加密技术。

非对称加密技术使用了一对密钥，即公钥和私钥。

公钥可以用于加密消息，而私钥则用于解密消息。

二、实验准备在进行PGP加密实验之前，我们需要准备一些工具和材料。

首先，我们需要下载和安装PGP软件，例如GnuPG。

其次，我们需要生成一对密钥，一个用作公钥，另一个用作私钥。

生成密钥时，我们需要输入一些个人信息，如姓名和电子邮件地址。

三、实验步骤1. 生成密钥对在GnuPG软件中，我们可以使用命令行或图形界面生成密钥对。

我们需要输入一些个人信息，并设置一个密码来保护私钥。

生成密钥对后，我们将得到一个公钥文件和一个私钥文件。

2. 密钥的导入和导出我们可以将生成的公钥导出为一个文件，并与他人共享。

其他人可以使用我们的公钥来加密消息，以确保只有我们能够解密。

同样，我们也可以导入他人的公钥，并使用其公钥来加密消息。

3. 加密和解密消息使用GnuPG软件，我们可以使用对方的公钥来加密消息。

在加密过程中，只有使用私钥才能解密。

我们可以通过命令行或图形界面来进行加密和解密操作。

四、实验结果通过实验，我们成功生成了一对密钥，并将公钥导出并与他人共享。

我们还成功使用对方的公钥来加密消息，并使用私钥来解密。

实验结果表明，PGP加密技术能够有效地保护个人隐私和数据安全。

五、实验总结PGP加密技术作为一种非对称加密技术，为我们提供了一种安全保护个人隐私和数据安全的手段。

通过实验，我们深入了解了PGP加密的原理和应用。

RSA非对称加密算法实验报告

学与工程学院
2009年9月
第一部分
信息加密技术实验
第一部分信息加密技术实验
一、实验目的：
在数据加密、解密的算法中，DES算法是典型的单密钥体制，RSA是典型的双密钥体制，目前均在大量使用。通过实验，让学生充分理解和掌握DES和RSA算法，PGP 加密工具的使用。以及通过网络进行数据加密传输的概念。
RSA实验：运行《RSATool》演示软件：产生公钥和私钥
第二项任务 DES加密解密工具2.1及其代码——支持字符串及文件加密，支持3重DES
1.DES 2.1 说明
先看看DES 2.1 的截图：
的简介： 2. DES 2.1 2.1的简介：
1.支持任意长度字符串加密解密 2.明文、密钥可以不足8字节 3.支持回车换行，Tab 等特殊字符 4.密文可以选择三种方式显示 5.支持3重DES 6.支持文件加密、解密 7.加密时显示进度
3.DES 算法介绍
关于DES算法的介绍大家可以看我博客里的另一篇文章，[原创]DES算法的介绍以及实
现（含上次DES程序1.0的源码），所以在此不在重述。
提供的 Public 函数 4. yxyDES2 Class Class提供的提供的Public Public函数
下面我们来看看yxyDES2 类（Class）里public函数和它们的用法： //功能:产生16个28位的key //参数:源8位的字符串(key),存放key的序号0-1 //结果:函数将调用private CreateSubKey将结果存于char SubKeys[keyN][16][48] void InitializeKey(char* srcBytes,unsigned int keyN); //功能:加密8位字符串 //参数:8位字符串,使用Key的序号0-1 //结果:函数将加密后结果存放于private szCiphertext[16] // 用户通过属性Ciphertext得到 void EncryptData(char* _srcBytes,unsigned int keyN); //功能:解密16位十六进制字符串 //参数:16位十六进制字符串,使用Key的序号0-1 //结果:函数将解密候结果存放于private szPlaintext[8] // 用户通过属性Plaintext得到 void DecryptData(char* _srcBytes,unsigned int keyN); //功能:加密任意长度字符串 //参数:任意长度字符串,长度,使用Key的序号0-1 //结果:函数将加密后结果存放于private szFCiphertextAnyLength[8192] // 用户通过属性CiphertextAnyLength 得到 void EncryptAnyLength(char* _srcBytes,unsigned int _bytesLength,unsigned int keyN); //功能:解密任意长度十六进制字符串 //参数:任意长度字符串,长度,使用Key的序号0-1 //结果:函数将加密后结果存放于private szFPlaintextAnyLength[8192] // 用户通过属性PlaintextAnyLength 得到 void DecryptAnyLength(char* _srcBytes,unsigned int _bytesLength, unsigned int keyN); //功能:Bytes到Bits的转换, //参数:待变换字符串,处理后结果存放缓冲区指针,Bits缓冲区大小 void Bytes2Bits(char *srcBytes, char* dstBits, unsigned int sizeBits); //功能:Bits到Bytes的转换, //参数:待变换字符串,处理后结果存放缓冲区指针,Bits缓冲区大小 void Bits2Bytes(char *dstBytes, char* srcBits, unsigned int sizeBits);

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

非对称加密实验
【实验环境】
ISES客户端
Microsoft CLR Debugger 2005或其它调试器
【实验内容】
通过运算器工具实现RSA和ElGamal算法的加解密计算
手工计算RSA密钥并检验，将其应用于签名中并验证
对RSA密钥生成、RSA密钥加密、ElGamal参数生成、ElGamal密钥生成和ElGamal加密进行算法跟踪
非对称加密实验
【实验原理】
非对称密码体制又称为公钥密码体制，加解密使用公私钥密钥对，私钥由密钥拥有者保管，公钥可以公开，基于公开渠道进行分发，解决了对称密钥体制中密钥管理、分发和数字签名等难题。

一、 RSA算法
RSA公钥算法由Rivest、Shamir、Adleman于1978年提出的，是目前公钥密码的国际标准。

算法的数学基础是Euler定理，是基于Deffie-Hellman的单项陷门函数的定义而给出的第一个公钥密码的实际实现，其安全性建立在大整数因子分解的困难性之上。

RSA算法的明文空间M=密文空间C=Z整数，其算法描述如下: n
(1) 密钥生成
随机选择两个大素数p和q，计算n=p•q，;选择一个随机整数e<，满足，计算整数;公开公钥(n,e)，安全的销毁p、q和，并保留(d,n)作为私钥。

(2) 加密
(3) 解密
使用中国剩余定理可以加速RSA密码算法的实现。

二、 ElGamal算法
ElGamal算法是Deffie-Hellman单项陷门函数的一个成功应用，把函数转化为公钥加密体制，其安全性建立在有限域上的离散对数问题。

ElGamal算法的描述如下:
(1) 密钥生成
随机选择一个素数p，计算p个元素的有限域的乘法群的一个随机乘法生成元g;均匀随机地在模p-1的整数集合中选取x，计算;把(p,g,y)作为公钥公开，把(p,g,x)作为私钥。

(2) 加密
均匀随机地在模p-1的整数集合中选取k，消息m<p，计算密文对(c1,c2):
(3) 解密
非对称加密实验
【实验步骤】
一、 RSA
(一) 加解密计算
(1) 打开实验实施，默认的选择即为RSA标签，显示RSA实验界面。

(2) 选择明文格式，输入要加密的明文信息。

(3) 选择密钥长度，此处以512比特为例，点击“生成密钥对”按钮，生成密钥对和参
数。

(4) 选择“标准方法”标签，在标签下查看生成的密钥对和参数，如图1.1.7-1所示。

图1.1.7-1
(5) 标准方法加解密
标准方法可选择公钥加密/私钥解密形式和公钥加密/私钥解密形式进行加解密，此处以公钥加密/私钥解密形式进行加解密，公钥加密/私钥解密可参照完成;注意在一次加解密过程中不要重新生成密钥对。

点击“公钥加密”按钮使用生成的公钥对明文进行加密，密文以十六进制显示在密文文本框中;清除明文文本框中的内容，点击“私钥解密”按钮对密文进行解密，明文默认以文本形式显示在明文文本框中，如图1.1.7-2所示;可选择以16进制查看明文。

图1.1.7-2
(6) 选择“中国剩余定理方法”标签，在标签下查看生成的密钥对和参数，如图1.1.7-3
所示。

图1.1.7-3
(7) 中国剩余定理方法加解密
点击“加密”按钮使用生成的公钥对明文进行加密，密文以十六进制显示在密文文本框中;清除明文文本框中的内容，点击“解密”按钮对密文进行解密，明文默认以文本形式显示在明文文本框中，如图1.1.7-4所示。

可选择以十六进制查看明文。

图1.1.7-4
(二) RSA密钥计算
(1) 点击“扩展实验”框中的“RSA计算”按钮，进入RSA计算窗体。

(2) 输入报文信息，点击“计算MD5值”生成报文信息的信息摘要，如图1.1.7-5所示。

图1.1.7-5
(3) 选择p、q值，计算n、φ(n)、e和d并输入相应的文本框中，点击“检验”按钮对
计算的各个参数值进行检验，如图1.1.7-6所示。

图1.1.7-6
(4) 检验无误后，根据上述计算得到的RSA私钥，计算报文MD5值即报文摘要的前8
位的签名值，并输入相应的文本框;点击“生成签名并检验”按钮，检验签名输入
是否正确并自动生成消息摘要前8位的签名值并显示，如图1.1.7-7所示。

图1.1.7-7
(5) 点击“验证”按钮，对输入的签名值进行验证，并给出相应的提示，如图1.1.7-8
所示。

图1.1.7-8
(三) 算法跟踪
点击“算法跟踪”框下的“RSA密钥生成”/“RSA加密”按钮，进入调试器，选择对应的算法函数对RSA密钥生成算法/RSA加密算法进行算法跟踪;跟踪完成后会自动返回实验界面显示计算结果;切换回调试器，停止调试，关闭调试器，不保存工程。

具体步骤可参照古典密码实验中实验步骤二。

二、 ElGamal
(一) 加解密计算
(1) 选择“ElGamal”标签，进入ElGamal实验界面。

(2) 选择明文形式，输入明文信息。

(3) 参数生成
点击“生成g和P”按钮，生成ElGamal参数p和g，如图1.1.7-9所示。

图1.1.7-9
(4) 密钥生成
点击“生成密钥”按钮，生成密钥Y和X，如图1.1.7-10所示。

图1.1.7-10
(5) 加密
点击“加密”按钮，使用公开密钥Y对明文加密，密文以十六进制形式显示在密文文本框中，如图1.1.7-11所示。

图1.1.7-11
(6) 解密
清除明文文本框中的内容，点击“解密”按钮对密文进行解密，明文默认以十六进制形式显示在明文文本框中，如图1.1.7-12所示;可选择以文本形式查看明文。

图1.1.7-12
(二) 算法跟踪
点击“算法跟踪”框下的“ElGamal参数生成”/“ElGamal密钥生
成”/“ElGamal加密”按钮，进入调试器，选择对应的算法函数对ElGamal参数生成过程、ElGamal密钥生成算法和ElGamal加密算法进行算法跟踪;跟踪完成后会自动返回实验界面显示计算结果;切换回调试器，停止调试，关闭调试器，不保存工程。