长方体和正方体单元复习知识点及练习
长方体和正方体知识点归纳和习题
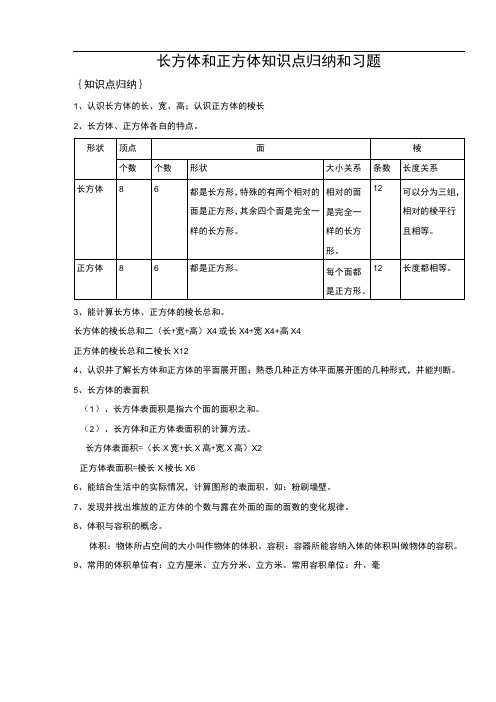
长方体和正方体知识点归纳和习题{知识点归纳}1、认识长方体的长、宽、高;认识正方体的棱长2、长方体、正方体各自的特点。
3、能计算长方体、正方体的棱长总和。
长方体的棱长总和二(长+宽+高)X4或长X4+宽X4+高X4正方体的棱长总和二棱长X124、认识并了解长方体和正方体的平面展开图;熟悉几种正方体平面展开图的几种形式,并能判断。
5、长方体的表面积(1)、长方体表面积是指六个面的面积之和。
(2)、长方体和正方体表面积的计算方法。
长方体表面积=(长X宽+长X高+宽X高)X2正方体表面积=棱长X棱长X66、能结合生活中的实际情况,计算图形的表面积。
如:粉刷墙壁。
7、发现并找出堆放的正方体的个数与露在外面的面的面数的变化规律。
8、体积与容积的概念。
体积:物体所占空间的大小叫作物体的体积。
容积:容器所能容纳入体的体积叫做物体的容积。
9、常用的体积单位有:立方厘米、立方分米、立方米。
常用容积单位:升、毫如:冰箱的容积用“升”作单位;我们饮用的自来水用“立方米”作单位。
10、长方体的体积二长X宽X高正方体的体积二棱长X棱长X棱长长方体(正方体)的体积二底面积X高11、能利用长方体(正方体)的体积及其他两个条件求出问题。
如:长方体的高二体积三(长X宽)12、相邻两个体积单位、容积单位之间的进率是1000。
如:1dm3=1000cm31L=1000mL1m3=1000dm3高级单位化低级单位乘进率,低级单位化高级单位除以进率。
13、不规则物体体积测量方法:将物体体积转化成可测量的水的体积。
如:容器中上升水的体积=不规则物体体积专题练习一、填空:1、长方体和正方体都有()个面,()条棱,()个顶点。
2、长方体的长是8厘米,宽是6厘米,高是5厘米,它的棱长和是()厘米;六个面中最大的一个面积是()平方厘米,表面积是()平方厘米。
3、2850平方厘米二()平方分米()平方厘米12.8米二()分米二()厘米4、一个棱长是1分米的正方体,锯成2个小长方体,其中一个长方体的表面积是()平方分米。
长方体和正方体经知识点归纳+经典例题

第三单元长方体和正方体日期:基础知识一、知识点一:长方体和正方体的认识1、长方体和正方体的特征:长方体有6个面,每个面都是长方形(特殊的有一组对面是正方形),相对的面完全相同;有12条棱,相对的棱平行且相等;有8个顶点。
正方形有6个面,每个面都是正方形,所有的面都完全相同;有12条棱,所有的棱都相等;有8个顶点。
2、长、宽、高:相交于一个顶点的三条棱的长度分别叫做长方体的长、宽、高。
3、长方体的棱长总和=(长+宽+高)×4用字母表示:(a+b+h)×4正方体的棱长总和= 棱长×12用字母表示:12a二、知识点二:长方体和正方体的表面积的计算4、表面积:长方体或正方体6个面的总面积叫做它的表面积。
5、长方体的表面积=(长×宽+长×高+宽×高)×2用字母表示:S=(ab+ah+bh)×2正方体的表面积= 棱长×棱长×6用字母表示:S=6a26、表面积单位:平方厘米、平方分米、平方米7、1m2 =100dm2 1dm2 =100cm2三、知识点三:长方体和正方体的体积的计算7、体积:物体所占空间的大小叫做物体的体积。
8、长方体的体积= 长×宽×高用字母表示:V=abh正方体的体积= 棱长×棱长×棱长用字母表示:V=a39、体积单位:立方厘米、立方分米和立方米1m3=1000dm3 1dm3=1000cm3 1m3=100 0000cm310、长方体和正方体的体积统一公式:长方体或正方体的体积=底面积×高用字母表示:V=Sh11、体积单位的互化:把高级单位化成低级单位,用高级单位数乘以进率;------大乘小把低级单位聚成高级单位,用低级单位数除以进率。
-----------小除大四、知识点三:长方体和正方体的容积的计算12、容积:容器所能容纳物体的体积。
(完整版)长方体和正方体知识点汇总(最新整理)
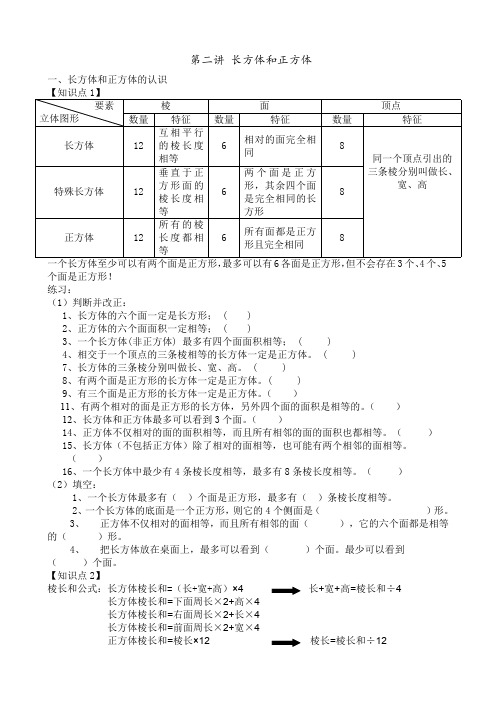
第二讲 长方体和正方体一、长方体和正方体的认识【知识点1】棱面顶点要素立体图形数量特征数量特征数量特征长方体12互相平行的棱长度相等6相对的面完全相同8特殊长方体12垂直于正方形面的棱长度相等6两个面是正方形,其余四个面是完全相同的长方形8正方体12所有的棱长度都相等6所有面都是正方形且完全相同8同一个顶点引出的三条棱分别叫做长、宽、高一个长方体至少可以有两个面是正方形,最多可以有6各面是正方形,但不会存在3个、4个、5个面是正方形!练习:(1)判断并改正:1、长方体的六个面一定是长方形; ( )2、正方体的六个面面积一定相等; ( )3、一个长方体(非正方体) 最多有四个面面积相等; ( )4、相交于一个顶点的三条棱相等的长方体一定是正方体。
( )7、长方体的三条棱分别叫做长、宽、高。
( )8、有两个面是正方形的长方体一定是正方体。
( )9、有三个面是正方形的长方体一定是正方体。
( )11、有两个相对的面是正方形的长方体,另外四个面的面积是相等的。
( )12、长方体和正方体最多可以看到3个面。
( ) 14、正方体不仅相对的面的面积相等,而且所有相邻的面的面积也都相等。
( ) 15、长方体(不包括正方体)除了相对的面相等,也可能有两个相邻的面相等。
( )16、一个长方体中最少有4条棱长度相等,最多有8条棱长度相等。
( )(2)填空:1、一个长方体最多有( )个面是正方形,最多有( )条棱长度相等。
2、一个长方体的底面是一个正方形,则它的4个侧面是( )形。
3、正方体不仅相对的面相等,而且所有相邻的面( ),它的六个面都是相等的( )形。
4、把长方体放在桌面上,最多可以看到( )个面。
最少可以看到( )个面。
【知识点2】棱长和公式:长方体棱长和=(长+宽+高)长+宽+高=棱长和÷4长方体棱长和=下面周长×2+高×4长方体棱长和=右面周长×2+长×4长方体棱长和=前面周长×2+宽×4正方体棱长和=棱长×12 棱长=棱长和÷12棱长和的变形:例如:有一个礼盒需要用彩带捆扎,捆扎效果如图,打结部分需要10厘米彩带,一共需要多长的彩带?分析:本题虽然并未直接提出求棱长和,但由于彩带的捆扎是和棱相互平行的, 因此,在解决问题时首先确定每部分彩带与那条棱平行,从而间接去求棱长和。
五年级数学长方体和正方体知识点及练习题

长方体和正方体的表面积知识点长方体和正方体都有6个面,12条棱,8个顶点。
长方体相对的4条棱相等,长方体的12条棱按长度可以分成3组。
正方体是长宽高都相等的长方体。
长方体是6个长方形(特殊情况下有两个相对的面试正方形)围成的立体图形,相对的两个面完全相同。
1、正方体的展开1).141型,中间一行4个作侧面,上下两个各作为上下底面,共有六种基本图形2).132型,中间3个作侧面,共3中基本图形3).222型,两行只能有1个正方形相连4).33型,两行只能有一个正方形相连一共11种2、长方体的表面积就是长方体六个面的总面积。
由于相对的面完全相同,所以可以先求出前面、后面和下面三个面的面积,再乘以2,就可以求出表面积了。
长方体的表面积 = 长×宽×2+长×高×2+宽×高×2=(长×宽+长×高+宽×高)×2正方体的六个面完全相同,所以计算时只要算出其中的一个面,再乘6就可以了。
正方体的表面积 = 棱长×棱长×63、在解决一些问题时,要充分考虑实际情况,想清楚要算几个面。
在解答时,可以把这几个面的面积分别算出来,再相加,也可以先算出六个面的面积总和,再减去不需要的那个(些)面。
一个抽屉有5个面,分别是前面、后面、左面、右面、底面。
所以做这样一个抽屉所需要的木板,只要算出这5个面的面积就可以了。
通风管顾名思义是通风用的,没有底面。
所以只要算四个侧面就可以了。
(1)具有六个面的长方体、正方体物品:油箱、罐头盒、纸箱子等;(2)具有五个面的长方体、正方体物品:水池、鱼缸等;(3)具有四个面的长方体、正方体物品:水管、烟囱等。
长方体和正方体表面积知识巩固一、填空题。
1、一个正方体的棱长之得84厘米,它的棱长是(),一个面的面积是(),表面积是(),体积是()。
2、一个长方体的长、宽、高都扩大2倍,它的表面积就()。
六年级上册数学第一单元知识点和题型长方体和正方体

一、长方体和正方体的定义长方体:长方体是一种特殊的长方形,其六个面都是矩形,相邻的两个面是相等的,相对的两个面是相似的,并且相邻的三条棱相交于一点,这样的立体叫做长方体。
正方体:正方体是一个特殊的长方体,它的所有边长相等,并且每个面都是正方形,相邻的两个面是相等的,相对的两个面是相似的,且相邻的四条棱相交于一点,这样的立体叫做正方体。
二、长方体和正方体的性质1. 面的个数和性质:长方体有六个矩形的面;正方体有六个正方形的面。
2. 顶点、棱、面的关系:长方体有八个顶点、十二条棱和六个面;正方体有八个顶点、十二条棱和六个面。
3. 对角线的长度:长方体的对角线长度为√(l² + w² + h²),其中l、w、h分别为长方体的长、宽、高;正方体的对角线长度为√3a,其中a为正方体的边长。
4. 体积和表面积:长方体的体积为lwh,其中l、w、h分别为长方体的长、宽、高,表面积为2lw + 2lh + 2wh;正方体的体积为a³,其中a为正方体的边长,表面积为6a²。
5. 对顶点、棱、面的关系:对每个顶点,有四条棱和三个面相交;对每条棱,有两个面相交;对每个面,有四条棱相交。
三、长方体和正方体的题型及解题方法1. 计算体积和表面积:给定长方体或正方体的边长,要求计算它们的体积和表面积,可以使用公式进行计算。
2. 计算对角线的长度:给定长方体或正方体的长、宽、高或边长,要求计算它们的对角线长度,可以使用勾股定理进行计算。
3. 判断给定的图形是长方体还是正方体:根据图形的特征,可以判断给定的立体是长方体还是正方体,主要依据是它的六个面是否都是矩形或正方形。
4. 求棱长:已知长方体或正方体的体积和某个棱长,要求计算其它两个棱长,可以使用体积的公式进行计算。
四、案例分析例题一:已知正方体的边长为5cm,求其体积和表面积。
解:正方体的体积为a³,表面积为6a²。
五年级数学下册期末总复习《3单元长方体和正方体》必记知识点

五年级数学下册期末总复习《3单元长方体和正方体》必记知识点一、长方体和正方体的认识1. **长方体的定义**:-由6个长方形(特殊情况有两个相对的面是正方形)围成的立体图形叫做长方体。
-在一个长方体中,相对面完全相同,相对的棱长度相等。
2. **正方体的定义**:-由6个完全相同的正方形围成的立体图形叫做正方体(也叫做立方体)。
-正方体有12条棱,它们的长度都相等,所有的面都完全相同。
3. **长方体和正方体的共同点**:-都有6个面、12条棱和8个顶点。
-面、棱和顶点的数目相同。
4. **长方体和正方体的区别**:-长方体的棱长不一定相等,面不一定都是正方形。
-正方体的棱长都相等,所有的面都是正方形。
二、长方体和正方体的表面积1. **表面积的定义**:-长方体或正方体6个面的总面积叫做它的表面积。
2. **表面积的计算公式**:-长方体的表面积= (长×宽+ 长×高+ 宽×高)×2-正方体的表面积= 棱长×棱长×6三、长方体和正方体的体积1. **体积的定义**:-物体所占空间的大小叫做物体的体积。
2. **体积的计算公式**:-长方体的体积= 长×宽×高-正方体的体积= 棱长×棱长×棱长四、长方体和正方体的棱长总和1. **棱长总和的定义**:-长方体或正方体12条棱的长度和叫做棱长总和。
2. **棱长总和的计算公式**:-长方体的棱长总和= (长+ 宽+ 高)×4-正方体的棱长总和= 棱长×12五、体积单位及进率1. **常用的体积单位**:-立方厘米(cm³)、立方分米(dm³)、立方米(m³)。
2. **体积单位间的进率**:- 1dm³= 1000cm³- 1m³= 1000dm³六、容积和容积单位1. **容积单位与体积单位的关系**:- 1L = 1dm³- 1mL = 1cm³2. **容积的计算方法**:-与体积的计算方法相同,但要从容器里面量长、宽、高。
长方体和正方体单元知识点

长方体和正方体单元知识点1. 长方体(Rectangular Prism):长方体是由6个矩形面组成的立体图形。
它的所有对面都是相等的,并且相对的面是平行的。
长方体有8个顶点、12条边和6个面。
1.1定义:长方体的定义可以用以下几个要素来描述:-一个有6个矩形面的立体图形。
-每个面都是直角相邻的。
-所有面的边长都不相等。
-所有对面都是平行的。
1.2特征:长方体具有以下特征:-所有边长不相等。
-所有对面都是平行的。
-每个面上的相对边长相等。
-所有的角都是直角。
1.3表面积计算:长方体的表面积可以通过计算每个面的面积,并将结果相加得到。
表面积 = 2lw + 2lh + 2wh其中,l、w和h分别代表长方体的长度、宽度和高度。
1.4体积计算:长方体的体积可以通过将长度、宽度和高度相乘来计算。
体积 = lwh2. 正方体(Cube):正方体是一种特殊的长方体,其所有边长相等。
正方体有8个顶点、12条边和6个面。
正方体具有更多的对称性和特殊性质。
2.1定义:正方体的定义可以用以下几个要素来描述:-一个具有6个正方形面的立体图形。
-所有边长相等。
-所有的角都是直角。
2.2特征:正方体具有以下特征:-所有边长相等。
-所有对面都是平行的。
-每个面上的角度都是直角。
-具有更多的对称性,即旋转或反射一个正方体的结果仍然是一个正方体。
2.3表面积计算:正方体的表面积可以通过计算每个面的面积,并将结果相加得到。
表面积=6s^2其中,s代表正方体的边长。
2.4体积计算:正方体的体积可以通过将边长三次幂(即三次方)来计算。
体积=s^3其中,s代表正方体的边长。
总结:长方体和正方体都是由矩形面组成的三维立体图形。
长方体具有所有边长不相等的特征,而正方体具有所有边长相等的特征。
它们在计算表面积和体积时的公式也有所不同。
长方体的表面积为2lw + 2lh + 2wh,体积为lwh;而正方体的表面积为6s^2,体积为s^3、正方体具有更多的对称性和特殊性质。
第3单元长方体和正方体单元复习(试题)-数学五年级下册 (2)

第3单元长方体和正方体综合复习知识点一:长方体和正方体的基本认识典例用一个长方体最多能画出()个不同的长方形。
A.1个B.2个C.3个跟踪训练1.长方体有条棱,相对的棱的长度相等。
在长方体所有的棱中,长度相等的棱最少有条。
2.用一个正方体只能画出种正方形,用一个长方体最多能画出种不同的长方形.35.长方体中最多有2个面是正方形。
(判断对错)3.看到的立体图形的一个面是正方形,这个立体图形可能是正方体,也可能是长方体。
(判断对错)4.长方体相邻的三条棱的长度之和是14厘米,这个长方体的棱长总和是42厘米。
(判断对错)5.6个完全相同的长方形(不含正方形)能拼成长方体。
(判断对错)知识点二:棱长和典例用一根长52厘米长的铁丝,正好可以弯成长6厘米、宽4厘米,高()厘米的长方体教具。
A.3B.4C.51.要焊接一个长11cm、宽7cm、高6cm的长方体框架,需要长11cm、宽7cm、高6cm的铁丝各()根.A.3B.4C.1218.2.一个正方体的棱长扩大3倍,它的棱长之和就扩大()A.27倍B.9倍C.3倍3.一个长方体框架长16cm、宽12cm、高8cm,如果把长方体框架改焊成正方体框架,正方体的棱长是多少?4.用1根长2m的铁丝焊接成1个长方体框架(铁丝无剩余,接头处忽略不计),它的长是35cm,宽是12cm,高是多少厘米?知识点三:表面积典例一个棱长5分米的正方体,在它的一个顶点处挖掉一个棱长1分米的小正方体,那么()A.表面积增加B.表面积不变C.表面积减少1.制作一个长方体的鱼缸,要用多少玻璃是求鱼缸的()。
A.棱长总和B.表面积C.体积D.容积2.一个正方体的棱长扩大到原来的2倍,它的表面积是原来的()倍。
A.2B.4C.83.一个长方体,长、宽、高分别是a厘米、b厘米、h厘米。
如果高增加2厘米,那么新的长方体的表面积比原来增加()平方厘米。
A.ab(h+2)B.2abC.2(2a+2b)D.2(2a+2b)+ab4.一个长方体的棱长总和是48分米,从一个顶点出发的三条棱长的和是分米,如果这三条棱的长度恰好是三个连续的自然数,这个长方体的表面积是平方分米。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
长方体和正方体单元复习
知识1:长方体和正方体的认识
展开图:141、231、222、33,相对的面中间隔一个
(1)判断和填空:
长方体的六个面一定是长方形; ( )
正方体的六个面面积一定相等; ( )
一个长方体(非正方体) 最多有四个面面积相等; ( )
相交于一个顶点的三条棱相等的长方体一定是正方体。
( )
一个长方体中,可能有4个面是正方形。
(? )
正方体是特殊的长方体。
( )
有两个面是正方形的长方体一定是正方体。
( )
一个长方体中最少有4条棱长度相等,最多有8条棱长度相等。
( )
(2)一个长方体最多有( )个面是正方形,最多有( )条棱长度相等。
(3)一个长方体的底面是一个正方形,则它的4个侧面是( )形。
(4)正方体不仅相对的面相等,而且所有相邻的面(? ),它的六个面都是相等的( )形。
(5)把长方体放在桌面上,最多可以看到( )个面。
最少可以看到( )个面。
知识2:棱长和公式
长方体棱长和=(长+宽+高)×4 长+宽+高=棱长和÷4
正方体棱长和=棱长×12 棱长=棱长和÷12
例题:
(1)看图2-6,并填空单位:厘米
这个长方体长( )厘米,宽( )厘米,高( )厘米。
由一个顶点引出的三条
棱的长度和是( )厘米。
棱长总和是( )厘米。
上下两个面是( )形。
(2)一个长方体的棱长总和是 80厘米,其中长是 10厘米,宽是 7厘米,高是( )厘米。
(3)把两个棱长 1厘米的正方体拼成一个长方体,这个长方体的棱长总和是( )厘米。
(4)至少需要(?? )厘米长的铁丝,才能做一个底面周长是18厘米,高3厘米的长方体框架。
(5)用长92厘米的铁丝围成一个长方体框架,长10厘米,高比宽少3厘米,这个长方体的宽和高分别是多少厘米?
(7)有一个礼盒需要用彩带捆扎,捆扎效果如图,打结部分需要10厘米彩带,一共需要多长的彩带?
知识3:长方体和正方体的表面积
【知识点1】
长方体表面积=(长×宽+长×高+宽×高)×2 =(a ×b+a ×c+b ×c )×2
30㎝ 20cm
20cm
【知识点3】棱长变化对表面积的影响:
➢ 正方体
正方体的棱长扩大n 倍,其棱长和也扩大n 倍,表面积扩大n 2倍,体积扩大n 3倍。
➢ 长方体
长方体的长宽高同时扩大n 倍,其棱长和也扩大n 倍,体积扩大n 3倍。
(1)大正方体棱长是小正方体棱长的2倍,则大正方体表面积是小正方体表面积的(?)倍。
(2)一个长方体长扩大2倍,高扩大4倍,宽不变,体积扩大( )倍。
知识3:单位换算、体积和容积
【知识点1】单位换算
长度单位:mm 、cm 、dm 、m 相邻两个单位进率为10
面积单位:mm 2、cm 2、dm 2、m 2 相邻两个单位进率为100
体积单位:mm 3、cm 3、dm 3、m 3 相邻两个单位进率为1000
容积单位:ml 、l 相邻两个单位进率为1000
特别的:1ml=cm 3 1l=1dm 3 1方=1m 3
不是同一类型的单位,数据不能比较大小,同一类型的单位中右边的单位比左边的单位大。
大单位化小单位乘以进率,小单位化大单位除以进率。
(1)立方分米=( )立方厘米 立方分米=( )立方分米( )立方厘米 9立方米500立方分米=( )立方米=( )立方分米
升=( )毫升=( )立方厘米
2100毫升=(?????? )立方厘米=(?????? )立方分米
(2)一个水池能装水400立方米,这是指( ),占地2公顷指的是( )。
一块橡皮擦的体积约是8( )。
一本书的封面约是2( )。
【知识点2】体积
物体所占空间的大小叫做物体的体积。
长方体的体积=长×宽×高 V=abh
长=体积÷宽÷高 a=V ÷b ÷h 宽=体积÷长÷高 b=V ÷a ÷h 高=体积÷长÷宽 h= V ÷a ÷b
正方体的体积=棱长×棱长×棱长 V=a ×a ×a
例题:
(1)一个正方体棱长2厘米,体积是( )立方厘米,如果这个正方体的棱长扩大2倍,它的体积是( )立方厘米。
(2)长方体的长为12厘米,高为8厘米,阴影部分的两个面的面积和是200平方厘米,这个长方体的体积是多少立方厘米?
(3)一个长方体的底面是一个周长为16分米的正方形,它的表面积是96平方分米,这个长
高级单位 进率×高级单位的
数 低级单位 低级单位的数÷进
率。
