长方体和正方体知识点
(完整版)长方体和正方体知识点汇总(最新整理)
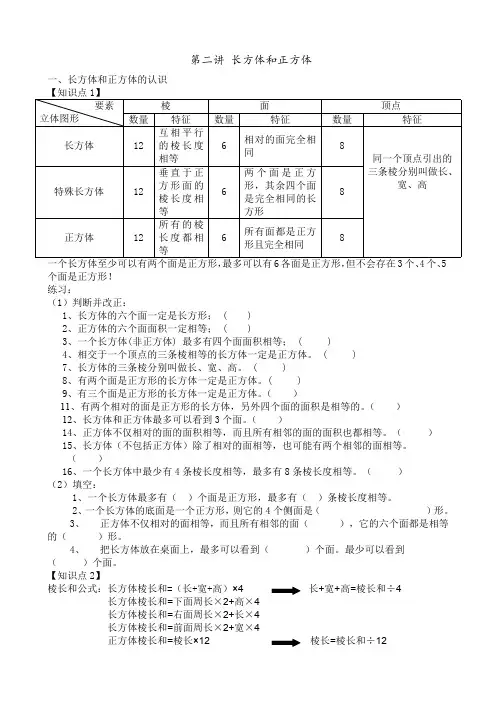
第二讲 长方体和正方体一、长方体和正方体的认识【知识点1】棱面顶点要素立体图形数量特征数量特征数量特征长方体12互相平行的棱长度相等6相对的面完全相同8特殊长方体12垂直于正方形面的棱长度相等6两个面是正方形，其余四个面是完全相同的长方形8正方体12所有的棱长度都相等6所有面都是正方形且完全相同8同一个顶点引出的三条棱分别叫做长、宽、高一个长方体至少可以有两个面是正方形，最多可以有6各面是正方形，但不会存在3个、4个、5个面是正方形！练习：（1）判断并改正：1、长方体的六个面一定是长方形； ( )2、正方体的六个面面积一定相等； ( )3、一个长方体(非正方体) 最多有四个面面积相等； ( )4、相交于一个顶点的三条棱相等的长方体一定是正方体。
( )7、长方体的三条棱分别叫做长、宽、高。
( )8、有两个面是正方形的长方体一定是正方体。
( )9、有三个面是正方形的长方体一定是正方体。
（ ）11、有两个相对的面是正方形的长方体，另外四个面的面积是相等的。
（ ）12、长方体和正方体最多可以看到3个面。
（ ） 14、正方体不仅相对的面的面积相等，而且所有相邻的面的面积也都相等。
（ ） 15、长方体（不包括正方体）除了相对的面相等，也可能有两个相邻的面相等。
（ ）16、一个长方体中最少有4条棱长度相等，最多有8条棱长度相等。
（ ）（2）填空：1、一个长方体最多有（ ）个面是正方形，最多有（ ）条棱长度相等。
2、一个长方体的底面是一个正方形，则它的4个侧面是（ ）形。
3、正方体不仅相对的面相等，而且所有相邻的面（ ），它的六个面都是相等的（ ）形。
4、把长方体放在桌面上，最多可以看到（ ）个面。
最少可以看到（ ）个面。
【知识点2】棱长和公式：长方体棱长和=（长+宽+高）长+宽+高=棱长和÷4长方体棱长和=下面周长×2+高×4长方体棱长和=右面周长×2+长×4长方体棱长和=前面周长×2+宽×4正方体棱长和=棱长×12 棱长=棱长和÷12棱长和的变形：例如：有一个礼盒需要用彩带捆扎，捆扎效果如图，打结部分需要10厘米彩带，一共需要多长的彩带？分析：本题虽然并未直接提出求棱长和，但由于彩带的捆扎是和棱相互平行的， 因此，在解决问题时首先确定每部分彩带与那条棱平行，从而间接去求棱长和。
长方体和正方体知识点汇总
长方体和正方体知识点汇总一、长方体长方体是一种具有六个面，每个面均为长方形的立体图形。
它的特点是长宽高不相等，分别对应着长方体的三条棱。
下面总结一些长方体的基本知识：1. 长方体的表面积公式为：S=2×(ab+bc+ac)，其中a、 b、 c 分别为长方体的三个面的长宽高。
2. 长方体的体积公式为：V=abc，其中a、b、c分别为长方体的三个面的长宽高。
3. 长方体的对角线长度公式为：d=√(a²+b²+c²)，其中a、b、c 分别为长方体的三个面的长宽高。
4. 长方体的中心对称轴是一条连接长方体两面中心点的直线，它与长方体的三条棱垂直。
5. 长方体的垂直截面是长方形，水平截面是正方形或长方形。
6. 长方体的立体对称轴有3条：一条是连接对角面中心的对称轴，另外两条是互相垂直的，分别连接相对边中心的对称轴。
7. 长方体的顶点个数为8个。
顶点是立方体的八个角。
二、正方体正方体是一种有六个面，每个面均为正方形的立体图形。
它具有的特点是长宽高相等，都是边长，下面总结一些正方体的基本知识：1. 正方体的表面积公式为：S=6a²，其中a为正方体的边长。
2. 正方体的体积公式为：V=a³，其中a为正方体的边长。
3. 正方体的对角线长度公式为：d=√3a，其中a为正方体的边长。
4. 正方体的中心对称轴是一条连接正方体两面中心点的直线，它与正方体的任何一边垂直。
5. 正方体的垂直截面和水平截面都是正方形。
6. 正方体的立体对称轴有4条：一条是连接对角面中心的对称轴，另外三条是互相垂直的，分别连接相对边中心的对称轴。
7. 正方体的顶点个数为8个。
顶点是正方体的八个角。
总结：长方体和正方体相比，长方体的三条棱长度不相等，而正方体的三条棱长度相等。
在实际生活中，我们可以用长方体来描述一些长宽高不相同的物品，例如房屋、柜子等；而正方体通常用来描述一些长宽高相同的物品，例如小盒子等。
人教版五年级数学下册第三单元《长方体和正方体》知识点汇总清单
人教版五年级数学下册第三单元《长方体和正方体》知识点汇总清单一、长方体和正方体的定义及特征长方体：有6个面的立体图形，每个面都是长方形，任意两个相邻面都是全等的，相对的面是平行的。
正方体：是一种特殊的长方体，所有的面都是正方形。
二、长方体和正方体的面、棱和顶点1. 面：长方体有6个面，分别是底面、顶面和4个侧面。
正方体同样有6个面，每个面都是正方形。
2. 棱：长方体有12条棱，正方体有12条棱。
3. 顶点：长方体有8个顶点，正方体也有8个顶点。
三、长方体和正方体的名字长方体和正方体的命名按底部的形状来命名，如下所示：1. 底面为长方形的长方体，我们称为长方体；2. 底面为正方形的长方体，我们称为正方体。
四、长方体和正方体的面积和体积1. 面积：长方体的面积计算公式：面积 = 底面积 + 侧面积 + 侧面积 + 侧面积 + 侧面积 + 侧面积 = 2ab + 2bc + 2ac（其中a、b、c分别为长方体的长、宽、高）正方体的面积计算公式：面积 = 正方形的边长 ×正方形的边长 ×6 = a × a × 6（其中a为正方体的边长）2. 体积：长方体的体积计算公式：体积 = 底面积 ×高 = 底面积 × c（其中c 为长方体的高）正方体的体积计算公式：体积 = 正方形的边长 ×正方形的边长 ×正方形的边长 = a × a × a（其中a为正方体的边长）五、长方体和正方体的应用及实例长方体和正方体在日常生活中有许多应用，比如：1. 盒子和容器：我们常见的纸箱、塑料盒子、储物箱等都是长方体或正方体的形状，它们能够容纳各种物品。
2. 建筑：很多建筑物的砖块、砖石等都是长方体形状的，如砖墙、柱子等建筑结构。
3. 学习用具：书包、文具盒等也常常是长方体或正方体的形状。
举例：1. 如果一座长方体的长、宽、高分别为3厘米、4厘米、5厘米，则该长方体的面积为36平方厘米，体积为60立方厘米。
长方体和正方体单元知识点
长方体和正方体单元知识点1. 长方体（Rectangular Prism）:长方体是由6个矩形面组成的立体图形。
它的所有对面都是相等的，并且相对的面是平行的。
长方体有8个顶点、12条边和6个面。
1.1定义：长方体的定义可以用以下几个要素来描述：-一个有6个矩形面的立体图形。
-每个面都是直角相邻的。
-所有面的边长都不相等。
-所有对面都是平行的。
1.2特征：长方体具有以下特征：-所有边长不相等。
-所有对面都是平行的。
-每个面上的相对边长相等。
-所有的角都是直角。
1.3表面积计算：长方体的表面积可以通过计算每个面的面积，并将结果相加得到。
表面积 = 2lw + 2lh + 2wh其中，l、w和h分别代表长方体的长度、宽度和高度。
1.4体积计算：长方体的体积可以通过将长度、宽度和高度相乘来计算。
体积 = lwh2. 正方体（Cube）:正方体是一种特殊的长方体，其所有边长相等。
正方体有8个顶点、12条边和6个面。
正方体具有更多的对称性和特殊性质。
2.1定义：正方体的定义可以用以下几个要素来描述：-一个具有6个正方形面的立体图形。
-所有边长相等。
-所有的角都是直角。
2.2特征：正方体具有以下特征：-所有边长相等。
-所有对面都是平行的。
-每个面上的角度都是直角。
-具有更多的对称性，即旋转或反射一个正方体的结果仍然是一个正方体。
2.3表面积计算：正方体的表面积可以通过计算每个面的面积，并将结果相加得到。
表面积=6s^2其中，s代表正方体的边长。
2.4体积计算：正方体的体积可以通过将边长三次幂（即三次方）来计算。
体积=s^3其中，s代表正方体的边长。
总结：长方体和正方体都是由矩形面组成的三维立体图形。
长方体具有所有边长不相等的特征，而正方体具有所有边长相等的特征。
它们在计算表面积和体积时的公式也有所不同。
长方体的表面积为2lw + 2lh + 2wh，体积为lwh；而正方体的表面积为6s^2，体积为s^3、正方体具有更多的对称性和特殊性质。
正方体长方体知识点归纳
正方体长方体知识点归纳一、正方体知识点1. 正方体的概念正方体就是那种超级规整的立体图形啦，它的六个面都是正方形，而且这六个正方形的大小完全一样哦。
就像是那种特别精致的魔方，每个小方块都是正方体的一个小缩影呢。
2. 正方体的棱长棱长就是正方体每条边的长度。
这个棱长可重要啦，它决定了正方体的大小。
比如说，棱长为3厘米的正方体就比棱长为2厘米的正方体要大一些。
而且呀，正方体的12条棱长度都相等，这就像是一个小团队，大家都一样长，没有谁特殊哦。
3. 正方体的表面积表面积呢，就是正方体六个面的面积之和。
一个面的面积是棱长乘以棱长，那正方体的表面积就是棱长×棱长×6啦。
想象一下给正方体穿上一层纸做的衣服，这层纸的大小就是正方体的表面积啦。
比如说棱长是4厘米的正方体，一个面的面积就是4×4 = 16平方厘米，那表面积就是16×6 = 96平方厘米。
4. 正方体的体积体积就是正方体所占空间的大小。
计算方法是棱长×棱长×棱长，就像在一个小盒子里能装多少东西一样。
例如棱长为5厘米的正方体，体积就是5×5×5 = 125立方厘米。
二、长方体知识点1. 长方体的概念长方体是一个有六个面的立体图形，不过和正方体不同的是，它的六个面不一定都是正方形，可能是长方形，当然也有可能有两个相对的面是正方形哦。
就像是我们生活中的书本、盒子之类的，很多都是长方体的形状。
2. 长方体的棱长长方体有12条棱，这12条棱可以分成三组，每组有4条棱，而且每组的4条棱长度是相等的呢。
比如说，一个长方体的长、宽、高分别是5厘米、3厘米、2厘米，那长这条棱对应的就有3条和它一样长的棱，宽和高也是这样。
3. 长方体的表面积长方体的表面积计算稍微复杂一点，公式是（长×宽+长×高+宽×高）×2。
这是因为长方体的六个面两两相对，而且面积有三种不同的情况，把这三种情况的面积加起来再乘以2就得到表面积啦。
正方体与长方体知识点总结
正方体与长方体知识点总结一、正方体1、正方体有8个顶点、12条棱、6个面。
2、公式: 棱长总和＝棱长×12棱长＝棱长总和÷12正方体表面积＝棱长×棱长×6正方体体积＝棱长×棱长×棱长(V=a·a·a=a³)二、长方体1、长方体有8个顶点、12条棱、6个面。
2、公式: 棱长总和=(长+宽+高)×4长=棱长总和÷4-宽-高宽=棱长总和÷4-长-高高=棱长总和÷4-长-宽长方体表面积＝(长×宽+长×高+宽×高)×2前面/后面：长×高左边/右面：宽×高上面/下面：长×宽长方体体积＝长×宽×高=底面积×高=横截面面积×长长=体积÷宽÷高宽=体积÷长÷高高=体积÷长÷宽三、常用知识点总结1、正方体的棱长扩大n倍，棱长总和也扩大(n)倍，表面积扩大(n×n)倍，体积扩大(n×n×n)倍。
2、面积与体积无法比较，因为它们的意义不同。
3、占地面积=底面积=长×宽长方体体积公式可改写为:长方体体积＝底面积×高高=体积÷底面积4、将一个物体投入水中，物体的体积=水面上升部分的体积。
5、将一个正方体模型熔化变成长方体模型，解题关键在于变化前后的体积不变。
6、单位换算口诀:大变小～乘进率～小数点向右移动小变大～除以进率～小数点向左移动。
7、几个同样大小的小正方体，搭成一个长方体，如何摆放长方体的表面积最大？（一条龙一样的摆放）如何摆放表面积最小？(形状越接近于正方体，表面积越小)。
四、关于涂色的正方体的一些规律正方体棱等分的份数三面涂色的个数（在顶点处）两面涂色的个数（在棱中间）一面涂色的个数（在面中间）没有涂色的正方体个数2 8个0 0 03 8个4 8个n 8个12x（3-2）=1212x（4-2）=2412x（n-2）6 x（3-2）²6 x（4-2）²6 x（n-2）²（3-2）³（4-2）³（n-2）³。
《长方体和正方体》必背概念知识点整理
第一单元《长方体和正方体》知识点一、长方体和正方体的特征：1.长方体的特征：长方体有6个面，每个面都是长方形（特殊的有一组对面是正方形），相对的面完全相同；有12条棱，相对的棱平行且相等；有8个顶点。
2.正方体的特征：正方体有6个面，每个面都是正方形，所有的面都完全相同；有12条棱，所有的棱都相等；有8个顶点。
3.长、宽、高：相交于一个顶点的三条棱的长度分别叫做长方体的长、宽、高。
4.长方体的棱长总和=（长＋宽＋高）×4 用字母表示：(a+b+h)×4正方体的棱长总和= 棱长×12 用字母表示：12a二、长方体和正方体的表面积的计算1.什么叫表面积：长方体或正方体6个面的总面积叫做它的表面积。
2.长方体的表面积=（长×宽＋长×高＋宽×高）×2用字母表示：S=（ab＋ah＋bh）×23.正方体的表面积= 棱长×棱长×6 用字母表示：S=6a24．常用的面积单位：平方厘米、平方分米、平方米5.面积单位间的进率：1m2 =100dm2 1dm2 =100cm2三、长方体和正方体的体积的计算1.什么叫体积：物体所占空间的大小叫做物体的体积。
2.长方体的体积= 长×宽×高用字母表示：V=abh3.正方体的体积= 棱长×棱长×棱长用字母表示：V=a34.常用的体积单位：立方厘米、立方分米和立方米5.体积单位间的进率：1m3=1000dm3 1dm3=1000cm3 1m3=100 0000cm36.长方体和正方体的体积统一公式：长方体或正方体的体积=底面积×高用字母表示：V=Sh7.体积单位的互化：把高级单位化成低级单位，用高级单位数乘进率；------大乘小把低级单位聚成高级单位，用低级单位数除以进率。
-----------小除以大8.容积：容器所能容纳物体的体积。
长方体和正方体数学知识点
长方体和正方体数学知识点长方体和正方体数学知识点知识点是在教育实践中，对某一个知识的泛称，多用于口语化，特指教科书上或考试的知识，下面是店铺整理的长方体和正方体数学知识点，一起来看看吧。
长方体和正方体数学知识点1长方体(正方体)的特征1.长方体的特征：有6个面，相对的面完全相同;有12条棱，相对的棱长度相等;有8个顶点2.正方体的特征：正方体的6个面完全相同;12条棱的长度全相等;有8个顶点。
3.长方体长、宽、高的意义：相交于同一顶点的三条棱的长度分别叫做长方体的长、宽、高。
长方体和正方体的表面积1.表面积的意义：长方体或正方体6个或5个面的总面积，叫做它的表面积。
2.长方体的表面积的计算方法：(2个)3.正方体表面积的计算方法：正方体的表面积=棱长2×6长方体和正方体的体积1.体积的意义：物体所占的空间的大小叫做体积。
2.体积单位：立方米、立方分米、立方厘米;字母表示：m3,dm3,cm3。
3.体积单位间的进率：1 m3 =1000dm3 dm3 =1000cm3.4.容积的意义：箱子、油桶等所能装下物体的体积，叫做箱子等的容积。
5.容积的单位和容积单位之间的进率：1L=1000ml6.容积单位和体积单位之间的换算：1L= dm3 1 cm3.=1 ml7.长方体体积计算公式和正方体体积计算公式。
8.容积与体积的'计算方法相同，只是要从里面量它的长、宽和高。
长方体和正方体数学知识点2长方体、正方体的特征1、长方体有（）个面，（）个点，（）条棱长。
相对的面（），每个面都是（）形，特殊情况有（）个面是正方形；棱长分为（）、（）和（），各有（）条。
长方体最少有（）个面是长方形。
2、长方体最多有（）个相对面是正方形，最多有（）个面的完全相同。
3、正方体有（）个面，这些面都是（）形，（）个点，（）条棱长。
它所有的棱长都（）。
4、要焊接一个长10cm，宽8 cm，高6 cm的长方体框架，要准备10cm，8 cm，6 cm的铁丝各（）条。
长方体和正方体相关知识点
长方体和正方体一、知识点1、长方体表面积=（长×宽+长×高+宽×高）×2 即：S=（ab+ah+bh）×22、长方体体积 = 长×宽×高 = 底面积×高即：V = abh = Sh3、正方体表面积= 棱长×棱长×6 即：S = 6a24、正方体体积 = 棱长×棱长×棱长 = a×a×a 即：V = a35、容积和体积的概念：容积是容器所能容纳物体的体积。
体积是指物体所占空间的大小。
6、单位：(1) 体积的单位及进率：1 m³ = 1000 dm³ 1 dm³ = 1000 cm³1cm³= 1000 mm³容积的单位及进率：1L=1000ml容积和体积的单位关系：1L=1dm³ 1ml=1cm³ 1m³=1000L长方体的棱长总和=长×4+宽×4+高×4=（长+宽+高）×4正方体的棱长总和=棱长×12三、补充长方体和正方体的表面积定义：长方体或正方体6个面的总面积，叫做它的表面积。
无底或无盖长方体的表面积（有五个面）=长×宽+长×高×2+宽×高×2=长×宽+（长×高+宽×高）×2无底又无盖长方体的表面积（有四个面）=长×高×2+宽×高×2=（长×高+宽×高）×21平方米=100平方分米 1平方分米=100平方厘米四、面积公式1、长方形的周长=（长+宽）×2 C=(a+b)×22、正方形的周长=边长×4 C=4a3、长方形的面积=长×宽S=ab4、正方形的面积=边长×边长S=a·a= a 25、三角形的面积=底×高÷2 S=ah÷26、平行四边形的面积=底×高S=ah7、梯形的面积=（上底+下底）×高÷2 S=（a＋b）h÷2。
完整版)长方体和正方体知识点总结
完整版)长方体和正方体知识点总结第二单元长方体和正方体总结长方体和正方体是几何学中常见的立体图形。
它们有许多共同的特征，也有一些不同之处。
共同点：长方体和正方体都有六个面，每个面都是一个矩形或正方形。
相对的面是完全相同的，相对的棱长也相等。
长方体和正方体都有8个顶点，每个顶点上的三条棱分别称为长方体的长、宽、高，正方体的棱长是相等的。
不同点：长方体的长、宽、高可以不相等，而正方体的长、宽、高必须相等。
计算方面，长方体的棱长总和可以用公式（长+宽+高）×4计算。
长方体的表面积可以用公式（长×宽+长×高+宽×高）×2计算，也可以用前后面积、左右面积和上下面积分别计算后相加。
正方体的表面积可以用公式棱长×棱长×6计算。
练题：1.已知一个长方体长、宽、高分别是10cm、7cm、4cm，求它的棱长总和。
2.已知一个长方体的棱长和是160dm，其中长是20dm，宽是8dm，求它的高和从一个顶点引出的三条棱的长度总和。
在解答问题时，要充分考虑实际情况，想清楚要算几个面。
例如，一个抽屉有5个面，分别是前面、后面、左面、右面、底面，所以做这样一个抽屉所需要的木板，只要算出这5个面的面积就可以了。
通风管顾名思义是通风用的，没有上面和底面，所以只要算四个侧面就可以了。
具有六个面的长方体或正方体物品包括油箱、罐头盒、纸箱子等。
具有五个面的长方体或正方体物品包括水池、鱼缸等。
具有四个面的长方体或正方体物品包括水管、烟囱等。
练题：1.一个棱长为8dm的正方体纸箱，做100个这样的纸箱至少需要多少平方米纸板？解：一个正方体的表面积为6a²，其中a为棱长，所以一个棱长为8dm的正方体纸箱的表面积为6×8²=384dm²。
做100个需要的表面积为100×384=dm²=38.4m²。
2.一只长0.4米，宽0.25米，深0.3米的长方形鱼缸，至少需要用多少平方米的玻璃？解：长方形鱼缸的底面积为0.4×0.25=0.1m²，两个长面的面积为2×0.4×0.3=0.24m²，两个短面的面积为2×0.25×0.3=0.15m²，所以这只鱼缸的表面积为0.1+0.24+0.24+0.15+0.15=0.88m²。
长方体和正方体知识点汇总
长方体和正方体知识点汇总长方体：1. 定义：长方体，又称作矩形长方体，是一种具有6个矩形面的立体图形。
每个面都是矩形，且相邻面互相垂直。
2. 属性：- 六个面：长方体有六个面，分别被称为底面、顶面、前面、后面、左面和右面。
- 顶点：长方体有8个顶点，每个顶点都是3个面的交点。
- 边：长方体有12条边，每个边都连接两个顶点。
- 对角线：长方体有4条对角线，每条对角线连接两个不相邻的顶点。
- 相邻面：相邻的面互相垂直，即任意两个相邻的面的法向量互为相反数。
3. 公式：- 表面积：长方体的表面积等于各个面积的总和。
表面积公式为：2(lw + lh + wh)，其中l为长度，w为宽度，h为高度。
- 体积：长方体的体积等于底面积乘以高度。
体积公式为：lwh，其中l为长度，w为宽度，h为高度。
4. 性质：- 对角线等长：长方体的对角线相等，且长度等于边长的根号3倍。
- 质心位置：长方体的质心位于两个对面的中点。
- 对称性：长方体具有三个对称面，即通过长方体的任意中心点可以找到三个对称点。
5. 典型问题：- 体积或表面积求解：根据已知条件计算长方体的体积或表面积。
- 折纸问题：长方体可以通过折纸构造，使用规定的折法可以将长方体从一个平面展开为一个矩形。
正方体：1. 定义：正方体是一种拥有六个相等的正方形面的立体图形。
每个面都是正方形，而且相邻面互相垂直。
2. 属性：- 六个面：正方体有六个面，每个面都是正方形，分别被称为顶面、底面、前面、后面、左面和右面。
- 顶点：正方体有8个顶点，每个顶点都是3个面的交点。
- 边：正方体有12条边，每个边都连接两个顶点。
- 对角线：正方体有4条对角线，每条对角线连接两个不相邻的顶点。
- 相邻面：相邻的面互相垂直，即任意两个相邻的面的法向量互为相反数。
3. 公式：- 表面积：正方体的表面积等于各个面积的总和。
表面积公式为：6s^2，其中s为边长。
- 体积：正方体的体积等于边长的立方。
长方体与正方体知识点总结
长方体与正方体知识点总结一、长方体和正方体的认识1、长方体定义：长方体是由六个长方形（特殊情况有两个相对的面是正方形）围成的立体图形。
特征：长方体有 6 个面，每个面都是长方形（可能有两个面是正方形），相对的面完全相同。
长方体有 12 条棱，相对的棱长度相等。
长方体有 8 个顶点。
2、正方体定义：正方体是用六个完全相同的正方形围成的立体图形。
特征：正方体有 6 个面，每个面都是正方形，6 个面完全相同。
正方体有 12 条棱，12 条棱长度都相等。
正方体有 8 个顶点。
3、长方体和正方体的关系正方体是特殊的长方体，当长方体的长、宽、高都相等时，就变成了正方体。
二、长方体和正方体的表面积1、表面积的定义长方体或正方体 6 个面的总面积，叫做它的表面积。
2、长方体的表面积公式：长方体的表面积＝（长×宽＋长×高＋宽×高）× 2例如：一个长方体的长是 5 厘米，宽是 4 厘米，高是 3 厘米。
它的表面积是：（5×4 ＋ 5×3 ＋ 4×3）× 2＝（20 ＋ 15 ＋ 12）× 2＝ 47× 2＝ 94（平方厘米）3、正方体的表面积公式：正方体的表面积＝棱长×棱长× 6例如：一个正方体的棱长是 5 厘米，它的表面积是：5×5×6 ＝ 150（平方厘米）三、长方体和正方体的体积物体所占空间的大小叫做物体的体积。
2、体积单位常用的体积单位有立方米、立方分米、立方厘米。
1 立方米＝ 1000 立方分米1 立方分米＝ 1000 立方厘米3、长方体的体积公式：长方体的体积＝长×宽×高例如：一个长方体的长是 6 分米，宽是 5 分米，高是 4 分米。
它的体积是：6×5×4 ＝ 120（立方分米）4、正方体的体积公式：正方体的体积＝棱长×棱长×棱长例如：一个正方体的棱长是 3 分米，它的体积是：3×3×3 ＝ 27（立方分米）四、容积1、容积的定义箱子、油桶、仓库等所能容纳物体的体积，通常叫做它们的容积。
长方体正方体知识点汇总
长方体正方体知识点汇总长方体和正方体都属于立体图形，具有一些共同和独特的特点。
下面是对长方体和正方体的综合了解和详细解释：一、长方体的定义和特点：长方体是一种有6个面的立体图形，这些面由矩形组成，且相邻面两两平行。
长方体具有以下特点：1. 面的特点：长方体有6个面，其中有3对平行面。
相邻面两两平行，且相对的面是相等的矩形。
2. 边的特点：长方体有12条边，每个顶点有3条边相交。
3. 顶点的特点：长方体有8个顶点，每个顶点都是3个面的交点。
4. 相邻面、边、顶点的关系：长方体中，两个相邻面的共用一条边，两个相邻面的共用一点，这个点同时也是四条边的端点。
5. 相对面的特点：长方体的相对面是相等的矩形，具有相同的形状和大小。
二、正方体的定义和特点：正方体是一种特殊的长方体，所有的面都是正方形，具有以下特点：1. 面的特点：正方体有6个面，都是正方形，且相邻面两两平行。
2. 边的特点：正方体有12条边，每个顶点有3条边相交。
3. 顶点的特点：正方体有8个顶点，每个顶点都是3个面的交点。
4. 相邻面、边、顶点的关系：正方体中，两个相邻面的共用一条边，两个相邻面的共用一点，这个点同时也是四条边的端点。
5. 相对面的特点：正方体的相对面是相等的正方形，具有相同的形状和大小。
三、长方体和正方体的性质：1. 体积：长方体和正方体的体积都可以通过公式V = l × w × h来计算，其中l为长，w为宽，h为高。
正方体的体积可以简化为V = a^3，其中a为边长。
2. 表面积：长方体和正方体的表面积都可以通过公式S = 2lw + 2lh + 2wh来计算，其中l为长，w为宽，h为高。
正方体的表面积可以简化为S = 6a^2，其中a为边长。
3. 对角线：长方体和正方体的对角线可以通过勾股定理来计算。
长方体的对角线长度为d = sqrt(l^2 + w^2 + h^2)，正方体的对角线长度为d = sqrt(3a^2)，其中l、w、h分别为长方体的长、宽、高，a为正方体的边长。
长方体和正方体知识点汇总
长方体和正方体知识点汇总长方体和正方体是几何学中常见的两种立体图形。
它们具有一些相同的特点，也存在一些不同之处。
本文将对长方体和正方体的知识点进行全面的汇总。
以下是对这两种立体图形的基本概念、性质和计算方法等方面进行详细介绍。
一、长方体的基本概念和性质长方体是指具有六个矩形面的立体图形，每个面都是矩形。
它具有以下几个基本概念和性质。
1. 面、棱和顶点：长方体由六个面组成，这些面分别是底面、顶面和四个侧面。
底面和顶面是相似的矩形，而四个侧面则是相似的长方形。
长方体还有12条边，这些边被称为棱。
长方体有8个顶点，每个顶点是三条棱的交点。
2. 对角线：长方体的对角线是连接长方体的两个非相邻顶点的线段。
一个长方体具有4条对角线。
3. 体积和表面积：长方体的体积是指长方体所包含的三维空间的大小，用单位立方计算。
长方体的体积等于底面积乘以高。
长方体的表面积是指长方体所有面的总面积，它等于底面积的两倍加上四个侧面的面积之和。
4. 对称性：长方体具有面对称和点对称。
面对称是指长方体的任意两个相对面是相似的矩形。
点对称是指对长方体中心点进行对称时，长方体保持不变。
二、正方体的基本概念和性质正方体是一种特殊的长方体，它具有六个相等的正方形面。
正方体在几何学中有着独特的特点和性质。
1. 面、棱和顶点：正方体由六个相等的正方形面组成。
正方体有12条边，这些边都具有相等的长度，并且每个顶点都是三条棱的交点。
2. 对角线：正方体的对角线是连接正方体的两个对角顶点的线段。
一个正方体具有4条对角线。
3. 体积和表面积：正方体的体积等于边长的立方，即体积=边长³。
正方体的表面积等于边长的平方的六倍，即表面积=6 ×边长²。
4. 对称性：正方体具有面对称和点对称。
面对称是指正方体的任意两个相对面是相等的正方形。
点对称是指对正方体的中心点进行对称时，正方体保持不变。
三、长方体和正方体的应用长方体和正方体在日常生活和工程中有着广泛的应用。
长方体、正方体的知识点
长方体、正方体的知识点长方体是一种具有六个面的立体图形，其每个面都是一个矩形。
长方体有固定的尺寸，可以根据其长、宽和高来确定。
而正方体是一种特殊的长方体，其所有的面都是相等的正方形，每个角都是直角。
1. 长方体的性质：a. 面：长方体有六个面，每个面都是一个矩形。
其中，相邻的面是平行的。
b. 边：长方体有12条边，每两条边相邻的都是平行的。
每个顶点都连接着三条边。
c. 顶点：长方体有8个顶点，每个顶点都连接着三条边。
d. 对角线：长方体的每个对面都有一条对角线，共6条对角线。
e. 体积：长方体的体积可以通过长、宽和高来计算，公式为体积=长×宽×高。
f. 表面积：长方体的表面积可以通过计算各个面的面积之和来获得，公式为表面积=2×（长×宽+长×高+宽×高）。
2. 正方体的性质：a. 面：正方体有六个面，每个面都是一个正方形。
其中，相邻的面是平行的。
b. 边：正方体有12条边，每两条边相邻的都是平行的。
每个顶点都连接着三条边。
c. 顶点：正方体有8个顶点，每个顶点都连接着三条边。
d. 对角线：正方体的每个对面都有一条对角线，共6条对角线。
e. 体积：正方体的体积可以通过边长（边长相等）来计算，公式为体积=边长×边长×边长。
f. 表面积：正方体的表面积可以通过边长（边长相等）来计算，公式为表面积=6×边长×边长。
3. 长方体和正方体的区别：a. 面形状：长方体的面是矩形，而正方体的面是正方形。
b. 边长：长方体的边长可以不相等，而正方体的边长是相等的。
c. 面积和体积计算：长方体的表面积和体积计算需要考虑长、宽、高的不同值，而正方体的面积和体积计算只需要一个边长即可。
4. 长方体和正方体的应用：a. 建筑：长方体和正方体是建筑中常见的立体图形。
很多建筑物的结构和形状可以用长方体或正方体来描述。
b. 数学问题：长方体和正方体经常在数学问题中出现，如几何形状的计算、体积和表面积的求解等。
长方体和正方体知识点汇总
长方体和正方体知识点汇总一、长方体和正方体的定义及性质1. 定义长方体：长方体是一种六个面都是矩形的立体图形，其中相对的两个面是长方形，其余四个面是正方形。
正方体：正方体是一种六个面都是正方形的立体图形，每个面的边长相等。
2. 性质（1）长方体的性质长方体有6个面，12条棱，8个顶点。
相对的面是长方形，其余四个面是正方形。
相邻的棱长相等，相对的棱长也相等。
长方体的对角线互相垂直，且相等。
（2）正方体的性质正方体有6个面，12条棱，8个顶点。
所有面都是正方形，边长相等。
相邻的棱长相等，相对的棱长也相等。
正方体的对角线互相垂直，且相等。
二、长方体和正方体的表面积与体积1. 长方体的表面积与体积（1）表面积长方体的表面积是指六个面的面积之和。
设长方体的长、宽、高分别为a、b、c，则长方体的表面积S为：S = 2(ab + ac + bc)（2）体积长方体的体积是指长、宽、高三个维度的乘积。
设长方体的长、宽、高分别为a、b、c，则长方体的体积V为：V = abc2. 正方体的表面积与体积（1）表面积正方体的表面积是指六个面的面积之和。
设正方体的边长为a，则正方体的表面积S为：S = 6a^2（2）体积正方体的体积是指边长的三次方。
设正方体的边长为a，则正方体的体积V为：V = a^3三、长方体和正方体的空间关系1. 长方体的空间关系长方体的底面与顶面平行，且底面与侧棱垂直。
长方体的侧面与底面垂直，且相邻侧面互相垂直。
长方体的对角线互相垂直，且相等。
2. 正方体的空间关系正方体的底面与顶面平行，且底面与侧棱垂直。
正方体的侧面与底面垂直，且相邻侧面互相垂直。
正方体的对角线互相垂直，且相等。
四、长方体和正方体的应用1. 长方体的应用长方体广泛应用于建筑设计、家具设计、包装设计等领域。
长方体的体积和表面积计算对于计算材料用量、确定空间大小等有重要作用。
2. 正方体的应用正方体在建筑设计、雕塑创作、数学建模等领域有广泛的应用。
长方体和正方体的知识点整理
长方体和正方体的知识点整理长方体和正方体是几何学中的两种常见立体图形。
它们在几何学、物理学和工程学等领域中具有广泛的应用。
下面是关于。
一、长方体的定义和性质：1. 长方体是一种六个面都是矩形的几何体，每对相对的面是相等并平行的。
2. 长方体具有8个顶点、12条棱和6个面。
3. 长方体的面包括底面、顶面、前后左右四个侧面。
4. 长方体的棱包括底边、顶边和侧棱。
5. 长方体的对角线是连接非相邻顶点的线段。
长方体的对角线的长度可以通过勾股定理计算。
6. 长方体的体积可以通过底面积与高度的乘积计算，即V = l × w × h，其中l、w、h分别表示长方体的长度、宽度和高度。
7. 长方体的表面积可以通过各个面的面积之和计算，即A = 2lw + 2lh + 2wh。
8. 对于长方体来说，当长方体的长度、宽度和高度相等时，它就是一个正方体。
二、正方体的定义和性质：1. 正方体是一种六个面都是正方形的几何体。
2. 正方体具有8个顶点、12条边和6个面。
3. 正方体的面包括底面、顶面、前后左右四个侧面。
4. 正方体的对角线是连接非相邻顶点的线段。
正方体的对角线的长度可以通过勾股定理计算。
5. 正方体的棱长度都相等。
6. 正方体的体积可以通过边长的立方计算，即V = a^3，其中a表示正方体的边长。
7. 正方体的表面积可以通过各个面的面积之和计算，即A = 6a^2。
8. 正方体的对称轴有4条，分别是通过两个相对的棱中点的线段。
三、长方体和正方体的应用：1. 长方体和正方体在建筑、家具和包装等领域中都有广泛应用。
例如，房屋的建筑结构常常利用长方体形状的砖块、瓷砖等构建。
2. 长方体和正方体在物流和仓储管理中起着重要作用。
货物、箱子和容器常常采用长方体和正方体的形状，以便更好地摆放和储存。
3. 长方体和正方体在数学教育中也是一个重要的学习对象。
学生通过研究长方体和正方体的性质和计算方法，提高他们的几何学能力。
长方体与正方体知识点总结
长方体与正方体知识点总结长方体和正方体是几何学中常见的三维立体图形。
本文将对长方体与正方体的定义、性质、公式以及应用进行总结。
一、长方体的定义与性质长方体是一种具有六个矩形面的立体图形，其中相对的面是相等的，并且每个面都是矩形。
长方体具有以下性质：1. 全面：长方体的六个面都是矩形面，每个面都是全面。
2. 全等：相对的面积相等，且相邻面是相等的。
3. 全直角：长方体的每个面都与相邻面垂直相交，形成直角。
4. 对角线相等：长方体的对角线长度相等。
5. 体对角线：长方体的一个对角线连接两个不相邻的顶点，叫做体对角线。
二、长方体的公式1. 表面积公式：长方体的表面积等于各个面积的总和，公式如下：表面积 = 2(长 ×宽 + 长 ×高 + 宽 ×高)2. 体积公式：长方体的体积等于底面积与高的乘积，公式如下：体积 = 长 ×宽 ×高三、正方体的定义与性质正方体是一种具有六个正方形面的立体图形，每个面都是正方形。
正方体具有以下性质：1. 全面：正方体的六个面都是正方形，每个面都是全面。
2. 全等：相对的面积相等，且相邻面是相等的。
3. 全直角：正方体的每个面都与相邻面垂直相交，形成直角。
4. 对角线相等：正方体的对角线长度相等。
5. 体对角线：正方体的对角线连接两个不相邻的顶点，叫做体对角线。
四、正方体的公式1. 表面积公式：正方体的表面积等于各个面积的总和，公式如下：表面积 = 6 × (边长 ×边长)2. 体积公式：正方体的体积等于边长的立方，公式如下：体积 = 边长 ×边长 ×边长五、长方体与正方体的应用由于长方体与正方体在生活与工作中广泛存在，所以它们的应用也十分广泛。
以下是一些常见的应用场景：1. 建筑领域：长方体和正方体常被用作建筑物的模型，能够帮助建筑师、设计师更好地展示建筑的外观和内部空间。
2. 包装与储物：长方体和正方体形状的箱子常被用于包装物品，方便储存和搬运。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
长方体和正方体知识点 Prepared on 24 November 2020
长方体（一）（二）复习重点
一、知识点一：长方体和正方体的认识
1、长方体的特征：长方体有6个面，每个面都是长方形（特殊的有一组对面是正方形），相对的面完全相同；有12条棱，相对的棱平行且相等；有8个顶点。
2、正方体的特征：正方形有6个面，每个面都是正方形，所有的面都完全相同；有12条棱，所有的棱都相等；有8个顶点。
3、长方体的长、宽、高各有4条。
长方体的棱长总和=（长＋宽＋高）×4或长方体的棱长总和=长×4＋宽×4＋高×4
4、正方体的棱长总和= 棱长×12
练习：1、一个正方体的棱长是2cm，它的棱长总和是（）cm
2、用36cm长的铁丝，可以围成一个长3cm，宽2cm，高（）cm的长方体。
3、8根长4cm，6根长3cm，4根长2cm的木棒，最多能围成（）种不同的长方体。
二、知识点二：长方体和正方体的表面积的计算
5、长方体或正方体6个面的总面积叫做它的表面积。
6、长方体的表面积=（长×宽＋长×高＋宽×高）×2
用字母表示：S=（ab＋ah＋bh）×2
正方体的表面积= 棱长×棱长×6
用字母表示：S=6a2
7、表面积单位：平方厘米、平方分米、平方米
8、1m2 =100dm2 1dm2 =100cm2
练习：1、长方体的长是5cm，宽和高都是4cm，这个长方体的表面积是
（）cm2
2、要在一个长6米，宽4米，深2米的游泳池的四周及底面贴上瓷砖，要贴上（）平方米的瓷砖。
3、做一个长2dm，宽3dm,高3m的长方形的烟囟，要用（）平方分米的铁板。
三、知识点三：长方体和正方体的体积的计算
9、体积：物体所占空间的大小叫做物体的体积。
10、长方体的体积= 长×宽×高用字母表示：V=abh
正方体的体积= 棱长×棱长×棱长用字母表示：V=a3
11、体积单位：立方厘米、立方分米和立方米
1m3=1000dm3 1dm3=1000cm3 1m3=100 0000cm3
12、长方体正方体体积统一计算公式：
长方体或正方体的体积=底面积×高用字母表示：V=Sh
13、单位换算：把高级单位化成低级单位，用高级单位数乘以进率；
把低级单位聚成高级单位，用低级单位数除以进率。
练习；1、千米＝（）米，20分＝（）时
240ml=（）l =（）dm3
=（）cm 56dm2=（）cm2
2、有一个长方体和一个正方体，长方体的长是5分米，宽是4分米，高是6分米，正方体的棱长是5分米，（）的体积大，大（）立方分米。
3、把一个体积是216立方分米的正方体棱长扩大2倍后，它的体积是（）方方分分。
4、有两个体积相等的长方体和正方体，正方体的棱长是6cm，长方体的底面积是18cm2，这个长方形的高是（）cm。
四、知识点四：长方体和正方体的容积的计算
14、容积：容器所能容纳物体的体积。
15、容积单位：升和毫升（L和ml）
1L=1000ml 1L= 1dm3 1ml= 1cm3
16、容积单位的计算单位：长方体和正方体容器容积的计算方法，跟体积的计算方法相同，但要从里面量长、宽、高。
17、有趣的测量：水面上升的体积就是物体的体积。
练习；1、填一填：
橡皮擦的体积是15（）；一个杯子的容积是500
（）；
一本书的封面的面积是165（）；一瓶牛奶约500（）；
一个讲台的体积约是（）；一本词典的体积约是900
（）；
2、一个长方体容器，底面长2分米，宽分米，放入一个土豆后水面升高了分米，这个土豆的体积是（）立方分米。
五、知识点五：正方体展开图。
练习；用自己喜欢的图标出上面展开图中相对的面。
六、知识点六：包装中的学问。
最节约材料的包装方法：用大面重叠。
练习；把两盒糖果包成一包（糖果盒是一个长20厘米，宽15厘米，高5厘米的长方体），共有（）种包装方法，至少要（）平方厘米的包装纸。