(完整版)长方体和正方体知识点复习整理
长方体和正方体整理与复习
40升＝40000立方厘米
（50× 40）x＝40000
x＝40000÷ 2000
x＝20
答：水深大约20厘米。
把一个棱长0.8米的正方体钢坯，锻造成一 个横截面面积是0.16平方米的长方体方钢。 锻造成的这块方钢长多少米？
0.8×0.8×0.8÷0.16＝3.2（米）
用包装纸把两个长6厘米，宽5厘米，高4厘米的长方 体礼盒包在一起，有几种包法，哪种包装方法最节 省材料？
长方体和正方体 的整理与复习
形
相同点
体 面 棱 顶点
面的形状
不同点 面的面积
棱长
长 方 体
6 个 面
12 条 棱
8 个 顶 点
6个面都是长方形， 有时有两个相对的 相对面的面积相等
面是正方形
相对应的 棱的长度 相等
8
正 6 12 个 方个 条 顶 体面 棱 点
6个面的面积都想等
6个面都是完全相同 的正方形
6、相邻的面是正方形的长方体是正方体。 （ √ ）
一件雕塑的底座是用混凝土浇注成的棱长2.6米 的正方体。（只列式不计算 ）
1.这件雕塑占地多少平方米？ 2.6×2.6＝6.76(m2)
2. 浇注这件雕塑底座需要混凝土多少立方米？
2.6×2.6×2.6=17.576(m3）
3. 给这件雕塑的底座四周贴上花岗石，贴花岗 石的面积是多少平方米？2.6×2.6×4=243;bh)
面积×长 米
叫做它们 ×2 的表面积。
平方分 米
V=abh
立方 米
容器所能容纳物
正 方 体
正方体表面积＝ 棱长×棱长×6
平方米
体的体积，叫做 正方体体 这个容器的容积。积＝棱长
[笔记]人教版五年级下册数学第三单元《长方体和正方体的认识》知识点
![[笔记]人教版五年级下册数学第三单元《长方体和正方体的认识》知识点](https://img.taocdn.com/s3/m/d72e64c3185f312b3169a45177232f60ddcce719.png)
第三单元《长方体和正方体》1.长方体：由六个长方形（特殊情况有两个相对的面是正方形）围成的立体图形叫长方体.长方体的任意一个面的对面都与它完全相同。
2.长、宽、高：长方体的每一个矩形都叫做长方体的面，面与面相交的线叫做长方体的棱，三条棱相交的点叫做长方体的顶点，相交于一个顶点的三条棱的长度分别叫做长方体的长、宽、高。
3.长方体的特征(1)长方体有6个面,每个面都是长方形,至少有两个相对的两个面完全相同。
特殊情况时有两个面是正方形，其他四个面都是长方形，并且完全相同。
(3)长方体有12条棱，相对的棱长度相等。
可分为三组，每一组有4条棱。
还可分为四组，每一组有3条棱。
(3)长方体有8个顶点。
每个顶点连接三条棱。
(4) 长方体相邻的两条棱互相（相互）垂直。
长方体是由6个长方形（特殊情况有两个相对的面是正方形）围成的立体图形。
在一个长方体中，相对的面完全相同，相对的棱长度相等。
顶点个数面棱个数大小关系条数长度关系8 6 相对的面相等12 平行的棱长相等4.棱长总和公式：长方体棱长总和=4条长+4条宽+4条高＝（长+高+宽）×4宽=棱长之和÷4－长－高长＝棱长之和÷4－宽－高高＝棱长之和÷4－宽－长二、正方体的认识：1. 正方体的认识：正方体是由6个完全相同的正方形围成的立体图形。
正方体有6个面，12条棱，8个顶点，每个面都是正方形，面积都相等。
每条棱的长度都相等。
正方体的长、宽、高都相等，统称棱长。
2.长方体和正方体的关系：正方体是一种特殊的长方体。
3．正方体棱长之和：棱长×１２=棱长之和棱长之和÷１２＝棱长4.长方体的表面积（1）长方体和正方体6个面的总面积，叫做它的表面积。
（2）表面积计算公式①.因为长方体有“上”、“下”、“前”、“后”、“左”、“右”6个面,相对的2个面相等，所以先算上下两个面，再算前后两个面，最后算左右两个面。
②长方体的表面积=（长×宽＋长×高＋宽×高）×2用字母表示： S=（ab＋ah＋bh）×2长方体表面积＝（长×宽＋长×高＋宽×高）×2设一个长方体的长、宽、高分别为a、b、c，则它的表面积S：S = 2ab + 2bc+ 2ca= 2 ( ab + bc + ca)长方体没盖的表面积＝长×宽＋长×高×2 ＋宽×高×2③特殊长方体的表面积（有两个面是正方形）正方形的两个面完全相同，其余四个面完全相同。
(完整版)长方体和正方体知识点汇总(最新整理)
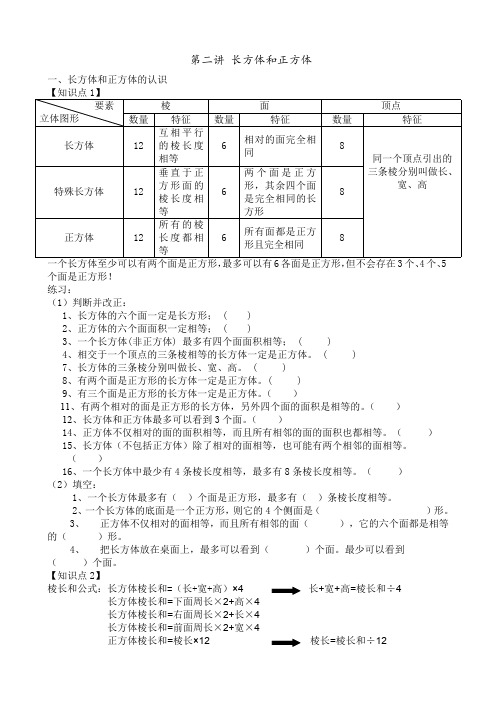
第二讲 长方体和正方体一、长方体和正方体的认识【知识点1】棱面顶点要素立体图形数量特征数量特征数量特征长方体12互相平行的棱长度相等6相对的面完全相同8特殊长方体12垂直于正方形面的棱长度相等6两个面是正方形，其余四个面是完全相同的长方形8正方体12所有的棱长度都相等6所有面都是正方形且完全相同8同一个顶点引出的三条棱分别叫做长、宽、高一个长方体至少可以有两个面是正方形，最多可以有6各面是正方形，但不会存在3个、4个、5个面是正方形！练习：（1）判断并改正：1、长方体的六个面一定是长方形； ( )2、正方体的六个面面积一定相等； ( )3、一个长方体(非正方体) 最多有四个面面积相等； ( )4、相交于一个顶点的三条棱相等的长方体一定是正方体。
( )7、长方体的三条棱分别叫做长、宽、高。
( )8、有两个面是正方形的长方体一定是正方体。
( )9、有三个面是正方形的长方体一定是正方体。
（ ）11、有两个相对的面是正方形的长方体，另外四个面的面积是相等的。
（ ）12、长方体和正方体最多可以看到3个面。
（ ） 14、正方体不仅相对的面的面积相等，而且所有相邻的面的面积也都相等。
（ ） 15、长方体（不包括正方体）除了相对的面相等，也可能有两个相邻的面相等。
（ ）16、一个长方体中最少有4条棱长度相等，最多有8条棱长度相等。
（ ）（2）填空：1、一个长方体最多有（ ）个面是正方形，最多有（ ）条棱长度相等。
2、一个长方体的底面是一个正方形，则它的4个侧面是（ ）形。
3、正方体不仅相对的面相等，而且所有相邻的面（ ），它的六个面都是相等的（ ）形。
4、把长方体放在桌面上，最多可以看到（ ）个面。
最少可以看到（ ）个面。
【知识点2】棱长和公式：长方体棱长和=（长+宽+高）长+宽+高=棱长和÷4长方体棱长和=下面周长×2+高×4长方体棱长和=右面周长×2+长×4长方体棱长和=前面周长×2+宽×4正方体棱长和=棱长×12 棱长=棱长和÷12棱长和的变形：例如：有一个礼盒需要用彩带捆扎，捆扎效果如图，打结部分需要10厘米彩带，一共需要多长的彩带？分析：本题虽然并未直接提出求棱长和，但由于彩带的捆扎是和棱相互平行的， 因此，在解决问题时首先确定每部分彩带与那条棱平行，从而间接去求棱长和。
五年级长方体和正方体概念和公式归纳
长方体和正方体概念一、长方体和正方体的各部分名称1.由6个长方形（特殊情况有两个相对的面是正方形）围成的立体图形叫做长方体。
在一个长方体中，相对面完全相同，相对的棱长度相等。
两个面相交的边叫做棱。
三条棱相交的点叫做顶点。
相交于一个顶点的三条棱的长度分别叫做长方体的长、宽、高。
3.由6个完全相同的正方形围成的立体图形叫做正方体（也叫做立方体）。
正方体有有6个面，8个顶点，12条棱，它们的长度都相等，所有的面都完全相同。
4.长方体和正方体的面、棱和顶点的数目都一样，只是正方体的棱长都相等，正方体可以说是长、宽、高都相等的长方体，它是一种特殊的长方体。
5.长方体有6个面，8个顶点，12条棱，相对的面的面积相等，相对的棱的长度相等。
一个长方体最多有6个面是长方形，最少有4个面是长方形，最多有2个面是正方形。
正方体有6个面，每个面都是正方形，每个面的面积都相等，有12条棱，每条的棱的长度都相等。
二、总棱长公式长方体的棱长总和=（长+宽+高）×4棱长总和÷4=长+宽+高正方体的棱长总和=棱长×12正方体的棱长=棱长总和÷12三、表面积1.长方体或正方体6个面和总面积叫做它的表面积。
2.长方体的表面积=（长×宽＋长×高＋宽×高）×2无底（或无盖）长方体表面积= 长×宽＋（长×高＋宽×高）×2无底又无盖长方体表面积=（长×高＋宽×高）×2正方体的表面积=棱长×棱长×6四、体积1.物体所占空间的大小叫做物体的体积。
2.长方体的体积=长×宽×高=底面积×高V=abh=sh长=体积÷宽÷高a=V÷b÷h宽=体积÷长÷高b=V÷a÷h高=体积÷长÷宽h= V÷a÷b3.正方体的体积=棱长×棱长×棱长 V=a×a×a注意：正方体的棱长扩大n倍，表面积扩大n的平方倍，体积扩大n的立方倍。
长方体正方体知识点及重点题型
长方体和正方体的知识点1 1 一、正方体部分①最少要八个．．相同．．的小正方体才能拼成一个较大的正方体。
②正方体有十一种展开图。
③正方形涂色B ：把一个正方体的表面都涂满颜色，然后切成棱长为1的小正方体。
（长方体同）三面有颜色：有8个，在顶点上二面有颜色：有(棱长－2)×12 在棱长上 实际上求棱长减去2以后正方体的棱长和一面有颜色：有(棱长－2)2 ×6在表面上 实际上求棱长减去2以后正方体的表面积没有颜色：(棱长－2)3 在正方体的内部 实际是求棱长减去2以后正方体的体积。
④正方体的棱长扩大到原来的2倍，表面积扩大到原来的4倍，增加了．．．原来的3倍，面积是原来的平方倍； 正方体的棱长扩大到原来的2倍体积扩大到8倍，增加了．．．原来的7倍。
正方体体积是原来的立方倍。
⑤设一个正方体的棱长为a ，则它的棱长和=12a ，表面积S ：S=6×a×a =6a 2 体积V= a×a×a = a3 长方体和正方体都有：12条棱、6个面、8个顶点正方体的总棱长= 棱长 × 12 （单位：长度单位）正方体的表面积 =（棱长 × 棱长）×6 （单位：平方单位）正方体的体积 = 棱长 × 棱长 × 棱长 即： V= a 3 （单位：立方单位）长方体（或正方体）的体积= 底面积×高 即： V=sh （单位：平方单位）⑥体积单位有：立方米、立方分米、立方厘米 1立方分米=1000立方厘米 1立方米=1000立方分米 容积单位有：立方米、升、 毫升 1升=1立方分米 1毫升=1立方厘米 1升=1000毫升二、长方体①长方体有六个面，12条棱，8个顶点，最多可以看到3个面，最少看到一个面，长方体不包括正方体， 最多有两个面是正方形，最多有四个面相等，最多有8条棱相等。
②长、宽、高均不相等的长方体的表面展开图：一四一式27种；二三一式18种；二二二式6种；三三式3种，共计54种。
五年级下数学常考考点：长方体和正方体
五年级下数学常考考点：长方体和正方体1、长方体和正方体的特征长方体的特征①长方体有6个面，每个面都是长方形(可能有两个面是正方形)，相对的两个面完全相同。
②长方体有12条棱，每相对的4条棱相等(按照相等的棱长可分为3组)。
③三条棱相交的点叫顶点。
长方体有8个顶点④相交于同一顶点的棱不相等，分别叫做长方体的长，宽，高。
以同一顶点上的长，宽，高为一组，可分为4组。
正方体的特征：①正方体有6个面，面积都相等;②正方体有12条棱，长度都相等，有8个顶点。
③正方体是一种特殊的长方体。
长方体和正方体都有6个面、12条棱、8个顶点。
长方体：由六个长方形(特殊情况有两个相对的面是正方形)围成的立体图形叫长方体。
正方体：长宽高都相等的长方体叫正方体。
正方体是特殊的长方体：长方体的表面积长方体的表面积公式：长方体的表面积=长×宽×2+长×高×2+宽×高×2;S=(ab+ah+bh)×2。
正方体的表面积公式：正方体的表面积=棱长×棱长×6;S=6 。
2、长方体和正方体的棱长(1)长方体的棱长总和=(长+宽+高)×4=长×4+宽×4+高×4(2)正方体的棱长总和=棱长×123、长方体和正方体的表面积长方体或正方体6个面和总面积叫做它的表面积。
(1)长方体的表面积=(长×宽+长×高+宽×高)×2(2)正方体的表面积=棱长×棱长×64、长方体和正方体的体积(1)长方体的体积=长×宽×高(2)正方体的体积=棱长×棱长×棱长V=a×a×a = a³(3)长方体或正方体底面的面积叫做底面积。
长方体(或正方体)的体积=底面积×高V=S h(横截面积相当于底面积，长相当于高)。
完整版)长方体和正方体的知识点整理
完整版)长方体和正方体的知识点整理长方体和正方体的知识整理一、概念长方体是由6个长方形（特殊情况下有两个相对的面是正方形）围成的立体图形。
在长方体中，相对的面完全相同，相对的棱长度相等。
两个面相交的边叫做棱，三条棱相交的点叫做顶点。
相交于一个顶点的三条棱的长度分别叫做长方体的长、宽、高。
正方体是由6个完全相同的正方形围成的立体图形。
正方体有12条棱，它们的长度都相等，所有的面都完全相同。
长方体和正方体的面、棱和顶点的数目都一样，只是正方体的棱长都相等，正方体可以说是长、宽、高都相等的长方体，它是一种特殊的长方体。
二、长方体和正方体的棱长和表面积长方体的棱长总和=（长+宽+高）×4，长=棱长总和÷4－宽－高，宽=棱长总和÷4－长－高，高=棱长总和÷4－长－宽。
正方体的棱长总和=棱长×12，正方体的棱长=棱长总和÷12.长方体或正方体的长、宽、高同时扩大几倍，棱长总和会扩大相同的倍数。
长方体的表面积=（长×宽＋长×高＋宽×高）×2，无底（或无盖）长方体表面积=长×宽＋（长×高＋宽×高）×2，无底又无盖长方体表面积=（长×高＋宽×高）×2，正方体的表面积=棱长×XXX×6.表面积的常用单位有：平方米、平方分米、平方厘米。
相邻两个面积单位之间的进率是100，1m=100dm，1dm=100cm。
三、生活实际油箱、罐头盒等都是6个面；游泳池、鱼缸、粉刷教室等都只有5个面；水管、烟囱等都只有4个面。
注意：长方体或正方体每截断一次会增加两个截面，所以这时的两个物体的表面积大于原来物体的表面积。
长方体或正方体的长、宽、高同时扩大几倍，其表面积会扩大倍数的平方倍。
比如，若长、宽、高各扩大2倍，则表面积会扩大到原来的4倍。
长方体和正方体的体积是指物体所占空间的大小。
(完整版)长方体和正方体知识点
一、知识点一：长方体和正方体的认识
6个面，每个面都是长方形（特殊的有一组对面是正方形），相对的面完全相同；有12条棱，相对的棱平行且相等；有8个顶点。
正方形有6个面，每个面都是正方形，所有的面都完全相同；有12条棱，所有的棱都相等；有8个顶点。
长方体的长、宽、高。
=（长＋宽＋高）×4
用字母表示：(a+b+h)×4
正方体的棱长总和= 棱长×12
用字母表示：12a
二、知识点二：长方体和正方体的表面积的计算
6个面的总面积叫做它的表面积。
=（长×宽＋长×高＋宽×高）×2用字母表示：S=（ab＋ah＋bh）×2
正方体的表面积= 棱长×棱长×6
用字母表示：S=6a2
6
7、1m2 =100dm2 1dm2 =100cm2
三、知识点三：长方体和正方体的体积的计算
= 长×宽×高
用字母表示：V=abh
正方体的体积= 棱长×棱长×棱长
用字母表示：V=a3
1m3=1000dm3 1dm3=1000cm3 1m3=100 0000cm3
长方体或正方体的体积=底面积×高
用字母表示：V=Sh
把高级单位化成低级单位，用高级单位数乘以进率；------大乘小
把低级单位聚成高级单位，用低级单位数除以进率。
-----------小除大
四、知识点三：长方体和正方体的容积的计算
L和ml）
1L=1000ml 1L= 1dm3 1ml= 1cm3
跟体积的计算方法相同，但要从里面量长、宽、高。
长方体与正方体总复习
【知识点讲解】长方体的棱长总和=（长+宽+高）×4＝长×4+宽×4+高×4 L=（a＋b＋h）×4 长=棱长总和÷4－宽－高a=L÷4－b－h宽=棱长总和÷4－长－高b=L÷4－a－h高=棱长总和÷4－长－宽h=L÷4－a－b正方体的棱长总和=棱长×12 L=a×12正方体的棱长=棱长总和÷12 a=L÷123、长方体或正方体6个面和总面积叫做它的表面积。
长方体的表面积=（长×宽＋长×高＋宽×高）×2 S=2（ab＋ah＋bh）无底（或无盖）长方体表面积= 长×宽＋（长×高＋宽×高）×2无底又无盖长方体表面积=（长×高＋宽×高）×2 S=2（ah＋bh）贴墙纸正方体的表面积=棱长×棱长×6 S=a×a×6 用字母表示：S= 6a2生活实际：油箱、罐头盒等都是6个面游泳池、鱼缸等都只有5个面水管、烟囱等都只有4个面。
注意1：用刀分开物体时，每分一次增加两个面。
（表面积相应增加）注意2：长方体或正方体的长、宽、高同时扩大几倍，表面积会扩大倍数的平方倍。
（如长、宽、高各扩大2倍，表面积就会扩大到原来的4倍）。
4、物体所占空间的大小叫做物体的体积。
长方体的体积=长×宽×高V=abh长=体积÷宽÷高a=V÷b÷h宽=体积÷长÷高b=V÷a÷h高=体积÷长÷宽h= V÷a÷b正方体的体积=棱长×棱长×棱长长方体或正方体底面的面积叫做底面积。
长方体（或正方体）的体积=底面积×高用字母表示：V=S h （横截面积相当于底面积，长相当于高）。
完整版)长方体和正方体知识点总结
完整版)长方体和正方体知识点总结第二单元长方体和正方体总结长方体和正方体是几何学中常见的立体图形。
它们有许多共同的特征，也有一些不同之处。
共同点：长方体和正方体都有六个面，每个面都是一个矩形或正方形。
相对的面是完全相同的，相对的棱长也相等。
长方体和正方体都有8个顶点，每个顶点上的三条棱分别称为长方体的长、宽、高，正方体的棱长是相等的。
不同点：长方体的长、宽、高可以不相等，而正方体的长、宽、高必须相等。
计算方面，长方体的棱长总和可以用公式（长+宽+高）×4计算。
长方体的表面积可以用公式（长×宽+长×高+宽×高）×2计算，也可以用前后面积、左右面积和上下面积分别计算后相加。
正方体的表面积可以用公式棱长×棱长×6计算。
练题：1.已知一个长方体长、宽、高分别是10cm、7cm、4cm，求它的棱长总和。
2.已知一个长方体的棱长和是160dm，其中长是20dm，宽是8dm，求它的高和从一个顶点引出的三条棱的长度总和。
在解答问题时，要充分考虑实际情况，想清楚要算几个面。
例如，一个抽屉有5个面，分别是前面、后面、左面、右面、底面，所以做这样一个抽屉所需要的木板，只要算出这5个面的面积就可以了。
通风管顾名思义是通风用的，没有上面和底面，所以只要算四个侧面就可以了。
具有六个面的长方体或正方体物品包括油箱、罐头盒、纸箱子等。
具有五个面的长方体或正方体物品包括水池、鱼缸等。
具有四个面的长方体或正方体物品包括水管、烟囱等。
练题：1.一个棱长为8dm的正方体纸箱，做100个这样的纸箱至少需要多少平方米纸板？解：一个正方体的表面积为6a²，其中a为棱长，所以一个棱长为8dm的正方体纸箱的表面积为6×8²=384dm²。
做100个需要的表面积为100×384=dm²=38.4m²。
2.一只长0.4米，宽0.25米，深0.3米的长方形鱼缸，至少需要用多少平方米的玻璃？解：长方形鱼缸的底面积为0.4×0.25=0.1m²，两个长面的面积为2×0.4×0.3=0.24m²，两个短面的面积为2×0.25×0.3=0.15m²，所以这只鱼缸的表面积为0.1+0.24+0.24+0.15+0.15=0.88m²。
长方体和正方体知识点及类型题总结
一，概念和定义：1，长方体：由6个长方形（特殊情况有两个相对的面是正方形）围成的立体图形叫做长方体。
1，棱长：两个面相交的边叫做棱。
2，顶点：三条棱相交的点叫做顶点。
3，长宽高：相交于一个顶点的三条棱的长度分别叫做长方体的长、宽、高。
2，长方体的特征： 1，有6个面，8个顶点，12条棱，相对的面的面积相等，相对的棱的长度相等。
2，一个长方体最多有6个面是长方形，最少有4个面是长方形，最多有2个面是正方形。
3，正方体：由6个完全相同的正方形围成的立体图形叫做正方体（也叫做立方体）。
4，正方体特点： 1，有6个面，8个顶点，12条棱，12条棱长度都相等，6个面的面积都相等。
2，正方体可以说是长、宽、高都相等的长方体，它是一种特殊的长方体。
5，长方体长、宽、高的意义：相交于同一顶点的三条棱的长度分别叫做长方体的长、宽、高。
6，表面积 1，意义：长方体或正方体6个面的总面积，叫做它的表面积。
2，长方体表面积：长方体的表面积=(长×宽+宽×高+长×高)×2 字母表示S=2（ab＋ah＋bh）3，正方体表面积：正方体的表面积=棱长×棱长×6（任意一个面积×6），字母表示 S=a×a×64，无底（或无盖）长方体表面积= （长×宽＋长×高＋宽×高）×2 - 长×宽5，无底又无盖长方体表面积=（长×宽＋长×高＋宽×高）×2 - （长×宽）×26，没盖的正方体表面积＝棱长×棱长×57，体积 1，意义：物体所占空间的大小叫做物体的体积。
2，体积单位：立方米，立方分米，立方厘米；用字母表示为：3，体积单位之间的进率：每两个相邻的体积单位之间的进率是1000.4，长方体的体积=长×宽×高=底面积×高字母表示V=abh 或 V=S h5，正方体的体积=棱长×棱长×棱长=底面积×高字母表示 V=a×a×a = a3读作“a的立方”表示3个a相乘，（即a·a·a）6，特殊体积：在一个有水的容器里放入一个物体（如：石头等），水面会上升，水面上升那部分水的体积，就是物体的体积。
长方体和正方体单元整理复习
建立模型
对于复杂的问题，可以尝试建 立数学模型，以便更直观地理
解问题并找到解决方案。
多做练习
通过大量的练习，可以加深对 知识点的理解，提高解题的准
确性和效率。
06 复习策略与建议
系统回顾本单元知识点
长方体和正方体的定义与性质
理解长方体和正方体的基本概念，掌握它们的面、棱、 顶点等要素的数量关系和位置关系。
01 03
性质
02
正方体的所有面都是全等的 正方形。
长方体与正方体关系
正方体是长方体的特例，当长 方体的三组对边分别相等时， 即为正方体。
长方体和正方体都有6个面、 12条棱和8个顶点。
长方体和正方体的表面积和体 积计算公式不同，需要根据具 体形状进行区分和应用。
02 长方体和正方体表面积计 算
03 长方体和正方体体积计算
长方体体积公式推导
长方体体积公式为
$V = l times w times h$，其中 $l$ 是长度，$w$ 是宽度，$h$ 是高度。
公式推导
长方体可以看作是由 $l$ 个长度为 $w$， 高度为 $h$ 的小长方体组成，因此总 体积就是 $l times w times h$。
05 易错点与注意事项
常见易错点总结
概念混淆
学生容易混淆长方体和正方体的 概念，特别是在面对复杂图形时。
计算错误
在计算表面积或体积时，学生可能 会因为疏忽或计算不准确而导致错 误。
单位问题
在解决实际问题时，学生可能会忽 略单位换算，从而导致答案错误。
避免错误方法指导
01
02
03
明确概念
在解题前，首先要明确题 目中涉及的是长方体还是 正方体，以及它们的基本 性质。
长方体和正方体知识点汇总
长方体和正方体知识点汇总一、长方体和正方体的认识1、长方体定义：长方体是由六个长方形（特殊情况有两个相对的面是正方形）围成的立体图形。
面：长方体有 6 个面，相对的面完全相同。
棱：长方体有 12 条棱，相对的棱长度相等。
按长度可分为三组，每一组有 4 条棱。
顶点：长方体有 8 个顶点。
2、正方体定义：正方体是用六个完全相同的正方形围成的立体图形。
面：正方体有 6 个面，每个面都是正方形，且 6 个面完全相同。
棱：正方体有 12 条棱，12 条棱的长度都相等。
顶点：正方体有 8 个顶点。
3、长方体和正方体的关系正方体是特殊的长方体，当长方体的长、宽、高都相等时，就变成了正方体。
二、长方体和正方体的表面积1、表面积的定义长方体或正方体 6 个面的总面积，叫做它的表面积。
2、长方体表面积的计算公式：长方体的表面积＝（长×宽＋长×高＋宽×高）× 2例如：一个长方体的长为 5 厘米，宽为 4 厘米，高为 3 厘米，其表面积为：（5×4 ＋ 5×3 ＋ 4×3）× 2 ＝ 94（平方厘米）3、正方体表面积的计算公式：正方体的表面积＝棱长×棱长× 6例如：一个正方体的棱长为 6 厘米，其表面积为：6×6×6 ＝ 216（平方厘米）三、长方体和正方体的体积1、体积的定义物体所占空间的大小叫做物体的体积。
2、体积单位常用的体积单位有立方厘米、立方分米、立方米。
1 立方厘米：棱长为 1 厘米的正方体，体积是 1 立方厘米。
1 立方分米：棱长为 1 分米的正方体，体积是 1 立方分米。
1 立方米：棱长为 1 米的正方体，体积是 1 立方米。
3、长方体体积的计算公式：长方体的体积＝长×宽×高例如：一个长方体的长为 6 厘米，宽为 5 厘米，高为 4 厘米，其体积为：6×5×4 ＝ 120（立方厘米）4、正方体体积的计算公式：正方体的体积＝棱长×棱长×棱长例如：一个正方体的棱长为 5 厘米，其体积为：5×5×5 ＝ 125（立方厘米）5、体积单位的换算1 立方米＝ 1000 立方分米1 立方分米＝ 1000 立方厘米四、长方体和正方体的容积1、容积的定义容器所能容纳物体的体积，叫做它的容积。
(完整版)长方体和正方体的体积知识点
1、体积和容积。
（1）体积：物体所占空间的大小（2）容积：容器所能容纳物体的体积像这个长方体木箱的体积除了里面能容纳物体的体积外，还有做成木箱的木板的体积。
一个物体的体积要比一个物体的容积大，因为体积还包括自身材料的体积。
2、体积（容积）单位。
（1）用列表的形式来表述体积单位的大小，以利于记忆。
体积与容积单位之间的关系：1立方厘米=1毫升 1立方分米=1升升和毫升之间的进率是1000，因为1升是1立方分米，1毫升是1立方厘米。
升和毫升相比，升是高级单位，毫升是低级单位，把高级单位的数量换算成低级单位的数量，都要乘相应的进率。
3、因为长方体的体积都是由它的长、宽、高决定的，它的体积=长×宽×高。
正方体是特殊的长方体，长=宽=高，因而它的体积是由棱长决定的，体积=棱长×棱长×棱长。
因为长方体和正方体的底面积是两条棱长决定的，即长方体底面积=长×宽；正方体的底面积=棱长×棱长；所以长方体和正方体的体积又可以说是由底面积和高决定的，它们的体积=底面积×高。
（1）长方体的体积=长×宽×高（2）正方体的体积=棱长×棱长×棱长（3）长方体的体积=底面积×高4、求这根长方体木料的体积要用“底面积×高”，从中间截成两段，表面积实质上增加了两个底面，如果是截成三段，就是截了两次，增加了四个面。
也就是说每截一次，增加两个面。
5、综合运用体积单位、长度单位的知识。
将一个大的形体分成一个小的形体。
将小正方体紧紧地排成一排，能排多少米，实际上就是将这些小正方体的棱长加起来，看有多长。
一、填空题。
1、把一个容积是500ml的量杯里先注入200ml的水，然后放入一个土豆，这时测量杯里的容量为350ml，这个土豆的体积是（）cm22、一个底面周长是1。
6分米的正方体鱼缸的容积是（）升。
3、把一个棱长2分米的正方体切成两个体积相等的长方体，其中一个长方体的表面积是（）平方分米。
长方体正方体知识点汇总
长方体正方体知识点汇总长方体和正方体都属于立体图形，具有一些共同和独特的特点。
下面是对长方体和正方体的综合了解和详细解释：一、长方体的定义和特点：长方体是一种有6个面的立体图形，这些面由矩形组成，且相邻面两两平行。
长方体具有以下特点：1. 面的特点：长方体有6个面，其中有3对平行面。
相邻面两两平行，且相对的面是相等的矩形。
2. 边的特点：长方体有12条边，每个顶点有3条边相交。
3. 顶点的特点：长方体有8个顶点，每个顶点都是3个面的交点。
4. 相邻面、边、顶点的关系：长方体中，两个相邻面的共用一条边，两个相邻面的共用一点，这个点同时也是四条边的端点。
5. 相对面的特点：长方体的相对面是相等的矩形，具有相同的形状和大小。
二、正方体的定义和特点：正方体是一种特殊的长方体，所有的面都是正方形，具有以下特点：1. 面的特点：正方体有6个面，都是正方形，且相邻面两两平行。
2. 边的特点：正方体有12条边，每个顶点有3条边相交。
3. 顶点的特点：正方体有8个顶点，每个顶点都是3个面的交点。
4. 相邻面、边、顶点的关系：正方体中，两个相邻面的共用一条边，两个相邻面的共用一点，这个点同时也是四条边的端点。
5. 相对面的特点：正方体的相对面是相等的正方形，具有相同的形状和大小。
三、长方体和正方体的性质：1. 体积：长方体和正方体的体积都可以通过公式V = l × w × h来计算，其中l为长，w为宽，h为高。
正方体的体积可以简化为V = a^3，其中a为边长。
2. 表面积：长方体和正方体的表面积都可以通过公式S = 2lw + 2lh + 2wh来计算，其中l为长，w为宽，h为高。
正方体的表面积可以简化为S = 6a^2，其中a为边长。
3. 对角线：长方体和正方体的对角线可以通过勾股定理来计算。
长方体的对角线长度为d = sqrt(l^2 + w^2 + h^2)，正方体的对角线长度为d = sqrt(3a^2)，其中l、w、h分别为长方体的长、宽、高，a为正方体的边长。
(新版)苏教版六年级数学长方体和正方体知识点归纳总结
(新版)苏教版六年级数学上册知识点归纳总结
第一单元长方体和正方体
1.长方体的表面积=（长×宽+宽×高+高×长）×2
正方体的表面积=棱长×棱长×6
2.长方体的体积=长×宽×高V =abh
3.正方体的体积=棱长×棱长×棱长V =a×a×a= a3
4.长方体（或正方体）的体积=底面积×高=横截面×长V=Sh
一、填空。
1.一个正方体的棱长为A，棱长之和是（），当A=6厘米时，这个正方体的棱长总和是（）厘米。
2.一个长方体最多可以有（）个面是正方形，则其余4个面是完全相等的长方形。
3.用铁丝焊接成一个长12厘米，宽10厘米，高5厘米的长方体的框架，至少需要铁丝（）厘米。
4.一个长方体的金鱼缸，长是8分米，宽是5分米，高是6分米，不小心前面的玻璃被打坏了，修理时配上的玻璃的面积是（）平方分米。
5.一个正方体的棱长总和是72厘米，它的棱长是（）厘米，它的表面积是（）平方厘米。
二、应用题。
1.天天游泳池，长25米，宽10米，深1.6米，在游泳池的四周和池底砌瓷砖，那么至少需要砌瓷砖多少平方米？
2.一个通风管的横截面是边长是0.5米的正方形,长2.5米.如果用铁皮做这样的通风管50只,需要多少平方米的铁皮?
3.一种牛奶盒长6厘米，宽5厘米，高10厘米。
这种牛奶盒的容积是多少毫升？
4.一块棱长8厘米的正方体铁块，如果用这根铁块熔成一个长10厘米、宽8厘米的长方体框架，它的高应该是多少厘米？
精品文档资料。
(完整版)长方体和正方体的表面积知识点及练习题
长方体和正方体的表面积知识点1、长方体的表面积就是长方体六个面的总面积。
由于相对的面完全相同，所以可以先求出前面、和下面三个面的面积，再乘以2，就可以求出表面积了。
长方体的表面积 = 长×宽×2+长×高×2+宽×高×2=（长×宽+长×高+宽×高）×2正方体的六个面完全相同，所以计算时只要算出其中的一个面，再乘6就可以了。
正方体的表面积 = 棱长×棱长×62、在解决一些问题时，要充分考虑实际情况，想清楚要算几个面。
在解答时，可以把这几个面的面积分别算出来，再相加，也可以先算出六个面的面积总和，再减去不需要的那个（些）面。
一个抽屉有5个面，分别是前面、后面、左面、右面、底面。
所以做这样一个抽屉所需要的木板，只要算出这5个面的面积就可以了。
通风管顾名思义是通风用的，没有底面。
所以只要算四个侧面就可以了。
（1）具有六个面的长方体、正方体物品：油箱、罐头盒、纸箱子等；（2）具有五个面的长方体、正方体物品：水池、鱼缸等；（3）具有四个面的长方体、正方体物品：水管、烟囱等。
长方体和正方体表面积知识巩固一、填空题。
１、一个正方体的棱长之得８４厘米，它的棱长是（），一个面的面积是（），表面积是（），体积是（）。
２、一个长方体的长、宽、高都扩大２倍，它的表面积就（）。
３、两个棱长２厘米的正方体木块，拼成一个长方体，这个长方体的表面积是（）。
４、把一个长１２厘米，宽和高都是３厘米的长方体分割成４个大小一样的正方体，表面积增加了（），每个正方体的表面积是（）。
５、用棱长１厘米的小正方体木块拼成一个较大的的正方体，至少要（）块这样的小木块，拼成的正方体的棱长是（），表面积是（）。
6、把一个棱长2分米的正方体切成两个体积相等的长方体，其中一个长方体的表面积是（）平方分米。
7、一个长方体的长是25厘米，宽是20厘米，高是18厘米，最大的面的长是（）厘米，宽是（）厘米，它的面积是（）平方厘米；最小的面长是（）厘米，宽是（）厘米，它的面积是（）平方厘米。
长方体和正方体知识点汇总
长方体和正方体知识点汇总一、长方体和正方体的定义及性质1. 定义长方体：长方体是一种六个面都是矩形的立体图形，其中相对的两个面是长方形，其余四个面是正方形。
正方体：正方体是一种六个面都是正方形的立体图形，每个面的边长相等。
2. 性质（1）长方体的性质长方体有6个面，12条棱，8个顶点。
相对的面是长方形，其余四个面是正方形。
相邻的棱长相等，相对的棱长也相等。
长方体的对角线互相垂直，且相等。
（2）正方体的性质正方体有6个面，12条棱，8个顶点。
所有面都是正方形，边长相等。
相邻的棱长相等，相对的棱长也相等。
正方体的对角线互相垂直，且相等。
二、长方体和正方体的表面积与体积1. 长方体的表面积与体积（1）表面积长方体的表面积是指六个面的面积之和。
设长方体的长、宽、高分别为a、b、c，则长方体的表面积S为：S = 2(ab + ac + bc)（2）体积长方体的体积是指长、宽、高三个维度的乘积。
设长方体的长、宽、高分别为a、b、c，则长方体的体积V为：V = abc2. 正方体的表面积与体积（1）表面积正方体的表面积是指六个面的面积之和。
设正方体的边长为a，则正方体的表面积S为：S = 6a^2（2）体积正方体的体积是指边长的三次方。
设正方体的边长为a，则正方体的体积V为：V = a^3三、长方体和正方体的空间关系1. 长方体的空间关系长方体的底面与顶面平行，且底面与侧棱垂直。
长方体的侧面与底面垂直，且相邻侧面互相垂直。
长方体的对角线互相垂直，且相等。
2. 正方体的空间关系正方体的底面与顶面平行，且底面与侧棱垂直。
正方体的侧面与底面垂直，且相邻侧面互相垂直。
正方体的对角线互相垂直，且相等。
四、长方体和正方体的应用1. 长方体的应用长方体广泛应用于建筑设计、家具设计、包装设计等领域。
长方体的体积和表面积计算对于计算材料用量、确定空间大小等有重要作用。
2. 正方体的应用正方体在建筑设计、雕塑创作、数学建模等领域有广泛的应用。
(完整版)长方体和正方体知识点总结+练习
第二单元长方体和正方体总结一、长方体和正方体的特征：形体相同点不同点关系面棱顶点面的形状面的大小棱长长方体 6 12 8一般六个面都是长方形（也有两个相对的面是正方形）。
相对的面面积相等平行的四条棱长度相等正方体是特殊的长方体正方体 6 12 8六个面都是正方形六个面的面积相等十二条棱长都相等长方体：①有6个面，相对的面完全相同；长方体放桌面上，最多只能看到3个面。
②有12条棱，相对的棱长长度相等，而且相对的棱互相平行；12条棱可以分为3组（分别为长、宽、高），每组的4条棱一样长；长方体的棱长总和=长×4+宽×4+高×4=（长+宽+高）×4③有8个顶点，每个顶点上的三条棱分别称为长方体的长、宽、高。
正方体：①有6个完全相同的面；正方体放桌面上，最多只能看到3个面。
②有12条长度相等的棱，每条棱的长度称为正方体的棱长；正方体的总棱长=棱长×12。
上下左后右前③有8个顶点。
练一练：1.一个长方体长、宽、高分别是10cm、7 cm、4 cm ，这个长方体的棱长和是多少厘米？（提示：根据长方体的总棱长公式计算）2.一个长方体的棱长和是160dm，其中，长是20dm，宽是8dm，它的高是多少？从一个顶点引出的三条棱的长度总和是多少？3.将一根铁丝长720厘米做成正方体，则正方体的棱长是多少厘米？二、长方体和正方体的表面积定义：长方体或正方体6个面的总面积，叫做它的表面积。
1.法一：(1)长方体的表面积（有六个面）=长×宽×2+长×高×2+宽×高×2=（长×宽+长×高+宽×高）×2（因为长方体相对的面完全相同）法二：前、后面：长×高×2=X左、右面：长×高×2=Y上、下面：长×宽×2=Z则长方体的表面积（有六个面）= X + Y + Z2.正方体的表面积（有六个面）=棱长×棱长×6（因为正方体的六个面完全相同）在解决一些问题时，要充分考虑实际情况，想清楚要算几个面。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
三长方体和正方体6个面，8个顶点，12条棱
【概念】
1、由6个长方形（特殊情况有两个相对的面是正方形）围成的立体图形叫做长方体。
在一个长方体中，相对面完全相同，相对的棱长度相等。
一个长方体最多有6个面是长方形，最少有4个面是长方形，最多有2个面是正方形。
2、两个面相交的边叫做棱。
三条棱相交的点叫做顶点。
相交于一个顶点的三条棱的长度分别叫做长方体的长、宽、高。
3、由6个完全相同的正方形围成的立体图形叫做正方体（也叫做立方体）。
正方体有12条棱，它们的长度都相等，所有的面都完全相同。
4、正方体是长、宽、高都相等的长方体，它是一种特殊的长方体。
注意：①两个棱长和相等的长方体或一个长方体和一个正方体，表面积不一定相等！
②表面积相等的两个长方体或一个长方体和一个正方体，棱长和也不一定相等！
③长方体的棱长总和=（长+宽+高）×4
长=棱长总和÷4－宽－高宽=棱长总和÷4－长－高
高=棱长总和÷4－长－宽
④正方体的棱长总和=棱长×12 棱长=棱长总和÷12
5、长方体或正方体6个面和总面积叫做它的表面积。
①长方体的表面积=（长×宽＋长×高＋宽×高）×2 S=2（ab＋ah＋bh）
②无底（或无盖）长方体表面积= 长×宽＋（长×高＋宽×高）×2
③无底又无盖长方体表面积=（长×高＋宽×高）×2
④正方体的表面积=棱长×棱长×6
【知识点2】长方体表面求法的变形：
①贴商标类型：只求四周面积。
例如：一个长方体包装盒，长宽高分别为8,4,5，需要在包装盒四周贴上商标，需要商标纸的面积是多少？
②游泳池类型：只求四周和底面。
例如：一座游泳池，长宽高分别为、10m，4m， 1.5m，需要在池内贴上边长为1dm的瓷砖，大约需要多少块瓷砖？
③抽纸盒类型：六个面面积减去缺口面积。
例如：一款抽纸盒，长宽高分别是20cm，12cm，5cm，上面有长14cm，宽3cm的抽纸口，做这款抽纸盒需要多少硬纸片？
④占地面积问题：只求底面面积。
例如：一个长方体蓄水池，长12m ，宽8m ，深3m ，这个水池占地面积多少平方米？
【知识点3】棱长变化对表面积的影响：
正方体
正方体的棱长扩大n 倍，其棱长和也扩大n 倍，表面积扩大n ²倍，体积扩大n ³倍。
长方体
长方体的长宽高同时扩大n 倍，其棱长和也扩大n 倍，表面积扩大n2倍，体积扩大n3倍。
（1）大正方体棱长是小正方体棱长的2倍，则大正方体表面积是小正方体表面积的（）倍。
（2）一个长方体的长、宽、高都扩大4倍，它的表面积就（）。
（3）一个正方体的棱长为4厘米扩大为2倍后，其棱长和为（ ）厘米，表面积为（）平方厘米比原来扩大了（）。
（5）一个长方体长扩大2倍，高扩大4倍，体积扩大（）倍。
6、物体所占空间的大小叫做物体的体积。
长方体的体积=长×宽×高 V=abh
长=体积÷宽÷高 a=V ÷b ÷h
宽=体积÷长÷高 b=V ÷a ÷h
高=体积÷长÷宽 h= V ÷a ÷b
正方体的体积=棱长×棱长×棱长 V=a ×a ×a= a 3
a 3读作“a 的立方”表示3个a 相乘，（即a ·a ·a ）
7、箱子、油桶、仓库等所能容纳物体的体积，通常叫做他们的容积。
常用的容积单位有升和毫升也可以写成L 和ml 。
1升=1立方分米 1毫升=1立方厘米 1升=1000毫升
计算公式相同 V=sh V=abh
【体积单位换算】 高级单位 低级单位 低级单位 高级单位
长度单位： mm 、cm 、dm 、m 相邻两个单位进率为10
面积单位： mm ²、cm ²、dm ²、m ² 相邻两个单位进率为100
体积单位： mm ³、cm ³、dm ³、m ³ 相邻两个单位进率为1000
容积单位： ml 、l 相邻两个单位进率为1000
特别的： 1ml=cm ³ 1l=1dm ³ 1方=1m ³
×进率
÷进率。