巴中市中考数学考试说明大纲
中考数学考试说明

2021年中考数学考试说明
2021年中考数学考试说明
数学
调整能力和知识要求
数学《考试说明》调整知识要求,梳理能力要求,替换部分参考样题,体现注重基础、能力立意,考查基础内容、知识结构和核心能力。
知识要求方面
知识要求方面,调整”反比例函数"和”抽样与数据分析”的内容要求。
比如,将反比例函数要求中的”结合图象与表达式,理解当k>0和k<0时,反比例函数图象的变化情况”调整到B级要求,并将"理解”改为”掌握”。
能力要求方面
能力要求方面,梳理运算能力和数据分析观念的描述,将”根据特定问题,分析运算条件”调整为”根据特定问题,观察、分析运算条件",将"整理、分析数据”调整为”运用统计方法对数据进行收集、整理和分析”。
参考样题及说明
《考试说明》中,参考样题主要体现试题的考查目的,包括知识的评价、能力的评价和思想的评价三方面。
下表是2021年数学学科《考试说明》参考样题调整题目及相应题目的考查目标。
以下是2021年全部科目的试题发布入口:
True地区
True中考试题
True中考答案
语文数学英语化学物理历史治
语文数学英语化学物理历史治
2021年中考结束后您可能还会关注:
中考
中考
中考
中考录取
中考策
中考状元
中考饮食
中考备考辅导
中考复习资料。
中考数学考试大纲(最新版)

中考数学考试大纲〔5〕无理数和实数的概念考试目标〔6〕实数与数轴上的点一一对【数与代数】应关系〔7〕对含有较大数字的信息作1.有理数〔1〕有理数的意义出合理的解释和推断〔2〕用数轴上的点表示有理数〔8〕用有理数估计一个无理数及有理数的相反数和绝对的大致范围值〔9〕近似数与有效数字的概念〔3〕有理数的大小比拟〔10〕二次根式的加、减、乘、〔4〕求有理数的相反数与绝对除运算法那么值〔绝对值内不含字母〕〔11〕实数的简单四那么运算〔5〕乘方的意义3.代数式〔6〕有理数的加、减、乘、除、〔1〕用字母表示数的意义乘方运算及混合运算〔以三〔2〕用代数式表示简单问题的步为主〕数量关系〔3〕解释一些简单代数式的实2.实数〔1〕平方根、算术平方根、立方际背景或几何意义根和二次根式的概念〔4〕求代数式的值〔2〕用根号表示平方根、立方根〔5〕整数指数幂的意义和根本〔3〕开方和乘方互为逆运算性质〔4〕求某些非负数的算术平方〔6〕用科学记数法表示数根,求实数的立方根〔7〕整式和分式的概念1〔8〕简单的整式加减运算及乘一元二次方程法运算〔其中的多项式相乘〔5〕用观察、画图或计算等方法仅指一次式相乘〕估计方程的解〔9〕平方差、完全平方公式的推〔6〕根据具体问题的实际意义,导及运用检验结果是否合理〔10〕提取公因式法和公式5.不等式与不等式组法〔用公式不超过两次,指〔1〕不等式的意义数是正整数〕因式分解〔2〕不等式的根本性质〔11〕运用分式根本性质进〔3〕解一元一次不等式及由两行约分和通分个一元一次不等式组成的〔12〕简单的分式加、减、乘不等式组,并在数轴上表示除运算出解集〔4〕不等式与不等式组的简单4.方程与方程组〔1〕根据具体问题中的数量关应用系,列出方程或方程组6.函数〔2〕解一元一次方程和二元一〔1〕常量、变量的意义次方程组〔2〕举出函数的实例〔3〕解可化为一元一次方程的〔3〕函数的概念及函数的三种分式方程〔方程中分式不超表示方法过两个〕〔4〕结合图象对简单实际问题〔4〕用因式分解法、公式法和配中的函数关系进展分析方法解简单的数字系数的〔5〕求简单整式、分式和简单实2际问题中的函数的自变量例函数的性质的取值范围〔15〕通过图象认识二次函〔6〕求函数值数的性质〔7〕用适当的函数表示法刻画〔16〕根据公式确定图象的某些实际问题中变量之间顶点、开口方向和对称轴的关系〔公式不要求记忆〕〔8〕结合对函数关系的分析,尝〔17〕运用一次函数图象求试对变量的变化规律进展二元一次方程组的近似解初步预测〔18〕利用二次函数图象求〔9〕一次函数、反比例函数和二一元二次方程组的近似解次函数的意义〔19〕利用一次函数、反比例〔10〕根据条件确定一函数和二次函数解决实际次函数和反比例函数的表问题示法【空间与图形】〔11〕通过对实际问题情境7.图形的认识的分析确定二次函数表达〔1〕认识点、线、面式〔2〕角的概念与表示〔12〕画一次函数、反比例函〔3〕认识度、分、秒,能进展数的图象度、分、秒的简单换算〔13〕用描点法画二次函数〔4〕角的大小比拟或估计的图象〔5〕角度的和差计算〔14〕理解一次函数和反比〔6〕角平分线及其性质3〔2〕画任意三角形的角平分线、8.相交线与平行线〔1〕补角、余角、对顶角等概念中线和高〔2〕等角的余角相等、等角的补〔3〕三角形中线及其性质角相等、对顶角相等〔4〕全等三角形的概念〔3〕垂线、垂线段等概念,了解〔5〕三角形全等的条件垂线段最短〔6〕等腰三角形、等边三角形和〔4〕点到直线的距离和两跳平直角三角形的有关概念行线之间的距离〔7〕等腰三角形、等边三角形和〔5〕过一点有且仅有一条直线直角三角形的性质垂直于直线〔8〕判定等腰三角形、直角三角〔6〕用三角尺或量角器过一点形的条件画一条直线的垂线〔9〕勾股定理及其简单运用〔7〕线段垂直平分线及其性质10.四边形〔8〕两直线平行同位角相等〔1〕多边形的概念〔9〕过直线外一点有且只有一〔2〕多边形的内角和与外角和条直线平行于直线公式〔10〕用三角尺和直尺过已〔3〕平行四边形、矩形、菱形、知直线外一点画这条直线正方形、梯形的概念的平行线〔4〕平行四边形、矩形、菱形、9.三角形正方形、梯形的性质〔1〕三角形的有关概念〔内角、〔5〕平行四边形、矩形、菱形、外角、中线、高、角平分线〕正方形、梯形之关系间的4〔6〕判定平行四边形、矩形、菱12.尺规作图形、正方形的条件〔1〕根本作图:作一条线段等于〔7〕等腰梯形的有关性质线段;作一个角等于已〔8〕判定等腰梯形的依据知角;作角的平分线;作线11.圆段的垂直平分线〔1〕圆及其有关概念〔2〕利用根本作图作三角形;已〔2〕弧、弦、圆心角的关系知三边作三角形;两边〔3〕点与圆、直线与圆以及圆与及其夹角作三角形;两圆的位置关系角及其夹边作三角形;〔4〕圆的简单性质底边及底边上的高作等腰〔5〕圆周角与圆心角的关系,直三角形径所对圆周角的特征〔3〕过不在同一直线上的三点〔6〕三角形的内心和外心作圆〔7〕切线的概念〔4〕对于尺规作图题,应保存作〔8〕切线与过切点的半径之间图痕迹的关系,会过圆上一点画圆〔5〕的切线13.视图与展开图〔9〕判定一条直线是否为圆的〔1〕画根本几何体〔直棱柱、圆切线柱、圆锥、球〕的三视图〔10〕计算弧长和扇形的面〔2〕判断简单物体〔根本几何体积,计算圆锥的侧面积和全地简单组合〕的三视图面积〔3〕根据三视图描述简单几何5体或简单物体的实物原型〔6〕平行四边形、圆是中心对称〔4〕直棱柱、圆锥的侧面展开图图形〔5〕根本几何体与其三视图、展〔7〕探索图形之间的变换关系开图〔球除外〕之间的关系;〔轴对称、平移、旋转及其通过典型实例,知道这种关组合〕系在现实生活中的应用〔如〔8〕应用轴对称、平移、旋转或物体的包装〕他们的组合进展图案设计〔6〕根据展开图判断立体模型〔9〕欣赏现实生活中的轴对称,14.图形与变换欣赏平移、旋转在现实生活〔1〕轴对称、平移和旋转的概念中的应用〔2〕轴对称、平移和旋转的根本15.图形的相似性质〔1〕比例的根本性质、线段的〔3〕按要求作出简单平面图形比、成比例线段经过一次或两次轴对称后〔2〕黄金分割的图形;作出简单图形平移〔3〕图形相似、三角形相似的概后的图形;作出简单图形旋念转后的图形〔4〕图形相似的简单性质〔4〕找出成轴对称的两个图形〔5〕两个三角形相似的判定依或轴对称图形的对称轴据〔5〕等腰三角形、矩形、菱形、〔6〕观察和认识现实生活中的等腰梯形、正多边形、圆的物体相似轴对称性及相关性质〔7〕利用图形的相似解决一些6实际问题〔3〕命题的构成〔区分条件与16.三角函数结论〕〔1〕锐角三角函数sinA,cosA,〔4〕逆命题的概念〔5〕两个互逆命题的关系tanA的概念〔2〕30°,45°,60°角的三〔6〕反证法的含义角函数值〔7〕综合法证明的格式〔3〕运用三角函数解决与直角〔8〕掌握以下“证明的依据〞三角形有关的简单实际问题一条直线截两条平行直17.图形与坐标线所得的同位角相等;两条直线〔1〕平面直角坐标系的概念被第三条直线所截,假设同位角相〔2〕在给定的直角坐标系中,等,那么这两条直线平行;假设两由坐标描出点的位置,由点的位个三角形的两边及其夹角〔或两置写出它的坐标角及其夹边,或三边〕分别相等,〔3〕在方格纸上建立适当的直那么这两个三角形全等;全等三角角坐标系,描述物体的位置形的对应边、对应角分别相等〔4〕在同一坐标系中感受图形〔9〕利用“证明的依据〞〔上变换后点的坐标的变化一条目〕中的根本领实证明以下〔5〕运用不同的方式确定物体命题:的位置平行线的性质定理〔内错角18.图形与证明相等、同旁内角互补〕〔1〕证明的作用、反例的作用平行线的判定定理〔内错角〔2〕定义、命题、定理的含义相等或同旁内角互补,那么两7直线平行〕数据三角形的内角和定理及推〔2〕抽样的意义论〔3〕总体、个体、样本的概念直角三角形全等的判定定〔4〕用样本估计总体的思想理〔5〕用扇形统计图表示数据角平分线性质定理及逆定〔6〕加权平均数的概念理,三角形三个内角的平分〔7〕加权平均数的计算线交于一点〔内心〕〔8〕选择适宜的统计量表示数垂直平分线性质定理及逆据的集中程度定理,三角形三边的垂直平〔9〕用样本的平均数估计总体分线交与一点〔外心〕的平均数三角形中位线定理〔10〕极差和方差的概念等腰三角形、等边三角形、〔11〕极差和方差的计算直角三角形的性质和判定〔12〕用极差和方差表示数据的定理离散程度平行四边形、矩形、菱形、〔13〕用样本的方差估计总体的正方形、等腰梯形的性质和方差判定定理〔14〕频数、频率的概念〔15〕频数分布的意义和作用【统计与概率】〔16〕列频数分布表、画频数分19.统计布直方图和频数折线图及其应用〔1〕收集、整理、描述和分析〔17〕根据统计结果作出合理的8判断和预测〔1〕有初步的研究问题的方法〔18〕从有关实际问题的资料中和经历。
中考数学试卷大纲

一、试卷结构1. 试卷总分:满分120分,考试时间120分钟。
2. 试卷结构:分为选择题、填空题、解答题三大块。
二、选择题(共20题,每题2分,满分40分)1. 数与代数(1)实数的运算及性质(2)一元一次方程及不等式(3)二元一次方程组(4)一元二次方程及根的判别式(5)函数及其性质2. 几何与代数(1)三角形、四边形及相似、全等(2)圆及圆的性质(3)平面直角坐标系与坐标计算(4)解析几何基础3. 统计与概率(1)平均数、中位数、众数(2)频率分布表(3)概率计算(4)随机事件三、填空题(共10题,每题3分,满分30分)1. 完成实数的运算2. 求一元一次方程的解3. 求二元一次方程组的解4. 求一元二次方程的解5. 求函数的值6. 判断三角形的性质7. 求圆的面积8. 在平面直角坐标系中求点的坐标9. 求概率10. 求平均数、中位数、众数四、解答题(共5题,每题10分,满分50分)1. 数与代数(一元二次方程、函数)题目:已知一元二次方程ax^2+bx+c=0(a≠0)的解为x1和x2,求:(1)若x1+x2=5,求a、b、c的值;(2)若x1x2=4,求a、b、c的值。
2. 几何与代数(三角形、四边形)题目:已知在三角形ABC中,AB=AC,BC=5cm,求:(1)求三角形ABC的面积;(2)求角B的度数。
3. 统计与概率题目:某班级有30名学生,成绩如下表所示:成绩区间 | 人数——|——0-60 | 560-70 | 1070-80 | 1080-90 | 590-100 | 0求:(1)求该班级的平均成绩;(2)求该班级的中位数;(3)求该班级的众数。
4. 综合题题目:已知平面直角坐标系中,点A(2,3),点B(-1,2),求:(1)直线AB的方程;(2)点C(x,y)在直线AB上,且AC的长度为5,求点C的坐标。
5. 应用题题目:某工厂生产一批产品,每天产量为100件,成本为1000元,售价为200元。
完整版)初中数学中考考试大纲

完整版)初中数学中考考试大纲初中数学中考考试大纲一、知识与技能1、数与代数考试内容:本部分主要考察有理数、实数、二次根式、代数式、整式、因式分解、分式、方程与方程组、不等式与不等式组、函数及其表示等知识点。
要求目标:学生需要掌握有理数的概念、大小比较、加减乘除乘方运算、数的开方等基本知识;理解实数、无理数的概念,以及近似数和有效数字的概念;掌握代数式、整式的概念和基本运算法则,以及因式分解、分式、方程与方程组、不等式与不等式组等知识;理解函数的概念和表示方法,能够求解一次函数和反比例函数等问题。
2、几何考试内容:本部分主要考察平面图形的性质、三角形的性质、圆的性质、相似与全等等知识点。
要求目标:学生需要掌握平面图形的基本性质,如线段、角、多边形等;掌握三角形的性质,如三角形内角和、中线定理、角平分线定理等;掌握圆的性质,如圆心角、弧长、切线等;理解相似和全等的概念,能够判断两个图形是否相似或全等。
3、数据与统计考试内容:本部分主要考察数据的收集、整理和表示方法,以及统计分析方法等知识点。
要求目标:学生需要掌握数据的收集、整理和表示方法,如频数、频率、累计频率等;掌握统计分析方法,如均值、中位数、众数、极差、方差等;能够进行简单的数据分析和统计。
4、应用题考试内容:本部分主要考察数学知识在实际问题中的应用能力。
要求目标:学生需要能够将数学知识应用到实际问题中,解决生活中的实际问题。
例如,能够解决关于比例、利润、利率、速度等方面的实际问题。
反比例函数的意义是指两个变量之间的关系是反比例关系,即其中一个变量的值增加,另一个变量的值就会相应地减少。
例如,当一个物品的价格上涨时,人们购买该物品的数量会下降。
反比例函数的表达式通常写作y=k/x,其中k是常数。
这个表达式中,y和x分别代表两个变量的值,k是比例系数。
当x增加时,y会相应地减少,反之亦然。
反比例函数的图像是一个开口朝下的双曲线。
反比例函数也可以写成y=k/x^n的形式,其中n是正整数。
2024年巴中市中考数学试卷及答案

2024年四川省巴中市中考数学试卷一、选择题1.在0,1,1-,π中最小的实数是()A.0B.1- C.1 D.π2.下列图形中,是轴对称图形的是()A. B. C. D.3.函数y =自变量的取值范围是()A.0x > B.2x >- C.2x ≥- D.2x ≠-4.下列运算正确的是()A.33a b ab+= B.325a a a ⋅=C.()8240a a a a ÷=≠ D.()222a b a b -=-5.实数,a b 在数轴上对应点的位置如图所示,下列结论正确的是()A.0ab >B.0a b +<C.a b >D.0a b -<6.如图,直线m n ∥,一块含有30︒的直角三角板按如图所示放置.若140∠=︒,则2∠的大小为()A.70︒B.60︒C.50︒D.40︒7.如图,ABCD Y 的对角线AC BD 、相交于点O ,点E 是BC 的中点,4AC =.若ABCD Y 的周长为12,则COE ∆的周长为()A.4B.5C.6D.88.某班学生乘汽车从学校出发去参加活动,目的地距学校60km,一部分学生乘慢车先行0.5h ,另一部分学生再乘快车前往,他们同时到达.已知快车的速度比慢车的速度每小时快20km,求慢车的速度?设慢车的速度为km /h x ,则可列方程为()A.60601202x x -=+ B.60601202x x -=-C.60601202x x -=+ D.60601202x x -=-9.一组数据10,0,11,17,17,31-,若去掉数据11,下列会发生变化的是()A.平均数B.中位数C.众数D.极差10.“今有方池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问:水深几何?”这是我国数学史上的“葭生池中”问题.即5AC =,1DC =,BD BA =,则BC =()A.8B.10C.12D.1311.如图,是用12个相似的直角三角形组成的图案.若1OA =,则OG =()A.125564B.12564C.6427D.32312.如图,在ABC ∆中,D 是AC 的中点,CE AB ⊥,BD 与CE 交于点O ,且BE CD =.下列说法错误的是()A.BD 的垂直平分线一定与AB 相交于点EB.3BDC ABD∠=∠C.当E 为AB 中点时,ABC 是等边三角形D.当E 为AB 中点时,34BOC AEC S S =△△非选择题二、填空题13.27的立方根为_____.14.过五边形的一个顶点有__________条对角线.15.已知方程220x x k -+=的一个根为2-,则方程的另一个根为______.16.如图,四边形ABCD 是O 的内接四边形,若四边形OABC 为菱形,则ADC ∠的度数是______.17.如图,矩形ABCD 的对角线AC 与BD 交于点O ,DE AC ⊥于点E ,延长DE 与BC 交于点F .若3AB =,4BC =,则点F 到BD 的距离为______.18.若二次函数()20y ax bx c a =++>的图象向右平移1个单位长度后关于y 轴对称.则下列说法正确的序号为______.(少选得1分,错选得0分,选全得满分)①2ba =②当3522a ≤≤时,代数式2258ab b +-+的最小值为3③对于任意实数m ,不等式20am bm a b +-+≥一定成立④()11,P x y ,()22,Q x y 为该二次函数图象上任意两点,且12x x <.当1220x x ++>时,一定有12y y <三、解答题19.(1)计算:()2sin305π3+--+︒(2)求不等式组26321054x x x x -<⎧⎪⎨+--≥⎪⎩①②的解集.(3)先化简,再求值:23211224x x x x -+⎛⎫-÷⎪++⎝⎭,其中1x =+20.为了解全校学生对篮球、足球、乒乓球、羽毛球四项球类运动的喜爱情况,在全校随机抽取了m 名学生进行问卷调查,每名学生只选择一项球类运动填写问卷.将调查结果绘制成如下统计图,请你根据图中所提供的信息解答下列问题.(1)求m =______,并补全条形统计图.(2)若该校共有1200名学生,请估计喜欢乒乓球运动的学生有多少名?(3)学校羽毛球队计划从甲、乙、丙、丁四名同学中挑选两名同学加入球队.请用画树状图或列表的方法计算恰好选中甲、乙两名同学的概率.21.某兴趣小组开展了测量电线塔高度的实践活动.如图所示,斜坡BE 的坡度i =,6m BE =,在B 处测得电线塔CD 顶部D 的仰角为45︒,在E 处测得电线塔CD 顶部D 的仰角为60︒.(1)求点B 离水平地面的高度AB .(2)求电线塔CD 的高度(结果保留根号).22.如图,在平面直角坐标系中,直线2y x =+与反比例函数()0ky k x=≠的图象交于A B 、两点,点A 的横坐标为1.(1)求k 的值及点B 的坐标.(2)点P 是线段AB 上一点,点M 在直线OB 上运动,当12BPO ABO S S =△△时,求PM 的最小值.23.如图,ABC 内接于O ,点D 为 BC的中点,连接AD BD 、,BE 平分ABC ∠交AD 于点E ,过点D 作DF BC ∥交AC 的延长线于点F .(1)求证:DF 是O 的切线.(2)求证:BD ED =.(3)若5DE =,4CF =,求AB 的长.24.综合与实践(1)操作与发现:平行四边形和梯形都可以剪开拼成一个矩形,拼接示意图如图1,图2.在图2中,四边形ABCD 为梯形,AB CD ,E F 、是AD BC 、边上的点.经过剪拼,四边形GHJK 为矩形.则EDK ≌△______.(2)探究与证明:探究将任意一个四边形剪开拼成一个平行四边形,拼接示意图如图3,图4,图5.在图5中,E F G H 、、、是四边形ABCD 边上的点.OJKL 是拼接之后形成的四边形.①通过操作得出:AE 与EB 的比值为______.②证明:四边形OJKL 为平行四边形.(3)实践与应用:任意一个四边形能不能剪开拼成一个矩形?若能,请将四边形ABCD 剪成4块,按图5的方式补全图6,并简单说明剪开和拼接过程.若不能,请说明理由.25.在平面直角坐标系中,抛物线()230y ax bx a =++≠经过()1,0A -,()3,0B 两点,与y 轴交于点C ,点P 是抛物线上一动点,且在直线BC的上方.(1)求抛物线的表达式.(2)如图1,过点P 作PD x ⊥轴,交直线BC 于点E ,若2PE ED =,求点P 的坐标.(3)如图2,连接AC PC AP 、、,AP 与BC 交于点G ,过点P 作PF AC ∥交BC 于点F .记ACG ,PCG ,PGF 的面积分别为123S S S 、、.当3221S S S S +取得最大值时,求sin BCP ∠的值.2024年四川省巴中市中考数学试卷答案一、选择题题号123456789101112答案BDCBDABABCCD11.【解析】解:∵12个相似的直角三角形∴3603012BOA BOC ︒∠=∠===︒ 3cos302OA OB OC OB OC OD ====︒= ∵1OA =∴1OB ==2413OC ==⨯31OD =⨯=,L∴664127OG =⨯=故选C12.【解析】解:连接DE ,如图1所示:CE AB ⊥ ,点D 是AC 的中点DE ∴为Rt AEC △斜边上的中线12DE AD CD AC ∴===BE CD=BE DE∴=∴点D 在线段BD 的垂直平分线上即线段BD 的垂直平分线一定与AB 相交于点E ,故选项A 正确,不符合题意;设ABD α∠=BE DE= EDB ABD α∴∠=∠=2AED EDB ABD α∴∠=∠+∠=DE AD= 2A AED α∴∠=∠=3BDC A ABD α∴∠=∠+∠=即3BDC ABD ∠=∠,故选B 正确,不符合题意;当E 为AB 中点时,则12BE AB =CE AB⊥ CE ∴是线段AB 的垂直平分线AC BC ∴=12BE AB =,12CD AC =,BE CD =AB AC ∴=AC BC AB∴==ABC ∴ 是等边三角形,故选C 正确,不符合题意;连接AO ,并延长交BC 于F ,如图2所示:当E 为AB 中点时点D 为AC 的中点∴根据三角形三条中线交于一点得:点F 为BC 的中点当E 为AB 中点时,ABC 是等边三角形60ABC BAC ∴∠=∠=︒,AF BC ⊥,AF 平分OAC ∠,BD 平分ABC∠30OBC OAC ∴∠=∠=︒OA OB∴=在Rt OBF △中,2OB OF=2OA OB OF∴==3AF OA OF OF∴=+=12OBC S BC OF ∆∴=⋅,1322ABC S BC AF BC OF ∆=⋅=⋅∴13OBC ABC S S ∆∆=,故选项D 不正确,符合题意.故选:D .二、填空题13.【答案】314.【答案】215.【答案】416.【答案】60°17.【答案】2120【解析】解:如图,过点F 作FH DB ⊥,垂足为H四边形ABCD 为矩形90BAD BCD ∴∠=∠=︒,AC BD=3AB = ,4BC=5AC BD ∴====1122ADC S AD DC AC DE ∴=⋅=⋅ ,即1143522DE ⨯⨯=⨯⨯解得:125DE =cos DE DC EDC DC DF ∴∠==,即12353DF=解得:154DF =94FC ∴===97444BF BC FC ∴=-=-=1122BDF S BD FH BF DC ∴=⋅=⋅ ,即11753224FH ⨯⨯=⨯⨯解得:2120FH =故答案为:2120.18.【答案】①③【解析】解:∵二次函数()20y ax bx c a =++>的图象的对称轴为直线2bx a=-而二次函数()20y ax bx c a =++>的图象向右平移1个单位长度后关于y 轴对称.∴102b a-+=∴2b a =,故①符合题意;∴2b a=∴2258a b b +-+25108a a =-+()2513a =-+∵3522a ≤≤∴当32a =时,2258a b b +-+取最小值174,故②不符合题意;∵102b a-+=∴对称轴为直线=1x -∵0a >当=1x -时,函数取最小值ab c-+当x m =时,函数值为2am bm c++∴2am bm c a b c++≥-+∴对于任意实数m ,不等式20am bm a b +-+≥一定成立,故③符合题意;当121x x <-<时∵1220x x ++>∴2111x x +>--∴12y y <当121x x -<<时,满足1220x x ++>∴1211x x +<+∴12y y <当121x x <<-时,不满足1220x x ++>,不符合题意,舍去,故④符合题意;综上:符合题意的有①③;故答案为:①③.三、解答题19.【答案】(1)5+;(2)613x -<≤;(3)21x -20.【答案】(1)200,图见详解(2)312名(3)16【小问1详解】解:4422%200m =÷=(名)喜欢乒乓球的人数;20044168852---=(名)补全统计图:故答案为:200;【小问2详解】解:521200312200⨯=(名)答:估计喜欢乒乓球运动的学生有312名;【小问3详解】解:画树状图得:一共有12种等可能出现的结果,符合条件的结果有2种∴恰好选中甲、乙两名同学的概率为21126=.21.【答案】(1)3m AB =;(2)电线塔CD 的高度()636m +.【小问1详解】解:∵斜坡BE 的坡度1:3i =∴1333AB AE ==∵3t n 3a AB BEA AE ∠==∴30BEA ∠=︒∵6mBE =∴()13m 2AB BE ==;【小问2详解】解:作BF CD ⊥于点F ,则四边形ABFC 是矩形,3m AB CF ==,BF AC=设mDF x =在Rt DBF △中,tan DFDBF BF∠=∴m tan DF BF x DBF==∠在Rt ABE △中,AE ==在Rt DCE V 中,()3m DC DF CF x =+=+,tan DCDEC EC ∠=∴()333tan 603x EC x +==+︒∴BF AE EC=+∴()333x x +=∴6x =答:电线塔CD的高度()6m +.22.【答案】(1)3k =,()3,1B --(2)2105【小问1详解】解:∵直线2y x =+与反比例函数()0k y k x=≠的图象交于A B 、两点,点A 的横坐标为1.∴123A y =+=∴()1,3A ∴133k =⨯=∴反比例函数为:3y x =;∴23y x y x =+⎧⎪⎨=⎪⎩解得:31x y =-⎧⎨=-⎩,13x y =⎧⎨=⎩∴()3,1B --;【小问2详解】解:∵12BPO ABO S S =△△∴BP AP =∵()1,3A ,()3,1B --∴()1,1P -,221310OA OB =+==∴OP AB⊥∴22112OP =+=,()()2210222PB =-=如图,当PM OB ⊥时,PM 最短;∴222210510BP OP PM OB ⋅⨯===;23.【答案】(1)证明见解析(2)证明见解析(3)254AB =【小问1详解】证明:如图,连接OD∵点D 为 BC 的中点∴OD BC⊥∵DF BC∥∴DF OD ⊥,且OD 是O 的半径∴DF 是O 的切线;【小问2详解】证明:∵点D 为 BC 的中点∴BD CD =∴CBD BAD∠=∠∵BE 平分ABC∠∴ABE CBE∠=∠∵DEB BAD ABE ∠=∠+∠,DBE CBD CBE∠=∠+∠∴DBE DEB∠=∠∴DB DE =;【小问3详解】解:如图,连接CD∵5DE =,BD DE=∴5BD =∵BD CD =∴5CD BD ==∵BC DF∥∴ACB F ∠=∠,而ACB ADBÐ=Ð∴ADB F∠=∠∵四边形ABDC 为O 的内接四边形∴180ABD ACD ACD DCF∠+∠=︒=∠+∠∴DCF ABD∠=∠∴FDC DAB∽∴FCCD DB AB=,而4CF =∴455AB=∴254AB =,经检验,符合题意;24.【答案】(1)EAG △(2)①1;②见详解(3)见详解【小问1详解】解:如图∵AB CD∴GAE D∠=∠由题意得E 为AD 中点,‘∴EA ED =’∵AEG DEK∠=∠∴EDK EAG△△≌故答案为:EAG △;【小问2详解】解:①如图,由操作知,点E 为AB 中点,将四边形EBFO 绕点E 旋转180︒得到四边形EAQL ∴AE BE=∴1AE BE=故答案为:1;②如图由题意得,E F G H 、、、是,,,AB BC CD DA 的中点,操作为将四边形EBFO 绕点E 旋转180︒得到四边形EAQL ,将四边形OHDG 绕点H 旋转180︒得到四边形JHAP ,将四边形OGCF 放在左上方空出则,AQ BF CF AP DG CG ====,BFO AQL∠=∠∵360DAB B C D ∠+∠+∠+∠=︒,,QAE B PAH D ∠=∠∠=∠,360DAB QAE PAH PAQ ∠+∠+∠+∠=︒∴PAQ C∠=∠∵180BFO CFO ∠+∠=︒∴180AQL AQK ∠+∠=︒∴,,K Q L 三点共线,同理,,K P J 三点共线由操作得,2,3L J∠=∠∠=∠∵12180,13180∠+∠=︒∠+∠=︒∴1180,1180L J ∠+∠=︒∠+∠=︒∴,OJ KL OL KJ∥∥∴四边形OJKL 为平行四边形;【小问3详解】解:如图,如图,取,,,AB BC CD DA 为中点为,,,E H G F ,连接FH ,过点E ,点G 分别作EM FH ⊥,GN FH ⊥,垂足为点,M N ,将四边形EBHM 绕点E 旋转180︒至四边形EAH M '',将四边形FDGN 绕点F 旋转180︒至四边形FAG N '',将四边形NGCH 放置左上方空出,使得点C 与点A 重合,CG 与AG '重合,CH 与AH '重合,点N 的对应点为点N '',则四边形MM N N ''''即为所求矩形.由题意得,90EMF EMH M '∠=∠=∠=︒,90GNH GNF N '∠=∠=∠=︒∴90N M MH ''∠=∠=︒,H M N M'''∥∴N G MM '''∥由操作得,14,23∠=∠∠=∠∵12180∠+∠=︒∴34180∠+∠=︒∴,,N H M ''''三点共线同理,,N G N ''''三点共线∵90N EMF M ''∠=∠=∠=︒∴四边形MM N N ''''为矩形如图,连接,,,,AC EF FG GH EH ∵,E H 为,BA BC 中点∴1,2EH AC EH AC =∥同理1,2FG AC FG AC =∥∴,FG EH FG EH = ∴EHM GFN ∠=∠∵90EMF GNH ∠=∠=︒∴EHM GFN ≌∴EM GN =,MH NF =∴FM NH=由操作得,AH BH '=,而BH CH =∴AH CH '=同理,AG CG'=∵360BAD D C B ∠+∠+∠+∠=︒,,D G AF B H AE ''∠=∠∠=∠,360BAD H AE G AF H AG ''''∠+∠+∠+∠=︒∴H AG C''∠=∠∵四边形MM N N ''''为矩形∴,N N MM N M N M'''''''''==∴N F FM H M H N ''''''+=+∴MF NF MF MH M H N H '''''+=+=+∴NH N H '''=同理''NG N G ='∴四边形NGCH 能放置左上方空出∴按照以上操作可以拼成一个矩形.25.【答案】(1)223y x x =-++(2)()2,3P (3)31010【小问1详解】解:∵抛物线()230y ax bx a =++≠与x 轴交于点()1,0A -,()3,0B ∴309330a b a b -+=⎧⎨++=⎩解得:12a b =-⎧⎨=⎩∴抛物线解析式为.223y x x =-++;【小问2详解】解:∵当0x =时,2233y x x =-++=∴()0,3C 设直线BC 的解析式为y kx n=+∴303k n n +=⎧⎨=⎩解得:13k n =-⎧⎨=⎩∴直线BC 的解析式为3y x =-+设()2,23P m m m -++,则223PD m m =-++∵PD x ⊥轴于点D∴(),3E m m -+,(),0D m ∴3DE m =-+∴()222333PE PD DE m m m m m=-=-++--+=-+∵2PE ED=∴()2323m m m -+=-+解得12m =,23m =(此时B ,D 重合,不合题意舍去)∴2m =∴()2,3P ;【小问3详解】解:∵PF AC∥∴ACG PFG∽ AC AG CG PF PG FG∴==∴23S GF PF S CG AC ==,12S PG PF S AG AC==∴32212S S PF S S AC+=作AN BC ∥交y 轴于N,作PQ y ∥轴交BC 于Q 直线BC 的解析式为3y x =-+,AN BC∥∴直线AN 的解析式为y x b '=-+将()1,0A -代入y x b '=-+,得:()01b =--+'解得:1b '=-∴直线AN 的解析式为=1y x --当0x =时,1N y =-()0,1N ∴-∴1ON =,4CN ON CO =+= AN BC ∥,PQ y∥∴PQF NCB ANC ∠=∠=∠,PFC ACF ∠=∠∵PFC FPQ PQF ∠=∠+∠,ACF NCB ACN ∠=∠+∠∴FPQ ACN∠=∠∴CAN PFQ∽ PF PQ AC CN∴=设()2,23P n n n -++,则(),3Q n n -+∴23PQ n n=-+∴22322122261394228S S PF PQ n n n S S AC CN -+⎛⎫+====--+ ⎪⎝⎭∴当32n =时,3221S S S S +有最大值98此时315,24P ⎛⎫ ⎪⎝⎭,33,22Q ⎛⎫ ⎪⎝⎭∴1539424PQ =-=,322CQ ==1,3ON OA OB OC ==== 45OBC ANC ∴∠=∠=︒ANC PQF∠=∠OBC PQF∴∠=∠BC == ,4AB =932323242,848PQ CQ BC AB ∴====PQ CQ BC AB∴=∴CPQ ACB∽ BCP CAB∴∠=∠AC ==310sin sin10OC BCP CAB AC ∴∠=∠==.。
(完整版)初中数学中考考试大纲

梯形的概念
√
等腰梯形的性质和判定
√
线段、矩形、平行四边形、三角形的中心及物理意义
√
运用三角形、四边形、正六边形进行镶嵌设计
√
7、圆
圆的有关概念
√
弧、弦、圆心角的关系
√
圆的性质
√
圆周角与圆心角的关系、直径所对圆周角的特征
√
三角形的内心与外心
√
切线的概念
√
切线与过切点的半径之间的关系
√
切线的判定
√
过圆上一点画圆的切线
图形坐标与坐标变化
√
用适当方式确定物体的位置
√
考试内容
考试
要求目标
单元
知识条目
a1
a2
a3
统计与概率
1、统计
数据的收集、整理
√
抽样、样本
√
统计图(条形图、折线图、扇形图)
√
众数、中位数、平均数、加权平均数
√
频数、频率的概念
√
频数分布的意义和作用
√
频数分布表和分布直方图
√
用频数分布直方图解决实际问题
√
(1)实世界中数量关系,具有初步的数感、符号感和抽象思维能力。这一目标主要包括能够在较复杂的层面上用数字和图表刻画现实生活中的现象,对一些数字信息作出合理解释与推断,并运用代数中的方程、不等式、函数等去刻画具体问题,建立合适的数学模型。
(2)对现实空间及图形有较丰富的认识,具体初步的空间观念和形象思维能力。这一目标包括能够通过动手操作、图形变换等多种方式探讨图形的形状、大小、位置关系、等量关系等,进行简单的图案设计、构建几何空间,并尝试用图形去从事推理活动。
(4)能够通过观察、实验、猜想、证明等数学活动过程,作出合理推理和演绎推理,能有条理地,清晰地阐述自己的观点。这一目标主要包括能够通过推理作出合理的判断与选择,尝试通过不同的方式去检验一个猜想,并能够用比较规范的逻辑推理形式表达自己的演绎推理过程。
(完整word版)中考数学考试大纲及要求明细
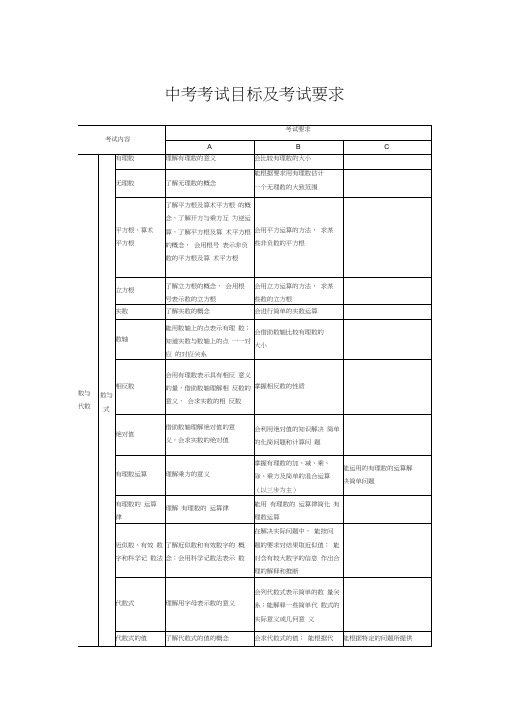
函数及其图象
了解常量和变量的意义; 了 解函数的概念和三种表示 方法;能举出函数的实例; 会确定简单的整式、 分式和 简单实际问题中的函数的 自变量取值范围, 并会求函 数值
能用适当的函数表示法刻 画某些实际问题中变量之 间的关系
能探索具体问题中的数量 关系和变化规律,并用函 数加以表示;结合函数关 系的分析,能对变量的变 化趋势进行初步推测;能 结合图象对简单实际问题 中的函数关系进行分析
掌握相反数的性质
绝对值
借助数轴理解绝对值的意
义,会求实数的绝对值
会利用绝对值的知识解决 简单的化简问题和计算问 题
有理数运算
理解乘方的意义
掌握有理数的加、减、乘、 除、乘方及简单的混合运算 (以三步为主)
能运用的有理数的运算解
决简单问题
有理数的 运算 律
理解 有理数的 运算律
能用 有理数的 运算律简化 有理数运算
近似数、有效 数字和科学记 数法
了解近似数和有效数字的 概念;会用科学记数法表示 数
在解决实际问题中, 能按问 题的要求对结果取近似值; 能对含有较大数字的信息 作出合理的解释和推断
代数式
理解用字母表示数的意义
会列代数式表示简单的数 量关系;能解释一些简单代 数式的实际意义或几何意 义
代数式的值
了解代数式的值的概念
能选择适当的方法解一元 二次方程;会用一元二次方 程根的判别式判断根的情 况
能利用根的判别式说明含 有字母系数的一元二次方 程根的情况及由方程根的 情况确定方程中待定系数 的取值范围; 会用配方法 对代数式作简单的变形; 会运用一元二次方程解决 简单的实际问题
不等式(组)
能根据具体问题中的大小 关系 了解不等式的意义
2023年中考数学考试说明

2023年中考数学考试说明考试时间与地点
2023年中考数学考试将于2023年6月15日上午9点开始,考试时间为120分钟。
考试地点将在考生所在的中学进行。
考试内容
考试内容包括:
1. 初中数学全部知识点,包括代数、几何、函数、排列组合等内容;
2. 科学解题方法和思维能力的测试;
3. 与日常生活和实际问题相关的数学应用能力测试。
考试形式
考试采取闭卷形式,考生不得携带任何纸质或电子辅助材料参加考试。
考试共设两个部分,第一部分为选择题,第二部分为填空题和解答题。
1. 选择题:共计60道,每题1分,共60分;
2. 填空题:共计30道,每题2分,共60分;
3. 解答题:共计5道,每题16分,共80分。
总分为200分。
注意事项
1. 考试前,请务必检查个人准考证信息,并提前到达考场;
2. 请携带2B铅笔、橡皮擦、直尺、圆规、三角板、计算器等必需品;
3. 在考试过程中,请保持安静,不得与他人交流和传递信息;
4. 考试结束后,请将试卷和答题卡放在指定地点。
祝各位考生取得优异成绩!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
巴中市2019年中考数学考试说明大纲
一、考试方式
①采取闭卷笔试的方式。
全卷满分为150分,答题时间为120分钟。
试卷由试题和答卷两部分组成,只交答卷。
②参加考试的学生带三角板、圆规、量角器、笔、计算器等进入考场。
二、试卷结构
1、基本结构
试题题型包括客观性试题和主观性试题两大类。
客观性试题指选择题和填空题。
选择题是四选一型的单项选择题;填空题只要求直接填写结果,不必写出计算过程或推证过程。
主观性试题指计算题、证明题、阅读题、画图题以及探索题、开放题等(常统称为解答题)。
解答题要有解题的主要过程,关键步骤不能省略。
2、题型比例
全卷约35个小题,每个小题的设问最多不超过3问,试卷采用选择题、填空题和解答题(包括开放性解答题)组成,其中客观性试题(选择题、填空题)的分值不超过试卷总分值的40%,开放性解答题的分值可占总分值的5%-10%。
3、知识与内容比例
数与代数约75分,空间与图形约58分,统计与概率约17
分。
4、试题难度比例
容易题60%;中等题30%;较难题10%
三、考试内容及要求
1、数与代数
认识有理数、实数、代数式(整式、分式、二次根式)、方程(一元一次方程、一元二次方程、可以化为一元一次方程的分式方程和二元一次方程组)、不等式(一元一次不等式、一元一次不等式组)、函数(一次函数、反比例函数、二次函数);掌握必要的运算(掌握有理数的加、减、乘、除、乘方及简单的混合运算(以三步为主));会进行有关实数的简单四则运算(不要求分母有理化);会进行简单的整式加、减运算、整式乘法运算。
会进行分式加、减、乘、除运算;会解一元一次方程、简单的二元一次方程组、可化为一元一次方程的分式方程,会解简单的数字系数的一元二次方程;会解简单的一元一次不等式,会解由两个一元一次不等式组成的不等式组;能探索具体问题中的数量关系和变化规律,并运用代数式、方程、不等式、函数等进行描述。
2、空间与图形
经历探索物体与图形的基本性质(平行线的性质,等腰三角形的性质,等边三角形的性质,直角三角形的性质,平行四边形的有关性质,矩形、菱形、正方形的有关性质,等腰梯
形的有关性质,正多边形、圆的性质)、变换(轴对称、平移、旋转、相似)、位置关系的过程,掌握三角形、四边形、圆的基本性质以及平移、旋转、轴对称、相似等的基本性质,初步认识视图(主视图、左视图、俯视图),掌握基本的识图、作图等技能,体会证明的必要性,能够根据“一条直线截两条平行直线所得的同位角相等”、“两条直线被第三条直线所截,若同位角相等,那么这两条直线平行”、“若两个三角形的两边及其夹角(或两角及其夹边,或三边)分别相等,则这两个三角形全等、”“全等三角形的对应边、对应角分别相等”等证明三角形和四边形相关的基本性质和
判定定理,掌握基本的推理技能。
3、统计与概率
从事收集、描述、分析数据,作出判断并进行交流的活动,感受抽样的必要性,体会用样本估计总体的思想(主要指用样本平均数、方差估计总体的平均数和方差),掌握必要的数据处理技能(会用扇形统计图表示数据,在具体的情境中会计算极差和方差);进一步丰富对概率的认识,知道大量重复实验时频率可作为事件发生概率的估计值,会运用列举法(包括列表、画树状图)计算一些事件发生的概率。
(。
