解三角形单元测试题
高一数学解三角形单元测试及答案

高一数学解三角形单元测试及答案解三角形本章测试本次测试共有12道选择题,每题5分,总分60分。
在每道题中,只有一个选项是正确的,请将正确选项填涂在答题卡上。
1.在三角形ABC中,已知a=2,b=2,B=π/6,则A=()A。
3π/4 B。
π/3 C。
4π/3 D。
π/42.在三角形ABC中,已知a²=b²+c²+bc,则角A为()A。
30° B。
45° C。
120° D。
150°3.已知三角形ABC中,A:B:C=11:4,则a:b:c的比值为()A。
1:1:3 B。
2:2:3 C。
1:1:2 D。
1:1:44.在三角形ABC中,a、b、c分别为三个内角A、B、C的对边,若a=2,b=1,B=29°,则此三角形的解为()A。
无解 B。
有一解 C。
有两解 D。
有无数解5.在三角形ABC中,∠C=90°,0<A<45°,则下列各式中,正确的是()A。
sinA>XXX>XXX<XXX<sinB6.一艘船自西向东航行,上午10时到达灯塔的南偏西75°、距塔68海里的M处,下午2时到达这座灯塔的东南方向的N 处,则这艘船航行的速度为()A。
176/22海里/时 B。
346海里/时 C。
22海里/时 D。
342/22海里/时7.已知三角形ABC的面积为S,三个内角A、B、C的对边分别为a、b、c,若4S=a²-(b-c)²,bc=4,则S=()A。
2 B。
4 C。
3 D。
15/28.已知三角形ABC的内角A、B、C所对的边分别为a、b、c,若cosC=1/4,4bcosA+acosB=3,则三角形ABC外接圆的半径为()A。
2/3 B。
2√2 C。
4 D。
69.在三角形ABC中,已知asinA/bsinB=(a²+c²-b²)/(b²+c²-a²),则三角形ABC的形状为()A。
解三角形单元测试题Penny

解三角形单元测试题 一、选择题:1. 在△ABC 中,c=3,B=300,则a 等于( ) AB .CD .22.在ABC ∆中,已知三边a 、b 、c 满足()()3a b c a b c ab +++-=,则C =( ) A .15 B .30 C .45 D .603. 已知△ABC 的周长为9,且4:2:3sin :sin :sin =C B A ,则cosC 的值为( )A .41-B .41C .32-D .324. 在△ABC 中,A =60°,b =1,其面积为3,则CB A cb a sin sin sin ++++等于( )A .33B .3392C .338D .2395. 在△ABC 中,AB =5,BC =7,AC =8,则BC AB ⋅的值为( ) A .79B .69C .5D .-56.△ABC 中,根据下列条件,确定△ABC 有两解的是( ) A.a=18,b=20,A=120° B.a=60,c=48,B=60° C.a=3,b=6,A=30° D.a=14,b=16,A=45°7. 设m 、m+1、m+2是钝角三角形的三边长,则实数m 的取值范围是( ) A.0<m <3 B.1<m <3C.3<m <4D.4<m <68. △ABC 中,若c=ab b a ++22,则角C 的度数是( ) A.60° B.120° C.60°或120° D.45°9.在△ABC 中,A B B A 22sin tan sin tan ⋅=⋅,那么△ABC 一定是( ) A .锐角三角形B .直角三角形C .等腰三角形D .等腰三角形或直角三角形10. 在ABC △中,cos cos sin sin A B A B >,则ABC △是( ) A.锐角三角形 B.直角三角形C.钝角三角形D.正三角形二、填空题13.在△ABC 中,有等式:①asinA=bsinB ;②asinB=bsinA ;③acosB=bcosA ;④sin sin sin a b cA B C+=+. 其中恒成立的等式序号为______________14. 在等腰三角形 ABC 中,已知sinA ∶sinB=1∶2,底边BC=10,则△ABC 的周长是 .15. 在△ABC 中,已知sinA ∶sinB ∶sinC=3∶5∶7,则此三角形的最大内角的度数等于___________.16. 在ABC △中,若12057A AB BC ∠===,,,则ABC △的面积S =_____________.三、解答题17. 已知在△ABC 中,A=450,BC=2,求解此三角形.18. 在△ABC 中,已知a-b=4,a+c=2b ,且最大角为120°,求△ABC 的三边长.19. 如图,测量河对岸的塔高AB 时,可以选与塔底B 在同一水平面内的 两个测点C 与D ,测得75BCD ︒∠=,60BDC ︒∠=,60CD =米, 并在点C 测得塔顶A 的仰角为60︒,求塔高20. 如图所示,我艇在A 处发现一走私船在方位角45°且距离为12海里的B 处正以每小时10海里的速度向方位角105°的方向逃窜,我艇立 即以14海里/小时的速度追击,求我艇追上走私船所需要的时间.21.在ABC △中,已知222sin sin sin A B C +=,求证:ABC △为直角三角形.22. 在△ABC 中,已知3cos 2cos a C c A =,且1tan 3A =,求B.23.已知ABC △中,AD 为BAC ∠的平分线,利用正弦定理证明AB BDAC DC=.222222442-41(4)(4) cos 222(4)100()14 10 6a b a b a c b c b A b c a b b b A bc b b b b -=⇒=++=⇒=+-+--+=⇒-=-==,代入 故易知:为最大角 解方程得:或舍去故三角形的三边长分别为:, ,正余弦定理单元测试参考答案 CDABD DBBDC13. ②④ 14.50, 15.120017. 已知在△ABC 中,A=450,BC=2,求解此三角形. 解答:作图观察,12060 232226sin sin sin sin 或故==⨯==⇒=C a A c C A a C c ,15180012,7518060=--===--==C A B C C A B C 时,当时,当13624645cos 2cos 2222±=-+=⇒-+=b b b bc a c b A 解方程得:将余弦定理作为方程来用!15120==B C ,故,三角形的解为:,1-3=AC 或 5706==B C ,,13+=AC 18. 在△ABC 中,已知a-b=4,a+c=2b ,且最大角为120°,求△ABC 的三边长. 解答:19.如图,测量河对岸的塔高AB 时,可以选与塔底B 在同一水平面内的两个测点C 与D ,测得75BCD ︒∠=,60BDC ︒∠=,60CD =米,并在点C 测得塔顶A 的仰角为60︒,求塔高解答:63022236060sin 45sin =⨯=⇒=CB CBCD290363060tan 60tan =⨯==⇒=CB AB CBAB答:塔高为290米。
2020届 人教A版__解三角形-单元测试

解三角形一、单选题1.在ABC ∆中,B=30︒,C=45︒,c=1,则最短边长为()A.3B.2C.12D.2【答案】B【解析】由题意,易知B C A <<,所以b 最小.由正弦定理,得sin 2sin 2c B b .C ==2.已知ABC ∆中,2=a ,3=b , 60=B ,那么=∠A ()A.45B.90C.135或45D.150或30【答案】A 【解析】试题分析:利用正弦定理,B bA a sin sin =得:22360sin 2sin sin 0===bB a A ,由于b a <,则B A <,于是045=A ,选A.考点:利用正、余弦定理解三角形.【易错点评】利用正弦定理求三角形的内角,当求出b a <22sin =A 时,容易得出045=A 或 135,这时务必要研究角A 的范围,由于,则B A <,说明角A 为锐角,所以045=A .3.已知ABC ∆满足a b >,则下列结论错误的是()A .AB >B .sin sin A B >C .cos cos A B<D .sin2sin2A B>【答案】D【解析】由大边对大角,可知A B >,所以A 正确;由正弦定理可知,sin sin A B >,所以B 正确;由A B >,且cos y x =在()0,π单调递减,可知cos cos A B <,所以C 正确;当90,30A B ==时,a b >,但sin2sin2A B <,所以D 错误。
故选D 。
点睛:本题考查三角函数与解三角形的应用。
本题中涉及到大边对大角的应用,正弦定理的应用,三角函数单调性的应用等,需要学生对三角模块的综合掌握,同时结合特殊值法去找反例,提高解题效率。
4.在∆ABC 中,,30,,1=∠==A x b a 则使∆ABC 有两解的x 的范围是()A、)332,1(B、),1(+∞C、)2,332(D、)2,1(【答案】D 【解析】试题分析:结合图形可知,三角形有两解的条件为,sin b x a b A a =><,所以01,sin 301b x x =><,12x <<,故选D 。
2020届人教A版__解三角形-单元测试

解三角形一、单选题1.已知α是三角形的一个内角,且32cos sin =+αα,则这个三角形( ) A .锐角三角形 B .钝角三角形 C .不等腰的直角三角形 D .等腰直角三角形 【答案】B 【解析】 试题分析:由题32cos sin =+αα, 则:()2225sin cos ,sin cos 0318αααα⎛⎫+==-< ⎪⎝⎭因为: sin 0,cos 0αα><,则三角形为钝角三角形。
考点:三角函数的变形及三角形形状的判断. 2.【答案】A【解析】本题考查向量的数量积及其最佳值问题如图示以为A 原点,以CA 和CB 所在直线为x 轴和y 轴建立直角坐标系,则()()()0,0,0,3,4,0A B C -,则()4,3CB = .设(),M x y 则()4,CM x y =+,由//CM CB 得443y x +=,即334y x =+,则()3,34x M x +,所以()()33,3,4,344x x AM x CM x =+=++;又AM CM ⊥,则0AM CM ⋅=,则()()()2223331617,34,34390444252x x x x x x x x x +⋅++=+++=++= 所以2251361440x x ++=解得3625x =-或4x =-(舍)所以()3648,2525M =-,所以()3648,2525AM =-设()()3,3,404a N a a +-≤≤,则()3,34a AN a =+,则()()()3648336348144,,33252542542525a a a AM AN a ⋅=-⋅+=-++⨯=即40a -≤≤时取最大值14425AM AN ⋅=故正确答案为A 3.在,则边的边长为( )A .B .3C .D .7【答案】A 【解析】试题分析:由题意得,三角形的面积,解得,在中,由余弦定理得,所以.考点:余弦定理及三角形的面积公式的应用.4.已知ABC ∆中,AB=AC=5,BC=6,则ABC ∆的面积为A .12B .15C .20D .25 【答案】A 【解析】试题分析:因为,ABC ∆中,AB=AC=5,BC=6,所以,BC4=,三角形的面积为12,选A 。
《解直角三角形》单元测试题
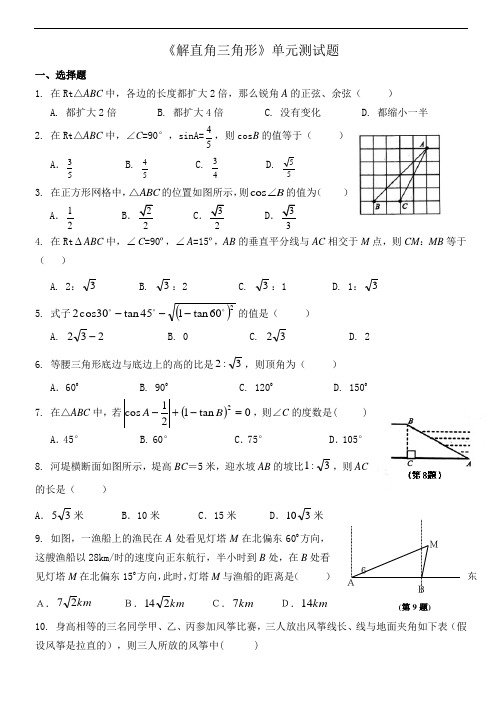
《解直角三角形》单元测试题一、选择题1. 在Rt △ABC 中,各边的长度都扩大2倍,那么锐角A 的正弦、余弦( ) A. 都扩大2倍 B. 都扩大4倍 C. 没有变化 D. 都缩小一半2. 在Rt △ABC 中,∠C =90°,sinA=54,则cos B 的值等于( ) A .53 B. 54 C. 43 D. 553. 在正方形网格中,ABC △的位置如图所示,则cos B ∠的值为( ) A .12B .22C .32D .334. 在Rt ∆ABC 中,∠C =90º,∠A =15º,AB 的垂直平分线与AC 相交于M 点,则CM :MB 等于( )A. 2:3B. 3:2C. 3:1D. 1:3 5. 式子()260tan 145tan 30cos 2---的值是( )A. 232-B. 0C. 32D. 2 6. 等腰三角形底边与底边上的高的比是3:2,则顶角为( ) A .600B. 900C. 1200D. 15007. 在△ABC 中,若()0tan 121cos 2=-+-B A ,则∠C 的度数是( ) A .45° B. 60° C .75°D .105° 8. 河堤横断面如图所示,堤高BC =5米,迎水坡AB 的坡比3:1,则AC 的长是( ) A .35米 B .10米C .15米D .310米9. 如图,一渔船上的渔民在A 处看见灯塔M 在北偏东60O方向,这艘渔船以28km/时的速度向正东航行,半小时到B 处,在B 处看见灯塔M 在北偏东15O方向,此时,灯塔M 与渔船的距离是( ) A.km 27 B.km 214 C.km 7 D.km 1410. 身高相等的三名同学甲、乙、丙参加风筝比赛,三人放出风筝线长、线与地面夹角如下表(假设风筝是拉直的),则三人所放的风筝中( )6ABM东(第9题)同学 甲 乙 丙 放出风筝线长 100m 100m 90m 线与地面夹角40º45º60ºA. 甲的最高B. 丙的最高C. 乙的最低D. 丙的最低 11. 如图,一棵大树被台风拦腰刮断,树根到刮断点的长度是,折断部分与地面成的夹角,那么原来树的长度是( )12.为了方便行人推车过某天桥,市政府在10m 高的天桥一侧修建了40m 长的斜道(如图所示).我们可以借助科学计算器求这条斜道倾斜角的度数.具体按键顺序是 ( ).11 12 二、填空题13. 锐角A 满足2 sin(A-150)=3,则∠A = . 14. 已知tan B =3,则sin 2B= . 15. 已知有一山坡水平方向前进了米,就升高了米,那么这个山坡的坡度是 .16.某人沿着有一定坡度的坡面前进了10米,此时他与水平地面的垂直距离为52米,则这个破面的坡度为 .17. 如图,已知直线1l ∥2l ∥3l ∥4l ,相邻两条平行直线间的距离都是1,如果正方形ABCD 的四个顶点分别在四条直线上,则sin α= .18. 如图所示,小明在家里楼顶上的点A 处,测量建在与小明家楼房同一水平线上相邻的电梯楼的高,在点A 处看电梯楼顶部点B 处的仰角为60°,在点A 处看这栋电梯楼底部点C 处的俯角为45°,两栋楼之间的距离为30m ,则电梯楼的高BC 为 米(保留根号)17 18 19 AB C DαA 1l 3l2l4l19. 已知如图,将两根宽度为的纸带交叉叠放,若为已知,则阴影部分面积为________20. 如图,在一段坡度为的山坡上种树,要求株距(即相邻两株树之间的水平距离)为米,那么斜坡上相邻两株树之间的坡面距离为________米 三、解答题 21计算:-120162cos 60-+2-8-tan 30-12+1÷⨯()(1)()22. 如图,在Rt △ABC 中,∠C =90°,AC =12,∠A 的平分线AD =83,求BC ,AB .23. 如图所示,海上有一灯塔P ,在它周围3海里处有暗礁,一艘客轮以9海里/时的速度由西向东航行,行至A 点处测得P 在它的北偏东60°的方向,继续行驶20分钟后,到达B 处又测得灯塔P 在它的北偏东45°方向.问客轮不改变方向继续前进有无触礁的危险?24. 如图,某中心广场灯柱被钢缆固定,已知米,且.求钢缆的长度;若米,灯的顶端距离处米,且,则灯的顶端距离地面多少米?25.如图,小华站在河岸上的点,看见河里有一小船沿垂直于岸边的方向划过来.此时测得小船的俯角是.若小华的眼睛与地面的距离是米,米,平行于所在的直线,迎水坡,坡长米,点、、、、、在同一平面内,则此时小船到岸边的距离的长是多少?(结果保留根号)26. 综合实践课上,张明所在小组要测量护城河的宽度.如图所示是护城河的一段,两岸AB 、CD ,河岸AB 上有一排大树,相邻两棵大树之间的距离均为10米.张明先用测角仪在河岸CD 的M 处测得∠α=36°,然后沿河岸走50米到达N 点,测得∠β=72°.请你根据这些数据帮他们算出河宽FR (结果保留两位有效数字). (参考数据:sin 36°≈0.59,cos 36°≈0.81,tan36°≈0.73,sin 72°≈0.95,cos 72°≈0.31,tan72°≈3.08)ABC DEFMNR αβ。
《解三角形》单元测试题2

《解三角形》单元测试题班级:__________学号:__________姓名:__________成绩:__________一、选择题。
1、一个三角形的三边之比为6:7:9,那么这三角形是A 、钝角三角形B 、锐角三角形C 、直角三角形D 、三内角之比为6:7:92、在ABC △中,已知4,6a b ==,60B =,则sin A 的值为A 、33B 、32C 、63D 、623、在ABC △中,::1:2:3A B C =,则sin :sin :sin A B C =A 、1:2:3B 、1:2:3C 、1:2:3D 、1:3:24、在ABC △中,sin :sin :sin 4:3:2A B C =,那么cos C 的值为A 、14B 、14-C 、78D 、11165、在ABC △中,13,34,7===c b a ,则最小角为A 、3πB 、6πC 、4πD 、12π 6、在ABC △中,60,16,A b == 面积3220=S ,则c =A 、610B 、75C 、55D 、497、在ABC △中,()()()a c a c b b c +-=+,则A =A 、30B 、60C 、120D 、1508、在ABC △中,根据下列条件解三角形,则其中有二个解的是A 、10,45,70b A C ===B 、60,48,60a c B ===C 、7,5,80a b A ===D 、14,16,45a b A ===9、在ABC △中,有一边是另一边的2倍,并且有一个角是30,那么这个三角形A 、一定是直角三角形B 、一定是钝角三角形C 、可能是锐角三角形D 、一定不是锐角三角形10、已知锐角三角形的边长分别是2,3,x ,则x 的取值范围是A 、15x <<B 、513x <<C 、05x <<D 、135x <<二、填空题。
A B C11、在ABC △中,3,2a b ==,45B =,则A =____________12、在ABC △中,60A =,且43c b =,则sin C =____________ 13、在ABC △中,已知7,8a b ==,13cos 14C =,则最大角的余弦值是___________ 14、在ABC △中,12,60,45a b A B +===,则a =____________三、解答题。
必修5解三角形第一单元测试题 (含答案)

数学必修5解三角形单元测试题(时间120分钟,满分150分)一、选择题:(每小题5分,共计60分)1.在△ABC 中,若BA sin sin >,则A 与B 的大小关系为( ) A. B A > B. B A < C. A ≥B D. A 、B 的大小关系不能确定 2. 在△ABC 中,b=3,c=3,B=300,则a 等于( )A .3B .123C .3或23D .2 3. 不解三角形,下列判断中正确的是( )A .a=2,b=4,A=300有两解B .a=30,b=25,A=1500有一解C .a=6,b=9,A=450有两解D .a=9,c=10,B=600无解4. 已知△ABC 的周长为9,且4:2:3sin :sin :sin =C B A ,则cosC 的值为( )A .41-B .41 C .32-D .32 5. 在△ABC 中,A =60°,b =1,其面积为3,则CB A cb a sin sin sin ++++等于( )A .33B .3392C .338D .2396.(2013年高考湖南卷)在锐角中ABC ∆,角,A B 所对的边长分别为,a b 若2sin 3,a B b A =则角等于( ) A.12π B.6π C.4π D.3π 7.已知锐角三角形的边长分别为1,3,a ,则a 的范围是( )A .()10,8B .()8,10 C . ()10,8D .()10,88.在△ABC 中,若cCb B a A sin cos cos ==,则△ABC 是( ) A .有一内角为30°的直角三角形B .等腰直角三角形C .有一内角为30°的等腰三角形D .等边三角形9. △ABC 中,若c=ab b a ++22,则角C 的度数是( ) A.60°或120° B.60° C. 45° D.120° 10. 在△ABC 中,若b=22,a=2,且三角形有解,则A 的取值范围是( ) A.0°<A <30° B.0°<A ≤45° C.0°<A <90° D.30°<A <60°11. 已知△ABC 的三边长6,5,3===c b a ,则△ABC 的面积为 ( )A . 14B .15C . 142D .15212.(2013年高考陕西卷)设△ABC 的内角A , B , C 所对的边分别为a , b , c ,若cos cos sin b C c B a A +=, 则△ABC 的形状为( )(A) 锐角三角形 (B)直角三角形 (C)钝角三角形 (D) 不确定 二、填空题(每小题5分,满分20分)13.(2013新课标Ⅱ)设θ为第二象限角,若1tan()42πθ+=,则sin cos θθ+=______. 14. 在等腰三角形 ABC 中,已知sinA ∶sinB=1∶2,底边BC=10,则△ABC 的 周长是 .15. 在△ABC 中,已知sinA ∶sinB ∶sinC=3∶5∶7,则此三角形的最大内角的 度数等于________.16. 已知△ABC 的三边分别是a 、b 、c ,且面积4222c b a S -+=,则角C=_______.三、解答题(70分)17. (本题满分10分)已知a =33,c =2,B =150°,求边b 的长及三角形面积.18. (本题满分12分)在△ABC 中,已知a-b=4,a+c=2b ,且最大角为120°,求△ABC 的三边长.19. (本题满分12分)在△ABC 中,证明:2222112cos 2cos ba b B a A -=-。
2020届人教A版-解三角形-单元测试(4)

解三角形一、单选题1.在ABC ∆中,,,4530,2===C A a 则ABC S ∆=A 、2B 、22C 、13+D 、()1321+【答案】C 【解析】 试题分析:2221051sin sin 22a c cc B A C =∴=∴==()11sin 260453122S ac B ∴==⨯⨯+=+ 考点:正弦定理及三角形面积公式2.△ABC 中,角A , B , C 所对的边分别是a , b , c , S 表示三角形的面积,若sin sin sin a A b B c C +=, ()22214S a c b =+-,则对△ABC 的形状的精确描述是( )A .直角三角形B .等腰三角形C .等腰或直角三角形D .等腰直角三角形 【答案】D【解析】试题分析:因为sin sin sin a A b B c C +=,由正弦定理可知222a b c +=,所以ABC ∆为直角三角形,又由三角形的面积公式,可知()22211sin 24ac B a c b =+-,即222sin cos 2a c b B B ac +-==,解得4B π∠=,综上所述,可得ABC ∆为等腰直角三角形,故选D .考点:三角形的综合应用.【方法点晴】本题主要考查了三角形的综合问题,其中解答中涉及到解三角形的正弦定理、余弦定理和三角形的面积公式等知识点综合问题,着重考查了学生分析问题和解答问题的能力,以及推理与运算能力,试题比较基础,属于基础题,本题的解答中根据正弦定理,得出ABC ∆为直角三角形,在利用三角形的面积公式和余弦定理,得出4B π∠=是解答关键.3.在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c.若2a =,b+c=7,cosB=14-,则c =( )A .3B .4C .5D .6 【答案】A【解析】由题意结合余弦定理222cos 2a c b B ac +-=可得: 224144c b c +-=-,①由7b c +=可知: 7b c =-,② 代入①式可得:()2247144c c c+--=-,求解关于边长的方程可得: 3c =. 本题选择A 选项.4.已知在ΔABC 中, sin :sin :sin 3:2:4A B C =,那么cos C 的值为 A .14-B .14C .23-D .23【答案】A【解析】因为sin :sin :sin 3:2:4A B C =, 所以::3:2:4a b c =.所以2223241cosC .2324+-==-⨯⨯本题选择A 选项.5.在△ABC 中,周长为7.5cm ,且sinA :sinB :sinC =4:5:6,下列结论: ①6:5:4::=c b a ②6:5:2::=c b a③cm c cm b cm a 3,5.2,2=== ④6:5:4::=C B A其中成立的个数是( )A .0个B .1个C .2个D .3 【答案】C 【解析】 试题分析:令sin sin sin a b ck A B C===,sin ,sin ,sin a k A b k B c k C ∴===. ::sin :sin :sin sin :sin :sin 4:5:6a b c k A k B k C A B C ∴===. 7.5a b c ++=,4567.52,7.5 2.5,7.53151515a cmb cmc cm ∴=⨯==⨯==⨯=.所以①③正确.故C 正确.考点:正弦定理. 6.的三内角A,B,C 所对边长分别是,若sinB−sinA sinC=√3a+ca+b,则角的大小为( ) A .B .C .D .【答案】B【解析】试题分析:由正弦定理得sinB−sinA sinC=√3a+c a+b⇒b−a c=√3a+c a+b⇒c 2+a 2−b 2=−√3ac ⇒cosB =c 2+a 2−b 22ac=−√32∵0<B <π∴B =5π6,选B考点:正弦定理,余弦定理7.设ABC ∆的内角A , B , C 的对边分别为a , b , c .若2a =, c =,1sin 2A =,且b c <,则B =( ) A .π6 B .π3 C .π2 D .2π3【答案】A【解析】因b c <, a c <,故由1sin 2A =可得30A =,由正弦定理可得:sin sin sin sin a c c A C A C a =⇒==,解之得120C =,即23C π=,则2366B ππππ=--=,应选答案A 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解三角形习题
一、选择题:(每小题5分,共计50分)
1.在△ABC 中,
c=3,B=300,则a 等于( ) A
.
.2
2. 在ABC ∆,内角,,A B C 所对的边长分别为,,.a b c 1
sin cos sin cos ,2
a B C c B A
b +=且a b >,则
B ∠= A.6π B.3π C.23π D.56
π 3.已知△ABC 的周长为9,且4:2:3sin :sin :sin =C B A ,则cosC 的值为
A .41-
B .41
C .3
2- D .32
4. 在△ABC 中,A =60°,b =1,其面积为3,则C
B A c
b a sin sin sin ++++等于( )
A .33
B .3392
C .338
D .2
39
5.在△ABC 中,AB =5,BC =7,AC =8,则BC AB ⋅的值为( ) A .79 B .69 C .5 D .-5
6.在△ABC 中,若b 2sin 2C +c 2sin 2B =2bc cos B cos C ,则此三角形为
A.直角三角形
B.等腰三角形
C.等边三角形
D.等腰直角三角形
7.已知锐角三角形的边长分别为1,3,a ,则a 的范围是( )
A .()10,8
B .
()10,8
C . ()
10,8
D .()
8,10
8. 在△ABC 中,222sin sin sin sin sin A B C B C ≤+-,则A 的取值范围是
A.(0,]6
π B.[,)6
ππ C.(0,]3
π D.[,)3
ππ
9.设,,,,,ABC A B C a b c ∆的内角所对的边为若三边的长为连续的三个正整数,且,320cos A B C b a A >>=,则sin :sin :sin A B C 为( ) A.4:3:2 B.5:6:7 C.6:5:4 D.5:4:3
10. ,,,,,ABC A B C a b c ∆在的内角所对的边为已知8b=5c,C=2B,则cosC=( ) A.725
B. 725-
C.725±
D.2425
二、填空题(每小题4分,满分16分)
11.在△ABC 中,有等式:①asinA=bsinB ;②asinB=bsinA ;③acosB=bcosA ;④
s i n s i n s i n a
b c
A B C
+=
+.
其中恒成立的等式序号为______________
12.设△ABC 的内角A ,B ,C ,所对的边分别是a ,b ,c.若()()+-++=a b c a b c ab ,则角C=______________。
13.已知△ABC 的三边分别是a 、b 、c ,且面积4
2
22c b a S -+=,则角C=____________.
14. 在△ABC 中,若a=2,b+c=7,cosB=1
4
-,则b=__________
15.22,,()ABC a b c S S a b c ∆=--的三边和面积满足:,且ABC ∆的外接圆周长为17π,则面积S 的最大值为____________ 三、解答题(84分)
16. 在△ABC 中,a =3,b
,∠B =2∠A .
(I)求cos A 的值; (II)求c 的值.
17. 在△ABC 中,已知a-b=4,a+c=2b ,且最大角为120°,求△ABC 的三边长.
18. 设ABC ∆的内角,,A B C 的对边分别为,,a b c ,()()a b c a b c ac ++-+=. (I)求B
(II)
若sin sin A C =
,求C
19. 设ABC ∆的内角,,A B C 所对边的长分别是,,a b c ,且3,1,2.b c A B ===
(Ⅰ)求a 的值; (Ⅱ)求sin()4
A π
+的值。
20. 如图1,甲船在A 处,乙船在A 处的南偏东45°方向,
距A 有
图1
C
°
9海里并以20海里/时的速度沿南偏西15°方向航行,若甲船以28海里/时的速度航行,应沿什么方向,用多少小时能尽快追上乙船? (本题满分12分)
21.在ABC ∆中,角A ,B ,C 对应的边分别是a ,b ,c 。
已知()cos23cos 1A B C -+=。
(I )求角A 的大小;
(II )若ABC ∆
的面积S =5b =,求sin sin B C 的值。
