第3章_决策树学习
机器学习模型之决策树

机器学习模型之决策树⽬录1、分类决策树模型决策树模型是⼀种基于规则的算法,其是⼀个⼆叉树结构,其中叶⼦节点为分类的类别,中间的节点为对不同的特征的选择。
其既可以做分类,也可以做回归,决策树学习算法包括特征选择,决策树的构建,剪枝。
1.1、特征选择特征选择在进⾏决策树分裂的过程中进⾏的算法,其主要思想是希望在选择某个特征作为分裂特征之后,整个系统的熵变⼩。
常⽤的特征选择算法有信息增益和信息增益⽐信息增益⾸先,要想了解信息增益的原理,我们就需要理解两个概念,熵和条件熵,熵是什么呢?熵表⽰系统的混乱程度,或者叫不确定程度。
设X为取有限个值的随机变量P(X=x i)=p i则熵表⽰为H(X)=−n∑i=1p i logp i我们可以看到,如果每个p i都⽐较均匀的话,那么熵值就会很⼤,意味着整个系统就会很不确定。
接下来我们引⼊条件熵,条件熵表⽰在某个随机变量下,另⼀个随机变量的混乱程度。
公式如下H(Y|X)=n∑i=1p i H(Y|X=x i)有了上述知识,我们就可以引出信息增益,其公式如下g(D,A)=H(D)−H(D|A)可以理解为,数据集D的熵为H(D),在A条件下的熵为H(D|A),那就是说,当我们指定A之后,整体下降的熵即为信息增益,也可以理解为A 帮助系统减少的混乱程度。
⼀般情况下,我们也将信息增益当做D和A的互信息。
在决策树中,我们如何来理解信息增益呢?最开始的熵H(D)表⽰系统最开始的混乱程度,其公式为H(D)=−K∑k=1|C k||D|∗log2|C k||D|其中K表⽰类别标签的数量,|C k|表⽰在类别标签为k下的样本数量,|D|表⽰数据集样本总数量,这句话理解为类别标签越平均,则原始数据整体混乱。
接着,我们再看下H(D|A)的公式H(D|A)=∑i=1n|D i||D|H(Di)其中H(D i)=−K∑k=1|D ik||D|∗log2|D Ik||D|上⾯这两个式⼦怎么理解呢?⾸先,由于是在条件A下,所以我们要先算出每个特征占据整个数据集的百分⽐⽤|D i||D|,接下来,我们就要计算在第i个特征下,这个特征的混乱程度,即H(D i),我们发现这个式⼦和H(D)基本类似,其原理也是⼀样,得到这个特征下的系统混乱程度,接下来,我们将所有特征所在的系统的混乱程度进⾏加和,最后,⽤信息增益公式(4)得到结果。
决策树(理论篇)

决策树(理论篇)定义 由⼀个决策图和可能的结果(包括资源成本和风险组成),⽤来创建到达⽬的的规划。
——维基百科通俗理解 给定⼀个输⼊值,从树节点不断往下⾛,直⾄⾛到叶节点,这个叶节点就是对输⼊值的⼀个预测或者分类。
算法分类ID3(Iterative Dichotomiser 3,迭代⼆叉树3代)历史 ID3算法是由Ross Quinlan发明的⽤于⽣成决策树的算法,此算法建⽴在奥卡姆剃⼑上。
奥卡姆剃⼑⼜称为奥坎的剃⼑,意为简约之法则,也就是假设越少越好,或者“⽤较少的东西,同样可以做好的事情”,即越是⼩型的决策树越优于⼤的决策树。
当然ID3它的⽬的并不是为了⽣成越⼩的决策树,这只是这个算法的⼀个哲学基础。
引⼊ 信息熵。
熵是热⼒学中的概念,是⼀种测量在动⼒学⽅⾯不能做功的能量总数,也就是当总体熵的增加,其做功能⼒也下降,熵的量度正是能量退化的指标——维基百科。
⾹农将“熵”的概念引⼊到了信息论中,故在信息论中被称为信息熵,它是对不确定性的测量,熵越⾼,不确定性越⼤,熵越低,不确定性越低。
那么到底何为“信息熵”?它是衡量信息量的⼀个数值。
那么何⼜为“信息量”?我们常常听到某段⽂字信息量好⼤,某张图信息量好⼤,实际上指的是这段消息(消息是信息的物理表现形式,信息是其内涵——《通信原理》)所包含的信息很多,换句话说传输信息的多少可以采⽤“信息量”去衡量。
这⾥的消息和信息并不完全对等,有可能出现消息很⼤很多,但所蕴含有⽤的信息很少,也就是我们常说的“你说了那么多(消息多),但对我来说没⽤(信息少,即信息量少)”。
这也进⼀步解释了消息量的定义是传输信息的多少。
进⼀步讲,什么样的消息才能构成信息呢? 我们为什么会常常发出感叹“某段⽂字的信息量好⼤”,得到这条消息时是不是有点出乎你的意料呢?⽐如,X男和X男在同⼀张床上发出不可描述的声⾳,这段消息对于你来讲可能就会发出“信息量好⼤”的感叹。
再⽐如,某情侣在同⼀张床上发出不可描述的声⾳,这段消息对于你来讲可能就是家常便饭,并不会发出“信息量好⼤”的感叹。
李航-统计学习方法-笔记-5:决策树
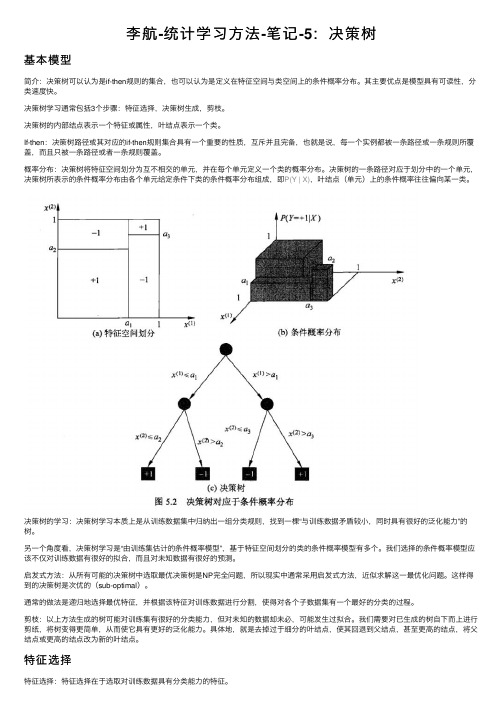
李航-统计学习⽅法-笔记-5:决策树基本模型简介:决策树可以认为是if-then规则的集合,也可以认为是定义在特征空间与类空间上的条件概率分布。
其主要优点是模型具有可读性,分类速度快。
决策树学习通常包括3个步骤:特征选择,决策树⽣成,剪枝。
决策树的内部结点表⽰⼀个特征或属性,叶结点表⽰⼀个类。
If-then:决策树路径或其对应的if-then规则集合具有⼀个重要的性质,互斥并且完备,也就是说,每⼀个实例都被⼀条路径或⼀条规则所覆盖,⽽且只被⼀条路径或者⼀条规则覆盖。
概率分布:决策树将特征空间划分为互不相交的单元,并在每个单元定义⼀个类的概率分布。
决策树的⼀条路径对应于划分中的⼀个单元,决策树所表⽰的条件概率分布由各个单元给定条件下类的条件概率分布组成,即P(Y | X),叶结点(单元)上的条件概率往往偏向某⼀类。
决策树的学习:决策树学习本质上是从训练数据集中归纳出⼀组分类规则,找到⼀棵“与训练数据⽭盾较⼩,同时具有很好的泛化能⼒”的树。
另⼀个⾓度看,决策树学习是“由训练集估计的条件概率模型”,基于特征空间划分的类的条件概率模型有多个。
我们选择的条件概率模型应该不仅对训练数据有很好的拟合,⽽且对未知数据有很好的预测。
启发式⽅法:从所有可能的决策树中选取最优决策树是NP完全问题,所以现实中通常采⽤启发式⽅法,近似求解这⼀最优化问题。
这样得到的决策树是次优的(sub-optimal)。
通常的做法是递归地选择最优特征,并根据该特征对训练数据进⾏分割,使得对各个⼦数据集有⼀个最好的分类的过程。
剪枝:以上⽅法⽣成的树可能对训练集有很好的分类能⼒,但对未知的数据却未必,可能发⽣过拟合。
我们需要对已⽣成的树⾃下⽽上进⾏剪纸,将树变得更简单,从⽽使它具有更好的泛化能⼒。
具体地,就是去掉过于细分的叶结点,使其回退到⽗结点,甚⾄更⾼的结点,将⽗结点或更⾼的结点改为新的叶结点。
特征选择特征选择:特征选择在于选取对训练数据具有分类能⼒的特征。
机器学习知到章节答案智慧树2023年三亚学院

机器学习知到章节测试答案智慧树2023年最新三亚学院第一章测试1.下面哪句话是正确的()参考答案:增加模型的复杂度,总能减小训练样本误差2.评估模型之后,得出模型存在偏差,下列哪种方法可能解决这一问题()参考答案:向模型中增加更多的特征3.以垃圾微信识别为例,Tom Mitchell的机器学习的定义中,任务T是什么?()参考答案:T是识别4.如何在监督式学习中使用聚类算法()?参考答案:在应用监督式学习算法之前,可以将其类别ID作为特征空间中的一个额外的特征;首先,可以创建聚类,然后分别在不同的集群上应用监督式学习算法5.想要训练一个ML模型,样本数量有100万个,特征维度是5000,面对如此大数据,如何有效地训练模型()?参考答案:对训练集随机采样,在随机采样的数据上建立模型;使用PCA算法减少特征维度;尝试使用在线机器学习算法6.机器学习兴起于()。
参考答案:1990年;1980年7.监督学习包括是()。
参考答案:分类;回归8.机器学习可以对电子商务产品评价进行好评与差评分类。
()参考答案:对9.机器学习必备知识包括数学基础、心理学基础、算法设计基础、商业模式基础。
()参考答案:错10.机器学习是一门多学科交叉专业,涵盖____、____、近似理论知识和复杂算法知识,使用计算机作为工具并致力于真实实时的模拟人类学习方式,并将现有内容进行知识结构划分来有效提高学习效率。
参考答案:null第二章测试1.关于k-NN算法,以下哪个选项是正确的?参考答案:可用于分类和回归2.k-NN算法在测试时间而不是训练时间上进行了更多的计算。
参考答案:对3.假设算法是k最近邻算法,在下面的图像中,____将是k的最佳值。
参考答案:104.一个kNN分类器,该分类器在训练数据上获得100%的准确性。
而在客户端上部署此模型时,发现该模型根本不准确。
以下哪项可能出错了?注意:模型已成功部署,除了模型性能外,在客户端没有发现任何技术问题参考答案:可能是模型过拟合5.以下是针对k-NN算法给出的两条陈述,其中哪一条是真的?1、我们可以借助交叉验证来选择k的最优值2、欧氏距离对每个特征一视同仁参考答案:1和26.你给出了以下2条语句,发现在k-NN情况下哪个选项是正确的?1、如果k的值非常大,我们可以将其他类别的点包括到邻域中。
决策树

预修剪技术
预修剪的最直接的方法是事先指定决策树生长的最 大深度, 使决策树不能得到充分生长。 目前, 许多数据挖掘软件中都采用了这种解决方案, 设置了接受相应参数值的接口。但这种方法要求 用户对数据项的取值分布有较为清晰的把握, 并且 需对各种参数值进行反复尝试, 否则便无法给出一 个较为合理的最大树深度值。如果树深度过浅, 则 会过于限制决策树的生长, 使决策树的代表性过于 一般, 同样也无法实现对新数据的准确分类或预测。
决策树的修剪
决策树学习的常见问题(3)
处理缺少属性值的训练样例 处理不同代价的属性
决策树的优点
可以生成可以理解的规则; 计算量相对来说不是很大; 可以处理连续和离散字段; 决策树可以清晰的显示哪些字段比较重要
C4.5 对ID3 的另一大改进就是解决了训练数据中连续属性的处 理问题。而ID3算法能处理的对象属性只能是具有离散值的 数据。 C4.5中对连续属性的处理采用了一种二值离散的方法,具体 来说就是对某个连续属性A,找到一个最佳阈值T,根据A 的取值与阈值的比较结果,建立两个分支A<=T (左枝)和 A>=T (右枝),T为分割点。从而用一个二值离散属性A (只 有两种取值A<=T、A>=T)替代A,将问题又归为离散属性的 处理。这一方法既可以解决连续属性问题,又可以找到最 佳分割点,同时就解决了人工试验寻找最佳阈值的问题。
简介
决策树算法是建立在信息论的基础之上的 是应用最广的归纳推理算法之一 一种逼近离散值目标函数的方法 对噪声数据有很好的健壮性且能学习析取(命题 逻辑公式)表达式
信息系统
决策树把客观世界或对象世界抽象为一个 信息系统(Information System),也称属性--------值系统。 一个信息系统S是一个四元组: S=(U, A, V, f)
决策树

决策树算法:什么是机器学习?机器学习(Machine Learning) 是近20 多年兴起的一门多领域交叉学科,涉及概率论、统计学、逼近论、凸分析、算法复杂度理论等多门学科。
机器学习理论主要是设计和分析一些让计算机可以自动学习的算法。
机器学习算法是一类从数据中自动分析获得规律,并利用规律对未知数据进行预测的算法。
机器学习在数据挖掘、计算机视觉、自然语言处理、生物特征识别、搜索引擎、医学诊断、检测信用卡欺诈、证券市场分析、DNA 序列测序、语言与手写识别、战略游戏与机器人运用等领域有着十分广泛的应用。
它无疑是当前数据分析领域的一个热点内容。
决策树定义:机器学习中决策树是一个预测模型;他代表的是对象属性与对象值之间的一种映射关系。
树中每个节点表示某个对象,而每个分叉路径则代表的某个可能的属性值,而每个叶结点则对应从根节点到该叶节点所经历的路径所表示的对象的值。
决策树仅有单一输出,若欲有复数输出,可以建立独立的决策树以处理不同输出。
从数据产生决策树的机器学习技术叫做决策树学习, 通俗说就是决策树。
决策树模型定义2.1(决策树)分类决策树模型是一种描述对实例进行分类的树形结构。
决策树由结点(node)和有向边(directed edge)组成。
□——决策点,是对几种可能方案的选择,即最后选择的最佳方案。
如果决策属于多级决策,则决策树的中间可以有多个决策点,以决策树根部的决策点为最终决策方案为最终决策方案。
○——状态节点,代表备选方案的经济效果(期望值),通过各状态节点的经济效果的对比,按照一定的决策标准就可以选出最佳方案。
由状态节点引出的分支称为概率枝,概率枝的数目表示可能出现的自然状态数目每个分枝上要注明该状态出现的概率。
△——结果节点,将每个方案在各种自然状态下取得的损益值标注于结果节点的右端。
决策树是如何工作的?决策树一般都是自上而下的来生成的。
选择分割的方法有好几种,但是目的都是一致的:对目标类尝试进行最佳的分割。
决策树ppt课件

分类问题背景介绍
分类问题是机器学习中一类重要 的问题,旨在将数据划分为不同
的类别。
在现实世界中,分类问题广泛存 在,如垃圾邮件识别、疾病诊断、
信用评分等。
分类算法的目标是通过学习训练 数据中的特征与类别之间的关系, 从而对新的未知数据进行类别预
测。
决策树在分类问题中优势
直观易理解
决策树在处理缺失值和异常值时容易受到干扰,可能导致模型性能下降。可以通过数据 预处理等方法减少缺失值和异常值对模型的影响。
CART算法实例演示
实例背景
假设有一个关于信用卡欺诈的数据集,包含多个特征(如交 易金额、交易时间、交易地点等)和一个目标变量(是否欺 诈)。我们将使用CART算法构建一个分类模型来预测交易 是否属于欺诈行为。
构建决策树时间较长
C4.5算法在构建决策树时需要计算每 个特征的信息增益比,当数据集较大 或特征较多时,构建决策树的时间可 能会较长。
C4.5算法实例演示
数据集介绍
以经典的鸢尾花数据集为例,该数据集包含150个 样本,每个样本有4个特征(花萼长度、花萼宽度、 花瓣长度、花瓣宽度)和1个标签(鸢尾花的类 别)。
建造年份等特征。
选择合适的决策树算法 (如CART、ID3等),
对数据进行训练。
模型评估与优化
采用均方误差等指标评 估模型性能,通过调整 参数、集成学习等方法
优化模型。
结果展示与解读
展示决策树图形化结果, 解释每个节点含义及预
测逻辑。
08
CATALOGUE
总结与展望
决策树模型总结回顾
模型原理
决策树通过递归方式将数据集划分为若干个子集,每个子 集对应一个决策结果。通过构建树形结构,实现分类或回 归任务。
决策树原理和简单例子

决策树原理和简单例子决策树是一种常用的机器学习算法,它可以用于分类和回归问题。
决策树的原理是基于一系列的规则,通过对特征的判断来对样本进行分类或预测。
下面将通过原理和简单例子来介绍决策树。
1. 决策树的原理决策树的构建过程是一个递归的过程,它将样本集合按照特征的不同取值分割成不同的子集,然后对每个子集递归地构建决策树。
构建决策树的过程是通过对特征的选择来确定每个节点的划分条件,使得信息增益或信息增益比最大。
2. 决策树的构建假设有一个分类问题,样本集合包含n个样本,每个样本有m个特征。
决策树的构建过程如下:(1) 若样本集合中的样本都属于同一类别,则构建叶子节点,并将该类别作为叶子节点的类别标签。
(2) 若样本集合中的样本特征为空,或者样本特征在所有样本中取值相同,则构建叶子节点,并将该样本集合中出现次数最多的类别作为叶子节点的类别标签。
(3) 若样本集合中的样本特征不为空且有多个取值,则选择一个特征进行划分。
常用的划分方法有信息增益和信息增益比。
(4) 根据选择的特征的不同取值将样本集合划分成多个子集,对每个子集递归地构建决策树。
(5) 将选择的特征作为当前节点的判断条件,并将该节点加入决策树。
3. 决策树的例子假设有一个二分类问题,样本集合包含10个样本,每个样本有2个特征。
下面是一个简单的例子:样本集合:样本1:特征1=0,特征2=1,类别=1样本2:特征1=1,特征2=1,类别=1样本3:特征1=0,特征2=0,类别=0样本4:特征1=1,特征2=0,类别=0样本5:特征1=1,特征2=1,类别=1样本6:特征1=0,特征2=0,类别=0样本7:特征1=1,特征2=0,类别=0样本8:特征1=0,特征2=1,类别=1样本9:特征1=1,特征2=1,类别=1样本10:特征1=0,特征2=1,类别=1首先计算样本集合的信息熵,假设正样本和负样本的比例都是1:1,信息熵为1。
选择特征1进行划分,计算信息增益:对于特征1=0的样本,正样本有2个,负样本有2个,信息熵为1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
表3-2 目标概念PlayTennis的训练样例
Day Outlook Temperature Humidity
D1
Sunny
Hot
High
D2
Sunny
Hot
High
D3 Overcast
Hot
High
D4
Rainy
Mild
High
D5
Rainy
Cool
Normal
D6
Rainy
Cool
Normal
• S的正反样例数量不等, 熵介于0,1之间
• 抛一枚均匀硬币的信息熵是多少? 解:出现正面与反面的概率均为0. 5,信息熵 是
q
E x p xi log p xi i1
(0.5log 0.5 0.5log 0.5)
1
• 用信息增益度量期望的熵降低
– 属性的信息增益,由于使用这个属性分割样例 而导致的期望熵降低
• 返回root
最佳分类属性
• 信息增益(Information Gain)
– 用来衡量给定的属性区分训练样例的能力 – ID3算法在增长树的每一步使用信息增益从候选属性中
选择属性
• 用熵度量样例的均一性
– 给定包含关于某个目标概念的正反样例的样例集S,那 么S相对这个布尔型分类的熵为
E n tr o p y (S ) p lo g 2 p plo g 2 p
ID3算法的核心问题是选取在树的每个节点要测试的属性。
表3-1 用于学习布尔函数的ID3算法
• ID3(Examples, Target_attribute, Attributes)
• 创建树的root节点
• 如果Examples都为正,返回label=+的单节点树root
• 如果Examples都为反,返回label=-的单节点树root
Gain=1(0.750.918 + 0.250) = 0.311
表3-2 目标概念PlayTennis的训练样例
Day Outlook Temperature Humidity
D1
Sunny
Hot
High
D2
Sunny
Hot
High
D3 Overcast
Hot
High
D4
Rainy
Mild
High
4 关联分析 Apriori
5 统计学习 EM
6 链接挖掘 PageRank
7 集装与推进 AdaBoost
8 分类
kNN
9 分类
Naïve Bayes
10 分类
CART
得票数 发表时间
作者
61
1993 Quinlan, J.R
60
1967 MacQueen, J.B
58
1995 Vapnik, V.N
D7 Overcast
Cool
Normal
D8
Sunny
Mild
High
D9
Sunny
Cool
Normal
D10
Rainy
Mild
Normal
D11
Sunny
Mild
Normal
D12 Overcast
Mild
High
D13 Overcast
Hot
Normal
D14
Rainy
Mild
High
Wind Weak Strong Weak Weak Weak Strong Strong Weak Weak Weak Strong Strong Weak Strong
• 如果Attributes为空,那么返回单节点root,label=Examples中最普遍的 Target_attribute值
• 否则开始
– AAttributes中分类examples能力最好的属性
– root的决策属性A
– 对于A的每个可能值vi
• 在root下加一个新的分支对应测试A=vi
概论
• 决策树学习是应用最广的归纳推理算法之一 • 是一种逼近离散值函数的方法 • 很好的健壮性 • 能够学习析取表达式 • ID3, Assistant, C4.5 • 搜索一个完整表示的假设空间 • 归纳偏置是优先选择较小的树 • 决策树表示了多个if-then规则
提纲
• 决策树定义 • 适用问题特征 • 基本ID3算法 • 决策树学习的归纳偏置 • 训练数据的过度拟合 •…
第3章 决策树学习 (Decision-Tree Algorithm)
ICDM 2006会议的算法投票结果
共有145人参加了ICDM 2006 Panel (会议的专题讨论),并对18种 候选算法进行投票,选出了机器学习10大算法
排名 主题
算法
1 分类
C4.5
2 聚类
k-Means
3 统计学习 SVM
决策树基本概念
关于分类问题
名称 人类 海龟
体温 恒温
表皮覆 盖
毛发
胎生 是
水生动 物
否
飞行动 物
否
有腿 是
冷血 鳞片
否
半
否
是
冬眠 类标号
否 哺乳动 物
否 爬行类
鸽子 恒温 羽毛
否
否
是
是
否
鸟类
鲸
恒温 毛发
是
是
否
否
否
X
分类与回归
分类目标属性y是离散的,回归目标属性y是连续的
哺乳类
y
决策树基本概念
解决分类问题的一般方法
big small 1+,1 1+,1 E=1 E=1
Gain=1(0.51 + 0.51) = 0
red blue 2+,1 0+,1 E=0.918 E=0
Gain=1(0.750.918 + 0.250) = 0.311
2+, 2 : E=1 shape
circle square 2+,1 0+,1 E=0.918 E=0
52
1994 Rakesh Agrawal
48
2000 McLachlan, G
46
1998 Brin, S.
45
1997 Freund, Y.
45
1996 Hastie, T
45
2001 Hand, D.J
34
1984 L.Breiman
陈述人
Hiroshi Motoda Joydeep Ghosh QiangYang Christos Faloutsos Joydeep Ghosh Christos Faloutsos Zhi-Hua Zhou Vipin Kumar Qiang Yang Dan Steinberg
D5
Rainy
Cool
Normal
D6
Rainy
Cool
Normal
D7 Overcast
Cool
Normal
D8
Sunny
Mild
High
D9
Sunny
Cool
Normal
D10
Rainy
Mild
Normal
D11
Sunny
Mild
Normal
D12 Overcast
Mild
High
D13 Overcast
– Gain(S,A)是在知道属性A的值后可以节省的二进 制位数;
计算属性的信息增益
<big, red, circle>: + <small, red, circle>: + <small, red, square>: <big, blue, circle>:
2+, 2 : E=1 size
2+, 2 : E=1 color
Gain(S,Humidity)=0.151
Gain(S,Wind)=0.048
Gain(S,Temperature)=0.029
根据信息增益标准,属性Outlook被选作根节点的决策属性,并 为它的每一个可能值(Sunny、Overcast和Rainy)在根节点下创 建分支,得到部分决策树显示在图3-4中。 2. 对非终端的后继节点再重复前面的过程以选择一个新的属性来分割 训练样例,这一次仅使用与这个节点关联的训练样例,直到满足结 束条件。
Hot
Normal
D14
Rainy
Mild
High
Wind Weak Strong Weak Weak Weak Strong Strong Weak Weak Weak Strong Strong Weak Strong
PlayTennis No No Yes Yes Yes No Yes No Yes Yes Yes Yes Yes No
计算属性的信息增益
S:[9+,5-] E(S)=0.940
Humidity
S:[9+,5-] E(S)=0.940
Wind
High
N
[3+,4-] E=0.985
[6+,1-] E=0.592
Gain (S, Humidity) = 0.940-(7/14)*0.985- (7/14)*0.592 =0.151
决策树基本概念
关于分类问题
分类(Classification)任务就是通过学习获 得一个目标函数(Target Function)f, 将每个属 性集x映射到一个预先定义好的类标号y。
分类任务的输入数据是记录的集合,每条记录 也称为实例或者样例。用元组(X,y)表示,其中,X 是属性集合,y是一个特殊的属性,指出样例的类标 号(也称为分类属性或者目标属性)
