渝北实验中学初2020级19——20学年度第一学期第一次考试
2019-2020学年渝北区实验中学校高三语文一模试卷及参考答案

2019-2020学年渝北区实验中学校高三语文一模试卷及参考答案一、现代文阅读(36分)(一)现代文阅读I(9分)阅读下面的文字,完成下面小题。
蚕儿陈忠实学校里来了一位新老师。
他很年轻,穿一身列宁式制服,胸前两排大纽扣,站在讲台上,笑着给我们介绍自己:“我姓蒋……”说着,他转过身,从粉笔盒儿里捏起一节粉笔,在木头黑板上,端端正正写下他的名字,说:“我叫蒋玉生。
”多新鲜啊!四十来个学生的小学,只有一位老师,称呼中是不必挂上姓氏的。
新老师自报姓名,无论如何算是一件新奇事。
有一天,我爬上村后那棵老桑树,摘了一抱最鲜最嫩的桑叶,扔给风葫芦,就往下溜,慌忙中,松了手,摔到地上,半天爬不起来,嘴里咸腻腻的,一摸,擦出血了,烧疼烧疼的。
我俩站在教室门口。
“脸上怎么弄破了?”他走到我跟前。
他牵着我的胳膊朝他住的小房子走去。
这回该吃一顿教鞭了!走进小房子,他从桌斗里翻出一团棉花,撕下一块,缠在一根火柴棒上,又在一只小瓶里蘸上红墨水一样的东西,就往我的脸上涂抹。
我感到伤口又扎又疼,心里却有一种异样的温暖。
他那按着我的头顶的手使我想到母亲按抚我的头脸的感觉。
“怎么弄破的?”他问。
“上树……摘桑叶。
”我怯生生地回答。
“摘桑叶做啥用?”他似乎很感兴趣。
“喂蚕儿。
”我也不怕了。
“噢!”他高兴了,“你们养蚕干什么?”“给墨盒儿做垫子。
”我说的话又多了,“把蚕儿放在一个空盒里,它就网出一片薄丝来了。
”“多有意思!”他高兴了,“把大家的蚕养在一起,搁到我这里,课后咱们去摘桑叶,给同学们每人网一张丝片儿,铺墨盒,你愿意吗?”“好哇!”我高兴地从椅子上跳下来。
于是,后晌,他领着我们满山满沟跑,采摘桑叶。
有时候,他从坡上滑倒了,青草的绿色液汁粘到裤子上,也不在乎。
初夏的傍晚,落日的余晖里,霞光把小河的清水染得一片红。
蒋老师领着我们,脱了衣服,跳进水里打泼剌,和我们打水仗。
我们联合起来,从他的前后左右朝他泼水。
他举起双手,闭着眼睛,脸上流下一股股水来,佯装着求饶的声调,投降了……这天早晨,我和风葫芦抱着桑叶,刚走进老师的房子,就愣住了。
2019-2020学年重庆渝北实验中学高三语文第一次联考试题及答案解析

2019-2020学年重庆渝北实验中学高三语文第一次联考试题及答案解析一、现代文阅读(36分)(一)现代文阅读I(9分)阅读下面的文字,完成下列小题。
孝是最为重要且影响最深的中华传统道德观念。
在生活方式已发生翻天覆地变化的今天,传统孝道仍然具有重要的社会作用。
不过,传统孝道精华与糟粕并存,这需要我们在正确地批判分析的基础上,推动其实现创造性转化和创新性发展。
要求子女在物质层面对父母尽赡养的义务,这是传统孝道最基本的规定。
但在儒家看来,仅做到这一点还不够,对父母的孝还必须要做到“敬”,即对待父母应时刻保持恭敬的态度。
无论是物质方面的“养”,还是精神层面的“敬”,都以顺从父母的意愿为标准,但父母的意愿未必正当,传统孝道的践行还应有更高层次的道德考量。
当父母的意愿不正当时,要用温和的方式去劝谏父母,从而避免让父母陷于不义。
传统孝道不但体现于父母生前,还涉及父母去世以后。
孔子挽:“生,事之以礼;死,葬之以礼,祭之以礼。
"子女不但在父母生前要对其以礼敬养,父母去世后还要以礼安葬、以礼祭祀。
生养、死葬、祭祀,在这三个环节都合乎礼制的要求,才算是实现了完满的孝道。
传统孝道的丰富内涵产生于古代宗法社会。
它是维系古代家庭、宗族与社会和谐的重要道德规范。
近现代以来,随着社会结构与生活方式的巨大变化,传统孝道显得越来越不合时宜。
受古代专制等级制度的长期影响,传统孝道被融入了大量维护专制、压抑人性的腐朽因素。
这集中体现于“三纲”教条中的“父为子纲",并通过《二十四孝》等通俗读物流传。
传统孝道的畸形化与父权的绝对化,阻碍了社会的发展。
近现代以来对传统孝道的批判,起到了削弱旧道德对国人的思想束缚、促进社会发展的积极作用。
而对于传统孝道本身而言,这些批判实际上也有助于推动其在新的时代条件下实现创新与发展。
但也应该看到,在当前社会,传统孝道对于促进社会和谐依然具有非常重要的现实意义。
不能因为传统孝道在历史演变中曾经绝对化、畸形化,就否定传统孝道本身,而应该将传统孝道的根本精神与其种种具体要求区分开来。
重庆市渝北区2019-2020学年中考数学一模考试卷含解析

重庆市渝北区2019-2020学年中考数学一模考试卷一、选择题(本大题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.如图,△ABC中,∠CAB=65°,在同一平面内,将△ABC绕点A旋转到△AED的位置,使得DC∥AB,则∠BAE等于()A.30°B.40°C.50°D.60°2.如图,正方形ABCD中,AB=6,G是BC的中点.将△ABG沿AG对折至△AFG,延长GF交DC 于点E,则DE的长是( )A.1 B.1.5 C.2 D.2.53.在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如图所示,如果5400cm,设金色纸边的宽为xcm,那么x满足的方程是()要使整幅挂图的面积是2A.213014000+-=x xx x+-=B.2653500C.213014000--=x x--=D.2653500x x4.定义:如果一元二次方程ax2+bx+c=0(a≠0)满足a+b+c=0,那么我们称这个方程为“和谐”方程;如果一元二次方程ax2+bx+c=0(a≠0)满足a﹣b+c=0那么我们称这个方程为“美好”方程,如果一个一元二次方程既是“和谐”方程又是“美好”方程,则下列结论正确的是()A.方有两个相等的实数根B.方程有一根等于0C.方程两根之和等于0 D.方程两根之积等于05.下列运算正确的是()A .22a +a=33aB .()32m =5mC .()222x y x y +=+D .63a a ÷=3a6.如图,在平面直角坐标系xOy 中,正方形ABCD 的顶点D 在y 轴上,且(3,0)A -,(2,)B b ,则正方形ABCD 的面积是( )A .13B .20C .25D .347.已知x 1,x 2是关于x 的方程x 2+bx ﹣3=0的两根,且满足x 1+x 2﹣3x 1x 2=5,那么b 的值为( ) A .4 B .﹣4 C .3 D .﹣38.有理数a ,b 在数轴上的对应点如图所示,则下面式子中正确的是( )①b <0<a ; ②|b|<|a|; ③ab >0; ④a ﹣b >a+b .A .①②B .①④C .②③D .③④9.如图是某公园的一角,∠AOB=90°,弧AB 的半径OA 长是6米,C 是OA 的中点,点D 在弧AB 上,CD ∥OB ,则图中休闲区(阴影部分)的面积是()A .91032π⎛⎫- ⎪⎝⎭米2B .932π⎛⎫- ⎪⎝⎭米2C .9632π⎛⎫- ⎪⎝⎭米2D .()693π-米2 10.如图,等腰直角三角板ABC 的斜边AB 与量角器的直径重合,点D 是量角器上60°刻度线的外端点,连接CD 交AB 于点E ,则∠CEB 的度数为( )A .60°B .65°C .70°D .75°11.如图,在△ABC中,点D是边AB上的一点,∠ADC=∠ACB,AD=2,BD=6,则边AC的长为()A.2 B.4 C.6 D.812.下列图形中一定是相似形的是( )A.两个菱形B.两个等边三角形C.两个矩形D.两个直角三角形二、填空题:(本大题共6个小题,每小题4分,共24分.)13.已知式子13xx-+有意义,则x的取值范围是_____14.若分式方程x a2x4x4=+--的解为正数,则a的取值范围是______________.15.如图,在平面直角坐标系中,Rt△ABO的顶点O与原点重合,顶点B在x轴上,∠ABO=90°,OA与反比例函数y=kx的图象交于点D,且OD=2AD,过点D作x轴的垂线交x轴于点C.若S四边形ABCD=10,则k的值为.16.学校乒乓球社团有4名男队员和3名女队员,要从这7名队员中随机抽取一男一女组成一队混合双打组合,可组成不同的组合共有_____对.17.如图,AB,AC分别为⊙O的内接正六边形,内接正方形的一边,BC是圆内接n边形的一边,则n 等于_____.18.如图,矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P与点B,C都不重合),现将△PCD沿直线PD折叠,使点C落到点F处;过点P作∠BPF的角平分线交AB于点E.设BP=x,BE=y,则下列图象中,能表示y与x的函数关系的图象大致是()三、解答题:(本大题共9个小题,共78分,解答应写出文字说明、证明过程或演算步骤.19.(6分)为响应市政府“创建国家森林城市”的号召,某小区计划购进A、B两种树苗共17棵,已知A 种树苗每棵80元,B种树苗每棵60元.若购进A、B两种树苗刚好用去1220元,问购进A、B两种树苗各多少棵?若购买B种树苗的数量少于A种树苗的数量,请你给出一种费用最省的方案,并求出该方案所需费用.20.(6分)数学课上,李老师和同学们做一个游戏:他在三张硬纸片上分别写出一个代数式,背面分别标上序号①、②、③,摆成如图所示的一个等式,然后翻开纸片②是4x1+5x+6,翻开纸片③是3x1﹣x﹣1.解答下列问题求纸片①上的代数式;若x是方程1x=﹣x﹣9的解,求纸片①上代数式的值.21.(6分)某商场以每件30元的价格购进一种商品,试销中发现这种商品每天的销售量m(件)与每件的销售价x(元)满足一次函数关系m=162﹣3x.请写出商场卖这种商品每天的销售利润y(元)与每件销售价x(元)之间的函数关系式.商场每天销售这种商品的销售利润能否达到500元?如果能,求出此时的销售价格;如果不能,说明理由.22.(8分)如图所示,一次函数y=kx+b与反比例函数y=mx的图象交于A(2,4),B(﹣4,n)两点.分别求出一次函数与反比例函数的表达式;过点B作BC⊥x轴,垂足为点C,连接AC,求△ACB的面积.23.(8分)如图,AB为⊙O的直径,点D、E位于AB两侧的半圆上,射线DC切⊙O于点D,已知点E是半圆弧AB上的动点,点F是射线DC上的动点,连接DE、AE,DE与AB交于点P,再连接FP、FB,且∠AED=45°.求证:CD∥AB;填空:①当∠DAE=时,四边形ADFP是菱形;②当∠DAE=时,四边形BFDP是正方形.24.(10分)铁岭市某商贸公司以每千克40元的价格购进一种干果,计划以每千克60元的价格销售,为了让顾客得到更大的实惠,现决定降价销售,已知这种干果销售量y(千克)与每千克降价x(元)(0<x<20)之间满足一次函数关系,其图象如图所示:求y与x之间的函数关系式;商贸公司要想获利2090元,则这种干果每千克应降价多少元?该干果每千克降价多少元时,商贸公司获利最大?最大利润是多少元?25.(10分)山地自行车越来越受中学生的喜爱.一网店经营的一个型号山地自行车,今年一月份销售额为30000元,二月份每辆车售价比一月份每辆车售价降价100元,若销售的数量与上一月销售的数量相同,则销售额是27000元.求二月份每辆车售价是多少元?为了促销,三月份每辆车售价比二月份每辆车售价降低了10%销售,网店仍可获利35%,求每辆山地自行车的进价是多少元?26.(12分)某校开展“我最喜爱的一项体育活动”调查,要求每名学生必选且只能选一项,现随机抽查了m名学生,并将其结果绘制成如下不完整的条形图和扇形图.请结合以上信息解答下列问题:m=;请补全上面的条形统计图;在图2中,“乒乓球”所对应扇形的圆心角的度数为;已知该校共有1200名学生,请你估计该校约有名学生最喜爱足球活动.27.(12分)如图,已知A(a,4),B(﹣4,b)是一次函数与反比例函数图象的两个交点.(1)若a=1,求反比例函数的解析式及b的值;(2)在(1)的条件下,根据图象直接回答:当x取何值时,反比例函数大于一次函数的值?(3)若a﹣b=4,求一次函数的函数解析式.参考答案一、选择题(本大题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.C【解析】试题分析:∵DC∥AB,∴∠DCA=∠CAB=65°.∵△ABC绕点A旋转到△AED的位置,∴∠BAE=∠CAD,AC=AD.∴∠ADC=∠DCA="65°." ∴∠CAD=180°﹣∠ADC﹣∠DCA="50°." ∴∠BAE=50°.故选C.考点:1.面动旋转问题;2. 平行线的性质;3.旋转的性质;4.等腰三角形的性质.2.C【解析】【分析】连接AE,根据翻折变换的性质和正方形的性质可证Rt△AFE≌Rt△ADE,在直角△ECG中,根据勾股定理求出DE的长.【详解】连接AE,∵AB=AD=AF,∠D=∠AFE=90°,由折叠的性质得:Rt △ABG ≌Rt △AFG ,在△AFE 和△ADE 中,∵AE=AE ,AD=AF ,∠D=∠AFE ,∴Rt △AFE ≌Rt △ADE ,∴EF=DE ,设DE=FE=x ,则CG=3,EC=6−x.在直角△ECG 中,根据勾股定理,得:(6−x)2+9=(x+3)2,解得x=2.则DE=2.【点睛】熟练掌握翻折变换、正方形的性质、全等三角形的判定与性质是本题的解题关键.3.B【解析】【分析】根据矩形的面积=长×宽,我们可得出本题的等量关系应该是:(风景画的长+2个纸边的宽度)×(风景画的宽+2个纸边的宽度)=整个挂图的面积,由此可得出方程.【详解】由题意,设金色纸边的宽为xcm ,得出方程:(80+2x )(50+2x )=5400,整理后得:2653500x x +-=故选:B.【点睛】本题主要考查了由实际问题得出一元二次方程,对于面积问题应熟记各种图形的面积公式,然后根据等量关系列出方程是解题关键.4.C【解析】试题分析:根据已知得出方程ax 2+bx+c=0(a≠0)有两个根x=1和x=﹣1,再判断即可.解:∵把x=1代入方程ax 2+bx+c=0得出:a+b+c=0,把x=﹣1代入方程ax 2+bx+c=0得出a ﹣b+c=0,∴方程ax 2+bx+c=0(a≠0)有两个根x=1和x=﹣1,∴1+(﹣1)=0,即只有选项C 正确;选项A 、B 、D 都错误;故选C .5.D【解析】【分析】根据整式的混合运算计算得到结果,即可作出判断.【详解】A 、22a 与a 不是同类项,不能合并,不符合题意;B 、()32m =6m ,不符合题意;C 、原式=22x 2y xy ++,不符合题意;D 、63a a ÷=3a ,符合题意,故选D .【点睛】此题考查了整式的混合运算,熟练掌握运算法则是解本题的关键.6.D【解析】作BE ⊥OA 于点E.则AE=2-(-3)=5,△AOD ≌△BEA (AAS ),∴OD=AE=5,22223534AD AO OD ∴=+=+= ,∴正方形ABCD 的面积是343434= ,故选D.7.A【解析】【分析】根据一元二次方程根与系数的关系和整体代入思想即可得解.【详解】∵x1,x2是关于x的方程x2+bx﹣3=0的两根,∴x1+x2=﹣b,x1x2=﹣3,∴x1+x2﹣3x1x2=﹣b+9=5,解得b=4.故选A.【点睛】本题主要考查一元二次方程的根与系数的关系(韦达定理),韦达定理:若一元二次方程ax2+bx+c=0(a≠0)有两个实数根x1,x2,那么x1+x2=,x1x2=.8.B【解析】分析:本题是考察数轴上的点的大小的关系.解析:由图知,b<0<a,故①正确,因为b点到原点的距离远,所以|b|>|a|,故②错误,因为b<0<a,所以ab<0,故③错误,由①知a-b>a+b,所以④正确.故选B.9.C【解析】【详解】连接OD,∵弧AB的半径OA长是6米,C是OA的中点,∴OC=12OA=12×6=1.∵∠AOB=90°,CD∥OB,∴CD⊥OA.在Rt△OCD中,∵OD=6,OC=1,∴2222CD OD OC6333=-=-=.又∵CD333sin DOCOD∠===,∴∠DOC=60°.∴2606193336336022DOCAODS S Sππ∆⋅⋅=-=-⨯⨯=-阴影扇形(米2).故选C.10.D【解析】【详解】解:连接OD∵∠AOD=60°,∴ACD=30°.∵∠CEB是△ACE的外角,∴△CEB=∠ACD+∠CAO=30°+45°=75°故选:D11.B【解析】【分析】证明△ADC∽△ACB,根据相似三角形的性质可推导得出AC2=AD•AB,由此即可解决问题. 【详解】∵∠A=∠A,∠ADC=∠ACB,∴△ADC∽△ACB,∴AC AD AB AC,∴AC2=AD•AB=2×8=16,∵AC>0,∴AC=4,故选B.【点睛】本题考查相似三角形的判定和性质、解题的关键是正确寻找相似三角形解决问题. 12.B【解析】【分析】如果两个多边形的对应角相等,对应边的比相等,则这两个多边形是相似多边形.【详解】解:∵等边三角形的对应角相等,对应边的比相等,∴两个等边三角形一定是相似形,又∵直角三角形,菱形的对应角不一定相等,矩形的边不一定对应成比例,∴两个直角三角形、两个菱形、两个矩形都不一定是相似形,故选:B.【点睛】本题考查了相似多边形的识别.判定两个图形相似的依据是:对应边成比例,对应角相等,两个条件必须同时具备.二、填空题:(本大题共6个小题,每小题4分,共24分.)13.x≤1且x≠﹣1.【解析】根据二次根式有意义,分式有意义得:1﹣x≥0且x+1≠0,解得:x≤1且x≠﹣1.故答案为x≤1且x≠﹣1.14.a<8,且a≠1【解析】分式方程去分母得:x=2x-8+a,解得:x=8- a,根据题意得:8- a>2,8- a≠1,解得:a<8,且a≠1.故答案为:a<8,且a≠1.【点睛】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,根据分式方程解为正数求出a 的范围即可.此题考查了分式方程的解,需注意在任何时候都要考虑分母不为2.15.﹣1【解析】【详解】∵OD=2AD,∴23 ODOA=,∵∠ABO=90°,DC⊥OB,∴AB∥DC,∴△DCO∽△ABO,∴23 DC OC ODAB OB OA===,∴22439 ODCOABSS⎛⎫==⎪⎝⎭VV,∵S四边形ABCD=10,∴S△ODC=8,∴OC×CD=8,OC×CD=1,∴k=﹣1,故答案为﹣1.16.1【解析】【分析】利用树状图展示所有1种等可能的结果数.【详解】解:画树状图为:共有1种等可能的结果数.故答案为1.【点睛】本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果n,再从中选出符合事件A或B的结果数目m,然后利用概率公式计算事件A或事件B的概率.17.12【解析】连接AO,BO,CO,如图所示:∵AB、AC分别为⊙O的内接正六边形、内接正方形的一边,∴∠AOB=36060o=60°,∠AOC=3604o=90°,∴∠BOC=30°,∴n=36030oo=12,故答案为12.18.C【解析】【分析】先证明△BPE∽△CDP,再根据相似三角形对应边成比例列出式子变形可得. 【详解】由已知可知∠EPD=90°,∴∠BPE+∠DPC=90°,∵∠DPC+∠PDC=90°,∴∠CDP=∠BPE,∵∠B=∠C=90°,∴△BPE∽△CDP,∴BP:CD=BE:CP,即x:3=y:(5-x),∴y=253x x-+(0<x<5);故选C.考点:1.折叠问题;2.相似三角形的判定和性质;3.二次函数的图象.三、解答题:(本大题共9个小题,共78分,解答应写出文字说明、证明过程或演算步骤.19.(1)购进A种树苗1棵,B种树苗2棵(2)购进A种树苗9棵,B种树苗8棵,这时所需费用为1200元【解析】【分析】(1)设购进A种树苗x棵,则购进B种树苗(12﹣x)棵,利用购进A、B两种树苗刚好用去1220元,结合单价,得出等式方程求出即可;(2)结合(1)的解和购买B种树苗的数量少于A种树苗的数量,可找出方案.【详解】解:(1)设购进A种树苗x棵,则购进B种树苗(12﹣x)棵,根据题意得:80x+60(12﹣x )=1220,解得:x=1.∴12﹣x=2.答:购进A种树苗1棵,B种树苗2棵.(2)设购进A种树苗x棵,则购进B种树苗(12﹣x)棵,根据题意得:12﹣x<x,解得:x>8.3.∵购进A、B两种树苗所需费用为80x+60(12﹣x)=20x+120,是x的增函数,∴费用最省需x取最小整数9,此时12﹣x=8,所需费用为20×9+120=1200(元).答:费用最省方案为:购进A种树苗9棵,B种树苗8棵,这时所需费用为1200元.20.(1)7x1+4x+4;(1)55.【解析】【分析】(1)根据整式加法的运算法则,将(4x1+5x+6)+(3x1﹣x﹣1)即可求得纸片①上的代数式;(1)先解方程1x=﹣x﹣9,再代入纸片①的代数式即可求解.【详解】解:(1)纸片①上的代数式为:(4x1+5x+6)+(3x1﹣x﹣1)=4x1+5x+6+3x1-x-1=7x1+4x+4(1)解方程:1x=﹣x﹣9,解得x=﹣3代入纸片①上的代数式得7x1+4x+4=7×(-3)²+4×(-3)+4=63-11+4=55即纸片①上代数式的值为55.【点睛】本题考查了整式加减混合运算,解一元一次方程,代数式求值,在解题的过程中要牢记并灵活运用整式加减混合运算的法则.特别是对于含括号的运算,在去括号时,一定要注意符号的变化.21.(1)y=﹣3x2+252x﹣1(2≤x≤54);(2)商场每天销售这种商品的销售利润不能达到500元.【解析】【分析】(1)此题可以按等量关系“每天的销售利润=(销售价﹣进价)×每天的销售量”列出函数关系式,并由售价大于进价,且销售量大于零求得自变量的取值范围.(2)根据(1)所得的函数关系式,利用配方法求二次函数的最值即可得出答案.【详解】(1)由题意得:每件商品的销售利润为(x﹣2)元,那么m件的销售利润为y=m(x﹣2).又∵m=162﹣3x,∴y=(x﹣2)(162﹣3x),即y=﹣3x2+252x﹣1.∵x﹣2≥0,∴x≥2.又∵m≥0,∴162﹣3x≥0,即x≤54,∴2≤x≤54,∴所求关系式为y=﹣3x2+252x﹣1(2≤x≤54).(2)由(1)得y=﹣3x2+252x﹣1=﹣3(x﹣42)2+432,所以可得售价定为42元时获得的利润最大,最大销售利润是432元.∵500>432,∴商场每天销售这种商品的销售利润不能达到500元.【点睛】本题考查了二次函数在实际生活中的应用,解答本题的关键是根据等量关系:“每天的销售利润=(销售价﹣进价)×每天的销售量”列出函数关系式,另外要熟练掌握二次函数求最值的方法.22.(1)反比例函数解析式为y=8x,一次函数解析式为y=x+2;(2)△ACB的面积为1.【解析】【分析】(1)将点A坐标代入y=mx可得反比例函数解析式,据此求得点B坐标,根据A、B两点坐标可得直线解析式;(2)根据点B坐标可得底边BC=2,由A、B两点的横坐标可得BC边上的高,据此可得.【详解】解:(1)将点A(2,4)代入y=mx,得:m=8,则反比例函数解析式为y=8x,当x=﹣4时,y=﹣2,则点B(﹣4,﹣2),将点A(2,4)、B(﹣4,﹣2)代入y=kx+b,得:2442k bk b+=⎧⎨-+=-⎩,解得:12kb=⎧⎨=⎩,则一次函数解析式为y=x+2;(2)由题意知BC=2,则△ACB的面积=12×2×1=1.【点睛】本题主要考查一次函数与反比例函数的交点问题,熟练掌握待定系数法求函数解析式及三角形的面积求法是解题的关键.23.(1)详见解析;(2)①67.5°;②90°.【解析】【分析】(1)要证明CD∥AB,只要证明∠ODF=∠AOD即可,根据题目中的条件可以证明∠ODF=∠AOD,从而可以解答本题;(2)①根据四边形ADFP是菱形和菱形的性质,可以求得∠DAE的度数;②根据四边形BFDP是正方形,可以求得∠DAE的度数.【详解】(1)证明:连接OD,如图所示,∵射线DC切⊙O于点D,∴OD⊥CD,即∠ODF=90°,∵∠AED=45°,∴∠AOD=2∠AED=90°,∴∠ODF=∠AOD,∴CD∥AB;(2)①连接AF与DP交于点G,如图所示,∵四边形ADFP是菱形,∠AED=45°,OA=OD,∴AF⊥DP,∠AOD=90°,∠DAG=∠PAG,∴∠AGE=90°,∠DAO=45°,∴∠EAG=45°,∠DAG=∠PEG=22.5°,∴∠EAD=∠DAG+∠EAG=22.5°+45°=67.5°,故答案为:67.5°;②∵四边形BFDP是正方形,∴BF=FD=DP=PB,∠DPB=∠PBF=∠BFD=∠FDP=90°,∴此时点P与点O重合,∴此时DE是直径,∴∠EAD=90°,故答案为:90°.【点睛】本题考查菱形的判定与性质、切线的性质、正方形的判定,解答本题的关键是明确题意,找出所求问题需要的条件,利用菱形的性质和正方形的性质解答.24.(1)y=10x+100;(2)这种干果每千克应降价9元;(3)该干果每千克降价5元时,商贸公司获利最大,最大利润是2250元.【解析】【分析】(1)由待定系数法即可得到函数的解析式;(2)根据销售量×每千克利润=总利润列出方程求解即可;(3)根据销售量×每千克利润=总利润列出函数解析式求解即可.【详解】(1)设y 与x 之间的函数关系式为:y =kx+b ,把(2,120)和(4,140)代入得,21204140k b k b +=⎧⎨+=⎩, 解得:10100k b =⎧⎨=⎩, ∴y 与x 之间的函数关系式为:y =10x+100;(2)根据题意得,(60﹣40﹣x)(10x+100)=2090,解得:x =1或x =9,∵为了让顾客得到更大的实惠,∴x =9,答:这种干果每千克应降价9元;(3)该干果每千克降价x 元,商贸公司获得利润是w 元,根据题意得,w =(60﹣40﹣x)(10x+100)=﹣10x 2+100x+2000,∴w =﹣10(x ﹣5)2+2250,∵a=-100<,∴当x =5时,w 2250=最大故该干果每千克降价5元时,商贸公司获利最大,最大利润是2250元.【点睛】本题考查的是二次函数的应用,此类题目主要考查学生分析、解决实际问题能力,又能较好地考查学生“用数学”的意识.25.(1)二月份每辆车售价是900元;(2)每辆山地自行车的进价是600元.【解析】【分析】(1)设二月份每辆车售价为x 元,则一月份每辆车售价为(x+100)元,根据数量=总价÷单价,即可得出关于x 的分式方程,解之经检验后即可得出结论;(2)设每辆山地自行车的进价为y 元,根据利润=售价﹣进价,即可得出关于y 的一元一次方程,解之即可得出结论.【详解】(1)设二月份每辆车售价为x 元,则一月份每辆车售价为(x+100)元,根据题意得:3000027000100x x=+,解得:x=900,经检验,x=900是原分式方程的解,答:二月份每辆车售价是900元;(2)设每辆山地自行车的进价为y元,根据题意得:900×(1﹣10%)﹣y=35%y,解得:y=600,答:每辆山地自行车的进价是600元.【点睛】本题考查了分式方程的应用、一元一次方程的应用,弄清题意,找准等量关系列出方程是解题的关键. 26.(1)150,(2)36°,(3)1.【解析】【分析】(1)根据图中信息列式计算即可;(2)求得“足球“的人数=150×20%=30人,补全上面的条形统计图即可;(3)360°×乒乓球”所占的百分比即可得到结论;(4)根据题意计算即可.【详解】(1)m=21÷14%=150,(2)“足球“的人数=150×20%=30人,补全上面的条形统计图如图所示;(3)在图2中,“乒乓球”所对应扇形的圆心角的度数为360°×15150=36°;(4)1200×20%=1人,答:估计该校约有1名学生最喜爱足球活动.故答案为150,36°,1.【点睛】本题考查了条形统计图,观察条形统计图、扇形统计图获得有效信息是解题关键.27. (1) 反比例函数的解析式为y =4x,b 的值为﹣1;(1) 当x <﹣4或0<x <1时,反比例函数大于一次函数的值;(3) 一次函数的解析式为y =x+1【解析】【分析】(1)由题意得到A (1,4),设反比例函数的解析式为y =k x (k≠0),根据待定系数法即可得到反比例函数解析式为y =4x;再由点B (﹣4,b )在反比例函数的图象上,得到b =﹣1; (1)由(1)知A (1,4),B (﹣4,﹣1),结合图象即可得到答案; (3)设一次函数的解析式为y =mx+n (m≠0),反比例函数的解析式为y =p x ,因为A (a ,4),B (﹣4,b )是一次函数与反比例函数图象的两个交点,得到44p a p b ⎧=⎪⎪⎨⎪=⎪-⎩, 解得p =8,a =1,b =﹣1,则A (1,4),B (﹣4,﹣1),由点A 、点B 在一次函数y =mx+n 图象上,得到2442m n m n +=⎧⎨-+=-⎩,解得12m n =⎧⎨=⎩,即可得到答案.【详解】(1)若a =1,则A (1,4),设反比例函数的解析式为y =k x(k≠0), ∵点A 在反比例函数的图象上,∴4=1k , 解得k =4,∴反比例函数解析式为y =4x; ∵点B (﹣4,b )在反比例函数的图象上,∴b =44-=﹣1, 即反比例函数的解析式为y =4x,b 的值为﹣1; (1)由(1)知A (1,4),B (﹣4,﹣1),根据图象:当x <﹣4或0<x <1时,反比例函数大于一次函数的值;(3)设一次函数的解析式为y =mx+n (m≠0),反比例函数的解析式为y =p x, ∵A (a ,4),B (﹣4,b )是一次函数与反比例函数图象的两个交点,∴44p a p b ⎧=⎪⎪⎨⎪=⎪-⎩,即44a p b p =⎧⎨-=⎩①②, ①+②得4a ﹣4b =1p ,∵a ﹣b =4,∴16=1p ,解得p =8,把p =8代入①得4a =8,代入②得﹣4b =8, 解得a =1,b =﹣1,∴A (1,4),B (﹣4,﹣1),∵点A 、点B 在一次函数y =mx+n 图象上, ∴2442m n m n +=⎧⎨-+=-⎩解得12m n =⎧⎨=⎩ ∴一次函数的解析式为y =x+1.【点睛】本题考查一次函数与反比例函数,解题的关键是待定系数法求函数解析式.。
重庆市渝北区2019-2020学年中考数学一模试卷含解析

重庆市渝北区2019-2020学年中考数学一模试卷一、选择题(本大题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的.) 1.如图,是由7个大小相同的小正方体堆砌而成的几何体,若从标有①、②、③、④的四个小正方体中取走一个后,余下几何体与原几何体的主视图相同,则取走的正方体是( )A .①B .②C .③D .④2.在△ABC 中,点D 、E 分别在AB 、AC 上,如果AD =2,BD =3,那么由下列条件能够判定DE ∥BC 的是( ) A .DE BC =23B .DE BC =25C .AE AC =23D .AE AC =253.如图,平面直角坐标中,点A (1,2),将AO 绕点A 逆时针旋转90°,点O 的对应点B 恰好落在双曲线y=(x>0)上,则k 的值为( )A .2B .3C .4D .64.长度单位1纳米米,目前发现一种新型病毒直径为25100纳米,用科学记数法表示该病毒直径是( ) A .米 B .米 C .米 D .米5.已知二次函数2y ax bx c =++的图象与x 轴交于点()2,0-、()1,0x ,且112x <<,与y 轴的正半轴的交点在()0,2的下方.下列结论:①420a b c -+=;②0a b c -+<;③20a c +>;④210a b -+>.其中正确结论的个数是( )个. A .4个B .3个C .2个D .1个6.如图,点A 、B 、C 、D 、O 都在方格纸的格点上,若△COD 是由△AOB 绕点O 按逆时针方向旋转而得,则旋转的角度为()A.30°B.45°C.90°D.135°7.如图,在△ABC中,∠ACB=90°,点D为AB的中点,AC=3,cosA=13,将△DAC沿着CD折叠后,点A落在点E处,则BE的长为()A.5 B.42C.7 D.528.如图,五边形ABCDE中,AB∥CD,∠1、∠2、∠3分别是∠BAE、∠AED、∠EDC的外角,则∠1+∠2+∠3等于A.90°B.180°C.210°D.270°9.如图,二次函数y=ax1+bx+c(a≠0)的图象与x轴正半轴相交于A、B两点,与y轴相交于点C,对称轴为直线x=1,且OA=OC.则下列结论:①abc>0;②9a+3b+c>0;③c>﹣1;④关于x的方程ax1+bx+c=0(a≠0)有一个根为﹣1a;⑤抛物线上有两点P(x1,y1)和Q(x1,y1),若x1<1<x1,且x1+x1>4,则y1>y1.其中正确的结论有()A.1个B.3个C.4个D.5个10.甲、乙两盒中分别放入编号为1、2、3、4的形状相同的4个小球,从甲盒中任意摸出一球,再从乙盒中任意摸出一球,将两球编号数相加得到一个数,则得到数()的概率最大.A .3B .4C .5D .611.如图,一张半径为1的圆形纸片在边长为4的正方形内任意移动,则在该正方形内,这张圆形纸片“能接触到的部分”的面积是( )A .4π-B .πC .12π+D .π154+12.已知抛物线y=ax 2+bx+c 与x 轴交于点A 和点B ,顶点为P ,若△ABP 组成的三角形恰为等腰直角三角形,则b 2﹣4ac 的值为( ) A .1B .4C .8D .12二、填空题:(本大题共6个小题,每小题4分,共24分.)13.如图,矩形ABCD 面积为40,点P 在边CD 上,PE ⊥AC ,PF ⊥BD ,足分别为E ,F .若AC =10,则PE+PF =_____.14.如果方程x 2-4x+3=0的两个根分别是Rt △ABC 的两条边,△ABC 最小的角为A ,那么tanA 的值为_______.15.如图,P 为正方形ABCD 内一点,PA :PB :PC=1:2:3,则∠APB=_____________ .16.已知二次函数2y ax bx c =++中,函数y 与x 的部分对应值如下: ... -1 0 1 2 3 ......105212...则当5y <时,x 的取值范围是_________.17.如图,将△ABC 绕点A 逆时针旋转100°,得到△ADE.若点D 在线段BC 的延长线上,则B Ð的大小为________.18.如图,在Rt△ABC中,AB=AC,D、E是斜边BC上的两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论:①∠EAF=45°;②△AED≌△AEF;③△ABE∽△ACD;④BE1+DC1=DE1.其中正确的是______.(填序号)三、解答题:(本大题共9个小题,共78分,解答应写出文字说明、证明过程或演算步骤.19.(6分)如图,六个完全相同的小长方形拼成了一个大长方形,AB是其中一个小长方形的对角线,请在大长方形中完成下列画图,要求:①仅用无刻度直尺,②保留必要的画图痕迹.在图1中画出一个45°角,使点A或点B是这个角的顶点,且AB为这个角的一边;在图2中画出线段AB的垂直平分线.20.(6分)为了加强学生的安全意识,某校组织了学生参加安全知识竞赛,从中抽取了部分的学生成绩进行统计,绘制统计图如图(不完整).类别分数段A 50.5~60.5B 60.5~70.5C 70.5~80.5D 80.5~90.5E 90.5~100.5请你根据上面的信息,解答下列问题.(1)若A组的频数比B组小24,求频数直方图中的a,b的值;(2)在扇形统计图中,D 部分所对的圆心角为n°,求n 的值并补全频数直方图;(3)若成绩在80分以上为优秀,全校共有2 000名学生,估计成绩优秀的学生有多少名? 21.(6分)(1)如图1,在矩形ABCD 中,点O 在边AB 上,∠AOC=∠BOD ,求证:AO=OB ; (2)如图2,AB 是⊙O 的直径,PA 与⊙O 相切于点A ,OP 与⊙O 相交于点C ,连接CB ,∠OPA=40°,求∠ABC 的度数.22.(8分)如图1,抛物线y=ax 2+bx+4过A (2,0)、B (4,0)两点,交y 轴于点C ,过点C 作x 轴的平行线与抛物线上的另一个交点为D ,连接AC 、BC .点P 是该抛物线上一动点,设点P 的横坐标为m (m >4).(1)求该抛物线的表达式和∠ACB 的正切值; (2)如图2,若∠ACP=45°,求m 的值;(3)如图3,过点A 、P 的直线与y 轴于点N ,过点P 作PM ⊥CD ,垂足为M ,直线MN 与x 轴交于点Q ,试判断四边形ADMQ 的形状,并说明理由.23.(8分)如图,四边形ABCD 为平行四边形,∠BAD 的角平分线AF 交CD 于点E ,交BC 的延长线于点F .(1)求证:BF=CD ;(2)连接BE ,若BE ⊥AF ,∠BFA=60°,BE=23,求平行四边形ABCD 的周长.24.(10分)直角三角形ABC 中,BAC 90∠=o ,D 是斜边BC 上一点,且AB AD =,过点C 作CE AD ⊥,交AD的延长线于点E,交AB延长线于点F.()1求证:ACB DCE∠∠=;()2若BAD45o∠=,AF22=+,过点B作BG FC⊥于点G,连接DG.依题意补全图形,并求四边形ABGD的面积.25.(10分)某中学为了了解在校学生对校本课程的喜爱情况,随机调查了部分学生对A B C D E,,,,五类校本课程的喜爱情况,要求每位学生只能选择一类最喜欢的校本课程,根据调查结果绘制了如下的两个不完整统计图.请根据图中所提供的信息,完成下列问题:(1)本次被调查的学生的人数为;(2)补全条形统计图(3)扇形统计图中,C类所在扇形的圆心角的度数为;(4)若该中学有2000名学生,请估计该校最喜爱C D,两类校本课程的学生约共有多少名.26.(122112(1)6tan303π-︒⎛⎫--+-⎪⎝⎭解方程:544101236x xx x-++=--27.(12分)勾股定理神秘而美妙,它的证法多样,其中的“面积法”给了李明灵感,他惊喜地发现;当两个全等的直角三角形如图(1)摆放时可以利用面积法”来证明勾股定理,过程如下如图(1)∠DAB=90°,求证:a 2+b 2=c 2证明:连接DB ,过点D 作DF ⊥BC 交BC 的延长线于点F ,则DF=b-a S 四边形ADCB =21122ADC ABC S S b ab +=-+V V S 四边形ADCB =211()22ADB BCD S S c a b a +=+-V V ∴221111()2222b abc a b a +=+-化简得:a 2+b 2=c 2 请参照上述证法,利用“面积法”完成如图(2)的勾股定理的证明,如图(2)中∠DAB=90°,求证:a 2+b 2=c 2 参考答案一、选择题(本大题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的.) 1.A 【解析】 【分析】根据题意得到原几何体的主视图,结合主视图选择. 【详解】解:原几何体的主视图是:.视图中每一个闭合的线框都表示物体上的一个平面,左侧的图形只需要两个正方体叠加即可. 故取走的正方体是①. 故选A . 【点睛】本题考查了简单组合体的三视图,中等难度,作出几何体的主视图是解题关键.【分析】根据平行线分线段成比例定理的逆定理,当AD AEDB EC=或AD AEAB AC=时,DE BDP,然后可对各选项进行判断.【详解】解:当AD AEDB EC=或AD AEAB AC=时,DE BDP,即23AEEC=或25AEAC=.所以D选项是正确的.【点睛】本题考查了平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例.也考查了平行线分线段成比例定理的逆定理.3.B【解析】【分析】作AC⊥y轴于C,ADx轴,BD⊥y轴,它们相交于D,有A点坐标得到AC=1,OC=1,由于AO绕点A 逆时针旋转90°,点O的对应B点,所以相当是把△AOC绕点A逆时针旋转90°得到△ABD,根据旋转的性质得AD=AC=1,BD=OC=1,原式可得到B点坐标为(2,1),然后根据反比例函数图象上点的坐标特征计算k的值.【详解】作AC⊥y轴于C,AD⊥x轴,BD⊥y轴,它们相交于D,如图,∵A点坐标为(1,1),∴AC=1,OC=1.∵AO绕点A逆时针旋转90°,点O的对应B点,即把△AOC绕点A逆时针旋转90°得到△ABD,∴AD=AC=1,BD=OC=1,∴B点坐标为(2,1),∴k=2×1=2.故选B.【点睛】本题考查了反比例函数图象上点的坐标特征:反比例函数y=(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.也考查了坐标与图形变化﹣旋转.先将25 100用科学记数法表示为2.51×104,再和10-9相乘,等于2.51×10-5米. 故选D 5.B 【解析】分析:根据已知画出图象,把x=−2代入得:4a−2b+c=0,把x=−1代入得:y=a−b+c>0,根据122cx x a⋅=<-,不等式的两边都乘以a(a<0)得:c>−2a ,由4a−2b+c=0得22c a b -=-,而0<c<2,得到102c-<-<即可求出2a−b+1>0.详解:根据二次函数y=ax 2+bx+c 的图象与x 轴交于点(−2,0)、(x 1,0),且1<x 1<2,与y 轴的正半轴的交点在(0,2)的下方,画出图象为:如图把x=−2代入得:4a−2b+c=0,∴①正确;把x=−1代入得:y=a−b+c>0,如图A 点,∴②错误; ∵(−2,0)、(x 1,0),且1<x 1,∴取符合条件1<x 1<2的任何一个x 1,−2⋅x 1<−2, ∴由一元二次方程根与系数的关系知122cx x a⋅=<-, ∴不等式的两边都乘以a(a<0)得:c>−2a , ∴2a+c>0,∴③正确;④由4a−2b+c=0得22c a b -=-, 而0<c<2,∴102c-<-< ∴−1<2a−b<0 ∴2a−b+1>0, ∴④正确.所以①③④三项正确. 故选B.点睛:属于二次函数综合题,考查二次函数图象与系数的关系, 二次函数图象上点的坐标特征, 抛物线与x轴的交点,属于常考题型. 6.C 【解析】 【分析】根据勾股定理求解. 【详解】设小方格的边长为1,得, OC=222222+= ,AO=222222+=,AC=4,∵OC 2+AO 2=22(22)(22)+=16, AC 2=42=16,∴△AOC 是直角三角形, ∴∠AOC=90°. 故选C . 【点睛】考点:勾股定理逆定理. 7.C 【解析】 【分析】连接AE ,根据余弦的定义求出AB ,根据勾股定理求出BC ,根据直角三角形的性质求出CD ,根据面积公式出去AE ,根据翻转变换的性质求出AF ,根据勾股定理、三角形中位线定理计算即可. 【详解】 解:连接AE ,∵AC=3,cos ∠CAB=13, ∴AB=3AC=9, 由勾股定理得,22AB AC -2,∠ACB=90°,点D 为AB 的中点,∴CD=12AB=92,S△ABC=12×3×62=92,∵点D为AB的中点,∴S△ACD=12S△ABC=922,由翻转变换的性质可知,S四边形ACED=92,AE⊥CD,则12×CD×AE=92,解得,AE=42,∴AF=22,由勾股定理得,DF=22AD AF=72,∵AF=FE,AD=DB,∴BE=2DF=7,故选C.【点睛】本题考查的是翻转变换的性质、直角三角形的性质,翻转变换是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.8.B【解析】【详解】试题分析:如图,如图,过点E作EF∥AB,∵AB∥CD,∴EF∥AB∥CD,∴∠1=∠4,∠3=∠5,∴∠1+∠2+∠3=∠2+∠4+∠5=180°,故选B9.D【分析】根据抛物线的图象与系数的关系即可求出答案. 【详解】解:由抛物线的开口可知:a <0,由抛物线与y 轴的交点可知:c <0,由抛物线的对称轴可知:2ba->0,∴b >0,∴abc >0,故①正确;令x=3,y >0,∴9a+3b+c >0,故②正确; ∵OA=OC <1,∴c >﹣1,故③正确; ∵对称轴为直线x=1,∴﹣2ba=1,∴b=﹣4a . ∵OA=OC=﹣c ,∴当x=﹣c 时,y=0,∴ac 1﹣bc+c=0,∴ac ﹣b+1=0,∴ac+4a+1=0,∴c=41a a+-,∴设关于x 的方程ax 1+bx+c=0(a≠0)有一个根为x ,∴x ﹣c=4,∴x=c+4=1a-,故④正确; ∵x 1<1<x 1,∴P 、Q 两点分布在对称轴的两侧, ∵1﹣x 1﹣(x 1﹣1)=1﹣x 1﹣x 1+1=4﹣(x 1+x 1)<0,即x 1到对称轴的距离小于x 1到对称轴的距离,∴y 1>y 1,故⑤正确. 故选D . 【点睛】本题考查的是二次函数图象与系数的关系,二次函数y=ax 1+bx+c 系数符号由抛物线开口方向、对称轴、抛物线与y 轴的交点抛物线与x 轴交点的个数确定.本题属于中等题型. 10.C 【解析】解:甲和乙盒中1个小球任意摸出一球编号为1、2、3、1的概率各为,其中得到的编号相加后得到的值为{2,3,1,5,6,7,8} 和为2的只有1+1; 和为3的有1+2;2+1; 和为1的有1+3;2+2;3+1; 和为5的有1+1;2+3;3+2;1+1; 和为6的有2+1;1+2; 和为7的有3+1;1+3; 和为8的有1+1. 故p (5)最大,故选C . 11.C 【解析】这张圆形纸片减去“不能接触到的部分”的面积是就是这张圆形纸片“能接触到的部分”的面积. 【详解】 解:如图:∵正方形的面积是:4×4=16;扇形BAO 的面积是:229013603604n r πππ⨯⨯==,∴则这张圆形纸片“不能接触到的部分”的面积是4×1-4×4π=4-π, ∴这张圆形纸片“能接触到的部分”的面积是16-(4-π)=12+π, 故选C . 【点睛】本题主要考查了正方形和扇形的面积的计算公式,正确记忆公式是解题的关键. 12.B 【解析】 【分析】设抛物线与x 轴的两交点A 、B 坐标分别为(x 1,0),(x 2,0),利用二次函数的性质得到P (-2b a ,244ac b a-),利用x 1、x 2为方程ax 2+bx+c=0的两根得到x 1+x 2=-b a ,x 1•x 2=ca,则利用完全平方公式变形得到AB=|x 1-x 224b ac a - ,接着根据等腰直角三角形的性质得到|244ac b a-|=1224b aca -简可得到b 2-1ac 的值. 【详解】设抛物线与x 轴的两交点A 、B 坐标分别为(x 1,0),(x 2,0),顶点P 的坐标为(-2b a ,244ac b a-),则x 1、x 2为方程ax 2+bx+c=0的两根, ∴x 1+x 2=-b a ,x 1•x 2=ca, ∴AB=|x 1-x 2212()x x -21212()4x x x x +-2()4b ca a--⋅=24b ac a -,∵△ABP 组成的三角形恰为等腰直角三角形,∴|244ac b a -|=12•24b ac a -,222(4)16b ac a -=2244b ac a-, ∴b 2-1ac=1. 故选B . 【点睛】本题考查了抛物线与x 轴的交点:把求二次函数y=ax 2+bx+c (a ,b ,c 是常数,a≠0)与x 轴的交点坐标问题转化为解关于x 的一元二次方程.也考查了二次函数的性质和等腰直角三角形的性质. 二、填空题:(本大题共6个小题,每小题4分,共24分.) 13.4 【解析】 【分析】由矩形的性质可得AO=CO=5=BO=DO ,由S △DCO =S △DPO +S △PCO ,可得PE+PF 的值. 【详解】解:如图,设AC 与BD 的交点为O ,连接PO ,∵四边形ABCD 是矩形 ∴AO=CO=5=BO=DO , ∴S △DCO =14S 矩形ABCD =10, ∵S △DCO =S △DPO +S △PCO , ∴10=12×DO×PF+12×OC×PE ∴20=5PF+5PE ∴PE+PF=4 故答案为4 【点睛】本题考查了矩形的性质,利用三角形的面积关系解决问题是本题的关键. 14.13或24【解析】①当3是直角边时,∵△ABC最小的角为A,∴tanA=13;②当3是斜边时,根据勾股定理,∠A的邻边=223122-=,∴tanA=2422=;所以tanA的值为13或24.15.135°【解析】【分析】通过旋转,把PA、PB、PC或关联的线段集中到同一个三角形,再根据两边的平方和等于第三边求证直角三角形,可以求解∠APB.【详解】把△PAB绕B点顺时针旋转90°,得△P′BC,则△PAB≌△P′BC,设PA=x,PB=2x,PC=3x,连PP′,得等腰直角△PBP′,PP′2=(2x)2+(2x)2=8x2,∠PP′B=45°.又PC2=PP′2+P′C2,得∠PP′C=90°.故∠APB=∠CP′B=45°+90°=135°.故答案为135°.【点睛】本题考查的是正方形四边相等的性质,考查直角三角形中勾股定理的运用,把△PAB顺时针旋转90°使得A′与C点重合是解题的关键.16.0<x<4【解析】【分析】根据二次函数的对称性及已知数据可知该二次函数的对称轴为x=2,结合表格中所给数据可得出答案.【详解】所以,x=4时,y=5,所以,y<5时,x的取值范围为0<x<4.故答案为0<x<4.【点睛】此题主要考查了二次函数的性质,利用图表得出二次函数的图象即可得出函数值得取值范围,同学们应熟练掌握.17.40°【解析】【分析】根据旋转的性质可得出AB=AD、∠BAD=100°,再根据等腰三角形的性质可求出∠B的度数,此题得解.【详解】根据旋转的性质,可得:AB=AD,∠BAD=100°,∴∠B=∠ADB=12×(180°−100°)=40°.故填:40°.【点睛】本题考查了旋转的性质以及等腰三角形的性质,根据旋转的性质结合等腰三角形的性质求出∠B的度数是解题的关键.18.①②④【解析】【分析】①根据旋转得到,对应角∠CAD=∠BAF,由∠EAF=∠BAF+∠BAE=∠CAD+∠BAE即可判断②由旋转得出AD=AF, ∠DAE=∠EAF,及公共边即可证明③在△ABE∽△ACD中,只有AB=AC、∠ABE=∠ACD=45°两个条件,无法证明④先由△ACD≌△ABF,得出∠ACD=∠ABF=45°,进而得出∠EBF=90°,然后在Rt△BEF中,运用勾股定理得出BE1+BF1=EF1,等量代换后判定④正确【详解】由旋转,可知:∠CAD=∠BAF.∵∠BAC=90°,∠DAE=45°,∴∠CAD+∠BAE=45°,∴∠BAF+∠BAE=∠EAF=45°,结论①正确;②由旋转,可知:AD=AF在△AED 和△AEF 中,=45AD AF DAE EAF AE AE ===⎧⎪∠∠︒⎨⎪⎩∴△AED ≌△AEF (SAS ),结论②正确;③在△ABE ∽△ACD 中,只有AB =AC ,、∠ABE =∠ACD =45°两个条件, 无法证出△ABE ∽△ACD ,结论③错误;④由旋转,可知:CD =BF ,∠ACD =∠ABF =45°, ∴∠EBF =∠ABE+∠ABF =90°, ∴BF 1+BE 1=EF 1. ∵△AED ≌△AEF , EF =DE , 又∵CD =BF ,∴BE 1+DC 1=DE 1,结论④正确. 故答案为:①②④ 【点睛】本题考查了相似三角形的判定,全等三角形的判定与性质, 勾股定理,熟练掌握定理是解题的关键 三、解答题:(本大题共9个小题,共78分,解答应写出文字说明、证明过程或演算步骤. 19.(1)答案见解析;(2)答案见解析. 【解析】试题分析:(1)根据等腰直角三角形的性质即可解决问题.(2)根据正方形、长方形的性质对角线相等且互相平分,即可解决问题. 试题解析:(1)如图所示,∠ABC=45°.(AB 、AC 是小长方形的对角线).(2)线段AB 的垂直平分线如图所示,点M 是长方形AFBE 是对角线交点,点N 是正方形ABCD 的对角线的交点,直线MN 就是所求的线段AB 的垂直平分线.20.(1)40(2)126°,1(3)940名【解析】【分析】(1)根据若A组的频数比B组小24,且已知两个组的百分比,据此即可求得总人数,然后根据百分比的意义求得a、b的值;(2)利用360°乘以对应的比例即可求解;(3)利用总人数乘以对应的百分比即可求解.【详解】(1)学生总数是24÷(20%﹣8%)=200(人),则a=200×8%=16,b=200×20%=40;(2)n=360×70200=126°.C组的人数是:200×25%=1.;(3)样本D、E两组的百分数的和为1﹣25%﹣20%﹣8%=47%,∴2000×47%=940(名)答估计成绩优秀的学生有940名.【点睛】本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.21.(1)证明见解析;(2)25°.【解析】试题分析:(1)根据等量代换可求得∠AOD=∠BOC,根据矩形的对边相等,每个角都是直角,可知∠A=∠B=90°,AD=BC,根据三角形全等的判定AAS证得△AOD≌△BOC,从而得证结论.(2)利用切线的性质和直角三角形的两个锐角互余的性质得到圆心角∠POA的度数,然后利用圆周角定理来求∠ABC的度数.试题解析:(1)∵∠AOC=∠BOD∴∠AOC -∠COD=∠BOD-∠COD∵四边形ABCD 是矩形 ∴∠A=∠B=90°,AD=BC ∴AOD BOC ∆≅∆ ∴AO=OB(2)解:∵AB 是O e 的直径,PA 与O e 相切于点A , ∴PA ⊥AB , ∴∠A=90°. 又∵∠OPA=40°, ∴∠AOP=50°, ∵OB=OC , ∴∠B=∠OCB.又∵∠AOP=∠B+∠OCB ,∴1252B OCB AOP ∠=∠=∠=︒. 22.(1)y=12x 2﹣3x+1;tan ∠ACB=13;(2)m=163;(3)四边形ADMQ 是平行四边形;理由见解析.【解析】 【分析】(1)由点A 、B 坐标利用待定系数法求解可得抛物线解析式为y=12x 2-3x+1,作BG ⊥CA ,交CA 的延长线于点G ,证△GAB ∽△OAC 得BG AG =OCOA,据此知BG=2AG .在Rt △ABG 中根据BG 2+AG 2=AB 2,可求得.继而可得 (2)作BH ⊥CD 于点H ,交CP 于点K ,连接AK ,易得四边形OBHC 是正方形,应用“全角夹半角”可得AK=OA+HK ,设K (1,h ),则BK=h ,HK=HB-KB=1-h ,AK=OA+HK=2+(1-h )=6-h .在Rt △ABK中,由勾股定理求得h=83,据此求得点K (1,83).待定系数法求出直线CK 的解析式为y=-13x+1.设点P 的坐标为(x ,y )知x 是方程12x 2-3x+1=-13x+1的一个解.解之求得x 的值即可得出答案; (3)先求出点D 坐标为(6,1),设P (m ,12m 2-3m+1)知M (m ,1),H (m ,0).及PH=12m 2-3m+1),OH=m ,AH=m-2,MH=1.①当1<m <6时,由△OAN ∽△HAP 知ON PH =OAAH.据此得ON=m-1.再证△ONQ ∽△HMQ 得ON HM =OQHQ.据此求得OQ=m-1.从而得出AQ=DM=6-m .结合AQ ∥DM 可得答案.②当m >6时,同理可得. 【详解】解:(1)将点A(2,0)和点B(1,0)分别代入y=ax2+bx+1,得4240{16440 a ba b++=++=,解得:123 ab⎧=⎪⎨⎪=-⎩;∴该抛物线的解析式为y=12x2﹣3x+1,过点B作BG⊥CA,交CA的延长线于点G(如图1所示),则∠G=90°.∵∠COA=∠G=90°,∠CAO=∠BAG,∴△GAB∽△OAC.∴42BG OCAG OA===2.∴BG=2AG,在Rt△ABG中,∵BG2+AG2=AB2,∴(2AG)2+AG2=22,解得:AG=255.∴BG=455,CG=AC+AG=25+255=1255.在Rt△BCG中,tan∠ACB═13BGCG=.(2)如图2,过点B作BH⊥CD于点H,交CP于点K,连接AK.易得四边形OBHC是正方形.应用“全角夹半角”可得AK=OA+HK,设K(1,h),则BK=h,HK=HB﹣KB=1﹣h,AK=OA+HK=2+(1﹣h)=6﹣h,∴22+h2=(6﹣h)2.解得h=83,∴点K(1,83),设直线CK的解析式为y=hx+1,将点K(1,83)代入上式,得83=1h+1.解得h=﹣13,∴直线CK的解析式为y=﹣13x+1,设点P的坐标为(x,y),则x是方程12x2﹣3x+1=﹣13x+1的一个解,将方程整理,得3x2﹣16x=0,解得x1=163,x2=0(不合题意,舍去)将x1=163代入y=﹣13x+1,得y=209,∴点P的坐标为(163,209),∴m=163;(3)四边形ADMQ是平行四边形.理由如下:∵CD∥x轴,∴y C=y D=1,将y=1代入y=12x2﹣3x+1,得1=12x2﹣3x+1,解得x1=0,x2=6,∴点D(6,1),根据题意,得P(m,12m2﹣3m+1),M(m,1),H(m,0),∴PH=12m2﹣3m+1,OH=m,AH=m﹣2,MH=1,①当1<m<6时,DM=6﹣m,如图3,∵△OAN∽△HAP,∴ON OA PH AH,∴21342ONm m -+=22m -, ∴ON=2682m m m -+-=(4)(2)2m m m ---=m ﹣1, ∵△ONQ ∽△HMQ , ∴ON OQ HM HQ=, ∴4ON OQ m OQ=-, ∴44m OQ m OQ-=-, ∴OQ=m ﹣1,∴AQ=OA ﹣OQ=2﹣(m ﹣1)=6﹣m ,∴AQ=DM=6﹣m ,又∵AQ ∥DM ,∴四边形ADMQ 是平行四边形.②当m >6时,同理可得:四边形ADMQ 是平行四边形.综上,四边形ADMQ 是平行四边形.【点睛】本题主要考查二次函数的综合问题,解题的关键是掌握待定系数法求函数解析式、相似三角形的判定与性质、平行四边形的判定与性质及勾股定理、三角函数等知识点.23.(1)证明见解析;(2)12【解析】【分析】(1)由平行四边形的性质和角平分线得出∠BAF=∠BFA ,即可得出AB=BF ;(2)由题意可证△ABF 为等边三角形,点E 是AF 的中点. 可求EF 、BF 的值,即可得解.【详解】解:(1)证明:∵ 四边形ABCD 为平行四边形,∴ AB=CD ,∠FAD=∠AFB又∵ AF 平分∠BAD ,∴ ∠FAD=∠FAB∴ ∠AFB=∠FAB∴ AB=BF∴ BF=CD(2)解:由题意可证△ABF 为等边三角形,点E 是AF 的中点在Rt △BEF 中,∠BFA=60°,BE=23, 可求EF=2,BF=4∴ 平行四边形ABCD 的周长为1224.(1)证明见解析;(2)补图见解析;ABGD S 2四边形=.【解析】【分析】()1根据等腰三角形的性质得到ABD ADB ∠=∠,等量代换得到ABD CDE ∠=∠,根据余角的性质即可得到结论;()2根据平行线的判定定理得到AD ∥BG ,推出四边形ABGD 是平行四边形,得到平行四边形ABGD 是菱形,设AB=BG=GD=AD=x ,解直角三角形得到22BF BG x == ,过点B 作BH AD ⊥ 于H ,根据平行四边形的面积公式即可得到结论.【详解】解:()1AB AD Q =, ABD ADB ∠∠∴=,ADB CDE ∠∠=Q ,ABD CDE ∠∠∴=,BAC 90∠=o Q ,ABD ACB 90∠∠∴+=o ,CE AE ⊥Q ,DCE CDE 90∠∠∴+=o ,ACB DCE ∠∠∴=;()2补全图形,如图所示:BAD 45∠=o Q ,BAC 90∠=o ,BAE CAE 45∠∠∴==o ,F ACF 45∠∠==o ,AE CF ⊥Q ,BG CF ⊥,AD //BG ∴,BG CF ⊥Q ,BAC 90∠=o ,且ACB DCE ∠∠=,AB BG ∴=,AB AD =Q ,BG AD ∴=,∴四边形ABGD 是平行四边形,AB AD =Q ,∴平行四边形ABGD 是菱形,设AB BG GD AD x ====,BF ∴==,AB BF x 2∴+==x ∴=过点B 作BH AD ⊥于H ,BH AB 12∴==.ABGD S AD BH ∴=⨯=四边形故答案为(1)证明见解析;(2)补图见解析;ABGD S 四边形.【点睛】本题考查等腰三角形的性质,平行四边形的判定和性质,菱形的判定和性质,解题的关键是正确的作出辅助线.25. (1)300;(2)见解析;(3)108°;(4)约有840名.【解析】【分析】(1)根据A 种类人数及其占总人数百分比可得答案;(2)用总人数乘以B 的百分比得出其人数,即可补全条形图;(3)用360°乘以C 类人数占总人数的比例可得;(4)总人数乘以C 、D 两类人数占样本的比例可得答案.【详解】解:(1)本次被调查的学生的人数为69÷23%=300(人),故答案为:300;(2)喜欢B类校本课程的人数为300×20%=60(人),补全条形图如下:(3)扇形统计图中,C类所在扇形的圆心角的度数为360°×90300=108°,故答案为:108°;(4)∵2000×90+36300=840,∴估计该校喜爱C,D两类校本课程的学生共有840名.【点睛】本题考查条形统计图、扇形统计图的综合运用.读懂统计图,从统计图中得到必要的信息是解题关键.条形统计图能清楚地表示出每个项目的数据.26.(1)10;(2)原方程无解.【解析】【分析】(1)原式利用二次根式性质,零指数幂、负整数指数幂法则,以及特殊角的三角函数值计算即可求出值;(2)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【详解】(1)原式=33169-⨯+=10;(2)去分母得:3(5x﹣4)+3x﹣6=4x+10,解得:x=2,经检验:x=2是增根,原方程无解.【点睛】此题考查了解分式方程,利用了转化的思想,解分式方程注意要检验.27.见解析.【解析】【分析】首先连结BD,过点B作DE边上的高BF,则BF=b-a,表示出S五边形ACBED,两者相等,整理即可得证.【详解】证明:连结BD,过点B作DE边上的高BF,则BF=b-a,∵S五边形ACBED=S△ACB+S△ABE+S△ADE=12ab+12b1+12ab,又∵S五边形ACBED=S△ACB+S△ABD+S△BDE=12ab+12c1+12a(b-a),∴12ab+12b1+12ab=12ab+12c1+12a(b-a),∴a1+b1=c1.【点睛】此题考查了勾股定理的证明,用两种方法表示出五边形ACBED的面积是解本题的关键.。
2019-2020学年重庆渝北区实验中学高一数学理月考试卷含解析

2019-2020学年重庆渝北区实验中学高一数学理月考试卷含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. α、β是两个不同的平面,下列命题:若平面内的直线垂直于平面内的任意直线,则;若平面内的任一直线都平行于平面,则;若平面垂直于平面,直线在平面内,则;若平面平行于平面,直线在平面内,则;其中正确命题的个数是A、B、C、D、参考答案:B2. 设函数,若,则实数的值为 ( )A.或0 B.或C.0或2 D.2参考答案:B3. 已知均为正数,且都不等于1,若实数满足,则的值等于()A、1B、2C、3D、4参考答案:A4. 温家宝总理在2010年政府工作报告中提出,今年中央财政拟安排“三农”投入8183亿元.用科学记数法表示“8183亿元”,并保留两个有效数字为()A.元B.元 C.元D.元参考答案:C略5. 若上述函数是幂函数的个数是()A.个 B.个 C.个 D.个参考答案:C解析:是幂函数6. 在下列区间中,函数=e x+4x-3的零点所在的区间为().A. B. C. D.参考答案:C7. 已知关于参数的二次函数的最小值是关于的函数,则的最小值为()。
以上结果都不对参考答案:。
当时,的最小值为,其中。
因为对称轴为,所以当时的最小值为,选。
8. 执行如图所示的程序框图,其输出的结果是A.1 B.C. D.参考答案:C9. 下列命题中错误的是:()A.如果α⊥β,那么α内一定存在直线平行于平面β;B.如果α⊥β,那么α内所有直线都垂直于平面β;C.如果平面α不垂直平面β,那么α内一定不存在直线垂直于平面β;D.如果α⊥γ,β⊥γ,α∩β=l,那么l⊥γ.参考答案:略10. 若,则(▲ )A. B. C. D.参考答案:C二、填空题:本大题共7小题,每小题4分,共28分11. 我国2001年底的人口总数为M,要实现到2011年底我国人口总数不超过N(其中M<N),则人口的年平均自然增长率p的最大值是______.参考答案:12. (5分)在三棱柱ABC﹣A1B1C1中,各棱长相等,侧掕垂直于底面,点D是侧面BB1C1C 的中心,则AD与平面BB1C1C所成角的大小是.参考答案:60°考点:直线与平面所成的角.专题:空间角.分析:三棱柱ABC﹣A1B1C1是正三棱柱,取BC的中点E,则∠ADE就是AD与平面BB1C1C所成角,解直角三角形求出∠ADE的大小,[来源:Z,xx,]即为所求.解答:由题意可得,三棱柱ABC﹣A1B1C1是正三棱柱,取BC的中点E,则AE⊥∠面BB1C1C,ED就是AD在平面BB1C1C内的射影,故∠ADE就是AD 与平面BB1C1C所成角,设三棱柱的棱长为1,直角三角形ADE中,tan∠ADE===,∴∠ADE=60°,故答案为60°.点评:本题考查直线与平面成的角的定义和求法,取BC的中点E,判断∠ADE就是AD与平面BB1C1C所成角,是解题的关键,属于中档题.13. 已知等比数列中,,,则参考答案:7014. 函数的周期是___________参考答案:15. 中,点在边中线上,,则·()的最小值为____________。
2019-2020学年重庆渝北实验中学高三生物一模试卷及参考答案

2019-2020学年重庆渝北实验中学高三生物一模试卷及参考答案一、选择题:本题共15小题,每小题2分,共30分。
每小题只有一个选项符合题目要求。
1.下列有关生物学实验的叙述,正确的是()A. 用苏丹Ⅲ染液可检测生物组织中维生素D的存在B. 取藓类小叶制作成临时装片,在显微镜下可观察到绿色颗粒成顺时针流动,而实际流动方为逆时针C. 利用光学微镜可观察到细胞膜的磷脂双分子层D. 经加热变性后的牛奶仍能用作蛋白质鉴定的材料2.现提供新配制的斐林试剂甲液(0.1 g/mL NaOH溶液)、乙液(0.05 g/mL CuSO4溶液)、蒸馏水,则充分利用上述试剂及必需的实验用具,能鉴别出下列哪些物质()①麦芽糖②蔗糖③胰岛素④脂肪A. 只有①B. ①和②C. ①和③D. ②、③和④3.下列关于生态平衡的说法,不正确的是()A.生态平衡就是生态系统的结构和功能处于相对稳定的一种状态B.处于生态平衡的生态系统的各种组成成分保持不变C.处于生态平衡的生态系统的物质和能量的输入和输出达到平衡状态D.生态平衡的调节机制是负反馈调节4.经人工处理过的一只成年狗,身体变得臃肿,行动呆笨而迟缓,精神萎靡,食欲不振,根据上述症状可以断定人工处理的方法是()A.摘除了狗的生殖腺B.摘除了狗的甲状腺C.给狗注射了大量的甲状腺激素D.给狗注射了大量的生长激素5.如图X、Y、Z是细胞中的三种有机化合物,X是细胞生命活动所需的主要能源物质,Y、Z为构成细胞膜的成分。
下列有关说法正确的是()A.X参与构成细胞膜上的糖被,糖被与细胞识别功能有关B. 胆固醇可优先通过细胞膜进入细胞内,与Y有关C. 细胞膜会被蛋白酶分解,说明组成细胞膜的物质中有ZD. 细胞膜上的Z是可以运动的,而Y是静止的6.某种野生猕猴桃(2n=58)是一种多年生且富含维生素C的小野果。
育种专家以野生猕猴桃的种子(基因型为aa)为实验材料,培育出抗虫无籽猕猴桃新品种,育种过程如下图所示。
2019-2020学年渝北区实验中学校高三英语第一次联考试卷及参考答案

2019-2020学年渝北区实验中学校高三英语第一次联考试卷及参考答案第一部分阅读(共两节,满分40分)第一节(共15小题;每小题2分,满分30分)阅读下列短文,从每题所给的A、B、C、D四个选项中选出最佳选项AIt looks like 2017 is shaping up to be a record-breaking year in movie History. Here is a list of some of the year’s biggest blockbusters so far.Kong: Skull IslandA reboot (重启) of King Kong would normally get laughed at in this day and age, but it looks like this modem version of the story will be worth watching. With US actress Brie Larson and UK actor Tom Hiddleston in the mix, this film is set to be this year’s biggest monster tale.Release Date:3/10/17Beauty and the BeastDirector Bill Condon is bringing back a part of our childhood in live action, complete with the songs we all remember and love. With British stars Emma Watson and Dan Stevens leading thecast, the classic Walt Disney story already sounds like it’ll be a delight for both children and adults.Release Date:3/17/17The Fate of the FuriousThere was doubt that we’d even get a Fast 8, especially after the fitting ending US actor Paul Walker’s character was given at the end of Furious 7. Fans thought they’d never see Dom and the rest of the crew back in action, but thankfully, US star Vin Diesel himself confirmed that The Fate of the Furious is fueling up for another go.Release Date:4/14/17Spider-Man: HomecomingSpider Man is heading home to Marvel Studios for the first time. The movie will show us Peter Parker’s high school days, and will continue the threads we saw formed during his initial appearance in Captain America: Civil War. We know that Michael Keaton is playing The Vulture in this story, and that both Happy Hogan and Tony Stark, played by US actors Jon Favreau and Robert Downey Jr., are along for the ride.Release Date:7/7/171.Which of the following movies can’t you see on May Day?A.Kong: Skull Island.B.Beauty and the Beast.C.The Fate of the Furious.D.Spider-Man: Homecoming.2.What can we know about Beauty and the Beast?A.It is fueling up for another go.B.It is produced by Marvel StudiosC.It’ll show us Peter Parker’s school days.D.It’ll be enjoyable for both children and adults.3.What does the underlined word “cast” probably mean?A.Characters.B.Actors.C.Directors.D.Teachers.BImust have always known reading was very important because the first memories I have as a child deal with books. There was not one night that I don’t remember mom reading me a storybook by my bedside. I was extremely inspired by the wonderful way the words sounded.I always wanted to know what my mom was reading. Hearing mom say, “I can’t believe what’s printed in the newspaper this morning,” made me want to grab it out of her hands and read it myself. I wanted to be like my mom and know all of the things she knew. So I carried around a book, and each night, just to be like her, I would pretend to be reading.This is how everyone learned to read. We would start off with sentences, then paragraphs, and then stories. It seemed an unending journey, but even as a six-year-old girl I realized that knowing how to read could open many doors. When mom said, “The C-A-N-D-Y is hidden on the top shelf,” I knew where the candy was. My progress in reading raised my curiosity, and I wanted to know everything. I often found myself telling my mom to drive more slowly, so that I could read all of the road signs we passed.Most of my reading through primary, middle and high school was factual reading. I read for knowledge, and to make A’s on my tests. Sometimes, I would read a novel that was assigned, but I didn’t enjoy this type of reading.I liked facts, things that are concrete. I thought anything abstract left too much room for argument.Now that I’m growing and the world I once knew as being so simple is becoming more complex, I find myself needing a way to escape. By opening a novel, I can leave behind my burdens and enter into a wonderful and mysterious world where I am now a new character. In these worlds I can become anyone. I don’t have to writedown what happened or what technique the author was using when he or she wrote this. I just read to relax.We’re taught to read because it’s necessary for much of human understanding. Reading is an important part of my life. Reading satisfies my desire to keep learning. And I’ve found that the possibilities that lie within books are limitless.4. Why did the author want to grab the newspaper out of mom’s hands?A. She wanted mom to read the news to her.B. She couldn’t wait to tear the newspaper apart.C. She couldn’t help but stopmom from reading.D. She was eager to know what had happened.5. According to Paragraph 3, the author’s reading of road signs shows___________.A. her own way to find herselfB. her eagerness to develop her reading abilityC. her growing desire to know the world around herD. her effort to remind mom to obey traffic rules6. The author takes novel reading as a way to___________.A. explore a mysterious landB. develop an interest in learningC. get away from a confusing worldD. learn about the adult world7. What could be the best title for the passage?A The Pleasure of Reading B. Growing Up with ReadingC. The Magic of ReadingD. Reading Makes a Full ManCI was in the second year of my Ph. D. program when a colleague asked what I would do if I had an extra hour every day. Without much consideration, I said I would use it to help others. The question kept coming to my mind. Like many graduate students, I was overwhelmed (难以承受的) with research, teaching, coursework, and some attempt at a personal life. Still, I asked myself, "Do I really need a 25th hour to help other people-or do I need to make better use of the 24 hours I have?"I needed something to help me return to my old self. After that conversation with my colleague, I googled (谷歌搜索) “volunteer opportunities near me”. A local organization that drives people to stores or appointments waslooking for volunteers. Having grown up in a rural village where everyone knew oneanother and my grandparents were always close by, I thought serving senior citizens in my new hometown might be just what I needed.A short time later, I started to volunteer for an organization that provides transportation for senior citizens and people with disabilities. To my surprise, adding this activity to my busy life was just what I needed to calm the confusion I was feeling as a first-generation international graduate student.I started to volunteer about 3 hours every weekend, the time I otherwise would have wasted oversleeping or scrolling (滚屏) through social media. Sharing stories with my riders was much more rewarding. What they told me about their lives helped me realize that in every corner of the world, humans are connected with the languageof emotions. And seeing how eager my riders were to spend time out and about inspired me to think about how to spend my time, which used to slip away. My previously overwhelming schedule began to feel manageable.I'm proud of who I have become, and I continue to reflect on how I'm using the most valuable thing in life: my time.8. Why did the author ask himself the question in Paragraph 1?A. He wanted to return to normal life.B. He was busy but wanted to help others.C. He couldn't bear too much school work.D. He couldn't answer his colleague's question.9. How did the author find the volunteer job?A. A colleague recommended it.B. A local organization offered it.C. He got it from his grandparents.D. He got it by surfing on the Internet.10. What made the author feel his volunteer job was worth doing?A. Communicating with his riders.B. Improving his language learning.C. Meeting his grandparents often.D. Realizing his previous dream.11. How did volunteering influence the author?A. It helped himbecome confident and efficient.B. He found a good way to live a free and quiet life.C. He realized he had wasted too much time pursuing his Ph.D.D. It inspired him to spare more time to accompany his grandparents.DA nurse has fulfilled (实现) a promise she made to her patient four years ago to one day attend her daughter's graduation from nursing school.Edina Habibovic, 22, graduated from Chamberlain University's College of Nursing in 2020. Her mother, Sevala Habibovic, 46, died in2017 after a two year fight with breast cancer.“I thought the medical field wasn't for me. Then, my mom got sick and I had all the experience going in and out of the hospital, ” Edina toldGood MorningAmerica. “When my mom passed away, I thought, ‘I want to dothis.’”she said.Sanja Josipovic, who at the time worked as a home health nurse with Northwestern Medicine in Winfield, Illinois, cared for Sevala inside her home. They often chatted and shared the latest news with each other over six months of care.“She was most worried about Edina because she was young and hadn't finished school yet, ” Sanja said. “We are like sisters; we care about and trust each other. She was a powerful and strong minded woman. She wasn't scared to die; she was just worried about her kids and husband.”Edina said her mother lived for being with her family and taking care of people. “When Sanja was working, my mom would still try to make her something to eat, no matter how sick she was, ” Edina added. When Sevala's life was coming to an end, she asked Sanja to take her place at her youngest daughter's nursing school graduation. “That was the only thing she was going to miss. Edina's graduation, ” said Sanja, who is a mother of three herself. She agreed.Due to COVID -19, there was no graduation or pinning ceremony. Edina's manager at Marianjoy Rehabilitation Hospital decided to host a pinning ceremony for her and have Sanja present the pin. “Sanja has fulfilled her promise, ” Edina said.Edina and Sanja are now caring for patients alongside one another as colleagues at Marianjoy.12. What does the underlined word “this” in paragraph 3 refer to?A. Leaving the hospitalB. Working as a nurseC. Facing death positivelyD. Caring for Edina's mother13. What can be learned about Sanja and Sevala?A. They enjoyed volunteeringB. They were cancer survivorsC. They had unhappy marriagesD. They developed a close bond14. What would be Sevala's regret?A. The loss of the chance to study medicineB. Her absence from Edina's school graduationC. Failing to keep the promise made to SanjaD. Never cooking a good meal for her husband15. How did Sanja fulfill her promise?A. By taking care of Edina and her familyB. By helping Edina enter her dream hospitalC. By attending a special ceremony for EdinaD. By managing to become Edina's colleague第二节(共5小题;每小题2分,满分10分)阅读下面短文,从短文后的选项中选出可以填入空白处的最佳选项。
重庆市渝北区2019-2020学年第一次中考模拟考试物理试卷含解析
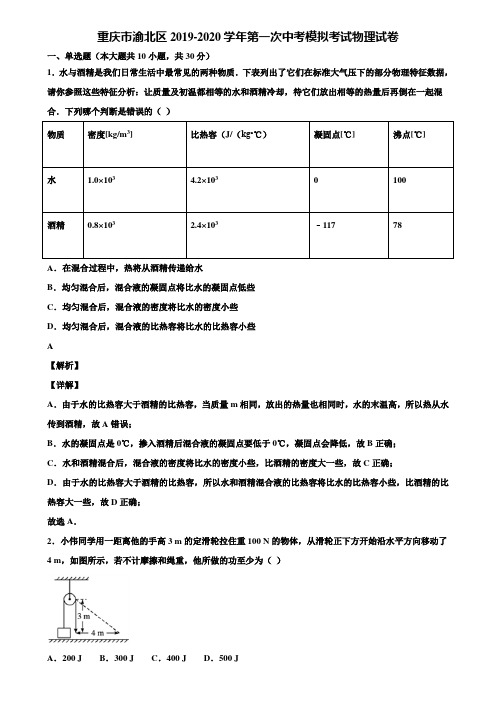
重庆市渝北区2019-2020学年第一次中考模拟考试物理试卷一、单选题(本大题共10小题,共30分)1.水与酒精是我们日常生活中最常见的两种物质.下表列出了它们在标准大气压下的部分物理特征数据,请你参照这些特征分析:让质量及初温都相等的水和酒精冷却,待它们放出相等的热量后再倒在一起混合.下列哪个判断是错误的()物质密度[kg/m3] 比热容(J/(kg•℃)凝固点[℃] 沸点[℃]水 1.0×103 4.2×1030 100酒精0.8×103 2.4×103﹣117 78A.在混合过程中,热将从酒精传递给水B.均匀混合后,混合液的凝固点将比水的凝固点低些C.均匀混合后,混合液的密度将比水的密度小些D.均匀混合后,混合液的比热容将比水的比热容小些A【解析】【详解】A.由于水的比热容大于酒精的比热容,当质量m相同,放出的热量也相同时,水的末温高,所以热从水传到酒精,故A错误;B.水的凝固点是0℃,掺入酒精后混合液的凝固点要低于0℃,凝固点会降低,故B正确;C.水和酒精混合后,混合液的密度将比水的密度小些,比酒精的密度大一些,故C正确;D.由于水的比热容大于酒精的比热容,所以水和酒精混合液的比热容将比水的比热容小些,比酒精的比热容大一些,故D正确;故选A.2.小伟同学用一距离他的手高3 m的定滑轮拉住重100 N的物体,从滑轮正下方开始沿水平方向移动了4 m,如图所示,若不计摩擦和绳重,他所做的功至少为()A.200 J B.300 J C.400 J D.500 JA【解析】滑轮为定滑轮,不省力,若不计绳重和摩擦,他至少做的功W总=W有用=Gh;利用勾股定理计算绳子现在的长度L=m=5m,所以物体被提高的高度为h=5m-3m=2m,W=Gh=100N×2m=200J故选A.3.下列关于生活用电的说法正确的是()A.家庭电路中开关接在火线或零线上都可以B.当保险丝熔断后,可以用铜丝代替C.使用测电笔时,手不要接触笔尾金属体,以免触电D.发生触电事故时,应立即切断电源D【解析】【详解】A.家庭电路的开关应该装在火线上,这样可防止断开开关后用电器仍带电,故A错误;B.铜丝的熔点高,用铜丝代替保险丝,在电流异常升高到一定的高度的时候,不能自身熔断切断电流,起不到保险作用,故B错误;C.用测电笔时,手必须要接触笔尾金属体,这样才能使测电笔发挥作用,故C错误;D.如果发生触电事故,应立即切断电源,然后施救,绝对不能用手将触电人拉开,否则可能使救人者触电,故D正确;故选D.4.如图所示,放在水平桌面上的物块用细线通过定滑轮与沙桶相连,当沙桶与沙的总质量为m时,物块恰好做匀速直线运动(忽略细线与滑轮之间的摩擦).以下说法正确的是A.物块受到的滑动摩擦力大小为mgB.物块的重力与它对桌面的压力是一对平衡力C.物块受到的滑动摩擦力与支持力是一对平衡力D.小桶匀速下降的过程中重力势能转化为动能A【解析】【详解】A、沙桶与沙的总重力为G=mg,使用定滑轮不能改变力的大小(忽略细线与滑轮之间的摩擦),则物块受到的拉力大小为mg;因为物块做匀速直线运动,拉力和滑动摩擦力是一对平衡力,所以滑动摩擦力的大小为mg,故A正确;B、物块的重力与它对桌面的压力没有作用在同一个物体上,不是一对平衡力,故B错误;C、物块受到的滑动摩擦力与支持力不在同一条直线上,不是一对平衡力,故C错误;D、小桶匀速下降的过程中,质量不变,高度减小,所以重力势能减小,但速度不变,动能不变,因此不是重力势能转化为动能,故D错误.5.如图所示电路,当开关S闭合后,L1、L2均能发光,电流表、电压表均有示数.过一会儿,两灯都不发光.电流表的示数为零,电压表的示数为电源电压,可能发生的故障是A.L l灯丝断了B.L1短路C.L2灯丝断了D.L2短路C【解析】【详解】A.如果灯泡L1灯丝断了,整个电路断路,电流表、电压表示数都为零.不符合题意;B.如果灯泡L1短路不能发光,但L2仍然发光.电流表、电压表示数都增大.不符合题意;C.如果灯泡L2灯丝断了,电路断路,两只灯泡都不亮,电流表示数为零,电压表测量电源电压.符合题意;D.如果灯泡L2短路不能发光,但L1仍然发光.电流表示数增大,电压表相当于与导线并联示数减小为零.不符合题意.故选C.6.下列实例中,为了增大压强的是()A.书包带做得很宽B.图钉帽做得面积较大C.铁轨铺在多根枕木上D.压路机做得很重D【解析】【详解】A.书包带做得较宽,是在压力一定时,通过增大受力面积来减小压强;故A不合题意;B.图钉帽做得面积较大,是在压力一定时,通过增大受力面积来减小压强;故B不合题意;C.铁轨铺在多根枕木上,是在压力一定时,通过增大受力面积来减小压强;故C不合题意;D.压路机做得很重,是在受力面积一定时,通过增大压力来增大压强;故D符合题意.7.在没有其他任何光照的情况下,舞台追光灯发出的绿光照在穿白上衣、红裙子的演员身上,观众看到她A.全身呈绿色B.上衣呈绿色,裙子呈紫色C.上衣呈绿色,裙子不变色D.上衣呈绿色,裙子呈黑色D【解析】不透明物体的颜色是由它反射的色光决定的,白色物体能反射所有色光,黑色物体吸收所有色光解答:追光灯发出的绿光照到白色的上衣上,白色的上衣能反射所有颜色的光,因此上衣看起来是绿色;而红色的裙子只能反射红光,不能反射其他颜色的光,因此绿光照射在上面时,裙子看起来是黑色。
