初中数学竞赛辅导资料
初中数学竞赛辅导
初中数学竞赛辅导资料3质数 合数甲内容提要1 正整数的一种分类： 质数的定义：如果一个大于1的正整数,只能被1和它本身整除,那么这个正整数叫做质数质数也称素数.合数的定义：一个正整数除了能被1和本身整除外,还能被其他的正整数整除,这样的正整数叫做合数.2 根椐质数定义可知① 质数只有1和本身两个正约数,② 质数中只有一个偶数2如果两个质数的和或差是奇数那么其中必有一个是2,如果两个质数的积是偶数那么其中也必有一个是2,3任何合数都可以分解为几个质数的积.能写成几个质数的积的正整数就是合数.乙例题例1两个质数的和等于奇数a a ≥5.求这两个数解：∵两个质数的和等于奇数∴必有一个是2所求的两个质数是2和a －2.例2己知两个整数的积等于质数m, 求这两个数解：∵质数m 只含两个正约数1和m,又∵－1－m=m∴所求的两个整数是1和m 或者－1和－m.例3己知三个质数a,b,c 它们的积等于30求适合条件的a,b,c 的值解：分解质因数：30＝2×3×5适合条件的值共有： ⎪⎩⎪⎨⎧===532c b a ⎪⎩⎪⎨⎧===352c b a ⎪⎩⎪⎨⎧===523c b a ⎪⎩⎪⎨⎧===253c b a ⎪⎩⎪⎨⎧===325c b a ⎪⎩⎪⎨⎧===235c b a 应注意上述六组值的书写排列顺序,本题如果改为4个质数a,b,c,d 它们的积等于210,即abcd=2×3×5×7那么适合条件的a,b,c,d 值共有24组,试把它写出来.例4试写出4个连续正整数,使它们个个都是合数.解：本题答案不是唯一的设N 是不大于5的所有质数的积,即N ＝2×3×5那么N ＋2,N ＋3,N ＋4,N ＋5就是适合条件的四个合数即32,33,34,35就是所求的一组数.本题可推广到n 个.令N 等于不大于n+1的所有质数的积,那么N ＋2, N ＋3,N ＋4,……N ＋n+1就是所求的合数.丙练习31， 小于100的质数共___个,它们是__________________________________ 2， 己知质数P 与奇数Q 的和是11,则P ＝＿＿,Q ＝＿＿3， 己知两个素数的差是41,那么它们分别是＿＿＿＿＿4， 如果两个自然数的积等于19,那么这两个数是＿＿＿如果两个整数的积等于73,那么它们是＿＿＿＿如果两个质数的积等于15,则它们是＿＿＿＿＿5, 两个质数x 和y,己知 xy=91,那么x=__,y=__,或x=__,y=__. 6, 三个质数a,b,c 它们的积等于1990.那么 ⎪⎩⎪⎨⎧===c b a7, 能整除311＋513的最小质数是＿＿8,己知两个质数A 和B 适合等式A ＋B ＝99,AB ＝M.求M 及B A ＋AB 的值 9,试写出6个连续正整数,使它们个个都是合数.10,具备什么条件的最简正分数可化为有限小数11,求适合下列三个条件的最小整数：① 大于1 ②没有小于10的质因数 ③不是质数12,某质数加上6或减去6都仍是质数,且这三个质数均在30到50之间,那么这个质数是＿＿＿13,一个质数加上10或减去14都仍是质数,这个质数是＿＿.。
初中数学竞赛辅导资料.doc
初中数学竞赛辅导资料初中数学竞赛辅导资料初一上目录1数的整除（一） 2倍数约数 3质数合数4 零的特性5a n的个位数6数学符号 7用字母表示数 8 抽屉原则初一下目录9一元一次方程解的讨论10二元一次方程的整数解11二元一次方程组解的讨论12用交集解题13用枚举法解题14经验归纳法15乘法公式16整数的一种分类初二上目录17 奇数偶数18 式的整除19因式分解20 恒等式证明21 比较大小22 分式23递推公式24 连续正整数25 十进制的记数法26 选择题解法(一)27识图28三角形边角性质初中数学竞赛辅导资料初二下目录29概念的定义30概念的分类31勾股定理32中位线33同一法34 反证法35两种对称36三点共线37不等关系38、垂直平行39线段、角相等40线段、角和差倍分41线段的比、积、幂42形如1/a+1/b=1/c问题的证明43面积法44数的整除（二）初三上目录45一元二次方程46完全平方式（数）47配方法48非负数49对称式50 基本对称式51待定系数52换元法53 条件等式54整数解55未知数多于方程的个数56列表法57逆推法58观察法59“或者”“并且”60解三角形初三下目录61函数的图象62绝对值63动态几何的定值64最大最小值65图象法66辅助圆67参数法证平几68选择题(二)69数的整除(三) 70正整数简单性质的复习美文欣赏1、走过春的田野，趟过夏的激流，来到秋天就是安静祥和的世界。
秋天，虽没有玫瑰的芳香，却有秋菊的淡雅，没有繁花似锦，却有硕果累累。
秋天，没有夏日的激情，却有浪漫的温情，没有春的奔放，却有收获的喜悦。
清风落叶舞秋韵，枝头硕果醉秋容。
秋天是甘美的酒，秋天是壮丽的诗，秋天是动人的歌。
2、人的一生就是一个储蓄的过程，在奋斗的时候储存了希望；在耕耘的时候储存了一粒种子；在旅行的时候储存了风景；在微笑的时候储存了快乐。
聪明的人善于储蓄，在漫长而短暂的人生旅途中，学会储蓄每一个闪光的瞬间，然后用它们酿成一杯美好的回忆，在四季的变幻与交替之间，散发浓香，珍藏一生！3、春天来了，我要把心灵放回萦绕柔肠的远方。
初中数学竞赛辅导资料
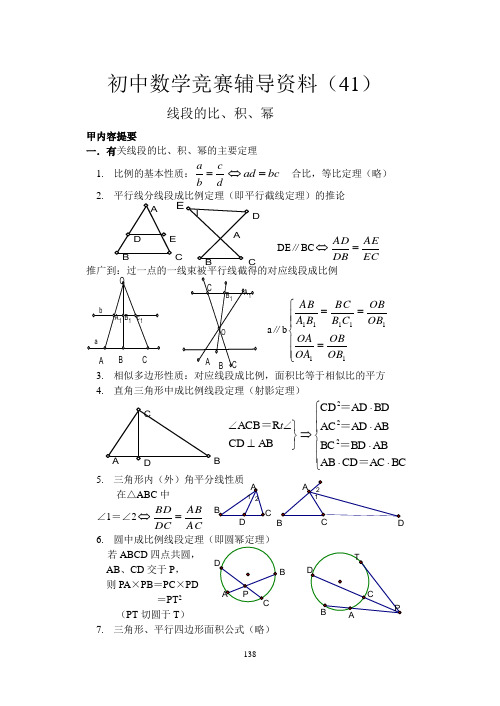
初中数学竞赛辅导资料（41）线段的比、积、幂甲内容提要一．有关线段的比、积、幂的主要定理 1. 比例的基本性质：dcb a =bc ad =⇔ 合比，等比定理（略） 2.DE ∥BC ECAEDB AD =⇔a ∥b ⎪⎪⎩⎪⎪⎨⎧===1111111OB OBOA OA OB OB C B BC BA AB3. 相似多边形性质：对应线段成比例，面积比等于相似比的平方4. 直角三角形中成比例线段定理（射影定理）⎪⎪⎩⎪⎪⎨⎧⋅⋅⋅⋅⋅⇒⎭⎬⎫⊥∠∠BC AC CD AB ABBD BC ABAD AC BDAD CD AB CD R ACB 222＝＝＝＝＝t 5. 三角形内（外）角平分线性质在△ABC 中 ∠1＝∠2ACABDC BD =⇔6. 若ABCD 四点共圆，AB 、CD 交于P ， 则PA ×PB ＝PC ×PD＝PT 2 （PT 切圆于T ）7. 三角形、平行四边形面积公式（略）CD E B A B C DB8.正弦定理：在△ABC 中，SinCcSinB b SinA a == 二．要运用相似三角形证明线段的积、幂，一般应把积、幂先化为比例式，然后由它来找相似三角形。
有时还要用等线段或等比代换。
乙例题例1． 过四边形ABCD 的对角线交点O 画CD 的平行线，分别与边BC ，AD 及AB 的延长线交于E ，F ，G 求证：GO 2=GEGF证明：设DC ，AB 的延长线相交于H ， ∵FG ∥DH ， 从过点B 的线束被平行线截得HD HCGO GE =从过点A 的线束被平行线截得HDHCGF GO = ∴GFGOGO GE = 即GO 2＝GEGF 例2.已知：CD 是Rt △ABC 斜边上的高，角平分线AE 交CD 于F 求证：CE 2＝DF ×BE分析：要CE 2＝DF ×BE 成立，应证DF CECE BE = 可证CE ＝CF （等角对等边）根据角平分线性质可得AC AB CE BE =，ADACDF CF = 只要AC 2＝ABAD 这符合直角三角形中成比例线段定理 证明 （略）例3.已知：△ABC 中最大角A 是最小角C 的2倍，三边长是连续整数 求：△ABC 的各边长解：设AC 为x, 则AB 是x-1,BC 为x+1 延长CA 到D 使AD=AB ，连结BD ，BA 则∠D ＝∠1 ∵∠BAC ＝∠1＋∠D ＝2∠D ， ∵∠BAC ＝2∠C ， ∴∠1＝∠D ＝∠C∴等腰△ABD ∽等腰△BCDCD BD BC AB ＝，1111+++=+-x x x x x ，解得x=5, ∴三边长分别为4,5,6 ( 本题也可作∠BAC 的平分线AE ，证明△EAB ∽△ACB)例4. 已知：⊙O 和⊙O 1相交于P ，外公切线AB ，A ，B 是切点，AP 交⊙OH B于C ，BP 交⊙O 1于D ，CE 和⊙O 1切于点E 求证：CE ＝CB证明：过点P 作两圆公切线PQ 交AB 于Q 由切线长定理，得QP ＝QA ＝QB ∴△APB 是Rt △，∠APB ＝Rt ∠ ∴BC 是⊙O 的直径，BC ⊥AB根据射影定理，得BC 2＝CP ×CA∵CE 切⊙O 1于E ，根据圆幂定理，得CE 2＝CP ×CA∴CE ＝CB例5.正方形OPQR 内接于△ABC ，已知△AOR ，△BOP ，△CRQ 面积是 S 1＝1，S 2＝3，S 3＝1。
关于初中数学竞赛的书籍
关于初中数学竞赛的书籍
初中数学竞赛是许多学生热衷的学科，以下是一些相关的书籍推荐：
1.《初中数学竞赛全解析》——这本书提供了各种数学竞赛题目的详细解析和解题思路，适合准备竞赛的学生查阅。
2. 《初中数学竞赛习题集》——该书汇集了大量经典数学竞赛题目，按照题型和难易程度进行分类，帮助学生巩固知识并提高解题能力。
3. 《初中数学竞赛冲刺指南》——这本书介绍了常见竞赛的出题规律和解题技巧，通过精选的例题和训练题，帮助学生提高应试能力。
4. 《初中数学竞赛辅导教材》——该教材系统地介绍了数学竞赛中常见的知识点和题型，并提供了大量的例题和习题供学生练习。
5. 《初中数学竞赛秘籍》——这本书总结了数学竞赛中常见的解题技巧和方法，通过实例讲解帮助学生理解和掌握。
这些书籍都可以在学校教材供应店或者在线书店购买到。
希望这些书籍能够帮助到对数学竞赛感兴趣的同学们。
初中数学竞赛辅导资料(3)
初中数学比赛指导资料(9)一元一次方程解的议论甲内容大纲1， 方程的解的定义： 能使方程左右两边的值相等的未知数的值叫做方程的解。
一元方程的解也叫做根。
比方：方程 2x ＋ 6＝ 0， x （ x-1） =0,|x|=6, 0x=0,0x=2 的解 分别是：x= － 3,x=0 或 x=1,x= ±6,全部的数，无解。
2， 关于 x 的一元一次方程的解（根）的状况：化为最简方程ax=b 后，议论它的解：当a ≠0 时，有独一的解x= b；a当 a=0 且 b ≠ 0 时，无解；当 a=0 且 b ＝ 0 时，有无数多解。
（∵不论 x 取什么值， 0x ＝ 0 都成立） 3, 求方程 ax=b(a ≠ 0)的整数解、正整数解、正数解当 a ｜ b 时，方程有整数解；当 a ｜ b ，且 a 、 b 同号时，方程有正整数解； 当 a 、 b 同号时，方程的解是正数。
综上所述，议论一元一次方程的解，一般应先化为最简方程 ax=b乙例题例 1 a 取什么值时，方程 a(a －2)x=4(a － 2) ①有独一的解？②无解？③有无数多解？④是正数解？ 解：①当 a ≠ 0 且 a ≠2 时，方程有独一的解，x=4a②当 a=0 时，原方程就是 0x= － 8，无解；③当 a=2 时，原方程就是0x=0 有无数多解④由①可知当 a ≠ 0 且 a ≠2 时，方程的解是x=4,∴只要 a 与 4 同号，a即当 a>0 且 a ≠ 2 时，方程的解是正数。
例 2 k 取什么整数值时，方程① k(x+1)=k － 2（ x －2）的解是整数？②（ 1－ x ） k=6 的解是负整数？ 解：①化为最简方程（k ＋2） x=4当 k+2 能整除 4，即 k+2= ± 1，± 2，± 4 时，方程的解是整数 ∴ k= －1，－ 3，0，－ 4， 2，－ 6 时方程的解是整数。
初中数学竞赛辅导材料目录
初中数学竞赛辅导材料目录一、初中数学竞赛基础知识1.数集及其运算-自然数、整数、有理数、实数、复数的概念及运算性质-数集的表示方法与运算法则2.代数式与方程-一元一次方程与一元一次不等式的解法及应用-一次函数的定义、性质与图像-一元二次方程的解法及应用3.几何基本概念-点、线、面、角的定义与性质-直线、射线、线段、平行线、垂直线的概念与判定-多边形、三角形、四边形的性质4.图形的相似与投影-图形的相似判定条件及相似比的计算-平面图形在对称、旋转、平移、投影中的性质与运用5.数据的整理与表示-数据的收集、整理、描述和分析方法-列联表的制作与应用-分组频数统计图的制作与读图6.立体几何-空间图形的基本概念及性质-空间图形的展开与剖析-空间图形的体积与表面积计算方法二、初中数学竞赛解题技巧与方法1.快速计算技巧-快速计算小技巧的应用（如乘法口诀、整数加减乘除的计算等）-快速计算较大数的方法（如分解因数、整理计算顺序等）2.思维训练与问题解决-近似计算与估算的方法与应用-分析解题条件与利用信息求解问题-数学问题的逻辑和推理方法3.策略与技巧-消元法与代入法的使用-枚举与特例法的应用-逆向思维与反证法的运用4.考试技巧与应试心理-数学竞赛常见题型的解题思路-如何正确阅读题目与审题技巧-考试时间分配与答题顺序规划-心理调适与压力应对方法三、数学竞赛真题及解析1.真题分析与解题方法讲解-分析数学竞赛真题的特点与难点-理解题目要求、辅助线的作法、巧用条件等解题技巧-真题解析与解题思路讲解2.解题思路总结与题型归纳-简述各种常见数学竞赛题型的解题思路-总结解题中常用的技巧与方法-提供大量的练习题目，以加强学生对各类题型的掌握以上为初中数学竞赛辅导材料的目录，通过系统的学习与实践，相信学生们可以提升数学竞赛的能力，取得更好的成绩。
祝学习愉快！。
初中数学竞赛辅导系列
例1 化简分式：
例２ 已知：x+y+z=3a(a≠0，且x，y，z不全相等)，求
15
15
此时, x 105
若a 3,b 7,则100 c 150 ,此时无解
21
21
综上,x 102,104,105,110,114,128,130,135,136,138
余数问题
在整数除法运算中，除了前面说过的“能整除”情形 外，更多的是不能整除的情形.
被除数=除数×商+余数. 通常把这一算式称为带余除式，它使我们容易从“余
例２ 有四个学生，他们的年龄恰好是一个比一个大1岁， 而他们的年龄的乘积是5040，那么，他们的年龄各是多少 ？
解：设他们的年龄分别是x-1, x , x+1 , x+2
(x 1)x(x 1)(x 2) 5040
(x2 x)(x2 x 2) 5040
(x2 x)2 2(x2 x) 5040 0
（4）能被4（或25）整除的数的特征：如果一个整数的末 两位数能被4（或25）整除，那么它必能被4（或25）整除.
（5）能被8（或125）整除的数的特征：如果一个整数的 末三位数能被8（或125）整除，那么它必能被8（或125） 整除.
（6）能被11整除的数的特征：如果一个整数的奇数位数 字之和与偶数位数字之和的差（大减小）能被11整除，那 么它必能被11整除.
质数中只有一个偶数，就是2，其他质数都是奇数.但 是奇数不一定是质数，例如，15，33，….
一个整数的因数中，为质数的因数叫做这个整数的质 因数，例如，2，3，7，都是42的质因数，6，14也是42的 因数，但不是质因数.
初中数学竞赛辅导讲义全
初中数学竞赛辅导讲义（初三）第一讲 分式的运算[知识点击]1、 分部分式：真分式化为另几个真分式的和，一般先将分母分解因式，后用待定系数法进行。
2、 综合除法：多项式除以多项式可类似于是有理数的除法运算，可列竖式来进行。
3、 分式运算：实质就是分式的通分与约分。
[例题选讲]例1．化简2312++x x + 6512++x x + 12712++x x 解：原式= )2)(1(1++x x + )3)(2(1++x x + )4)(3(1++x x = 11+x - 21+x + 21+x - 31+x + 31+x - 41+x =)4)(1(3++x x 例2． 已知 z z y x -+ = y z y x +- = x z y x ++- ，且xyz ≠0，求分式xyz x z z y y x ))()((+-+的值。
解：易知：z y x + = y z x + = x z y + =ｋ 则⎪⎩⎪⎨⎧=+=+=+)3()2()1(kx z y ky z x kz y x （1）+（2）+（3）得：(ｋ-2)(x+y+z)=0 ｋ=2 或 x+y+z=0 若ｋ=2则原式= k 3 = 8 若 ｘ+ｙ+ｚ=0，则原式= k 3 =-1例3．设 12+-mx x x =1，求 12242+-x m x x 的值。
解：显然X 0≠，由已知x mx x 12+- =1 ，则 x +x 1 = ｍ + 1 ∴ 22241x x m x +- = ｘ2 + 21x - ｍ2= (x +x1)2-2 –ｍ2 =( ｍ +1)2-2- ｍ2= 2ｍ -1 ∴原式=121-m 例4．已知多项式3x 3 +ax 2 +3x +1 能被x 2+1整除，求ａ的值。
解：13313232+++++x ax x X ax1- ａ=0 ∴ ａ=1例5：设ｎ为正整数，求证311⨯ + 511⨯ + …… +)12)(12(1+-n n ＜ 21 证：左边=21（1 - 31 + 31 - 51 + …… + 121-n - 121+n ） aaax ax xO x -++++1133223=21（1- 121+n ） ∵n 为正整数，∴121+n ＜ 1 ∴1- 121+n ＜ 1 故左边＜ 21[小结归纳]1、部分分式的通用公式：)(1k x x + = k 1 （x 1 - kx +1） 2、参数法是解决比例问题特别是连比问题时非常有效的方法，其优点在于设连比值为K ，将连等式化为若干个等式，把各字母用同一字母的解析式表示，从而给解题带来方便。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
初中数学竞赛专题选讲
识图
一、内容提要
1.几何学是研究物体形状、大小、位置的学科。
2.几何图形就是点，线，面，体的集合。
点是组成几何图形的基本元素。
《平面几何学》只研究在同一平面内的图形的形状、大小和相互位置。
3.几何里的点、线、面、体实际上是不能脱离物体而单独存在的。
因此单独研究点、线、面、体，要靠正确的想像
点：只表示位置，没有大小，不可再分。
线：只有长短，没有粗细。
线是由无数多点组成的，即“点动成线”。
面：只有长、宽，没有厚薄。
面是由无数多线组成的，“线动成面”。
4.因为任何复杂的图形，都是由若干基本图形组合而成的，所以识别图形的组合关系是学好几何的重要基础。
识别图形包括静止状态的数一数，量一量，比一比，算一算；运动状态中的位置、数量的变化，图形的旋转，摺叠，割补，并合，比较等。
还要注意一般图形和特殊图形的差别。
二、例题
例1.数一数甲图中有几个角（小于平角）？乙图中有几个等腰三角形？丙图中有几全等三角形？丁图中有几对等边三角形？
E
解：甲图中有10个角：∠AOB, ∠AOC,∠BOC,∠BOD,∠COD, ∠COE,∠DOE,∠DOA,∠EOA,∠EOB.如果OA和OC成一直线，则少一个∠AOC，余类推。
乙图中有5个等腰三角形：△ABC，△ABD，△BDC，△BDE，△DEC
丙图中有全等三角形4对：(设AC和DB相交于O)
△AOB≌△COD，△AOD≌△BOC，△ABC≌△CDA，△BCD≌△DAB。
丁图中共有等边三角形48个：
边长1个单位：顶点在上▲的个数有 1＋2＋3＋4＋5＝15
顶点在下▼的个数有 1＋2＋3＋4＝10
边长2个单位：顶点在上▲的个数有 1＋2＋3＋4＝10
顶点在下▼的个数有 1＋2＝3
边长3个单位：顶点在上▲的个数有 1＋2＋3＝6
边长4个单位：顶点在上▲的个数有 1＋2＝3
边长5个单位：顶点在上▲的个数有 1
以上要注意数一数的规律
例2.设平面内有6个点A 1，A 2，A 3，A 4，A 5，A 6，其中任意3个点都不在同
一直线上，如果每两点都连成一条线，那么共有线段几条？如果要使图形不
出现有4个点的两两连线，那么最多可连成几条线段？试画出图形。
（1989年全国初中数学联赛题）
解：从点A 1与其他5点连线有5条，从点A 2与其他4点（A 1除外）连线
有4条，从A 3与其他3点连线有3条（A 1，A 2除外）……以此类推，6个
点两两连线共有线段1＋2＋3＋4＋5＝15（条），或用每点都与其他5点
连线共5×6再除以2（因重复计算）。
要使图形不出现有4个点的两两连线，那么每点只能与其他4个点连线，
共有（6×4）÷2＝12（条）如下图：其中有3对点不连线：A 1A 4，A 2A 5，
A 3A 6
A 3
1 2
例3.如图水平线与铅垂线相交于O ，某甲沿水平线，某乙铅垂线同时匀速
前进，当甲在O 点时，乙离点O 为500米，2分钟后，甲、乙离点O 相
等；又过8分钟，甲、乙再次离点O 相等。
求甲和乙的速度比。
解：如图设甲0，乙0为开始位置，甲1，乙1为前进2分钟后位置，甲2，乙2
乙2
为再前进8分钟的位置。
再设甲，乙的速度分别为每分钟x,y 米，根据题意得
⎩
⎨⎧-=-=500101025002y x y x 甲 O 甲1 甲2
解得12x=8y
乙1 ∴x ∶y=2∶3
乙0 答甲和乙的速度比是2比3。
例4.在三角形内（不在边上）有3个点，连同原三角形三个顶点，共6
个点，以这6个点为顶点，作出所有不重迭的三角形共有几个？
（1989年全国初中数学联赛题）
解：如图△ABC 中一个点D ，与A ，B ，C 各点连结可得3个不重迭的三
角形；再增加1个点E ，这时可连结不重迭的三角形共5个，再增加1个
点F ，又可增加2个不重迭的三角形，共有7个。
一般规律是每增加1个点，可增加不重迭的三角形2个
A A
A
F
D E E
B C D D
B C
三、练习
1. 数一数：甲图中有直角三角形＿＿个，乙图中有等腰直角三角＿＿个，
丙图中有全等三角形＿＿对。
C
甲 乙
2. 平面上有5个点A ，B ，C ，D ，E ，其中A ，B ，C 三点在同一直线上，
那么以这5个点为端点的线段共有＿＿＿条，记作_____＿＿＿＿＿＿
＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿
3. 以O 为端点画6条射线OA ，OB ，OC ，OD ，OE,OF,那么可组成的
角（小于平角）最多是＿＿个，最少是＿＿＿个，试分别画出草图。
4. 在三角形内有n 个点（n 为整数）与原三角形3个顶点共n ＋3个点，
以这些点为顶点可连成不重迭的三角形最多有＿＿＿＿个。
5. 下图中三角形＿＿＿个其中等腰三角形＿＿个，直角三角形＿＿＿个，
全等的等腰三角形＿＿组，每组＿＿个， 全等的直角三角形＿＿＿组，每组＿＿个。
6. 如图长方形ABCD 中，E ，F ，G 分别在边 BC ，CD ，DA 上，以A 为一个顶点，其他两点
在B ，C ，D ，E ，F ，G 中任选，总共可组成的
三角形的个数是＿＿（1987年泉州市初二数学双基赛题）
7. 平面上有6个点A ，B ，C ，D ，E ，F 其中任意3个点都不在同一直
线上，如果不使图形出现有3个点两两连线，那么最多可连接线段几
条？试画出草图.
OC ⊥AB 于O ，OD ⊥OE 于O ，写出图中 相等的角：＿＿＿＿＿＿＿＿＿＿＿＿＿＿ 互余的角：＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿ 互补的角：＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿
C 如图长方形ABC
D 中，AB ＝5，BC ＝4，
AE ＝BF ＝1，CG ＝DH ＝2
F 那么四边形EFGH 的面积是＿＿（平方单
10.如图A ，B ，C ，D 四点在同一直线上，到A ，B ，C ，D 各点距离之和
为最小值的点在什么位置？有几个符合条件的点？距离之和的最小值可
用哪些线段的长度来表示？（1987年全国初中数学联赛题）
A B C D
11.正方形的边长为a ，以四条边长为直径，向形内作4个半圆，求这四个
半圆相交所成的菊花形面积。
12.下列四图，都是由全等正方形组成的图形，其中哪一个能围成正方体？
答：（ ）
(D)
13. 甲，乙两人沿着圆周同时匀速前进，开始他们位于一条直径的两端，相
向而行，第一次相遇时，乙走了100米，第二次相遇时，甲还差60
米走完一圈。
求这个圆的周长。
提示：可设 圆周长为x 米，并引入参数V 甲，V 乙 列方程组解之
14.正方形ABCD 边长为a ，在点A 处有个质点P ， 在点B 处有个质点 Q ， 两个质点同时依反时针方向，沿正方形的边线作匀速的运动，过4秒
钟，P 在C 处追上Q 。
那么 P A
① 再过 ＿＿秒钟， P 在＿处第二次追上Q O
②出发6秒钟时，P，Q这间相距＿＿a Q
C D
15.有长3cm，宽2cm的长方形纸片1991张，将它们按照下图所示的方法，摆在平面上，那么这1991张纸片覆盖的面积是（）
（1991年泉州市初二数学双基赛题）（A）3982 （B）3986 （C）3990 （D）3999
16.一条线段（与圆相交）可把一个圆分成两部分，问四条线段最多可把圆分成＿＿＿＿部分。
（1991年泉州市初二数学双基赛题）
17.把一个矩形分成6个正方形（如图），其中最小的一个面积是1（单位平
方）那么这个矩形的面积是＿＿＿（单位平方）
练习题参考答案
1. 5，8，4
2. 10
3. 15, 12
4. 1+2n
5. 16,8,8 .4,2.2,4
6. 14
7. 9
9. 11
10. 有无数多个点，在线段BC 上（包括端点），和是AD ＋BC
11. （)12-πa 2
12. (A)
13. 480
14. ① 16，C ② 0.5a
15.(B)
16. 11
17. 4。