力距 转动定律 转动惯量共26页文档
合集下载
力矩转动定律转动惯量解析课件

02
CATALOGUE
转动惯量基础概念
转动惯量的定义
转动惯量
描述刚体绕固定轴转动的惯性大 小的物理量。
定义公式
I = Σ(m * r^2),其中m为刚体的 质量,r为刚体上任意质点到转动 轴的距离。
转动惯量的性质
转动惯量只与刚体的质量分布 和转动轴的位置有关,与刚体 的运动状态无关。
对于同一刚体,不同的转动轴 位置,其转动惯量可能不同。
力矩转动定律转动 惯量解析课件
contents
目录
• 力矩转动定律概述 • 转动惯量基础概念 • 力矩与转动惯量的关系 • 转动惯量的计算方法 • 转动惯量的应用实例
01
CATALOGUE
力矩转动定律概述
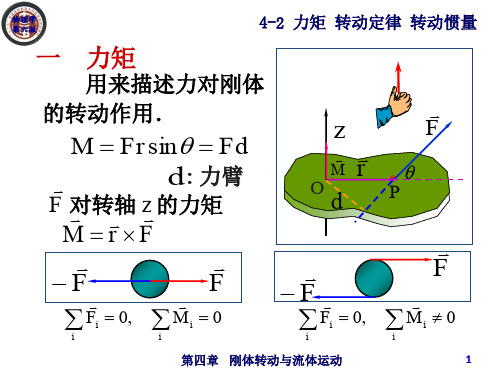
力矩的定义
力矩是描述力的转动效果的物理量,其大小等于力和力臂的乘积。
力矩是一个向量,其大小等于力和力臂的乘积。力臂是从转动轴到力的垂直距离 。在二维平面中,力矩可以表示为M=F×r,其中F是力,r是力臂。
CATALOGUE
转动惯量的应用实例
飞轮的设计与优化
飞轮的设计
飞轮是利用转动惯量储存能量的重要 装置,其设计需要考虑转动惯量的大 小、质量分布、转速等因素。
飞轮的优化
为了提高飞轮的储能效率和稳定性, 需要对飞轮进行优化设计,如采用轻 质高强度的材料、优化飞轮的形状和 尺寸等。
陀螺仪的设计与优化
陀螺仪的设计
陀螺仪是利用角动量守恒原理工作的惯性导 航和姿态测量器件,其设计需要考虑转动轴 的稳定性、转动惯量的大小和分布等因素。
陀螺仪的优化
为了提高陀螺仪的测量精度和稳定性,需要 对陀螺仪进行优化设计,如采用高性能的轴 承材料、减小摩擦力矩等。
电机转子的设计与优化
力矩 刚体绕定轴转动定律-精品文档

力矩 刚体绕定轴转动定律
一、刚体绕定轴转动的力矩
z
F//
F
F对点O转动的力矩:
MO
O
Mz
y
x
r
P
F
F对定轴z转动的力矩:
M r F O r F r F //
M r F z
二、定轴转动定律
M β z J
M J Fr 2 M Fr 39 . 2 [ rad /s ]
mg T ma
Tr J
J
r
O
T
F
mg
(2)
ar
21 . 8 [ rad /s]
2
例: 均匀细直棒m 、l ,可绕轴 O 在竖直平面内转动 初始时它在水平位置 m l O 求: 它由此下摆 角时的
转动惯量与转轴有关
例: 求圆环绕中心轴旋转的转动惯量
2 解: dm 转动惯量 d JR d m
2 J R d m R d m mR 2 2 0 0 L L
dl R o
m
例: 求圆盘绕中心轴旋转的转动惯量 m 2 mr m d S 解: d 2 2πrdr 2 dr πR R dm 转动惯量 d J r2d m
M r d f df 的力矩 d
R
2 d M mgR 圆盘摩擦力矩 M 0 2 1 2d 3 mgR mR
d M
d 3 转动定律 MJ dt 3R0 t 0 3 R t d t d 0 4g g 04
2
d t
例: 一均质棒,长度为 l,现有一水平打 击力F 作用于距轴 l 处。 求: l =? 时, 轴对棒作用力的水平分量为 0。
一、刚体绕定轴转动的力矩
z
F//
F
F对点O转动的力矩:
MO
O
Mz
y
x
r
P
F
F对定轴z转动的力矩:
M r F O r F r F //
M r F z
二、定轴转动定律
M β z J
M J Fr 2 M Fr 39 . 2 [ rad /s ]
mg T ma
Tr J
J
r
O
T
F
mg
(2)
ar
21 . 8 [ rad /s]
2
例: 均匀细直棒m 、l ,可绕轴 O 在竖直平面内转动 初始时它在水平位置 m l O 求: 它由此下摆 角时的
转动惯量与转轴有关
例: 求圆环绕中心轴旋转的转动惯量
2 解: dm 转动惯量 d JR d m
2 J R d m R d m mR 2 2 0 0 L L
dl R o
m
例: 求圆盘绕中心轴旋转的转动惯量 m 2 mr m d S 解: d 2 2πrdr 2 dr πR R dm 转动惯量 d J r2d m
M r d f df 的力矩 d
R
2 d M mgR 圆盘摩擦力矩 M 0 2 1 2d 3 mgR mR
d M
d 3 转动定律 MJ dt 3R0 t 0 3 R t d t d 0 4g g 04
2
d t
例: 一均质棒,长度为 l,现有一水平打 击力F 作用于距轴 l 处。 求: l =? 时, 轴对棒作用力的水平分量为 0。
力矩转动定律转动惯量

J mjrj2 m1r12 m2r22 mjrj2
❖ 质量连续分布
J mjrj2 r2dm dm:质量元 j
4-2 力矩 转动定律
上页 下页 首页 目录
物理学
第五版 刚体对某一转轴的转动惯量等于每个质元的质
量与这一质元到转轴的距离平方的乘积之总和。
质量为线分布 质量为面分布 质量为体分布
可见,转动惯量与l 无关。所以,实心圆柱对其
轴的转动惯量也是mR2/2。
4-2 力矩 转动定律
上页 下页 首页 目录
物第理五版学例2: 求长为L、质量为m的均匀细棒的转动惯量。 (1)转轴通过棒一端并与棒垂直。 (2)转轴通过棒 的中心并与棒垂直;
解:取如图坐标,dm=dx , =m/L
A L
B
J A r2dm
x
L x2dx mL2 / 3 0
AC L/2
B L/2 x
JC r2dm
L
Jc
2 L
x2dx
mL2
/12
2
4-2 力矩 转动定律
上页 下页 首页 目录
物理学
第五版
四、
平行轴定理
质量为 m 的刚体,如
果对其质心轴的转动惯量
为 JC ,则对任一与该轴平
行,相距为 d 的转轴的转
动惯量
JO JC md 2
dt
刚体定轴转动的角加速度与它所受的合外力
矩成正比,与刚体的转动惯量成反比.
讨论:
(1) M 一定,J
α 转动惯量是转动
惯性大小的量度;
(2) 是矢量式(但在定轴转动中力矩只有两个
方向)。
4-2 力矩 转动定律
上页 下页 首页 目录
物理学
❖ 质量连续分布
J mjrj2 r2dm dm:质量元 j
4-2 力矩 转动定律
上页 下页 首页 目录
物理学
第五版 刚体对某一转轴的转动惯量等于每个质元的质
量与这一质元到转轴的距离平方的乘积之总和。
质量为线分布 质量为面分布 质量为体分布
可见,转动惯量与l 无关。所以,实心圆柱对其
轴的转动惯量也是mR2/2。
4-2 力矩 转动定律
上页 下页 首页 目录
物第理五版学例2: 求长为L、质量为m的均匀细棒的转动惯量。 (1)转轴通过棒一端并与棒垂直。 (2)转轴通过棒 的中心并与棒垂直;
解:取如图坐标,dm=dx , =m/L
A L
B
J A r2dm
x
L x2dx mL2 / 3 0
AC L/2
B L/2 x
JC r2dm
L
Jc
2 L
x2dx
mL2
/12
2
4-2 力矩 转动定律
上页 下页 首页 目录
物理学
第五版
四、
平行轴定理
质量为 m 的刚体,如
果对其质心轴的转动惯量
为 JC ,则对任一与该轴平
行,相距为 d 的转轴的转
动惯量
JO JC md 2
dt
刚体定轴转动的角加速度与它所受的合外力
矩成正比,与刚体的转动惯量成反比.
讨论:
(1) M 一定,J
α 转动惯量是转动
惯性大小的量度;
(2) 是矢量式(但在定轴转动中力矩只有两个
方向)。
4-2 力矩 转动定律
上页 下页 首页 目录
物理学
力矩转动定律转动惯量

PB y
31
第32页/共42页
a
mB g
mA mB mC 2
解 得
FT1
mA
mAmB g mB mC
2
FT2
(mA mC 2)mB g mA mB mC 2
A mA
mC 0时: FT1 FT2
32
第33页/共42页
C mC
mB B
FT1
mA
mAmB g mB mC
2
FT2
(mA mC 2)mB g mA mB mC 2
的角加速度和角速度. M J
35
第36页/共42页
36
解: 受力分析,力矩(O)分析
重力对O点的力矩
M mgd
J
d L sin
2
有: 1 mgl sin J
2
m,l
O
θ
FN
mg
d
式中 J 1 ml2 3
得 3g sin
2l
第37页/共42页
由角加速度的定义
dω dω dθ ω dω
F
F
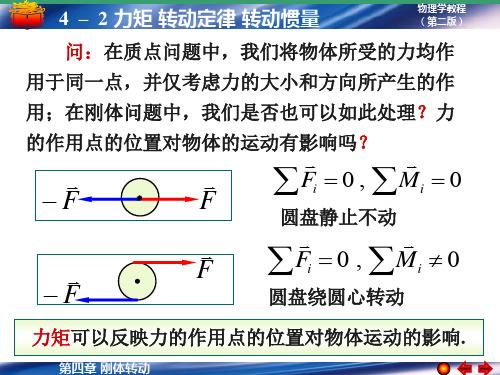
Fi 0 , Mi 0
M rF
M Frsin Fd
3
第4页/共42页
4、一对力偶的力矩
M Fd
F
F
ol
F 0 M 0
F'
ro
F
F 0 M 0
M F l F l Fl
22
M Fr Fr 0
4
第5页/共42页
讨论
(1)若力 F 不在转动平面内,把力分
解为平行和垂直于转轴方向的两个分量
如令 mC 0 ,可得
A mA
FT1
FT2
4-2 力矩 转动定律 转动惯量
19
物理学 第六版
4-2 力矩 转动定律 转动惯量
解 (1) 用隔离法分 别对各物体作受力分析, 取如图所示坐标系.
A
mA
FN
mA FT1
PA
O
x
C
mC
mB B
FT1
FC
PC
FT2
FT2
O
mB
PB y
第四章 刚体转动与流体运动
20
物理学 第六版
4-2 力矩 转动定律 转动惯量
第四章 刚体转动与流体运动
1
物理学 第六版
4-2 力矩 转动定律 转动惯量
讨论
(1)若力
F
不在转动平面内,把力分
解为平行 和垂 直于 转轴方向的两个分量
F
Fz
F
其中 Fz对转 轴的
力矩为零,故 F 对转
轴的力矩 M zk
r
F
z
F
k
O rFz
F
M z rF sin
索跨过一半径为R、质量为mC的圆柱形滑轮 C,并系在另一质量为mB 的物体B上,B 竖 直悬挂.滑轮与绳索间无滑动, 且滑轮与
轴承间的摩擦力可略去不计.(1)两物体的 线加速度为多少? 水平和竖直两段绳索的
张力各为多少?(2) 物体 B 从静止落下距 离 y 时,其速率是多少?
第四章 刚体转动与流体运动
4
物理学 第六版
4-2 力矩 转动定律 转动惯量
解 设水深h,坝长L,在坝面上取面积 元 dA Ldy ,作用在此面积元上的力
dF pdA pLdy
力矩转动惯量定轴转动定律

AB O
h
1 2
l
转动惯量的计算
解: (1)建立图示坐标系,设棒的质量线密度为, 则质元的质量为dm=dx。
A
JO r 2dm
x dx
1 2
l
2
1 2
l
1 l3
12
O x dx x
1 2
l
JO
1 ml 2 12
转动惯量的计算
(2)建立图示坐标系。
J A r 2dm
解: 建立图示坐标系,
R
设圆盘的质量面密度为
,则质元的质量为
dr
r
dm=2rdr。
J r 2dm
0R 2r 3dr
m
R2
R4
2 J
1 mR2 2
转动惯量的计算
例题2 求质量为m、长为l的均匀细棒对下面三种转 轴的转动惯量: (1)转轴通过棒的中心O并和棒垂直; (2)转轴通过棒的一端A并和棒垂直; (3)转轴通过棒上距中心为h的一点B并和棒垂直。
平行轴定理
JB
1 ml 2 12
mh2
JO
1 ml 2 12
JA
1 ml 2 3
JA
JO
m( l )2 2
定理表述:刚体绕平行于质心轴的转轴的转动惯量 J, 等于绕质心轴的转动惯量 JC 加上刚体质量与两轴间
的距离平方的乘积。
表达式: J Jc md 2
§3-2 力矩 转动惯量 定轴转动定律
,平放在粗糙的水平桌面上,盘与桌面间摩擦系数
为。令圆盘最初以角速度0绕通过中心且垂直盘面
的轴旋转,问它经过多少时间才停止转动?
h
1 2
l
转动惯量的计算
解: (1)建立图示坐标系,设棒的质量线密度为, 则质元的质量为dm=dx。
A
JO r 2dm
x dx
1 2
l
2
1 2
l
1 l3
12
O x dx x
1 2
l
JO
1 ml 2 12
转动惯量的计算
(2)建立图示坐标系。
J A r 2dm
解: 建立图示坐标系,
R
设圆盘的质量面密度为
,则质元的质量为
dr
r
dm=2rdr。
J r 2dm
0R 2r 3dr
m
R2
R4
2 J
1 mR2 2
转动惯量的计算
例题2 求质量为m、长为l的均匀细棒对下面三种转 轴的转动惯量: (1)转轴通过棒的中心O并和棒垂直; (2)转轴通过棒的一端A并和棒垂直; (3)转轴通过棒上距中心为h的一点B并和棒垂直。
平行轴定理
JB
1 ml 2 12
mh2
JO
1 ml 2 12
JA
1 ml 2 3
JA
JO
m( l )2 2
定理表述:刚体绕平行于质心轴的转轴的转动惯量 J, 等于绕质心轴的转动惯量 JC 加上刚体质量与两轴间
的距离平方的乘积。
表达式: J Jc md 2
§3-2 力矩 转动惯量 定轴转动定律
,平放在粗糙的水平桌面上,盘与桌面间摩擦系数
为。令圆盘最初以角速度0绕通过中心且垂直盘面
的轴旋转,问它经过多少时间才停止转动?
力矩转动定律转动惯量ppt
物理学教程 (第二版)
* 例4 如图一斜面长 l = 1.5m, 与水平面的夹角 = 5o.
有两个物体分别静止地位于斜面的顶端, 然后由顶端沿
斜面向下滚动, 一个物体是质量 m1 = 0.65kg、半径为R1 的实心圆柱体, 另一物体是质量为 m2 = 0.13 kg 、半径 R2 = R1 = R 的薄壁圆柱筒. 它们分别由斜面顶端滚到斜 面底部各经历多长时间?
直放置的细杆处于非稳定平衡状态,当其受到微小扰
动时,细杆将在重力作用下由静止开始绕铰链O 转动.
试计算细杆转动到与竖直线成 角时的角加速度和角
速度.
解 细杆受重力和
铰链对细杆的约束力
FN
作用,由转动定律得
1 mgl sin J
2
m FN
l2
l oP
第四章 刚体转动
4 – 2 力矩 转动定律 转动惯量
圆盘绕圆心转动
力矩可以反映力的作用点的位置对物体运动的影响.
第四章 刚体转动
4 – 2 力矩 转动定律 转动惯量
物理学教程 (第二版)
一 力矩
刚体绕 O z 轴旋 转 , 力 F 作用在刚体上点 P ,
且在转动平面内,
矢.
r
为由点O 到力的作用点 P 的径 M
F
对转轴Z
的力矩
M rF
M Frsin Fd
例2 有一半径为R质量为 m 匀质圆盘, 以角速度ω0绕
通过圆心垂直圆盘平面的轴转动.若有一个与圆盘大小相
同的粗糙平面(俗称刹车片)挤压此转动圆盘,故而有正压
力N 均匀地作用在盘面上, 从而使其转速逐渐变慢.设正
压力N 和刹车片与圆盘间的摩擦系数均已被实验测出.试
问经过多长时间圆盘才停止转动?
4-2-力矩-转动定律-转动惯量

0
2
第24页,共47页。
而 m π R2
所以 J 1 mR2 2
注意
刚体的转动惯量与以下三个因素有关: (1)与刚体的几何形状有关.
(2)与刚体的体密度 有关.
(3)与转轴的位置有关.
在定轴转动定律中,不论是对M还是对于J, 首先都要明确的是转轴的位置,只有轴确定,
M和J才有意义。
第25页,共47页。
为R=0.100 m,一根不能伸长的轻绳,一端固定在定滑轮
上,另一端系有一质量为m=5.00 kg的物体,如图所示.已
知定滑轮的初角速度 w0=10.0 rad/s,方向垂直纸面向 里.求:
(1) 定滑轮的角加速度的大小和方向; (2) 定滑轮的角速度变化到0时,物体
0
R
上升的高度;
M
(3) 当物体回到原来位置时,定滑轮
PmA AO
FT1
x
FT1
PC
FC FT2
C
mC FT2
mB B
FT2
O
mB
PB y
解 (1)隔离物体分别 对物体A、B 及滑轮作受力 分析,取坐标如图,运用 牛顿第二定律 、转动定律 列方程 .
FT1 mAa
mBg FT2 mBa
RFT2 RFT1 J
a R
第34页,共47页。
y
x
dF y
O
Q
第12页,共47页。
dF [ p0 g(h y)]Ldy
dF对通过点Q的轴的力矩 dM ydF
h
M 0 y[ p0 g(h y)]Ldy
y
1 2
p0 Lh2
1 6
gLh3
h dF O
dy 代入数据,得:
