5.4 Four fundamental subspaces
N(A) R(AT ). Replacing A byAT N(AT ) R(A) .
Review of properties of orthogonal complements
Th2 If S is a subspace of Rn, then dim S + dim S = n. Furthermore, if {x1, ···, xr } is a basis for S and {xr+1, ···, xn} is a basis for S , then {x1, ···, xr , xr+1, ···, xn} is a basis for Rn.
Review of properties of orthogonal complements (continued)
Th3 If S is a subspace of Rn, then Rn = S ⊕S . From Th2
Th4 If S is a subspace of Rn, then (S ) S. From Th3
Four fundamental subspaces
Introduction
Four fundamental subspaces have important applications in many areas.
In this section we define four fundamental subspaces and show fundamental subspaces theorem and their orthogonalities.
Orthogonal decompositions of Euclidean vector spaces
If A is an m × n matrix, we have orthogonal decompositions of Euclidean vector spaces related to four fundamental subspaces.
spaces 4. Example
Definitions of four fundamental subspaces
If A is an m × n matrix, there are four fundamental subspaces:
row space of A in Rn : R(AT ) column space of A in Rm : R(A) null space of A in Rn : N(A) null space of AT in Rm : N(AT )
null space are orthogonal.
Next theorem tells us they are orthogonal complements of each other actually.
Fundamental subspaces theorem
Th1 If A is an m × n matrix, then
How are they related to each other?
Remark. Row space of a matrix and its null space are orthogonal.
R1 A x = 0,
A
R
2
,
Rix = (RiT) T x = 0, i =1, 2, 3.
Example
1 1 2
Ex.
Let
A=
0
1
1
.
1 3 4
Find the bases for N(A), R(AT ), N(AT ), and R(A). Solution.
R3 RiT and x are orthogonal, i =1, 2, 3.
Since any row vector of a matrix and any vector in its
null space are orthogonal, row space of a matrix and its
Proof of fundamental subspaces theorem
We have R(AT ) ⊥N(A). This implies that
N(A) R(AT ) . If x R(AT ) ,
then x is orthogonal to each of the column vectors of AT and, consequently, Ax = 0. Thus, x must be an element of N( A) and hence
Then we give the orthogonal decompositions of Euclidean vector spaces.
And we show an example to find the four fundamental subf four fundamental subspaces 2. Fundamental subspaces theorem 3. Orthogonal decompositions of Euclidean vector
Rn N(A) R(AT ),
By Th3
R(AT ) and N(A) are subspaces of Rn
Rm N(AT ) R(A).
R(A) and N(AT) are subspaces of Rm
How to find four fundamental subspaces? Finding bases
N(A) = R(AT ),
and N(AT) =R(A) .
Remark. Row space of a matrix and its null space are orthogonal complements. Column space of a matrix and the null space of its transpose are orthogonal complements.
四阶微分方程组 英文
四阶微分方程组英文The Four-Dimensional Differential Equation SystemThe study of differential equations has long been a fundamental aspect of mathematics, with applications spanning a wide range of scientific and engineering disciplines. Among the most complex and intriguing forms of these equations are the four-dimensional differential equation systems, which possess a unique set of properties and challenges. In this essay, we will delve into the intricacies of these systems, exploring their mathematical foundations, their applications, and the insights they provide into the natural world.At the core of a four-dimensional differential equation system lies the concept of a system of coupled partial differential equations, where the variables depend on four independent variables, typically representing the three spatial dimensions and time. These systems are often used to model complex physical phenomena that involve the interplay of multiple interrelated processes, such as fluid dynamics, electromagnetic fields, and quantum mechanics.One of the defining characteristics of four-dimensional differentialequation systems is their inherent complexity. The addition of a fourth dimension to the problem domain introduces a level of complexity that is not present in lower-dimensional systems. This complexity manifests itself in the form of increased mathematical rigor, the need for advanced numerical methods, and the challenge of visualizing and interpreting the solutions.Despite the challenges, the study of four-dimensional differential equation systems has yielded numerous insights and advancements in various fields. In the realm of fluid dynamics, for example, these systems are used to model the behavior of fluids in three-dimensional space, taking into account the temporal evolution of the flow. This has led to a deeper understanding of phenomena such as turbulence, vortex formation, and the behavior of fluids in complex geometries.In the field of electromagnetism, four-dimensional differential equation systems are employed to describe the propagation of electromagnetic waves, including the behavior of light, radio waves, and other forms of radiation. These models have been instrumental in the development of advanced communication technologies, as well as in the study of the interactions between electromagnetic fields and matter.Furthermore, in the realm of quantum mechanics, four-dimensionaldifferential equation systems play a crucial role in the description of the behavior of subatomic particles and the evolution of quantum states. The Schrödinger equation, a fundamental equation in quantum mechanics, is a four-dimensional differential equation system that describes the wave function of a particle and its evolution over time.The mathematical complexity of four-dimensional differential equation systems has also led to the development of sophisticated numerical methods and computational tools. These tools enable researchers and engineers to simulate and analyze the behavior of these systems, allowing for the prediction of complex phenomena and the design of innovative technologies.One of the challenges in working with four-dimensional differential equation systems is the difficulty in visualizing and interpreting the solutions. The addition of a fourth dimension makes it challenging to represent the solutions in a way that is intuitive and easily understandable. However, advancements in computer graphics and visualization techniques have helped to overcome this obstacle, allowing researchers to gain deeper insights into the behavior of these systems.Despite the challenges, the study of four-dimensional differential equation systems continues to be an active and vibrant area ofresearch, with applications in a wide range of fields. As our understanding of these systems deepens, we can expect to see further advancements in fields such as fluid dynamics, electromagnetism, and quantum mechanics, leading to new discoveries and technological breakthroughs.In conclusion, the four-dimensional differential equation system is a fascinating and complex area of study that has far-reaching implications for our understanding of the natural world. Its mathematical intricacies, computational challenges, and diverse applications make it a rich and rewarding field of inquiry, with the potential to unlock new insights and drive innovation in a wide range of scientific and engineering disciplines.。
新视野大学英语第四册Unit4课文翻译
新视野大学英语第四册Unit4课文翻译新视野大学英语第四册Unit 4课文翻译新视野大学英语第四册第四单元的课文跟电信网络有关，下面是店铺分享的课文翻译，欢迎大家阅读!新视野大学英语第四册Unit 4课文翻译一个将会大大提高发展中国家生活水准的转变正方兴未艾。
一些不久前还是信息闭塞的地方正在迅速获得最新的通信技术，这将促进他们吸纳国内外投资。
亚洲、拉丁美洲和东欧的许多国家也许需要10年时间来改善其交通、电力供应和其他公用设施。
但是只一根直径小于半毫米的光纤电缆就可以比由铜丝制成的粗电缆承载更多的信息。
由于安装了光纤电缆、数字转换器和最新的无线传输系统，从北京到布达佩斯的一系列城区和工业区正在直接步入信息时代。
一个蛛网般的数字和无线通信网络已经发展到亚洲的大部分地区和东欧的部分地区。
所有这些发展中地区都把先进的通信技术看作一种跨越经济发展诸阶段的途径。
例如，信息技术的广泛应用有望缩短劳动密集型的组装工业转向涉及工程、营销和设计的那些产业所需的时间。
现代通信技术“将使中国、越南这样的国家比那些困于旧技术的国家拥有巨大的优势”。
这些国家应以多快的速度向前发展是人们争论的一个问题。
许多专家认为，越南在目前急需电话的情况下，却要求所有的移动电话都必须是昂贵的数字型电话，这种做法太超前了。
一位专家说：“这些国家缺乏成本估算和选择技术的经验。
”然而毋庸争辩，通信技术将是区分输赢的关键因素。
看一看俄罗斯的情况吧。
由于其坚实的数学和科学教育基础，它应该在信息时代有繁荣的发展。
问题是，它的国内电话系统是一堆生锈的20世纪30年代的老古董。
为了解决这一问题，俄罗斯已经开始铺设光纤电缆，并制定了投入400亿美元建设多项通信工程的战略计划。
但是由于其经济陷于低迷，几乎没有资金来着手解决最基本的问题。
与俄罗斯相比，在未来10年中，中国大陆计划对通信设备投入1,000亿美元。
从某种意义上说，中国的落后成了一种有利因素，因为这一发展正好发生在新技术比铜线电缆系统更便宜的时候。
2024高考英语二轮备考策略
Researches on NEMT
Characteristics of NEMT
3 text themes: Human and nature, Human and society, Human and himself.
19 texts: 10 listening texts, 5 reading texts, 2 filling-task texts, and 2 writing texts.
1 testing rationale.
One core: the assessment system, based on "cultivate youngsters' moral, find out the talents and lead teaching and learning", answering "why to test in this way".
2 Design essential vocabulary tests not only before the beginning of a unit but also the end of a book.
For vocabulary
3 Design various dictation forms to help student remember necessary words and phrases. 4 Make best of our textbooks.
2
3
代词
1 0 1
冠词
1 1 1
无提示词
介词
从属 连词
1
0
0
2
0
1
并列 连词
1 1 1
线性代数-常用单词词组-中英对照
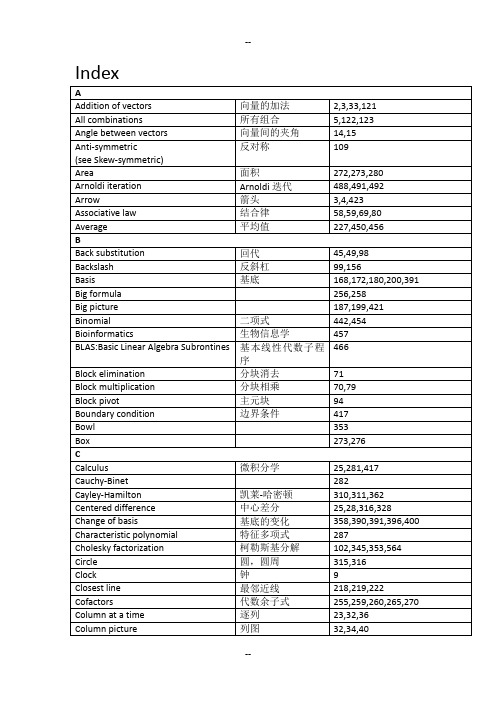
Dual problem对偶问题442,446EEconomics 经济学435,439Eigencourse 457,458Eigenvalue 特征值283,287,374,499 Eigenvalue changes 特征值变换439284,294,300 Eigenvalues of 的特征值297Eigenvalues of 的特征值362Eigenvalues of 的特征值Eigenvector basis 基底的特征向量399Eigenvectors 特征向量283,287,374Eigshow 290,368Elimination 消元法45-66,83,86,135Ellipse 椭圆290,346,366,382Energy 能量343,409Engineering 工程409,419Error 误差211,218,219,225,481,483 Error equation 误差方程477Euler angles 欧拉角474Euler’s formula 欧拉公式311,426,430,497Even 偶数113,246,258,452 Exponential 指数的314,319,327FFactorization 因式分解95,110,235,348,370,374 False proof 假证明305,338Fast Fourier Transform 快速傅立叶变换393,493,511,565Feasible set 可行集440,441FFT(see Fast见快速傅里叶变换509-514Fourier Transform)Fibonacci 菲波那契75,266,268,301,302,306,308 Finite difference 有限差分315-317,417Finite elements 有限元412,419First-order system 一阶方程组315,326Fixed-free 固定-自由410,414,417,419Force balance 平衡力412FORTRAN 16,38Forward difference 前向差分30Four Fundamental Subspaces 四个基本子空间184-199,368,424,507 Fourier series 傅立叶序列233,448,450,452Fourier Transform 傅立叶变换393,509-514Fredholm Alternative 弗雷德霍姆择一203Free 自由133,135,137,144,146,155 Full column rank 列满秩157,170,405Full row rank 行满秩159,405Function space 函数空间121,448,449 Fundamental Theorem of Linear线性代数基本定理188,198,368Algebra(see Four Fundamental Subspaces)GGaussian elimination 高斯消元法45,49,135Gaussian probability distribution 高斯概率分布455Gauss-Jordan 高斯-约当83,84,91,469Gauss-Seidel 高斯-塞德尔481,484,485,489Gene expression data 基因表达数据457Geometric series 等比数列436Gershgorin circles 格尔什戈林圆491Gibbs phenomenon 吉布斯效应451Givens rotation 吉文斯旋转471Google 谷歌368,369,434Gram-Schmidt 格拉姆-施密特223,234,236,241,370,469 Graph 图表74,143,307,311,420,422,423 Group 群119,354HHalf-plane 半平面7Heat equation 热方程式322,323Heisenberg 海森堡305,310Hilbert space 希尔伯特空间447,449Hook e’s Law 虎克定律410,412Householder reflections 镜像变换237,469,472Hyperplane 超平面30,42IIll-conditioned matrix 病态矩阵371,473,474Imaginary 虚数289Independent 独立的26,27,134,168,200,300 Initial value 初值313Inner product 内积11,56,108,448,502,506 Input and output basis 基底输入输出399Integral 积分24,385,386Interior point method 内点法445Intersection of spaces 交空间129,183Inverse matrix 逆矩阵24,81,27082Inverse of的逆Invertible 可逆的86,173,200,248Iteration 迭代481,482,484,489,492JJacobi 雅可比481,483,485,489Jordan form 约当型356,357,358,361,482 JPEG 364,373KKalman filter 卡尔曼滤波器93,214Kernel 核377,380Kirchhoff’s Laws 基尔霍夫定律143,189,420,424-427 Krylov 克雷洛夫491,492L225,480norm 和范数Lagrange multiplier 拉格朗日乘子445Lanczos method 兰索斯方法490,492LAPACK 线性代数软件包98,237,486Leapfrog method 跳步法317,329Least squares 最小平方218,219,236,405,408,453184,186,192,425Left nullspace左零空间Left-inverse 左逆的81,86,154,405Length 长度12,232,447,448,501Line 线34,40,221,474Line of springs 线弹簧411Linear combination 线性组合1,3Linear equation 线性方程23Linear programming 线性规划440Linear transformation 线性变换44,375-398Linearity 线性关系44,245,246Linearly independent 线性独立26,134,168,169,200 LINPACK 线性系统软件包465Loop 环路307,425,426Lower triangular 下三角9598,100,474Lucas numbers 卢卡斯数306MMaple 38,100Mathematica 38,100MATLAB 17,37,237,243,290,337,513 Matrix(see full page 570) 矩阵22,384,387Matrix exponential 矩阵指数314,319,327Matrix multiplication 矩阵乘法58,59,67,389----。
新视野大学英语读写教程第4册(第三版)课后段落翻译
第一单元一、英译汉亚里士多德是古希腊的哲学家和科学家。
他的作品涵盖了许多学科，包括物理学、生物学、动物学、逻辑学、伦理学、诗歌、戏剧、音乐、语言学、政治和政府，构成了第一个综合的西方哲学体系。
亚里士多德是第一个将人类的知识领域划分为不同学科的人，如数学，生物学和伦理学。
他相信人所有的观念和所有的知识在根本上都是基于感知能力。
他对自然科学的看法构成了他许多作品的基础。
他几乎对他所处时期的每一个人类知识领域都作出了贡献。
他的作品包含了人们所知的最早的关于逻辑的正式研究，即使在今天，亚里士多德哲学所涵盖的方方面面仍是学术研究的重要课题。
他的哲学对所有的西方哲学理论的发展有着经久不衰的影响。
在去世2,300多年后，亚里士多德仍是最有影响力的哲学家和科学家之一。
二、汉译英The Doctrine of the Mean is the core of Confucianism. The so-called "mean" by Confucius doesn't mean "compromise" but a "moderate" and "just-right" way when understanding and handling objective things. Confucius advocated that this thought should not only be treated as a way to understand and deal with things but also be integrated into one's daily conduct to make it a virtue through self-cultivation and training. The Doctrine of the Mean is not only the core of Confucianism but also an important component of traditional Chinese culture. From the time it came into being to the present, it has played an invaluable role in the construction of national spirit, the transmission of national wisdom, and the development of national culture.第二单元二、英译汉人们普遍认为，威廉•莎士比亚是最伟大的英语作家和世界杰出的戏剧家。
2025版高考英语一轮复习Unit4Cyberspace讲义北师大版必修2
⑨hard disk硬盘
子话题2 计算机编程
①account lockout账号封锁②adapter适配器
③alias小应用程序④domain controller域名限制器
⑤attack攻击⑥back end后端
⑦decipher破译⑧cipher密码
⑨database数据库
9．suggestionn．建议，提议→suggestvt.建议，提议
10．terroristn．恐怖分子→terrorismn．恐怖主义→terrorn．恐怖→terrifyvt.使恐怖；使惊吓→terrifyingadj.令人恐怖的→terrifiedadj.感到恐怖的
纵联1.以“ ical”结尾的形容词一览
[练通]
单句语法填空
①You'd better focus your attentionon/uponyour studies.
②The key question isin_focus; why not reach a decision?
③Instead of focusingon_your wounded feelings, learn to look for the love, beauty and kindness around you.
5．arrangementn．支配→arrangevt.支配
6．settlevi.定居vt.解决，使定居→settlementn．解决；定居地
7．attractiveadj.吸引人的，有魅力的→attractionn．吸引力；具有吸引力的事物或人→attractvt.吸引
8．entertainmentn．消遣；款待→entertainv．消遣；款待→entertainingadj.使开心的；好玩的
斯坦福 数学基础54集中英译
斯坦福大学开设的数学基础54集（Math 54）是一门专门为工程师和自然科学领域的学生设计的数学课程。
它不仅涵盖了微积分和线性代数等基础数学知识，还涉及了部分常微分方程和离散数学的内容。
而且，Math 54 注重理论与实践的结合，旨在培养学生解决实际问题的数学能力。
1. Math 54 的课程设置Math 54 为期一学期，主要包括以下几个部分的内容：微积分部分：介绍微积分的基本概念和技巧，包括导数、积分、微分方程等内容。
线性代数部分：介绍向量空间、矩阵、线性变换、特征值与特征向量等内容。
常微分方程部分：概述一阶和高阶微分方程的解法，包括分离变量法、特征方程法、变参数法等。
离散数学部分：介绍命题逻辑、集合论、图论等内容。
其课程设置合理，内容丰富，有助于学生全面掌握数学基础知识。
2. Math 54 的教学模式Math 54 采用了大学数学教学中常见的讲授和讨论相结合的教学模式。
教师在课堂上对数学知识进行讲解，并通过例题训练学生的解题能力。
课程还设置了小组讨论与作业等环节，学生通过交流与合作，提高解决数学问题的能力。
3. Math 54 的教学目标Math 54 旨在培养学生的数学思维和解决实际问题的能力。
通过学习此课程，学生将能够掌握微积分、线性代数、常微分方程和离散数学的基本理论和方法，并能够运用这些知识解决工程和自然科学领域的实际问题。
4. Math 54 的师资力量Math 54 的教师团队由斯坦福大学数学系的教授和讲师组成。
这些教师在数学领域拥有丰富的教学经验和深厚的学术造诣，能够为学生提供优质的数学教育。
斯坦福大学数学基础54集（Math 54）作为一门为工程师和自然科学领域的学生设计的数学课程，以其丰富的内容、合理的设置、高水平的教学与师资力量，为学生提供了扎实的数学学习基础，有助于他们在工程和科学领域取得成功。
Math 54作为一门为工程师和自然科学领域的学生设计的数学课程，一直以来都备受青睐。
2021版高考英语一轮复习Unit4Astronomythescienceofthestars词汇训
2021版高考英语一轮复习Unit4Astronomythescienceofthestars词汇训练新人教版必修3基础知识默写篇一、分层单词写作词汇1. prep.与……不同;不像2. adv. 因此,因此3. adj.温顺的;文雅的4. n.气候阅读词汇1.astronomy n.2.system n.3.globe n.4.atmosphere n.5.fundamental adj.6.chain n.7.multiply vt.& vi.8.gravity n.9.satellite n.10.physicist n.11.crash vi.&vt.12.spaceship n.13.pull n.&vt.14.float vi.&vt.& n.15.oxygen n.拓展词汇1. adj.猛烈的;猛烈的;强暴的→ n.暴力→adv. 暴力地;猛烈地2. adj.有害的→ n.& v.损害→adj.无害的3. vi.存在;生存→n.存在;生存4. vi.&vt.(使)困惑;(使)为难 n.谜;难题→adj.困惑不解的→adj.令人困惑的5. n.生物学→ n.生物学家二、高频短语1. 及时;终于2. 熟悉;把握;明白得3. 产生;分娩4. 轮到某人5. 阻止;禁止6. 感到快乐;感到振奋7. 既然8. 突发;爆发9. 紧密注意;当心;提防10. 挡住(光线)三、经典句型1.This produced a chain reaction,which (使生命的进展成为可能).2. (专门多科学家所相信的是)the continued presence of water allowed the earth to dissolve harmful gases and acids into the oceans and seas.st month I (我足够有幸有机会)to make a trip into space with my friend Li Yanping, an astronomer.4.When we get closer to the moon,we shall feel its gravity pulling us,but it will(不像地球的引力那么大).5.But when I tried to step forward,I found I was carried (地球上的两倍远)and fell over.6....walking does need a bit of practice (既然重力改变了).基础知识运用篇一、语境词汇运用(一)词汇拼写(注意单词或短语的形式变化)1.Worse still, being addicted to cellphones might also lead to teena gers’ poor performance at school, (因此)adding to their elders’ worries.2.The final of the match was going on in an exciting (气氛) and won hearty applause at times.3.She (拉;拖) him gently towards her just now.4.Some (差不多的) mistakes are not allowed to make when you are doing the work.5.As we know, the earth is becoming warmer and warmer due to the global (气候)change.6. (不像) most people in the office who come to work by car, I usually come to work by bus.7.When the Chinese women volleyball team turned up, all the fans (感到振奋).8.Please tell me when Mr. Smith is arriving at the train station so that I can pick him up (及时).9.Once he has made up his mind, no one can him (阻止)carrying out the pla n.10.At last the firefighters put out the fire in the supermarket, which (突发;爆发)at ten this morning.11.You’ve made me suffer in the past, so now you, (轮到你), suffer again!12.She married at 17 and (分娩)her first child shortly after.13.She bought a heavy curtain to (挡住)the light.(二)单句填空1.He often says that he doesn’t believe in any (religious) and only believes in himself.2.The factory gives off gases. They may do to our health.(harm)3.Do you believe the of ghosts? Perhaps they only in the minds of some people.(exist)4.The look on her face suggested she was about the math problem.(puzzle)5.The robbers hit them . They couldn’t bear it any more so they decided to answer with and began their fightback. (violent)二、经典句型仿写1.了解唐朝的历史会使你更容易明白得唐诗。
线性代数 英文讲义
Example The set {(1, 1, 1)T, (2, 1, -3)T, (4, -5, 1)T} is an
orthogonal set in R3.
Theorem 5.5.1 If { v1, v2, …, vn} is an orthogonal set of
nonzero vectors in an inner product space V, then v1, v2, …,vn are linearly independent.
Example Let X be the subspace of R3 spanned by e1, and
let Y be the subspace spanned by e2.
Example Let X be the subspace of R3 spanned by e1 and e2,
and let Y be the subspace spanned by e3.
Corollary 5.1.2 ( Cauchy-Schwarz Inequality)
If x and y are vectors in either R2 or R3 , then (2) xTy≤‖x‖‖y‖
with equality holding if and only if one of the vectors is 0 or one vector is a multiple of the other.
Corollary 5.5.3 Let { u1, u2, …, un} be an orthonoemal basis
α=
u， v v
and the vector projection of u onto v is given by
(完整word版)线性代数课程专业词汇表
线性代数课程专业词汇表英文单词或词组中文翻译书中出现页码Linear equation 线性方程 1Linear system(s) 线性方程组 1Consistent 有解 2Inconsistent 无解 2Solution set of linear system 线性方程组的解集合 2Equivalent systems 等价的线性方程组 3Row operations 行变换 5Strict triangular form 严格三角形式 5Back substitution 回代法 6Equivalent systems 等价的线性方程组 6Coefficient matrix 系数矩阵 7Coefficient matrix 系数矩阵 7Augmented matrix 增广矩阵 8Pivot 主元 8Free variables 自由未知量 14Lead variables 前变量 14Gaussian elimination 高斯消元法 15Overdetermined linear system 方程个数超过未知数个数的方程组 15 Row echelon form 行阶梯形 15Underdetermined linear system 方程个数低于未知数个数的方程组 17 Gauss-Jordan reduction 高斯-若当归纳法 18Reduced row echelon form 减少的行阶梯形 18Homogeneous linear system 齐次线性方程组 22Homogeneous system 齐次线性方程组 22nontrivial solution 非零解 22Trivial solution 平凡解，全零解 22Matrix algebra 矩阵代数 30Scalars 常数 30Column vector(s) 列向量 31Euclidean n-space 欧几里得空间 31Row vector(s) 行向量 31Vector(s）向量 31Addition of matrices 矩阵加法 32Addition of matrices 矩阵加法 32Equality of matrices 矩阵相等 32Scalar multiplication for matrices 矩阵的数乘 32Scalar multiplication of matrices 矩阵的数乘 32Zero matrix 零矩阵 33Scalar product 内积 34Linear combination 线性组合 36Consistency Theorem 解的存在性定理 37Multiplication of matrices 矩阵乘法 38Identity matrix 单位矩阵 47Inverse matrix 逆矩阵 48Invertible matrix 可逆矩阵 48Nonsingular matrix 非奇异矩阵 48Singular matrix 奇异矩阵 49Transpose of a matrix 矩阵的转置 49Transpose of matrix 矩阵的转置 49Symmetric matrix 对称矩阵 51Symmetric matrix 对称矩阵 51Adjacency matrix 邻接矩阵 52Graph(s) 图 52Angle between vectors 向量的夹角 56Markov chain(s） Markov链 57Elementary matrix 初等矩阵 62Row equivalent 行等价 64Row equivalent matrices 行等价矩阵 64Diagonal matrix 对角矩阵 67Lower triangular 下三角 67Triangular factorization 三角分解 67Triangular matrix 三角形矩阵 67Triangular matrix 三角形矩阵 67Upper triangular 上三角 67Upper triangular matrix 上三角矩阵 67LU factorization LU分解 68Matrix factorizations 矩阵分解 68Partitioned matrices 分块矩阵 72Vandermonde matrix 范德蒙矩阵 72Block multiplication 分块乘法 74Inner product 内积 78Determinant(s) 行列式 90Cofactor 代数余子式 93Minor 余子式 93Cofactor expansion 代数余子式展开 94Determinant of matrix 矩阵的行列式 95Skew symmetric 反对称 105Adjoint of a matrix 伴随矩阵 106Cramer’s rule 克莱姆法则 107Cryptography 密码学 108Addition of vectors 向量的加法 119Closure properties 封闭性 119Vector space 向量空间 119Zero vector 零向量 119C[a,b] 区间[a,b]上的连续函数 120Isomorphism between vector spaces 向量空间的同构 123Subspace(s) 子空间 123Zero subsapce 零空间 125Nullspace 零化空间 127Nullspace of matrix 矩阵的零化空间 127Span 张成 128Spanning set 生成集 129Linearly dependent 线性相关 136Linearly independent 线性无关 136Basis 基 145Dimension 维数 147Finite dimensional 有限维 147Infinite dimensional 无限维 147Standard basis 标准基 150change of basis 基的变换 151Coordinate vector 坐标向量 152Transition matrix 过渡矩阵 155Coordinates 坐标 157Column space 列空间 162Column space of matrix 矩阵的列空间 162Rank of a matrix 矩阵的秩 162Rank of matrix 矩阵的秩 162Row space 行空间 162Row space of matrix 矩阵的行空间 162Nullity 零化度 164Rank-Nullity Theorem Rank-Nullity定理 164Left inverse 左可逆 170Right inverse 右逆 170Full rank 满秩 171Linear transformation(s) 线性变换 175Linear operator 线性算子 176Image 象 181Kernel 核 181Contraction 收缩 192Dilation 扩张 192Similarity 相似性 199Similar matrices 相似矩阵 202Trace 迹 206Angle between vectors 向量的夹角 211Euclidean length 欧几里得长度 211Distance in 2-space 2维空间的距离 212Cauchy-Schwarz inequality 柯西-施瓦兹不等式 213 Orthogonality 正交性 213Scalar projection 数量投影 214equation of plane 平面方程 215Nonmal vector 正规向量 215Angle between vectors 向量的夹角 216Pythagorean Law Pythagorean 定理 216Correlations 相关 219Correlation matrix 相关矩阵 221Covariance 协方差 222Covariance matrix 协方差矩阵 222Factor analysis 因子分析 222Fundamental subspaces 基本子空间 227Range of a matrix 矩阵的值域 227Direct sum 直和 229Least squares problem(s) 最小二乘法问题 234Projection onto column space 列空间上的投射 236Normal equations 正规方程 237Inner product space 内积空间 245Length in inner product spaces 内积空间中的长度 246 Orthogonal set(s) 正交集合 255Orthonormal set(s) 标准正交集 255orthonormal basis 标准正交基 256Orthonormal basis 标准正交基 256Orthogonal matrices 正交矩阵 258Orthogonal matrix 正交矩阵 258Approximation of functions 函数的逼近 264Fourier coefficients 傅里叶系数 266Fourier matrix 傅里叶矩阵 269Gram-Schmidt process Gram-Schmidt过程 274Dimension Theorem 维数定理 283Orthogonal polynomials 正交多项式 283Hermite polynomials Hermite 多项式 287Jacobi polynomials Jacobi多项式 287Lagrange’s interpolating formula Lagrange 插值公式 288 Gaussian quadrature 高斯求积 289Characteristic value(s) 特征值 301Characteristic vector 特征向量 301Eigenvalue 特征值 301Eigenvector 特征向量 301Characteristic equation 特征方程 302Characteristic polynomial 特征多项式 302Eigenspace 特征空间 302Nilpotent 幂零的 311Companion matrix 友矩阵 313Linear differential equations 线性微分方程 313Initial value problems 初值问题 314Diagonalizable matrix 可对角化的矩阵 326Distance in n-space n维空间的距离 332Complex matrix 复矩阵 346Hermite matrix Hermite 矩阵 346Unitary matrix 酉矩阵 347Unitary matrix 酉矩阵 347Normal matrices 正规矩阵 351Singular values 奇异值 356Conic sections 二次曲线部分 371Quadratic equation in n variables n个变量的二次方程 376 Quadratic form in n variables n个变量的二次型 376 Definite quadratic form 定二次型 378Indefinite quadratic form 不定二次型 378Negative definite matrix 负定矩阵 378Negative definite quadratic form 负定二次型 378 Negative semidefinite matrix 半负定矩阵 378Negative semidefinite quadratic form 半负定二次型 378 Positive definite matrix 正定矩阵 378Positive definite quadratic form 正定二次型 378Positive semidefinite matrix 半正定矩阵 378Positive semidefinite quadratic form 半正定二次型 378 Local maximum 极大值 382Local minimum 极小值 382Positive definite matrix 正定矩阵 384Leading principal submatrix 顺序主子矩阵 385 Nonnegative matrix 非负矩阵 392Nonnegative vector 非负向量 392Positive matrix 正矩阵 392Positive matrix 正矩阵 392Reducible matrix 可约矩阵 394Frobenius theorem Frobenius 定理 395Absolute error 绝对误差 411Relative error 相对误差 411Back substitution 回代法 419QR factorization QR分解 448。