Ch2轴向拉压4-5节-2003
合集下载
轴向拉压.ppt

x1
Pb
Aa b
由b
+ve
-ve
压
(b) 图2-49
x2
Pa
Aa b
u
ab P
AEa b
材料力学, 土木2003, 2004年9月, 金培鹏副教授
第二章 轴向拉伸和压缩
Pa
a b
Pa
a b
青海大学建工系
当 A
E=70 GPa, A=100 mm2 时
LMax
y,Max g
3.6 km
v
g
2E
L2Max
2.6 m
横向收缩是多少?
如杆为直径为D的圆截面杆, 则有:
x
dD D
y
g y
E
dDMax
gD L
E
材料力学, 土木2003, 2004年9月, 金培鹏副教授
第二章 轴向拉伸和压缩
竖直悬挂的重力杆. 若杆的最大正应力为 Max, 杆的最大长度是多少,
LMax, 杆的伸长是多少?
RA
y
y
A
L, A, , E,
x
g
Fyy(y)
FBD:
y
B v
Fy 0
Fyy m g
Fyy Ay g Fyy Ag y y g y
图2-33
青海大学建工系
2.7.1 直接分析法
要解静定问题, 需要更多方程 力的平衡方程 变形协调条件 虎克定律
e.g. y
RAx
x
E, A
第二章轴向拉伸和压缩精品文档25页

脱离体(图b、c)。根据平衡条件可求得:
F
F
F
F a
G1 3m F
a
G2
3m
b
b
240 370 (a)
G1
G1
F
F
FN a a-a (b)
例题2−3图
G2
FN b b-b (c)
截面a−a:
F y 0 , F N a F G 1 1 2 . 5 0 1 . 5 k 2 N
截面b−b:
杆和AC杆的应力分别为
3m
FNAB
A
σAB F A N A AB B 3 4.8 0 8 1 1 0 3 0 60 16 1360 P a16 M 3PaC
FNAC
σAC F A N A AC C 18 .7 2 .3 1 11 4 0 30 6 4 16P 0 a 6M 4 Pa
4m
σαpαcoα sσco2αs
ταpαsiα n1 2σsi2 nα 正应力的最大值发生在α = 0的截面,即横截面上,其值为
σα0 σmaxσ
当 α π 时对应的斜截面上,切应力取得最大值
4
ταπ 4
τmax
σ 2
§2−5 拉压杆的变形、胡克定律
拉压杆的变形
F
d1 d
F
F
d1
d
F
l
l
l1
l1
§2−1 轴向拉伸和压缩的概念
轴向拉压变形的受力及变形特点: F
F
杆件受一对方向相反、作用线与
杆件的轴线重合的外力作用。杆 F
F
件发生轴线方向的伸长或缩短。
§ 2−2 轴力与轴力图
横截面上的内力——轴
按截力面法求解步骤:
第一讲-轴向拉压

专题一 杆件的轴向拉伸与压缩
构件正常工作的要求
a.强度
抵抗破坏的能力
b.刚度
抵抗变形的能力
c.稳定性 保持原有稳定状态的能力
杆件变形的基本形式
a.轴向拉压 b.剪切 c.扭转 d.弯曲
杆件轴线弯成曲线 杆件长度方向的改变 相邻横截面绕轴线发生相对转动 横截面沿外力方向发生相对错动
轴向拉伸压缩杆件的内力和应力
轴力正负号规定 拉力为正( + ) 压力为负( - )
截面法求内力过程 (1) 求哪个截面内力,在哪儿截开 (2) 留下一部分,弃去部分对留下部分的作用效果代之以内力 (3) 对留下部分建立平பைடு நூலகம்方程
拉压杆斜截面的应力
拉压杆的变形
轴向拉压杆的变形能
V
1 2
FNl
l FNl
→
V
FN2l 2EA
EA
应变能密度
v
V V
1 Fl 2
Al
1
2
适用于拉压杆
构件正常工作的要求
a.强度
抵抗破坏的能力
b.刚度
抵抗变形的能力
c.稳定性 保持原有稳定状态的能力
杆件变形的基本形式
a.轴向拉压 b.剪切 c.扭转 d.弯曲
杆件轴线弯成曲线 杆件长度方向的改变 相邻横截面绕轴线发生相对转动 横截面沿外力方向发生相对错动
轴向拉伸压缩杆件的内力和应力
轴力正负号规定 拉力为正( + ) 压力为负( - )
截面法求内力过程 (1) 求哪个截面内力,在哪儿截开 (2) 留下一部分,弃去部分对留下部分的作用效果代之以内力 (3) 对留下部分建立平பைடு நூலகம்方程
拉压杆斜截面的应力
拉压杆的变形
轴向拉压杆的变形能
V
1 2
FNl
l FNl
→
V
FN2l 2EA
EA
应变能密度
v
V V
1 Fl 2
Al
1
2
适用于拉压杆
轴向拉压

F
D 2
4
p 8.84 kN
N 4F 6 2 34.7 10 Pa A d
强度足够
应用2:设计截面尺寸
N
A
P35例2-3 起重链条,承受的轴向最大拉力 F=15kN,许用应力 [ ] 40 MPa ,试 确定圆钢的直径d
应用3:确定许可载荷
(MPa)
400
低碳钢压缩 应力应变曲线
E(b)
C(s上) (e) B 200 D(s下) A(p)
f1(f)
低碳钢拉伸 应力应变曲线
g
Ey= E=tg tg O O1 O2 0.1 0.2
2 灰铸铁拉压时的力学性能
by
灰铸铁的 压缩曲线
bL
灰铸铁的 拉伸曲线
= 45o~55o
强度 刚度 稳定性 材料抵抗塑性变形和断裂的能力 材料抵抗弹性变形的能力 构件保持其原有平衡形态能力
3.
构件受力的情况 载荷:机构或者机械工作时,作用在构件上的力
集中载荷 通过极小的面积(构件本身相比)传递给构 件的压力称为集中载荷 均匀分布载荷 分布载荷 均匀分布作用于构件某段长度或者面积上的外力 线性载荷 不均匀分布载荷
一等截面直杆,受轴向内力P1、 P2、P3的作用,已知 P1=8kN,P2=10kN,P3=6kN , 试求AB、BC、CD各段上轴力。 N1
解:N1=P1=8KN N2=P1-P2=-2KN N3=P1+P2-P3=4KN
N2 N3
应 力
内力的大小是否直接决定了构件被破坏? 比较两材料相同而粗细不同拉杆, 在相同拉力作用下,当拉力增大时 的,试想那根杆先被拉断? 单位面积上承受的内力称为应力 其单位是兆帕(MPa),N/mm2
D 2
4
p 8.84 kN
N 4F 6 2 34.7 10 Pa A d
强度足够
应用2:设计截面尺寸
N
A
P35例2-3 起重链条,承受的轴向最大拉力 F=15kN,许用应力 [ ] 40 MPa ,试 确定圆钢的直径d
应用3:确定许可载荷
(MPa)
400
低碳钢压缩 应力应变曲线
E(b)
C(s上) (e) B 200 D(s下) A(p)
f1(f)
低碳钢拉伸 应力应变曲线
g
Ey= E=tg tg O O1 O2 0.1 0.2
2 灰铸铁拉压时的力学性能
by
灰铸铁的 压缩曲线
bL
灰铸铁的 拉伸曲线
= 45o~55o
强度 刚度 稳定性 材料抵抗塑性变形和断裂的能力 材料抵抗弹性变形的能力 构件保持其原有平衡形态能力
3.
构件受力的情况 载荷:机构或者机械工作时,作用在构件上的力
集中载荷 通过极小的面积(构件本身相比)传递给构 件的压力称为集中载荷 均匀分布载荷 分布载荷 均匀分布作用于构件某段长度或者面积上的外力 线性载荷 不均匀分布载荷
一等截面直杆,受轴向内力P1、 P2、P3的作用,已知 P1=8kN,P2=10kN,P3=6kN , 试求AB、BC、CD各段上轴力。 N1
解:N1=P1=8KN N2=P1-P2=-2KN N3=P1+P2-P3=4KN
N2 N3
应 力
内力的大小是否直接决定了构件被破坏? 比较两材料相同而粗细不同拉杆, 在相同拉力作用下,当拉力增大时 的,试想那根杆先被拉断? 单位面积上承受的内力称为应力 其单位是兆帕(MPa),N/mm2
轴向拉压解析PPT课件
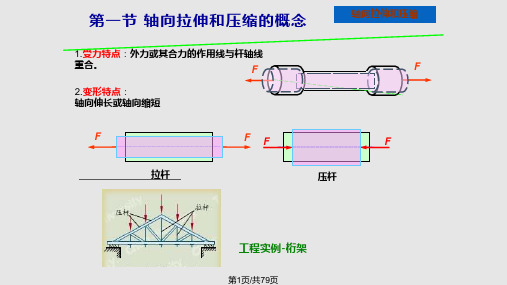
p = F A
F (2)一点的总应力 p p = lim F = dF
3.应力分量
A0 A dA
(1)正应力σ (normal stress):与截面垂直的法向 分量。规定其离开截面为正;指向截面为负。
(2)切应力τ(shear stress) :与截面相切的切向分 量。规定其对截面内部的一点产生顺时针向力矩的
F F
①全应力:
F
p
=
F cos
A
=0
cos
p
②正应力:
FN
= p cos = cos2
p
③切应力:
=
p
sin
=
0
2
sin 2
第16页/共79页
讨论:
①横截面上正应力最大,剪应力为零,即α=00时, σmax=σ 。
②45°斜截面上剪应力最大,即α=450时, τmax=σ/2 。
③90°纵向截面上剪应力,正应力都为零。
第一节 轴向拉伸和压缩的概念
1.受力特点:外力或其合力的作用线与杆轴线
重合。
F
2.变形特点: 轴向伸长或轴向缩短
轴向拉伸和压缩 F
F 拉杆
FF
F
压杆
工程实例-桁架
第1页/共79页
第二节 内力、截面法、轴力及轴力图
1.轴力、截面法(method of (s1e)轴c力tiFoN:ns杆)件发生轴向拉压时横截面上的内力。
p 切应力为正,反之为负。
4.应力特征 :
(1)必须明确截面及点的位置。
(2)是矢量。
(3)单位:Pa(帕)和MPa(兆帕) 1MPa=106Pa
第9页/共79页
第三节 横截面及斜截面上的应力
轴向拉伸与压缩

第二章
§2-1 §2-2 §2-3 §2-4
轴向拉伸和压缩
轴向拉伸和压缩的概念 轴向拉(压)杆横截面上的内力及轴力图 轴向拉(压)杆内的应力 拉(压)杆的变形
§2-5 强度条件•安全系数•许用应力
1
§2-1 轴向拉伸和压缩的概念
2
受力特点:直杆受到一对大小相等,作用 线与其轴线重合的外力F作用。 变形特点:杆件发生纵向伸长或缩短。
杆的受力简图为 拉伸
F F F
压缩
F
3
§2-2 轴向拉(压)杆横截面上的内力及内力图
1.内力与截面法: 1)内力 定义: 在外力作用下,构件内部各部分之间因 相对位置改变而引起的附加的相互作用力— —附加内力。 特点: ①连续分布于截面上各处; ②随外力的变化而变化。
4
§2-2 轴向拉(压)杆横截面上的内力及内力图
BC段(2-2截面)
FR A
∑F
x
=0
FN2 − FR − F1 = 0
14
B 2
FN2 = 50kN(拉)
FR
1
F1=40kN
2 2
F2=55kN F3=25kN
3 4 4
F4= 20kN
A 1
B
C
3 D
E
CD段(3-3截面)
FN3
3 3
FN 3 = −5kN(压)
F3 D E
4 4
F4
同理
FN 4 = 20kN(拉)
FN4
F4 E
15
FR
1
F1=40kN
2 2
F2=55kN F3=25kN
3 4 4
F4= 20kN
A 1
B
C
§2-1 §2-2 §2-3 §2-4
轴向拉伸和压缩
轴向拉伸和压缩的概念 轴向拉(压)杆横截面上的内力及轴力图 轴向拉(压)杆内的应力 拉(压)杆的变形
§2-5 强度条件•安全系数•许用应力
1
§2-1 轴向拉伸和压缩的概念
2
受力特点:直杆受到一对大小相等,作用 线与其轴线重合的外力F作用。 变形特点:杆件发生纵向伸长或缩短。
杆的受力简图为 拉伸
F F F
压缩
F
3
§2-2 轴向拉(压)杆横截面上的内力及内力图
1.内力与截面法: 1)内力 定义: 在外力作用下,构件内部各部分之间因 相对位置改变而引起的附加的相互作用力— —附加内力。 特点: ①连续分布于截面上各处; ②随外力的变化而变化。
4
§2-2 轴向拉(压)杆横截面上的内力及内力图
BC段(2-2截面)
FR A
∑F
x
=0
FN2 − FR − F1 = 0
14
B 2
FN2 = 50kN(拉)
FR
1
F1=40kN
2 2
F2=55kN F3=25kN
3 4 4
F4= 20kN
A 1
B
C
3 D
E
CD段(3-3截面)
FN3
3 3
FN 3 = −5kN(压)
F3 D E
4 4
F4
同理
FN 4 = 20kN(拉)
FN4
F4 E
15
FR
1
F1=40kN
2 2
F2=55kN F3=25kN
3 4 4
F4= 20kN
A 1
B
C
第一章 轴向拉伸和压缩1 材料力学

T Qz
z
My N x 主矢
N 轴力; Qy, Qz 剪力;
T 扭矩; My, Mz 弯矩 。
2020/11/11
9
截面法的步骤 1 沿截面假想地截开,留下一部分作为研究对
象,弃去另一部分;
2 用作用于截面上的内力代替弃去部分对留下部
分的作用;
3
对留下部分,列平衡方程求出内力。
2020/11/11
2020/11/11
18
为了得到正应力分布规律,先研究杆件变形。
ac
杆的变形 F
a'
c'
F
变形后a' b',c' d'
b'
d'
(1) 仍为直线;
bd
(2) 仍互相平行且垂直于轴线;
平面假设
变形前为平面的横截面,变形后仍保持为平面,
而2020且/11/11仍垂直于轴线。
19
平面假设 F
ac
a'
c'
下面建立变形与力之间的关系
应变
l
2020/11/11
l
23
2. 横向变形 横向变形量
bb1b
横向应变 b
试验证明
b
当应力不超过比例极限时,有:
泊松比或横向变形系数。
上式也可写成:
2020/11/11
24
在弹性范围内,有变形 x 与外力 F 成正比的弹性定律
Fkx
它是由英国力学家胡克(Robert Hooke, 1635-1703) 于1678年发现的,实际上早于他1500年前,东汉的经学 家和教育家郑玄(公元127-200)就已经发现
AB段:
轴向拉压精简讲义

低碳钢压缩 低碳钢拉伸
33
第34页/共51页
脆性材料:脆性材料压缩的性质与拉伸时有较大区别。铸铁压缩时的应力-应 变曲线与拉伸时的应力-应变曲线相比,抗压强度远比抗拉强度高,约为抗拉 强度的4~5倍。压缩时有较大塑性变形,破坏形式为沿45º左右斜面断裂
铸铁压缩
铸铁拉伸
o
ε
34
第35页/共51页
塑性材料与脆性材料的区别
( pb d d)sin
0
2
pbd 2
sind
0
pbd
FN
FR 2
pbd 2
FN pbd pd 40MPa
A
2第b50页/共521页
感谢您的观看!
50
第51页/共51页
[练习4] 图示砖柱,高h=3.5m,横截面面积
A=370×370mm2,砖砌体的容重γ=18KN/m3。柱顶
受 有 轴 向 压 力 F = 5 0 K N , 试 做 此G砖柱A的y轴 力 图 。
F
F
50
y
nnຫໍສະໝຸດ FNyF Ay FNy 0
350
FNy F Ay 50 2.46y
58.6
一、轴力计算和轴力图
41
第42页/共51页
[练习1]
求图示直杆1-1和2-2截面上的轴力
1
2
2F
2F
F
F
1
2
2F
2
F
2
第43页/共51页
[练习2] 计算各截面轴力
1F
2F
3
1
2
3
10KN
10KN 1
2
6KN
1
2
第44页/共51页
33
第34页/共51页
脆性材料:脆性材料压缩的性质与拉伸时有较大区别。铸铁压缩时的应力-应 变曲线与拉伸时的应力-应变曲线相比,抗压强度远比抗拉强度高,约为抗拉 强度的4~5倍。压缩时有较大塑性变形,破坏形式为沿45º左右斜面断裂
铸铁压缩
铸铁拉伸
o
ε
34
第35页/共51页
塑性材料与脆性材料的区别
( pb d d)sin
0
2
pbd 2
sind
0
pbd
FN
FR 2
pbd 2
FN pbd pd 40MPa
A
2第b50页/共521页
感谢您的观看!
50
第51页/共51页
[练习4] 图示砖柱,高h=3.5m,横截面面积
A=370×370mm2,砖砌体的容重γ=18KN/m3。柱顶
受 有 轴 向 压 力 F = 5 0 K N , 试 做 此G砖柱A的y轴 力 图 。
F
F
50
y
nnຫໍສະໝຸດ FNyF Ay FNy 0
350
FNy F Ay 50 2.46y
58.6
一、轴力计算和轴力图
41
第42页/共51页
[练习1]
求图示直杆1-1和2-2截面上的轴力
1
2
2F
2F
F
F
1
2
2F
2
F
2
第43页/共51页
[练习2] 计算各截面轴力
1F
2F
3
1
2
3
10KN
10KN 1
2
6KN
1
2
第44页/共51页
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§2-4拉(压)杆的变形(Deformation of Axial Forced Bar)· 胡克定律(Hooke’s Law)
桁架节点位移:
例: 图(a)所示托架,杆1和杆2均为 钢杆,弹性模量E=200GPa,横截面面积 分别为A1=200mm2,A2=250mm2,荷 载P=10kN,l1=2m。试求节点A的位移。 解:1,求各杆轴力:(取节点A
其中: m ---横向变形系数(or: 泊松比Poisson’s Ratio)
例题2-5 求例题2-4中所示薄壁圆环在内压力 p=2MPa作用下的径向应变和圆环直径的改变量。 已知材料的弹性模量E=210GPa。 解:在例题2-4中已经求出圆环在任一横截面 上的正应力=40MPa,若正应力不超过材料的比 例极限,则可按公式(2-6)算出沿正应力方向 (即沿圆周方向)的线应变e为
e ma PDl 2 2 EA 2l
§2-5 拉(压)杆内的应变能 Strain Energy of Axial Forced Bar
1 2 Ee 2 t e 2 2E 2
变形能Strain Energy and比能Energy Density (Strain Energy per Unit Volume): 外力作功(T)→引起构件变形→产生内力→( ~e)将外力功(T)转化 为内能(U)----因是构件变形引起,故称为变形能。 当(≤e
解:1,计算应力:(索上端支反力 R0=P+A l 。用截面法求得x截面 的内力为Nx=R0-Ax=A(l-x)+P 故:Nmax=Al+P)。索为等截面的,其 x截面上的应力为 x=Nx/A=(l-x)+P/A。最大应力发生在索的最上 端横截面上,其值为 max=Nmax/A=l+P/A 2,计算变形: Dl dDl
3,计算D端位移: (D端位移DD即为杆的总变形,应为各段变形的代数和)。即:
Nl N l N l 103 103 301 20 2 401 D D Dl Dl Dl Dl 0.767mm EA EA2 EA 200103 500 300 500 1 1
2
1 U ( N1Dl1 N 2 Dl2 ) 2
P 2 P 20 kN sin 30 N2 N1 cos30 1.732P 17.32kN N1
N1l1 20103 2 103 Dl1 1.0mm (伸长) EA 200103 200 1 N 2l2 17.32103 1.732103 Dl2 0.6mm (缩短) EA2 200103 250
根据上式即可算出圆环在内压力p作用下的直径(d=222mm)增大量为
D d e d d e d 1.9 104 200 0.038mm
例:图示阶梯形钢杆,AB段 和CD段的横截面面积相等A1= 500mm2,BC段横截面积A2= 300mm2。已知材料的弹性模量 E=200GPa。 试求:1,各杆段的应力。 2,D端的位移。
解: 1 P 2l 2P 2l (a)杆: U a PDl 2
2 2EAd Ed
Ub
P2 l
(b)杆:
2 EAd
4
P 2 3l
2 4 P l (1 3 ) 2 EA2d 8EAd 4
(c)杆:
P 2 dx P2 l 4l 2 Uc 0 d 2 (l x) 2 dx l 2 EA( x ) 2E 2 P 2l 2 1 2 0 2 2 l x Ed (l x) Ed 0 2 P 2l 2 P 2l Ed 2
( N1Dl1 N 2 Dl2 ) P (201 17.32 0.6) 10 3.04mm
§2-5 拉(压)杆内的应变能 Strain Energy of Axial Forced Bar
例: 求图示三根圆截面杆的应变能,并比较其大小,设三杆用 同一种线弹性材料制成,弹性模量为E。
§2-5 拉(压)杆内的应变能
Strain Energy of Axial Forced Bar
弹性体在受力后要发生变形,同时弹性体内将积蓄能量。例如钟表 的发条(弹性体)被拧紧(发生变形)以后,在它放松的过程中将带动齿轮系 使指针转动,这样,发条就作了功。这说明拧紧了的发条具有作功的本领, 这是因为发条在拧紧状态下积蓄有能量。为了获得计算这种能量的依据, 下面研究弹性体在受外力作用而变形的过程中,外力所作的功与弹性体内 所积蓄的能量在数量上的关系。
轴向变形下的外力功 Work of External Forced in Axial Deformation: eP T T Dl de ∵dW=dT=PdDl ∴ W T dT 0 PdDl 故: t 0 V Al
§2-5 拉(压)杆内的应变能 Strain Energy of Axial Forced Bar
材 料 力 学
第二章 轴向拉伸和压缩
(Ch2. Axial Tension and Compression)
§2-4拉(压)杆的变形(Deformation of Forced Bar)· 胡克定律(Hooke’s Law)
Dl = l1- l
Axial
变形Deformation:
横向Lateral变形:
External Work in Elastic Range:
1 P 2l EADl 2 T PDl 2 2 EA 2l
1 2 Ee 2 t e 2 2E 2
弹能模量:
(Modulus of Resilience)
ue de
0
ee
韧性模量(Modulus of Toughness) : umax 0
e
E 40 1.9 10 4 210 103
§2-4拉(压)杆的变形(Deformation of Axial Forced Bar)· 胡克定律(Hooke’s Law)
圆环的周向应变e等于其径向应变ed,因为
(d Dd ) d ) Dd e ed d d
现以受重力作用且仅发生弹性变形的拉杆为例,利用能量守恒原理来 找出上述关系。设杆(图2-11)的上端固定,在其下端的小盘上逐渐增加重 量。每加一点重量,杆将相应地有一点伸长,已在盘上的重物也相应地下沉, 因而重物的位能将减少。由于重量是逐渐增加的,故在加载过程中,可认为 杆没有动能改变。按能量守恒原理,略去其它微小的能量损耗不计,重物失 去的位能将全部转变为积蓄在杆内的能量。因为杆的变形是弹性变形,故 在卸除荷载以后,这种能量又随变形的消失而全部转换为其它形式的能量。 通常将这种伴随着弹性变形的增减而改变的能量称为弹性应变能。 在所讨论的情况下,应变能就等于重物所失去的位能。
线应变Linear Strain:1,轴向应变Axial Strain:ε =Dl/l=const
Dd = d1- d
2,横向应变Lateral Strain:
e’= Dd / d
显然: e ·’ <0 e
受力变形关系: Dl = Nl / EA (or:σ =Ee ; σ ≤σ p) 其中: E----弹性模量Elastic Modulus; EA---杆的轴向刚度Axial Rigidity of Bar σ p---比例极限Proportional Limit 纵横向应变关系: e ’= -me (σ ≤σ p)
计算结果为负,说明D端发生向左的位移。
例:某矿井升降机如图(a)所示,因 吊索很长,其自重引起的应力和变形应 予以考虑。设钢索长为l,横截面面积为 A,材料容重为,弹性模量为E。试求: 钢索在自重和起吊载荷P作用下产生的 应力和变形(设起吊是匀速的)。
§2-4拉(压)杆的变形(Deformation of Axial Forced Bar)· 胡克定律(Hooke’s Law)
AH AA2 Dl2 0.6mm ()
AV AA3 AO OA3
Dl1 Dl2 1.0 0.6 3.0m m sin 30 tg 30 0.5 0.577 ()
2 2 A AH AV 0.6 2 3.0 2 3.1 mm 节点A的总位移为:
为研究对象,画受力图如图(b),由平衡条 件求得两杆轴力分别为)
N1 P 2 P 20 kN(拉) sin 30
N2 N1 cos30 1.732P 17.32kN (压)
2,求各杆的变形:
N1l1 20103 2 103 Dl1 1.0mm AA (伸长) 1 EA 200103 200 1 (缩短)
§2-4拉(压)杆的变形(Deformation of Axial Forced Bar)· 胡克定律(Hooke’s Law)
解:1,绘轴力图如图(b)所示。 2,求各段应力:
AB
N BC 20 103 N AB 30 103 NCD 40103 60MPa BC 66.7MPa CD 80MPa A1 500 A2 300 A1 500
由于两杆的变形,节点A位移至A’ 点,A’点是以B为圆心,(l1+Dl1)为 半径作圆弧与以C为圆心,(l2+Dl2) 为半径作圆弧的交点。由于变形相 对于杆的原长很微小,这种作图方法 和计算A’点位移很不方便,但正因为 变形微小,可将上述两圆弧用过A1和 A2两点并分别垂直于杆1和杆2的 两垂线代替(图(c))。此图称为节点 A的位移图。由节点A的位移图可知,节点A的水平位移AH和垂直位移AV分别为
e max
大→此材料抵抗冲击和突加荷载的可靠性也越大)。
0
de 是使试件断裂所需要的比功,故tf越
注:U 和 u 恒为正。
