传热学第八章
合集下载
传热学-第八章

T E Eb T C0 100
4
15
4
8.3.2 实际物体的光谱辐射力
上面公式只是针对方向和光谱平均的情况,但实际上,真实 表面的发射能力是随方向和光谱变化的。
对应于黑体的辐射力Eb,光谱辐射力Eb和定向辐射强度I, 分别引入了三个修正系数,即,发射率,光谱发射率( )和定
M 1.0 - 1.3 金属: 非金属:M 0.95 - 1.0 M 1.0 一般计算:
表8-2为常见材料的发射率实验值。 物体表面的发射率与物质种类、表面温度和表面状况有关。
21
§8-4
实际固体的吸收比和基尔霍夫定律
上一节简单介绍了实际物体的发射情况,那么当外界 的辐射投入到物体表面上时,该物体对投入辐射吸收 的情况又是如何呢?本节将对其作出解答。 8.4.1实际物体的吸收比
第八章 热辐射基本定律及 辐射特性
1
§8-1 热辐射的基本概念
8.1.1 热辐射的定义及特点
(1) 定义:由热运动产生的,以电磁波形式传递的能量;
(2) 特点:a 任何物体,只要温度高于0 K,就会不停地向周 围空间发出热辐射;b 可以在真空中传播;c 伴随能量形 式的转变;d 具有强烈的方向性;e 辐射能与温度和波长 均有关;f 发射辐射取决于温度的4次方。 8.1.2 电磁波谱 电磁辐射包含了多种形式,如图8-1所示,而我们所感兴趣 的,即工业上有实际意义的热辐射区域一般为0.1~100μ m。 电磁波的传播速度: c = fλ 式中:f — 频率,s-1; λ— 波长,μm
2
电
磁
辐
射
波
谱
图8-1
3
物体对热辐射的吸收、反射和穿透 当热辐射投射到物体表面上时,一般 会发生三种现象,即吸收、反射和穿 透,如图7-2所示。
传热学_第八章

即
X 1, 2 1 A1 cos 1 cos 2 dA2 dA1 A1 A2 r 2
2、代数分析法
利用角系数的相对性、完整性及可加性,通过 求解代数方程而获得角系数的方法称为代数分析 法。 (1)三个非凹表面组成的封闭系统
图8-5
三个非凹表面组成的封闭系统
由角系数完整性
X 1, 2 X 1, 3 1 X 2 ,1 X 2 , 3 1 X 3 ,1 X 3 , 2 1
一. 角系数的定义 角系数是进行辐射换热计算时空间热组的 主要组成部分。 定义:把表面1发出的辐射能中落到表面2 上的百分数称为表面1对表面2的角系数, 记为X1,2。 同理,表面2发出的辐射能中落到表面1 上的百分数称为表面2对表面1的角系数, 记为X 2, 1
二.
角系数的性质
研究角系数的性质是用代数法(代数分析 法)求解角系数的前提:
(b) 空间辐射热阻
2、两灰表面组成的封闭腔的辐射换热
图8-9
两个物体组成的辐射换热系统
Eb1
J1
1 1 A1 1
1 A1, 2 X 1, 2
J2
1 2 A2 2
Eb 2
两表面封闭系统辐射换热等效网络图
利用上述两个单元格电路,可以容易 地画出组成封闭系统的两个灰体表面间辐 射换热的等效网络,如图所示。根据等效 网络,可以立即写出换热量计算式:
图8-7 黑体系统的辐射换热
二、两漫灰表面组成的封闭系统的辐 射换热计算
1、有效辐射 (1)投入辐射:单位时间内投射到单位面积上的 总辐射能,记为G。 (2)有效辐射:单位时间内离开单位面积的总辐 射能为该表面的有效辐射,记为J。
自身射辐射E 有效辐射包括 投入辐射 G 被反射辐射的部分 G 表面的反射比,可表示成
传热学第8章

黑体光谱辐射力分布图
Eb 5 T
C1 C2 T 5 exp 1 T
f T
实例:金属加热时的颜色变化 (随着温度升高,可见光在总能量中 所占比例逐渐增加)
黑体光谱辐射力通用曲线 2.维恩位移定律 ——黑体辐射峰值波长与热力学温度乘积为常数
d.光谱定向辐射力
或
E E d
0
——在某给定辐射方向上,单位时间内、物体单位辐射面积、在 单位立体角内发射的波长λ 附近单位波长间隔内的能量。
E ,
d E W m 2 sr m dd
2
或
E
E dd
, 2 0
第二节 热辐射的基本定律
——单位时间内、物体单位辐射面积向半球空间所发射全部波长 的总能量。
E
2
E d
2
2 I cos d W m
c.光谱辐射力 ——单位时间内、物体单位辐射面积、在波长λ 附近的单位波长 间隔内,向半球空间所发射的能量。
dE E W m 2 m d
E Eb
基尔霍夫定律基本表达式: , T a , T
——物体发射辐射能的能力愈强,吸收辐射能的能力也愈强
对漫射表面: T a T
对灰表面: T a T
对漫射灰表面: T aT
对黑表面: T aT 1
吸收比 反射比
穿透比 (某一频率下)
a 1
光谱 光谱 光谱 吸收比 反射比 穿透比
2.辐射能投射实际物体:
大多数固体和液体: a 气体: a
1
《传热学》课件——第八章 导热

1 )稳态传热过程(定常过程)
凡是物体中各点温度不随时间而变的热传递过程均称稳 态传热过程。
2 )非稳态传热过程(非定常过程)
凡是物体中各点温度随时间的变化而变化的热传递过 程均称非稳态传热过程。
各种热力设备在持续不变的工况下运行时的热传递 过程属稳态传热过程;而在启动、停机、工况改变时 的传热过程则属 非稳态传热过程。
壁,对此写出傅里叶定律的表达式
q dt
dx
x
对此式分离变量后积分得: qdx dt 0
tw1
对稳定导热,热流密度q为常数,将上式积分得:
tw2
q
t tw1 x
上式说明:单层平壁稳定导热壁内的温度分 布呈直线分布。
当x=δ时,t=tw2代入上式,得:
热流密度:
q tw1 tw2
2)时间 工程热力学:不考虑传热的时间。计算总热量Q。 传热学:考虑时间。计算热流量(单位时间传热量)φ。
3) 工程热力学:研究平衡态; 传热学:研究过程和非平衡态
所以,传热学与工程热力学研究的问题不同。
10
火电厂中的传热现象
动力
11
火电厂中的传热现象
动力
锅炉中的传热
汽轮机散热
凝汽器换热
12
火电厂中的传热现象
1
2
3
t r1 r 2 r 3
t
i 3 i
i 1
i
34
三层平壁稳定导热的温度分布
t
t r
热流量: A tw1 tw2
t
t R
A
31
导热热阻与热路图
动力
A tw1 tw2
t
t
R
A
R A
(K /W )平壁面积为A时的导热热阻
凡是物体中各点温度不随时间而变的热传递过程均称稳 态传热过程。
2 )非稳态传热过程(非定常过程)
凡是物体中各点温度随时间的变化而变化的热传递过 程均称非稳态传热过程。
各种热力设备在持续不变的工况下运行时的热传递 过程属稳态传热过程;而在启动、停机、工况改变时 的传热过程则属 非稳态传热过程。
壁,对此写出傅里叶定律的表达式
q dt
dx
x
对此式分离变量后积分得: qdx dt 0
tw1
对稳定导热,热流密度q为常数,将上式积分得:
tw2
q
t tw1 x
上式说明:单层平壁稳定导热壁内的温度分 布呈直线分布。
当x=δ时,t=tw2代入上式,得:
热流密度:
q tw1 tw2
2)时间 工程热力学:不考虑传热的时间。计算总热量Q。 传热学:考虑时间。计算热流量(单位时间传热量)φ。
3) 工程热力学:研究平衡态; 传热学:研究过程和非平衡态
所以,传热学与工程热力学研究的问题不同。
10
火电厂中的传热现象
动力
11
火电厂中的传热现象
动力
锅炉中的传热
汽轮机散热
凝汽器换热
12
火电厂中的传热现象
1
2
3
t r1 r 2 r 3
t
i 3 i
i 1
i
34
三层平壁稳定导热的温度分布
t
t r
热流量: A tw1 tw2
t
t R
A
31
导热热阻与热路图
动力
A tw1 tw2
t
t
R
A
R A
(K /W )平壁面积为A时的导热热阻
传热学-第八章

2. 传热学与工程热力学的关系
(1) 热力学 + 传热学 = 热科学(Thermal Science)
关心的是热量传 递的过程,即热 量传递的速率。
铁块, M1 300oC
系统从一个平衡态到 另一个平衡态的过程 中传递热量的多少。
热力学: tm
Φ
传热学: t ( x, y, z , )
Φ f ( )
空间飞行器重返大气层冷却;超高音速飞行器 (Ma=10)冷却;核热火箭、电火箭;微型火箭(电 火箭、化学火箭);太阳能高空无人飞机
b c d
微电子: 电子芯片冷却 生物医学:肿瘤高温热疗;生物芯片;组织与器 官的冷冻保存 军 事:飞机、坦克;激光武器;弹药贮存
e
f
制
冷:跨临界二氧化碳汽车空调/热泵;高温
G.
B.
J.
Fourier , 1822 年)
F. B. Jaeger/ M.
Riemann/ H. S. Jakob
Carslaw/ J.
对流换热 (Convection heat transfer) 不可压缩流动方程 (M.Navier,1823年) 流体流动Navier-Stokes基本方程 (G.G.Stokes,1845年) 雷诺数(O.Reynolds,1880年) 自然对流的理论解(L.Lorentz, 1881年) 管内换热的理论解(L.Graetz, 1885年;W.Nusselt,1916 年) 凝结换热理论解 (W.Nusselt, 1916年) 强制对流与自然对流无量纲数的原则关系 (W.Nusselt,1909年/1915年) 流体边界层概念 (L.Prandtl, 1904年) 热边界层概念 (E.Pohlhausen, 1921年) 湍流计算模型 (L.Prandtl,1925年;Th.Von Karman, 1939年;R.C. Martinelli, 1947年)
传热学第八章
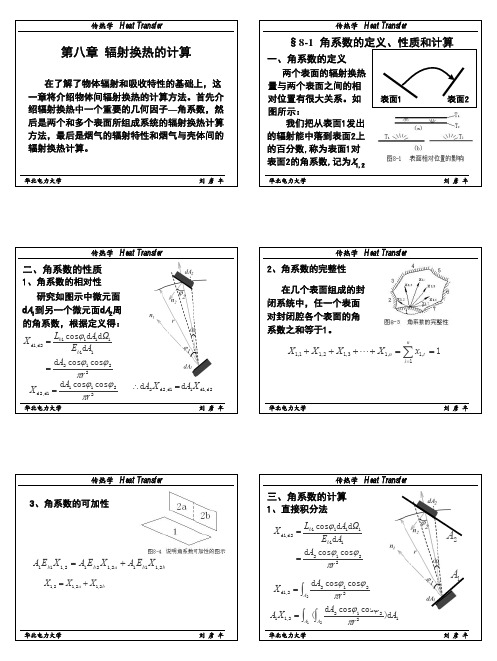
ε (λ, s) = α (λ, s) = f (分压P, 温度T , 射线行程S)
华北电力大学
刘彦丰
Lλ , 0
体层的单色穿透比,所以
τ (λ, s) = Lλ,s / Lλ,0 = e−kλs
Lλ , x
Lλ ,s
x dx
s
α (λ, s) = 1−τ (λ, s) = 1− e−kλs
根据基尔霍夫定律,还可以得到光谱发射率等于
光谱吸收比
ε (λ, s) = α (λ, s) = 1− e−kλs
传热学 Heat Transfer
§8-1 角系数的定义、性质和计算
一、角系数的定义
两个表面的辐射换热
量与两个表面之间的相
对位置有很大关系。如 图所示:
我们把从表面1发出
表面1
表面2
的辐射能中落到表面2上
的百分数,称为表面1对 表面2的角系数,记为X1,2
华北电力大学
刘彦丰
传热学 Heat Transfer
华北电力大学
刘彦丰
3、代数法
传热学 Heat Transfer
利用角系数的相对性、完整性及可加性来获得 角系数的方法。
1 2
表面2
华北电力大学
表面1
刘彦丰
传热学 Heat Transfer
X1,2 X 2,1
+ +
X1,3 X 2,3
=1 =1
完整性
X 3,1
+
X3,2
=1
A1 X 1,2 A1 X 1,3
=
A1 X1,2 (Eb1
−
Eb2 )
=
Eb1
− Eb2 1
A1 X1,2
华北电力大学
刘彦丰
Lλ , 0
体层的单色穿透比,所以
τ (λ, s) = Lλ,s / Lλ,0 = e−kλs
Lλ , x
Lλ ,s
x dx
s
α (λ, s) = 1−τ (λ, s) = 1− e−kλs
根据基尔霍夫定律,还可以得到光谱发射率等于
光谱吸收比
ε (λ, s) = α (λ, s) = 1− e−kλs
传热学 Heat Transfer
§8-1 角系数的定义、性质和计算
一、角系数的定义
两个表面的辐射换热
量与两个表面之间的相
对位置有很大关系。如 图所示:
我们把从表面1发出
表面1
表面2
的辐射能中落到表面2上
的百分数,称为表面1对 表面2的角系数,记为X1,2
华北电力大学
刘彦丰
传热学 Heat Transfer
华北电力大学
刘彦丰
3、代数法
传热学 Heat Transfer
利用角系数的相对性、完整性及可加性来获得 角系数的方法。
1 2
表面2
华北电力大学
表面1
刘彦丰
传热学 Heat Transfer
X1,2 X 2,1
+ +
X1,3 X 2,3
=1 =1
完整性
X 3,1
+
X3,2
=1
A1 X 1,2 A1 X 1,3
=
A1 X1,2 (Eb1
−
Eb2 )
=
Eb1
− Eb2 1
A1 X1,2
传热学第八章辐射换热的计算

02
辐射换热的计算方法
辐射换热的基本公式
斯蒂芬-玻尔兹曼方程
描述了物体在任意温度下的辐射功率,是辐射换热的基本公式。
辐射力方程
表示物体发射和吸收的辐射能与物体表面温度和周围环境温度之间 的关系。
辐射传递方程
表示在给定温度和光谱发射率下,物体表面发射和吸收的辐射能与 物体表面温度之间的关系。
辐射换热的角系数法
表面传热系数的计算方法
通过实验测定或经验公式计算表面传热系数, 需要考虑表面粗糙度和涂层的影响。
表面传热系数的应用
适用于简化模型或近似计算中的辐射换热计算。
辐射换热的积分方程法
积分方程的建立
根据斯蒂芬-玻尔兹曼方程和边界条件建立积分方程。
积分方程的求解方法
采用数值方法求解积分方程,如有限元法、有限差分 法等。
太阳能利用
通过优化太阳能集热器的设计,提高太阳能辐射的吸收和 转换效率,降低太阳能利用成本,有助于减少化石能源的 消耗和碳排放。
05
辐射换热的发展趋势与展 望
新型材料的辐射换热特性研究
总结词
随着科技的发展,新型材料不断涌现,对新型材料的辐射换热特性研究成为当 前热点。
详细描述
新型材料如碳纳米管、石墨烯等具有独特的物理和化学性质,其辐射换热特性 与传统材料有所不同。研究这些新型材料的辐射换热特性有助于发现新的传热 机制,提高传热效率。
感谢观看
THANKS
传热学第八章辐射 换热的计算
目 录
• 辐射换热的基本概念 • 辐射换热的计算方法 • 辐射换热的实际应用 • 辐射换热的优化与控制 • 辐射换热的发展趋势与展望
01
辐射换热的基本概念
定义与特性
定义
第八章热辐射的基本定律_传热学

发射的一切波长的能量
d () I () dA cos d
单位:W/m2· sr
2) Lambert定律:
黑体表面具有漫辐射性质,在半球空间各个方向辐射强度相等
I 1 I 2 ...... I n
E I cos I n cos En cos
如果已知黑体温度,则可以求得最大单色辐射力 Eb, max 所对应的波长 max
25
讨论:黑体温度在3800K以下时,其峰值波长处在红外线区域。 因此,在一般工程中所遇到的辐射换热,基本上属于红外辐射。
思考:金属在加热过程中,随 着温度的升高,金属颜色呈暗 红、红、黄、白,请解释这一 现象。
Fb 0-T
T E c1 b d T d T f T 5 0 T C2 5 b b T exp 1 T
30
根据黑体辐射函数,可以计算出给定温度下λ1-λ2波段内的 黑体辐射力为:
Eb 1- 2 Eb Fb 0- 2T Fb 0-1T
f (T )
23
三、维恩位移定律
黑体的峰值波长 max 与热力学温度T之间的函数关系
Eb
c15 ec
2
( T )
1
根据普朗克定律,将Eb 对 波长求极值,可得: maxT 2897.6m.K
随着温度T的升高,最大单色辐射 力 Eb, 所对应的峰值波长 max max 逐渐向短波方向移动
• 实际物体的辐射力并不严格遵从四次方定律,怎么办? 认为E∝T4 由此引起的误差修正归入用实验方法确定的中 因此除了与物性有关,还与物体本身的温度有关
39
2 实际物体的光谱辐射力E
E Eb
d () I () dA cos d
单位:W/m2· sr
2) Lambert定律:
黑体表面具有漫辐射性质,在半球空间各个方向辐射强度相等
I 1 I 2 ...... I n
E I cos I n cos En cos
如果已知黑体温度,则可以求得最大单色辐射力 Eb, max 所对应的波长 max
25
讨论:黑体温度在3800K以下时,其峰值波长处在红外线区域。 因此,在一般工程中所遇到的辐射换热,基本上属于红外辐射。
思考:金属在加热过程中,随 着温度的升高,金属颜色呈暗 红、红、黄、白,请解释这一 现象。
Fb 0-T
T E c1 b d T d T f T 5 0 T C2 5 b b T exp 1 T
30
根据黑体辐射函数,可以计算出给定温度下λ1-λ2波段内的 黑体辐射力为:
Eb 1- 2 Eb Fb 0- 2T Fb 0-1T
f (T )
23
三、维恩位移定律
黑体的峰值波长 max 与热力学温度T之间的函数关系
Eb
c15 ec
2
( T )
1
根据普朗克定律,将Eb 对 波长求极值,可得: maxT 2897.6m.K
随着温度T的升高,最大单色辐射 力 Eb, 所对应的峰值波长 max max 逐渐向短波方向移动
• 实际物体的辐射力并不严格遵从四次方定律,怎么办? 认为E∝T4 由此引起的误差修正归入用实验方法确定的中 因此除了与物性有关,还与物体本身的温度有关
39
2 实际物体的光谱辐射力E
E Eb
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
传热学 黑体辐射能按波段的分布
Ebλ
如何求得某个波段范围内黑体的辐射能?
Eb0 Eb d
0
λ1 λ2 λ
波长1与 2之间的辐射能计算如下: Eb 1-2 Eb d Eb d- Eb d
1 0 0 2 2 2
Eb 0-2 Eb 0-1
•
远红外加热技术
传热学
3 物体对热辐射的吸收、反射和穿透
当热辐射投射到物体表面上时, 一般会发生三种现象,即吸收、 反射和穿透,如图所示。
G
G
G
G
G G G G G G G 1 G G G
absorptivity
reflectivity transmissivity
单位:sr(球面度)
Ac 2 r
dAc d 2 r
传热学
r sind
dAc
rd
dAc d 2 r
Ac 2 r
r
d
dA
dAc rd r sin d d 2 2 r r
sindd
传热学 定向辐射强度I(, ) 1) 定义 在单位时间内、单位可见辐射面积上、单位 立体角内发射的一切波长的能量
传热学 1、Stefan-Boltzmann定律:揭示了黑体辐射力与温度K
的关系。
黑体辐射力:
Eb T
4
• -Stefan-Boltzmann常数
5.6710-8 W/(m2· 4) K • Cb-黑体辐射系数 5.67 W/(m2· 4) K
T Eb C b 100
越大;
•
温度均匀是为了保 证辐射均匀且各向 同性。
黑体模型
传热学
§8-2 黑体辐射的基本定律
黑体辐射有三个基本定律 Stefan-Boltzmann
Planck’s Law
Lambert’s Law
从不同角度描述了一定温度下的 黑体辐射的基本规律
传热学 1、Stefan-Boltzmann定律:揭示了黑体辐射力与温度K
传热学 2、Planck定律:揭示了黑体光谱辐射力与波长、温度之
间的关系
Eb
c15 ec
2
( T )
1
式中: λ— 波长,m
T — 黑体温度,K
c1 — 第一辐射常数,3.742×10-16 Wm2; c2 — 第二辐射常数,1.4388×10-2 WK;
传热学
黑体的光谱辐射力随温度升高而增 大,短波区增大速度比长波区大。 在一定的温度下,黑体的光谱辐射力随 波长的增加,先是增大,然后有减小, 其中有一峰值 Eb, max
传热学
三 Lambert’s Law
2) Lambert定律:黑体表面具有漫辐射性质,在半球 空间各个方向辐射强度相等
I 1 I 2 ...... I n
E I cos I n cos En cos
传热学 Lambert定律 1) 定向辐射强度与方向无关的规律 2)除了黑体表面,还有漫射表面服从Lambert定律
4
黑体辐射力Eb受温度T影响很大,温度增加2倍,辐射力 注:黑体的所有辐射参数有下角标b 增加16倍。
传热学 2、Planck定律:解释了黑体辐射力按波长分布的规律,
即黑体光谱辐射力与波长、温度之间的关系。
光谱辐射力:单位时间内,物体的每单位面积、在波 长附近的单位波长间隔内,向半球空间所发射的能 量,E,单位为W/(m2. m )
表面不平整尺寸小于辐射波长
镜反射
表面不平整尺寸大于辐射波长
漫反射
传热学
三 黑体模型
1 为什么? 2 黑体模型
•
比较标准,对比研究实际物体的辐射特性
可以全部吸收透射到其表面上的所有波长
的辐射能;理想的吸收体
•
现实世界中并不存在严格意义上的黑体;
•
实验室模型
传热学 带有小孔的温度均匀的空腔
•
小孔的孔径越小
传热学
通常,将黑体的波段辐射力表示成同温度下黑体 辐射力E b的百分数,记为Fb 0-T
Fb 0-T
Fb 0-T
Eb 0- Eb
T
0
Eb d
bT 4
0
T E c1 b d T d T f T 0 T5 C2 5 b b T exp 1 T
传热学
讨论:集热器玻璃表面温度低,它的长波辐射对玻璃阻挡 短波透过玻璃。这种特性能够减少集热器表面透过玻璃 向外的辐射热损失。
如果用这种玻璃作为房屋的窗子,结果如何?
传热学
三 Lambert’s Law
兰贝特定律给出了黑体辐射能按空间分布的规律。 一般用立体角来描述空间方向和大小。
1 立体角
定义:球面面积除以球半径的平方
传热学 2. 特点 • 任何物体,只要温度高于0 K,就会不停 地向周围空间发出热辐射;固有属性
• 可以在真空中传播;
• 伴随能量形式的转变;
• 具有强烈的方向性;
• 辐射能与温度和波长均有关
传热学
二 热辐射具有电磁波的共性
电磁辐射包含了多种形式,而我们所感兴趣的, 即工业上有实际意义的热辐射区域一般波长为 0.1~100μm。
E I cos I n cos En cos
又称余弦定律 3) 黑体的在辐射力法向方向最大,切线方向为零
传热学 5 黑体定向辐射强度与辐射力之间的关系
d () Eb I b cos d dA 2
dA d 2 sin d d r
传热学
二 热辐射具有电磁波的共性
f=C
e hv
式中:f — 频率,s-1; λ— 波长,μm
2 电磁波谱
传热学
•
• •
理论上覆盖整个电磁波谱;
对于太阳辐射(约5800K):0.22m; 可见光0.380.76m 红外线0.76251000m
•
一般工业范围内(2000K以下): 0.38100m 0.7620m 25 m 微波
max 如果已知黑体温度,则可以求得最大光谱辐射力 Eb, 所对应的波长 max
传热学
讨论:黑体温度在3800K以下时,其峰值波长处在红外线区域。 因此,在一般工程中所遇到的辐射换热,基本上属于红外辐射。
思考:金属在加热过程中,随 着温度的升高,金属颜色呈暗 红、红、黄、白,请解释这一 现象。
的关系。
辐射力E
emissive power
• 为了定量表述单位黑体表面在一定温度下向
外界辐射能量的多少而引入的概念。
半球空间
dA
传热学 1、Stefan-Boltzmann定律:揭示了黑体辐射力与温度K
的关系。
辐射力E
emissive power
• 单位时间内,物体的单位表面积向半球 空间发射的所有波长的能量总和。 • 单位:W/m2 • E从总体上表征了物体辐射能力的大小。 • 辐射力与空间有关,与方向有关
§8-1 热辐射的基本概念
一 热辐射
1. 定义 热辐射-thermal radiation
物体由于热的原因(温度高于 0 K)而发射电磁波的 现象。
辐射换热-radiation heat transfer
物体之间通过热辐射交换热量的过程。 当系统达到热平衡时,辐射换热量为零,但热辐 射仍然不断进行。
传热学
第八章
热辐射基本定律及 物体的辐射特性
传热学
物质由基本微观粒子组成,当原子内部的电子受激和振动时,产生 交替变化的电场和磁场,发出电磁波向空间传播,此为辐射。
不同的激发方式,产生电磁波的波长不同,它们投射到物体上产生 的效应不同。
由于自身温度或者热的原因而激发产生的电磁波传播,称为热辐射
传热学
传热学 Planck定律与Stefan-Boltzmann的关系 Stefan-Boltzmann定律 Planck定律
确定黑体辐射力Eb
确定黑体辐射力Eb与波长,温度的关系
b
Eb E d
0
Eb
c15 ec
2
( T )
1
Eb E d
0 b
0
c1 5 d bT 4 W / m 2 ec2 ( T ) 1
I b cos sin d d Ib d
0 2 2 0
cos sin d
Ib
对于漫射表面,辐射力是任意方向辐射强度的 倍
传热学
四 小结
Stefan-Boltzmann’s Law Planck’s Law Lambert’s Law 总体 按波长分布 在空间分布
解:利用黑体辐射函数表来完成 1T 0.35 5762 2017m.K,查表可得Fb 0-1T =0.0696
2T 2.7 5762 15557m.K,查表可得Fb 0-2T =0.9717
在给定波长范围内,透射到玻璃上的能量占总能量的 百分数为:0.9717-0.0696=90.21% 太阳辐射透过该玻璃的百分数为:90.21%×0.85=76.68%
E 定向发射率: E b 单色定向发射率: , E , Eb , E , ,T E b, , ,T
温度为T的单色定向发射率: , ,T
• 一般通过实验测定
• 只取决于物体本身,与外界无关
传热学
2 计算式
E Eb T 4
3 说明
• 实际物体的辐射力并不严格遵从四次方定律 • 怎么办? 认为E∝T4 由此引起的误差修正归入用实验方法确定的中
传热学 维恩位移定律
黑体的峰值波长 max 与热力学温度T之间的函数关系
