【免费下载】概率论与数理统计第三章二维随机变量及其概率分布例题

合集下载

概率统计第三章

第三章二维随机变量及其分布练习题 3.1一、判断题1(X,Y)的分布可确定 X 与 Y 的边缘分布。

()、由2、设、是两个随机变量，则是二维随机变量。

3、设二维随机变量 (,)的联合分布函数为 F (x, y) ，则 F ( x, y)P{x,y} 1 P{x,y} 。

() 4、设二维随机变量(,) 的联合分布函数为 F (x, y) 则，P{ x1x2 , y1y2 } F (x2 , y2 ) F ( x1 , y1 )()5、由( X,Y)的两个边缘分布可确定 ( X ,Y )的联合分布()6、若(X,Y)为离散型二维随机变量，则P{ X a,Y b}P{ x a, y b} (其中 a,b 为常数)() 7、设( , )的概率分布为0133 1010131 1010则， U的概率分布为U012343。

( )P1010 10二、填空题1.设二维随机变量 ( , ) 的联合概率分布为01200.10.2010.30.10.120.100.1则 P0 =____。

2.设二维随机变量 ( , ) 的概率密度e y0 x yx, y0其他而的边缘密度为y ，则 2 =________。

3.设二维随机变量 ( , ) 的概率密度为1 0 x 1,0 y1x, y0其他则概率 P0.5,0.6 =________。

4.设二维随机变量 ( , ) 的概率密度为4xy0 x1,0y1x, y0其他则 P 01 , 12 41=___________，P{} =_________，P{} =_________。

5.(X ,Y)是二维连续型随机变量，用(X ,Y)的联合分布函数 F ( x, y)表示下列概率（1）p( a X b, Y c)__________ __________;（2）p( X a, Y b)____________________ ;（3） p(0 Y a ) __________ __________;（4） p( X a, Y b) ____________________ .练习题 3.2一、选择题1、设,为随机变量，则事件1,1的逆事件为 ().A1, 1 ;B1, 1 ;C1, 1 ;D1 1 .2、p ij P{x i ,y j }( i, j1,2,) 是离散型二维随机变量( ,) 的（）。

概率论与数理统计3.1.2 二维离散型随机变量及其联合分布律

pk
xi
pi1 pi2 ... pij ...
分布律的性质 (1)非负性：pk 0 , k 1, 2, ;

(2)规范性： pk 1. k 1
3.联合分布律的性质
(1) 非负性: pij 0，i, j 1, 2, ;

(2) 规范性: pij 1 i1 j1
p{(X 0,Y 0)} P{(X 1,Y 0)} P{(X 1,Y 1)}
0.3 0.3 0.1 0.7
注 P{(X ,Y ) D}
p{X xi ,Y y j}
pij
：
( xi , y j )D
( xi , y j )D
P{X 0,Y 0} P{X 0}p{Y 0}
33 9 5 5 25
Y X
0
1
P{X 0,Y 1} 3 2 6
5 5 25
P{X 1,Y 0} 2 3 6 5 5 25
P{X 1,Y 1} 2 2 4
0 1
9
6
25
25
625
例1 袋中有2只白球，3只黑球，现摸球两次，定义
1 X 0
第一次摸到白球,求 (1) 有放回取球下(X,Y)的分布律。第一次摸到黑球 (2) 不放回取球下(X,Y)的分布律。
Y

1 0
第二次摸到白球第二次摸到黑球
(3)不放回下 P{X Y}.
例1 袋中有2只白球，3只黑球，现摸球两次，定义
1 X 0
第一次摸到白球,求 (1) 有放回取球下(X,Y)的分布律。第一次摸到黑球 (2) 不放回取球下(X,Y)的分布律。

第三章二维随机变量及其分布《概率论与数理统计》西南交大峨眉校区

X
0 1
pX ( xi )
3 2 5 5
9 6
25 25
5
6 4
25 25
5
pY ( y j )
3
2
1
（2）不放回取球
Y
X
0 1
0
1
pX ( xi )
3 2 5 5
6 6
20 20
5
6 2
20 20
5
pY ( y j )
3
2
1
三、二维离散型随机变量的独立性
定义 5：对二维离散型随机变量 ( X , Y ) 的任意一对可能取值 ( xi , y j ) ，若满足：
例如，研究某一社区儿童的生长发育状况，常需要将身高和体重作为一个整体来研究，才能合理地对生长发育状况做出评价。故：样本空间该社区的全体儿童，身高 H ( ) 和体重 W ( ) 是定义在样本空间上的两个随机变量，则

( H ( ),W ( )) 是二维随机变量。
( X xi , Y y2 )
( X xi , Y yn ) ，
按照互不相容事件的概率加法定理，可得：
pX ( xi ) = P( X xi , Y y1 ) P( X xi , Y y2 )
P( X xi , Y yn )
P( X xi , Y y j ) p( xi , y j )
Y
X
0 1
0
1
9 6
25 25
6 4
25 25
二维离散型随机变量的联合概率函数的性质
① 非负性： pij 0 ； ② 归一性：

概率论与数理统计第三章习题及答案

概率论与数理统计习题第三章多维随机变量及其分布习题3-1 盒子里装有3只黑球、2只红球、2只白球，在其中任取4只球.以X 表示取到黑球的只数，以Y 表示取到红球的只数，求X 和Y 的联合分布律.（X ，Y ）的可能取值为(i , j )，i =0，1，2，3， j =0，12，i + j ≥2，联合分布律为 P {X=0, Y=2 }=351472222=C C C P {X=1, Y=1 }=35647221213=C C C C P {X=1, Y=2 }=35647122213=C C C C P {X=2, Y=0 }=353472223=C C C P {X=2, Y=1 }=351247121223=C C C C P {X=2, Y=2 }=353472223=C C C P {X=3, Y=0 }=352471233=C C C P {X=3, Y=1 }=352471233=C C C P {X=3, Y=2 }=0习题3-2 设随机变量),(Y X 的概率密度为⎩⎨⎧<<<<--=其它,0,42,20),6(),(y x y x k y x f（1）确定常数k ；（2）求{}3,1<<Y X P （3）求{}5.1<X P ；（4）求{}4≤+Y X P . 分析：利用P {(X , Y)∈G}=⎰⎰⎰⎰⋂=oD G Gdy dx y x f dy dx y x f ),(),(再化为累次积分，其中⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧<<<<=42,20),(y x y x D o解：（1）∵⎰⎰⎰⎰+∞∞-+∞∞---==2012)6(),(1dydx y x k dy dx y x f ，∴81=k （2）83)6(81)3,1(321⎰⎰=--=<<dy y x dxY X P （3）3227)6(81),5.1()5.1(425.10=--=∞<≤=≤⎰⎰dy y x dx Y X P X P （4）32)6(81)4(4020=--=≤+⎰⎰-dy y x dxY X P x习题3-3 将一枚硬币掷3次，以X 表示前2次出现H 的次数，以Y 表示3次中出现H 的次数，求Y X ,的联合分布律以及),(Y X 的边缘分布律。

概率论与数理统计(理工类,第四版)吴赣昌主编课后习题答案第三章

第三章多维随机变量及其分布3.1 二维随机变量及其分布习题1设(X,Y)的分布律为X\Y12311/61/91/1821/3a1/9求a.分析：dsfsd1f6d54654646解答：由分布律性质∑i⋅jPij=1,可知1/6+1/9+1/18+1/3+a+1/9=1,解得a=2/9.习题2(1)2.设(X,Y)的分布函数为F(x,y)，试用F(x,y)表示：(1)P{a<X≤b,Y≤c};解答：P{a<X≤b,Y≤c}=F(b,c)-F(a,c).习题2(2)2.设(X,Y)的分布函数为F(x,y)，试用F(x,y)表示：(2)P{0<Y≤b};解答：P{0<Y≤b}=F(+∞,b)-F(+∞,0).习题2(3)2.设(X,Y)的分布函数为F(x,y)，试用F(x,y)表示：(3)P{X>a,Y≤b}.解答：P{X>a,Y≤b}=F(+∞,b)-F(a,b).习题3(1)3.设二维离散型随机变量的联合分布如下表：试求：(1)P{12<X<32,0<Y<4;解答：P{12<X<23,0<Y<4P{X=1,Y=1}+P{X=1,Y=2}+P{X=1,Y=3}=P{X=1,Y=1}+P{X=1,Y=2}+P{X=1,Y=3}=14+0+0=14.习题3(2)3.设二维离散型随机变量的联合分布如下表：试求：(2)P{1≤X≤2,3≤Y≤4};解答：P{1≤X≤2,3≤Y≤4}=P{X=1,Y=3}+P{X=1,Y=4}+P{X=2,Y=3}+P{X=2,Y=4}=0+116+0+14=516.习题3(3)3.设二维离散型随机变量的联合分布如下表：试求：(3)F(2,3).解答：F(2,3)=P(1,1)+P(1,2)+P(1,3)+P(2,1)+P(2,2)+P(2,3)=14+0+0+116+14+0=916.习题4设X,Y为随机变量，且P{X≥0,Y≥0}=37,P{X≥0}=P{Y≥0}=47,求P{max{X,Y}≥0}.解答：P{max{X,Y}≥0}=P{X,Y至少一个大于等于0}=P{X≥0}+P{Y≥0}-P{X≥0,Y≥0}=47+47-37=57.习题5(X,Y)只取下列数值中的值：(0,0),(-1,1),(-1,13),(2,0)且相应概率依次为16,13,112,512,请列出(X,Y)的概率分布表，并写出关于Y的边缘分布.解答：(1)因为所给的一组概率实数显然均大于零，且有16+13+112+512=1,故所给的一组实数必是某二维随机变量(X,Y)的联合概率分布. 因(X,Y)只取上述四组可能值，故事件：{X=-1,Y=0},{X=0,Y=13,{X=0,Y=1},{X=2,Y=13,{X=2,Y=1}均为不可能事件，其概率必为零. 因而得到下表：Y01/31pk7/121/121/3习题6设随机向量(X,Y)服从二维正态分布N(0,0,102,102,0),其概率密度为f(x,y)=1200πex2+y2200,求P{X≤Y}.解答：由于P{X≤Y}+P{X>Y}=1，且由正态分布图形的对称性，知P{X≤Y}=P{X>Y},故P{X≤Y}=12.习题7设随机变量(X,Y)的概率密度为f(x,y)={k(6-x-y),0<x<2,2<y<40,其它, (1)确定常数k;(2)求P{X<1,Y<3};(3)求P{X<1.5};(4)求P{X+Y≤4}.解答：如图所示(1)由∫-∞+∞∫-∞+∞f(x,y)dxdy=1,确定常数k.∫02∫24k(6-x-y)dydx=k∫02(6-2x)dx=8k=1,所以k=18.(2)P{X<1,Y<3}=∫01dx∫2318(6-x-y)dy=38.(3)P{X<1.5}=∫01.5dx∫2418(6-x-y)dy=2732.(4)P{X+Y≤4}=∫02dx∫24-x18(6-x-y)dy=23.习题8已知X和Y的联合密度为f(x,y)={cxy,0≤x≤1,0≤y≤10,其它,试求：(1)常数c;(2)X和Y的联合分布函数F(x,y).解答：(1)由于1=∫-∞+∞∫-∞+∞f(x,y)dxdy=c∫01∫01xydxdy=c4,c=4.(2)当x≤0或y≤0时，显然F(x,y)=0;当x≥1,y≥1时，显然F(x,y)=1;设0≤x≤1,0≤y≤1,有F(x,y)=∫-∞x∫-∞yf(u,v)dudv=4∫0xudu∫0yvdv=x2y2.设0≤x≤1,y>1,有F(x,y)=P{X≤1,Y≤y}=4∫0xudu∫01ydy=x2.最后，设x>1,0≤y≤1,有F(x,y)=P{X≤1,Y≤y}=4∫01xdx∫0yvdv=y2.函数F(x,y)在平面各区域的表达式F(x,y)={0,x≤0或y≤0x2,0≤x≤1,y>1x2y2,0≤x≤1,0≤y≤1.y2,x>习题9设二维随机变量(X,Y)的概率密度为f(x,y)={4.8y(2-x),0≤x≤1,x≤y≤10,其它,求边缘概率密度fY(y).解答：fX(x)=∫-∞+∞f(x,y)dy={∫0x4.8y(2-x)dy,0≤x≤10,其它={2.4x2(2-x),0≤x≤10,其它.fY(y)=∫-∞+∞f(x,y)dx={∫0y4.8y(2-x)dx,0≤y≤10,其它={2.4y(4y-y2),0≤y≤10,其它.习题10设(X,Y)在曲线y=x2,y=x所围成的区域G里服从均匀分布，求联合分布密度和边缘分布密度. 解答：区域G的面积A=∫01(x-x2)dx=16,由题设知(X,Y)的联合分布密度为f(x,y)={6,0≤x≤1,x2≤y≤x0,其它,从而fX(x)=∫-∞+∞f(x,y)dy=6∫x2xdy=6(x-x2),0≤x≤1,即fX(x)={6(x-x2),0≤x≤10,其它,fY(y)=∫-∞+∞f(x,y)dx=6∫yydx=6(y-y),0≤y≤1,即fY(y)={6(y-y),0≤y≤10,其它.3.2 条件分布与随机变量的独立性习题1二维随机变量(X,Y)的分布律为从而(X,Y)的联合概率分布为P{X≤a,∣X∣≤a}=P{X≤a}⋅P{∣X∣≤a},而事件{∣X∣≤a}⊂{X≤a},故由上式有P{∣X∣≤a}==P{X≤a}⋅P{∣X∣≤a},⇒P{∣X∣≤a}(1-P{X≤a})=0⇒P{∣X≤a∣}=0或1=P{X≤a}⋅(∀a>0)但当a>0时，两者均不成立，出现矛盾，故X与∣X∣不独立.习题9设X和Y是两个相互独立的随机变量，X在(0,1)上服从均匀分布，Y的概率密度为fY(y)={12e-y2,y>00,y≤0,(1)求X与Y的联合概率密度；(2)设有a的二次方程a2+2Xa+Y=0,求它有实根的概率.解答：(1)由题设易知fX(x)={1,0<x<10,其它,又X,Y相互独立，故X与Y的联合概率密度为f(x,y)=fX(x)⋅fY(y)={12e-y2,0<x<1,y>00,其它;(2)因{a有实根}={判别式Δ2=4X2-4Y≥0}={X2≥Y},故如图所示得到：P{a有实根}=P{X2≥Y}=∫∫x2>yf(x,y)dxdy=∫01dx∫0x212e-y2dy=-∫01e-x22dx=1-[∫-∞1e-x22dx-∫-∞0e-x22dx]=1-2π[12π∫-∞1e-x22dx-12π∫-∞0e-x22dx]=1-2π[Φ(1)-Φ(0),又Φ(1)=0.8413,Φ(0)=0.5,于是Φ(1)-Φ(0)=0.3413,所以P{a有实根}=1-2π[Φ(1)-Φ(0)]≈1-2.51×0.3413=0.1433.3.3 二维随机变量函数的分布习题1设随机变量X和Y相互独立，且都等可能地取1,2,3为值，求随机变量U=max{X,Y}和V=min{X,Y}的联合分布.解答：由于U≥V,可见P{U=i,V=j}=0(i<j).此外，有P{U=V=i}=P{X=Y=i}=1/9(i=1,2,3),P{U=i,V=j}=P{X=i,Y=j}+P{X=j,Y=i}=2/9(i>j),于是，随机变量U和V的联合概率分布为=∫01dy∫y2y12dx=14,P{U=1,V=1}=1-P{U=0,V=0}-P{U=0,V=1}-P{U=1,V=0}=1/2,即U\V01011/401/41/2习题4设(X,Y)的联合分布密度为f(x,y)=12πe-x2+y22,Z=X2+Y2,求Z的分布密度.解答：FZ(z)=P{Z≤z}=P{X2+Y2≤z}.当z<0时，FZ(z)=P(∅)=0;当z≥0时，FZ(z)=P{X2+Y2≤z2}=∫∫x2+y2≤z2f(x,y)dxdy=12π∫∫x2+y2≤z2e-x2+y22dxdy=12π∫02πdθ∫0ze-ρ22ρdρ=∫0ze-ρ22ρdρ=1-e-z22.故Z的分布函数为FZ(z)={1-e-z22,z≥00,z<0.Z的分布密度为fZ(z)={ze-z22,z>00,z≤0.习题5设随机变量(X,Y)的概率密度为f(x,y)={12(x+y)e-(x+y),x>0,y>00,其它,(1)问X和Y是否相互独立？(2)求Z=X+Y的概率密度.解答：(1)fX(x)=∫-∞+∞f(x,y)dy={∫0+∞12(x+y)e-(x+y)dy,x>00,x≤0\under2line令x+y=t{∫x+∞12te-tdt=12(x+1)e-x,x>00,x≤0,由对称性知fY(y)={12(y+1)e-y,y>00,y≤0,显然f(x,y)≠fX(x)fY(y),x>0,y>0,所以X与Y不独立.(2)用卷积公式求fZ(z)=∫-∞+∞f(x,z-x)dx.当{x>0z-x>0即{x>0x<z时，f(x,z-x)≠0,所以当z≤0时，fZ(z)=0;当z>0时，fZ(z)=∫0z12xe-xdx=12z2e-z.于是，Z=X+Y的概率密度为fZ(z)={12z2e-z,z>00,z≤0.习题6设随机变量X,Y相互独立，若X服从(0,1)上的均匀分布，Y服从参数1的指数分布，求随机变量Z=X+Y的概率密度.解答：据题意，X,Y的概率密度分布为fX(x)={1,0<x<10,其它,fY(y)={e-y,y≥00,y<0,由卷积公式得Z=X+Y的概率密度为fZ(z)=∫-∞+∞fX(x)fY(z-x)dx=∫-∞+∞fX(z-y)fY(y)dy=∫0+∞fX(z-y)e-ydy.由0<z-y<1得z-1<y<z,可见：当z≤0时，有fX(z-y)=0,故fZ(z)=∫0+∞0⋅e-ydy=0;当z>0时，fZ(z)=∫0+∞fX(z-y)e-ydy=∫max(0,z-1)ze-ydy=e-max(0,z-1)-e-z,即fZ(z)={0,z≤01-e-z,0<z≤1e1-z-e-z,z>1.习题7设随机变量(X,Y)的概率密度为f(x,y)={be-(x+y),0<x<1,0<y<+∞,0,其它.（1）试确定常数b；（2）求边缘概率密度fX(x),fY(y)；（3）求函数U=max{X,Y}的分布函数.解答：（1）由∫-∞+∞∫-∞+∞f(x,y)dxdy=1，确定常数b.∫01dx∫0+∞be-xe-ydy=b(1-e-1)=1，所以b=11-e-1，从而f(x,y)={11-e-1e-(x+y),0<x<1,0<y<+∞,0,其它.（2）由边缘概率密度的定义得fX(x)={∫0+∞11-e-1e-(x+y)dy=e-x1-e-x,0<x<1,0,其它，fY(x)={∫0111-e-1e-(x+y)dx=e-y,0<y<+∞,0,其它（3）因为f(x,y)=fX(x)fY(y)，所以X与Y独立，故FU(u)=P{max{X,Y}≤u}=P{X≤u,Y≤u}=FX(u)F Y(u)，其中FX(x)=∫0xe-t1-e-1dt=1-e-x1-e-1,0<x<1，所以FX(x)={0,x≤0,1-e-x1-e-1,0<x<1,1,x≥1.同理FY(y)={∫0ye-tdt=1-e-y,0<y<+∞,0,y≤0，因此FU(u)={0,u<0,(1-e-u)21-e-1,0≤u<1,1-e-u,u≥1.习题8设系统L是由两个相互独立的子系统L1和L2以串联方式联接而成，L1和L2的寿命分别为X与Y,其概率密度分别为ϕ1(x)={αe-αx,x>00,x≤0,ϕ2(y)={βe-βy,y>00,y≤0,其中α>0,β>0,α≠β,试求系统L的寿命Z的概率密度.解答：设Z=min{X,Y},则F(z)=P{Z≥z}=P{min(X,Y)≤z}=1-P{min(X,Y)>z}=1-P{X≥z,Y≥z}=1-[1P{X<z}][1-P{Y<z}]=1-[1-F1{z}][1-F2{z}]由于F1(z)={∫0zαe-αxdx=1-e-αz,z≥00,z<0,F2(z)={1-e-βz,z≥00,z<0,故F(z)={1-e-(α+β)z,z≥00,z<0,从而ϕ(z)={(α+β)e-(α+β)z,z>00,z≤0.习题9设随机变量X,Y相互独立，且服从同一分布，试证明：P{a<min{X,Y}≤b}=[P{X>a}]2-[P{X>b}]2.解答：设min{X,Y}=Z,则P{a<min{X,Y}≤b}=FZ(b)-FZ(a),FZ(z)=P{min{X,Y}≤z}=1-P{min{X,Y}>z}=1-P{X>z,Y>z}=1-P{X>z}P{Y>z}=1-[P{X>z}]2,代入得P{a<min{X,Y}≤b}=1-[P{X>b}]2-(1-[P{X>a}]2)=[P{X>a}]2-[P{X>b}]2.证毕.复习总结与总习题解答习题1在一箱子中装有12只开关，其中2只是次品，在其中取两次，每次任取一只，考虑两种试验：(1)放回抽样；(2)不放回抽样.我们定义随机变量X,Y如下：X={0,若第一次取出的是正品1,若第一次取出的是次品, Y={0,若第二次取出的是正品1,若第二次取出的是次品,试分别就(1),(2)两种情况，写出X和Y的联合分布律.解答：(1)有放回抽样，(X,Y)分布律如下：P{X=0,Y=0}=10×1012×12=2536; P{X=1,Y=0}=2×1012×12=536,P{X=0,Y=1}=10×212×12=536, P{X=1,Y=1}=2×212×12=136,(2)不放回抽样，(X,Y)的分布律如下：P{X=0,Y=0}=10×912×11=4566, P{X=0,Y=1}=10×212×11=1066,P{X=1,Y=1}=2×112×11=166,习题2假设随机变量Y服从参数为1的指数分布，随机变量Xk={0,若Y≤k1,若Y>k(k=1,2),求(X1,X2)的联合分布率与边缘分布率.解答：因为Y服从参数为1的指数分布，X1={0,若Y≤11,若Y>1, 所以有P{X1=1}=P{Y>1}=∫1+∞e-ydy=e-1,P{X1=0}=1-e-1,同理P{X2=1}=P{Y>2}=∫2+∞e-ydy=e-2,P{X2=0}=1-e-2,因为P{X1=1,X2=1}=P{Y>2}=e-2，P{X1=1,X2=0}=P{X1=1}-P{X1=1,X2=1}=e-1-e-2,P{X1=0,X2=0}=P{Y≤1}=1-e-1,P{X1=0,X2=1}=P{X1=0}-P{X1=0,X2=0}=0,故(X1,X2)联合分布率与边缘分布率如下表所示：习题3在元旦茶话会上，每人发给一袋水果，内装3只橘子，2只苹果，3只香蕉. 今从袋中随机抽出4只，以X记橘子数，Y记苹果数，求(X,Y)的联合分布.解答：X可取值为0,1,2,3,Y可取值0,1,2.P{X=0,Y=0}=P{∅}=0,P{X=0,Y=1}=C30C21C33/C84=2/70,P{X=0,Y=2}=C30C22C32/C84=3/70,P{X=1,Y=0}=C31C20C33/C84=3/70,P{X=1,Y=1}=C31C21C32/C84=18/70,P{X=1,Y=2}=C31C22C31/C84=9/70,P{X=2,Y=0}=C32C20C32/C84=9/70,P{X=2,Y=1}=C32C21C31/C84=18/70,P{X=2,Y=2}=C32C22C30/C84=3/70,P{X=3,Y=0}=C33C20C31/C84=3/70,P{X=3,Y=1}=C33C21C30/C84=2/70,P{X=3,Y=2}=P{∅}=0,所以，(X,Y)的联合分布如下：习题4设随机变量X与Y相互独立，下表列出了二维随机变量(X,Y)的联合分布律及关于X与Y解答：由题设X与Y相互独立，即有pij=pi⋅p⋅j(i=1,2;j=1,2,3), p⋅1-p21=p11=16-18=124,又由独立性，有p11=p1⋅p⋅1=p1⋅16故p1⋅=14.从而p13=14-124-18, 又由p12=p1⋅p⋅2, 即18=14⋅p⋅2.从而p⋅2=12. 类似的有p⋅3=13,p13=14,p2⋅=34.将上述数值填入表中有习题5设随机变量(X,Y)的联合分布如下表：求：(1)a值；(2)(X,Y)的联合分布函数F(x,y)；(3)(X,Y)关于X,Y的边缘分布函数FX(x)与FY(y).解答：(1)\because由分布律的性质可知∑i⋅jPij=1, 故14+14+16+a=1,∴a=13.(2)因F(x,y)=P{X≤x,Y≤y}①当x<1或y<-1时，F(x,y)=0;②当1≤x<2,-1≤y<0时，F(x,y)=P{X=1,Y=-1}=1/4;③当x≥2,-1≤y<0时，F(x,y)=P{X=1,Y=-1}+P{X=2,Y=-1}=5/12;④当1≤x<2,y>0时，F(x,y)=P{X=1,Y=-1}+P{X=1,Y=0}=1/2;⑤当x≥2,y≥0时，F(x,y)=P{X=1,Y=-1}+P{X=2,Y=-1}+P{X=1,Y=0}+P{X=2,Y=0}=1;综上所述，得(X,Y)联合分布函数为F(x,y)={0,x<1或y<-11/4,1≤x<2,-1≤y<05/12,x≥2,-1≤y<01/2,1≤x<2,y≥01,x≥2,y≥0.(3)由FX(x)=P{X≤x,Y<+∞}=∑xi<x∑j=1+∞pij, 得(X,Y)关于X的边缘分布函数为：FX(x)={0,x<114+14,1≤x<214+14+16+13,x≥2={0,x<11/2,1≤x<21,x≥2,同理，由FY(y)=P{X<+∞,Y≤y}=∑yi≤y∑i=1+∞Pij, 得(X,Y)关于Y的边缘分布函数为FY(y)={0,y<-12/12,-1≤y<01,y≥0.习题6设随机变量(X,Y)的联合概率密度为f(x,y)={c(R-x2+y2),x2+y2<R0,x2+y2≥R,求：(1)常数c; (2)P{X2+Y2≤r2}(r<R).解答：(1)因为1=∫-∞+∞∫-∞+∞f(x,y)dydx=∫∫x2+y2<Rc(R-x2+y)dxdy=∫02π∫0Rc(R-ρ)ρdρdθ=cπR33,所以有c=3πR3.(2)P{X2+Y2≤r2}=∫∫x2+y2<r23πR3[R-x2+y2]dxdy=∫02π∫0r3πR3(R-ρ)ρdρdθ=3r2R2(1-2r3R).习题7设f(x,y)={1,0≤x≤2,max(0,x-1)≤y≤min(1,x)0,其它,求fX(x)和fY(y).解答：max(0,x-1)={0,x<1x-1,x≥1, min(1,x)={x,x<11,x≥1,所以，f(x,y)有意义的区域(如图)可分为{0≤x≤1,0≤y≤x},{1≤x≤2,1-x≤y≤1},即f(x,y)={1,0≤x≤1,0≤y≤x1,1≤x≤2,x-1≤y≤1,0,其它所以fX(x)={∫0xdy=x,0≤x<1∫x-11dy=2-x,1≤x≤20,其它,fY(y)={∫yy+1dx=1,0≤y≤10,其它.习题8若(X,Y)的分布律为则α,β应满足的条件是¯, 若X与Y独立，则α=¯,β=¯.解答：应填α+β=13;29;19.由分布律的性质可知∑i⋅jpij=1, 故16+19+118+13+α+β=1,即α+β=13.又因X与Y相互独立，故P{X=i,Y=j}=P{X=i}P{Y=j}, 从而α=P{X=2,Y=2}=P{X=i}P{Y=j},=(19+α)(14+α+β)=(19+α)(13+13)=29,β=P{X=3,Y=2}=P{X=3}P{Y=2}=(118+β)(13+α+β)=(118+β)(13+13)，∴β=19.习题9设二维随机变量(X,Y)的概率密度函数为f(x,y)={ce-(2x+y),x>0,y>00,其它,(1)确定常数c; (2)求X,Y的边缘概率密度函数；(3)求联合分布函数F(x,y); (4)求P{Y≤X};(5)求条件概率密度函数fX∣Y(x∣y); (6)求P{X<2∣Y<1}.解答：(1)由∫-∞+∞∫-∞+∞f(x,y)dxdy=1求常数c.∫0+∞∫0+∞ce-(2x+y)dxdy=c⋅(-12e-2x)\vline0+∞⋅(-e-y)∣0+∞=c2=1,所以c=2.(2)fX(x)=∫-∞+∞f(x,y)dy={∫0+∞2e-2xe-ydy,x>00,x≤0={2e-2x,x>00,x≤0,fY(y)=∫-∞+∞f(x,y)dx={∫0+∞2e-2xe-ydx,y>00,其它={e-y,y>00,y≤0.(3)F(x,y)=∫-∞x∫-∞yf(u,v)dvdu={∫0x∫0y2e-2ue-vdvdu,x>0,y>00,其它={(1-e-2x)(1-e-y),x>0,y>00,其它.(4)P{Y≤X}=∫0+∞dx∫0x2e-2xe-ydy=∫0+∞2e-2x(1-e-x)dx=13.(5)当y>0时，fX∣Y(x∣y)=f(x,y)fY(y)={2e-2xe-ye-y,x>00,x≤0={2e-2x,x>00,x≤0.(6)P{X<2∣Y<1}=P{X<2,Y<1}P{Y<1}=F(2,1)∫01e-ydy=(1-e-1)(1-e-4)1-e-1=1-e-4.习题10设随机变量X以概率1取值为0, 而Y是任意的随机变量，证明X与Y相互独立.解答：因为X的分布函数为F(x)={0,当x<0时1,当x≥0时, 设Y的分布函数为FY(y),(X,Y)的分布函数为F(x,y)，则当x<0时，对任意y, 有F(x,y)=P{X≤x,Y≤y}=P{(X≤x)∩(Y≤y)}=P{∅∩(Y≤y)}=P{∅}=0=FX(x)FY(y);当x≥0时，对任意y, 有F(x,y)=P{X≤x,Y≤y}=P{(X≤x)∩(Y≤y)}=P{S∩(Y≤y)}=P{Y≤y}=Fy(y)=FX(x)FY(y),依定义，由F(x,y)=FX(x)FY(y)知，X与Y独立.习题11设连续型随机变量(X,Y)的两个分量X和Y相互独立，且服从同一分布，试证P{X≤Y}=1/2. 解答：因为X,Y独立，所以f(x,y)=fX(x)fY(y).P{X≤Y}=∫∫x≤yf(x,y)dxdy=∫∫x≤yfX(x)fY(y)dxdy=∫-∞+∞[fY(y)∫-∞yfX(x)dx]dy=∫-∞+∞[fY(y)FY(y)]dy=∫-∞+∞FY(y)dFY(y)=F2(y)2∣-∞+∞=12,也可以利用对称性来证，因为X,Y独立同分布，所以有P{X≤Y}=P{Y≤X},而P{X≤Y}+P{X≥Y}=1, 故P{X≤Y}=1/12.习题12设二维随机变量(X,Y)的联合分布律为若X与Y相互独立，求参数a,b,c的值.解答：关于X的边缘分布为由于X与Y独立，则有p22=p2⋅p⋅2 得b=(b+19)(b+49) ①p12=p1⋅p⋅2 得19=(a+19)(b+49) ②由式①得b=29, 代入式②得a=118. 由分布律的性质，有a+b+c+19+19+13=1,代入a=118,b=29, 得c=16.易验证，所求a,b,c的值，对任意的i和j均满足pij=pi⋅×p⋅j.因此，所求a,b,c的值为a=118,b=29,c=16.习题13已知随机变量X1和X2的概率分布为且P{X1X2=0}=1.(1)求X1和X2的联合分布律；(2)问X1和X2是否独立？解答：(1)本题是已知了X1与X2的边缘分布律，再根据条件P{X1X2=0}=1, 求出联合分布. 列表如下：P{X1=1,X2=1}=0,P{X1=-1,X2=1}=0.再由p⋅1=p-11+p11+p01, 得p01=12, p-10=p-1⋅=p-11=14,p10=p1⋅-p11=14,从而得p00=0.(2)由于p-10=14≠p-1⋅⋅p⋅0=14⋅12=18, 所以知X1与X2不独立.习题14设(X,Y)的联合密度函数为f(x,y)={1πR2,x2+y2≤R20,其它,(1)求X与Y的边缘概率密度；(2)求条件概率密度，并问X与Y是否独立？解答：(1)当x<-R或x>R时，fX(x)=∫-∞+∞f(x,y)dy=∫-∞+∞0dy=0;当-R≤x≤R时，fX(x)=∫-∞+∞f(x,y)dy=1πR2∫-R2-x2R2-x2dy=2πR2R2-x2.于是fX(x)={2R2-x2πR2,-R≤x≤R0,其它.由于X和Y的地位平等，同法可得Y的边缘概率密度是：fY(y)={2R2-y2πR2,-R≤y≤R0,其它.(2)fX∣Y(x∣y)=f(x,y)fY(y)注意在y处x值位于∣x∣≤R2-y2这个范围内，f(x,y)才有非零值，故在此范围内，有fX∣Y(x∣y)=1πR22πR2⋅R2-y2=12R2-y2,即Y=y时X的条件概率密度为fX∣Y(x∣y)={12R2-y2,∣x∣≤R2-y20,其它.同法可得X=x时Y的条件概率密度为fY∣X(y∣x)={12R2-x2,∣y∣≤R2-x20,其它.由于条件概率密度与边缘概率密度不相等，所以X与Y不独立.习题15设(X,Y)的分布律如下表所示X\Y -112-12 1/102/103/102/101/101/10求：(1)Z=X+Y; (2)Z=max{X,Y}的分布律.解答：与一维离散型随机变量函数的分布律的计算类似，本质上是利用事件及其概率的运算法则. 注意，Z的相同值的概率要合并.概率(X,Y)X+YXYX/Ymax{X,Y}1/102/103/102/101/101/10(-1,-1)(-1,1)(-1,2)(2,-1)(2,1)(2,2)-2011341-1-2-2241-1-1/2-221-112222于是(1)习题16设(X,Y)的概率密度为f(x,y)={1,0<x<1,0<y<2(1-x)0,其他，求Z=X+Y的概率密度.解答：先求Z的分布函数Fz(z)，再求概率密度fz(z)=dFz(z)dz.如右图所示.当z<0时，Fz(z)=P{X+Y≤z}=0;当0≤z<1时，Fz(z)=P{X+Y≤z}=∫∫x+y≤zf(x,y)dxdy=∫0zdx∫0z-x1dy=∫0z(z-x)dx=z2-12x2∣0z=12z2；当1≤z<2时，Fz(z)=∫02-zdx∫0z-xdy+∫2-z1dx∫02(1-x)dy=z(2-z)-12(2-z)2+(z-1)2；当z≥2时，∫∫Df(x,y)dxdy=∫01dx∫02(1-x)dy=1.综上所述Fz(z)={0,z<012z2,0≤z<1z(2-z)-12(2-z)2+(z-1)2,1≤z<21,z≥2，故fz(z)={z,0≤z<12-z,1≤z<20,其它.习题17设二维随机变量(X,Y)的概率密度为f(x,y)={2e-(x+2y),x>0,y>00,其它,求随机变量Z=X+2Y的分布函数.解答：按定义FZ(Z)=P{x+2y≤z},当z≤0时，FZ(Z)=∫∫x+2y≤zf(x,y)dxdy=∫∫x+2y≤z0dxdy=0.当z>0时，FZ(Z)=∫∫x+2y≤zf(x,y)dxdy=∫0zdx∫0(z-x)/22e-(x+2y)dy=∫0ze-x⋅(1-ex-z)dx=∫0z(e-x-e-z)dx=[-e-x]∣0z-ze-z=1-e-z-ze-z,故分布函数为FZ(Z)={0,z≤01-e-z-ze-z,z>0.习题18设随机变量X与Y相互独立，其概率密度函数分别为fX(x)={1,0≤x≤10,其它, fY(y)={Ae-y,y>00,y≤0,求：(1)常数A; (2)随机变量Z=2X+Y的概率密度函数.解答：(1)1=∫-∞+∞fY(y)dy=∫0+∞A⋅e-ydy=A.(2)因X与Y相互独立，故(X,Y)的联合概率密度为f(x,y)={e-y,0≤x≤1,y>00,其它.于是当z<0时，有F(z)=P{Z≤z}=P{2X+Y≤z}=0;当0≤z≤2时，有F(z)=P{2X+Y≤z}=∫0z/2dx∫0z-2xe-ydy=∫0z/2(1-e2x-z)dx;当z>2时，有F(z)=P{2X+Y≤2}=∫01dx∫0z-2xe-ydy=∫01(1-e2x-z)dx.利用分布函数法求得Z=2X+Y的概率密度函数为fZ(z)={0,z<0(1-e-z)/2,0≤z<2(e2-1)e-z/2,z≥2.习题19设随机变量X,Y相互独立，若X与Y分别服从区间(0,1)与(0,2)上的均匀分布，求U=max{X,Y}与V=min{X,Y}的概率密度.解答：由题设知，X与Y的概率密度分别为fX(x)={1,0<x<10,其它, fY(y)={1/2,0<y<20,其它,于是，①X与Y的分布函数分别为FX(x)={0,x≤0x,0≤x<11,x≥1, FY(y)={0,y<0y/2,0≤y<21,y≥2,从而U=max{X,Y}的分布函数为FU(u)=FX(u)FY(u)={0,u<0u2/2,0≤u<1u/2,1≤u<21,u≥2,故U=max{X,Y}的概率密度为fU(u)={u,0<u<11/2,1≤u<20,其它.②同理，由FV(v)=1-[1-FX(v)][1-FY)]=FX(v)+FY(v)-FX(v)FY(v)=FX(v)+FY(v)-FU(v),得V=min{X,Y}的分布函数为FV(v)={0,v<0v2(3-v),0≤v<11,v≥1,故V=min{X,Y}的概率密度为fV(v)={32-v,0<v<10,其它.注：(1)用卷积公式，主要的困难在于X与Y的概率密度为分段函数，故卷积需要分段计算；(2)先分别求出X,Y的分布函数FX(x)与FY(y), 然后求出FU(u)，再求导得fU(u); 同理先求出FV(v), 求导即得fV(v).。

《概率论与数理统计》习题三答案-设二维随机变量(x,y)

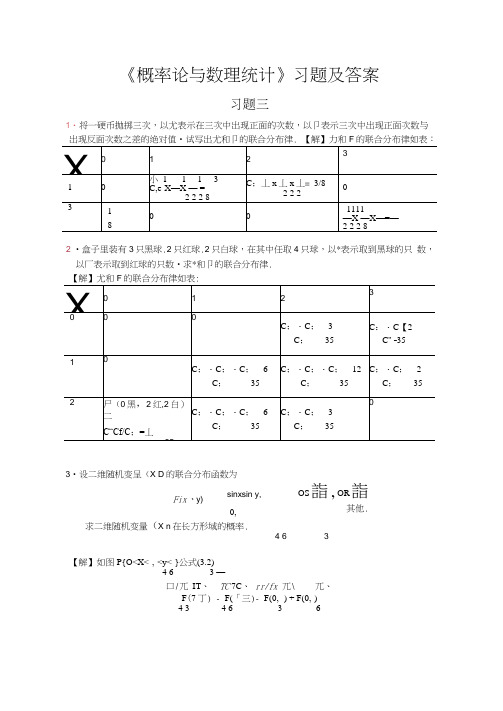
《概率论与数理统计》习题及答案习题三1・将一硬币抛掷三次，以尤表示在三次中出现正面的次数，以卩表示三次中出现正面次数与2 •盒子里装有3只黑球.2只红球.2只白球，在其中任取4只球，以*表示取到黑球的只数，以厂表示取到红球的只数•求*和卩的联合分布律.3•设二维随机变呈（X D 的联合分布函数为求二维随机变量（X n 在长方形域的概率.4 63【解】如图P{O<X<-,-<y<-}公式(3.2)4 6 3 —口/兀 IT 、 TC 7C 、 rr/fx 兀\ 兀、F (7 丁) - F(「三)- F(0, -) + F(0,-) 4 3 4 6 3 6Fix 、y)sinxsin y,0,OS詣,OR 詣其他.=sin —>sin — 一 sin —•sin — 一 sin O ・sin — + sin 0>sin= ^(73-1).4说明：也可先求出密度函数，再求概率。

4•设随机变量（匕D 的分布密度Ae H3r+4v \ x>0,y>0, 0, 其他.£' £' 12e _(3M+4v,di/dv _J(l-e _3x )(1-e -4-) y > 0,x > 0,0° ° =| o,其他(3) P{0<X<l,0<y<2)= p{o<x<i,o<y<2}=fj ： 12e _<3t *4v,d.vdy = (l-e-3 )(l-e _8)« 0.9499.5.设随机变量(X D 的概率密度为k(6 一兀一 y), 0 < x < 2, 2 <f (儿 y)=<0,(1) 确定常数k; (2) 求 P{X<\. K3}； (3) 求 HK1.5}； (4)求 PUHW4}.【解】(1)由性质有fix. y)=<求：(1)(2) (3) 常数川随机变量（x n 的分布函数;P{owg 0WK2}・【解】（1）由匚匚 fg y)dxdy =门「Ae 「'i &dy =£ = 1得(2)J=12由定义，有j* J f(x, y)dvdy = J ( J k(6 - x - y)dydx =8k = 1,故 R = -8(2) P{X v 1, Y v 3} = J ：/(x,y)dydx一曲•皿 €⑶ P{ X v 1.5} = JJ /(x, y)dAdy如图a [J/(x, y)d.vdyATP 曲 i —y)dy = ||.⑷ P{X+r<4}= JJ /(x,y)dxdy 如图y)dxdyX+YS4Dy6•设尤和F 是两个相互独立的随机变量，尤在（0, 0.2）上服从均匀分布，卩的密度函数为—r求:（1） X 与卩的联合分布密度；（2） P{Y^X\.【解】（1）因尤在（0, 0.2）上服从均匀分布，所以X 的密度函数为0, 其他.x<1.5fx(x )= 0 210<x<0.2,所以f(^y)X.Y 独立办(x)M(y)(2) P (y<X)= JJ fg y)dvdy 如图［f25e"5v dvdyy<x D=£'2 dxj ： 25e® dy = J (「(一5e 亠 + 5)<Lv =e _l a 0.3679・7•设二维随机变疑(x n 的联合分布函数为求(上D 的联合分布密度.&设二维随机变呈(儿力的概率密度为求边缘概率密度. 【解】办(X )=匚/'(X,刃dy「4・8y(2-x)dy \lAx 2(l-x)y 0 <x< h o. 1°，其他f Y (y) =匚/(兀刃 dxJ 4.8y(2 -x)dx _ J2.4y(3 -4y + y 2), 0 < y < 1, o =|o, 其他,y > o. 其他.0,25e _5v ,0,0<x<0.2且y >0, 其他.F5刃屮十*严)0.x > 0, y > 0,其他【解】oxdy0、 x >0,y> 0,其他.4.8y(2-A 0,0<x<l,0<y<x,其他y)=<求边缘概率密度.【解】办（尤）=匚f（x，y）dyI e~v dy=Jx ・=<0, ・A(y) = JJ/GvoOdx10.设二维随机变量（X D的概率密度为cFy, X2 < y < 1,0, 其他匚匚 /(也y )^2如图|7 fg y)dxdy1)=f dvj1, ex2 ydy = * c = 1.21c = —•4fx W =匚/a，y)dyy)=<fix、e0,0<x< ”其他(1)(2)试确定常数c；求边缘概率密度.x> 0,其他.0,f S e'v cLv=< Jo0,y>0, a 其他.yiw o Xf (x、y)=<【解】（1）题10图【解】办（兀）=匚/（血刃⑪f ldy = 2x.= J-x 0.ildv = 1 + y,一1 vy <0,所以丄，I y l< x < 1,2x 0, 其他J ；pyd ），0,—x~(l — %4), —lSxSl,8 0,其他.0,7 ?0<y<t 厶0,其他.11 •设随机变量（上D 的概率密度为 1, 0,f (%, y)=<|y| < x, 0 < x < 1,其他求条件概率密度fnx （y I X ）,A (y) =匚/(""nf ldx = 1 -y, 0,0<y<h 其他.0< x< 1, 其他.AirCviy) =/g)A(y)1o,-y < A： <1,其他.345P{X=x t} 11 _ 1 c[ = To2 _ 2 c[ = io3 _ 3 c[ = lo610201 _ 1 cf ~io2 _ 2 c[_lo310 3001 _ 1 c[= 10110P{y = y i}1To3 To61012•袋中有五个1, 2. 3, 4, 5,从中任取三个，记这三个中最小的为兀最大的为X （1）求X与『的联合概率分布；（2）X与卩是否相互独立？【解】（1）尤与卩的联合分布律如下表⑵因吩=啊一3}=劭存侖工存吟+ = 3}故尤与卩不独立（2）尤与卩是否相互独立？(2)因P{X= 2}.P{Y = 0.4} = 0.2x0.8 = 0.160.15 = P(X = 2,K = 0.4),1）上服从均匀分布，F 的概率密度为y > 0,其他.（1）求尤和卩的联合概率密度；（2）设含有日的二次方程为才+2炉扫0,试求臼有实根的概率.（2）方程a 2+2Xa + Y = 0有实根的条件是△ = (2X)2-43 0故斤2 K,从而方程有实根的概率为：P{X 2>r )= JJ /(x,y)drdyA 2>V= I -V^[①⑴-①(0)]= 0.1445.15 •设才和F 分别表示两个不同电子器件的寿命（以小时计），并设X 和卩相互独立，且服从同一分布，其概率密度为[1000f 3 ==〔0,求Z^X/Y 的概率密度.故尤与卩不独立.【解】（1） 14•设*和卩是两个相互独立的随机变量，*在（0,0,x > 1000, 其他fi (y)=【解】如图,z 的分布函数巧⑵= P{Z<z} = P[—<z}当O 〈z<l 时，（这时当尸1000时，尸型2）（如图a ） 106Fz ⑵=”詈"dy =打dy 打毎dx〉•注(1) 当zWO 时，巧（z ）= o2zz> 1, /z ⑵£2y0,0<z<l, 其他.ZT 5 Z ' I ， 2z—,0 < z < h 2 0, 其他.16 •设某种型号的电子管的寿命（以小时计）近似地服从M160,20‘）分布•随机地选取4 求其中没有一只寿命小于180的概率.【解】设这四只寿命为上（住123,4）,则尤二2（160 , 202）,只,(2)当时，（这时当尸10’时，尸102）（如图b ）传⑵=JI 詈dg ，=叵呱；詈"103 106 12z从而P{minCX,, X 2, X 3, X 4) > 180)X.之间独AtPfX, > 180}<P{X 2 > 180}P{X 3>180)eP{X 4>180)=[1 一P{XV80}]・[1 一P{X? v 180}]41-P{X 3<180}J41-P{X 4<180}]= [1-0(1)]4=(O 」58『 =0・00063・17•设匕F 是相互独立的随机变量，其分布律分别为P{X-k} =p (&), A=0, L 2,…，P{JM=g (r), r=0, U 2,….证明随机变疑卅卩的分布律为PC}二工 p (k)q(i -灯,，二0, 1> 2, •••・【证明】因X 和卩所有可能值都是非负整数，所以^Z = i} = {X + Y = i]= {X=0,Y = i}U{X = l" = i — l}U ・・・U{X=/』= 0}于是P{Z = i} = y P{X =k,Y = i-k}X.Y 相互独立 y P{X = k}.P{Y = i-k}R.O'女.0= ±P(k)q(i -k)£■(>1&设兀卩是相互独立的随机变量，它们都服从参数为”，p 的二项分布.证明Z=X+Y 服从参数为2m, p 的二项分布•【证明】方法一：贰F 可能取值为0, 1, 2,…，2n.kP {X +Y = R } =工p{xf-0= [1-P{X 1 <180)]4=180-160H20 jjk= ^P(X =i^P{Y = k-i}J-0方法二：设“】，“2,・「"n ； “J , P2 ，…，"J 均服从两点分布(参数为P ),则於 “l+“2+・・・+〃m U +"/ +•••+“/ •於片 “|+〃2+・・・+“/"「+"/ +•••+“/ ,所以，卅F 服从参数为(2/7.P )的二项分布.X0 1 2 3 4 5 0 0 0.01 0. 03 0. 05 0. 07 0. 09 1 0.01 0. 02 0. 04 0. 05 0. 06 0. 08 2 0.01 0. 03 0. 05 0. 05 0. 05 0. 06 30.010. 020. 040. 060. 060. 05(1)求刊后2 I 比2}, P{K=3 I 后0}(2) 求J^max (X JO 的分布律； (3) 求itmin (X JO 的分布律； (4)求炉卅卩的分布律.【解】⑴吩—J ；/二「P{X=2,Y = 2} j^P{X=i,Y = 2} J-0P{X=0V = 3} £p{X=0，UI(2) P{V=i} = P{max(X.Y) = i} = P{X=i,Y<i} + P{X <i.Y = i]r-li=》P{X =i,Y = £} +》P{X =«Y = f},7 = 0,1,2,3,4.5 JO10P F2n-k(2n\J >0.05 ~ 0^25P{Y = 3IX =0}=P{Y = 3,X =0) P{X=0}0.01 _ 1 0^03~3p"q 21所以J/的分布律为J^max (Z Y)0 1 2 3 4 5p0. 040. 160. 28 0. 240. 28(3) P{U=i} = P{min(X,Y) = i}= P{X =i.Y>i} + P{X >i,Y = i]35= ^P{X=i y Y = k}+ Z P{X=k,Y = i} k7(4) 类似上述过程，有1 2 3 4 56780?020?06 6773671902467196712 676520•雷达的圆形屛幕半径为乩设目标出现点(上力在屏幕上服从均匀分布. (1)求 P{J>0 I (2)设 JhnaxU ； y\9【解】因(上力的联合概率密度为Jj/(’y)dby>0 y>x ___________jj/(A-,y)do-i = 0J,2,3,于是V0. 280. 30 0. 25 0. 17/(儿 y)= < 1TI R 20, X 1 + y 2 <R\其他.(1) P{Y>0\Y>X} =P{Y>0”>X}P{Y>X}y>x3/8 _ 3172 "4(2) P{M>Q] = P{max(X.y )>0} = l-P{max(X,Y)<0}= l-P{X<0,r<0} = l-JJ f(x. y)db.r<0 y<021 •设平面区域〃由曲线y-\/x 及直线尸0, A=l,x=e 2所围成，二维随机变量(上力在区域〃上服从均匀分布，求(尤D 关于尤的边缘概率密度在齐2处的值为多少？r c 2 1【解】区域〃的面枳为S o = | -cLv = lnx f =2. (XK)的联合密度函数为 J1 V1 <x<e 2,0< y < —,x 其他.(X D 关于才的边缘密度函数为所以人⑵冷22•设随机变量尤和卩相互独立，下表列出了二维随机变量(儿力联合分布律及关于/和卩的边/3P{F 对二P ：X\ Xz1/8 1/8"{y=y.} =P >1/61【解】因P{Y = y j } = P j =XP{X=x i ,Y = y j },(-1故 P{Y = y }} = P{X=x r Y = y {} + P{X=x 2.Y = yi }.从而 P{X=x v Y = y,}丄1 _ 1 "6^8" 24* 而才与卩独立，故 P{X =x i ]^P{Y = yj} = P{X =x p y = y.). 从而 P{X=x l }x- = P{X=x }>Y = y }] = —.624即：P{X 十眾又 P{X=x }} = P{X=x }.Y = y }} + P{X=x^Y = y 2} + P{X=x {.Y = y 3}.£/(x,y)= 20,1 <x<e 2, 其他.即丄=-L + l + P{X=xr = yJ,4 24 8 i••狎从而P{X=x r Y = y3} = ^. 丄乙13同理P{Y = y2} = -. P{X=x2.Y = y2} = -2o3 1 1 1 又工卩{丫=儿} = 1・故川丫=儿} =1_7_3 = ?3同理P{X=x2} = -.从而P{X=x2,Y = y i} = P{Y = y i}-P{X=x r Y = y.} = L-^ = L 故23•设某班车起点站上客人数才服从参数为人（/1>0）的泊松分布，每位乘客在中途下车的概率为p（o<p<l）,且中途下车与否相互独立，以F表示在中途下车的人数，求：（1）在发车时有”个乘客的条件下，中途有刃人下车的概率；（2）二维随机变量（尤，力的概率分布. 【解】仃)P{Y = m\X=n} = C；；p m(1 -p)n'm,0</n</?,H = 0J,2,• • •.(2) P{X=mY = m} = P{X=n}>P{Y = m\X= n}A 1', n < m <n,n = 0,1,2,・・・・1 2 )24•设随机变量*和卩独立，其中才的概率分布为FL 而卩的概率密度为fg(0.3 0.7；求随机变量決於F 的概率密度g(u).【解】设尸(刃是F 的分布函数，则由全概率公式，知作於卩的分布函数为G(u) = P{X +Y <u} = 0.3P{X +Y <u \ X = \} + 0.7P{X + Y <u \ X = 2}= 0・3P{mX=l} + 0・7P{YS — 2IX=2} 由于才和卩独立，可见G(w) = 0・3P{ y<z/-l} + 0.7P{y<M-2} = 0・3F (M —l) + 0・7F(" — 2)・由此，得〃的概率密度为g(“)= G f(u) = 0.3F\u -1) + 0.7F (“ 一 2)=0・3/(" — 1) + 0・7/(“一2)・25. 25.设随机变量*与F 相互独立，且均服从区间［0.3］上的均匀分布，求/^{max(X H W1}.解：因为随即变量服从［0, 3］上的均匀分布，于是有因为兀卩相互独立，所以0<x<3,0<y<3,x<0, y<0,x>3, y>3.推得 P{max{X,y}<l)=l.26.设二维随机变量(尢力的概率分布为10 1 1 a0.2 0 0. 1 b0.210. 1c其中a 、b 、c 为常数，且X 的数学期望Eg 0.2/{卩冬0|辰0}二0・5,记Z-X^Y.求://!£fM = <30<x<3,(X x<0,x>3;£/(>') = * 30,0<y<3, y < 0,y > 3.fg y)=1-9（1） a 、b 、c 的值；（2） Z 的概率分布；（3） P{X^ ・解（1）由概率分布的性质知，0“心0・6=1由 E （X ） = -0.2,可得-a + c = -OA.得a +b = 0.3.解以上关于血b 9 c 的三个方程得a = 0・2,b = 0・l,c = 0.1.(2) Z 的可能取值为2, L 0, h 2,P{Z = _2} = P{X =_1,丫 = _1} = 0.2,P{Z = —1} = P{X=—1" = O} + P{X=O,Y = —1}=O ・1,P{Z = O} = P{X=—1,Y = 1} + P{X=OV = O} + P{X=1V = —1} = O ・3,P{Z = 1} = P{X =1V = O} + P{X=OV = 1} = O ・3,P{Z = 2} = P{X=l" = l} = 0.1,即z 的概率分布为P{X=Z} = P{Y = 0}=0」+b + 0・2 = 0・l + 0・l + 0・2 = 0・4.即 a+b+c = 0. 4.再由p{r<o|x<o ( =p{x<o,r<o )P{X<0}= 0.5a +b + 0.5。

概率论与数理统计作业(第三章)

院（系）班姓名学号第三章随机向量练习3.1 二维随机向量及其分布一、填空1.设二维随机变量),(Y X 的概率密度为, 510,49,(,)0, C x y f x y其它 ,则C ;2. 设二维随机变量),(Y X 的概率密度为(2)2, 0,0,(,)0, x y e x y f x y 其它,则{1}P X Y ;3.设二维随机变量),(Y X 的分布函数为1, 0,0,(,)0, x y x y e e e x y F x y 其它,则二维随机变量),(Y X 的概率密度为 ; 4. 设二维随机变量),(Y X 的概率密度为22220(,)(16)(25)f x y x y,则二维随机变量),(Y X 的分布函数为 ;5.用),(Y X 的联合分布函数),(y x F 表示下述概率：（1） },{c Y b X a P ; （2） },{b Y a X P ; （3） }0{a Y P ; （4） },{b Y a X P . 二、选择题1、设随机变量101,1,2111424i X i，且满足条件12{+=0}=1P X X ，则12{}P X X ( )A.0B.14 C. 12D.1 2.已知随机变量),(Y X 在区域{(,)|11,11}D x y x y 上服从均匀分布，则下列概率等于14的是（） A. {0}P X Y B. {0}P X YC. {(,)0}P MAX X YD. {(,)0}P Min X Y三．掷二枚硬币，以X 表示第一枚硬币出现正面的次数，Y 表示第二枚硬币出现正面的次数，试求二维随机变量),(Y X 的联合分布。

四、设二维随机变量),(Y X 的概率密度2, 01,02,(,)30, xyx x y f x y 其它 ,试求{1}P X Y 。

五、设二维随机变量),(Y X的概率密度222222( ,(,)0, C R x y R f x y x y R,求:(1) 系数C ; (2) ),(Y X 落在222()x y r r R 内的概率。

概率论与数理统计：c3_1 二维随机变量及其分布

例3.1.8
命题 3 .1 .1 若 X , Y ～ N 1 , 1 2 ; 2 , 2 2 ; 则
X
~
N
1
,
2 1
Y
~
N
2
,
2 2
2021/3/5
16
例：炮弹发射试验
炮弹在地面的命中点位置要由两个随机变量( X , Y )来确定。
飞机在空中飞行的位置由三个随机变量( X , Y, Z )来确定。
3 若f x , y在x , y处连续。则
2Fx, y
f x, y
xy
2021/3/5
11
二维随机变量及其分布
4 若G R2 , 有
p X ,Y G f x, y dxdy
5
x
,
y的
边
缘
概
率
G
密
度
为
fX x
f x , ydy
fY y
f x , ydx
证：FX x F x ,
定义：对任意实数对 ( x , y ) ∈R2 记
{ X ≤ x , Y ≤ y } = { X ≤ x } ∩{ Y ≤ y }
称二元函数
F(x,y)=P{X≤x,Y≤y}
为( X , Y ) 的联合分布函数.
一维随机变量 X、Y 的分布函数FX(x)与 FY(y)称
为( X, Y ) 的边缘分布函数。
X
2021/3/5
23
解：
fY
y
f
x,
y
dx
0 y0
1
1 y
2
x
2
dx y
0 y1
1
y
2

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

概率论与数理统计第三章二维随机变量及其概率分布例题1．甲乙两人独立地进行两次射击，命中率分别为0.2、0.5，把X 、Y 分别表示甲乙命中的次数，求（X,Y ）联合分布律。

2．袋中有两只白球，两只红球，从中任取两只以X 、Y 表示其中黑球、白球的数目，求（X,Y ）联合分布律。

3．设，且P{}=1，求（）的X 1=(‒1011/41/21/4)
X 2=(011/21/2)X 1X 2=0X 1，X 2联合分布律，并指出是否独立。

X 1，X 24．设随机变量X 的分布律为Y=，求（X,Y ）联合分布律。

X 2X Y 01
概率论与数理统计第三章二维随机变量及其概率分布例题
5．设（X,Y ）的概率分布为且事件{X=0}与{X+Y=1}独立求a ，b 。

6. 设某班车起点上车人数X 服从参数λ(λ>0)的泊松分布，每位乘客中途下车的概率为P （0<P<1）相互独立。

以Y 表示中途下车的人数。

（1）求在发车时有n 个人的情况下，中途m 个人下车的概率；（2）求（X,Y ）联合分布律。

7. 设二维随机变量（X,Y ）联合分布函数F(x.y)=A(B+arctan ) (C+arctan )。

x 2y
3（1）A 、B 、C （2）(X,Y)的联合密度f(x,y) （3）（X,Y ）的边缘密度，f z (x)f Y (y)8.设f(x,y)= 为二维随机变量（X,Y ）的联合密度函数，求：{C(x +y)00≤y ≤x ≤1其它01/3B 1
a 1/4
概率论与数理统计第三章二维随机变量及其概率分布例题（1）C 的值（2）， (3)P{X+Y ≤1}并判别X 与Y 是否独立。

f z (x)f Y (y)9．设f(x,y)= 为（X,Y ）的密度函数，求{10 |y |<x,0<x <1其它：(1) f X (x ), f Y (y ) (3)P{X>1/2|Y>0}(2) f Y|X (y|x ), f X|Y (x|y )10. 设f(x,y)= 为（X,Y ）的密度函数，求 {12x 2y 0 1x ≤y ≤x,x ≥1 其它 f X|Y (x|y )11. 设f(x,y)= 为（X,Y ）的密度函数，求的联合分布
{4xy 0 0≤x ≤1,0≤y ≤1 其它（X,Y ）
概率论与数理统计第三章二维随机变量及其概率分布例题
函数。

12.设X,Y 独立，均服从(0,1)上的均匀分布，Z 的密度函数f Z (Z )。

13. 设f(x,y)= 为（X,Y ）的密度函数，Z=X+Y,求的密度函{2（x +y ）0 0≤x ≤y ≤1 其它 Z 数。

f Z (Z )14.设X,Y 独立，X~N(μ,),Y~V(-π,π),Z=X+Y,求，结果用Φ(x)表示。

σ2
f Z (Z )
15.设（X,Y ）的联合密度函数为f(x,y)=,Z=X+Y,求Z 的概率密度。

12πδ12δ22e ‒12(x 2δ12+y 2δ22
)16.
设f(x,y)= 为（X,Y ）的密度函数，Z=X+2Y,求的密度函数
{2e ‒x ‒2y 0 x >0,y >0 其它 Z 。

f Z (Z )17. 设X,Y 独立，均服从N (0,1),Z==, 求的密度函数。

X 2+Y 2 Z f Z (Z )
18. 设X,Y 独立，均服从U (-1,1),Z==, 求的密度函数。

XY Z f Z (Z )19. 设X,Y 独立，均服从U (0,1),Z==, 求的密度函数。

X Y Z f Z (Z )20. 设X,Y 独立，其分布函数分别为，分别求max{X,Y},min{X,Y}的分布函数。

f Z (x )f Y (y )。