九年级数学: 24.1.3弧、弦、圆心角练习题含答案
人教版九年级数学上册 24.1.3 弧、弦、圆心角 同步练习卷
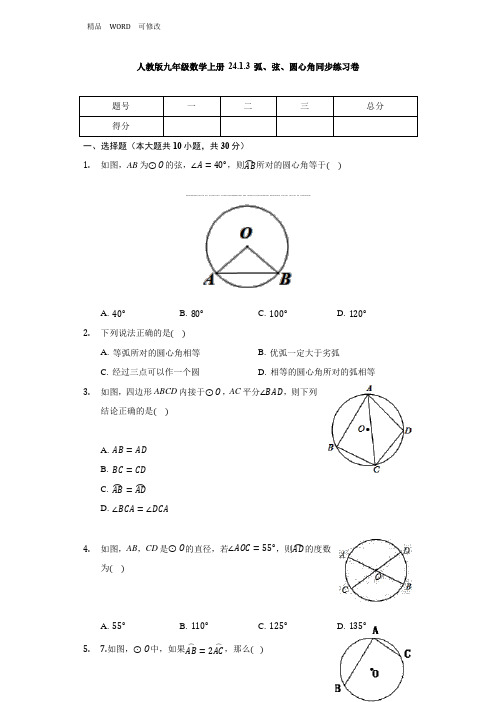
人教版九年级数学上册24.1.3 弧、弦、圆心角同步练习卷题号一二三总分得分一、选择题(本大题共10小题,共30分)1.如图,AB为⊙O的弦,∠A=40°,则AB⏜所对的圆心角等于()A. 40°B. 80°C. 100°D. 120°2.下列说法正确的是()A. 等弧所对的圆心角相等B. 优弧一定大于劣弧C. 经过三点可以作一个圆D. 相等的圆心角所对的弧相等3.如图,四边形ABCD内接于⊙O,AC平分∠BAD,则下列结论正确的是()A. AB=ADB. BC=CDC. AB⏜=AD⏜D. ∠BCA=∠DCA4.如图,AB,CD是⊙O的直径,若∠AOC=55°,则AD⏜的度数为()A. 55°B. 110°C. 125°D. 135°5.7.如图,⊙O中,如果AB⌢=2AC⌢,那么()A. AB=ACB. AB=2ACC. AB<2ACD. AB>2AC6.如图,在⊙O中AC⏜=BD⏜,∠AOB=40°,则∠COD的度数()A. 20°B. 40°C. 50°D. 60°7.如图,AB,CD是⊙O的直径,AE⏜=BD⏜.若∠AOE=32°,则∠COE的度数是()A. 32°B. 60°C. 68°D. 64°8.如图,在⊙O中,已知弦AB长为16cm,C为弧AB的中点,OC交AB于点M,且OM∶MC=3∶2,则CM长为()A. 2cmB. 4cmC. 6cmD. 8cm9.如图,AB是⊙O的直径,C,D分别是⊙O上的两点,OC⊥OD,AC=2cm,BD=√2cm,则⊙O的半径是()A. √3cmB. 2cmC. √5cmD. 3cm10.如图,AB是⊙O的直径,C是AB⏜的中点,连接OC,点E,F分别是OA,OC上的点,若EF//AC,则∠EFC的度数为()A. 45°B. 60°C. 135°D. 160°二、填空题(本大题共5小题,共15分)11.已知圆O的半径长为6,若弦AB=6√3,则弦AB所对的圆心角等于______ .12.如图,在⊙O中,点C为弧AB的中点,OC交弦AB于D,如果AB=8,OC=5,那么OD的长为______.13.如图,在⊙O中,AB⏜=CD⏜,∠AOB与∠COD的关系是______.14.如图,AB是⊙O的直径,弦CD⊥AB于点E,如果AC⏜=CD⏜,则∠ACD的度数是______.15.如图所示,PO是⊙O直径所在的直线,且PO平分∠BPD,OE⊥AB,OF⊥CD,则:①AB=CD;②AB⌢=CD⌢;③PO=PE;④BG⌢=DG⌢;⑤PB=PD.其中结论正确的是_________.(填序号)三、解答题(本大题共5小题,共55分)16.如图,已知AB为圆O的直径,M,N分别为OA,OB的中点,CM⊥AB,DN⊥AB,垂足分别为M,N,连结OC,OD,求证:AC⏜=BD⏜.17.如图,已知⊙O的弦AB,E,F是弧AB上两点,AE⏜=BF⏜,OE、OF分别交于AB于C、D两点,求证:AC=BD.18.如图,在⊙O中,AB⏜=BC⏜,∠BOC=32°,求∠D的度数.19.如图,以□ABCD的顶点A为圆心,AB为半径作⊙A,分别交BC,AD于E,F两点,交BA的延长线于G,判断EF⌒和FG⌒是否相等,并说明理由.20.已知:在△ABC中,以AC边为直径的⊙O交BC于点D,在劣弧AD⏜上到一点E使∠EBC=∠DEC,延长BE依次交AC于G,交⊙O于H.(1)求证:AC⊥BH;(2)若∠ABC=45°,⊙O的直径等于10,BD=8,求①CGCD的值;②EH的长.1、最困难的事就是认识自己。
人教版九年级上数学《24.1.3弧、弦、圆心角》练习题(含答案)

24.1.3 弧、弦、圆心角01 基础题知识点1 圆心角的概念及其计算 1.下面图形中的角是圆心角的是(D)A B C D2.已知⊙O 的半径为5 cm ,弦AB 的长为5 cm ,则弦AB 所对的圆心角∠AOB =60°. 知识点2 弧、弦、圆心角之间的关系 3.下列说法正确的是(B)A .相等的圆心角所对的弧相等B .在同圆中,等弧所对的圆心角相等C .弦相等,圆心到弦的距离相等D .圆心到弦的距离相等,则弦相等4.(兰州中考)如图,在⊙O 中,点C 是AB ︵的中点,∠A =50°,则∠BOC =(A)A .40°B .45°C .50°D .60°5.(教材P85练习T2变式)(贵港中考)如图,AB 是⊙O 的直径,BC ︵=CD ︵=DE ︵,∠COD =34°,则∠AEO 的度数是(A)A .51°B .56°C .68°D .78°6.如图,已知A ,B ,C ,D 是⊙O 上的点,∠1=∠2,则下列结论中正确的有(D) ①AB ︵=CD ︵;②BD ︵=AC ︵;③AC =BD ;④∠BOD =∠AOC.A .1个B .2个C .3个D .4个7.如图,AB 是⊙O 的直径,BC ,CD ,DA 是⊙O 的弦,且BC =CD =DA ,则∠BCD 的度数为(C)A .100°B .110°C .120°D .135°8.如图,AB ,DE 是⊙O 的直径,C 是⊙O 上的一点,且AD ︵=CE ︵.BE 与CE 的大小有什么关系?为什么?解:BE =CE.理由如下: ∵AB ,DE 是⊙O 的直径, ∴∠AOD =∠BOE. ∴AD ︵=BE ︵.∵AD ︵=CE ︵,∴BE ︵=CE ︵. ∴BE =CE.9.如图,M 为⊙O 上一点,OD ⊥AM 于点D ,OE ⊥BM 于点E.若OD =OE ,求证:AM ︵=BM ︵.证明:连接OM. ∵OD ⊥AM ,OE ⊥BM ,∴AD =MD ,ME =BE ,∠ODM =∠OEM =90°.在Rt △DMO 和Rt △EMO 中,⎩⎪⎨⎪⎧OD =OE ,OM =OM ,∴Rt △DMO ≌Rt △EMO(HL). ∴DM =EM.∴AM =BM. ∴AM ︵=BM ︵.易错点 对圆中的有关线段的关系运用不当而致错10.如图,A ,B ,C ,D 是⊙O 上的四点,且AD =BC ,则AB 与CD 的大小关系为(B)A .AB>CDB .AB =CDC .AB<CD D .不能确定 02 中档题11.如图,已知A ,B ,C 在圆O 上,D ,E ,F 是三边的中点.若AB ︵=AC ︵,则四边形AEDF 的形状是(B)A .平行四边形B .菱形C .正方形D .矩形12.已知⊙O 中,M 为AB ︵的中点,则下列结论正确的是(C)A .AB >2AM B .AB =2AMC .AB <2AMD .AB 与2AM 的大小不能确定13.如图,AB 是半圆O 的直径,E 是OA 的中点,F 是OB 的中点,ME ⊥AB 于点E ,NF ⊥AB 于点F.在下列结论中:①AM ︵=MN ︵=BN ︵;②ME =NF ;③AE =BF ;④ME =2AE. 正确的有①②③.14.如图,AB 是⊙O 的直径,AC ︵=CD ︵,∠COD =60°. (1)△AOC 是等边三角形吗?请说明理由; (2)求证:OC ∥BD.解:(1)△AOC 是等边三角形. 理由:∵AC ︵=CD ︵, ∴∠AOC =∠COD =60°. 又∵OA =OC ,∴△AOC 是等边三角形.(2)证明:∵∠AOC =∠COD =60°, ∴∠BOD =180°-(∠AOC +∠COD)=60°. ∵OD =OB ,∴△ODB 为等边三角形. ∴∠ODB =60°.∴∠ODB =∠COD =60°. ∴OC ∥BD.15.(教材P84例3变式)如图,A ,B ,C 为圆O 上的三等分点. (1)求∠BOC 的度数;(2)若AB =3,求圆O 的半径长及S △ABC .解:(1)∵A ,B ,C 为圆O 上的三等分点, ∴AB ︵=BC ︵=AC ︵.∴∠BOC =13×360°=120°.(2)过点O 作OD ⊥AB 于点D , ∵A ,B ,C 为圆O 上的三等分点, ∴AB =AC =BC =3, 即△ABC 是等边三角形. ∴∠BAO =∠OBA =30°.则AD =32,故DO =32,OA =3,即圆O 半径长为 3.∴S △ABC =3×12×DO·AB =934.03 综合题16.如图,∠AOB =90°,C ,D 是AB ︵的三等分点,连接AB 分别交OC ,OD 于点E ,F ,求证:AE =BF =CD.证明:连接AC ,BD. ∵C ,D 是AB ︵的三等分点, ∴AC ︵=CD ︵=DB ︵. ∴AC =CD =DB. 又∠AOB =90°,∴∠AOC =∠COD =∠BOD =13∠AOB =13×90°=30°.∵OA =OB ,∴∠OAB =∠OBA =45°. ∴∠AEC =∠AOC +∠OAB =75°. 在△AOC 中,OA =OC ,∴∠ACO =180°-∠AOC 2=180°-30°2=75°.∴∠AEC =∠ACO.∴AE =AC. 同理BF =BD. ∴AE =BF =CD.。
人教版九年级数学上册 第二十四章 圆 24.1.3 弧、县、圆心角 课后练习

人教版九年级数学上册第二十四章圆24.1.3 弧、县、圆心角课后练习一、选择题1.如图,AB为⊙O直径,CD为弦,AB⊥CD于E,连接CO,AD,∠BAD=20°,下列结论中正确的有()①CE =OE②∠C=50° ③ ACD = ADC ④AD=2OEA.①④B.②③C.②③④D.①②③④2.如图,半径为R的⊙O的弦AC=BD,AC、BD交于E,F为BC上一点,连AF、BF、AB、AD,下列结论:⊙AE=BE;⊙若AC⊥BD,则AD=R;⊙在⊙的条件下,若CF CD=,AB=,则BF+CE=1.其中正确的是()A.⊙⊙B.⊙⊙C.⊙⊙D.⊙⊙⊙3.如图,AB是⊙O的直径,C是线段OB上的一点(不与点B重合),D,E是半圆上的点且CD与BE交于点F,用①DB DE=,②DC⊥AB,③FB=FD中的两个作为题设,余下的一个作为结论组成一个命题,则组成真命题的个数为()A.0B.1C.2D.34.如图,AB是O的直径,AB=4,C为AB的三等分点(更靠近A点),点P是O上一个动点,取弦AP的中点D,则线段CD的最大值为()A.2B C.D5.如图:已知AB是⊙O的直径,点C在⊙O上,点D在半径OA上(不与点O,A重合).若∠COA=60°,∠CDO=70°,∠ACD的度数是()A .60°B .50°C .30°D .10°6.已知点A 、B 、C 、D 、E 、F 是半径为r 的⊙O 的六等分点,分别以A 、D 为圆心,AE 和DF 长为半径画圆弧交于点P .以下说法正确的是( )①∠PAD=∠PDA=60º; ②△PAO ≌△ADE ;③r ;④AO ∶OP ∶PA=1.A .①④B .②③C .③④D .①③④7.下列命题是假命题的是( )A .在同圆或等圆中,同弧或等弧所对的圆周角相等B .平分弦的直径垂直于弦C .两条平行线间的距离处处相等D .正方形的两条对角线互相垂直平分8.如图 ⊙MN 是⊙O 的直径,MN=8⊙∠AMN=40°,点B 为弧AN 的中点,点P 是 直径MN 上的一个动 点,则PA+PB 的最小值为( )A .√3B .2√3C .3√3D .4√39.如图,点A 是半圆上的一个三等分点,点B 为弧AD 的中点,P 是直径CD 上一动点,⊙O 的半径是2,则PA PB +的最小值为( ⊙A .2BC 1D .10.如图,在平面直角坐标系xOy 中()(),3,0,3,0A B -,若在直线y x m =-+上存在点P 满足60APB ∠=︒,则m 的取值范围是( )A m≤≤B.m≤≤C m≤≤D.m≤≤二、填空题11.如图,在等腰直角三角形ABC中,∠ACB=90°,AB=8,点E是AB的中点,以AE为边作等边△ADE(点D与点C 分别在AB异侧),连接CD,则△ACD的面积是_________.12.点A、C为半径是3的圆周上两点,点B为弧AC的中点,以线段BA、BC为邻边作菱形ABCD,顶点D恰在该圆直径的三等分点上,则该菱形的边长为_____.13.如图,MN是⊙O的直径,OM=2,点A在⊙O上,30∠⊙B为弧AN的中点,P是直径MN上一动点,AMN=则PA+PB的最小值为______________.14.如图,AB、CD是⊙O的两条弦,若⊙AOB+⊙C=180°,⊙COD=⊙A,则⊙AOB=________15.如图⊙A⊙B⊙C⊙D是⊙O上的四个点⊙若AB CD BC AD+=+⊙且弦AB=8⊙CD=4⊙则⊙O的半径为________⊙三、解答题16.如图,在平面直角坐标系中,点P 是y 轴正半轴上一点,⊙P 与x 轴交与A ,B 两点,与y 轴交与C 点,OC 、OA 分别是方程214480x x -+=的两个根(OC >OA ),点D 是弧AC 上的一动点,点F 是弧AD 的中点.(1)求⊙P 的半径;(2)试判断∠CF A 与∠EFC 的大小关系,并说明理由;(3)随着D 点的运动,CE 的长度变化吗?若不变,请求出其值;若变化,请求出其变化范围.17.某处靠近海岸的海域有一片暗礁,当地海洋管理部门在海岸上建造了两座灯塔A ,B ,通告所有船只不要进入以AB 为弦的弓形区域(阴影部分)内(含边界)以免触礁,如图所示.现有一艘货轮P 正向暗礁区域靠近,当APB ∠多大时,才能避开暗礁?18.如图,在正方形ABCD 中,点E 在边AD 上运动(不运动至两端点),射线BE ,CD 交于点F ,O 为BDF ∆的外接圆,连结OA ,OF ,OB .(1)求OFB ∠的度数.(2)求证:180AOF AEF ∠+∠=︒.(3)若正方形ABCD 的边长为2.①当E 为AD 中点时,求四边形OAEF 的面积.②设OD ,BF 交于点M ,设BED ∆,EMD ∆,MFD ∆的面积分别为1S ,2S ,3S ,当BA 平分OBF ∠时,123::S S S =_________(直接写出答案).19.(理论学习)学习图形变换中的轴对称知识后,我们容易在直线l 上找到点P ,使AP BP +的值最小,如图1所示,根据这一理论知识解决下列问题:(1)(实践运用)如图2,已知O 的直径CD 为4,弧AD 所对圆心角的度数为60︒,点B 是弧AD 的中点,请你在直径CD 上找一点P ,使BP AP +的值最小,并求BP AP +的最小值.(2)(拓展延伸)在图3中的四边形ABCD 的对角线AC 上找一点P ,使APB APD ∠=∠.(尺规作图,保留作图痕迹,不必写出作法).20.如图,在平面直角坐标系中,二次函数y =a (x ﹣1)(x ﹣5)(a >0)的图象与x 轴交于A 、B 两点(点A 在点B 的左侧),与y 轴交于P 点,过其顶点C 作直线CH ⊥x 轴于点H .(1)若∠APB =30°,请直接写出满足条件的点P 的坐标;(2)当∠APB 最大时,请求出a 的值;(3)点P 、O 、C 、B 能否在同一个圆上?若能,请求出a 的值,若不能,请说明理由.(4)若a =15,在对称轴HC 上是否存在一点Q ,使∠AQP =∠ABP ?若存在,请直接写出点Q 的坐标;若不存在,请说明理由.21.在平面直角坐标系xOy 中,点A (x 1,y 1),B (x 2,y 2),若x 1x 2+y 1y 2=0,且A ,B 均不为原点,则称A 和B 互为正交点.比如:A (1,1),B (2,﹣2),其中1×2+1×(﹣2)=0,那么A 和B 互为正交点.(1)点P 和Q 互为正交点,P 的坐标为(﹣2,3),①如果Q 的坐标为(6,m ),那么m 的值为多少;②如果Q 的坐标为(x ,y ),求y 与x 之间的关系式;(2)点M 和N 互为正交点,直接写出∠MON 的度数;(3)点C,D是以(0,2)为圆心,半径为2的圆上的正交点,以线段CD为边,构造正方形CDEF,圆心F在正方形CDEF的外部,求线段OE长度的取值范围.22.如图,在⊙O中,AB⊙DE为⊙O的直径,C是⊙O上一点,且AD=CE⊙⊙1⊙BE与CE有什么数量关系?为什么?⊙2)若∠BOE=60°,则四边形OACE是什么特殊的四边形?请说明理由.23.如图,AB为⊙O的直径,点C是⊙O上一点,CD是⊙O的切线,∠CDB=90°,BD交⊙O于点E.(1)求证:=AC CE.(2)若AE=12,BC=10.①求AB的长;②如图2,将BC沿弦BC折叠,交AB于点F,则AF的长为【参考答案】1.B 2.D 3.D 4.D 5.D 6.C 7.B 8.D 9.D 10.D11.4+12或13.14.108°15.16.解:(1)解方程214480x x-+=,得16x=,28x=,OA OC<,6OA ∴=,8OC =,连接AP ,设⊙P 的半径为r ,则在Rt AOP △中,222AP OP AO =+,即()22268r r =+-, 解得254r =; (2)连接AC ,AP ,BP∵12AFB APB ACO PAC ∠=∠=∠+∠, 且1122CFB CPB CPA ∠=∠=∠, ∴CFA CFB AFB ∠=∠+∠,180EFC CFB ∠=︒-∠,∴21801800CFA EFC CFB AFB CPA ACO PAC ∠-∠=∠+∠-︒=∠+∠+∠-︒=, ∴∠CF A 与∠EFC 相等;(3)不变;∵点F 是弧AD 的中点,∴ECF ACF ∠=∠,易得CEF CAF ≌,∴10CE AC ===.17.解:货轮P 在航行时,只要使∠APB<55°,即在ACB 外行驶,就能避开暗礁. 18.(1) 解:∵∠ADB=45°, ∠ADF=90°,∴∠BDF=135°∴优弧BF =270°.∴BF =90°,∠BOF =90°∵OB=OF ,∴∠OFB=∠OBF=45°故答案为:45°(2)证明:连结OD (如图1),∵OB=OD ,OA=OA ,AB=AD ,∴△OAB ≌△OAD (SSS ).∴∠OAB=∠OAD=360901352︒-︒=︒. ∵∠OFB=45°,∴∠AOF+∠AEF=360°-135°-45°=180°图1(3)①作OH ⊥AD ,OG ⊥FD ,垂足分别为H ,G ,连结OD (如图2),图2由AE=ED ,易得△ABE ≌△DFE ,∴FD=AB=2,由OD=OF ,OG ⊥FD ,得GD=12FD = 由OH ⊥AD ,OG ⊥FD ,∠ADF=90°,得矩形OHDG ,∴OH=GD=1.由∠OAH=∠OAB -∠HAB=135°-90°=45°,得∠HOA=∠HAO=45°∴AH=OH=1,OG=HD=AH+AD=1+2=3.∵△OAD 的面积=21122AD OH ⨯⨯==,△ODF 的面积=23322DF OG ⨯⨯==, △FDE 的面积=12122ED DF ⨯⨯==, ∴四边形OAEF 的面积=△OAD 的面积+△ODF 的面积-△FDE 的面积=1+3-1=3. ②OD 与BF 交于点M 如图3:BA 平分OBF ∠∴OBA ABE MDE ∠=∠=∠又∵AEB MED ∠=∠ ∴AEB MED ∆∆∴90EMD BAE ∠=∠=︒∵OF=OB∴BM=MF设圆的半径为r∵OBA ABE MED MFD ∠=∠=∠=∠∵90FDE FMD ∠=∠=︒∴DEF MED ∆∆∴2DM ME MF =2(r ME =1)ME r =,1)(1BE BM ME r r =-== BED ∆,EMD ∆,MFD ∆的面积分别为1S ,2S ,3S ,三个三角形的高均为MD∴312::::(1:1)1):(2:1S S BE ME MF r r S ===图3故答案为:1):(2:1-19.解:(1)作点B 关于CD 的对称点E ,则点E 在圆上,连接AE 交CD 于点P ,则AP BP +最短,连接OA OB OE ,,. 60AOD ∠=︒,B 是弧AD 的中点,30AOB DOB ∴∠=∠=︒,B 关于CD 的对称点E ,3090DOE DOB AOE ∴∠=∠=︒∴∠=︒,又2OA OE ==,OAE ∴是等腰直角三角形,∴AE =(2)如图,作点B 关于AC 的对称点B′,连接DB′交AC 于点P , 由AC 是BB′的垂直平分线,可得∠APB=∠APD.20.解:(1)作△PAB 的外接圆⊙D ,连接DP 、DA 、DB ,如图1 ∴DP =DA =DB ,∵C 为抛物线顶点且CH ⊥x 轴∴CH 为抛物线对称轴,即CH 垂直平分AB∴D 在直线CH 上∵∠APB =30°∴∠ADB =2APB =60°∴△ABD 是等边三角形∵当y =0时,a (x ﹣1)(x ﹣5)=0 解得:x 1=1,x 2=5 ∴A (1,0),B (5,0)∴DP =DA =AB =4,H (3,0),直线CH :x =3∴AH =2,DH =∴D (3,设P (0,p )(p >0)∴PD2=32+(﹣p)2=42解得:p1=+p2=∴点P坐标为(0,+0,(2)作△PAB的外接圆⊙E,连接EP、EA、EB,如图2∵∠AEB=2∠APB∴∠AEB最大时,∠APB最大∵AB=4是定值∴EH最小时,∠AEB最大,此时⊙E与y轴相切于点P ∴EP⊥y轴于P∴四边形OHEP是矩形∴PE=OH=3∴EA=PE=3∴Rt△AEH中,EH==∴OP=EH∴点P坐标为(0,代入抛物线解析式得:5a∴a(3)点P、O、C、B能在同一个圆上.连接PB,取PB中点F,连接FO、FC∵∠POB=90°∴OF=PF=FB=12 PB∴点P、O、B在以点F为圆心、FB的长为半径的圆上若点C在⊙F上,则FC=FB∵抛物线解析式y=a(x﹣1)(x﹣5)=ax2﹣6ax+5a=a(x﹣3)2﹣4a ∴P(0,5a),C(3,﹣4a)∵B(5,0),F为PB中点∴F55,22a ⎛⎫ ⎪⎝⎭∴22222 22551169552525 34,5222442244a a a a FC a FB⎛⎫⎛⎫⎛⎫⎛⎫=-++=+=-+=+⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭∴22 11692525 4444a a +=+解得:a1a2∴a的值为6(4)对称轴HC上存在一点Q,使∠AQP=∠ABP作△PAB的外接圆⊙G,连接GP、GA,设⊙G与直线CH交于点Q ∴∠AQP=∠ABP当a=15时,点P(0,1)设G(3,b)(b>0)∴GP2=32+(b﹣1)2,GA2=(3﹣1)2+b2∵GP=GA∴32+(b﹣1)2=(3﹣1)2+b2解得:b=3∴G(3,3),GQ=GA=∴点Q坐标为(3,3+ 3,3.21.(1)①由题意:﹣2×6+3m=0,解得m=4,故答案为4.②由题意:﹣2x+3y=0,∴y=23 x.(2)设M(m,n),N(p,q),∴直线OM的解析式为y=nmx,直线ON的解析式为y=qpx,∵点M和N互为正交点,∴mp +nq =0,∴k OM •k ON =nq mp=﹣1, ∴OM ⊥ON .∴∠MON =90°.(3)如图1中,连接EF 交CD 于H ,作FQ ⊥CD 于Q .由题意DF =CF =2,CD =DE =,DQ =QC =FQ ,∵FQ ∥DE ,∴QH :DH =FQ :DE =FH :EH =1:2,∴HQ =3,FH 3=,∴EH =2FH =3,∴EF =FH +EH =在△OFE 中,EF ﹣OF ≤OE ≤EF +OF ,∴当点E 在y 轴的正半轴上时,O 、F 、E 共线,此时OE 的值最大,最大值为 ∵原点O 在正方形CDEF 的外部,∴当点E 在y 轴负半轴上时,OE 的值最小,最小值为2.∴符合条件的OE 的范围为:2≤OE22.⊙1⊙∵AB⊙DE 是⊙O 的直径,∴∠AOD=∠BOE⊙∴AD BE =⊙∵AD CE =⊙∴BE CE ⊙∴BE=CE⊙⊙2)连结OC⊙∵∠BOE=60°⊙BE=CE⊙∴∠COE=60°⊙∵OC=OE⊙∴△COE是等边三角形,∵∠AOC=180°⊙60°⊙60°=60°⊙OA=OC⊙∴△AOC是等边三角形,∴OE=CE=OA=AC=OC⊙∴四边形OACE是菱形.23.解:(1)如图1,连接OC交AE于M,∵DC与⊙C相切于点C,∴OC⊥DC,即:∠OCD=90°,∵AB是⊙O的直径,∴∠AEB=90°,∵∠CDB=90°,∴CD∥AE,∴OC⊥AE,∴弧AC=弧CE;(2)①由(1)知,∠D=∠OCD=∠DEM=∠EMC=90°,∴四边形CMED是矩形,∴CD=ME=AM=12AE=6,在Rt△BCD中,根据勾股定理得,BD8,∴cos∠DBC=45,∵∠CAM=∠DBC,∴cos∠CAM=AMAC=45,∴AC=152,在Rt△ABC中,根据勾股定理得,AB=252;②如图2,在Rt△ABE中,根据勾股定理得,BE=7 2连接EF,∵弧AC=弧CE,∴∠ABC=∠DBC,由折叠知,BF=BE,∴AF=AB﹣BF=252﹣72=9,故答案为:9.。
人教版九年级上册数学 24.1.3弧、弦、圆心角 同步练习(含解析)

24.1.3弧、弦、圆心角同步练习一.选择题1.如图,半径为R的⊙O的弦AC=BD,且AC⊥BD于E,连结AB、AD,若AD=,则半径R的长为()A.1B.C.D.2.如图,△ABC的顶点A、B、C均在⊙O上,若∠ABC+∠AOC=75°,则∠OAC的大小是()A.25°B.50°C.65°D.75°3.如图,AB是⊙O的直径,点D,C在⊙O上,∠DOC=90°,AC=2,BD=2,则⊙O 的半径为()A.B.C.D.4.如图:AB为半圆的直径,AB=4,C为OA中点,D为半圆上一点,连CD,E为的中点,且CD∥BE,则CD的长为()A.B.C.D.5.如图,AB为⊙O的直径,C为AB上一点,AD∥OC,AD交⊙O于点D,连接AC,CD,设∠BOC=x°,∠ACD=y°,则下列结论成立的是()A.x+y=90B.2x+y=90C.2x+y=180D.x=y6.如图,已知AB和CD是⊙O的两条等弦.OM⊥AB,ON⊥CD,垂足分别为点M、N,BA、DC的延长线交于点P,联结OP.下列四个说法中:①;②OM=ON;③P A=PC;④∠BPO=∠DPO,正确的个数是()A.1B.2C.3D.47.如图,在⊙O中,AB,CD是两条弦,OM⊥CD,ON⊥AB,如果AB=CD,则下列结论不正确的是()A.∠AON=∠DOM B.AN=DM C.OM=DM D.OM=ON8.如图,已知A,B,C,D是圆上的点,弧AD=弧BC,AC,BD交于点E,则下列结论正确的是()A.AB=AD B.BE=CD C.AC=BD D.BE=AD二.填空题9.如图,AB和DE是⊙O的直径,弦AC∥DE,若弦BE=3,则弦CE=.10.如图,已知点C是⊙O的直径AB上的一点,过点C作弦DE,使CD=CO.若的度数为40°,则的度数是.11.如图,AB是⊙O的直径,点D、C在⊙O上,∠DOC=90°,AD=2,BC=,则⊙O 的半径长为.12.如图,在⊙O中,,∠1=30°,的度数为.13.如图,AB是⊙O的直径,M、N分别是AO,BO的中点,CM⊥AB,DN⊥AB,则的度数.14.如图,AB是⊙O的直径,弧BC、弧CD与弧DE相等,∠COD=40°,则∠AOE=.15.如图,AB为⊙O的直径,△P AB的边P A,PB与⊙O的交点分别为C、D.若==,则∠P的大小为度.三.解答题16.如图,⊙O中的弦AB=CD,AB与CD相交于点E.求证:(1)AC=BD;(2)CE=BE.17.如图,AB、AC是⊙O的两条弦,且AB=AC,点D是的中点,连接并延长BD、CD,分别交AC、AB的延长线于点E、F.(1)求证:DF=DE;(2)若BD=6,CE=8,求⊙O的半径.参考答案1.解:∵弦AC=BD,∴,∴,∴∠ABD=∠BAC,∴AE=BE;连接OA,OD,∵AC⊥BD,AE=BE,∴∠ABE=∠BAE=45°,∴∠AOD=2∠ABE=90°,∵OA=OD,∴AD=R,∵AD=,∴R=1,故选:A.2.解:∵根据圆周角定理得:∠AOC=2∠ABC,∵∠ABC+∠AOC=75°,∴∠AOC=×75°=50°,∵OA=OC,∴∠OAC=∠OCA=(180°﹣∠AOC)=65°,故选:C.3.解:作半径OE⊥AB,连接DE,作BF⊥DE于F,如图,∵∠DOC=90°,∠BOE=90°,∴∠DOE=∠AOC,∴DE=AC=2,∵∠BDE=180°﹣×90°=135°,∴∠BDF=45°,∴DF=BF=BD=×2=2,在Rt△BEF,BE==2,∵△BOE为等腰直角三角形,∴OB=×2=.故选:D.4.解:如图,连接EO并延长与DC的延长线相交于点K,连接BD交OE于点H,∵E为弧AD中点,∴OE⊥AD,BH=DH,∵BE∥CD,∴∠EBH=∠KDH,∠E=∠K,∴△BHE≌△DHK(AAS),∴BE=KD=2x,EH=KH,∵BE∥CD,∴△KCO∽△EBO,∴,∵AB是半圆⊙O的直径,AB=4,C为OA的中点,∴,∴KO=1,KC=x,∴KE=KO+OE=1+2=3,∴EH=KH=1.5,OH=0.5,∵BE2﹣EH2=BH2=BO2﹣OH2,∴4x2﹣1.52=22﹣0.52,解得:x=,∴CD=KD﹣KC=2x﹣x=x=,故选:B.5.解:连接BC,由圆周角定理得,∠BAC=∠BOC=x°,∵AB为⊙O的直径,∴∠ACB=90°,∴∠B=90°﹣x°,∵四边形ABCD是⊙O的内接四边形,∴∠D=180°﹣∠B=90°+x°,∵OA=OC,∴∠OCA=∠OAC=x°,∵AD∥OC,∴∠DAC=∠OCA=x°,∴∠ACD=180°﹣∠DAC﹣∠D,即y=180°﹣x°﹣(90°+x°)=90°﹣x°,∴x+y=90,故选:A.6.解:如图连接OB、OD;∵AB=CD,∴=,故①正确∵OM⊥AB,ON⊥CD,∴AM=MB,CN=ND,∴BM=DN,∵OB=OD,∴Rt△OMB≌Rt△OND,∴OM=ON,故②正确,∵OP=OP,∴Rt△OPM≌Rt△OPN,∴PM=PN,∠OPB=∠OPD,故④正确,∵AM=CN,∴P A=PC,故③正确,故选:D.7.解:∵AB=CD,OA=OD,OB=OC,∴△OAB≌△ODC(SSS),∠AOB=∠DOC,∵OM⊥CD,ON⊥AB,∴OM=ON,DM=CM,AN=NB,∴AN=DM,∵OA=OD,ON=OM,∴Rt△AON≌Rt△DOM(HL),∴∠AON=∠DOM,∴A,B,D正确,故选:C.8.解:∵,∴,∴,∴AC=BD,故选:C.9.解:连接OC,∵AC∥DE,∴∠A=∠1.∠2=∠ACO,∵∠A=∠ACO,∴∠1=∠2.∴CE=BE=3.10.解:连接OD、OE,∵的度数为40°,∴∠AOD=40°,∵CD=CO,∴∠ODC=∠AOD=40°,∵OD=OE,∴∠ODC=∠E=40°,∴∠DOE=100°,∴∠AOE=60°,∴∠BOE=120°,∴的度数是120°.故答案为120°.11.解:延长CO交⊙O于R,连AR,DR,过D作DM⊥AR于M,∵∠DOC=90°,∴∠DOR=90°,∴∠DAR=180°﹣×90°=135°,∴∠DAM=45°,∵DM⊥AM,DA=2,∴DM=AM=,∴MR=2,DR=,∵2OD2=DR2,∴OD=故答案为12.解:∵在⊙O中,,∴∠AOC=∠BOD,∴∠1+∠BOC=∠2+∠BOC,∴∠1=∠2=30°,∴的度数为30°,故答案为:30°13.解:∵AB是⊙O的直径,M、N分别是AO,BO的中点,∴2OM=OC,2ON=OD,∵CM⊥AB,DN⊥AB,∴∠CMO=∠DNO=90°,∴∠MCO=∠NDO=30°,∴∠MOC=∠NOD=60°,∴∠COD=180°﹣60°﹣60°=60°,∴的度数是60°,故答案为:60°14.解:∵,∠COD=40°,∴∠BOC=∠COD=∠EOD=40°,∴∠AOE=180°﹣∠BOE=60°.故答案为60°.15.解:连接OC、OD,∵==,∴∠AOC=∠COD=∠DOB=60°,∵OA=OC,OB=OD,∴△AOC和△BOD都是等边三角形,∴∠A=60°,∠B=60°,∴∠P=60°,故答案为:60.16.证明:(1)∵AB=CD,∴=,即+=+,∴=,∴AC=BD;(2)∵=,∴∠ADC=∠DAB,∴EA=ED,∵AB=CD,即AE+BE=CE+DE,∴CE=BE.17.(1)证明:连接AD,∵点D是的中点,∴∠CAD=∠BAD,∴CD=BD,在△CAD和△BAD中,,∴△CAD≌△BAD(SAS),∴∠ACD=∠ABD,∴∠DCE=∠DBF,在△CED和△BFD中,,∴△CED≌△BFD(ASA),∴DF=DE;(2)解:∵四边形ABDC是圆内接四边形,∴∠DBF=∠ACD,∵∠ACD=∠ABD,∴∠ABD=∠DBF,∴∠ABD=90°,∴∠ECD=∠ABD=90°,∴AD是⊙O的直径,∵CD=BD=6,CE=8,∴DE==10,∴EB=10+6=16,在Rt△ABE中,AB2+BE2=AE2,设AB=AC=x,则x2+162=(x+8)2,解得x=12,∴AB=12,在Rt△ABD中,AB2+BD2=AD2,∴AD==6,∴⊙O的半径为3.。
人教版九年级上册上册数学 24.1.3弧、弦、圆心角 同步测试(含解析)

24.1.3弧、弦、圆心角同步测试一.选择题(共10小题)1.如图所示,AB是⊙O直径,CM是AO的垂直平分线,DN是OB的垂直平分线,则下列结论正确的是()A.==B.=<C.=>D.<<2.已知,如图,∠AOB=∠COD,下列结论不一定成立的是()A.AB=CDB.=C.△AOB≌△CODD.△AOB、△COD都是等边三角形3.如果两个圆心角相等,那么()A.这两个圆心角所对的弦相等B.这两个圆心角所对的弧相等C.这两个圆心角所对的弦的弦心距相等D.以上说法都不对4.⊙O中,M为的中点,则下列结论正确的是()A.AB>2AMB.AB=2AMC.AB<2AMD.AB与2AM的大小不能确定5.下列说法中正确的有()①直径相等的圆一定是等圆;②两个半圆一定是等弧;③平分弦的直径垂直于弦;④等弧所对的弦相等;⑤相等的圆心角所对的弦相等.A.①②③B.①③④C.①④⑤D.①④6.如图,A,B,C,D是⊙O上的四个点,AD∥BC.那么与的数量关系是()A.=B.>C.<D.无法确定7.如图⊙O的半径为1cm,弦AB、CD的长度分别为,则弦AC、BD所夹的锐角α为()A.75°B.45°C.60°D.30°8.已知AB是⊙O的直径,弧AC的度数是30°.如果⊙O的直径为4,那么AC2等于()A.B.C.D.29.如图,AB是半圆的直径,∠BAC=20°,D是的中点,则∠DAC的度数是()A.30°B.35°C.45°D.70°10.下列说法中正确的是()①圆心角是顶点在圆心的角;②两个圆心角相等,它们所对的弦相等;③两条弦相等,圆心到这两弦的距离相等;④在等圆中,圆心角不变,所对的弦也不变.A.①③B.②④C.①④D.②③二.填空题(共5小题)11.已知圆O的半径为5,弦AB的长为5,则弦AB所对的圆心角∠AOB=.12.如图,在⊙O中,直径AB∥弦CD,若∠COD=120°,则∠BOD=°.13.如图,AB是直径,==,∠BOC=50°,∠AOE的度数是.14.如图,AB是⊙O的直径,如果∠COA=∠DOB=60°,那么与线段OA相等的线段是;与相等的弧是.15.如图,AD为直径,∠AOB=∠BOC=∠COD,O为圆心,那么(1)弧AB所对的圆心角是;(2)弧BD所对的圆心角是.三.解答题(共3小题)16.如图,已知⊙O中,点A,B,C,D在圆上,且AB=CD,求证:AC=BD.17.已知,如图,⊙O的两条弦AB,CD相交于点E,且AB=CD,连结BC,AD,求证:AE=CE.18.如图,在⊙O中,弦AB∥弦CD,∠A=28°,∠B=45°,=3,求的度数.参考答案1.解:连接AC,OC,OD,BD,∵CM是AO的垂直平分线,DN是OB的垂直平分线,∴AC=OC,BD=OD,∵OC=OD=OA=OB,∴△AOC,△BOD是等边三角形,∴∠AOC=∠BOD=60°,∵AB是⊙O直径,∴∠COD=60°,∴==,故选:A.2.解:∵∠AOB=∠COD,∴AB=CD,=,∵OA=OB=OC=OD,∴△AOB≌△COD,∴ABC成立,则D不成立,故选:D.3.解:在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等,所对的弦的弦心距相等.故选:D.4.解:连接BM.∵M为的中点,∴AM=BM,∵AM+BM>AB,∴AB<2AM.故选:C.5.解:①直径相等的圆一定是等圆,本小题说法正确;②两个半径相等的半圆一定是等弧,本小题说法错误;③平分弦(不是直径)的直径垂直于弦,本小题说法错误;④等弧所对的弦相等,本小题说法正确;⑤在同圆或等圆中,相等的圆心角所对的弦相等,本小题说法错误;故选:D.6.证明:连接AC,∵AD∥BC,∴∠DAC=∠ACB,∴=.故选:A.7.解:连接OA、OB、OC、OD,∵OA=OB=OC=OD=1,AB=,CD=1,∴OA2+OB2=AB2,∴△AOB是等腰直角三角形,△COD是等边三角形,∴∠OAB=∠OBA=45°,∠ODC=∠OCD=60°,∵∠CDB=∠CAB,∠ODB=∠OBD,∴α=180°﹣∠CAB﹣∠OBA﹣∠OBD=180°﹣∠OBA﹣(∠CDB+∠ODB)=180°﹣45°﹣60°=75°.8.解:如图,连接OC.过点C作CD⊥OA于点D.∵⊙O的直径为4,∴AB=4,∴OA=OC=2.∵弧AC的度数是30°,∴∠COD=30°,∴CD=1,∴OD==,则AD=2﹣,∵AB是直径,∴∠ACB=90°.∴AC2=AD•AB=(2﹣)×4=8﹣4.故选:C.9.解:连接BC,∵AB是半圆的直径,∴∠C=90°,∵∠BAC=20°,∴∠CBA=90°﹣∠BAC=70°,∵D是的中点,∴∠DAC=∠ABC=35°.10.解:圆心角是顶点在圆心的角,所以①正确;在同圆和等圆中,两个圆心角相等,它们所对的弦相等,所以②错误;③在同圆和等圆中,两条弦相等,圆心到这两弦的距离相等,所以③错误;在等圆中,圆心角不变,所对的弦也不变,所以④正确.故选:C.11.解:如图,∵OA=OB=5,AB=5,∴OA=OB=AB,∴△OAB为等边三角形,∴∠AOB=60°.故答案为60°.12.解:∵OC=OD,∴∠C=∠D,∵∠COD=120°,∴∠C=∠D=30°,∵AB∥CD,∴∠BOD=∠D=30°,故答案为30.13.解:∵==,∴∠BOC=∠COD=∠DOE=50°,∴∠AOE=180°﹣3×50°=30°.故答案为30°.14.解:∵AB是⊙O的直径,∠COA=∠DOB=60°,∴∠AOC=∠COD=∠BOD=60°;又∵OA=OC=OD=OB,∴△OAC、△OCD、△BOD是全等的等边三角形;∴OA=AC=OC=CD=OD=BD=OB;∴,故答案为:AC,OC,CD,OD,BD,OB;、.15.解:(1)弧AB所对的圆心角是∠AOB=60°;(2)弧BD所对的圆心角是∠BOD=120°.故答案为60°,120°.16.解:∵AB=CD,∴=,∴+=+,即=,∴AC=BD.17.证明:∵AB=CD,∴=,∴﹣=﹣,即=,∴AD=BC,在△AED和△CEB中,,∴△AED≌△CEB,∴AE=CE.18.解:连接AE,DE,∵∠A=28°,=3,∴∠AED=3∠A=84°,∠ADE=∠B=45°,∴∠EAD=180°﹣∠ADE﹣∠AED=51°,∴的度数是102°.。
人教版九年级上册数学24.1.3弧、弦、圆心角 练习

24.1.3弧、弦、圆心角一、选择题.1.如果两个圆心角相等,那么( )。
A .这两个圆心角所对的弦相等;B .这两个圆心角所对的弧相等C .这两个圆心角所对的弦的弦心距相等;D .以上说法都不对2.在同圆中,圆心角∠AOB=2∠COD ,则两条弧⌒AB 与⌒CD 关系是( )。
A .⌒AB =2⌒CD B .⌒AB >2⌒CDC .⌒AB <2⌒CD D .不能确定3.如图,⊙O 中,如果⌒AB =2⌒AC ,那么( )。
A .AB=ACB .AB=AC C .AB<2ACD .AB>2AC4.下列说法正确的是(A .等弦所对的圆心角相等 B. 等弦所对的弧相等C. 等弧所对的圆心角相等D. 相等的圆心角所对的弧相等5.半径为R 的⊙O 中,弦AB=2R ,弦CD=R ,若两弦的弦心距分别为OE 、OF ,则OE ∶OF 等于( )A.2∶1B.3∶2C.2∶3D.0二、填空题1.一条弦长恰好为半径长,则此弦所对的弧是半圆的_________。
2.如图,AB 和DE 是⊙O 的直径,弦AC ∥DE ,若弦BE=3,则弦CE=________。
3.半径为2cm 的⊙O 中有长2 cm 的弦AB 4.交通工具上的轮子都是做圆的,这是运用了圆的性质中的_________.三、解答题1.如图,在⊙O 中,C 、D 是直径AB 上两点,且AC=BD ,MC ⊥AB ,ND ⊥AB ,M 、N•在⊙O 上。
AAO CBA (1)求证; ⌒AM =⌒BN 。
(2)若C 、D 分别为OA 、OB 中点,则⌒AM =⌒MN =⌒BN 成立吗?2. 在⊙O 中, AB⌒ =AC ⌒ , ∠ACB=60°.求证: ∠AOB = ∠BOC = ∠AOC.3.如图以平行四边形ABCD 的顶点A 为圆心,AB 为半径作圆,分别交BC 、AD 于E 、F ,若 ∠D=50°,求⌒BE 的度数和⌒BF 的度数。
人教版九年级数学上册24.1.3弧、弦、圆心角同步测试及答案【优】

弧、弦、圆心角1.若AB ︵,CD ︵是同一圆上的两段弧,且AB ︵=CD ︵,则弦AB 与弦CD 之间的关系是( C )A .AB <CD B .AB >CDC .AB =CD D .不能确定【解析】 同圆或等圆中等弧所对的弦相等.2.如图24-1-27所示,AB 是⊙O 的直径,C ,D 是BE ︵上的三等分点,∠AOE =60°,则∠COE为( C )A .40°B .60°C .80°D .120°【解析】 易知∠EOB =180°-60°=120°.∵C ,D 是BE ︵的三等分点,∴BC ︵=CD ︵=DE ︵,∴∠BOC=∠COD =∠DOE ,∴∠COE =23∠EOB ,∴∠COE =23×120°=80°.故选C.图24-1-27图24-1-28图24-1-293.如图24-1-28,AB 是⊙O 的弦,OD ⊥AB 于D ,延长OD 交⊙O 于E ,则下列说法错误的是( D )A .AD =BDB .∠AOE =∠BOEC.AE ︵=BE ︵ D .OD =DE【解析】 由垂径定理得A ,C 正确.又由AE ︵=BE ︵得∠AOE =∠BOE ,故B 正确,故选D.4.如图24-1-29,AB 是⊙O 的直径,点C ,D 在⊙O 上,∠BOC =110°,AD ∥OC ,则∠AOD =( D )A .70°B .60°C .50°D .40°【解析】 ∠AOC =180°-∠BOC =180°-110°=70°.∵AD ∥OC ,∴∠A =∠AOC =70°.∵OA =OD ,∴∠A =∠D =70°.∴∠AOD =180°-∠A -∠D =180°-70°×2=40°.故选D.5.已知AB ︵,CD ︵是同圆的两段弧,且AB ︵=2CD ︵,则弦AB 与2CD 之间的关系为( B )A .AB =2CD B .AB <2CDC .AB >2CD D .不能确定【解析】 如图,在圆上截取DE ︵=CD ︵,则有AB ︵=CE ︵,∴AB =CE .∵CD +DE =2CD >CE =AB ,∴AB <2CD .6.如图24-1-30,AB 是⊙O 的直径,BC ,CD ,DA 是⊙O 的弦,且BC =CD =DA ,则∠BCD=( B )A .105°B .120°C .135°D .150°图24-1-30图24-1-317.如图24-1-31所示,AB 是⊙O 的直径,如果∠COA =∠DOB =60°,那么与线段OA 相等的线段有__OC ,OD ,OB ,AC ,CD ,DB __;与AC ︵相等的弧有__CD ︵和DB ︵__.8.如图24-1-32,在⊙O 中,AB ︵=AC ︵,∠A =42°,则∠B =__69°__.【解析】 ∵AB ︵=AC ︵,∴AB =AC ,∴∠B =∠C =12(180°-∠A )=12×(180°-42°)=69°.图24-1-32图24-1-339.如图24-1-33,AB 为半圆O 的直径,OC ⊥AB ,OD 平分∠BOC ,交半圆于点D ,AD 交OC 于点E ,则∠AEO 的度数是__67.5°__.【解析】 因为OD 平分∠BOC ,所以∠BOD =12∠BOC =12×90°=45°.因为OA =OD ,所以∠A =∠D .又因为∠BOD =∠A +∠D =2∠A ,所以∠A =12∠BOD =12×45°=22.5°,所以∠AEO =90°-22.5°=67.5°.10.如图24-1-34所示,D ,E 分别是⊙O 的半径OA ,OB 上的点,CD ⊥OA ,CE ⊥OB ,CD =CE ,则AC 与CB 的大小关系是__AC =CB __.图24-1-3411.如图24-1-35,已知在△ABC 中,∠ACB =90°,∠B =35°,以C 为圆心、CA 为半径的圆交AB 于D 点,则弧AD 为__70__度.【解析】 连接CD ,∵∠ACB =90°,∠B =35°,∴∠A =90°-∠B =55°.∵CA =CD ,∴∠A =∠CDA =55°,∴∠ACD =180°-2∠A =70°.12.如图24-1-36,AB ,BC ,AC 都是⊙O 的弦,且∠AOB =∠BOC .求证:(1)∠BAC =∠BCA ;(2)∠ABO =∠CBO .图24-1-36【解析】 (1)在⊙O 中,有圆心角∠AOB =∠BOC ,则可知该圆心角所对的弦相等,即AB =BC ,在△ABC 中,AB =BC ,则∠BAC =∠BCA .(2)图中共有4个等腰三角形,根据它们的底角分别相等,可以得出结论.证明:(1)∵∠AOB =∠BOC ,∴AB =BC ,∴∠BAC =∠BCA .(2)∵OB =OA ,∴∠ABO =∠BAO ,同理得∠CBO =∠BCO ,∠CAO =∠ACO .又∵∠BAC =∠BCA ,∴∠BAO =∠BCO ,∴∠ABO =∠CBO .13.如图24-1-37所示,已知AB 为⊙O 的直径,M ,N 分别为OA ,OB 的中点,CM ⊥AB ,DN⊥AB ,垂足分别为M ,N .求证:AC ︵=BD ︵.图24-1-37第13题答图【解析】 证两弧相等,可根据其定义和圆心角、弦、弧三者之间的关系定理与推论来证明. 证明:如图所示,连接OC ,OD ,则OC =OD .又OM =12OA ,ON =12OB ,OA =OB , ∴OM =ON ,∴Rt △CMO ≌Rt △DNO ,∴∠COA =∠DOB ,∴AC ︵=BD ︵.14.如图24-1-38所示,A ,B ,C 为⊙O 上的三点,且有AB ︵=BC ︵=CA ︵,连接AB ,BC ,CA .(1)试确定△ABC 的形状;(2)若AB =a ,求⊙O 的半径.图24-1-38第14题答图解: (1)∵AB ︵=BC ︵=CA ︵(已知),∴AB =BC =CA (在同圆中相等的弧所对的弦相等),∴△ABC 为等边三角形.(2)如图,连接OA ,OB ,OC ,过O 作OE ⊥BC ,垂足为E .∵AB ︵=BC ︵=CA ︵(已知),∴∠AOB =∠BOC =∠COA (在同圆中相等的弧所对的圆心角相等).又∵∠AOB +∠BOC +∠COA =360°(周角的定义),∴∠BOC =120°.又∵OB =OC ,OE ⊥BC ,∴∠BOE =∠COE =60°,BE =EC =12BC =12AB =12a (等腰三角形三线合一). ∴∠OBE =90°-∠BOE =30°.∴OE =12OB . 根据勾股定理得BE 2+OE 2=OB 2,∴⎝⎛⎭⎫12a 2+⎝⎛⎭⎫12OB 2=OB 2,解得OB =33a (负值已舍),即⊙O 的半径为33a . 15.如图24-1-39,A ,B ,C ,D ,E ,F 是⊙O 的六等分点.连接AB ,AD ,AF ,求证:AB +AF =AD .【解析】 连接OB ,OF ,得到等边△AOB ,△AOF ,据此并结合圆的性质,即可推理出AB =AF =AO =OD ,从而得到AB +AF =AD .图2439解:连接OB ,OF .∵A ,B ,C ,D ,E ,F 是⊙O 的六等分点,∴AD 是⊙O 的直径,且∠AOB =∠AOF =60°,又∵OA =OB ,OA =OF ,∴△AOB ,△AOF 是等边三角形,∴AB =AF =AO =OD ,∴AB +AF =AO +OD =AD .16.已知如图24-1-40,A 点是半圆上一个三等分点,B 点是AN ︵的中点,P 是直径MN 上一动点,⊙O 的半径为1,则AP +BP 的最小值为多少?第16【解析】 利用圆的对称性,找到AP +BP 取最小值时的P 点,再结合弧与圆心角的关系得到直角三角形,运用勾股定理求解.解:作A 关于MN 的对称点A ′,根据圆的对称性,则A ′必在圆上,连接BA ′交MN 于P ,连接P A ,则P A +PB 最小,此时P A +PB =P A ′+PB =A ′B ,连接OA ,OA ′,OB .∵AN ︵=13MN ︵,∴∠AON =∠A ′ON =60°. ∵AB ︵=BN ︵,∴∠BON =12∠AON =30°, ∴∠A ′OB =90°,∴A ′B =OA ′2+OB 2=12+12=2,即AP +BP 的最小值是 2.。
24.1.3 弧、弦、圆心角 人教版数学九年级上册同步练习(含答案)

24.1.3弦.弧.圆周角1.如图,在⊙O中,AB是弦,C是弧AB上一点.若∠OAB=25°,∠OCA=40°,则∠BOC的度数为( )A.30°B.40°C.50°D.60°2.如图,«Skip Record If...»是«Skip Record If...»的直径,弦«Skip Record If...»交«Skip Record If...»于点E,若«Skip Record If...»,则«Skip Record If...»的度数为()A.«Skip Record If...»B.«Skip Record If...»C.«Skip Record If...»D.«Skip Record If...»3.如图1是一座立交桥的示意图(道路宽度忽略不计)A为入口,F,G为出口,其中直行道为AB,CG,EF,且AB=CG=EF,弯道为以点O为圆心的一段弧,且«Skip Record If...»,«Skip Record If...»,«Skip Record If...»,所对的圆心角均为90°,甲、乙两车由A 口同时驶入立交桥,均以10m/s的速度行驶,从不同出口驶出,其间两车到点O的距离y(m)与时间x(s)的对应关系如图2所示,结合题目信息,下列说法正确的是( )A.甲车从F口出,乙车从G口出B.甲车驶出立交桥时,乙车在«Skip Record If...»上C.甲乙两车同时在立交桥上的时间为10sD.图中立交桥总长为140 m4.如图,«Skip Record If...»为«Skip Record If...»的直径,点D是弧«Skip Record If...»的中点,过点D作«Skip Record If...»于点E,延长«Skip Record If...»交«Skip Record If...»于点F,若«Skip Record If...».则«Skip Record If...»的直径长为()A.15B.13C.10D.165.如图,AB是⊙O的直径,C.D是⊙O上的两点,且点C为弧BAD的中点,连接CD.CB.OD,CD与AB交于点F.若∠AOD=100°,则∠ABC的度数为( )A.15°B.20°C.25°D.30°6.如图,在⊙O中,«Skip Record If...»,∠AOD=150°,∠BOC=80°,则∠AOB的度数是()A.20°B.25°C.30°D.35°7.下列说法中,正确的是()A.等弦所对的弧相等B.等弧所对的弦相等C.圆心角相等,所对的弦相等D.弦相等所对的圆心角相等8.如图,A.B是⊙O上的两点,∠AOB=120°,C是«Skip Record If...»的中点,则四边形OACB是( )A.梯形B.矩形C.菱形D.正方形9.如图,半径为5的⊙A中,弦«Skip Record If...»所对的圆心角分别是«Skip Record If...»,«Skip Record If...».已知«Skip Record If...»,«Skip Record If...»,则弦«Skip Record If...»的弦心距等于()A.«Skip Record If...»B.«Skip Record If...»C.4D.310.如图,⊙O中,弦AB⊥CD,垂足为E,F为«Skip Record If...»的中点,连接AF、BF、AC,AF交CD于M,过F作FH⊥AC,垂足为G,以下结论:①«Skip Record If...»;②HC=BF:③MF=FC:④«Skip Record If...»,其中成立的个数是( )A.1个B.2个C.3个D.4个11.若将一个圆等分成三个扇形,则其中一个扇形圆心角的度数为________«Skip Record If...».12.如图,在半径为5的«Skip Record If...»中,«Skip Record If...»,则弦«Skip Record If...»的长度为______.13.如图,在⊙O中,若«Skip Record If...» ,则AC与2CD的大小关系是:AC__2CD.(填“>”,“<”或“=”)14.如图,在圆«Skip Record If...»中,若«Skip Record If...»,且«Skip Record If...»,求«Skip Record If...»的长度.15.如图,MB,MD是⊙O的两条弦,点A,C分别在弧MB,弧MD上,且AB=CD,点M是弧AC的中点.(1)求证:MB=MD;(2)过O作OE⊥MB于E,OE=1,⊙O的半径是2,求MD的长.参考答案1.A【分析】根据等腰三角形的性质求出∠OBA=∠OAB=25°,∠OAC=∠OCA=40°,再根据三角形内角和定理求出∠AOB和∠AOC,再求出答案即可.【详解】解:∵OA=OB,∠OAB=25°,∴∠OBA=∠OAB=25°,∴∠AOB=180°﹣∠OAB﹣∠OBA=130°,∵OA=OC,∠OCA=40°,∴∠OAC=∠OCA=40°,∴∠AOC=180°﹣∠OAC﹣∠OCA=100°,∴∠BOC=∠AOB﹣∠AOC=130°﹣100°=30°,故选:A.【点拨】本题考查圆心角的定义,等腰三角形的性质,三角形内角和定理,解题关键是掌握圆心角的定义.2.B【分析】连接OC,根据圆周角定理求出∠AOC,求出«Skip Record If...»的度数,根据直角三角形的性质求出∠BCD=70°,根据平行线的性质求出∠D,求出«Skip Record If...»的度数,求出«Skip Record If...»的度数可得∠AOE,再求出答案即可.【详解】解:连接OC,∵AB⊥CD,∴∠CFB=90°,∵∠CBA=15°,∴∠AOC=2∠CBA=30°,∠BCD=90°-∠CBA=75°,∴«Skip Record If...»的度数是30°,∵DE∥BC,∴∠BCD+∠D=180°,∴∠D=105°,∴«Skip Record If...»的度数是210°,∴«Skip Record If...»的度数是360°-210°=150°,∴«Skip Record If...»的度数是150°-30°=120°,∴∠AOE=120°,∴«Skip Record If...»故选:B.【点拨】本题考查了圆周角定理,圆心角、弧、弦之间的关系等知识点,能熟记知识点是解此题的关键.3.B【分析】结合题意函数图象可分析出在直道AB,CG以及EF上的行驶时间均为3s,在弯道BC,CD,DE上的行驶时间均为2s,从而结合速度进行逐项分析即可.【详解】A.分析图2可知,甲车先驶出立交桥,乙车后驶出,因此甲车从G口出,乙车从F口出,原说法错误,不符合题意;B.根据图2甲的图象可知甲车在立交桥上由A到G共计用时5+3=8s,其中由B到C用时2s,由于甲乙的速度相同,则乙从A到D用时3+2×2=7s,从A到E用时3+3×2=9s,因此第8s 时,乙车在«Skip Record If...»上,原说法正确,符合题意;C.根据B选项的分析可知,两车同时在立交桥上的时间为8s,原说法错误,不符合题意;D.根据题意,立交桥总长为:«Skip Record If...»,原说法错误,不符合题意;故选:B.【点拨】考本题考查函数图象与实际行程问题,涉及到圆心角等相关知识点,理解函数图象对应的实际意义是解题关键.4.A【分析】连接«Skip Record If...»,首先证明«Skip Record If...»,设«Skip Record If...»,在«Skip Record If...»中,利用勾股定理构建方程即可解决问题.【详解】解:如图,连接«Skip Record If...».«Skip Record If...»,«Skip Record If...»,«Skip Record If...»,«Skip Record If...»点«Skip Record If...»是弧«Skip Record If...»的中点,«Skip Record If...»«Skip Record If...»,«Skip Record If...»«Skip Record If...»,«Skip Record If...»,«Skip Record If...»,设«Skip Record If...»,在«Skip Record If...»中,则有«Skip Record If...»,解得«Skip Record If...»,«Skip Record If...»,故答案是:A.【点拨】本题考查勾股定理,垂径定理,圆心角,弧,弦之间的关系等知识,解题的关键是学会利用参数构建方程解决问题,属于中考常考题型.5.B【分析】先根据邻补角的性质求出∠BOD,再根据点C为弧BAD的中点,求出∠BOC的度数,再根据等腰三角形的性质即可求出∠ABC的度数.【详解】∵∠AOD=100°,∴∠BOD=180°-∠AOD=80°,∵点C为弧BAD的中点∴∠BOC=∠DOC=«Skip Record If...»(360°-80°)=140°∵OC=OB∴∠ABC=∠BCO=«Skip Record If...»(180°-140°)=20°故选B.【点拨】此题主要考查圆内角度求解,解题的关键是熟知圆心角、弧的关系.6.D【分析】首先根据题意得出«Skip Record If...»,然后得到«Skip Record If...»,然后利用角度之间的关系求解即可.【详解】«Skip Record If...»,«Skip Record If...»,«Skip Record If...»,«Skip Record If...».∵∠AOD=150°,∠BOC=80°,«Skip Record If...»,故选:D.【点拨】本题主要考查圆心角、弧、弦的关系,准确识图并灵活运用相关知识是解题的关键.7.B【分析】根据圆心角,弦,弧之间的关系判断,注意条件.【详解】A中,等弦所对应的弧可以相等也可以互补构成新圆;B中,等弧所对应的弦相等,故选BC中,圆心角相等所对应的弦可能互补;D中,弦相等,圆心角可能互补;故选B【点拨】本题考查了圆心角,弧,弦之间的观,此类试题属于难度较大的试题,其中,弦和圆心角等一些基本知识容易混淆,从而很难把握.8.C【分析】连接OC,如图,利用圆心角、弧的关系得到∠AOC=∠BOC=«Skip Record If...»∠AOB=60°,可判断△OAC和△OCB都是等边三角形,所以OA=AC=OB=BC,于是可判断四边形OACB 为菱形.【详解】解:连接OC,如图,∵C是«Skip Record If...»的中点,∴∠AOC=∠BOC=«Skip Record If...»∠AOB=«Skip Record If...»×120°=60°,∵OA=OC,OC=OB,∴△OAC和△OCB都是等边三角形,∴OA=AC=OB=BC,∴四边形OACB为菱形.故选:C.【点拨】本题考查了圆心角、弧、弦的关系:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.也考查了菱形的判定.9.D【分析】作AH⊥BC于H,作直径CF,连结BF,先利用等角的补角相等得到∠DAE=∠BAF,再利用圆心角、弧、弦的关系得到DE=BF=6,由AH⊥BC,根据垂径定理得CH=BH,易得AH 为△CBF的中位线,然后根据三角形中位线性质得到AH=«Skip Record If...»BF=3.【详解】解:作AH⊥BC于H,作直径CF,连结BF,如图,∵∠BAC+∠EAD=180°,∠BAC+∠BAF=180°,∴∠DAE=∠BAF,∴«Skip Record If...»,∴DE=BF=6,∵AH⊥BC,∴CH=BH,而CA=AF,∴AH为△CBF的中位线,∴AH=«Skip Record If...»BF=3,故选:D.【点拨】本题考查了圆心角、弧、弦的关系.也考查了垂径定理和三角形中位线性质,解题的关键是熟练运用相应的定理.10.C【分析】根据弧,弦,圆心角之间的关系,圆周角定理以及三角形内角和定理一一判断即可.【详解】解:∵F为«Skip Record If...»的中点,∴«Skip Record If...»,故①正确,∴∠FCM=∠FAC,∵∠FCG=∠ACM+∠FCM,∠AME=∠FMC=∠ACM+∠FAC,∴∠AME=∠FMC=∠FCG>∠FCM,∴FC>FM,故③错误,∵AB⊥CD,FH⊥AC,∴∠AEM=∠CGF=90°,∴∠CFH+∠FCG=90°,∠BAF+∠AME=90°,∴∠CFH=∠BAF,∴«Skip Record If...»,∴HC=BF,故②正确,∵∠AGF=90°,∴∠CAF+∠AFH=90°,∴«Skip Record If...»=180°,∴«Skip Record If...»=180°,∴«Skip Record If...»,故④正确,故选:C.【点评】本题考查圆心角,弧,弦之间的关系,三角形内角和定理等知识,解题的关键是熟练掌握基本知识,属于中考选择题中的压轴题.11.120【分析】根据圆的性质计算,即可得到答案.【详解】根据题意,将一个圆等分成三个扇形,则其中一个扇形圆心角的度数为:«Skip Record If...» 故答案为:120.【点拨】本题考查了圆的知识;解题的关键是熟练掌握圆和圆心角的性质,从而完成求解.12.«Skip Record If...»【分析】作OC⊥AB,根据垂径定理得到AC=BC=«Skip Record If...»AB,根据直角三角形的性质求出OC,根据勾股定理求出AC,得到答案.【详解】解:作«Skip Record If...»于C,则«Skip Record If...»,«Skip Record If...»,«Skip Record If...»,«Skip Record If...»,«Skip Record If...»,由勾股定理得,«Skip Record If...»,«Skip Record If...»,故答案为:«Skip Record If...»【点拨】本题考查的是垂径定理、圆心角、弧、弦的关系定理,正确作出辅助性、灵活运用定理是解题的关键.13.«Skip Record If...»【分析】如图,连接AB.BC,根据题意知,AB=BC=CD,又由三角形三边关系得到AB+BC>AC得到:AC<2CD.【详解】解:如图,连接AB.BC,∵«Skip Record If...»∴AB=BC=CD,在△ABC中,AB+BC>AC.∴AC<2CD.故答案是:<.【点拨】本题主要考查了圆心角、弧、弦的关系,解题的关键是利用三角形三边关系得到AB+BC>AC.14.«Skip Record If...»【分析】由弦与弧的关系,得到«Skip Record If...»,然后得到«Skip Record If...»,即可得到«Skip RecordIf...».【详解】解:∵«Skip Record If...»,∴«Skip Record If...»,∴«Skip Record If...»即«Skip Record If...»∴«Skip Record If...».【点拨】本题考查了弦与弧的关系,解题的关键是熟练掌握所学的知识,正确得到«Skip Record If...».15.(1)见解析;(2)«Skip Record If...»【分析】(1)根据圆心角、弦、弧、弦心距之间的关系得出«Skip Record If...»即可;(2)根据垂径定理,勾股定理求出ME,进而求出MB即可.【详解】证明:(1)∵AB=CD,∴«Skip Record If...»,又∵点M是弧AC的中点,∴«Skip Record If...»,∴«Skip Record If...»,即:«Skip Record If...»,∴MB=MD;(2)过O作OE⊥MB于E,则ME=BE,连接OM,在Rt△MOE中,OE=1,⊙O的半径OM=2,∴ME=«Skip Record If...»=«Skip Record If...»=«Skip Record If...»,∴MD=MB=2ME=2«Skip Record If...».【点拨】本题考查圆心角、弦、弧之间的关系,垂径定理、勾股定理等知识,掌握垂径定理、勾股定理是正确计算的前提.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二十四章 圆 24.1.3 弧、弦、圆心角 同步练习题
1.在同圆或等圆中,相等的圆心角所对的弧 ,所对的弦 ;两个圆心角及它们所对的两条弧、两条弦中如果有一组量相等,那么其余各组量也 .
2.一条弦把圆分成1:3两部分,则弦所对的圆心角为________.
3.弦心距是弦的一半时,弦与直径的比是________,弦所对的圆心角是_____.
4.如图,AB 为圆O 的直径,»»BC
BD =,∠A=25°,则∠BOD=______.
5.如图,AB 、CD 是⊙O 的两条弦,M 、N 分别为AB 、CD 的中点,且∠AMN=∠CNM , AB=6,则CD=_______.
6.如果两条弦相等,那么( )
A .这两条弦所对的弧相等
B .这两条弦所对的圆心角相等
C .这两条弦的弦心距相等
D .以上答案都不对
7.如图,在圆O 中,直径MN ⊥AB ,垂足为C ,则下列结论中错误的是( )
A .AC=BC
B .»
»AN BN = C .¼¼AM BM = D .OC=CN
8.在⊙O 中,圆心角∠AOB=90°,点O 到弦AB 的距离为4,则⊙O 的直径的长
B
A
为()
A.
B.
C.24 D.16
9.如图,在半径为2cm的圆O内有长为
cm的弦AB,则此弦所对的圆心角
∠AOB为(• )
A.60° B.90° C.120° D.150°
10.如图,C、D为半圆上三等分点,则下列说法:①;②∠AOD =∠DOC=∠BOC;③AD=CD=BC;④△AOD沿OD翻折与△COD重合.其
中正确的是
(填序号).
11.如图所示,AB、CD为⊙的两条直径,E是圆上一点,连接DE,如果DE ∥AB,,则∠BOC的度数为.
12.如图所示,已知C 为»AB 的中点,OA ⊥CD 于M ,CN ⊥OB 于N ,若OA=r ,•ON=•a ,
•则CD=_______.
13.如图,直角坐标系中一条圆弧经过网格点A 、B 、C ,其中B 点坐标为(4, 4),•则该圆弧所在圆的圆心坐标为_________.
14.如图所示,在△ABC 中,∠A=70°,⊙O 截△ABC•的三边所得的弦长相等, 则∠BOC=( )
A .140°
B .135°
C .130°
D .125°
15.如图所示,已知AB 是⊙O 的直径,M 、N 分别是AO 、BO 的中点,CM ⊥AB ,
DN ⊥AB ,•求证:»
»AC BD .
C A
D
O N
M C
A O
16.如图:⊙O1和⊙O2是等圆,P是O1O2的中点,过P作直线AD交⊙O1于A、B,交⊙O2于C、D,求证:AB=CD.
17.如图所示,点O是∠EPF平分线上的一点,以点O为圆心的圆与角的两边分别交于点A、B和C、D
(1)求证:AB=CD
(2)若角的顶点P在圆上或在圆内,(1)的结论还成立吗?若不成立,请说明理由;•若成立,请加以证明
参考答案:
1.相等相等相等2. 90°
3.:2 90°4. 50°
5. 6
6. D
7. D
8. B
9. C
10.• ①②③④
11. 120°
12.
13.(2,0)
14.D
15.提示:连接OC,OD,由OM=1
2OA,ON=1
2
OB,得OM=ON,OC=OD,
∴Rt△CMO≌Rt△DNO,•∵∠COA=∠DOB,∴»»
AC BD
=
16.提示:过点O1作O1M⊥AB于M,过点O2作O2N⊥CD于N,再证明△O1MP≌△O2NP,•得OM=ON,∴AB=CD
17.(1)证明:过点O分别作PB、PD的垂线,垂足分别为M、N,∵点O是∠EPF•平分线上的点,∴OM=ON,从而AB=CD.
(2)结论成立,证明略.。
