面面垂直测试题

合集下载

面面垂直基础训练题基础训练题(有详解)(有详解)

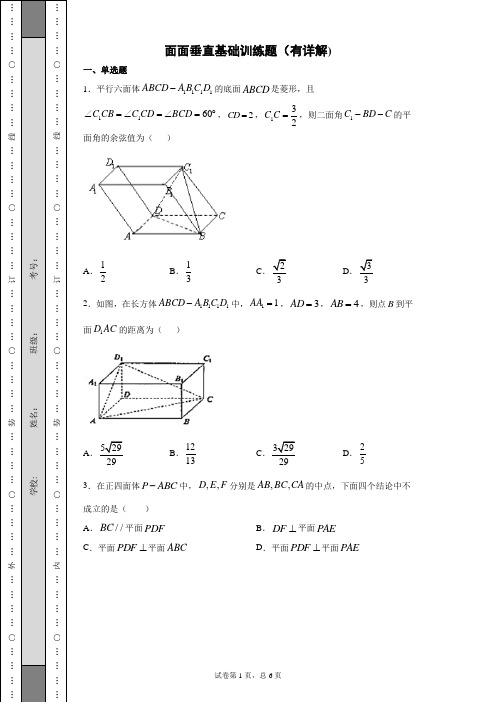
面面垂直基础训练题（有详解)一、单选题1．平行六面体1111ABCD A B C D -的底面ABCD 是菱形，且1160C CB C CD BCD ∠=∠=∠=︒，2CD =，132C C =，则二面角1C BD C --的平面角的余弦值为（）A ．12B ．13C ．3D 2．如图，在长方体1111ABCD A B C D -中，11AA =，3AD =，4AB =，则点B 到平面1D AC 的距离为（）A B ．1213C D ．253．在正四面体P ABC -中，,,D E F 分别是,,AB BC CA 的中点，下面四个结论中不成立的是（） A ．//BC 平面PDF B ．DF ⊥平面PAE C ．平面PDF ⊥平面ABC D ．平面PDF ⊥平面PAE二、解答题4．如图，在直角梯形ABCD 中，//AB DC ，90BAD ∠=，4AB =，2AD =，3DC =，点E 在CD 上，且2DE =，将ADE 沿AE 折起，使得平面ADE ⊥平面ABCE （如图）.G 为AE 中点.（1）求证:DG ⊥平面ABCE ；（2）求四棱锥D ABCE -的体积；（3）在线段BD 上是否存在点P ，使得//CP 平面ADE ？若存在，求BPBD的值；若不存在，请说明理由.5．如图，四棱锥P ABCD -的底面是菱形，PO ⊥底面ABCD ，O 、E 分别是AD 、AB 的中点，6AB =，5AP =，60BAD ∠=︒.（1）求证：平面PAC ⊥平面POE ；（2）求直线PB 与平面POE 所成角的正弦值；（3）若F 是边DC 的中点，求异面直线BF 与PA 所成角的正切值.6．如图1所示，在矩形ABCD 中， 2,4AB AD ==， E 为 C D 的中点，沿 AE 将AED∆折起，如图2所示， O H M 、、分别为AE BD AB 、、的中点，且 2DM =．（1）求证： //OH 平面DEC ；（2）求证：平面ADE ⊥平面 ABCE ．7．如图，在三棱锥P —ABC 中，△PBC 为等边三角形，点O 为BC 的中点，AC⊥PB，平面PBC⊥平面ABC ．（1）求直线PB 和平面ABC 所成的角的大小；（2）求证：平面PAC⊥平面PBC ；（3）已知E 为PO 的中点，F 是AB 上的点，AF ＝λAB ．若EF∥平面PAC ，求λ的值． 8．如图，三棱柱111ABC A B C -中，1BC CC =，平面11A BC ⊥平面11BCC B .证明：（1） //AC 平面11A BC ；（2）平面1AB C ⊥平面11A BC ．9．如图，已知四棱锥P ABCD -中，PD ⊥平面ABCD ，底面ABCD 为直角梯形，AD CD ⊥，//AB CD ，2CD AB =.（Ⅰ）求证：平面PAB ⊥平面PAD ；（Ⅱ）在侧棱PC 上是否存在点M ，使得//BM 平面PAD ，若存在，确定点M 位置；若不存在，说明理由．10．如图，ABC ∆是边长为2的正三角形.若1AE =，AE ⊥平面ABC ，平面BCD ⊥平面ABC ，BD CD =，且BD CD ⊥.（1）求证：AE 平面BCD ；（2）求证：平面BDE ⊥平面CDE .11．如图所示，在三棱柱111ABC A B C -中，V ABC 与111A B C △都为正三角形，且1AA ⊥平面ABC ，1F F ，分别是11AC A C ，的中点.求证：（1）平面11AB F ∥平面1C BF ；（2）平面11AB F ⊥平面11ACC A .12．如图，在平行四边形ABCM 中，3AB AC ==，90ACM ∠=︒，以AC 为折痕将ACM ∆折起，使点M 到达点D 的位置，且AB DA ⊥.（Ⅰ）证明：平面ACD ⊥平面ABC ；（Ⅱ）Q 为线段AD 上一点，P 为线段BC 上一点，且13BP DQ DA ==，求二面角Q PA C --的大小的正切值．13．在如图所示的几何体中，四边形ABCD 是正方形， MA ⊥平面ABCD ，//,PD MA E G F 、、分别为MB PB PC 、、的中点，且2AD PD MA ==.（1）求证：平面//EFG 平面PMA ；（2）求证：平面P DC EFG ⊥平面；14．在四棱锥P ABCD -中，PA ⊥平面ABCD ，//AD BC ，1AB =，2BC =，60ABC ∠=（Ⅰ）设平面PBC ⋂平面PAD l =，求证：//BC l （II ）求证：平面PAC ⊥平面PAB15．如图，四棱锥P -ABCD 的底面是矩形，PA ⊥平面ABCD ，E ，F 分别是AB ，PD 的（Ⅱ）求证：平面PEC⊥平面PCD．参考答案1．D 【解析】【分析】作出二面角1C BD C --的平面角，利用余弦定理计算出二面角的余弦值. 【详解】连接AC 交BD 于O ，连接1C O ，由于四边形ABCD 是菱形，所以BD CO ⊥.由于1111CD CB C CD C CB C C C C=⎧⎪∠=∠⎨⎪=⎩，所以11C CD C CB ∆≅∆，所以11C D C B =，所以1BD C O ⊥.故1C OC ∠是二面角1C BD C --的平面角.由于1160C CB C CD BCD ∠=∠=∠=︒，2CD =，132C C =，所以2,1BD OB OD ===,1113602C B C D===,所以132C O ==，而OC =在三角形1C OC中，由余弦定理得199344cos 3322C OC +-∠==.故选D.【点睛】本小题主要考查利用几何法求二面角的余弦值，考查空间想象能力和逻辑推理能力，属于中档题. 2．B【解析】【分析】根据等体积法：11D ACD D ACD V V --=得到1111,33ACD ACD S h S DD ⨯=⨯分别求出三角形的面积代入上式得到结果. 【详解】连接BD 交AC 于O 点，根据长方形对角线互相平分得到O 点为BD 的中点，故点B 到面1D AC 的距离等于点D 到面1D AC 的距离，根据11D ACD D ACD V V --=，设点D 到面1D AC 的距离为h,故得到1111,33ACD ACD S h S DD ⨯=⨯115,AC AD CD == 根据余弦定理得到11113cos 2AD CAD C AD C S ===，6ACDS =将面积代入上式得到h=1213. 故答案为：B. 【点睛】本题考查了点面距离的求法，点面距可以通过建立空间直角坐标系来求得点面距离，或者寻找面面垂直，再直接过点做交线的垂线即可;当点面距离不好求时，还可以等体积转化. 3．C 【解析】【分析】由//DF BC ，能证明//BC 平面PDF ；由已知推导出AE BC ⊥，PE BC ⊥，从而BC ⊥平面PAE ，进而DF ⊥平面PAE ；由已知得平面PAE ⊥平面ABC ，从而平面PDE 与平面ABC 不垂直；由DF ⊥平面PAE ，推导出平面PDF ⊥平面PAE ．【详解】∵在正四面体P ABC -中，,,D E F 分别是,,AB BC CA 的中点， ∴//DF BC ，∵DF ⊂平面PDF ，BC ⊄平面PDF ， ∴//BC 平面PDF ，故A 正确；∵AB AC PB PC ===，E 是BC 中点， ∴AE BC ⊥，PE BC ⊥， ∵AE PE E ⋂=， ∴BC ⊥平面PAE ， ∵//DF BC ，∴DF ⊥平面PAE ，故B 正确； ∵DF ⊥平面PAE ，DF ⊂平面ABC ， ∴平面PAE ⊥平面ABC ，∵平面PAE ⋂平面PDE PE =，且PE 与平面ABC 不垂直， ∴平面PDE 与平面ABC 不垂直，故C 错误； ∵DF ⊥平面PAE ，且DF ⊂平面PDF ， ∴平面PDF ⊥平面PAE ，故D 正确,故选C ．【点睛】本题通过对多个命题真假的判断，综合考查线面平行、线面垂直、面面垂直，属于难题.这种题型综合性较强，也是高考的命题热点，同学们往往因为某一处知识点掌握不好而导致“全盘皆输”，因此做这类题目更要细心、多读题，尽量挖掘出题目中的隐含条件，另外，要注意从简单的自己已经掌握的知识点入手，然后集中精力突破较难的命题. ．4．(1)见证明；(2) (3)34BP BD = 【解析】【分析】（1）证明DG AE ⊥，再根据面面垂直的性质得出DG ⊥平面ABCE ；（2）分别计算DG 和梯形ABCE 的面积，即可得出棱锥的体积；（3）过点C 作//CF AE 交AB 于点F ，过点F 作//FP AD 交DB 于点P ，连接PC ，可证平面//CFP 平面ADE ，故//CP 平面ADE ，根据//FP AD 计算BPBD的值. 【详解】（1）证明：因为G 为AE 中点，2AD DE ==，所以DG AE ⊥.因为平面ADE ⊥平面ABCE ，平面ADE平面ABCE AE =，DG ⊂平面ADE ，所以DG ⊥平面ABCE ．（2）在直角三角形ADE 中，易求AE =则AD DEDG AE⋅==．所以四棱锥D ABCE -的体积为1(14)232D ABCE V -+⨯=⨯=（3）过点C 作//CF AE 交AB 于点F ，则:1:3AF FB =．过点F 作//FP AD 交DB 于点P ，连接PC ,则:1:3DP PB =．又因为CF//A E ，AE ⊂平面,ADE CF ⊄平面ADE , 所以CF //平面ADE ．同理//FP 平面ADE ．又因为CF PF F ⋂=，所以平面CFP //平面ADE ．因为CP ⊂平面CFP ，所以//CP 平面ADE ．所以在BD 上存在点P ，使得//CP 平面ADE ，且34BP BD =. 【点睛】本题主要考查线面垂直的性质与判定，线面平行的性质与判定以及四棱锥的体积，考查学生的空间想象能力和推理论证能力.计算柱锥台的体积的关键是根据条件找出相应的底面积和高，如果给出的几何体不规则，需要利用求体积的一些特殊方法：分割法、补体法、转化法等，它们是解决一些不规则几何体体积计算常用的方法.5．（1）见解析；（2）86；（3）9【解析】【分析】（1）根据四边形ABCD 是菱形，证得AC BD ⊥，由平行得到OE AC ⊥，结合PO AC ⊥，证得AC ⊥平面POE ，由此证得平面PAC ⊥平面POE .（2）作出线面角，然后解直角三角形求得线面角的正弦值.（3）作出异面直线所成的角，然后利用余弦定理求得角的余弦值，进而求得其正切值.【详解】（1）证明：ABCD 是菱形，AC BD ⊥，//OE BD OE AC ∴⊥，PO ⊥底面ABCD ，PO AC ⊥，OE ，OP ⊂平面POEOE OP O =，AC ∴⊥平面POE ，AC ⊂平面PAC∴平面PAC ⊥平面POE（2）过点B 作BM OE ⊥于M ，易证PO BM ⊥，OE ，OP ⊂平面POEOE OP O =，BM ∴⊥平面POE ，PM ∴是PB 在平面POE 上的射影BPM ∠即为所求，在Rt PMB ∆中，2BM =，PB =sin BM BPM PB ∠==（3）分别取AB ，PB 中点H ，T ，易证//DH BF ，//TH PADHT ∴∠即为异面直线BF 与PA 所成角或其补角在DHT ∆中，DH =，52HT =，DT =cos 10DHT ∴∠= tan 9DHT ∴∠=【点睛】本小题主要考查面面垂直的证明，考查线面角的正弦值的求法，考查线线角的正切值的求法，考查空间想象能力和逻辑推理能力，属于中档题.6．（1）见解析；（2）见解析【解析】【分析】（1）取BC 中点Q ，连接OQ ，通过证明线线平行，证得平面//DEC 平面OHQ ，由此证得 //OH 平面DEC .（2）连接OD ，OM ，根据等腰三角形的性质，证得DO AE ⊥，利用勾股定理证得DO OM ⊥，由此证得OD ⊥平面ABCE ，进而证得平面ADE ⊥平面 ABCE .【详解】（1）证明：取BC 中点Q ，连接OQ （如图），易证//OQ 平面DEC//HQ 平面DEC ，OQ ，HQ ⊂平面OHQ ，OQ HQ Q =∴平面//DEC 平面OHQ ，OH ⊂平面OHQ ，//OH ∴平面DEC（2）证明：连接OD ，OM ，DA DE =，O 为AE 中点DO AE ∴⊥，222DO OM DM +=，DO OM ∴⊥AE ，OM ⊂平面ABCE ，AE OM O =，OD ∴⊥平面ABCEOD ⊂平面ADE ∴平面ADE ⊥平面ABCE【点睛】本小题主要考查线面平行的证明，考查面面垂直的证明，考查空间想象能力和逻辑推理能力，属于中档题.7．（1）060；（2）证明见解析；（3）13λ=【解析】【分析】（1）先找到直线PB 与平面ABC 所成的角为PBO ∠,再求其大小；（2）先证明PO AC ⊥, 再证明平面PAC⊥平面PBC ；（3）取CO 的中点G,连接EG ,过点G 作FG||AC,再求出λ的值.【详解】（1）因为平面PBC⊥平面ABC ，PO⊥BC, 平面PBC∩平面ABC=BC,PO PBC ⊂平面, 所以PO ⊥平面ABC,所以直线PB 与平面ABC 所成的角为PBO ∠,因为0=60PBO ∠，所以直线PB 与平面ABC 所成的角为060.(2)因为PO ⊥平面ABC,所以PO AC ⊥,因为AC ⊥PB ，,,PO PB PBC POPB P ⊂=平面,所以AC ⊥平面PBC,因为AC ⊂平面PAC,所以平面PAC⊥平面PBC.(3)取CO 的中点G ,连接EG ,过点G 作FG||AC,由题得EG||PC,所以EG||平面APC,因为FG||AC ，所以FG||平面PAC,EG,FG ⊂平面EFO,EG ∩FG=G ,所以平面EFO||平面PAC,因为EF ⊂平面EFO,所以EF||平面PAC.此时AF=11,33AB λ∴=. 【点睛】本题主要考查空间几何元素垂直关系的证明，考查线面角的求法，考查空间几何中的探究性问题，意在考查学生对这些知识的理解掌握水平和分析推理能力.8．（1）证明见解析；（2）证明见解析.【解析】【分析】（1）根据三棱柱特点可知11//AC A C ，根据线面平行判定定理证得结论；（2）由四边形11BCC B 为菱形可得11B C BC ⊥，根据面面垂直的性质可知1B C ⊥平面11A BC ，根据面面垂直的判定定理证得结论.【详解】（1）几何体为三棱柱 ⇒四边形11ACC A 为平行四边形 11//AC A C ⇒又11A C ⊂平面11A BC ，AC ⊄平面11A BC //AC ∴平面11A BC（2）1BC CC =且四边形11BCC B 为平行四边形∴四边形11BCC B 为菱形 11B C BC ⊥∴又平面11A BC ⊥平面11BCC B ，平面11A BC ⋂平面111BCC B BC =1B C ∴⊥平面11A BC又1B C ⊂平面1AB C ∴平面1AB C ⊥平面11A BC【点睛】本题考查直线与平面平行、平面与平面垂直关系的证明，涉及到空间几何体的结构、面面垂直性质定理的应用等知识，属于常考题型.9．（Ⅰ）见解析；（Ⅱ）见解析【解析】【分析】（Ⅰ）先证明PD AB ⊥和AD AB ⊥，进而求出AB ⊥平面PAD ，然后就可以证出平面PAB ⊥平面PAD（Ⅱ）连接MN ，AN ，易得MN 是PCD ∆的中位线，即可证明四边形ABMN 为平行四边形，然后，利用定义，即可求证//BM平面PAD 【详解】（Ⅰ）证明：因为PD ⊥平面ABCD ，所以PD AB ⊥．又因为AD CD ⊥，//AB CD ，所以AD AB ⊥．又AD PD D =I ，,AD PD ⊂平面PAD ．可得AB ⊥平面PAD ．又AB Ì平面PAB ，所以平面PAB ⊥平面PAD ．（Ⅱ）当点M 是PC 的中点时，//BM 平面PAD ．证明如下：设PD 的中点为N ，连接MN ，AN ，易得MN 是PCD ∆的中位线，所以//MN CD ，12MN CD =．由题设可得//AB CD ，2CD AB =，所以//MN AB ，MN AB =．所以四边形ABMN 为平行四边形，所以//BMAN ．又BM ⊄平面PAD ，AN ⊂平面PAD ，所以//BM 平面PAD ．【点睛】本题考查面面垂直与线面平行的证明，属于基础题10．（1）见解析；（2）见解析【解析】【分析】（1）取BC 的中点M ，连接DM ，由平面BCD ⊥平面ABC ，得DM ⊥平面ABC ，再证AE DM 即可证明（2）证明CD ⊥平面BDE ，再根据面面垂直的判定定理从而进行证明．【详解】（1）取BC 的中点M ，连接DM ，因为BD CD =，且BD CD ⊥，2BC =.所以1DM =，DM BC ⊥.又因为平面BCD ⊥平面ABC ，所以DM ⊥平面ABC ，又AE ⊥平面ABC ，所以AE DM又因为AE ⊄平面BCD ，DM ⊂平面BCD ，所以AE 平面BCD .（2）连接AM ，由（1）知AE DM ，又1AE =，1DM =，所以四边形DMAE 是平行四边形，所以DE AM .又ABC ∆是正三角形，M 为BC 的中点，∴AM BC ⊥，因为平面BCD ⊥平面ABC ，所以AM ⊥平面BCD ，所以DE ⊥平面BCD .又CD ⊂平面BCD ，所以DE CD ⊥.因为BD CD ⊥，BD DE D ⋂=，所以CD ⊥平面BDE .因为CD ⊂平面CDE ，所以平面BDE ⊥平面CDE .【点睛】本题考查了线面平行的证明，线面垂直，面面垂直的判定定理，考查空间想象和推理能力，熟记定理是关键，是一道中档题．11．(1)见解析.(2)见解析.【解析】【分析】（1）由1,F F 分别是11,AC A C 的中点，证得1111,B F BF AF C F ∥∥，由线面平行的判定定理，可得11B F //平面1C BF ，1AF //平面1C BF ，再根据面面平行的判定定理，即可证得平面11AB F ∥平面1C BF .（2）利用线面垂直的判定定理，可得11B F ⊥平面11ACC A ，再利用面面垂直的判定定理，即可得到平面11AB F ⊥平面11ACC A .【详解】（1）在三棱柱111ABC A B C -中，因为1,F F 分别是11,AC A C 的中点，所以1111,B F BF AF C F ∥∥，根据线面平行的判定定理，可得11B F //平面1C BF ，1AF //平面1C BF又11111,B F AF F C F BF F ==，∴平面11AB F ∥平面1C BF .（2）在三棱柱111ABC A B C -中，1AA ⊥平面111A B C ，所以111B F AA ⊥，又1111B F AC ⊥，1111A C AA A =，所以11B F ⊥平面11ACC A ，而11B F ⊂平面11AB F ，所以平面11AB F ⊥平面11ACC A .【点睛】本题考查线面位置关系的判定与证明，熟练掌握空间中线面位置关系的定义、判定、几何特征是解答的关键，其中垂直、平行关系证明中应用转化与化归思想的常见类型：(1)证明线面、面面平行，需转化为证明线线平行；(2)证明线面垂直，需转化为证明线线垂直；(3)证明线线垂直，需转化为证明线面垂直．12．（Ⅰ）详见解析；【解析】【分析】（Ⅰ）证明AB AC ⊥，结合AB DA ⊥，证明AB ⊥平面ACD ，然后证明平面ACD ⊥平面ABC ；（Ⅱ）过Q 作//QN DC 交AC 于点N ，过N 作NO AP ⊥交AP 于点O ；证明DC ⊥平面ABC ，推出QN AP ⊥，结合NO AP ⊥，推出AP ⊥平面QNO ，即可证明QO AP ⊥，NOQ ∠就是二面角Q PA C --的平面角；通过求解三角形的相关知识即可求解二面角Q PA C --大小的正切值．【详解】（Ⅰ）平行四边形ABCM 中，90ACM ∠= 90BAC ∴∠=，即AB AC ⊥ 又AB DA ⊥，DA AB A = AB ∴⊥平面ACDAB ⊂平面ABC ∴平面ACD ⊥平面ABC（Ⅱ）在ACD ∆中，过Q 作//QN DC 交AC 于点N ，过N 作NO AP ⊥交AP 于点O 由（Ⅰ）知平面ACD ⊥平面ABC平面ACD ⋂平面ABC AC =，90DCA ∠=o DC ∴⊥平面ABC//QN DC QN ∴⊥平面ABC ，AP ⊂平面ABC QN AP ∴⊥又NO AP ⊥，QN NO N = AP ∴⊥平面QNOQO ⊂平面NQO QO AP ∴⊥NOQ ∴∠就是二面角Q PA C --的平面角在CAP ∆中，3CA =，23CP CB ==45ACP ∠=(2222232342co 5s 5AP AC CP AC CP ACP ∴=+-⋅⋅∠=+-⨯⨯︒=AP ∴=在CAP ∆中，sin sin CP AP CAP ACP=∠∠，即：sin 2CAP =∠sin sin CAP NAO ∴∠==∠ ACD ∆中，//QN DC ，且223DQ AC ==，223QN CD == 在Rt NAO ∆中，sin 2NO AN NAO =∠==. 在Rt NOQ ∆中，2tan 4NQ NOQ NO ∠===∴二面角Q PA C --大小的正切值2【点睛】本题考查二面角的平面角的求法，直线与平面垂直的判定定理的应用，考查空间想象能力以及计算能力；准确找到二面角的平面角是解决本题的关键.13．（1）证明过程详见解析（2）证明过程详见解析；【解析】【分析】(1)由三角形中位线定理可得//,//EG PM GF BC ，由正方形的性质可得//BC AD ，GF AD //，由线面平行的判定定理可得//EG 平面PMA ， //GF 平面PMA ，从而可得结果；(2)由线面垂直的性质证明PD BC ⊥,正方形的性质可得BC DC ⊥，结合//GF BC ，可得GF ⊥平面PDC ，从而可得平面EFG ⊥平面PDC ；【详解】(1)∵E G F 、、分别为MB PB PC 、、的中点，∴//,//EG PM GF BC ，又∵四边形ABCD 是正方形，∴//BC AD ，∴GF AD //，∵EG GF 、在平面PMA 外， PM AD 、在平面PMA 内，∴//EG 平面PMA ， //GF 平面PMA ，又∵EG GF 、都在平面EFG 内且相交，∴平面//EFG 平面PMA .(2)证明：由已知MA ⊥平面,//ABCD PD MA ，∴PD ⊥平面ABCD .又BC ⊂平面ABCD ，∴PD BC ⊥.∵四边形ABCD 为正方形，∴BC DC ⊥，又PD DC D =，∴BC ⊥平面PDC ，在PBC ∆中，∵G F 、分别为PB PC 、的中点，∴//GF BC ，∴GF ⊥平面PDC .又GF ⊂平面EFG ，∴平面EFG ⊥平面PDC .【点睛】本题主要考查正方体的性质、线面垂直的判定定理及面面垂直的判定定理以及线面平行、面面平行的判定定理，属于中档题.解答空间几何体中垂直关系时，一般要根据已知条件把空间中的线线、线面、面面之间垂直关系进行转化，转化时要正确运用有关的定理，找出足够的条件进行推理；证明直线和平面垂直的常用方法有：（1）利用判定定理；（2）利用判定定理的推论()||,a b a b αα⊥⇒⊥；（3）利用面面平行的性质(),||a a ααββ⊥⇒⊥；（4）利用面面垂直的性质，当两个平面垂直时，在一个平面内垂直于交线的直线垂直于另一个平面.14．（Ⅰ）见解析；（II ）见解析.【解析】【分析】（Ⅰ）根据线面平行判定定理可知//BC 平面PAD ；利用线面平行性质定理可证得结论；（II ）根据线面垂直性质定理可得PA AC ⊥，利用余弦定理求得AC ，根据勾股定理可证得AC AB ⊥，利用线面垂直判定定理证得AC ⊥平面PAB ，根据面面垂直判定定理可证得结论.【详解】（Ⅰ）//BC AD ，AD ⊂平面PAD ，BC Ë平面PAD//BC ∴平面PADBC ⊂平面PBC ，且平面PBC ⋂平面PAD l =//BC l ∴（II ）PA ⊥平面ABCD ，AC ⊂平面ABCD PA AC∴⊥ 1AB =，2BC =，60ABC ∠=，由余弦定理得：3AC ==222AB AC BC ∴+= AC AB∴⊥ 又AC PA ⊥，PA AB A =，PA ⊂平面PAB ，AB Ì平面PABAC ∴⊥平面PAB又AC ⊂平面PAC ∴平面PAC ⊥平面PAB【点睛】本题考查立体几何中的线面平行的证明与性质、面面垂直的证明、线面垂直的证明与性质应用，考查学生对于空间中直线与平面、平面与平面位置关系相关定理的掌握情况.15．（Ⅰ）见解析（Ⅱ）见解析【解析】【分析】（Ⅰ）取PC 的中点G ，连结FG 、EG ，AF ∥EG 又EG⊂平面PCE ，AF ⊄平面PCE ，AF ∥平面PCE ；（Ⅱ）由（Ⅰ）得EG ∥AF ，只需证明AF ⊥面PDC ，即可得到平面PEC ⊥平面PCD ．【详解】证明：（Ⅰ）取PC 的中点G ，连结FG 、EG ，∴FG 为△CDP 的中位线，FG ∥CD ，FG =12CD ． ∵四边形ABCD 为矩形，E 为AB 的中点，∴AE ∥CD ，AE =12CD ． ∴FG =AE ，FG ∥AE ，∴四边形AEGF 是平行四边形，∴AF∥EG又EG⊂平面PCE，AF⊄平面PCE，∴AF∥平面PCE；（Ⅱ）∵PA=AD．∴AF⊥PDPA⊥平面ABCD，∴PA⊥CD，又因为CD⊥AB，AP∩AB=A，∴CD⊥面APD∴CD⊥AF，且PD∩CD=D，∴AF⊥面PDC由（Ⅰ）得EG∥AF，∴EG⊥面PDC又EG⊂平面PCE，∴平面PEC⊥平面PCD．【点睛】本题考查了空间线面平行、面面垂直的判定，属于中档题．。

面面垂直答案

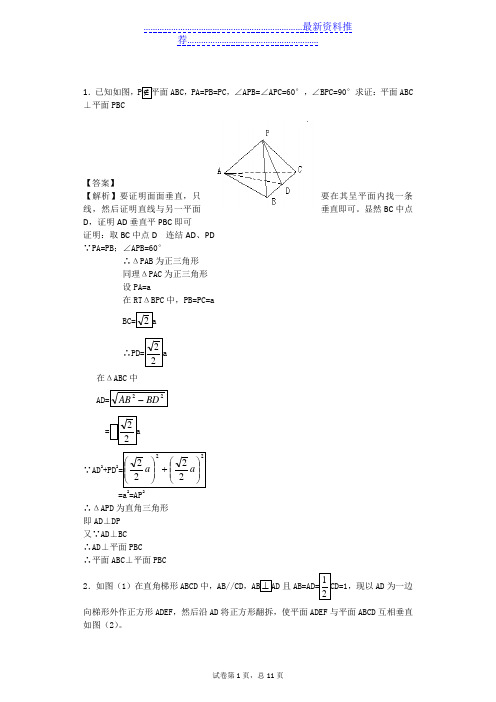
1．已知如图，P ∉平面ABC ，PA=PB=PC ，∠APB=∠APC=60°，∠BPC=90°求证：平面ABC ⊥平面PBC【答案】【解析】要证明面面垂直，只要在其呈平面内找一条线，然后证明直线与另一平面垂直即可。

显然BC 中点D ，证明AD 垂直平PBC 即可证明：取BC 中点D 连结AD 、PD ∵PA=PB ；∠APB=60°∴ΔPAB 为正三角形同理ΔPAC 为正三角形设PA=a在RT ΔBPC 中，PB=PC=a BC=2a∴PD=22a 在ΔABC 中 AD=22BD AB -=22a ∵AD 2+PD 2=222222⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛a a =a 2=AP 2∴ΔAPD 为直角三角形即AD ⊥DP 又∵AD ⊥BC ∴AD ⊥平面PBC∴平面ABC ⊥平面PBC2．如图（1）在直角梯形ABCD 中，AB//CD ，AB ⊥AD 且AB=AD=12CD=1，现以AD 为一边向梯形外作正方形ADEF ，然后沿AD 将正方形翻拆，使平面ADEF 与平面ABCD 互相垂直如图（2）。

（1）求证平面BEC（2）求直线BD与平面BEF所成角的正弦值。

【答案】⑴证见解析【解析】（1）由折前折后线面的位置关系得所以（2根据线面角的定义可求直线BD与平面BEF所成角的正弦值。

3．（本小题满分14分）如图，在正方体ABCD－A1B1C1D1中，E、F为棱AD、AB的中点．（1）求证：EF∥平面CB1D1；（2）求证：平面CAA1C1⊥平面CB1D1．【答案】（Ⅰ）略（Ⅱ）略【解析】（1）证明：连结BD.E、F为棱AD、AB……………4分又B1D1⊂≠EF∥平面CB1D1.……………7分（2）AA1⊥平面A1B1C1D1，而B1D1⊂≠平面A1B1C1D1，∴AA1⊥B1D1.…9分A1B1C1D1中，A1C1⊥B1D1，∴B1D1⊥平面CAA1C1.B1D1⊂≠平面CB1D1，∴平面CAA1C1⊥平面CB1D1．……14分4．如图，四棱锥中，底面为平行四边形，A BCDEF图2A BE C图1FDACA11(1)证明：平面⊥PBC 平面PBD ；(2)若二面角D BC P --为6π，求AP 与平面PBC 所成角的正弦值。

(压轴题)高中数学必修二第一章《立体几何初步》测试题(包含答案解析)(3)

一、选择题1．现有一个三棱锥形状的工艺品P ABC -，点P 在底面ABC 的投影为Q ，满足12QABQAC QBC PABPACPBCS S S S S S ===△△△△△△，22222213QA QB QC AB BC CA ++=++，93ABCS =，若要将此工艺品放入一个球形容器（不计此球形容器的厚度）中，则该球形容器的表面积的最小值为（）A ．42πB ．44πC ．48πD ．49π2．如图，在长方体1111ABCD A B C D -中，1AB AD ==，12AA =，M 为棱1DD 上的一点．当1A M MC +取得最小值时，1B M 的长为（）A 3B 6C ．23D ．263．已知三棱柱111ABC A B C -的所有顶点都在球O 的表面上，侧棱1AA ⊥底面111A B C ，底面111A B C △是正三角形，1AB 与底面111A B C 所成的角是45°.若正三棱柱111ABC A B C -的体积是3O 的表面积是（） A ．28π3B ．14π3C ．56π3D ．7π 34．在我国古代，将四个角都是直角三角形的四面体称为“鳖臑”．在“鳖臑”ABCD 中，AB ⊥平面BCD ，BD CD ⊥且AB BD CD ==，若该四面体的体积为43，则该四面体外接球的表面积为（）A ．8πB ．12πC ．14πD ．16π5．在长方体1111ABCD A B C D -中，12,3AB BC AA ===，E 是BC 的中点，则直线1ED 与直线BD 所成角的余弦值是（） A ．728B ．728-C ．3714D ．3714-6．已知正三棱柱111ABC A B C -中，1AB AA =，M 是1CC 的中点，则异面直线AM 与1A B 所成角的大小为（）A ．π6B ．π4C ．π3D ．π27．某几何体的三视图（单位：cm ）如图所示，则该几何体的体积（单位：3cm ）为（）A ．43B ．2C ．4D ．68．如图，在四棱锥E ABCD -中，底面ABCD 是正方形，且平面ABCD ⊥平面AEB ，则（）A ．DEC ∠可能为90︒B ．若AEB △是等边三角形，则DEC 也是等边三角形C ．若AEB △是等边三角形，则异面直线DE 和AB 所成角的余弦值为24D ．若AEB △是直角三角形，则BE ⊥平面ADE9．《九章算术》是古代中国乃至东方的第一步自成体系的数学专著，书中记载了一种名为“刍甍”的五面体（如图），其中四边形ABCD 为矩形，//EF AB ，若3AB EF =，ADE 和BCF △都是正三角形，且2AD EF =，则异面直线AE 与CF 所成角的大小为（）A ．6π B ．4π C ．3π D ．2π 10．一个正方体的平面展开图及该正方体的直观图如图所示，在正方体中，设BC 的中点为M ，GH 的中点为N ，下列结论正确的是（）A ．//MN 平面ABEB ．//MN 平面ADEC ．//MN 平面BDHD ．//MN 平面CDE11．某三棱锥的三视图如图所示，已知网格纸上小正方形的边长为1，则该三棱锥的体积为（）A ．43 B ．83C ．3D ．412．已知直线a 、b 都不在平面α内，则下列命题错误的是（） A ．若//a b ，//a α，则//b α B ．若//a b ，a α⊥，则b α⊥ C ．若a b ⊥，//a α，则b α⊥D ．若a b ⊥，a α⊥，则//b α二、填空题13．如图，已知直四棱柱1111ABCD A B C D -的所有棱长均相等，3BAD π∠=，E 是棱AB的中点，设平面α经过直线1A E ，且α平面111,B BCC l α=⋂平面112C CDD l =，若α⊥平面11A ACC ，则异面直线1l 与2l 所成的角的余弦值为_______．14．如图在菱形ABCD 中，2AB =，60A ∠=，E 为AB 中点，将AED 沿DE 折起使二面角A ED C '--的大小为90，则空间A '、C 两点的距离为________；15．点A 、B 、C 、D 在同一个球的球面上，3AB BC AC ===，若四面体ABCD 体积的最大值为32，则这个球的表面积为______. 16．如图，四边形ABCD 是矩形，且有2AB BC =，沿AC 将ADC 翻折成AD C '，当二面角D AC B '--的大小为3π时，则异面直线D C '与AB 所成角余弦值是______.17．已知长方体1234ABCD A B C D -，底面是边长为4的正方形，高为2，点O 是底面ABCD 的中心，点P 在以O 为球心，半径为1的球面上，设二面角111P A B C --的平面角为θ，则tan θ的取值范围是________.18．如图，在三棱锥V ABC -中，22AB =VA VB =，1VC =，且AV BV ⊥，AC BC ⊥，则二面角V AB C --的余弦值是_____．19．已知扇形的面积为56π，圆心角为63π，则由该扇形围成的圆锥的外接球的表面积为_________．20．棱长为a 的正四面体的外接球的表面积为______．三、解答题21．在如图所示几何体中，平面PAC ⊥平面ABC ，//PM BC ，PA PC =，1AC =，22BC PM ==，5AB =．若该几何体左视图（侧视图）的面积为34．（1）画出该几何体的主视图（正视图）并求其面积S ；（2）求出多面体PMABC 的体积V ．22．如图，在四棱锥P ABCD -中，底面ABCD 是正方形，32,3,PB PD PA AD ====点,E F 分别为线段,PD BC 的中点.（1）求证://EF 平面ABP ; （2）求证:平面AEF ⊥平面PCD ; （3）求三棱锥C AEF -的体积23．如图所示，已知在三棱锥A BPC -中，,AP PC AC BC ⊥⊥，M 为AB 的中点，D为PB 的中点，且PMB △为正三角形．（Ⅰ）求证：//DM 平面APC ；（Ⅱ）求证：平面ABC ⊥平面APC ；（Ⅲ）若4,20BC AB ==，求三棱锥D BCM -的体积．24．如图，四棱锥P ABCD -中，底面ABCD 为矩形，PA ⊥底面ABCD ，E 为PD 的中点．（1）证明：//PB 平面AEC ；（2）设1AP =，3AD =，四棱锥P ABCD -的体积为1，求证：平面PAC ⊥平面PBD ．25．如图，在平面四边形A ABC '中，90CAB CA A '∠=∠=，M 在直线AC 上，A A A C ''=，AB AM MC ==，A AC '绕AC 旋转．（1）若A AC '所在平面与ABC 所在平面垂直，求证：A C '⊥平面A AB '．（2）若二面角A AC B '--大小为60，求直线A B '与平面ABM 所成角的正弦值．26．在三棱锥P ABC -中，G 是底面ABC 的重心，D 是线段PC 上的点，且2PD DC =.（1）求证：DG//平面PAB ；（2）若PAB △是以PB 为斜边的等腰直角三角形，求异面直线DG 与PB 所成角的余弦值.【参考答案】***试卷处理标记，请不要删除一、选择题 1．D 解析：D 【分析】作QM AB ⊥，连接PM ，易证AB PM ⊥，由112122QAB PABAB QMS S AB PM ⨯⨯==⨯⨯△△,得到2PM QM =，再根据12QAB QAC QBC PABPACPBCS S S S S S ===△△△△△△，由对称性得到AB BC AC ==，然后根据22222213QA QB QC AB BC CA ++=++，93ABCS =6,3AB AQ ==，在AOQ△中，由222AO OQ AQ =+求解半径即可.【详解】如图所示：作QM AB ⊥与M ，连接PM ，因为PQ ⊥平面ABC ，所以PQ AB ⊥，又QM PQ Q ⋂=，所以AB ⊥平面PQM ，所以AB PM ⊥，所以112122QAB PAB AB QM S S AB PM ⨯⨯==⨯⨯△△, 2PM QM =,因为12QAB QAC QBC PABPACPBCS S S S S S ===△△△△△△，由对称性得AB BC AC ==,又因为22222213QA QB QC AB BC CA ++=++，93ABCS=所以21sin 60932ABCSAB =⨯⨯= 解得6,3AB AQ == 所以3,23,3QM PM PQ ===，设外接球的半径为r ，在AOQ △中，222AO OQ AQ =+，即()(222323r r =-+，解得72r =，所以外接球的表面积为2449S r ππ==，即该球形容器的表面积的最小值为49π. 故选：D 【点睛】关键点点睛：本题关键是由1 2QAB QAC QBCPAB PAC PBCS S SS S S===△△△△△△得到三棱锥是正棱锥，从而找到外接球球心的位置而得解..2．A解析：A【分析】本题首先可通过将侧面11CDD C绕1DD逆时针转90展开得出当1A、M、2C共线时1A M MC+取得最小值，此时M为1DD的中点，然后根据11B A⊥平面11A D DA得出111B A A M⊥，最后根据221111M AB B A M=+即可得出结果.【详解】如图，将侧面11CDD C绕1DD逆时针转90展开，与侧面11ADD A共面，连接12A C，易知当1A、M、2C共线时，1A M MC+取得最小值，因为1AB AD==，12AA=，所以M为1DD的中点，12A M=因为11B A⊥平面11A D DA，1A M⊂平面11A D DA，所以111B A A M⊥，则222211111(2)3M B A A MB=+=+=故选：A.【点睛】关键点点睛：本题考查根据线面垂直判断线线垂直，能否根据题意得出当M为1DD的中点时1A M MC+取得最小值是解决本题的关键，考查计算能力，考查数形结合思想，是中档题.3．A解析：A【分析】首先得到11AB A∠是1AB与底面111A B C所成的角，再通过三棱柱的体积得到三棱柱的底面等边三角形的边长，最后通过球的半径，球心到底面距离，底面外接圆半径的关系计算．【详解】因为侧棱1AA ⊥底面111A B C ，则11AB A ∠是1AB 与底面111A B C 所成的角，则1145AB A ∠=︒．故由11111tan tan 451AA AB A A B ∠=︒==，得111AA A B =．设111AA A B a ==，则111313323224ABC A B C a V a a a -=⨯⨯⨯==三棱柱，解得2a =．所以球O 的半径22232722233R ⎛⎫⎛⎫+⨯⨯= ⎪ ⎪ ⎪⎝⎭⎝=⎭，所以球O 的表面积22728π4π4π33S R ⎛⎫==⨯= ⎪ ⎪⎝⎭．故选：A ．【点睛】解决球与其他几何体的切、接问题，关键在于仔细观察、分析，弄清相关元素的关系和数量关系，选准最佳角度作出截面(要使这个截面尽可能多地包含球、几何体的各种元素以及体现这些元素之间的关系)，达到空间问题平面化的目的．4．B解析：B 【分析】由题意计算2,AB BD CD ===分析该几何体可以扩充为长方体，所以只用求长方体的外接球即可. 【详解】因为AB ⊥平面BCD ，BD CD ⊥且AB BD CD ==， 43A BCD V -=，而114323A BCD V BD CD AB -=⨯⨯⨯=,所以2AB BD CD ===，所以该几何体可以扩充为正方体方体，所以只用求正方体的外接球即可.设外接球的半径为R ，则23R =所以外接球的表面积为2412S R ππ== 故选：B 【点睛】多面体的外接球问题解题关键是找球心和半径，求半径的方法有：(1)公式法；(2) 多面体几何性质法；(3)补形法；(4)寻求轴截面圆半径法；(5)确定球心位置法．5．C解析：C 【分析】连接11D B 、1D E 、DE ，先证明四边形11BB D D 为平行四边形，得到11//B D BD ，故异面直线1ED 与BD 所成的角即为相交直线1ED 与11D B 所成的角，由余弦定理可得答案. 【详解】连接11D B 、1D E 、DE ，因为棱11//BB DD ，11BB DD =，所以四边形11BB D D 为平行四边形，所以11//B D BD ，故异面直线1ED 与BD 所成的角即为相交直线1ED 与11D B 所成的角11B D E ∠，因为12,3AB AD AA ===,1BE CE ==，所以2211111122B D D C B C =+=213110B E =+=222415ED CE DC +=+==，所以222115914D E ED D D ==+=+，由余弦定理得，从而22211111111137cos 24214B D D E B E B D E B D D E +-∠===⨯⨯. 故选：C 【点睛】本题考查异面直线所成角的余弦值的求法，关键点是找到异面直线所成的角，考查空间中线线的位置关系等基础知识，考查运算求解能力，是中档题．6．D解析：D 【分析】取AC 中点E ，连接1,A E BE ，先通过BE ⊥平面11ACC A 可得BE AM ⊥，再由1ACM A AE ≅可得1AM A E ⊥，即可得出AM ⊥平面1A BE ，即1AM A B ⊥.【详解】取AC 中点E ，连接1,A E BE ，ABC 为正三角形，BE AC ∴⊥，正三棱柱111ABC A B C -中，1CC ⊥平面ABC ，BE ⊂平面ABC ，1CC BE ∴⊥，1ACCC C =，BE ∴⊥平面11ACC A ，AM ⊂平面11ACC A ，BE AM ∴⊥，在直角三角形ACM 和直角三角形1A AE 中，1,AC A A CM AE ==,1ACM A AE ∴≅， 1CAM AA E ∴∠=∠，12CAM A EA π∴∴∠+∠=，则1AM A E ⊥，1BE A E E ⋂=，AM ∴⊥平面1A BE ，1A B ⊂平面1A BE ，1AM A B ∴⊥，故异面直线AM 与1A B 所成角的大小为2π.【点睛】本题考查异面直线所成角的求解，解题的关键是通过证明AM ⊥平面1A BE 判断出1AM A B ⊥.7．B解析：B 【分析】根据三视图判断出几何体的结构，利用椎体体积公式计算出该几何体的体积. 【详解】根据三视图可知，该几何体为如图所示四棱锥，该棱锥满足底面是直角梯形，且侧棱ED ⊥平面ABCD ，所以其体积为11(12)22232V =⨯⨯+⨯⨯=，故选：B. 【点睛】方法点睛：该题考查的是有关根据几何体三视图求几何体体积的问题，解题方法如下：（1）首先根据题中所给的几何体的三视图还原几何体；（2）结合三视图，分析几何体的结构特征，利用体积公式求得结果.8．C解析：C 【分析】对A ，直角三角形的斜边大于直角边可判断；对B ，由>=EC EB DC 可判断；对C ，可得CDE ∠即异面直线DE 和AB 所成角，即可求出；对D ，EAB ∠（或EBA ∠）为直角时，BE 与平面ADE 不垂直. 【详解】对A ，由题意，若90DEC ∠=︒，则DC EC >，但EC BC CD >=，故A 不正确；对B ，若AEB △是等边三角形，显然有>=EC EB DC ，所以DEC 不会是等边三角形，故B 不正确；对C ，若AEB △是等边三角形，设边长为2，则22DE EC ==//AB CD ，则CDE ∠即异面直线DE 和AB 所成角，易求2cos 422CDE ∠==，故C 正确；对D ，当AEB △是以AEB ∠为直角的直角三角形时，BE ⊥平面ADE ，当AEB △是以EAB ∠（或EBA ∠）为直角的直角三角形时，BE 与平面ADE 不垂直，故D 不正确．故选：C. 【点睛】本题考查四棱锥的有关位置关系的判断，解题的关键是正确理解长度关系，正确理解位置关系的变化.9．D解析：D 【分析】过点F 作//FG AE 交AB 于点G ，连接CG ，则异面直线AE 与CF 所成角为CFG ∠或其补角，然后在CFG △中求解. 【详解】如下图所示，在平面ABFE 中，过点F 作//FG AE 交AB 于点G ，连接CG ，则异面直线AE 与CF 所成角为CFG ∠或其补角，设1EF =，则3AB =，2BC CF AE ===，因为//EF AB ，//FG AE ，所以，四边形AEFG 为平行四边形，所以，2FG AE ==，1AG =，2BG =，由于2ABC π∠=，由勾股定理可得2222CG BC BG =+=所以，222CG CF FG =+，则2CFG π∠=.故选：D. 【点睛】思路点睛：平移线段法是求异面直线所成角的常用方法，其基本思路是通过平移直线，把异面直线的问题化归为共面直线问题来解决，具体步骤如下：（1）平移：平移异面直线中的一条或两条，作出异面直线所成的角；（2）认定：证明作出的角就是所求异面直线所成的角；（3）计算：求该角的值，常利用解三角形；（4）取舍：由异面直线所成的角的取值范围是0,2π⎛⎤⎥⎝⎦，当所作的角为钝角时，应取它的补角作为两条异面直线所成的角．10．C解析：C 【分析】根据题意，得到正方体的直观图及其各点的标记字母，取FH 的中点O ,连接ON ,BO ，可以证明MN ‖BO ,利用BO 与平面ABE 的关系可以判定MN 与平面ABE 的关系，进而对选择支A 作出判定；根据MN 与平面BCF 的关系，利用面面平行的性质可以判定MN 与平面ADE 的关系，进而对选择支B 作出判定；利用线面平行的判定定理可以证明MN 与平面BDE 的平行关系，进而判定C ；利用M ,N 在平面CDEF 的两侧，可以判定MN 与平面CDE 的关系，进而对D作出判定.【详解】根据题意，得到正方体的直观图及其各点的标记字母如图所示，取FH的中点O,连接ON,BO，易知ON与BM平行且相等，∴四边形ONMB为平行四边形，∴MN‖BO,∵BO与平面ABE（即平面ABFE)相交，故MN与平面ABE相交，故A错误；∵平面ADE‖平面BCF,MN∩平面BCF=M,∴MN与平面ADE相交，故B错误；∵BO⊂平面BDHF,即BO‖平面BDH,MN‖BO,MN⊄平面BDHF,∴MN‖平面BDH,故C正确；显然M,N在平面CDEF的两侧，所以MN与平面CDEF相交，故D错误.故选：C.【点睛】本题考查从面面平行的判定与性质，涉及正方体的性质，面面平行，线面平行的性质，属于小综合题，关键是正确将正方体的表面展开图还原，得到正方体的直观图及其各顶点的标记字母，并利用平行四边形的判定与性质找到MN的平行线BO.11．A解析：A【分析】首先由三视图还原几何体，然后由几何体的空间结构特征求解三棱锥的体积即可.【详解】-，由三视图可知，在棱长为2的正方体中，其对应的几何体为棱锥P ABC该棱锥的体积：11142223323V Sh ⎛⎫==⨯⨯⨯⨯= ⎪⎝⎭. 故选：A. 【点睛】方法点睛：(1)求解以三视图为载体的空间几何体的体积的关键是由三视图确定直观图的形状以及直观图中线面的位置关系和数量关系，利用相应体积公式求解；(2)若所给几何体的体积不能直接利用公式得出，则常用等积法、分割法、补形法等方法进行求解．12．C解析：C 【分析】利用线面平行的性质和判定定理可判断A 选项的正误；由线面垂直的定义可判断B 选项的正误；根据已知条件判断b 与α的位置关系，可判断C 选项的正误；根据已知条件判断b 与α的位置关系，可判断D 选项的正误. 【详解】由于直线a 、b 都不在平面α内.在A 中，若//a α，过直线a 的平面β与α的交线m 与a 平行，因为//a b ，可得//b m ，b α⊄，m α⊂，所以，//b α，A 选项正确；在B 中，若a α⊥，则a 垂直于平面α内所有直线，//a b ，则b 垂直于平面α内所有直线，故b α⊥，B 选项正确；在C 中，若a b ⊥，//a α，则b 与α相交或平行，C 选项错误；在D 中，若a b ⊥，a α⊥，则//b α或b α⊂，b α⊄，//b α∴，D 选项正确.故选：C. 【点睛】方法点睛：对于空间线面位置关系的组合判断题，解决的方法是“推理论证加反例推断”，即正确的结论需要根据空间线面位置关系的相关定理进行证明，错误的结论需要通过举出反例说明其错误，在解题中可以以常见的空间几何体（如正方体、正四面体等）为模型进行推理或者反驳．二、填空题13．【分析】取的中点连接证明平面平面平面即平面然后分别取的中点证明平面平面可得可得异面直线与所成的角即与所成的角由余弦定理可得答案【详解】由直四棱柱的所有棱长均相等所以是菱形连接且所以因为平面平面所以且解析：910【分析】取AD 的中点F ，连接1A F ，证明平面1A EF ⊥平面11A ACC ，平面1A EF 即平面α，然后分别取1111B C D C 、的中点M N 、，证明平面1//A EF 平面MNC ，可得//CM 1l ，//CN 2l ，可得异面直线1l 与2l 所成的角即CM 与CN 所成的角，由余弦定理可得答案.【详解】由直四棱柱1111ABCD A B C D -的所有棱长均相等，3BAD π∠=，所以ABCD 是菱形，连接AC BD 、，1111AC B D 、，且ACBD O =，11111A C B D O ⋂=，所以BD AC ⊥，1111B D A C ⊥，因为1AA ⊥平面ABCD ，BD ⊂平面ABCD ，所以1AA BD ⊥，且1AA AC A =，所以BD ⊥平面11A ACC ，取AD 的中点F ，连接1A F ，连接EF 交AC 与G ，所以//EF BD ，且G 是AO 的中点，所以EF ⊥平面11A ACC ，所以平面1A EF ⊥平面11A ACC ，又1A E ⊂平面1A EF ，所以平面1A EF 即平面α，分别取1111B C D C 、的中点M N 、，连接MN 交11A C 与H 点，H 即为11O C 的中点，所以1A H GC =，且1//A H GC ，所以四边形1A HCG 是平行四边形，所以1//A G HC ，1AG ⊄平面CMN ，CH ⊂平面CMN ，所以//A G 平面CMN ，又因为11//////EF BD B D MN ，EF ⊄平面CMN ，MN ⊂平面CMN ，所以//MN 平面CMN ，又1AG EF G =，所以平面1//A EF 平面MNC ，且平面11B C CB ⋂平面MNC MC =，平面11D C CD平面MNC NC =，所以//CM 1l ，//CN 2l ，所以异面直线1l 与2l 所成的角即CM 与CN 所成的角，设2AB =，则直四棱柱1111ABCD A B C D -的所有棱长均为2，由3BAD π∠=，所以112BD AB B D ===，11112MN D B ==，且CM CN ====，由余弦定理得222551922510CM CN MN MCN CM CN +-+-∠===⨯⨯.故答案为：910. 【点睛】本题考查了异面直线所成的角，关键点是作出平面α及找出异面直线所成的角，考查了学生分析问题、解决问题的能力及空间想象力.14．【分析】由二面角的大小为可得平面平面得到平面由勾股定理可得答案【详解】连接所以是等边三角形所以因为为中点所以所以即所以因为平面平面平面平面所以平面平面所以所以故答案为：【点睛】对于翻折问题解题时要认解析：22 【分析】由二面角A ED C '--的大小为90，可得平面A ED '⊥平面EDCB ，得到A E '⊥平面EDCB ，由勾股定理可得答案. 【详解】连接DB CE 、，2AB AD ==，60A ∠=，所以ABD △、CBD 是等边三角形，所以2AD BD CD ===，因为E 为AB 中点，1AE A E '==，所以DE AB ⊥，DE A E ⊥'，3DE =30EDB ∠=，所以90EDC ∠=，即DE CD ⊥，所以222347EC ED CD =+=+=，因为平面A ED '⊥平面EDCB ，DE A E ⊥'，平面A ED'平面EDCB DE =，所以A E '⊥平面EDCB ，EC ⊂平面EDCB ，所以A E EC '⊥，所以221722A C A E EC ''=+=+=故答案为：2【点睛】对于翻折问题，解题时要认真分析图形，确定有关元素间的关系及翻折前后哪些量变了，哪些量没有变，根据线线、线面、面面关系正确作出判断，考查了学生的空间想象力..15．【分析】先由题意得到的面积以及外接圆的半径记的外接圆圆心为为使四面体体积最大只需与面垂直由此求出设球心为半径为根据为直角三角形由勾股定理列出等式求出球的半径即可得出结果【详解】根据题意知是一个等边三解析：254π【分析】先由题意，得到ABC 的面积，以及ABC 外接圆的半径，记ABC 的外接圆圆心为Q ，为使四面体ABCD 体积最大，只需DQ 与面ABC 垂直，由此求出2DQ =，设球心为O ，半径为R ，根据AQO 为直角三角形，由勾股定理列出等式，求出球的半径，即可得出结果. 【详解】根据题意知，ABC 是一个等边三角形，其面积为()2213333322S ⎛⎫=-= ⎪ ⎪⎝⎭，ABC 外接圆的半径为1312sin 60r =⨯=，记ABC 的外接圆圆心为Q ，则1AQ r ==；由于底面积ABCS不变，高最大时体积最大，所以DQ 与面ABC 垂直时体积最大，最大值为133ABCS DQ ⋅=，2DQ ∴=，设球心为O ，半径为R ，则在直角AQO 中，222OA AQ OQ =+，即2221(2)R R =+-，54R ∴=，则这个球的表面积为：2525444S ππ⎛⎫== ⎪⎝⎭.故答案为：254π. 【点睛】思路点睛：求解几何体与球外接问题时，一般需要先确定底面外接圆的圆心位置，求出底面外接圆的半径，根据球的性质，结合题中条件确定球心位置，求出球的半径，进而即可求解.16．【分析】作于于可得等于二面角的平面角从而可得然后求得而因此可得是异面直线与所成角（或补角）这样在求解可得【详解】如图作于于则连接根据二面角平面角的定义知与的夹角等于二面角的平面角所以因为所以设则在矩解析：12．【分析】作DM AC ⊥于M ，BN AC ⊥于N ，可得,MD NB '<>等于二面角D AC B '--的平面角，从而可得DMD '∠，然后求得DD '，而//AB CD ，因此可得D CD '∠是异面直线D C '与AB 所成角（或补角）．这样在DCD '求解可得．【详解】如图，作DM AC ⊥于M ，BN AC ⊥于N ，则//DM BN ，连接,D M DD ''，根据二面角平面角的定义知MD '与NB 的夹角等于二面角D AC B '--的平面角，所以,3MD NB π'<>=，因为//DM BN ，所以23DMD π'∠=，设1BC =，则AB ==ABCD 中，AC =3DM ==，3D M DM '==，则22222212cos 22333332DD DM D M DM D M π⎛⎛⎛⎫'''=+-⋅=+-⨯-= ⎪ ⎝⎭⎝⎭⎝⎭，所以DD '=因为//AB CD ，所以D CD '∠是异面直线D C '与AB 所成角（或补角）．DCD '是正三角形，3D CD π'∠=，1cos 2D CD '∠=．所以异面直线D C '与AB 所成角余弦值是12．故答案为：12．【点睛】关键点点睛：本题考查求异面直线所成的角，解题方法根据异面直线所成角定义作出它们所成的角，然后解三角形可得，解题关键是利用图中MD '与NB 的夹角等于二面角D AC B '--的平面角，从而求得DMD '∠，只要设1BC =，可求得DD '，从而求得结论．17．【分析】根据题意画出相应的图形结合题意找出什么情况下取最大值什么情况下取最小值利用和差角正切公式求得最值得到结果【详解】根据题意如图所示：取的中点过点作球的切线切点分别为可以判断为的最小值为的最大值解析：4747,⎡⎤-+⎢⎥⎣⎦【分析】根据题意，画出相应的图形，结合题意，找出什么情况下取最大值，什么情况下取最小值，利用和差角正切公式求得最值，得到结果. 【详解】根据题意，如图所示：取11A B 的中点H ，过H 点作球O 的切线，切点分别为,M N ，可以判断1O HN ∠为θ的最小值，1O HM ∠为θ的最大值，且1112tan 12OO O HO HO ∠===，1OH OM ON ===，所以HM HN ==tan tan NHO OHM ∠=∠=，11tan tan()1O HN O HO NHO ∠=∠-∠====+1184tan tan()631O HM O HO OHM +∠=∠+∠====，所以tan θ的取值范围是44,33⎡+⎢⎣⎦，故答案为：⎣⎦. 【点睛】方法点睛：该题考查的是有关二面角的求解问题，解题方法如下：（1）先根据题意画图；（2）结合题意，找出在什么情况下取最大值和最小值；（3）结合图形求得相应角的正切值；（4）利用和差角正切公式求得结果.18．【分析】取的中点连接证明出可得出面角的平面角为计算出利用余弦定理求得由此可得出二面角的余弦值【详解】取的中点连接如下图所示：为的中点则且同理可得且所以二面角的平面角为由余弦定理得因此二面角的余弦值为解析：34【分析】取AB 的中点O ，连接VO 、OC ，证明出VO AB ⊥，OC AB ⊥，可得出面角V AB C --的平面角为VOC ∠，计算出VO 、OC ，利用余弦定理求得cos VOC ∠，由此可得出二面角V AB C --的余弦值. 【详解】取AB 的中点O ，连接VO 、OC ，如下图所示：VA VB =，O 为AB 的中点，则VO AB ⊥，且AV BV ⊥，22AB =122VO AB ∴== 同理可得OC AB ⊥，且2OC =V AB C --的平面角为VOC ∠，由余弦定理得2223cos 24VO OC VC VOC VO OC +-∠==⋅，因此，二面角V AB C --的余弦值为34. 故答案为：34. 【点睛】本题考查二面角余弦值的计算，考查二面角的定义，考查计算能力，属于中等题.19．【分析】由扇形的面积及圆心角可得扇形的半径再由扇形的弧长等于圆锥的底面周长可得底面半径再由外接球的半径与圆锥的高和底面半径的关系求出外接球的半径进而求出球的表面积【详解】设扇形的长为l 半径为R 则解得解析：36π【分析】由扇形的面积及圆心角可得扇形的半径，再由扇形的弧长等于圆锥的底面周长可得底面半径，再由外接球的半径与圆锥的高和底面半径的关系求出外接球的半径，进而求出球的表面积. 【详解】设扇形的长为l ，半径为R ，则22111656222S lR R παπ====，解得30R =l 为锥底面周长2r π，∴底面的半径5r =∴225R r -=．设外接球的半径为1R ，∴()222115(5)R R =-+，解得13R =，∴该外接球的表面积为21436R ππ=，故答案为：36π.【点睛】本题考查扇形的弧长与圆锥的底面周长的关系及外接球的半径和圆锥的高及底面半径的关系，和球的表面积公式的应用，属于中档题.20．【分析】由正四面体性质可知球心在棱锥高线上利用勾股定理可求出半径R 即可求出球的面积【详解】正四面体的棱长为：底面三角形的高：棱锥的高为：设外接球半径为R 解得所以外接球的表面积为：；故答案为：【点睛】解析：232a π 【分析】由正四面体性质可知，球心在棱锥高线上，利用勾股定理可求出半径R ，即可求出球的面积. 【详解】正四面体的棱长为：a ，a =，=，设外接球半径为R ，222)()33R a R a =-+，解得4R a =，所以外接球的表面积为：22342a ππ⎫⨯=⎪⎪⎝⎭；故答案为：232a π．【点睛】本题考查球的表面积的求法，解题的关键是根据球心的位置，在正四面体中求出球的半径．三、解答题21．（1）主视图（正视图）见解析，4S =；（2）4V =. 【分析】（1）根据侧视图计算出PAC △的边AC 上的高，进而可作出几何体PMABC 的主视图，利用梯形的面积公式可求得几何体的主视图的面积；（2）分别取AC 、PC 的中点O 、N ，连接PO 、AN ，推导出AN ⊥平面BCPM ，计算出AN 和梯形BCPM 的面积，利用锥体的体积公式可求得多面体PMABC 的体积V . 【详解】（1）在几何体PMABC 中，平面PAC ⊥平面ABC ，设PAC △的边AC 上的高为h ，则该几何体的侧视图的面积为1324AC h ⋅=，得32h =，又因为22BC PM ==，所以，该几何体的主视图（正视图）如下图所示：由图可知，该几何体的主视图为直角梯形，其面积为()1233322S +⨯==⨯；（2）分别取AC 、PC 的中点O 、N ，连接PO 、AN ，如下图所示：PA PC =，O 为AC 的中点，所以，PO AC ⊥，由（1）可知，3PO h ==1122AO CO AC ===，由勾股定理可得221PC PA AO PO ==+=，所以，PAC △为等边三角形，N 为PC 的中点，AN PC ∴⊥，且3sin 602AN AC ==. 1AC =，2BC =，5AB =222AC BC AB ∴+=，BC AC ∴⊥，平面PAC ⊥平面ABC ，平面PAC平面ABC AC =，BC ⊂平面ABC ，BC ∴⊥平面PAC ，AN 、PC ⊂平面PAC ，BC AN ∴⊥，BC PC ⊥， PC BC C =，AN ∴⊥平面BCPM ， //PM BC ，PM PC ∴⊥，所以，梯形BCPM 的面积为()322BCPM BC PM PC S +⋅==梯形，因此，1133333224BCPM V S AN =⋅=⨯⨯=梯形. 【点睛】方法点睛：求空间几何体体积的方法如下：（1）求解以三视图为载体的空间几何体的体积的关键是由三视图确定直观图的形状以及直观图中线面的位置关系和数量关系，利用相应体积公式求解；（2）若所给几何体的体积不能直接利用公式得出，则常用等积法、分割法、补形法等方法进行求解．22．（1）证明见解析；（2）证明见解析；（3）98. 【分析】（1）取PA 的中点G ，连接,BG EG ，证明四边形EFBG 为平行四边形，得出//EF BG ，再由线面平行的判定定理证明即可；（2）先证明PA ⊥平面ABCD ，从而得出PA CD ⊥，再由等腰三角形的性质得出AE PD ⊥，最后由面面垂直的判定定理证明即可；（3）以AFC △为底，12PA 为高，由棱锥的体积公式得出答案.【详解】（1）如图，取PA 的中点G ，连接,BG EG .因为点,E G 分别为,PD PA 的中点，所以1//,2EG AD EG AD =又因为F 是BC 的中点，四边形ABCD 是正方形，所以//BF EG 且BF EG = 故四边形EFBG 为平行四边形，所以//EF BG 因为BG ⊂平面,ABP EF 不在平面ABP 内，所以//EF 平面ABP .（2）由条件知32,3PB PD PA AD AB =====，所以PAB △和PAD △都是等腰直角三角形，,PA AB PA AD ⊥⊥ 又因为,,ABAD A AB AD =⊂平面,ABCD 所以PA ⊥平面ABCD因为CD ⊂平面ABCD ，所以PA CD ⊥又因为,,AD CD PA AD A ⊥⋂=所以CD ⊥平面PAD ，所以CD AE ⊥因为E 是PD 的中点，所以AE PD ⊥又因为,,PD CD D PD CD ⋂=⊂平面PCD ，所以AE ⊥平面PCD 因为AE ⊂平面,AEF 所以平面AEF ⊥平面PCD . （3）由图可知C AEF E ACF V V --=，1111319333232228E ACF ACF V S PA -=⨯=⨯⨯⨯⨯⨯=△，即三棱锥C AEF -的体积为98【点睛】关键点睛：在证明线线平行时，关键是证明四边形EFBG 为平行四边形，从而得出//EF BG .23．（1）见详解；（2）见详解；（3）107 【分析】(1)先证DM AP ∥，可证//DM 平面APC .(2)先证AP ⊥平面PBC ，得⊥AP BC ，结合AC BC ⊥可证得BC ⊥平面APC . (3)等积转换，由D BCM M DBC V V --＝，可求得体积. 【详解】证明：因为M 为AB 的中点，D 为PB 的中点，所以MD 是ABP △的中位线，MD AP .又MD 平面APC ，AP ⊂平面APC ，所以MD 平面APC .（2）证明：因为PMB △为正三角形，D 为PB 的中点，所以MD PB ⊥.又MDAP ，所以AP PB ⊥.又因为AP PC ⊥，PB PC P ＝，所以AP ⊥平面PBC .因为BC ⊂平面PBC ，所以⊥AP BC . 又因为BC AC ⊥，AC AP A ⋂＝，所以BC ⊥平面APC . (3)因为AP ⊥平面PBC ，MDAP ，所以MD ⊥平面PBC ，即MD 是三棱锥M DBC -的高. 因为20AB =，M 为AB 的中点，PMB △为正三角形，。

人教版高中数学必修第二册第三单元《立体几何初步》测试卷(包含答案解析)

一、选择题1．已知空间中不同直线m 、n 和不同平面α、β，下面四个结论：①若m 、n 互为异面直线，//m α，//n α，//m β，βn//，则//αβ；②若m n ⊥，m α⊥，βn//，则αβ⊥；③若n α⊥，//m α，则n m ⊥；④若αβ⊥，m α⊥，//n m ，则βn//.其中正确的是（）A ．①②B ．②③C ．③④D ．①③ 2．古代数学名著《数学九章》中有云：“有木长三丈，围之八尺，葛生其下，缠木两周，上与木齐，问葛长几何？”意思为：圆木长3丈，圆周为8尺，葛藤从圆木的底部开始向上生长，绕圆木两周，刚好顶部与圆木平齐，问葛藤最少长多少尺(注：1丈即10尺)（） A ．30尺 B ．32尺 C ．34尺 D ．36尺 3．如图，在长方体1111ABCD A B C D -中，13,2,4AA AB AD ===，点M 是棱AD 的中点，点N 在棱1AA 上，且满足12AN NA =，P 是侧面四边形11ADD A 内的一动点（含边界），若1//C P 平面CMN ，则线段1C P 长度的取值范围是（）A ．[3,17]B ．[2,3]C ．[6,22]D ．[17,5] 4．某几何体的三视图如图所示（单位：cm ），则该几何体的侧面积（单位：2cm ）是（）A ．10B ．105+C ．1625+D ．135+5．设l 是直线，α，β是两个不同的平面，则正确的结论是（）A ．若l ∥α，l ∥β，则α∥βB ．若l ∥α，l ⊥β，则α⊥βC ．若α⊥β，l ⊥α，则l ⊥βD ．若α⊥β，l ∥α，则l ⊥β6．在棱长为a 的正方体1111ABCD A B C D －中，M 为AB 的中点，则点C 到平面1A DM的距离为（）A ．6aB ．6aC ．2aD ．12a 7．如图所示，在棱长为a 的正方体1111ABCD A B C D -中，E 是棱1DD 的中点，F 是侧面11CDD C 上的动点，且1//B F 面1A BE ，则F 在侧面11CDD C 上的轨迹的长度是（）A ．aB ．2aC 2aD ．22a 8．3P －ABC 的顶点都在球O 的球面上，PA ⊥平面ABC ，PA ＝2，∠ABC ＝120°，则球O 的体积的最小值为（）A ．73 B 287 C 1919 D ．193π 9．已知三棱锥A BCD -的所有棱长都为2，且球O 为三棱锥A BCD -的外接球，点M 是线段BD 上靠近D 的四等分点，过点M 作平面α截球O 得到的截面面积为Ω，则Ω的取值范围为（）A ．π3π,42⎡⎤⎢⎥⎣⎦B ．3π3π,42⎡⎤⎢⎥⎣⎦C ．π3π,22⎡⎤⎢⎥⎣⎦D ．,42ππ⎡⎤⎢⎥⎣⎦ 10．设,m n 是两条不同的直线，,αβ是两个不同的平面，则下列命题正确的是（） A ．若m n ⊥，//n α，则m α⊥ B ．若//m β，βα⊥，则m α⊥ C ．若m β⊥，n β⊥，n α⊥，则m α⊥ D ．若m n ⊥，n β⊥，βα⊥，则m α⊥ 11．在三棱锥P ABC -中，AB BC ⊥，P 在底面ABC 上的投影为AC 的中点D ，1DP DC ==.有下列结论：①三棱锥P ABC -的三条侧棱长均相等；②PAB ∠的取值范围是,42ππ⎛⎫ ⎪⎝⎭； ③若三棱锥的四个顶点都在球O 的表面上，则球O 的体积为23π；④若AB BC =，E 是线段PC 上一动点，则DE BE +的最小值为622+. 其中正确结论的个数是（）A ．1B ．2C ．3D ．412．如图，正方体1111ABCD A B C D -的棱长为2，点O 为底面ABCD 的中心，点P 在侧面11BB C C 的边界及其内部运动．若1D O OP ⊥，则11D C P △面积的最大值为（）A 25B ．455C 5D ．2513．设α、β为两个不同的平面，l 、m 为两条不同的直线，且l α⊂，m β⊂，则下列命题中真命题是（）A ．若l β⊥，则αβ⊥B ．若l m ⊥，则αβ⊥C ．若αβ⊥，则l m ⊥D ．若//αβ，则//l m 14．αβ、是两个不同的平面，mn 、是平面α及β之外的两条不同直线，给出四个论断：①m n ⊥；②αβ⊥；③n β⊥；④.m α⊥以其中三个论断作为条件，余下一个作为结论，其中正确命题的个数是（）A ．1个B ．2个C ．3个D ．4个二、解答题15．如图，在正四棱柱1111ABCD A B C D -中（底面是正方形的直四棱柱），底面正方形ABCD 的边长为1，侧棱1AA 的长为2，E 、M 、N 分别为11A B 、11B C 、1BB 的中点．AD平面EMN；（1）求证：1//AD与BE所成角的余弦值．（2）求异面直线116．如图所示的四棱锥E-ABCD中，底面ABCD为矩形，AE＝EB＝BC＝2，AD⊥平面ABE，且CE上的点F满足BF⊥平面ACE.（1）求证：AE∥平面BFD；（2）求三棱锥C-AEB的体积.17．如图甲，平面四边形ABCD中，已知45∠=，90︒A︒∠=∠=，ADC︒C，105 ==，现将四边形ABCD沿BD折起，使得平面ABD⊥平面BDC (如图乙)，设2AB BD点E，F分别是棱AC，AD的中点.（1）求证：DC⊥平面ABC；（2）求三棱锥A BEF -的体积.18．在四棱锥P ABCD -中，//AD BC ，BC CD ⊥，120ABC ∠=︒，4=AD ，3BC =，=2AB ，3=CD CE ，⊥AP ED ．（1）求证：DE ⊥面PEA ；（2）已知点F 为AB 中点，点P 在底面ABCD 上的射影为点Q ，直线AP 与平面ABCD 所成角的余弦值为3，当三棱锥-P QDE 的体积最大时，求异面直线PB 与QF 所成角的余弦值．19．如图，在长方体1111ABCD A B C D -中，1AB AD ==，12AA =，点P 为棱1DD 的中点.（1）证明：1//BD 平面PAC ；（2）求异面直线1BD 与AP 所成角的大小.20．如图，在四棱锥P ABCD -中，PA ⊥平面ABC ，//,90AD BC ABC ︒∠=，2AD =，23AB =6BC =．（1）求证：平面PBD ⊥平面PAC ；（2）PA 长为何值时，直线PC 与平面PBD 所成角最大？并求此时该角的正弦值． 21．已知三棱柱ABC -A 1B 1C 1中BC =1，CC 1=BB 1=2，AB =2，∠BCC 1=60°，AB ⊥侧面BB 1C 1C（1）求证：C 1B ⊥平面ABC ；（2）求三棱柱ABC -A 1B 1C 1的体积，（3）试在棱CC 1(不包含端点C ，C 1)上确定一点E ，使得EA ⊥EB 1；22．如图，在平行四边形ABCD 中，4AB =，60DAB ∠=︒．点G ，H 分别在边CD ，CB 上，点G 与点C ，D 不重合，GH AC ⊥，GH 与AC 相交于点O ，沿GH 将CGH 翻折到EGH 的位置，使二面角E GH B --为90°，F 是AE 的中点．（1）请在下面两个条件：①AB AD =，②AB BD ⊥中选择一个填在横线处，使命题P ：若________，则BD ⊥平面EOA 成立，并证明．（2）在（1）的前提下，当EB 取最小值时，求直线BF 与平面EBD 所成角的正弦值． 23．如图，已知PA ⊥平面ABCD ，ABCD 为矩形，M 、N 分别为AB 、PC 的中点，,2,2PA AD AB AD ===.（1）求证：平面MPC ⊥平面PCD ；（2）求三棱锥B MNC -的高.24．如图，在棱长为1的正方体1111ABCD A B C D -中，点O 是BD 中点．（1）求证:平面11BDD B ⊥平面1C OC ；（2）求二面角1C BD C --的正切值．25．如图，已知三棱柱111ABC A B C -中，AB AC =，D 为BC 上一点，1A B 平面1AC D ．（1）求证：D 为BC 的中点;（2）若平面ABC ⊥平面11BCC B ，求证：1AC D ∆为直角三角形.26．如图，在四棱锥P ABCD -中，//AB CD ，2CD AB =，CD ⊥AD ，平面PAD ⊥平面ABCD ，,E F 分别是CD 和PC 的中点．求证：（1）BF //平面PAD（2）平面BEF ⊥平面PCD参考答案【参考答案】***试卷处理标记，请不要删除一、选择题1．D解析：D【分析】由线面和面面平行和垂直的判定定理和性质定理即可得解．【详解】解：对于①，由面面平行的判定定理可得，若m 、n 互为异面直线，//m α，//n β，则//αβ或相交，又因为//m β，//n α，则//αβ，故①正确；对于②，若m n ⊥，m α⊥，//n β，则//αβ或α，β相交，故②错误，对于③，若n α⊥，//m α，则n m ⊥；故③正确，对于④，若αβ⊥，m α⊥，//n m ，则//n β或n β⊂，故④错误，综上可得：正确的是①③，故选：D ．【点睛】本题考查命题真假的判断，考查空间中线线、线面、面面间的位置关系等基础知识，考查运算求解能力，属于中档题．2．C解析：C【分析】由题意，圆柱的侧面展开图是矩形，葛藤长是两个矩形相连所成矩形的对角线的长，画出图形，即可求出葛藤长.【详解】由题意，圆柱的侧面展开图是矩形，葛藤长是两个矩形相连所成矩形的对角线的长. 如图所示矩形ABCD 中，30AD =尺，2816AB =⨯=尺，所以葛藤长2222301634AC AD AB =+=+=尺.故选：C .【点睛】本题考查圆柱的侧面展开图，考查学生的空间想象能力，属于基础题. 3．C解析：C【分析】首先找出过点1C 且与平面CMN 平行的平面，然后可知点P 的轨迹即为该平面与侧面四边形11ADD A 的交线段，进而可以利用解三角形的知识求出线段1C P 长度的取值范围．【详解】如图所示：，取11A D 的中点G ，取MD 的中点E ，1A G 的中点F ，1D D 的三等分点H 靠近D ，并连接起来．由题意可知1//C G CM ，//GH MN ，所以平面1//C GH 平面CMN ．即当点P 在线段GH 上时，1//C P 平面CMN ．在1H C G 中，2212222C G =+=2212222C H =+=22GH =，所以1H C G 为等边三角形，取GH 的中点O ，122sin606C O ==，故线段1C P 长度的取值范围是[6,22]．故选：C ．【点睛】本题主要考查线面平行，面面平行的判定定理和性质定理的应用，以及解三角形，意在考查学生的逻辑推理能力和数学运算能力，属于中档题．4．B解析：B【分析】由三视图可知，该几何体的直观图为直四棱柱1111ABCD A B C D -，由矩形的面积公式得出该几何体的侧面积.【详解】由三视图可知，该几何体的直观图为直四棱柱1111ABCD A B C D -，如下图所示2211125AD A D ==+=∴该几何体的侧面积为122222521025⨯+⨯+⨯=+故选：B【点睛】本题主要考查了由三视图计算几何体的侧面积，属于中档题.5．B解析：B【分析】根据直线、平面间平行、垂直的位置关系判断．【详解】若l ∥α，l ∥β，则α∥β或,αβ相交，A 错；若l ∥α，由线面平行的性质得，知α内存在直线b 使得//l b （过l 作平面与α相交，交线即是平行线），又l ⊥β，∴b β⊥，∴α⊥β，B 正确；若α⊥β，l ⊥α，则不可能有l ⊥β，否则由l ⊥α，l ⊥β，得//αβ，矛盾，C 错；若α⊥β，l ∥α，则l 与β可能平行，可能在平面内，可能相交也可能垂直，D 错．故选：B ．【点睛】本题考查空间直线、平面间平行与垂直关系的判断，掌握直线、平面间位置关系是解题关键．6．A解析：A 【分析】根据等体积法有11A CDM C A DM V V --=得解. 【详解】画出图形如下图所示，设C 到平面1A DM 的距离为h ，在△1A DM 中115,2,2A M DM a A D a === 1A ∴到DM 的距离为3a则根据等体积法有11A CDM C A DM V V --=，即11113232322a a a a a h ⋅⋅⋅⋅=⋅⋅⋅⋅，解得6h a =，故选:A.【点睛】本题考查利用等体积法求距离，属于基础题.7．D解析：D 【分析】解：设G ，H ，I 分别为CD 、1CC 、11C D 边上的中点，证明平面1//A BGE 平面1B HI ，得到1//B F 面1A BE ，则F 落在线段HI 上，求出11222HI CD a == 【详解】解：设G ，H ，I 分别为CD 、1CC 、11C D 边上的中点，1//A B EG ,则1A BEG 四点共面，11//,//EG HI B H A E , 平面1//A BGE 平面1B HI ，又1//B F 面1A BE ，F ∴落在线段HI 上，正方体1111ABCD A B C D -中的棱长为a ， 1122HI CD a ∴==，即F 在侧面11CDD C 上的轨迹的长度是2a ．故选：D ．【点睛】本题考查利用线面平行求线段长度，找到动点的运动轨迹是解题的关键，属于基础题.8．B解析：B 【分析】根据三棱锥的体积求出S △ABC 33，在三角形ABC 中，根据余弦定理和正弦定理求出△ABC 外接圆的半径r 的最小值，从而可求出外接球半径的最小值和外接球体积的最小值. 【详解】设AB ＝c ，BC ＝a ，AC ＝b 313×S △ABC ×2，解得S △ABC 33. 因为∠ABC ＝120°，S △ABC 3312ac sin 120°，所以ac ＝6，由余弦定理可得b 2＝a 2＋c 2－2ac cos 120°＝a 2＋c 2＋ac ≥2ac ＋ac ＝3ac ＝18，当且仅当a ＝c 时取等号，此时b min ＝2.设△ABC 外接圆的半径为r ，则sin120b＝2r (b 最小，则外接圆半径最小)，故3232＝2r min ，所以r min ＝6.如图，设O 1为△ABC 外接圆的圆心，D 为PA 的中点，R 为球的半径，连接O 1A ，O 1O ，OA ，OD ，PO ，易得OO 1＝1，R 2＝r 2＋OO ＝r 2＋1，当r min ＝6时，2min R ＝6＋1＝7，R min ＝7，故球O 体积的最小值为43π3min R ＝437)3287. 故选：B 【点睛】本题考查了三棱锥的体积公式，考查了球的体积公式，考查了正弦定理，考查了余弦定理，属于中档题.9．B解析：B 【分析】求出三棱锥A BCD -的外接球半径R ，可知截面面积的最大值为2πR ，当球心O 到截面的距离最大时，截面面积最小，此时球心O 到截面的距离为OM ，截面圆的半径的最小值22R OM -，进而可求出截面面积的最小值. 【详解】三棱锥A BCD -是正四面体，棱长为2，将三棱锥A BCD -放置于正方体中，可得正方体的外接球就是三棱锥A BCD -的外接球. 因为三棱锥A BCD -的棱长为22，可得外接球直径22226R =++=6R =，故截面面积的最大值为2263πππ2R ==⎝⎭. 因为M 是BD 上的点，当球心O 到截面的距离最大时，截面面积最小，此时球心O 到截面的距离为OM ，△OBD 为等腰三角形，过点O 作BD 的垂线，垂足为H ，222662,122OD OH OD HD ⎛⎫==-=-= ⎪ ⎪⎝⎭，得222113244OM OH HM =+=+=，则所得截面半径的最小值为22633444R OM -=-=，所以截面面积的最小值为233ππ()44=. 故Ω的取值范围为3π3π,42⎡⎤⎢⎥⎣⎦.故选：B. 【点睛】外接球问题与截面问题是近年来的热点问题，平常学习中要多积累，本题考查学生的空间想象能力、推理能力及计算求解能力，属于中档题.10．C解析：C 【分析】根据空间中直线与平面、平面与平面位置关系相关定理依次判断各个选项可得结果. 【详解】对于A ，当m 为α内与n 垂直的直线时，不满足m α⊥，A 错误；对于B ，设l αβ=，则当m 为α内与l 平行的直线时，//m β，但m α⊂，B 错误；对于C ，由m β⊥，n β⊥知：//m n ，又n α⊥，m α∴⊥，C 正确；对于D ，设l αβ=，则当m 为β内与l 平行的直线时，//m α，D 错误.故选：C . 【点睛】本题考查立体几何中线面关系、面面关系有关命题的辨析，考查学生对于平行与垂直相关定理的掌握情况，属于基础题.11．C解析：C 【分析】作出三棱锥P ABC -的图象，逐一判断各命题，即可求解．【详解】作出三棱锥P ABC -的图象，如图所示：．对于①，根据题意可知，PD ⊥平面ABC ，且1DP DC ==，所以2PA PB PC ===①正确；对于②，在PAB △中，2PA PB ==02AB <<，所以2cos 222AB PAB PA ⎛∠== ⎝⎭，即PAB ∠的取值范围是,42ππ⎛⎫⎪⎝⎭，②正确；对于③，因为DP DA DB DC ===，所以三棱锥P ABC -外接球的球心为D ，半径为1，其体积为43π，③不正确；对于④，当AB BC =时，BD AC ⊥，所以2BC =将平面PBC 沿翻折到平面PAC 上，则DE BE +的最小值为线段BD 的长，在展开后的DCB 中，6045105DCB ∠=+=，根据余弦定理可得6221221cos1052BD =+-⨯⨯⨯=， ④正确．故选：C ．【点睛】本题主要考查棱锥的结构特征，三棱锥外接球的体积求法，以及通过展开图求线段和的最小值，意在考查学生的直观想象能力和数学运算能力，属于中档题．12．C解析：C 【分析】取1BB 的中点F ，由题意结合正方体的几何特征及平面几何的知识可得1OD OC ⊥，1OD OF ⊥，由线面垂直的判定与性质可得1OD CF ⊥，进而可得点P 的轨迹为线段CF ，找到1C P 的最大值即可得解.取1BB 的中点F ，连接OF 、1D F 、CF 、1C F ，连接DO 、BO 、OC 、11D B 、1D C ，如图：因为正方体1111ABCD A B C D -的棱长为2，所以11B F BF ==,2DO BO OC ===11122D B DC ==1BB ⊥平面ABCD ，1BB ⊥平面1111D C B A ，11C D ⊥平面11BB C C ，所以22116OD OD DD =+=223OF OB BF =+=2211113D F D B B F =+=，所以22211OD OF D F +=，22211OD OC D C +=，所以1OD OC ⊥，1OD OF ⊥，由OCOF O =可得1OD ⊥平面OCF ，所以1OD CF ⊥，所以点P 的轨迹为线段CF ，又221111152C F B C B F C C =+=>=,所以11D C P △面积的最大值1111125522S C F D C =⋅=⨯=. 故选：C. 【点睛】本题考查了正方体几何特征的应用，考查了线面垂直的判定与性质，关键是找到点P 的轨迹，属于中档题.13．A解析：A 【分析】利用平面与平面垂直的判定定理，平面与平面垂直、平行的性质定理判断选项的正误即可．由α，β为两个不同的平面，l 、m 为两条不同的直线，且l α⊂，m β⊂，知：在A 中，l β⊥，则αβ⊥，满足平面与平面垂直的判定定理，所以A 正确；在B 中，若l m ⊥，不能得到l β⊥，也不能得到m α⊥，所以得不到αβ⊥，故B 错误；在C 中，若αβ⊥，则l 与m 可能相交、平行或异面，故C 不正确；在D 中，若//αβ，则由面面平行的性质定理得l β//，不一定有//l m ，也可能异面，故D 错误．故选：A ．【点睛】本题考查命题真假的判断，考查空间中线线、线面、面面间的位置关系等基础知识，考查运算求解能力，是中档题．14．B解析：B 【分析】分别以①②③④作为结论，另外三个作条件，根据线面垂直和面面垂直的判定定理依次判断真假. 【详解】若m n ⊥，αβ⊥，n β⊥，则m 与α可能平行可能相交，即①②③不能推出④；同理①②④不能推出③；若m n ⊥，n β⊥，m α⊥，两个平面的垂线互相垂直则这两个平面垂直，则αβ⊥，即①③④能够推出②；若αβ⊥，n β⊥，m α⊥，两个平面互相垂直，则这两个平面的垂线互相垂直，即m n ⊥，所以②③④能够推出①. 所以一共两个命题正确. 故选：B 【点睛】此题考查空间直线与平面位置关系的辨析，根据选择的条件推出结论，关键在于熟练掌握空间垂直关系的判定和证明.二、解答题15．（1）证明见解析（2）85【分析】（1）通过证明1//AD MN 可证1//AD 平面EMN ；（2）由（1）知11//AD BC ,所以1EBC ∠（或其补角）为异面直线1AD 与BE 所成的角，根据余弦定理计算可得结果. 【详解】（1）连1BC ，1EC ，如图：因为//AB CD ，AB CD =，且11//CD C D ，11CD C D =，所以11//AB C D ，11AB C D =，所以四边形11ABC D 为平行四边形，所以11//AD BC ，因为M 、N 分别为11B C 、1BB 的中点，所以1//MN BC ，所以1//AD MN ，因为1AD ⊄平面EMN ，MN ⊄平面EMN ，所以1//AD 平面EMN .（2）由（1）知11//AD BC ，所以1EBC ∠（或其补角）为异面直线1AD 与BE 所成的角，依题意知12BB =，112EB =，111B C =，所以22211117444BE BB EB =+=+=，2221111415BC BB B C =+=+=，222111115144EC EB B C =+=+=，所以2221111cos 2BE BC EC EBC BE BC +-∠==⋅17554417252+-⨯⨯88585=. 【点睛】思路点睛：平移线段法是求异面直线所成角的常用方法，其基本思路是通过平移直线，把异面直线的问题化归为共面直线问题来解决，具体步骤如下：（1）平移：平移异面直线中的一条或两条，作出异面直线所成的角；（2）认定：证明作出的角就是所求异面直线所成的角；（3）计算：求该角的值，常利用解三角形；（4）取舍：由异面直线所成的角的取值范围是0,2π⎛⎤⎥⎝⎦，当所作的角为钝角时，应取它的补角作为两条异面直线所成的角．16．（1）证明见解析；（2）43. 【分析】（1）由ABCD 为矩形，易得G 是AC 的中点，又BF ⊥平面ACE ，BC ＝BE ，则F 是EC 的中点，从而FG ∥AE ，再利用线面平行的判定定理证明.（2）根据AD ⊥平面ABE ，易得AE ⊥BC ，再由BF ⊥平面ACE ，得到AE ⊥BF ，进而得到AE ⊥平面BCE ，然后由C AEB A BCE V V --=求解. 【详解】（1）如图所示：因为底面ABCD 为矩形，所以AC ，BD 的交点G 是AC 的中点，连接FG ， ∵BF ⊥平面ACE ，则CE ⊥BF ，而BC ＝BE ， ∴F 是EC 的中点， ∴FG ∥AE .又AE ⊄平面BFD ，FG ⊂平面BFD ， ∴AE ∥平面BFD .（2）∵AD ⊥平面ABE ，AD ∥BC ， ∴BC ⊥平面ABE ，则AE ⊥BC . 又BF ⊥平面ACE ，则AE ⊥BF ， ∴AE ⊥平面BCE .∴三棱锥C -AEB 的体积11142223323C AEB A BCE BCE V V S AE --⎛⎫==⋅=⨯⨯⨯⨯= ⎪⎝⎭△.【点睛】方法点睛：1、判断或证明线面平行的常用方法：（1）利用线面平行的定义，一般用反证法；（2）利用线面平行的判定定理(a ⊄α，b ⊂α，a ∥b ⇒a ∥α)，其关键是在平面内找(或作)一条直线与已知直线平行，证明时注意用符号语言的叙述；（3）利用面面平行的性质定理(α∥β，a ⊂α⇒a ∥β)；（4）利用面面平行的性质(α∥β，a ⊄β，a ∥α⇒a ∥β)． 17．（1）证明见解析；（2）312. 【分析】（1）在图甲中先证AB BD ⊥，在图乙中由面面垂直的性质定理先证AB CD ⊥，由条件可得DC BC ⊥，进而可判定DC ⊥平面AB C ；（2）利用等体积法进行转化计算即可. 【详解】（1）图甲中，∵AB BD =且45A ︒∠=，45ADB ︒∴∠=，()()180180454590ABD ADB A ︒︒︒︒︒∴∠=-∠+∠=-+=，即AB BD ⊥，图乙中，∵平面ABD ⊥平面BDC ，且平面ABD 平面BDC BD =， ∴AB ⊥平面BDC ，又CD ⊂平面BDC ，∴AB CD ⊥，又90DCB ︒∠=，∴DC BC ⊥，且AB BC B ⋂=，又AB ，BC ⊂平面AB C ，∴DC ⊥平面AB C ；（2）因为点E ，F 分别是棱AC ，AD 的中点，所以//EF DC ，且12EF DC =，所以EF ⊥平面ABC ，由（1）知，AB ⊥平面BDC ，又BC ⊂平面BDC ，所以AB BC ⊥，105ADC ︒∠=，45ADB ︒∠=，1054560CDB ADC ADB ︒︒︒∴∠=∠-∠=-=，90906030CBD CDB ︒︒︒︒∴∠=-∠=-=，cos3022BC BD ︒∴=⋅=⨯=1sin 30212DC BD ︒=⋅=⨯=，所以12ABC S AB BC =⨯⨯△12ABE ABC S S ==△△1122EF DC ==，所以111332A BEF F ABE ABE V V EF S --==⋅⋅=⋅=△ 【点睛】方法点睛：计算三棱锥体积时，常用等体积法进行转化，具体的方法为：①换顶点，换底面；②换顶点，不换底面；③不换顶点，换底面.18．（1）证明见解析；（2．【分析】（1）在直角梯形ABCD 中先求出,,CD CE BE ，然后可求得,DE AE ，从而可证明DE AE ⊥，由线面垂直判定定理证明线面垂直；（2）由（1）得面面垂直，知Q 在AE 上，PAQ ∠为直线AP 与平面ABCD 所成的角，cos 3AQ PAQ AP ∠==，设AQ x =（0x <≤-P QDE 的体积，由二次函数知识求得最大值，及此时x 的值，得Q 为AE 中点，从而有//FQ BE ，PBE ∠为异面直线PB 与QF 所成角（或补角），由余弦定理可得．【详解】（1）证明：//AD BC ，BC CD ⊥，120ABC ∠=︒，4=AD ，3BC =，=2AB ，∴CD ===CD ，∴1CE =，CD =2BE =，由余弦定理得222cos120AE BE AB BE B =+-⋅︒22122222232⎛⎫=+-⨯⨯⨯-= ⎪⎝⎭，又2222(3)12DE CD CE =+=+=，∴222DE AE AD ，∴AD DE ⊥，∵AP DE ⊥，又AP AE A =，AP AE ⊂、平面APE ，∴DE ⊥平面APE ．（2）由（1）DE ⊥平面APE ．DE ⊂平面ABCD ，∴平面ABCD ⊥平面PAE ，∴Q 点在AE 上，PAQ ∠为直线AP 与平面ABCD 所成的角， 3cos AQ PAQ AP ∠==，设AQ x =（023x <≤），则2PQ x =，23QE x =-， 12(23)232QDE S x x =⨯⨯-=-△， 212(23)33P QDE QDE V PQ S x x -=⋅=--△22(3)223x =--+≤，当且仅当3x =时等号成立，则当P QDE V -最大时，3AQ =，∴Q 为AE 中点，∵F 为AB 中点，∴//FQ BC ，∴PBE ∠为异面直线PB 与QF 所成角（或补角），1,3QB QE ==，则由PQ ⊥平面ABCD 得3,7PE PB ==，又2BE =，则2227cos 214PB BE PE PBE PB BE +-∠==⋅， ∴异面直线PB 与QF 所成角的余弦值为714．【点睛】本题考查线面垂直的判定定理，考查直线与平面所成的角，异面直线所成的角，三棱锥的体积等，旨在考查学生的空间想象能力，运算求解能力，逻辑推理能力．属于中档题．19．（1）证明见解析；（2）30.【分析】（1）AC 和BD 交于点O ，则O 为BD 的中点．推导出1//PO BD ．由此能证明直线1//BD 平面PAC ；（2）由1//PO BD ，得APO ∠即为异面直线1BD 与AP 所成的角或其补角．由此能求出异面直线1BD 与AP 所成角的大小．【详解】（1）证明：设AC 和BD 交于点O ，则O 为BD 的中点.连结PO ，又因为P 是1DD 的中点，所以1//PO BD .又因为PO ⊂平面PAC ，1BD ⊄平面PAC所以直线1//BD 平面PAC.（2）解：由（1）知，1//PO BD ，所以APO ∠即为异面直线1BD 与AP 所成的角或其补角.因为2PA PC ==212AO AC ==且PO AO ⊥，所以212sin 22AO APO AP ∠===. 又(0,90APO ︒︒⎤∠∈⎦，所以30APO ∠=︒故异面直线1BD 与AP 所成角的大小为30.【点睛】方法点睛：异面直线所成的角的求法方法一：（几何法）找→作（平移法、补形法）→证（定义）→指→求（解三角形）方法二：（向量法）cos m nm n α=，其中α是异面直线,m n 所成的角，,m n 分别是直线,m n 的方向向量.20．（1）证明见解析；（2）PA =PC 与平面PBD 所成角最大，此时该角的正弦值为35. 【分析】（1）根据已知条件，得到BD PA ⊥，再利用正切函数的性质，求得0030,BAC 60ABD ∠=∠=，得到BD AC ⊥，进而可证得平面PBD ⊥平面PAC ；（2）建立空间坐标系，得到()BD =-，()0,2,DP t =-，()2PC t =-，进而得到平面PBD的一个法向量为1,3,n ⎛= ⎝⎭，进而可利用向量的公式求解【详解】（1）∵PA ⊥平面,ABCD BD ⊂平面ABCD ，∴BD PA ⊥，又tan tan AD BC ABD BAC AB AB∠==∠== ∴0030,BAC 60ABD ∠=∠=，∴090AEB ∠=，即BD AC ⊥（E 为AC 与BD 交点）．又PA AC ，∴BD ⊥平面PAC ，又因为BD ⊂平面PBD ，所以，平面PAC ⊥平面PBD（2）如图，以AB 为x 轴，以AD 为y轴，以AP 为z 轴，建立空间坐标系，如图，设AP t =，则()()()(),,0,2,0,0,0,B C D P t ，则()BD =-，()0,2,t DP =-，()23,6,PC t =-，设平面PBD 法向量为(),,n x y z =，则00n BD n DP ⎧⋅=⎨⋅=⎩，即2020y y tz ⎧-+=⎪⎨-+=⎪⎩，取1x =，得平面PBD 的一个法向量为1,3,n t ⎛= ⎪ ⎪⎝⎭，所以cos ,48PC n PC n PC n⋅==因为22144515175t t +++=≥，当且仅当t = 所以5c 3353os ,PC n ≤=，记直线PC 与平面PBD 所成角为θ，则sin cos ,PC n θ=，故3sin 5θ≤，即23t =时，直线PC 与平面PBD 所成角最大，此时该角的正弦值为35．【点睛】关键点睛：解题关键在于利用定义和正切函数的性质，得到BD ⊥平面PAC ，进而证明平面PAC ⊥平面PBD ；以及建立空间直角坐标系，求出法向量，进行求解直线PC 与平面PBD 所成角的最大值，难度属于中档题21．（1）证明见解析；（2）62；（3）E 为CC 1的中点时，EA ⊥EB 1. 【分析】(1）证明11,AB BC BC BC ⊥⊥然后证明1C B ⊥平面ABC ；(2）求出ABC S ，求出13C B =，然后求解三棱柱111ABC A B C -的体积；(3）在棱CC 1(不包含端点C ，C 1)上取一点E ，连接BE ，证明1EB ⊥平面ABE ，得到EA ⊥EB 1.【详解】（1）∵BC =1，CC 1=BB 1=2，AB =2，∠BCC 1=60°，AB ⊥侧面BB 1C 1C∴AB ⊥BC 1在△BCC 1中，由余弦定理得BC =3，则BC 2+BC 2=CC 2，∴BC ⊥BC 1又∵BC ∩AB =B ，且AB ，BC ⊂平面ABC， ∴C 1B ⊥平面ABC .（2）由已知可得S △ABC =12AB ·BC =12×2×1=22由（1）知C 1B ⊥平面ABC ，C 1B =3，所以三棱柱ABC -A 1B 1C 1的体积V =S △ABC ·C 1B =2×3=62. （3）在棱CC 1(不包含端点C ，C 1)上取一点E ，连接BE .∵EA ⊥1EB ，AB ⊥1EB ，AB ∩AE=A ，AB ，AE ⊂平面ABE ，∴1EB ⊥平面ABE .又∵BE ⊂平面ABE ，∴BE ⊥1EB .不妨设CE =x (0<x <2)，则C 1E =2x -，在△BCE 中，由余弦定理得BE =221x x +-在△B 1C 1E 中，∠B 1C 1E =120°，由余弦定理得B 1E 2=257x x -+在Rt △BEB 1中，由B 1E 2+BE 2=B 1B 2，得()()222225714x x x x -+++-=，解得x =1或x =2(舍去).故E 为CC 1的中点时，EA ⊥EB 1.【点睛】关键点点睛：在确定动点位置时，设CE =x (0<x <2)，则C 1E =2x -，根据条件，建立关于x 的方程，求解确定动点位置，属于常用方法.22．（1）答案见解析；（2）11. 【分析】（1）选择①，结合直二面角的定义，证明BD ⊥平面EOA 内的两条相交直线,EO AO ；（2）设AC 与BD 交于点M ，4AB =，60DAB ∠=︒，则AC =CO x =，可得EB 关于x 的函数，求出EB 取得最小值时x 的值，连结EM ，作QF EM ⊥于F ，连结BF ，求出sin QBF ∠的值，即可得答案；【详解】解：（1）命题P ：若AB AD =，则BD ⊥平面EOA .∵AC GH ⊥，∴AO GH ⊥，EO GH ⊥，又二面角E GH B --的大小为90°，∴90AOE ∠=︒，即EO AO ⊥，∴EO ⊥平面ABCD ，∴EO BD ⊥，又AB BC =，∴AO BD ⊥， AO EO O =，∴BD ⊥平面EOA .（2）设AC 与BD 交于点M ，4AB =，60DAB ∠=︒，则AC =设CO x =，OM x =，222216OB OM MB x =+=-+，2222216EB EO OB x =+=-+，当x =min EB =连结EM ，作QF EM ⊥于F ，连结BF ，由（1）知BD ⊥平面EOA ，∴BD QF ⊥，∴QF ⊥平面EBD ，∴QBF ∠即为QB 与平面EBD 所成角，在Rt EMB 中，10EB =，2BM =，6EM =，30AE =，由()222222(2)22QB AE AB BE QB +=+⇒=， 62QF =， ∴33sin 11QF QBF QB ∠==，即QB 与平面EBD 所成角得正弦值为3311.【点睛】求线面角首先要根据一作、二证、三求找出线面角，然后利用三角函数的知识，求出角的三角函数值即可.23．（1）证明见解析；（2）2. 【详解】（1）取PD 的中点G ，连接NG ，AG ，如图所示：因为G ，N 分别为PD ，PC 的中点，所以//GN CD ，1=2GN CD . 又因为M 为AB 的中点，所以//AM CD ，1=2AM CD . 所以//AM GN ，=AM GN ，四边形AMNG 为平行四边形，所以//AG MN .又因为22213PM PA AM =+=+=22123MC MB BC =+=+= 所以PM MC =，则MN PC ⊥.又因为AD PA =，G 为PD 中点，所以AG PD ⊥.又因为//AG MN ，所以MN PD ⊥.所以MN PD MN PCMN PC PD P ⊥⎧⎪⊥⇒⊥⎨⎪=⎩平面PCD . 又MN ⊂平面MPC ，所以平面MPC ⊥平面PCD .（2）设点B 到平面MNC 的距离为h ，因为B MNC N MBC V V --=，所以111332MNC MBC S h S PA ⋅=⋅△△.因为12MBC S BC MB =⋅⋅=△，112MN AG PD ====，NC ===所以122MNC S MN NC =⋅⋅=△所以1132322h ⨯⨯=⨯2h =. 【点睛】关键点点睛：本题主要考查了面面垂直的证明和三棱锥的高，属于中档题，其中等体积转化B MNC N MBC V V --=为解决本题的关键.24．（1）证明见解析；（2.【分析】（1）在正方体1111ABCD A B C D -中，易证1,C O BD CO BD ⊥⊥，由线面垂直的判定定理得到BD ⊥平面1C OC ，然后再利用面面垂直的判定定理证明.（2）由（1）知BD ⊥平面1C OC ，且平面1C BD ⋂平面CBD BD =，得到1C OC ∠是二面角1C BD C --的平面角，然后在1Rt C OC ∆中求解.【详解】（1）∵在正方体1111ABCD A B C D -中，点O 是BD 中点，又11BC DC = ， BC DC = ，∴ 1,C O BD CO BD ⊥⊥11,C O CO O C O =⊂平面1,C OC CO ⊂平面1C OC ，BD ∴⊥平面1C OC ，又∵BD ⊂平面11BDD B ，∴平面11BDD B ⊥平面1C OC ．…（2）由（1）知：平面1C BD ⋂平面CBD BD =，11,C O BD C O ⊥⊂半平面1;,C BD CO BD CO ⊥⊂ 半平面;CBD所以1C OC ∠是二面角1C BD C --的平面角则在正方体1111ABCD A B C D -中121,2C C OC ==∴在1Rt C OC ∆中，11tan 2C C C OC OC∠== 故二面角1C BD C --的正切值为2 ．【点睛】本题主要考查线面垂直，面面垂直的判定定理以及二面角的求法，还考查了逻辑推理和运算求解的能力，属于中档题. 25．(1)见解析(2)见解析【分析】（1）连接A 1C 交AC 1于O ，连接OD ，利用线面平行的性质定理和中位线的定义，即可证明D 为BC 的中点；（2）由等腰三角形的性质和面面垂直的性质定理，证明AD ⊥C 1D 即可．【详解】证明:(1) 联结1A C 交1AC 于O ，联结OD .∵四边形11ACC A 是棱柱的侧面， ∴四边形11ACC A 是平行四边形.∵O 为平行四边形11ACC A 对角线的交点， ∴O 为1A C 的中点.∵1A B 平面1AC D ，平面1A BC ⋂平面1AC D OD =，1A B ⊂平面1A BC ，∴1A B OD∴OD 为1A BC ∆的中位线， ∴D 为BC 的中点.（2）∵AB AC =，D 为BC 的中点，∴AD BC ⊥.∵平面ABC ⊥平面11BCC B ,AD ⊂平面ABC ，平面ABC平面11BCC B BC =，∴AD ⊥平面11BCC B .∵1C D ⊂平面11BCC B ，∴AD ⊥ 1C D ，∴1AC D ∆为直角三角形.【点睛】本题考查线面平行的性质定理和面面垂直的性质定理的应用.26．（1）证明见解析；（2）证明见解析.【分析】（1）若要证BF //平面PAD ，只要BF 所在面和平面PAD 平行即可；（2）若要证平面BEF ⊥平面PCD ，只要证平面PCD 内的一条直线和平面BEF 垂直即可.【详解】（1）∵AB CD ∥，2CD AB =，E 是CD 的中点， ∴AB DE ，即ABED 是平行四边形．∴BE AD ．∵BE ⊄平面,PAD AD ⊄平面PAD ， ∴BE 平面PAD ，又EF PD ，EF ⊄平面PAD ，PD ⊂平面PAD ， ∴EF 平面PAD ，EF ，BE ⊂平面BEF ，且EFBE E =，∴平面BEF 平面PAD ． ∵BF ⊂平面BEF ，∴BF ∥平面PAD ．（2）由题意，平面PAD ⊥平面ABCD ，且两平面交线为AD ，CD ⊂平面ABCD ，CD AD ⊥，∴CD ⊥平面PAD ．∴CD PD ⊥．∴CD EF ⊥．又CD BE ⊥，BE ，EF ⊂平面BEF ，且EE EF E ⋂=，∴CD ⊥平面BEF ．∵CD ⊂平面PCD ，∴平面BEF ⊥平面PCD ．【点睛】本题考查了线面平行和面面垂直的证明，解决此类问题的关键是能利用线面关系的定理和性质进行逻辑推理，往往使用逆推法进行证明，需要较强的空间感和空间预判，属于较难题.。

面面垂直的性质习题详细答案

变种2
如果一个平面内的两条相交直线与另一个平面垂直，求证这两个平面垂直。
提高题
如果一个平面内的两条相交直线与另一个平面垂直，求证这两个平面的交线与原直线垂直。
综合பைடு நூலகம்解析与解答
• 综合题1：已知一个平面内的两条相交直线与另一个平面垂直，求证这两个平面的交线与原直线垂直。
综合题解析与解答
面面垂直的性质习题详细答案
contents
目录
• 面面垂直的性质概述 • 习题解析 • 习题解答技巧 • 面面垂直的性质习题答案 • 习题拓展与提高
01 面面垂直的性质概述
定义与定理
定义
两个平面互相垂直，当且仅当一个平面内的任意直线都与另一个平面垂直。
定理
如果两个平面互相垂直，那么其中一个平面内的任意直线都与另一个平面垂直。
机械工程
在机械设计中，面面垂直的性质常常用于确定零件的安装角度和位置，以确保机器的正常运转。
地理学
在地理学中，地球的经纬线分布和角度计算也涉及到面面垂直的性质，例如在计算地球上的纬度、经度等数值时，需要利用到面面
垂直的性质。
02 习题解析
基础习题解析
总结词
掌握基础概念
题目
两个平面垂直，其中一个平面内有一条直线，那么这条直线与另一个平面的关系是什么？
由于直线a⊥平面α，且直线b⊥直线a，根据面面垂直的性质定理，直线b必然在平面 α内。
中等难度习题答案
总结词
中等难度习题在考察面面垂直性质的基础上，增加了对空间想象能力和推理能力的考察。
题目3
已知平面α与平面β互相垂直，点A属于平面α，点B属于平面β，且AB与两平面的交线分别交于C和D两点，若AC=CD，求证线段BD的长度。

面面垂直习题（模版）

面面垂直习题（模版）第一篇：面面垂直习题（模版）例1如图,在四面体P-ABC中,PC⊥平面ABC,AB=BC=CA=PC,求二面角B-AP-C的正切值。

解：如图，过B作BE⊥AC于E，过E作EF⊥PA于F，连接BF∵PC⊥平面ABC，PC⊂平面PACC ∴平面PAC⊥平面ABC ,∴BE⊥平面PAC由三垂线定理，有BF⊥PA,∴∠BFE是二面角B-PA-C平面角，设PC=1,由E是AC的中点，∴BE=32,EF=12sin45=0B24∴tg∠BFE=BEEF=6例2:如图, PA⊥平面ABC,AC⊥BC,AF⊥PC于F.求证:AF⊥平面PBC.证明:∵PA⊥平面ABCBC ⊂平面ABC∴ PA⊥BC又AC⊥BC PA∩AC=A∴ BC⊥平面PAC⊂平面PAC又BC P F A C B∴平面PBC⊥平面PAC⊂平面PAC,∵AF⊥PCAF平面PBC∩平面PAC=PC∴ AF⊥平面PBC如图，△ABC为正三角形，EC⊥平面ABC，BD∥CE，且CE＝CA ＝2BD，求证：平面ADE⊥平面ACE.EDCAB如图在空间四边形ABCS中，SA⊥平面ABC，平面SAB ⊥平面SBC(1)求证：AB⊥BC ；(2)若设二面角S-BC-A为45︒，SA＝BC，求二面角A-SC-B的大小SEaA 2aC已知线段AB的两端点在直二面角-αCDβ-的两个面内,且与α、β分别成30︒和45︒角，求AB和CD所成的角C如图PA垂直于矩形ABCD所在平面，E是AB的中点，二面角P-CD-B 为45︒求证：平面PEC⊥平面PCDG CE B第二篇：面面垂直性质定理及习题面面垂直性质定理及习题《必修2》1.2.4一、学习目标撰稿：第四组审稿：高二数学组时间：2009-9-81．理解面面垂直的性质定理2．会用性质定理解决有关问题3．线线、线面、面面之间的位置关系及相互转化4．利用面面位置关系解决有关问题二、学习重点面面垂直的性质定理及应用学习难点“线线、线面、面面”判定及性质定理的应用三、知识链接1．面面垂直的判定定理2．面面平行的判定与性质定理3．直线与面平行、垂直的判定与性质定理四、学习过程1．回顾上节内容，问：如果两个平面垂直，那么一个面内的直线是否一定垂直于另一个平面？通过以上讨论，得平面与平面垂直的性质定理（1）符号语言：（2）图形语言：2．如何对定理加以证明：性质定理体现了什么关系？它反映了面面垂直与线面垂直之间的密切关系，两者可以互相转化。

高考数学总复习 9-5 线面、面面垂直的判定与性质但因为测试新人教B版

高考数学总复习 9-5 线面、面面垂直的判定与性质但因为测试新人教B 版1.(2011·北京西城模拟)已知两条不同的直线a ，b 和两个不同的平面α，β，且a ⊥α，b ⊥β，那么α⊥β是a ⊥b 的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件 [答案] C⎭⎪⎬⎪⎫⎭⎪⎬⎪⎫[解析] α⊥βa ⊥α⇒a ∥β或a ⊂β b ⊥β⇒a ⊥b ；⎭⎬⎫⎭⎪⎬⎪⎫a ⊥αa ⊥b ⇒b ∥α或b ⊂αb ⊥β⇒α⊥β.2．(文)(2011·唐山模拟)已知一个平面α，那么对于空间内的任意一条直线a ，在平面α内一定存在一条直线b ，使得a 与b ( )A ．平行B ．相交C ．异面D ．垂直[答案] D[解析] 当a 与α相交时，平面内不存在直线与a 平行；当a ∥α时，平面内不存在直线与a 相交；当a ⊂平面α时，平面α内不存在直线与a 异面；无论a 在何位置，a 在平面α内总有射影a ′，当b ⊂α，b ⊥a ′时，有b ⊥a ，故选D.(理)(2011·青岛模拟)设两个平面α，β，直线l ，下列三个条件：①l ⊥α；②l ∥β；③α⊥β.若以其中两个作为前提，另一个作为结论，则可构成三个命题，这三个命题中正确命题的个数为( )A ．3B ．2C ．1D ．0[答案] C [解析]⎭⎪⎬⎪⎫l ⊥αl ∥β⇒α⊥β； ⎭⎪⎬⎪⎫α⊥βl ⊥α⇒/ l ∥β，此时可能l ⊂β，⎭⎪⎬⎪⎫l ∥βα⊥β⇒/ l ⊥α，此时l 与α还可能平行、斜交，故选C.3．(文)(2011·东莞模拟)若l 为一条直线，α、β、γ为三个互不重合的平面，给出下面三个命题： ①α⊥γ，β⊥γ⇒α⊥β；②α⊥γ，β∥γ⇒α⊥β； ③l ∥α，l ⊥β⇒α⊥β.其中的真命题有()A．0个B．1个C．2个D．3个[答案] C[解析]①中α与β可能平行，故①错，②③正确．(理)(2011·北京市朝阳区模拟)设α，β，γ是三个不重合的平面，l是直线，给出下列命题①若α⊥β，β⊥γ，则α⊥γ；②若l上两点到α的距离相等，则l∥α；③若l⊥α，l∥β，则α⊥β；④若α∥β，l⊄β，且l∥α，则l∥β.其中正确的命题是()A．①②B．②③C．②④D．③④[答案] D[解析]对于①：若α⊥β，β⊥γ，则可能α⊥γ，也可能α∥γ.对于②：若l上两点到α的距离相等，则l∥α，显然错误．当l⊥α，l∩α＝A时，l上到A距离相等的两点到α的距离相等．③④显然正确．4．(2011·安徽省皖南八校联考)设l，m是两条不同的直线，α是一个平面，则下列命题正确的是()A．若l⊥m，m⊂α，则l⊥αB．若l⊥α，m⊂α，则l⊥mC．若l∥α，l∥m，则m∥αD．若l∥α，m∥α，则l∥m[答案] B[解析]直线垂直于平面中两条相交直线，才能垂直于平面，故A错；C中m可能包含在平面α中；D中两条直线可能平行、相交或异面．5.(2011·广东省深圳市高三调研)如下图，在立体图形D－ABC中，若AB＝CB，AD＝CD，E是AC的中点，则下列结论正确的是()A．平面ABC⊥平面ABDB．平面ABD⊥平面BDCC．平面ABC⊥平面BDE，且平面ADC⊥平面BDED．平面ABC⊥平面ADC，且平面ADC⊥平面BDE[答案] C[解析] 要判断两个平面的垂直关系，就需找一个平面内的一条直线与另一个平面垂直．因为AB ＝CB ，且E 是AC 的中点，所以BE ⊥AC ，同理有DE ⊥AC ，于是AC ⊥平面BDE .因为AC 在平面ABC 内，所以平面ABC ⊥平面BDE .又由于AC ⊂平面ACD ，所以平面ACD ⊥平面BDE .所以选C.6．(文)(2011·济宁三模)在正三棱柱ABC －A 1B 1C 1中，若AB ＝2，AA 1＝1，则点A 到平面A 1BC 的距离为( ) A.34B.32C.334D. 3[答案] B[解析] 解法1：取BC 中点E ，连接AE 、A 1E ，过点A 作AF ⊥A 1E ，垂足为F .∵A 1A ⊥平面ABC ，∴A 1A ⊥BC ， ∵AB ＝AC .∴AE ⊥BC . ∴BC ⊥平面AEA 1. ∴BC ⊥AF ，又AF ⊥A 1E ， ∴AF ⊥平面A 1BC .∴AF 的长即为所求点A 到平面A 1BC 的距离． ∵AA 1＝1，AE ＝3，∴AF ＝32. 解法2：VA 1－ABC ＝13S △ABC ·AA 1＝13×3×1＝33.又∵A 1B ＝A 1C ＝5，在△A 1BE 中，A 1E ＝A 1B 2－BE 2＝2.∴S △A 1BC ＝12×2×2＝2.∴VA －A 1BC ＝13×S △A 1BC ·h ＝23h .∴23h ＝33，∴h ＝32.∴点A 到平面A 1BC 距离为32. (理)(2011·海淀检测)若正四棱柱ABCD －A 1B 1C 1D 1的底面边长为1，AB 1与底面ABCD 成60°角，则A 1C 1到底面ABCD 的距离为( )A.33B ．1 C. 2 D. 3[答案] D[解析] 依题可知∠B 1AB ＝60°，平面A 1B 1C 1D 1∥平面ABCD ，A 1C 1⊂平面A 1B 1C 1D 1， ∴B 1B 即为所求距离，在△ABB 1中得， B 1B ＝ 3.故选D.7．(文)(2011·扬州模拟)已知直线l ，m ，n ，平面α，m ⊂α，n ⊂α，则“l ⊥α”是“l ⊥m 且l ⊥n ”的________条件．(填“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”之一)[答案] 充分不必要[解析] 若l ⊥α，则l 垂直于平面α内的任意直线，故l ⊥m 且l ⊥n ，但若l ⊥m 且l ⊥n ，不能得出l ⊥α. (理)(2011·揭阳模拟)设x 、y 、z 是空间不同的直线或平面，对下列四种情形：①x 、y 、z 均为直线；②x 、y 是直线，z 是平面；③z 是直线，x 、y 是平面；④x 、y 、z 均为平面，其中使“x ⊥z 且y ⊥z ⇒x ∥y ”为真命题的序号是________．[答案] ②③[解析] 当x 、y 为直线，z 为平面时，有x ⊥z ，y ⊥z ⇒x ∥y ；当x 、y 为平面，z 为直线时，有x ⊥z ，y ⊥z ⇒x ∥y ，故②③正确．[点评] 由正方体交于同一个顶点的三条棱和三个面知①④均使命题为假命题．8．(2011·苏州模拟)已知m ，n 是两条不同的直线，α，β为两个不同的平面，下列四个命题： ①若m ⊥α，n ⊥β，m ⊥n ，则α⊥β； ②若m ∥α，n ∥β，m ⊥n ，则α∥β； ③若m ⊥α，n ∥β，m ⊥n ，则α∥β； ④若m ⊥α，n ⊥β，α⊥β，则m ⊥n .其中正确的命题是(填上所有正确命题的序号)________． [答案] ①④⎭⎪⎬⎪⎫⎭⎪⎬⎪⎫[解析] ①m ⊥α m ⊥n ⇒n ⊂α或n ∥α n ⊥β⇒α⊥β；②如下图，m 为B 1C 1，n 为A 1B 1，α为平面ADD 1A 1，β为平面ABCD ，满足②的条件，故②错；③在上图中，将A 1B 1、B 1C 1改为m 、n ，满足m ⊥α，n ⊥β，m ⊥n ，故③错；⎭⎪⎬⎪⎫⎭⎪⎬⎪⎫④n ⊥β α⊥β⇒n ∥α或n ⊂α m ⊥α⇒m ⊥n .9．如下图所示，在四棱锥P －ABCD 中，P A ⊥底面ABCD ，且底面各边都相等，M 是PC 上的一动点，当点M 满足________时，平面MBD ⊥平面PCD .(只要填写一个你认为是正确的条件即可)[答案] DM ⊥PC[解析] ∵ABCD 为正方形，∴BD ⊥AC ， ∵P A ⊥平面ABCD ，∴BD ⊥P A ，∵P A ∩AC ＝A ，∴BD ⊥平面P AC ，∴BD ⊥PC ，故当DM ⊥PC (或BM ⊥PC )时，有PC ⊥平面MBD ，从而有平面PCD ⊥平面MBD .10．(文)(2010·山东临沂)在直平行六面体AC 1中，四边形ABCD 是菱形，∠DAB ＝60°，AC ∩BD ＝O ，AB ＝AA 1.(1)求证：C1O∥平面AB1D1；(2)求证：平面AB1D1⊥平面ACC1A1.[证明](1)连接A1C1交B1D1于O1，连接AO1.在平行四边形AA1C1C中，C1O1∥AO，C1O1＝AO，∴四边形AOC1O1为平行四边形，∴C1O∥AO1.∵C1O⊄平面AB1D1，AO1⊂平面AB1D1，∴C1O∥平面AB1D1.(2)在直平行六面体AC1中，A1A⊥平面A1B1C1D1，∴A1A⊥B1D1.∵四边形A1B1C1D1为菱形，∴B1D1⊥A1C1.∵A1C1∩AA1＝A1，A1C1⊂平面ACC1A1，AA1⊂平面ACC1A1，∴B1D1⊥平面ACC1A1.∵B1D1⊂平面AB1D1，∴平面AB1D1⊥平面ACC1A1.(理)(2011·广东省广州市调研)如下图，在四棱锥P－ABCD中，平面P AD⊥平面ABCD，AB∥DC，△P AD是等边三角形，已知BD＝2AD＝4，AB＝2DC＝2 5.(1)求证：BD ⊥平面P AD ； (2)求三棱锥A －PCD 的体积．[解析] (1)证明：在△ABD 中，由于AD ＝2，BD ＝4，AB ＝25，∴AD 2＋BD 2＝AB 2.∴AD ⊥BD . 又平面P AD ⊥平面ABCD ，平面P AD ∩平面ABCD ＝AD ，BD ⊂平面ABCD ，∴BD ⊥平面P AD . (2)解：过P 作PO ⊥AD 交AD 于O .又平面P AD ⊥平面ABCD ，∴PO ⊥平面ABCD .∵△P AD 是边长为2的等边三角形，∴PO ＝ 3. 由(1)知，AD ⊥BD ，在Rt △ABD 中，斜边AB 边上的高为h ＝AD ×BD AB ＝455.∵AB ∥DC ，∴S △ACD ＝12CD ×h ＝12×5×455＝2.∴V A －PCD ＝V P －ACD ＝13S △ACD ×PO ＝13×2×3＝233.11.(2011·广东广州一模)已知l ，m 是不同的两条直线，α，β是不重合的两个平面，则下列命题中为真命题的是( )A ．若l ⊥α，α⊥β，则l ∥βB ．若l ∥α，α⊥β，则l ∥βC ．若l ⊥m ，α∥β，m ⊂β，则l ⊥αD ．若l ⊥α，α∥β，m ⊂β，则l ⊥m [答案] D[解析]⎭⎪⎬⎪⎫⎭⎪⎬⎪⎫l ⊥αα∥β⇒l ⊥β m ⊂β⇒l ⊥m .12．(文)设m 、n 是两条不同的直线，α、β是两个不同的平面，考察下列命题，其中正确的命题是( ) A ．m ⊥α，n ⊂β，m ⊥n ⇒α⊥β B ．α∥β，m ⊥α，n ∥β⇒m ⊥n C ．α⊥β，m ⊥α，n ∥β⇒m ⊥n D ．α⊥β，α∩β＝m ，n ⊥m ⇒n ⊥β [答案] B[解析] 如下图(1)满足m ⊥α，n ⊂β，m ⊥n ，但β∥α，故A 错；⎭⎪⎬⎪⎫⎭⎪⎬⎪⎫α∥βm ⊥α⇒m ⊥β n ∥β⇒m ⊥n ，故B 对；如图(2)满足α⊥β，m ⊥α，n ∥β，但m ∥n ，故C 错；如图(3)α⊥β，α∩β＝m ，AB ⊥m 于B ，BC ⊥m 于B ，直线AC 为直线n ，显然满足D 的条件，但不能得出n ⊥β.故D 错．∴选B. (理)如下图，在长方体ABCD －A 1B 1C 1D 1中，AB ＝BC ＝2，A 1D 与BC 1所成的角为π2，则BC 1与平面BB 1D 1D 所成角的正弦值为( )A.63B.12C.155D.32[答案] B[解析] 连接B 1C ，∴B 1C ∥A 1D ， ∵A 1D 与BC 1所成的角为π2，∴B 1C ⊥BC 1，∴长方体ABCD －A 1B 1C 1D 1为正方体，取B 1D 1的中点M ，连接C 1M ，BM ，∴C 1M ⊥平面BB 1D 1D ，∴∠C 1BM 为BC 1与平面BB 1D 1D 所成的角，∵AB ＝BC ＝2，∴C 1M ＝2，BC 1＝22，∴sin ∠C 1BM ＝C 1M C 1B ＝12，故选B.13．(文)(2010·河北唐山)如下图，在直四棱柱ABCD －A 1B 1C 1D 1中，∠ADC ＝90°，且AA 1＝AD ＝DC ＝2，M ∈平面ABCD ，当D 1M ⊥平面A 1C 1D 时，DM ＝________.[答案] 2 2[解析] ∵DA ＝DC ＝DD 1且DA 、DC 、DD 1两两垂直，故当点M 使四边形ADCM 为正方形时，D 1M ⊥平面A 1C 1D ，∴DM ＝2 2.(理)(2011·西安模拟)在三棱柱ABC －A 1B 1C 1中，各棱长相等，侧棱垂直于底面，点D 是侧面BB 1C 1C 的中心，则AD 与平面BB 1C 1C 所成角的大小是________．[答案] 60° [解析]如上图，取BC 中点E ，连结DE 、AE 、AD ，依题意知三棱柱为正三棱柱，易得AE ⊥平面BB 1C 1C ，故∠ADE 为AD 与平面BB 1C 1C 所成的角．设各棱长为1，则AE ＝32，DE ＝12，tan ∠ADE ＝AE DE ＝3212＝3，∴∠ADE ＝60°.14．(文)如下图，已知在直四棱柱ABCD －A 1B 1C 1D 1中，AD ⊥DC ，AB ∥DC ，DC ＝DD 1＝2AD ＝2AB ＝2.(1)求证：DB ⊥平面B 1BCC 1；(2)设E 是DC 上一点，试确定E 的位置，使得D 1E ∥平面A 1BD ，并说明理由．[解析] (1)证明：∵AB ∥DC ，AD ⊥DC ，∴AB ⊥AD ，在Rt △ABD 中，AB ＝AD ＝1，∴BD ＝2，易求BC ＝2，又∵CD ＝2，∴BD ⊥BC . 又BD ⊥BB 1，B 1B ∩BC ＝B ，∴BD ⊥平面B 1BCC 1. (2)DC 的中点即为E 点．∵DE ∥AB ，DE ＝AB ， ∴四边形ABED 是平行四边形．∴AD綊BE .又AD 綊A 1D 1，∴BE 綊A 1D 1，∴四边形A 1D 1EB 是平行四边形．∴D 1E ∥A 1B .∵D 1E ⊄平面A 1BD ，A 1B ⊂平面A 1BD ，∴D 1E ∥平面A 1BD .(理)(2011·北京模拟)如下图，正方形ADEF 与梯形ABCD 所在的平面互相垂直，AD ⊥CD ，AB ∥CD ，AB ＝AD ＝2，CD ＝4，M 为CE 的中点．(1)求证：BM ∥平面ADEF ； (2)求证：平面BDE ⊥平面BEC .[解析] (1)证明：延长DA 与CB 相交于P ， ∵AB ＝AD ＝2，CD ＝4，AB ∥CD ， ∴B 为PC 的中点，又M 为CE 的中点，∴BM ∥EP ， ∵BM ⊄平面ADEF ，EP ⊂平面ADEF ， ∴BM ∥平面ADEF .(2)证明：由(1)知，BC ＝12PC ＝12PD 2＋CD 2＝22，又BD ＝AD 2＋AB 2＝22， ∴BD 2＋BC 2＝CD 2，∴BD ⊥BC . 又平面ADEF ⊥平面ABCD ，ED ⊥AD ， ∴ED ⊥平面ABCD ，∴ED ⊥BC ， ∵ED ∩BD ＝D ，∴BC ⊥平面BDE ，又BC ⊂平面BEC ， ∴平面BDE ⊥平面BEC .15．(文)(2011·北京文，17)如下图，在四面体P ABC 中，PC ⊥AB 、P A ⊥BC ，点D 、E 、F 、G 分别是棱AP 、AC 、BC 、PB 的中点．(1)求证：DE ∥平面BCP ； (2)求证：四边形DEFG 为矩形；(3)是否存在点Q ，到四面体P ABC 六条棱的中点的距离相等？说明理由． [解析] (1)因为D ，E 分别为AP ，AC 的中点，所以DE ∥PC ，又因为DE ⊄平面BCP ，PC ⊂平面BCP ，所以DE ∥平面BCP .(2)因为D ，E ，F ，G 分别为AP ，AC ，BC ，PB 的中点，所以DE ∥PC ∥FG ，DG ∥AB ∥EF ，所以四边形DEFG 为平行四边形，又因为PC ⊥AB ，所以DE ⊥DG ，所以四边形DEFG 为矩形． (3)存在点Q 满足条件，理由如下：连接DF ，EG ，设Q 为EG 的中点，由(2)知，DF ∩EG ＝Q ，且QD ＝QE ＝QF ＝QG ＝12EG ，分别取PC ，AB 的中点M ，N ，连接ME ，EN ，NG ，MG ，MN .与(2)同理，可证四边形MENG 为矩形，其对角线交点为EG 的中点Q ，且QM ＝QN ＝12EG ，所以Q 为满足条件的点．(理)(2011·北京石景山测试)在棱长为1的正方体ABCD －A 1B 1C 1D 1中，E ，F ，G 分别为棱BB 1，DD 1和CC 1的中点．(1)求证：C 1F ∥平面DEG ； (2)求三棱锥D 1－A 1AE 的体积；(3)试在棱CD 上求一点M ，使D 1M ⊥平面DEG .[解析] (1)证明：∵正方体ABCD －A 1B 1C 1D 1中，F ，G 分别为棱DD 1和CC 1的中点， ∴DF ∥GC 1，且DF ＝GC 1.∴四边形DGC 1F 是平行四边形．∴C 1F ∥DG . 又C 1F ⊄平面DEG ，DG ⊂平面DEG ， ∴C 1F ∥平面DEG .(2)解：正方体ABCD －A 1B 1C 1D 1中，有A 1D 1⊥平面AA 1E .∴A 1D 1是三棱锥D 1－A 1AE 的高，A 1D 1＝1. ∴VD 1－A 1AE ＝13·S △A 1AE ·D 1A 1＝13×12×1×1×1＝16.(3)解：当M 为棱CD 的中点时，有D 1M ⊥平面DEG . 正方体ABCD －A 1B 1C 1D 1中，有BC ⊥平面CDD 1C 1，又∵D 1M ⊂平面CDD 1C 1，BC ∥EG ， ∴EG ⊥D 1M .又∵tan ∠GDC ＝tan ∠MD 1D ＝12，∴∠GDC ＝∠MD 1D ，∴∠MD 1D ＋∠D 1DG ＝∠GDC ＋∠D 1DG ＝90°，∴D 1M ⊥DG . 又DG ∩EG ＝G ，∴D 1M ⊥平面DEG .1．定点A 和B 都在平面α内，定点P ∉α，PB ⊥α，C 是α内异于A 和B 的动点，且PC ⊥AC .那么，动点C 在平面α内的轨迹是( )A ．一条线段，但要去掉两个点B ．一个圆，但要去掉两个点C ．一个椭圆，但要去掉两个点D ．半圆，但要去掉两个点 [答案] B[解析] 连接BC ，∵PB ⊥α，∴AC ⊥PB . 又∵PC ⊥AC ，∴AC ⊥BC .∴C 在以AB 为直径的圆上．故选B.2．(2010·芜湖十二中)已知两条不同的直线m 、n ，两个不同的平面α、β，则下列命题中的真命题是( ) A ．若m ⊥α，n ⊥β，α⊥β，则m ⊥n B ．若m ∥α，n ∥β，α∥β，则m ∥n C ．若m ⊥α，n ∥β，α⊥β，则m ⊥n D ．若m ∥α，n ⊥β，α⊥β，则m ∥n [答案] A [解析]⎭⎬⎫⎭⎪⎬⎪⎫m ⊥αα⊥β⇒m ∥β或m ⊂β n ⊥β⇒m ⊥n ，故A 正确；如图(1)，m ⊥α，n ⊥α满足n ∥β，但m ∥n ，故C 错；如图(2)知B 错；如图(3)正方体中，m∥α，n⊥β，α⊥β，知D错．3．(2011·北京海淀区期末)已知m，n是两条不同的直线，α，β是两个不同的平面．下列命题中不正确的是() A．若m∥α，α∩β＝n，则m∥nB．若m∥n，m⊥α，则n⊥αC．若m⊥α，m⊥β，则α∥βD．若m⊥α，m⊂β，则α⊥β[答案] A[解析]选项A中，直线m与直线n也可能异面，因此A不正确．4．(2011·郑州二检)已知α，β，γ是三个不同的平面，命题“α∥β，且α⊥γ⇒β⊥γ”是真命题．如果把α，β，γ中的任意两个换成直线，另一个保持不变，在所得的所有新命题中，真命题有()A．0个B．1个C．2个D．3个[答案] C[解析]依题意得，命题“a∥b，且a⊥γ⇒b⊥γ”是真命题(由“若两条平行线中的一条与一个平面垂直，则另一条也与这个平面垂直”可知)；命题“a∥β，且a⊥c⇒β⊥c”是假命题(直线c可能位于平面β内，此时结论不成立)；命题“α∥b，且α⊥c⇒b⊥c”是真命题(因为α∥b，因此在平面α内必存在直线b1∥b；又α⊥c，因此c⊥b1，∴c⊥b)．综上所述，其中真命题有2个，选C.5.(2011·盘锦月考)如下图所示，△ABC为正三角形，EC⊥平面ABC，BD∥CE，EC＝CA＝2BD，M是EA的中点．求证：(1)DE＝DA；(2)平面BDM ⊥平面ECA .[证明] (1)如下图所示，取EC 中点F ，连接DF . ∵EC ⊥平面ABC ，BD ∥EC ，∴BD ⊥平面ABC ，∴BD ⊥AB ， ∵BD ∥EC ，BD ＝12EC ＝FC ，∴EC ⊥BC .∴四边形FCBD 是矩形，∴DF ⊥EC . 又BA ＝BC ＝DF ，∴Rt △DEF ≌Rt △ADB ，∴DE ＝DA .(2)如图所示，取AC 中点N ，连接MN 、NB ， ∵M 是EA 的中点，∴MN 綊12EC .由BD 綊12EC ，且BD ⊥平面ABC ，可得四边形MNBD 是矩形，于是DM ⊥MN .∵DE ＝DA ，M 是EA 的中点，∴DM ⊥EA . 又EA ∩MN ＝M ，∴DM ⊥平面ECA ，而DM ⊂平面BDM ，∴平面ECA ⊥平面BDM .6．(2011·辽宁文，18)如下图，四边形ABCD 为正方形，QA ⊥平面ABCD ，PD ∥QA ，QA ＝AB ＝12PD .(1)证明：PQ ⊥平面DCQ ；(2)求棱锥Q －ABCD 的体积与棱锥P －DCQ 的体积的比值．[解析] (1)由条件知PDAQ 为直角梯形．因为QA ⊥平面ABCD ，所以平面PDAQ ⊥平面ABCD ，交线为AD . 又四边形ABCD 为正方形，DC ⊥AD ，所以DC ⊥平面PDAQ ，可得PQ ⊥DC .[来源:Z+xx+] 在直角梯形PDAQ 中可得DQ ＝PQ ＝22PD ，则PQ ⊥QD .所以PQ ⊥平面DCQ . (2)设AB ＝a .由题设知AQ 为棱锥Q －ABCD 的高，所以棱锥Q －ABCD 的体积V 1＝13a 3，由(1)知PQ 为棱锥P －DCQ 的高，而PQ ＝2a ，△DCQ 的面积为22a 2，所以棱锥P －DCQ 的体积V 2＝13a 3. 故棱锥Q －ABCD 的体积与棱锥P －DCQ 的体积的比值为1.7.已知点P 是菱形ABCD 外一点，∠DAB ＝60°，其边长为a ，侧面P AD 是正三角形，其所在平面垂直于底面ABCD ，G 为AD 的中点．(1)求证：AD ⊥PB ；(2)若E 为BC 边中点，能否在棱PC 上找一点F ，使平面DEF ⊥平面ABCD .并证明你的结论．[分析] (1)要证AD ⊥PB ，∵△P AD 为正三角形，G 为AD 中点，∴AD ⊥PG ，故只需证明AD ⊥平面PBG 即可．(2)假设存在点F 使平面DEF ⊥平面ABCD ，则平面DEF 必过平面ABCD 的垂线，由于PG ⊥平面ABCD ，而PG 不可能在平面DEF 内，故需过直线DE 作平面PBG 的平行平面，由此可得点F 的位置．[解析] (1)证明：连接BG ，PG .∵四边形ABCD 是菱形且∠DAB ＝60°.∴BG ⊥AD . 又△P AD 为正三角形，且G 是AD 中点，∴PG ⊥AD . ∵PG ∩BG ＝G ，∴AD ⊥平面PBG . 又PB ⊂平面PBG ，∴AD ⊥PB .(2)解：当F是PC中点时，平面DEF⊥平面ABCD. 证明如下：取PC的中点F，连接DE、EF、DF.在△PBC中，EF∥PB.在菱形ABCD中，BG∥DE.∴平面DEF∥平面PGB.∵平面P AD⊥平面ABCD，PG⊥AD.∴PG⊥平面ABCD. 又PG⊂平面PGB.∴平面PGB⊥平面ABCD.∴平面DEF⊥平面ABCD.。

(常考题)人教版高中数学选修一第一单元《空间向量与立体几何》测试(答案解析)(3)

一、选择题1．已知正三棱锥P ABC -的侧面PAB 上动点Q 的轨迹是以P 为焦点，AB 为准线的抛物线，若点Q 到底面ABC 的距离为d ，且2PQ d =，点H 为棱PC 的中点，则直线BH 与AC 所成角的余弦值为（） A ．8585 B ．21 C ．38585 D ．321 2．已知在平行六面体中,3,4,5,120,60,60ABCD A B C D AB AD AA BAD BAA DAA '''''''-===∠=︒∠=︒∠=︒，则AC '的长为（）A ．52B ．9C ．85D ．73 3．在一直角坐标系中，已知(1,6),(3,8)A B --，现沿x 轴将坐标平面折成60︒的二面角，则折叠后,A B 两点间的距离为（）A ．241B ．41C ．17D ．217 4．在三棱锥P ABC -中，PA ，AB ，AC 两两垂直，D 为棱PC 上一动点，2PA AC ==，3AB =.当BD 与平面PAC 所成角最大时，AD 与平面PBC 所成角的正弦值为（）A ．1111B ．21111C ．31111D ．411115．ABC 中，90ACB ∠=︒，22AB BC ==，将ABC 绕BC 旋转得PBC ，当直线PC 与平面PAB 所成角正弦值为66时，P 、A 两点间的距离为（）A 2B ．2C ．42D ．4 6．已知MN 是正方体内切球的一条直径，点P 在正方体表面上运动，正方体的棱长是2，则PM PN →→⋅的取值范围为（）A ．[]0,4B ．[]0,2C ．[]1,4D ．[]1,2 7．已知二面角l αβ--的两个半平面α与β的法向量分别为,a b ，且,a b 6π<>=，则二面角l αβ--的大小为（）A ．6πB ．56πC ．6π或56πD ．6π或3π 8．如图，在三棱柱11ABC A B C -中，底面ABC 为正三角形，侧棱垂直于底面，14,6AB AA ==.若E 是棱1BB 的中点，则异面直线1A E 与1AC 所成角的余弦值为（）A ．13B ．21313C ．31313D ．13 9．如图,在四面体OABC 中,D 是BC 的中点,G 是AD 的中点,则OG 等于（）A ．111333OA OB OC ++ B ．111234OA OB OC ++ C ．111244OA OB OC ++ D ．111446OA OB OC ++ 10．正方形ABCD 沿对角线BD 折成直二面角，下列结论：①AD 与BC 所成的角为60︒：②AC 与BD 所成的角为90︒：③BC 与面ACD 所成角的正弦值为63：④二面角A BC D --2：其中正确结论的个数为（）A ．4B ．3C ．2D ．1 11．已知在四面体ABCD 中，点M 是棱BC 上的点，且3BM MC =，点N 是棱AD 的中点，若MN x AB y AC z AD =++其中,,x y z 为实数，则x y z ++的值是（）A ．12B ．12-C ．－2D ．212．以下四个命题中正确的是（）A ．空间的任何一个向量都可用其他三个向量表示B ．若{},,a b c 为空间向量的一组基底，则{},,a b b c c a +++构成空间向量的另一组基底 C ．ABC ∆为直角三角形的充要条件是0AB AC ⋅=D ．任何三个不共线的向量都可构成空间向量的一个基底13．如图，在所有棱长均为 a 的直三棱柱 ABC —A 1B 1C 1 中，D ,E 分别为 BB 1,A 1C 1 的中点，则异面直线 AD ,CE 所成角的余弦值为（）A ．12B ．32C ．15D ．45二、填空题14．在三棱锥P -ABC 中，PA ，AB ，AC 两两垂直，D 为棱PC 上一动点，2PA AC ==，3AB =.当BD 与平面PAC 所成角最大时，AD 与平面PBC 所成角的正弦值为________. 15．正四面体ABCD 的棱长为a ，点E 、F 分别是BC 、AD 的中点，则AE AF ⋅的值为_____________.16．如图，已知平面α⊥平面β，l αβ=，∈A l ，B l ∈，AC α⊂，BD β⊂，AC l ⊥，BD l ⊥，且4AB =，3AC =，12BD =，则CD =_________________.17．设空间任意一点O 和不共线三点A B C ，，，且点P 满足向量关系OP xOA yOB zOC =++，若,,,P A B C 四点共面，则x y z ++=______．18．设E ,F 是正方体1AC 的棱AB 和11D C 的中点,在正方体的12条面对角线中,与截面1A ECF 成60︒角的对角线的数目是______.19．若(2,3,1)a =-，(2,0,3)b =，(0,2,2)c =，则()a b c ⋅+=_____20．在空间直角坐标系O xyz -中，已知(1,0,2)A -，(0,1,1)B -，点,C D 分别在x 轴，y 轴上，且AD BC ⊥，那么CD →的最小值是______.21．已知()()1,1,0,1,0,2a b ==-，且ka b +与2a b -的夹角为钝角，则实数k 的取值范围为_____．22．如图，在四棱锥P ABCD -中，底面ABCD 是底边为1的菱形，60BAD ∠=，2PB =，PA PD =，当直线PB 与底面ABCD 所成角为30时，二面角P CD A --的正弦值为______.23．已知非零向量n b 、及平面α，向量n 是平面α的一个法向量,则0n b ⋅=是“向量b 所在直线在平面α内”的____________条件.24．如图，在空间四边形OABC 中，M ，N 分别为OA 、BC 的中点，点G 在线段MN 上，且3MG GN =，用向量OA 、OB 、OC 表示向量OG ，设OG x OA y OB z OC =⋅+⋅+⋅，则x 、y 、z 的和为______.25．如图，在三棱柱111ABC A B C -中，AB ，AC ，1AA 两两互相垂直，122AA AB AC ==，M ，N 是线段1BB ，1CC 上的点，平面AMN 与平面ABC 所成（锐）二面角为3π，当1B M 最小时，AMB ∠=__________.26．在平行六面体1111ABCD A B C D -中，已知1160BAD A AB A AD ∠=∠=∠=︒，14,3,5AD AB AA ===，1AC =__．【参考答案】***试卷处理标记，请不要删除一、选择题1．C解析：C【分析】建立空间直角坐标系，用向量法求直线BH 与AC 所成角的余弦值【详解】设△ABC 的中心为O ，如图示：以OA 为x 轴，过O 平行于BC 的Oy 为y 轴，OP 为z 轴建立空间直角坐标系，不妨设|BC |=2，则有：()23330,0,0,,,1,0,,1,0333O A B C ⎛⎫⎛⎫⎛⎫--- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭过Q 作QD ⊥底面ABC 于D ,QE ⊥AB 于E ，由抛物线的定义知：|QE |=|PD |=2d ，|QD |=d . 在Rt △QDE 中，∠QDE =90°，所以°s 1in ,302QD QDE QDE QE ∠==∴∠=，即侧面于底面所成的二面角为30°.设()0,0,P z 则有31333z ==，所以()311331,,,,,3,1,0,626626H BH AC ⎛⎫⎛⎫--=-=-- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭ 设直线BH 与AC 所成角为θ，则||cos |cos ,|||||BH AC BH AC BH AC θ==⨯ (()()()()22222233|310|331310626⎛⎫+-⨯-+ ⎪⎝⎭=⎛⎫⎛⎫⎛⎫+-+⨯-+-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ 38585= 即直线BH 与AC 所成角的余弦值为38585故选：C【点睛】向量法解决立体几何问题的关键：(1)建立合适的坐标系；(2)把要用到的向量正确表示；(3)利用向量法证明或计算.2．D解析：D【分析】直接利用AC AB BC CC AB AD AA '''=++=++，然后利用平面向量的数量积进行计算.【详解】如图，可得AC AB BC CC AB AD AA '''=++=++，故22||()AC AB AD AA ''=++222=|||||2()+|AB AD AA AB AD AB AA AD AA '''++⋅+⋅+⋅222111345234-+35+45222⎡⎤⎛⎫=+++⨯⨯⨯⨯⨯⨯ ⎪⎢⎥⎝⎭⎣⎦ =73. ∴=73AC '故选：D.【点睛】本题考查了几何体的对角线长的求解，根据已知条件，构造向量，将几何体的对角线长的求解转化为向量模的运算，是解答本题的关键，属于中档题.3．D解析：D【分析】画出图形，作,AC CD BD CD ⊥⊥，则6,8,4AC BD CD ===，可得0,0AC CD BD CD ⋅=⋅=，沿x 轴将坐标平面折成60︒的二面角，故两异面直线,CA DB 所成的角为60︒，结合已知，即可求得答案.【详解】如图为折叠后的图形，其中作,AC CD BD CD ⊥⊥则6,8,4AC BD CD ===，∴0,0AC CD BD CD ⋅=⋅=沿x 轴将坐标平面折成60︒的二面角∴两异面直线,CA DB 所成的角为60︒．可得：.cos6024CA DB CA DB ︒⋅=⋅= 故由AB AC CD DB =++得22||||AB AC CD DB =++ 2222+22AC CD DB AC CD CD DB AC DB +++⋅⋅+⋅= 2222+22AC CD DB AC CD CD DB CA DB +++⋅⋅-⋅= 36166448=++-68=||17AB ∴=故选：D.【点睛】本题考查了立体几何体中求线段长度，解题的关键是作图和掌握空间向量的距离求解公式，考查了分析能力和空间想象能力，属于中档题.4．C解析：C【分析】首先利用线面角的定义，可知当D 为PC 的中点时，AD 取得最小值，此时BD 与平面PAC 所成角最大，再以点A 为坐标原点，建立如图所示的空间直角坐标系A xyz -，利用向量坐标法求线面角的正弦值.【详解】,AB AC AB PA ⊥⊥，且PA AC A =，AB ∴⊥平面PAC ，易证AB ⊥平面PAC ，则BD 与平面PAC 所成角为ADB ∠，3tan AB ADB AD AD∠==，当AD 取得最小值时，ADB ∠取得最大值在等腰Rt PAC ∆中，当D 为PC 的中点时，AD 取得最小值.以A 为坐标原点，建立如图所示的空间直角坐标系A xyz -，则(0,0,0)A ，(3,0,0)B ，(0,2,0)C ，(0,0,2)P ，(0,1,1)D ，则(0,1,1)AD =，(0,2,2)PC =-，(3,2,0)BC =-设平面PBC 的法向量为(,,)n x y z =，则0n PC n BC ⋅=⋅=，即220320y z x y -=⎧⎨-+=⎩令3y =，得(2,3,3)n =. 因为311cos ,11222n AD 〈〉==⨯，所以AD 与平面PBC 311. 故选：C【点睛】关键点点睛：本题重点考查线面角，既考查了几何法求线面角，又考查向量法求线面角，本题关键是确定点D 的位置，首先利用线面角的定义确定点D 的位置，再利用向量法求线面角. 5．B解析：B【分析】取PA 的中点D ，连接CD ，因为CA =CP ，则CD ⊥PA ，连接BD ，过C 作CE ⊥BD ，E 为垂足，由题意得到∠CPE 就是直线PC 与平面PAB 所成角，利用直线PC 与平面PAB 所成角的正弦值为66PC 3CE ，再求出CD ，可得PD ，即可得出结论．【详解】取PA 的中点D ，连接CD ，因为CA =CP ，则CD ⊥PA ，连接BD ，过C 作CE ⊥BD ，E 为垂足，由已知得BC ⊥CA ， BC ⊥CP ， CA CP C =，则BC ⊥平面PAC ，得到BC ⊥PA ，CD BC C ⋂=，可得PA ⊥平面BCD ，又PA ⊂平面PAC ∴平面BCD ⊥平面PBA ，平面BCD 平面PBA =BD ，由两个平面互相垂直的性质可知：CE ⊥平面PBA ，∴∠CPE 就是直线PC 与平面PAB 所成角，∵直线PC 与平面PAB 所成角的正弦值为6，PC ＝AC =3， ∴CE ＝622PC =，设CD ＝x ，则BD ＝21x +，21121122x x ∴⋅⋅=⋅+⋅ ， ∴x ＝1，∵PC ＝3，∴PD ＝2，∴PA ＝2PD ＝22．故选：B ．【点睛】本题考查直线与平面所成角的求法，考查空间想象能力和分析推理能力以及计算能力，属于中档题．6．B解析：B【分析】利用向量的线性运算和数量积运算律可将所求数量积化为21PO →-，根据正方体的特点可确定PO →的最大值和最小值，代入即可得到所求范围.【详解】设正方体内切球的球心为O ，则1OM ON ==，2PM PN PO OM PO ON PO PO OM ON OM ON →→→→→→→→→→→→⎛⎫⎛⎫⎛⎫⋅=+⋅+=+⋅++⋅ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭， MN 为球O 的直径，0OM ON →→∴+=，1OM ON →→⋅=-，21PM PN PO →→→∴⋅=-，又P 在正方体表面上移动，∴当P 为正方体顶点时，PO →3P 为内切球与正方体的切点时，PO →最小，最小值为1，[]210,2PO →∴-∈，即PM PN →→⋅的取值范围为[]0,2. 故选：B .【点睛】本题考查向量数量积的取值范围的求解问题，关键是能够通过向量的线性运算将问题转化为向量模长的取值范围的求解问题.7．C解析：C【分析】由于方向量的方向性，平面的法向量有正向量或负向量；当a 、b 为异号向量，二面角为π减去两法向量夹角；当a 、b 为同号向量，二面角即为两法向量的夹角，由此即可求得二面角l αβ--【详解】两个半平面α与β的法向量分别为,a b ，且,a b 6π<>=由于向量的方向性，法向量与平面有两种情况当a 、b 为异号向量，如下图示：,a b 6π<>=∴有二面角l αβ--为56π 当a 、b 为同号向量，如下图示：,a b 6π<>=∴有二面角l αβ--为6π 综上，有二面角l αβ--为6π或56π 故选：C本题考查了二面角与平面法向量夹角的关系，依据法向量的夹角判断平面所成二面角的大小，注意法向量的方向性，讨论在不同情况下二面角的大小8．A解析：A【分析】以{},,a b c 为基底表示出11,A E AC ，利用向量夹角公式计算出异面直线1A E 与1AC 所成角的余弦值.【详解】设1,,AB a AC b AA c===，则{},,a b c 构成空间的一个基底， 111112A E AB B E a c =+=-， 11AC AC CC b c =+=+， 111111cos ,||||A E AC A E AC A E AC ⋅〈〉=⋅1()21||2a cbc a c b c ⎛⎫-⋅+ ⎪⎝⎭=-⋅+ ()222112212a b b c a c c a c b c ⋅-⋅+⋅-=⎛⎫-⋅+ ⎪22222144cos 600062124a a c c b b c c ⨯⨯︒-+-⨯=-⋅+⋅+⋅+===. 所以异面直线1A E 与1AC . 故选：A【点睛】本小题主要考查异面直线所成角的求法，属于中档题.9．C解析：C【分析】因为在四面体OABC 中,D 是BC 的中点,G 是AD 的中点,12OE OA AD =+,即可求得答案.在四面体OABC 中,D 是BC 的中点,G 是AD 的中点 ∴12OG OA AD =+ 11()22OA AB AC =+⨯+ 1()4OA OB OA OC OA =+⨯-+- 111244OA OB OC =++ 故选:C.【点睛】本题主要考查了向量的线性运算,解题关键是掌握向量基础知识和数形结合,考查了分析能力和空间想象能力,属于基础题.10．A解析：A【分析】取BD 中点O ，连结AO ，CO ，以O 为原点，OC 为x 轴，OD 为y 轴，OA 为z 轴，建立空间直角坐标系，利用向量法和空间中线线、线面、面面间的位置关系逐一判断四个命题得结论.【详解】解：取BD 中点O ，连结AO ，CO ，∵正方形ABCD 沿对角线BD 折成直二面角，∴以O 为原点，OC 为x 轴，OD 为y 轴，OA 为z 轴，建立空间直角坐标系，设1OC =，则()0,0,1A ，()0,1,0B -，()1,0,0C ，()0,1,0D ，()0,1,1AD =-，()1,1,0BC =， 1cos 22AD BCAD BC AD BC ⋅⋅===⋅， ∴异面直线AB 与CD 所成的角为60︒，故①正确： ()1,0,1AC =-，()0,2,0BD =，∵0AC BD ⋅=，∴AC BD ⊥，故②正确：设平面ACD 的一个法向量为(),,t x y z =，由00t AC x z t AD y z ⎧⋅=-=⎨⋅=-=⎩，取1z =，得()1,1,1t =，()1,1,0BC =，设BC 与面ACD 所成角为θ，则6sin cos ,32BC t BC t BC t θ⋅====⋅⋅，故③正确：平面BCD 的法向量()0,0,1n =，()0,1,1BA =，()1,1,0BC =，设平面ABC 的法向量(),,m x y z =，则0m BA y z m BC x y ⎧⋅=+=⎨⋅=+=⎩，取1x =，得()1,1,1m =-， cos ,3m nm n m n⋅<>==⋅， ∴6sin ,3m n <>=. ∴二面角A BC D --的平面角正切值是：2，故④正确.故选：A.【点睛】本题考查利用空间向量法解决立体几何中的问题，属于综合题.11．B解析：B【分析】利用向量运算得到131442MN AB AC AD =--+得到答案. 【详解】 ()3113142442MN MB BA AN AB AC AB AD AB AC AD =++=--+=--+故12x y z ++=-故选：B【点睛】本题考查了空间向量的运算，意在考查学生的计算能力.12．B解析：B【分析】根据空间向量基底的定义：任何三个不共面的向量都可构成空间向量的一组基底，逐一分析A ，B ，D 可判断这三个结论的正误；根据向量垂直的充要条件，及直角三角形的几何特征，可判断C 的真假.【详解】对A ，空间的任何一个向量都可用其他三个不共面的向量表示，A 中忽略三个基底不共面的限制，故A 错误；对B ，若{},,a b c 为空间向量的一组基底，则,,a b c 三个向量互不共面；则,,a b b c c a +++，也互不共面，故{,,}a b b c c a +++可又构成空间向量的一组基底，故B 正确；对C ，0AB AC ABC ⋅=⇔∆的A ∠为直角ABC ⇒∆为直角三角形，但ABC ∆为直角三角形时，A ∠可能为锐角，此时0AB AC ⋅>，故C 错误；对D ，任何三个不共面的向量都可构成空间向量的一组基底，三个向量不共线时可能共面，故D 错误；故选：B ．【点睛】本题以命题的真假判断为载体考查空间向量的基底概念、向量垂直的充要条件，考查对概念的理解与应用，属基础题．13．C解析：C【分析】取AC 的中点O ，以,,OB OC OE 为,,x y z 轴建立坐标系，求得向量,AD CE 的坐标，利用向量的夹角公式，即可求解.【详解】由题意，取AC 的中点O ，以,,OB OC OE 为,,x y z 轴建立坐标系，则(0,,0),(,0,),(0,,0),(0,0,)2222a a a A D C E a ，则3(,,),(0,,)222a a a AD a CE a ==-，设AD 与CE 成的角为θ ，则222223012222cos 534444a a a a a a a a a a θ⨯-⨯+⨯==++⋅+，故选：C.【点睛】本题主要考查了空间向量的应用，以及异面直线所成角的求解，其中解答中建立适当的空间直角坐标系，利用向量的夹角公式求解是解答的关键，着重考查了推理与运算能力，属于基础题.二、填空题14．【分析】首先可证平面PAC 则BD 与平面PAC 所成角为所以当D 为PC 的中点时取得最大值如图建立空间直角坐标系利用空间向量法求出线面角的正弦值；【详解】解：因为PAABAC 两两垂直所以平面PAC 则BD 与解析：311 【分析】首先可证AB ⊥平面PAC ，则BD 与平面PAC 所成角为ADB ∠，所以当D 为PC 的中点时ADB ∠取得最大值，如图建立空间直角坐标系，利用空间向量法求出线面角的正弦值；【详解】解：因为PA ，AB ，AC 两两垂直，PA AC A =所以AB ⊥平面PAC ，则BD 与平面PAC 所成角为ADB ∠，所以3tan AB ADB AD AD∠==，当AD 取得最小值时，ADB ∠取得最大值在等腰Rt PAC △中，当D 为PC 的中点时，AD 取得最小值，以A 为坐标原点，建立如图所示的空间直角坐标系A -xyz ，则(0,0,0)A ，(3,0,0)B ，(0,2,0)C ，(0,0,2)P ，(0,1,1)D ，则(0,1,1)AD =，(0,2,2)PC =-，(3,2,0)BC =-，设平面PBC 的法向量为(,,)n x y z =，则0n PC n BC ⋅=⋅=，即220320y z x y -=⎧⎨-+=⎩，令3y =，得(2,3,3)n =.因为cos ,11n AD 〈〉==，所以AD 与平面PBC .【点睛】 (1)求直线与平面所成的角的一般步骤：①找直线与平面所成的角，即通过找直线在平面上的射影来完成；②计算，要把直线与平面所成的角转化到一个三角形中求解．(2)作二面角的平面角可以通过垂线法进行，在一个半平面内找一点作另一个半平面的垂线，再过垂足作二面角的棱的垂线，两条垂线确定的平面和二面角的棱垂直，由此可得二面角的平面角． 15．【分析】结合由数量积定义计算【详解】正四面体中点EF 分别是BCAD 的中点连接则而所以平面又平面所以即所以故答案为：【点睛】关键点点睛：本题考查向量的数量积运算解题时选择用向量的加减数乘运算表示出要计解析：24a 【分析】AE AB BE =+，结合AD BC ⊥，由数量积定义计算．【详解】正四面体ABCD 中，点E 、F 分别是BC 、AD 的中点，连接,AE DE ，则,BC AE BC DE ⊥⊥，而AE DE E =，所以BC ⊥平面ADE ，又AD ⊂平面ADE ，所以AD BC ⊥，即AF BE ⊥，所以21()cos 6024a AE AF AB BE AF AB AF BE AF a a ⋅=+⋅=⋅+⋅=⨯⨯︒=．故答案为：24a ．【点睛】关键点点睛：本题考查向量的数量积运算，解题时选择用向量的加减数乘运算表示出要计算的向量，然后由数量积定义计算，是基本方法，实质上也可以应用空间向量基本定理表示向量，把向量的运算转化为空间向量的基底进行运算．16．13【分析】根据面面垂直得线面垂直进而得再根据向量模的平方求得结果【详解】因为平面平面所以因为所以故答案为：13【点睛】本题考查面面垂直性质定理利用空间向量求线段长考查基本分析论证与求解能力属中档题解析：13【分析】根据面面垂直得线面垂直，进而得AC BD ⊥,再根据向量模的平方求得结果.【详解】因为平面α⊥平面β，l αβ=，AC α⊂,AC l ⊥，所以AC β⊥，因为BD β⊂，所以AC BD ⊥，CD CA AB BD =++2222222CD CA AB BD CA AB CA BD AB BD ∴=+++⋅+⋅+⋅2222341200013||13CD =+++++=∴= 故答案为：13【点睛】本题考查面面垂直性质定理、利用空间向量求线段长，考查基本分析论证与求解能力，属中档题.17．【分析】先根据不共线三点用平面向量基底表示;再根据平面向量基本定理表示求和即得结果【详解】因为四点共面三点不共线所以因为因为是任意一点故可不共面所以故故答案为：1【点睛】本题考查用基底表示向量以及平解析：1【分析】先根据不共线三点A B C ，，，用平面向量基底AB AC ，表示PA ;再根据平面向量基本定理表示,,x y z ，求和即得结果.【详解】因为,,,P A B C 四点共面，三点A B C ，，不共线，所以,,,m n R PA mAB nAC ∃∈=+()(),(1)OA OP m OB OA n OC OA OP m n OA mOB nOC -=-+-∴=++--因为OP xOA yOB zOC =++，因为O 是任意一点，故,,OA OB OC 可不共面，所以1,,x m n y m z n =++=-=-，故1x y z ++=.故答案为：1【点睛】本题考查用基底表示向量以及平面向量基本定理应用，考查基本分析求解能力，属基础题. 18．【分析】由于平面不是特殊的平面故建系用法向量求解以为原点建系正方体三边为坐标轴求出平面的法向量求解面对角线和的夹角即可求得答案【详解】以点为原点所在直线为轴所在直线为轴所在直线为轴设正方体棱长为2如解析：4【分析】由于平面1A ECF 不是特殊的平面,故建系用法向量求解,以D 为原点建系,正方体三边为坐标轴,求出平面1A ECF 的法向量n ,求解面对角线和n 的夹角,即可求得答案.【详解】以点D 为原点,AD 所在直线为x 轴,DC 所在直线为y 轴,1DD 所在直线为z 轴设正方体棱长为2,如图:则(2,0,0),(0,0,0),(2,2,0),(0,2,0)A D B C1111(2,0,2),(2,2,2,),(0,2,2),(0,0,2)A B C D ,(2,1,0),(0,1,2)E F∴ 1(2,1,0),((0,1,2),(2,2,0)EC A E AC =-==-1(2,2,0),(2,0,2)BD BC =--=-- 11(0,2,2),(0,2,2)B A A B =--=-当面对角线与截面1A ECF 成60︒角,∴ 需保证直线与法向量的夹角为30︒,即其余弦值3±设平面1A ECF 的法向量(,,)n x y z =100n EC n A E ⎧⋅=⎪⎨⋅=⎪⎩ 可得:2020y z x y -=⎧⎨-+=⎩ ,取2y = ∴ (1,2,1)n = ,则||6n =cos ,62||||8n AC AC n n AC ⋅<>===≠±⋅ cos,2BDn <>== 1cos ,B C n<>=≠ 1cos ,2B A n <>==- 1cos ,2A B n <>=≠± 当两条面对角线平行时,求解其中一条与面1A ECF 的法向量n 夹角即可.平面11AA D D 中1AD 与EF 平行,故不符合题意.综上所述,符合题意的面对角线为:1111,,,BD B D AB DC 共4条. 故答案为:4.【点睛】本题考查了线面角求法,根据题意画出几何图形,掌握正方体结构特征是解本题的关键.对于立体几何中角的计算问题,可以利用空间向量法,利用向量的夹角公式求解,属于基础题. 19．3【分析】根据向量加法以及向量数量积的坐标表示得结果【详解】【点睛】本题考查空间向量加法与数量积考查基本求解能力属于基础题解析：3【分析】根据向量加法以及向量数量积的坐标表示得结果.【详解】()()() 2,3,12,2,5465 3.a b c ⋅+=-⋅=-+=，【点睛】本题考查空间向量加法与数量积，考查基本求解能力. 属于基础题. 20．【分析】设0则由知所以由此能求出其最小值【详解】设001-即（当时取最小值）故答案为：【点睛】方法点睛：求最值常用的方法有：（1）函数法；（2）数形结合法；（3）导数法；（4）基本不等式法要根据已知【分析】设(C x ，0，0)，(0D ，y ，0)，则(1,,2)AD y →=-，(,1,1)BC x →=-，由20AD BC x y →→=--=，知2x y =+．所以||CD →【详解】设(C x ，0，0)，(0D ，y ，0)，(1A -，0，2)，(0B ，1，-1)，∴(1,,2)AD y →=-，(,1,1)BC x →=-， AD BC ⊥，∴20AD BC x y →→=--=，即2x y =+．(,,0)CD x y →=-，∴||CD →=2．（当1y =-时取最小值）【点睛】方法点睛：求最值常用的方法有：（1）函数法；（2）数形结合法；（3）导数法；（4）基本不等式法.要根据已知条件灵活选择方法求解. 21．【分析】利用去掉反向的情形即得【详解】由所以解得若与反向则则所以所以与的夹角为钝角则且综上的范围是故答案为：【点睛】思路点睛：本题考查向量的夹角与向量的数量积的关系根据向量夹角求参数时可由是两个非零解析：()7,22,5⎛⎫-∞-⋃- ⎪⎝⎭ 【分析】利用()()20a b ka b <+⋅-去掉反向的情形即得．【详解】由()()1,1,0,1,0,2a b ==-，()1,,2ka b k k +=-，()23,22a b -=-，所以()()()231240a a k k b b k -=+⋅⨯-+-<，解得75k <若ka b +与2a b -反向，则()20a ka b b λλ-<+=，则21k λλ=⎧⎨=-⎩，所以2k =- 所以ka b +与2a b -的夹角为钝角则75k <且2k ≠-综上k 的范围是()7,22,5⎛⎫-∞-⋃- ⎪⎝⎭．故答案为：()7,22,5⎛⎫-∞-⋃- ⎪⎝⎭ 【点睛】思路点睛：本题考查向量的夹角与向量的数量积的关系，根据向量夹角求参数时，可由,a b 是两个非零向量，则,a b 夹角是锐角时，0a b ⋅>，,a b 夹角是钝角时，0a b ⋅<，反之要注意,a b 可能同向也可能反向．属于中档题.22．1【分析】取中点过作于点；由等腰三角形三线合一和线面垂直的判定定理可证得平面从而得到；再根据线面垂直判定定理得到面由线面角定义可知通过勾股定理可求得由此可知在直线上从而得到面面垂直关系可知二面角为从解析：1【分析】取AD 中点E ，过P 作PF BE ⊥于F 点；由等腰三角形三线合一和线面垂直的判定定理可证得AD ⊥平面PBE ，从而得到AD PF ⊥；再根据线面垂直判定定理得到PF ⊥面ABCD ，由线面角定义可知30PBF ∠=，通过勾股定理可求得EF BE =，由此可知F 在直线CD 上，从而得到面面垂直关系，可知二面角为90，从而得到正弦值.【详解】取AD 中点E ，连接BE 并延长，过P 作PF BE ⊥于F 点PA PD =，E 为AD 中点 PE AD ⊥∴四边形ABCD 为菱形，60BAD ∠= ABD ∴∆为等边三角形 BE AD ∴⊥,PE BE ⊂平面PBE ，PE BE E ⋂= AD ∴⊥平面PBEPF ⊂平面PBE AD PF ∴⊥又PF BF ⊥，,BF AD ⊂平面ABCD ，BFAD E = PF ∴⊥面ABCD ∴直线PB 与底面ABCD 所成角为PBF ∠ sin 2sin301PF PB PBF ∴=⋅∠=⨯=在PBE ∆中，由余弦定理得：22232cos 444222PE PB BE PB BE PBE =+-⋅∠=+-⨯=2EF ∴==，又2BE = F ∴在CD 延长线上 PF ∴⊂平面PCD ∴平面PCF ⊥平面ABCD∴二面角P CD A --的大小为90，正弦值为1故答案为：1【点睛】本题考查立体几何中二面角的求解问题，涉及到线面垂直的判定与性质、面面垂直的判定定理、直线与平面所成角、勾股定理等知识的应用；关键是能够通过线面垂直关系确定直线与平面所成角的位置.23．必要不充分【分析】根据充分条件和必要条件的定义进行判断即可【详解】解：若向量是平面的法向量则若则则向量所在直线平行于平面或在平面内即充分性不成立若向量所在直线平行于平面或在平面内则向量是平面的法向量解析：必要不充分【分析】根据充分条件和必要条件的定义进行判断即可．【详解】解：若向量n 是平面α的法向量，则n α⊥，若0n b =，则//b α，则向量b 所在直线平行于平面α或在平面α内，即充分性不成立，若向量b 所在直线平行于平面α或在平面α内，则//b α，向量n 是平面α的法向量，∴n α⊥，则n b ⊥，即0n b =，即必要性成立，则0n b =是向量b 所在直线平行于平面α或在平面α内的必要条件，故答案为：必要不充分【点睛】本题主要考查充分条件和必要条件的判断，根据向量和平面的位置关系是解决本题的关键．24．【分析】利用向量的加法公式得出再由得出的值即可得出的和【详解】即故答案为：【点睛】本题主要考查了用空间基底表示向量属于中档题解析：78【分析】利用向量的加法公式得出111222MN OA OB OC =-++，再由1324OG OM MG OA MN =+=+，得出,,x y z 的值，即可得出,,x y z 的和. 【详解】MN MA AB BN =++11111()22222OA OB OA OC OB OA OB OC =+-+-=-++ 13131112424222OG OM MG OA MN OA OA OB OC ⎛⎫∴=+=+=+-++ ⎪⎝⎭813388OA OB OC =++ 133,,888x y z ∴=== 即78x y z ++=故答案为：78【点睛】本题主要考查了用空间基底表示向量，属于中档题. 25．【分析】根据题意建立空间直角坐标系设出的长写出各个点的坐标求得平面与平面的法向量利用法向量及二面角大小求得的等量关系即可判断当取最小时各自的长即可求得的正切值进而求得的大小【详解】因为三棱柱中两两互解析：6π【分析】根据题意,建立空间直角坐标系,设出,CN BM 的长,写出各个点的坐标,求得平面AMN 与平面ABC 的法向量,利用法向量及二面角大小,求得,CN BM 的等量关系.即可判断当1B M 取最小时,CN BM 各自的长.即可求得AMB ∠的正切值,进而求得AMB ∠的大小.【详解】因为三棱柱111ABC A B C -中,AB ,AC ,1AA 两两互相垂直,建立如下图所示的空间直角坐标系:122AA AB AC ==,M ,N 是线段1BB ,1CC 上的点可设,,1BM a CN b AB ===,则12,1AA AB ==所以()()0,0,0,1,0,0A B ,()()1,0,,0,1,M a N b则()()1,0,,0,1,AM a AN b ==设平面AMN 的法向量为(),,m x y z =则00AM m AN m ⎧⋅=⎨⋅=⎩,代入可得00x az y bz +=⎧⎨+=⎩,令1z =代入解得x a y b =-⎧⎨=-⎩ 所以(),,1m a b =--平面ABC 的法向量()0,0,1n =由题意可知平面AMN 与平面ABC 所成（锐）二面角为3π 则由平面向量数量积定义可知22cos31m n m n a b π⋅==⋅++ 化简可得223a b += 1B M 最小值,即a 取得最大值,当0b =时,a 取得最大值为3a = 所以3tan 33AB AMB MB ∠=== 所以6AMB π∠=故答案为:6π 【点睛】本题考查了空间向量在立体几何中的应用,由法向量法结合二面角求值,属于中档题. 26．【分析】先由空间向量的基本定理将向量用一组基底表示再利用向量数量积的性质计算即可【详解】∵六面体ABCD ﹣A1B1C1D1是平行六面体∵=++∴=（++）2=+++2+2+2又∵∠BAD=∠A1AB【分析】先由空间向量的基本定理，将向量1AC 用一组基底1AA AD AB ，，表示，再利用向量数量积的性质22a a =，计算1AC 即可【详解】∵六面体ABCD ﹣A 1B 1C 1D 1是平行六面体，∵1AC =1AA +AD +AB ∴21AC =（1AA +AD +AB ）2=21AA +2AB +2AD +21AA AD ⋅+21AA AB ⋅+2AB AD ⋅ 又∵∠BAD=∠A 1AB=∠A 1AD=60°，AD=4，AB=3，AA 1=5， ∴21AC =16+9+25+2×5×4×cos60°+2×5×3×cos60°+2×3×4×cos60°=97 ∴197AC =【点睛】本题考察了空间向量的基本定理，向量数量积运算的意义即运算性质，解题时要特别注意空间向量与平面向量的异同。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

面面垂直测试题
1.如图，ABCD 是正方形，O 是正方形的中心，PO ⊥底面ABCD ，E 是PC 的中点。

2．如图，在三棱锥P ABC -中，90ABC ∠=o ，PA ⊥平面ABC ，E ,F 分别为PB ,PC 的
中点.
（1）求证：//EF 平面ABC ；
（2）求证：平面AEF ⊥平面PAB . F
E
A
C P
3如图在三棱锥-P ABC 中，,,D E F 分别为棱,,PC AC AB 的中点，已知
,6,8,5PA AC PA BC DF ⊥===，
求证（1）直线//PA 平面DEF ；
（2）平面BDE ⊥平面ABC .
4．如图，在四棱锥P ABCD -中，底面ABCD 是正方形，侧面PAD ⊥底面ABCD ．
（Ⅰ）若E ，F 分别为PC ，BD 中点，求证：EF ∥平面PAD ；
（Ⅱ）求证：PA ⊥CD ；
（Ⅲ）若2PA PD AD ==，求证：平面PAB ⊥平面PCD ． F E
D C B P
求证：（1）PA ∥平面BDE
（2）平面PAC ⊥平面BDE
5．已知三棱柱ABC-A 1B 1C 1中，侧棱垂直于底面,AC=BC,点D 是AB 的中点．
(1)求证：BC 1∥平面CA 1D ；(2)求证：平面CA 1D⊥平面AA 1B 1B ；
(3)若底面ABC 为边长为2的正三角形，BB 1
=3求三棱锥B 1-A 1DC 的体积．
6．如图，已知四棱锥A BCDE -，1AB BC AC BE ====，2CD =，
CD ⊥平面ABC ，BE ∥CD ，F 为AD 的中点．
（1）求证：EF ∥平面ABC ；
（2）求证：平面ADE ⊥平面ACD ；
（3）求四棱锥A BCDE -的体积．
7．如图，在四棱锥P-ABCD 中，底面ABCD 是平行四边形，且PA ⊥底面ABCD ，BD PC ⊥，
E 是PA 的中点.
（1）求证：平面PAC ⊥平面EBD ；
（2）若PA=AB=2，求三棱锥P-EBD 的高.
A
D
B C C
A
B
面面垂直测试题
1.证明：(1)∵O 是AC 的中点，E 是PC 的中点，∴OE ∥AP ，
又∵OE ⊂平面BDE ，PA ⊄平面BDE ，∴PA ∥平面BDE
(2)∵PO ⊥底ABCD,ABCD BD 面⊂∴PO ⊥BD ，又∵AC ⊥BD ，且AC I PO=O
∴BD ⊥平面PAC ，而BD ⊂平面BDE ，∴平面PAC ⊥平面BDE
2.证明:（1）在PBC ∆中，F E ,Θ分别为PC PB ,的中点BC EF //∴ 3分
又⊂BC 平面ABC ，⊄EF 平面ABC //EF ∴平面ABC 7分
（2）由条件，⊥PA 平面ABC ，⊂BC 平面ABC
BC PA ⊥∴︒=∠90ABC Θ，即BC AB ⊥， 10分
由//EF BC ，∴EF AB ⊥，EF PA ⊥
又A AB PA =⋂，AB PA ,都在平面PAB 内 EF ∴⊥平面PAB
又⊂EF Θ平面AEF ∴平面AEF ⊥平面PAB
3.（1）由于,D E 分别是,PC AC 的中点，则有//PA DE ，又PA DEF ⊄平面，
DE DEF ⊂平面，所以//PA DEF 平面．
（2）由（1）//PA DE ，又PA AC ⊥，所以PE AC ⊥，又F 是AB 中点，所以
132DE PA ==，142EF BC ==，又5DF =，所以222DE EF DF +=，所以
DE EF ⊥，,EF AC 是平面ABC 内两条相交直线，所以DE ABC ⊥平面，又
DE ⊂平面BDE ，所以平面BDE ⊥平面ABC ．
4.（3)（Ⅲ）在△PAD 中，因为PA PD AD ==，所以PA PD ⊥．由（Ⅱ）可知PA ⊥CD ，且=CD PD D I ，所以PA ⊥平面PCD ．
又因为PA ⊂平面PAB ，所以平面PAB ⊥平面PCD
5.由（Ⅱ）可知PA ⊥CD ，且=CD PD D I ，所以PA ⊥平面PCD ．又因为PA ⊂平面PAB ，
所以平面PAB ⊥平面PCD ．
证明（1）连接AC 1交A 1C 于点E ，连接DE
因为四边形AA 1C 1C 是矩形，则E 为AC 1的中点
又D 是AB 的中点，DE∥BC 1，
又DE ⊂面CA 1D ，BC 1⊄面CA 1D ，BC 1∥面CA 1 (４分)
证明（2）AC=BC ，D 是AB 的中点，AB⊥CD，
又AA 1⊥面ABC ，CD ⊂面ABC ，AA 1⊥CD，
AA 1∩AB=A，CD⊥面AA 1B 1B ，CD ⊂面CA 1D ，
平面CA 1D⊥平面AA 1B 1B (８分)
（3）解：1111B A DC C A B D V V --=,则（2）知CD⊥面ABB 1B ，所以高就是，BD=1，BB 1，
所以A 1D=B 1D=A 1B 1=2,11A B D S ∆=111C A B D V -== (1２分) 6.解：（1）取AC 中点G ，连结FG ，BG ，F G Q ，
分别是AD ，AC 的中点， FG ∴∥CD ，且112FG DC ==.
BE Q ∥CD ， FG ∴与BE 平行且相等.
所以四边形BEFG 为平行四边形，EF ∴∥BG . 3分
又EF ⊄平面ABC ，BG ⊂平面ABC .EF ∴∥平面ABC . 4分
（2）ABC ∆Q 为等边三角形，G 为AC 的中点，BG AC ∴⊥. 又DC ⊥平面ABC ，BG ⊂平面ABC .DC BG ∴⊥， 6‘ 又AC DC C =I ，BG ∴⊥平面ADC . 7分
EF Q ∥BG ，EF ∴⊥平面ADC ， 8分
EF ⊂Q 平面ADE ，∴平面ADE ⊥平面ADC . 10分
（3）取BC 中点H ,连结AH .AB BC AC ==Q , AH BC ∴⊥.
DC ⊥Q 平面ABC ，AH ⊂平面ABC DC AH ∴⊥，
又BC DC C =I ， ∴AH ⊥平面BCDE ，
AH ∴是四棱锥A BCDE -的高，且AH =， 12分
11(12)1332BCDE V S AH +⨯=⋅=⨯=梯形.
7（1）因为PA ⊥平面ABCD ，所以PA ⊥BD ．又BD ⊥PC ，所以BD ⊥平面PAC ，
因为BD ⊂平面EBD ，所以平面PAC ⊥平面EBD ． 5分
（2）由（1）可知，BD ⊥AC ，所以ABCD 是菱形，∠BAD ＝120︒．所以11
22
ABD S BD AC ∆=⋅= 7分设AC ∩BD ＝O ，连结OE ，则（1）可知，BD ⊥OE ．所以1
2EBD S BD OE ∆=⋅=．
设三棱锥P -EBD 的高为h ，则
11
33
EBD ABD S h S AE ∆∆⋅=⋅，即11133h =，解得h =． 12分。