函数y=sin(ωx+φ)的图象的三种变换
函数y=A sin(ωx+φ)的图象
x
2x
sin 2 x
0 0 0
4 2
1
2
0
3 4 3 2
－1
2
0
x
1 x 2 1 sin x 2
0 0 0
2
1
2
3
3 2
－1
4 2
0
0
列表并描点作图：
x
2x
sin 2 x
0 0 0
4 2
1
2
0
3 4 3 2
－1
2
0
x
1 x 2 1 sin x 2
y 3 2 1
y 3 sin(2 x ) 3
6
o
12
-1 -2 -3
3
7 12
5 6
2 x
y sin x
问题：函数y=3sin(2x+π/3)的图象是由函数 y＝sinx的图象经过怎样的变化得到呢？
方法1： 按 , , A顺序变换 ( )
y
3
2
y=3sin(2x+ 3 )
(二)探索对 y=sin(x+ ), x∈R的图象的影响.
1 例2．作函数 y sin 2 x及 y sin x 的简图． 2 2 ， x 0， 时的简图． 先作 解：函数 y sin 2 x 的周期 T 2 1 2 4 ，先作 x 0， 时的简图． 函数 y sin x 的周期T 4 1 2 2 列表：
方 法 y sin x 一
向左平移
个单位 3
y sin( x ） 3
横坐标缩短到 原来的 1 倍 2
高中数学同步教学 函数y=asin(ωx+φ)的图像变换
三角函数图像间的变换
【例 1】 已知函数 f(x)=sin +
为 π,则将函数 y=f(x)的图像向
π
4
(∈R,ω>0)的最小正周期
平移
个单位长
度可得到函数 g(x)=cos ωx 的图像.(填写一个正确答案即可)
π
解析:由 T=π,得 ω=2,因此 f(x)=sin 2 + 4 . 因为g(x)=cos
C.y=sin
D. = sin
-
π
2 10
-
π
2 20
题型一
题型二
题型三
题型四
π
解析:将函数 y=sin x 的图像上所有的点向右平移 10 个单位长度,
π
3
π
, 所以ω=2,φ=− .
3
,
题型一
题型二
题型三
题型二
题型四
利用图像变换求函数解析式
【例 2】 将函数 y=sin x 的图像上所有的点向右平移
π
10
个单位
长度, 再把所得各点的横坐标伸长到原来的 2 倍(纵坐标不变), 所得
图像的函数解析式是(
)
π
π
A.y=sin 2- 10
B. = sin 2- 5
的5倍,可得函数
的图像;再将所得图像上的各点的
横坐标不变,纵坐标伸长为原来的5倍,可得函数
的
图像.
答案:(1)左
1
5sin
5
π
4
(2)右
π
8
(3)下
1
5
1
(4) = sin 5 =
3.由函数y=sin x的图像得到函数y=Asin(ωx+φ)+b(A>0,ω>0)的图
三角函数图形的变换
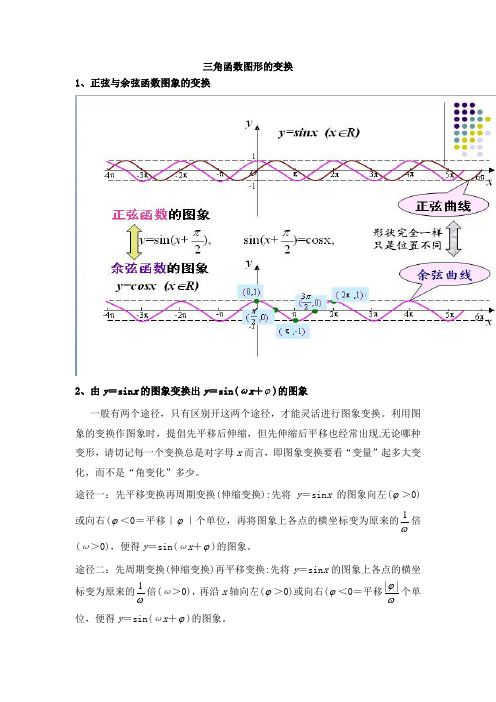
三角函数图形的变换1、正弦与余弦函数图象的变换2、由y ＝sin x 的图象变换出y ＝sin(ωx ＋ϕ)的图象一般有两个途径，只有区别开这两个途径，才能灵活进行图象变换。
利用图象的变换作图象时，提倡先平移后伸缩，但先伸缩后平移也经常出现无论哪种变形，请切记每一个变换总是对字母x 而言，即图象变换要看“变量”起多大变化，而不是“角变化”多少。
途径一：先平移变换再周期变换(伸缩变换):先将y ＝sin x 的图象向左(ϕ＞0)或向右(ϕ＜0＝平移｜ϕ｜个单位，再将图象上各点的横坐标变为原来的ω1倍(ω＞0)，便得y ＝sin(ωx ＋ϕ)的图象。
途径二：先周期变换(伸缩变换)再平移变换:先将y ＝sin x 的图象上各点的横坐标变为原来的ω1倍(ω＞0)，再沿x 轴向左(ϕ＞0)或向右(ϕ＜0＝平移ωϕ||个单位，便得y ＝sin(ωx ＋ϕ)的图象。
作y =sin x （长度为2π的某闭区间）的图象 得y =sin(x +φ) 的图象得y =sin ωx 的图象 得y =sin(ωx +φ) 的图象 得y =sin(ωx +φ) 的图象 得y =Asin(ωx +φ)的图象，先在一个周期闭区间上再扩充到R 上沿x 轴平 移|φ|个单位 横坐标 伸长或缩短 横坐标伸 长或缩短沿x 轴平 移|ωϕ|个单位 纵坐标伸 长或缩短纵坐标伸 长或缩短【经典例题】图像变换一：左右平移1、把函数R x x y ∈=,sin 图像上所有的点向左平移4π个单位，所得函数的解析式为 _________2、把函数R x x y ∈=,cos 图像上所有的点向右平移5π个单位，所得函数的解析式为 _________图像变换二：纵向伸缩3、对于函数R x x y ∈=,s i n 3的图像是将R x x y ∈=,sin 的图像上所有点的______(“横”或”纵”)坐标______（伸长或缩短）为原来的______而得到的图像。
《函数y=Asin(ωx+φ)的图象(第二课时)》教案
《函数y=Asin(ωx+φ)的图象（第二课时）》教案师：结合信息技术动态演示=1ω时，动点G 的轨迹以及动点G 对应的函数解析式．我们知道，动点M 在单位圆1O 上以单位角速度（即=1ω）按逆时针方向运动，如果动点M 以1Q 为起点（此时π=6），经过x s 后运动到点P ，那么点P 的纵坐标就等于πsin +6x （），所以以,x y （）为坐标描点G ，点G 的轨迹对应的函数解析式是π=sin +6y x （）．问题4：若取=2ω，动点1M 以1Q 为起点，在单位圆1O 上以角速度=2ω按逆时针方向运动，经过x s 后运动到点1P ，那么点1P 的纵坐标是什么？生：点1P 的纵坐标就等于πsin 2+6x （）． 追问：此时，以,x y （）为坐标描点H ，点H 的轨迹对应的函数解析式是什么？生：点H 的轨迹对应的函数解析式是π=sin 2+6y x （）．师：结合信息技术动态演示=2ω时，动点H 的轨迹．问题5：函数π=sin 2+6y x （）与π=sin +6y x （）的图象之间存在怎样的变换关系？你能从质点的匀速圆周运动规律和函数图象上点的坐标变化的角度进行解释吗？生：思考、交流．师：引导学生分析，学生遇到困难时进行点拨．师生分析：如图，从匀速圆周运动的变化规律看，在单位圆上，两个动点都以1Q 为起点，以=1ω和=2ω的不同角速度绕单位圆逆时针方向运动，到达同一位置P 时，=2ω时的运动时间始终是=1ω时运动时间的12．对应地，设,G x y （）是函数π=sin +6y x （）图象上的一点，那么1,2K x y （）就是函数π=sin 2+6y x （）图象上的相应点．问题6：如上我们找到了两个函数图象上任意点的变化，那么如何从函数π=sin +6y x （）的图象得到函数π=sin 2+6y x （）的图象？生：思考，交流．师：引导学生理解图象变换的本质是图象上点的变换．总结：函数π=sin 2+6y x （）的图象是把函数πsin()6y x =+的图象上所有点的横坐标缩短到原来的12（纵坐标不变）得到的．并且π=sin 2+6y x （）的周期为π，是π=sin +6y x （）的周期的12．问题7：如果ω取12，3，13时，对应的函数π=sin +6y ωx （）的图象与π=sin +6y x （）的图象之间存在怎样的变换关系？生：仿照上面的研究过程分析、交流． 师：以1=2ω为例，动点的转速是=1ω时的12，以1Q 为起点，到达点P 的时间是=1ω时的2倍，所以把π=sin +6y x （）图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），就得到1π=sin +26y x （）的图设计意图：引导学生类比参数 ，ω对函数=sin +y ωx φ（）图象影响的研究过程，明确参数0A A （＞）对函数=sin +y A ωx φ（）图象影响的研究思路．结合筒车模型，引导学生理解A 的实际意义，为后面的探索做好准备．问题10：若取=2A ，设射线1OQ 与以1O 为圆心、2为半径的圆交于点1T ，如果单位圆上以1Q 为起点的动点M ，以=2ω的转速经过x s 后到达圆周上的点P ，那么点P 的纵坐标是πsin 2+6x （），相应地，动点1M 在以1O 为圆心、2为半径的圆上，以1T 为起点，=2ω的转速经过x s 后到达圆周上的点T ，那么点T 的纵坐标是什么？师：借助信息技术演示．生：点T 的纵坐标就等于π2sin 2+6x （）． 追问：此时，以,x y （）为坐标描点H ，点H 的轨迹对应的函数解析式是什么？生：点H 的轨迹对应的函数解析式是π=2sin 2+6y x （）． 问题11：函数π=2sin 2+6y x （）与π=sin 2+6y x （）的图象之间存在怎样的变换关系？你能从质点的匀速圆周运动规律和函数图象上点的坐标变化的角度进行解释吗？生：借助前面的研究过程，分析、交流．师：在学生困难的地方进行点拨，借助信息技术动态演示，引导学生得出一般性的结论．师生分析：如图，从匀速圆周运动的变化规律看，在以1O 为圆心，半径分别为1和2的圆上，两个动点分别以1Q 和1T 为起点，=2ω的转速经过x s 后分别到达圆周上的点P 和点T ，易得点T 的纵坐标是点P 的纵坐标的2倍．对应地，设,K x y （）是函数π=sin 2+6y x （）图象上的一点，那么,2N x y （）就是函数π=2sin 2+6y x （）图象上的相应点．问题12：如上我们找到了两个函数图象上任意点的变化，那么如何从函数π=sin 2+6y x （）的图象得到函数π=2sin 2+6y x （）的图象？ 生：思考，交流．总结：函数π=2sin 2+6y x （）的图象是把函数π=sin 2+6y x （）的图象上所有点的纵坐标伸长到原来的2倍（横坐标不变）得到的．问题13：如果A 取12，3，13时，对应的函数π=sin 2+6y A x （）的图象与π=sin 2+6y x （）的图象之间存在怎样的变换关系？你能给出0A A （＞）的变化对函数=sin +y A ωx φ（）图象影响的一般化结论吗？ 生：仿照上面的研究过程分析、交流．师：借助信息技术动态演示，引导学生总结一般性的论．师生总结：以1=2A 为例，把函数π=sin 2+6y x （）的图象上所有点的纵坐标缩短到原来的12（横坐标不变），就得到1π=sin 2+26y x （）的图象． 一般地，函数=sin +y A ωx φ（）的图象，可以看作是把函数=sin +y ωx φ（）的图象上所有点的纵坐标伸长（当1A ＞时）或缩短（当课后篇巩固提升合格考达标练1.函数y=sin(2x-π3)在区间[-π2,π]上的简图是()x=0时,y=sin(-π3)=-√32<0,故可排除B,D;当x=π6时,sin(2×π6-π3)=sin0=0,排除C.2.要得到函数y=sin(x-π3)的图象,只需将函数y=sin(x+π6)的图象()A.向右平移π3个单位长度B.向左平移π3个单位长度C.向右平移π2个单位长度D.向左平移π6个单位长度y=sin[(x-π2)+π6]=sin(x-π3),所以应将函数y=sin(x+π6)的图象向右平移π2个单位长度.3.(2021天津高一联考)为了得到函数y=sin2x+π4的图象,只需把函数y=sin2x+π6的图象上所有的点()A.向左平移π12个单位长度B.向右平移π12个单位长度C.向左平移π24个单位长度D.向右平移π24个单位长度解析由题得函数y=sin 2x+π4=sin 2x+π24+π6,故要得到函数y=sin 2x+π4的图象,只需将函数y=sin 2x+π6的图象向左平移π24个单位长度即可,故选C . 4.某同学用“五点法”画函数y=A sin(ωx+φ)A>0,ω>0,|φ|<π2在一个周期内的简图时,列表如下:2则根据表格可得出A= ,ω= ,φ=.3 -π4A=2,T=34π-π12=2πω,∴ω=3,∴ωx+φ=3x+φ.∵当x=π12时,3x+φ=π4+φ=0,∴φ=-π4.5.把函数f (x )=cos (2x -π6)图象上所有点的横坐标缩短到原来的12,得到函数g (x )的图象,则g (x )的最小正周期是 .g (x )=cos (4x -π6),故最小正周期T=2π4=π2.6.(2021天津河西高一期末)将函数y=2sin 2x 的图象向左平移π12个单位长度,再将图象上每个点的横坐标和纵坐标都变为原来的12倍,则所得图象的函数解析式为 .答案y=sin 4x+π6解析将函数y=2sin 2x 的图象向左平移π12个单位长度,可得y=2sin 2x+π6的图象;再将图象上每个点的横坐标和纵坐标都变为原来的12倍,则所得图象的函数解析式为y=sin 4x+π6.7.(2021吉林公主岭高一期末)已知函数f (x )=2sin 2x+π6+1.(1)用“五点法”画出它在一个周期内的闭区间上的图象(完成横、纵坐标列表); (2)写出函数y=f (x )图象的对称中心坐标及对称轴的方程.列表如下:描点连线作图如下:(2)由图象可得对称中心的坐标为kπ2−π12,1,k ∈Z ,对称轴方程为x=kπ2+π6,k∈Z .等级考提升练8.已知函数f(x)=sinωx+π4(ω>0)的最小正周期为π,为了得到函数g(x)=cos ωx的图象,只要将y=f(x)的图象()A.向左平移π8个单位长度B.向右平移π8个单位长度C.向左平移π4个单位长度D.向右平移π4个单位长度解析函数f(x)的最小正周期为π,则ω=2ππ=2,所以f(x)=sin2x+π4.f(x)=sin2x+π4=cosπ2-2x+π4=cosπ4-2x=cos2x-π4=cos2x-π8.要想得到函数g(x)=cos 2x=cos2x-π8+π8的图象,只需把函数f(x)的图象向左平移π8个单位长度即可.故选A.9.(2021甘肃天水高一期末)为了得到函数y=√2sin2x+π4的图象,只要把函数y=√2cos 2x图象上所有的点()A.向左平移π8个单位长度B.向右平移π8个单位长度C.向左平移π4个单位长度D.向右平移π4个单位长度解析只要把函数y=√2cos 2x=√2sin2x+π2图象上所有的点向右平移π8个单位长度,可得函数y=√2sin2x+π4的图象,故选B.10.如图为一半径是2米的水轮,水轮圆心O 距离水面1米,已知水轮每分钟旋转5圈,水轮上的点P 到水面的距离y (单位:米)与时间x (单位:秒)满足函数关系y=A sin(ωx+φ)+1A>0,ω>0,|φ|<π2,则( )A.ω=π6,A=2 B.ω=2π15,A=1 C.ω=π6,A=3 D.ω=2π15,A=2T=605=2πω,可得ω=π6,由图可知y 的最大值为3,sin(ωx+φ)=1时取得最大值,∴3=A+1,解得A=2.11.将函数y=sin 2x 的图象上各点的横坐标伸长到原来的2倍,纵坐标不变,得到函数y=f (x )的图象,则( )A.y=f (x )的图象关于直线x=π8对称 B.f (x )的最小正周期为π2 C.y=f (x )的图象关于点π2,0对称D.f (x )在-π3,π6上单调递增解析函数y=sin 2x 的图象上各点的横坐标伸长到原来的2倍,可得y=sin x ,即f (x )=sin x.根据正弦函数的图象及性质可知,对称轴x=π2+k π,k ∈Z ,所以A 错误;最小正周期T=2π,所以B 错误;对称中心坐标为(k π,0),k ∈Z ,所以C 错误.单调递增区间为2k π-π2,π2+2k π,k ∈Z ,所以f (x )在-π3,π6上单调递增.故选D .12.(多选题)(2021江苏苏州高一期末)为了得到函数y=cos 2x+π4的图象,只要把函数y=cos x 图象上所有的点( )A.向左平移π4个单位长度,再将横坐标变为原来的2倍 B .向左平移π4个单位长度,再将横坐标变为原来的12倍 C .横坐标变为原来的12倍,再向左平移π8个单位长度D .横坐标变为原来的12倍,再向左平移π4个单位长度解析把函数y=cos x 图象上所有的点向左平移π4个单位长度,得到y=cos x+π4的图象;再将横坐标变为原来的12倍,得到y=cos 2x+π4的图象.或把函数y=cos x 图象上所有的点横坐标变为原来的12倍,得到y=cos 2x 的图象;再向左平移π8个单位长度,可得y=cos 2x+π4的图象.故选BC .13.(多选题)要得到y=cos 2x 的图象C 1,只要将y=sin 2x+π3的图象C 2( ) A.向左平移π12个单位长度 B.向右平移11π12个单位长度C .先作关于x 轴对称的图象C 3,再将图象C 3向右平移5π12个单位长度 D .先作关于x 轴对称的图象C 3,再将图象C 3向左平移π12个单位长度解析对于A,将y=sin 2x+π3的图象C 2向左平移π12个单位长度,可得y=sin 2x+π12+π3=sin 2x+π2=cos 2x 的图象C 1,故选项A 正确;对于B,将y=sin 2x+π3的图象C 2向右平移11π12个单位长度,可得y=sin [2(x -11π12)+π3]=sin 2x -3π2=cos 2x 的图象C 1,故选项B 正确; 对于C,先作C 2关于x 轴对称的图象,即y=-sin 2x+π3的图象C 3,再将图象C 3向右平移5π12个单位长度,得到y=-sin [2(x -5π12)+π3]=-sin 2x -π2=cos 2x 的图象C 1,故选项C 正确;对于D,先作C 2关于x 轴对称的图象,即y=-sin 2x+π3的图象C 3,再将图象C 3向左平移π12个单位长度,得到y=-sin [2(x +π12)+π3]=-sin 2x+π2=-cos 2x 的图象,故选项D 不正确.14.已知函数f (x )=sin (ωx +π4)(ω>0)的最小正周期为π,为了得到g (x )=sin (12x +π4)的图象,只需将y=f (x )的图象上 .4倍,纵坐标不变f (x )的最小正周期为π,∴2πω=π.∴ω=2.∴f (x )=sin (2x +π4).又g (x )=sin (12x +π4)=sin [2×(14x)+π4],∴只需将y=f (x )的图象上所有点的横坐标伸长为原来的4倍,纵坐标不变,得到g (x )=sin12x+π4的图象. 15.已知f (x )=2sin(ωx+φ)ω>0,|φ|≤π2在0,4π3上单调,且f π3=0,f4π3=2,则f (0)= .1 由题意知14·2πω=4π3−π3,所以ω=12.由f4π3=0,得12×4π3+φ=2k π+π2,k ∈Z , 所以φ=-π6+2k π,k ∈Z . 又因为|φ|≤π2,所以φ=-π6, 即f (x )=2sin12x -π6, 则f (0)=2sin -π6=-1.16.将函数f (x )=sin(ωx+φ)ω>0,-π2≤φ<π2图象上每一点的横坐标缩短为原来的一半,纵坐标不变,再向右平移π6个单位长度得到y=sin x 的图象.(1)求函数f (x )的解析式;(2)当x ∈[0,3π]时,方程f (x )=m 有唯一实数根,求m 的取值范围.将y=sin x 的图象向左平移π6个单位长度可得y=sin (x +π6)的图象,保持纵坐标不变,横坐标变为原来的2倍,可得y=sin (12x +π6)的图象,故f (x )=sin (12x +π6).(2)令2kπ+π2≤12x+π6≤2kπ+3π2(k∈Z),则4kπ+2π3≤x≤4kπ+8π3(k∈Z).又x∈[0,3π],所以x∈[0,2π3],f(x)单调递增,x∈[2π3,8π3],f(x)单调递减,x∈[8π3,3π],f(x)单调递增,所以f(x)max=1,f(x)min=-1,当x=0时,m=12,当x=3π时,m=-√32.故使方程f(x)=m有唯一实数根的m的取值范围为m∈(-√32,12)∪{-1,1}.新情境创新练17.某同学用“五点作图法”画函数f(x)=A sin(ωx+φ)ω>0,|φ|<π2在某一个周期内的图象时,列表并填入了部分数据,如下表:2(1)请将上表数据补充完整,并写出函数f(x)的解析式;(2)将f(x)图象上所有点向左平移θ(θ>0)个单位长度,得到g(x)的图象.若g(x)图象的一个对称中心为5π12,0,求θ的最小值.根据表中已知数据,可得A=5,{π3ω+φ=π2,5π6ω+φ=3π2,解得ω=2,φ=-π6.数据补全如下表:211函数解析式为f(x)=5sin2x-π6.(2)由(1)知f(x)=5sin2x-π6,则g(x)=5sin2x+2θ-π6.因为函数y=sin x图象的对称中心为(kπ,0),k∈Z,令2x+2θ-π6=kπ,k∈Z,解得x=kπ2+π12-θ,k∈Z.由于函数y=g(x)的图象关于点5π12,0成中心对称,所以令kπ2+π12-θ=5π12,k∈Z,解得θ=kπ2−π3,k∈Z.由θ>0可知,当k=1时,θ取得最小值π6.。
正弦型函数y=A sin(ωx+φ)的图像 课件-高一上学期数学人教A版(2019)必修第一册
y
2
1
0
π
2π
3π
4π x
-1
ω的作用：使正弦函数的周期发生变化。
你能得到y=sin （ x)与y=sinx 图象的关系吗？
函数 y sin(x) 的图象，可以看作
是把 y sin( x) 的图象上所有点的横坐
标* 1 倍（纵坐标不变）而得到的. 0
T 2
练习：求下列函数的最大值、最小值、 周期
先观察y=2sinx、y= 1 sinx与y=sinx的图象间的关系
y
2
2
1
0
π
2π x
-1
-2
你能得到y=Asinx与y=sinx 图象的关系吗？
1.y=Asinx（A>0)的图象是由y=sinx的图象上所 有点的横坐标不变，纵坐标*A倍而成. 2.值域 [ -A, A]最大值A,最小值-A
正弦型函数y =Asin(ωx + )的图象
5、 3 2
1
5
y sin( x ) 1
2 2
ymax 2
ymin
2
T 2
正弦型函数y =Asin(ωx + )的图象和性质
3、 的作用：研究 y=sin(x+ )与y=sinx 图象的关系
先观察y = sin（x+ ）、y = sin（x － ）
2
2
与 y=sinx 的图象间的关系
y
2
1
0
π
2π
3π
4π x
-1
作y=sin
1 2
x的图象
1x
0
2
x
0
sin 12x 0
1、列表
高中数学三角函数函数yasin(ωxφ)的图象与性质函数y=asin(ωx+φ)的图象与性质
跟踪演练 1 要得到 y＝cos2x－π4的图象，只要将 y＝sin 2x 的
图象( )
A．向左平移π8个单位
B．向右平移π8个单位
C．向左平移π4个单位
D．向右平移π4个单位
第十二页，共三十页。
解析 y＝sin 2x＝cosπ2－2x＝cos2x－π2 ＝cos2x－π4＝cos2x－π8－π4 若设 f(x)＝sin 2x＝cos 2x－π8－π4， 则 fx＋π8＝cos2x－π4，∴向左平移π8个单位．
第二十七页，共三十页。
(2)y＝sin x―周―期―变―换→y＝sin ωx―相―位―变―换→
y＝sin[ω(x＋ωφ )]＝sin(ωx＋φ)―振―幅―变―换→
y＝Asin(ωx＋φ)． 注意：两种途径的变换顺序不同，其中变换的量也有所不同： (1)是先相位变换后周期变换，平移|φ|个单位．(2)是先周期变换 后相位变换，平移|ωφ|个单位．
指出其变换步骤．
第二页，共三十页。
1 预习(yùxí)导学
实
2 课堂(kètáng)讲义
3 当堂(dānɡ tánɡ)检测
功
第三页，共三十页。
挑战自我，点点落
重点难点，个个击破 当堂训练，体验成
[知识(zhī shi)链接]
1．“五点法”作图 画正弦函数 y＝sin x，x∈[0,2π]的图象，五个关键点是 (0,0)， π2，1，(π，0)，32π，－1，(2π，0) ．
第二十六页，共三十页。
课堂(kètáng)小结
1.由y＝sin x的图象，通过变换可得到函数y＝Asin(ωx＋φ)(A＞0，ω＞0)
的图象，其变化(biànhuà)途径有两条：
(1)y＝sin x―相―位―变―换→y＝sin(x＋φ)―周―期―变―换→ y＝sin(ωx＋φ)―振―幅―变―换→y＝Asin(ωx＋φ)．
人教A版高中数学必修4-1.5函数y=Asin(ωxφ)的图象-课件
三 、 教学目标
１.知识与能力目标：
理解三个参数A、ω、φ对函数y=Asin(ωx+φ) 图象的影响；揭示函数y=Asin(ωx+φ)的图象与 正弦曲线的变换关系，
２.过程与方法目标：
结合具体函数图象的变化，领会由简单到复杂 ，由特殊到一般的化归思想，通过A、ω、φ变化 与函数y=Asin(ωx+φ)图象变换的关系，加深对数 形结合思想的理解。
函数.
那么函数 y Asin( x )与函数y=sinx
有什么关系呢?
从解析式上来看函数y=sinx就是函数
y Asin( x )在A=1，ω=1， 0 的情况.
下面就来探索 、、A 对函数
y Asin( x )
的图象的影响.
***检测复习***
y sin x, x [0,2 ]的图象
合
函数y=sinx(>0)图象:
作 探
究
y=sinx 横坐标变为本来的1/倍 y=sinx
纵坐标不变
小试牛刀
2. 要得到函数 y=sin3x 的图象，只需将 y=sinx 图象（ B ）
A. 横坐标伸长到本来的3倍 ，纵坐标不变 B.横坐标缩小到本来的1/3倍 ，纵坐标不变 C.纵坐标扩大到本来的3倍，横坐标不变 D.纵坐标缩小到本来的1/3倍，横坐标不变
1 sin x 0
2
1 2
0
1 2
0
函数 y 2sin x、y 1 sin x与y sin x 的图象
2
间的变化关系.
y
自
2
主 学
1
习
O
3
2
x
2
-1
y 1 sin x
-2
函数y=A sin (ωx+φ)的性质与图象课件
函数的最大值和最小值，通常称为振幅.
名师点析
函数＝ 的图象经过变换得到＝（ + ）（ > 0， > 0）的图象的步骤
高中数学
必修第二册
北师大版
四、探究＝（ + ）性质的一般步骤
第4步，借助图象讨论性质.
实际上，这也是讨论周期函数的一般方法和步骤.
高中数学
必修第二册
北师大版
名师点析
函数＝sin（ + ）（ > 0， > 0）的性质
（1）定义域为R；（2）值域：［−，］.
π
（3）奇偶性：当＝π， ∈ 时，是奇函数；当＝π+ 2 ， ∈ 时，是偶函数；当 ≠
函数＝ （ + ）的图象，可以看作将函数＝ 图象上的所有点向左（ > 0）或向右（ < 0）
平移||个单位长度得到的.
函数＝ （ + ）与函数＝ 有相同的周期，由 + ＝0，得＝− ，即函数＝ 图象
上的点（0，0）平移到点 − , 0 .函数＝ （ + ）的图象，可以看作将函数＝ 图象上的所
图象的对称中心、对称轴或求值.
（2）若函数＝sin（ + ）为奇函数，则＝， ∈ ，若函数＝（ + ）为偶函数，则
π
＝ 2 +π， ∈ .
高中数学
必修第二册
北师大版
跟踪训练
π
1.已知函数（）＝sin + 2 （0<<π），
π
4
π
＝0，则函数（）的图象的对称轴方程为（ Ｃ ）