第十一讲频率特性的基本概念和波特图
合集下载
频率特性
这些统称放大电路的频率响应。 这些统称放大电路的频率响应。 幅频特性偏离中频值的现象称为幅度频率失真; 相频特性偏离中频值的现象称为相位频率失真。 产生频率失真的原因是: 产生频率失真的原因是: 1.放大电路中存在电抗性元件 放大电路中存在电抗性元件， 1.放大电路中存在电抗性元件，例如 耦合电容、旁路电容、分布电容、 耦合电容、旁路电容、分布电容、变压 分布电感等; 器、分布电感等; 2.三极管的 是频率的函数。 2.三极管的β(ω)是频率的函数。 在研究频率特性时， 在研究频率特性时，三极管的低频小信号 模型不再适用，而要采用高频小信号模型。 模型不再适用，而要采用高频小信号模型。
1 1 式中 ω L = = 。 RC
RC 高通电路
τ
下限截止频率、 下限截止频率、模和相角分别为 f / fL 1 f0 = fL = Av = ϕ = 90o − arctg( f f ) 2πRC L 1 + ( f )2 fL
HPF
HPF
RC高通电路的频率响应 高通电路的频率响应
RC电路的电压增益： 电路的电压增益： 电路的电压增益 V ( s) R2 AVH ( s ) = o = Vi ( s ) R2 + 1 / sC 2
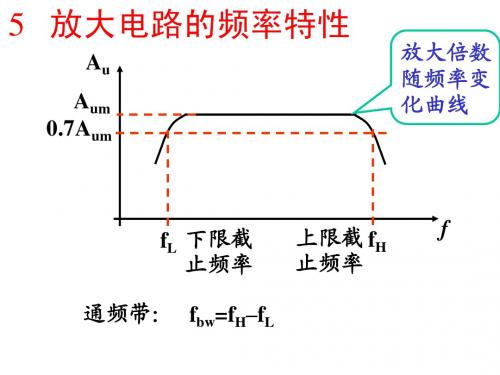
5 放大电路的频率特性
Au Aum 0.7Aum 放大倍数 随频率变 化曲线
fL 下限截 止频率 通频带： 通频带： fbw=fH–fL
上限截 fH 止频率
f
5.1 放大电路的频率特性概述
幅度频率特性
相位频率特性
幅频特性是描绘输入信号幅度 固定， 固定，输出信号的幅度随频率变化 而变化的规律。 而变化的规律。即 & &i &∣= ∣Vo /V∣= f (ω ) ∣A
频率特性法
§5-2
一、幅相频率特性
1、代数形式
频率特性表达方法
即极坐标图，也称为 Nyquist 图
G( j) P() jQ()
2、指数形式
由G ( j ) A( )e j ( )
3、幅相特性表示法 极坐标图形式
二、对数频率特性 即 Bode 图
G ( j ) A( )e j ( ) A( ) P 2 ( ) Q 2 ( ) Q ( ) P ( )
对数幅频特性绘在以 10 为底的对数坐标中，幅值的对数值用分贝（dB）表示
L() 20lg A()
纵轴是 L(w)，横轴实际上是 lgw，由于是用 w 标注，所以又转化成 w 的值，这使得每一单位 的 w 增加量为 10 倍，这 10 倍频记为 dec。横轴的起点不为 0。.
§5-3
一、比例环节
2 2
1 T
1
L( ) 20 lg A( ) 20 log 1 20 lg (1 2T 2 ) (2T ) 2
六、时滞环节或延迟环节
传递函数 : G ( s) e s j 频率特性 : G ( j )e 幅频特性 : A( ) 1 相频特性 : ( ) G ( j ) cos j sin e j cos j sin G ( j ) 1
积分环节的对数频率特性
四、微分环节
G (s) s G ( j ) j 代数式 G ( j ) j 0 j 指数式 G ( j ) j 90
L( w) 20 lg | G( jw) | 20 lg w G( jw) 90
理想微分环节的副相频率特性
五、振荡环节(0<§<1)
高等教育出版社第六版《电路》第011章电路的频率响应.ppt
H ( j)
200j
( j 2)(j 10)
解：
H ( j)
(1
10j j )(1
j )
2 10
HdB
20lg10 20lg
j
20lg1
j
2
20lg1
j
10
Φ 90 arctan arctan
2
10
28
幅频波特图
H dB
20lg10 20lg
（2）并联，B = 0，即 Im[Y ] 0
L1
L2
1 1 0
C
L1
L2
1
C
L1
1
C
L2， (L1
L2 )
1
C
02
1 (L1 L2 ) C
24
§11-5 波特图
用对数坐标描绘的频率响应图称为频响波特图。
H( j) H( j) ej(j)
lnH(j) lnH(j) j(j)
横坐标是频率，按对数分度，单位是 rad / s 。 幅频波特图的纵坐标表示函数值，均匀分度，单位是dB。
Q
1
1 4Q
2
Q
C3 时， HC ( jC3) 0
(Q 0.707)
17
2、H
C
(
j
)
U C U S
( (
j)、H j)
L
(
j
)
U U
L S
( (
j j
) )
的频率特性 ：
HC
(
j
)
jQ
jQ( 2
1)
UC ( j) US ( j1)
a cQ 0.707低通函数1HL
5 第五章 频率特性及其图示
s j
系统的频率特性就等于在系统传递函数 G(s)中以s=jω代入后所得的结果G(jω)。
频率特性的特点（2）
（2）G(jω)是以ω为自变量的复变函数
G( j ) G( )e j ( ) G( ) ( ) Re G( j ) j Im G( j )
幅频特性
极坐标
相特性曲线）。
OA 端点A形成轨迹曲线，称为Gj的极坐标图（幅
G( j ) G( j ) e
jG ( j1 )
当ω ： 时， 0
A
极坐标图
0
极轴
直角坐标
G( j ) R( ) jI ( )
jI
IA
极坐标图
A R
0
RA
在直角坐标上表示的曲线也称为极坐标图
两种坐标形式间的转换
G ( ) G ( j ) Re 2 ( ) Im 2 ( ) 1 Im( ) ( ) tg Re( )
Re( ) G( )cos ( ) Im( ) G( )sin ( )
极坐标图（Nyquist图）在直角坐标系或者极坐标系表示均可。
k
j 1)
G ( )
K ( i ) 2 1
m
k 1 i 1
i 1 n
(Tk ) 2 1
1
K a b
( ) tg ( i ) tg (Tk )
1 k 1
0：G(0) K；（0） 0
：G() 0；（） n m)90 （ K a)：n m 2 如 (T1j 1)(T2j 1) K b)：n m 3 如 (T1j 1)(T2j 1)(T3j 1)
系统的频率特性就等于在系统传递函数 G(s)中以s=jω代入后所得的结果G(jω)。
频率特性的特点（2）
（2）G(jω)是以ω为自变量的复变函数
G( j ) G( )e j ( ) G( ) ( ) Re G( j ) j Im G( j )
幅频特性
极坐标
相特性曲线）。
OA 端点A形成轨迹曲线，称为Gj的极坐标图（幅
G( j ) G( j ) e
jG ( j1 )
当ω ： 时， 0
A
极坐标图
0
极轴
直角坐标
G( j ) R( ) jI ( )
jI
IA
极坐标图
A R
0
RA
在直角坐标上表示的曲线也称为极坐标图
两种坐标形式间的转换
G ( ) G ( j ) Re 2 ( ) Im 2 ( ) 1 Im( ) ( ) tg Re( )
Re( ) G( )cos ( ) Im( ) G( )sin ( )
极坐标图（Nyquist图）在直角坐标系或者极坐标系表示均可。
k
j 1)
G ( )
K ( i ) 2 1
m
k 1 i 1
i 1 n
(Tk ) 2 1
1
K a b
( ) tg ( i ) tg (Tk )
1 k 1
0：G(0) K；（0） 0
：G() 0；（） n m)90 （ K a)：n m 2 如 (T1j 1)(T2j 1) K b)：n m 3 如 (T1j 1)(T2j 1)(T3j 1)
自动控制原理频率特性及其表示法.2021完整版PPT
系统的频率特性是一个与输入正弦信号的幅 值及相位均无关的复数量。
自动控制原理
6
1 频率特性的基本概念
系统的幅频特性 | G( j)|| C( j) | R( j)
反映了输出量与输入量幅值之比与频率 的关系。
系统的相频特性
( ) C (j ) R (j )
反映了输出量与输入量相位之差与频率 的关系。
❖ 幅相频率特性
极坐标图—Nyquist图（奈奎斯特图、简称奈氏图）。
❖ 对数频率特性
对数坐标图—Bode图（伯德图，简称伯氏图）
❖ 对数幅相频率特性
复合坐标图—Nichocls图（尼柯尔斯图，简称尼氏 图）；一般常用于闭环系统的频率特性分析。
自动控制原理
15
2 频率特性的表示
❖ 幅相频率特性 可以表示成代数形式或极坐标形式。
设系统或环节的传递函数为
G (s)bmsmbm 1sm 1.. ..b0 ansnan1sn1.. .a0
自动控制原理
16
幅相频率特性
令 s j，可得系统或环节的频率特性 代数形式：
G (j) b m (j)m b m 1 (j)m 1 . .b .0 R () j(I) a n (j)n a n 1 (j)n 1 . .a .0
性能、稳态性能。
自动控制原理
12
1 频率特性的基本概念
系统的稳态输出量与输入量具有相同的频率 频率特性(幅频、相频)是频率的函数 ，这是
系统中的储能元件引起的。
实际系统具有“低通”滤波器特性 实际系统的输出量都随频率的升高而出现失真，
幅值衰减。
频率特性可应用到某些非线性系统的分析中去
自动控制原理
13
自动控制原理
自动控制原理
6
1 频率特性的基本概念
系统的幅频特性 | G( j)|| C( j) | R( j)
反映了输出量与输入量幅值之比与频率 的关系。
系统的相频特性
( ) C (j ) R (j )
反映了输出量与输入量相位之差与频率 的关系。
❖ 幅相频率特性
极坐标图—Nyquist图（奈奎斯特图、简称奈氏图）。
❖ 对数频率特性
对数坐标图—Bode图（伯德图，简称伯氏图）
❖ 对数幅相频率特性
复合坐标图—Nichocls图（尼柯尔斯图，简称尼氏 图）；一般常用于闭环系统的频率特性分析。
自动控制原理
15
2 频率特性的表示
❖ 幅相频率特性 可以表示成代数形式或极坐标形式。
设系统或环节的传递函数为
G (s)bmsmbm 1sm 1.. ..b0 ansnan1sn1.. .a0
自动控制原理
16
幅相频率特性
令 s j，可得系统或环节的频率特性 代数形式：
G (j) b m (j)m b m 1 (j)m 1 . .b .0 R () j(I) a n (j)n a n 1 (j)n 1 . .a .0
性能、稳态性能。
自动控制原理
12
1 频率特性的基本概念
系统的稳态输出量与输入量具有相同的频率 频率特性(幅频、相频)是频率的函数 ，这是
系统中的储能元件引起的。
实际系统具有“低通”滤波器特性 实际系统的输出量都随频率的升高而出现失真，
幅值衰减。
频率特性可应用到某些非线性系统的分析中去
自动控制原理
13
自动控制原理
第11章电路原理课件
1
相对抑 制比
通频带
10. 谐振电路的能量
1 2 1 2 W WL WC Li CuC 2 2
2 2 2 2 W WL WC 1 LI m 1 CU C CQ US m 2 2
I
?
+
Us _
R j L
i 2 I 0 cos 0t 2
US cos 0t R
1 1 jjC
uC 2U C cos(0t 900 ) 2QU S sin 0t
1 2 1 L 2 2 2 Li CuC 2 U S cos 2 (0t ) CQ 2U S sin 2 (0t ) 2 2 R 1 2 1 2 2 2 1 L 1 L L CQ 2 2 Li Cu CQ US Q Q 2 2 C R R C R C 2 2 U Cm 2 1 2 2 2 ) CU Cm W C(QUS ) CUC C ( 2 2
1 由 L C 可得： o
– + U UL – + U – C –
谐振角 频率
R U
+
R jXL – jXC
1 LC
谐振频率（固有频率）
1 f f0 2π LC
1 f0 2π LC
2.使RLC串联电路发生（或避免）谐振的条件
1） L C 不变，改变 ； (调频) 2）电源频率不变，改变 L 或 C ( 常改变C )。
R U
+
R jXL – jXC
４. 谐振时电路中的能量变化
电路向电源吸收的无功功率 Q=0 ，谐振时电路能量 交换在电路内部的电场与磁场间进行。电源只向电阻R 提供能量。 P=RI02=U2/R，电阻功率最大。
频率响应分析法
频率响应分析法5.1 频率特性的基本概念 5.1.1频率特性的定义5.1.2频率特性和传递函数的关系 5.1.3频率特性的图形表示方法 5.2 幅相频率特性（Nyquist 图） 5.2.1典型环节的幅相特性曲线 5.2.2开环系统的幅相特性曲线 5.3 对数频率特性（Bode 图） 5.3.1典型环节的Bode 图 5.3.2开环系统的Bode 图5.3.3最小相角系统和非最小相角系统 5.4 频域稳定判据 5.4.1奈奎斯特稳定判据5.4.2奈奎斯特稳定判据的应用 5.4.3对数稳定判据 5.5 稳定裕度5.5.1稳定裕度的定义 5.5.2稳定裕度的计算5.6 利用开环频率特性分析系统的性能5.6.1)(ωL 低频渐近线与系统稳态误差的关系 5.6.2)(ωL 中频段特性与系统动态性能的关系5.6.3)(ωL 高频段对系统性能的影响 5.7 闭环频率特性曲线的绘制 5.7.1用向量法求闭环频率特性 5.7.2尼柯尔斯图线5.8 利用闭环频率特性分析系统的性能 5.8.1闭环频率特性的几个特征量 5.8.2闭环频域指标与时域指标的关系 引言频率响应法的特点1）由开环频率特性→闭环系统稳定性及性能 2）二阶系统频率特性↔时域性能指标 高阶系统频率特性↔时域性能指标3）物理意义明确许多元部件此特性都可用实验法确定工程上广泛应用 4）在校正方法中，频率法校正最为方便 5.1频率特性的基本概念1.定义1: ()sin ()()2. ()()3. ()()ss r t A t c t r t G s s j G j c t r t ωωω=⎧⎪=⎨⎪⎩时，与的幅值比，相角差构成的复数中，令得出为频率特性的富氏变换与的富氏变换之比一、 地位：三大分析方法之一二、 特点：1)2)()3)⎧⎪→⎨⎪⎩图解法，简单不直接解闭环根，从开环闭环特征特别适用于校正，设计近似法，不完全精确以右图R －C 网络为例：r cc r c c u iR u i Cu q u CuR u =+↓===+ ()(1)r c U s CRs U =+⋅ ()1()()1T CR c r U s G s U s Ts ===+ 设()sin r u t A t ω=求()c u t22()1tT c A T u t e t t T ωωωω-⎡⎤∴=-⎥+⎦22)1tT A T e t arctg t T ωωωω-=+-+ 瞬态响应稳态响应网络频率特性()()()()()ss ss c r c t G j G j r t G j arctgT ωωωϕϕω⎧⎪⎪===⎨⎪⎪∠=-=-⎩幅频特性：相频特性频率特性定义一：——频率特性物理意义：频率特性()G j ω是当输入为正弦信号时，系统稳态输出（也是一个与输入同频率的正弦信号）与输入信号的幅值比，相角差。
第三章.放大器的频率特性
A ( ) ( ) A V V
o ( j ) V AV ( ) i ( j ) V
( ) o ( ) i ( )
称为幅频响应
称为相频响应
4
中频区
普通音响系统放大电路 的幅频响应
其中
f H — —上限频率 f L — —下限频率
40
3dB 3dB 频率点 频率点 （半功率点） （半功率点）
分析方法
9
3.1.2 频率特性的基本概念
对低频段 , 由于耦合电容和射级旁路电容的容抗变大 , 低频段时 1/ωC<<R不成立。电容不能视为短路，等效电路 如图所示。
10
对高频段, 影响频率响应的主要因素是三极管极间电 容和接线，这两者电容在电路中与其他支路是并联的，等 效电路如图所示。
11
基本RC电路的频率响应
U s
U o
29
中频区电压放大倍数
A usm
' U Uo Ui R R o i L Us Ui U s R R rbe s i
Ri Rb // rbe Rb1 // Rb 2 // rbe
R'L Rc // RL
30
2．低频区频率响应的分析
E
Cb
e
20
混合π型等效电路
21
1．密勒定理
• 密勒定理原理图
I 1
U 1
K
I 2 U 2
U U ( 1 K ) U ( 1 U / U ) 1 U U 1 2 1 1 1 2 I1 Z1 Z Z Z
22
简化过程 U U U U 2 1 2 2 I2 ) Z Z Z /(1 1 / K 2
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
3、基本放大器高、低截止频率的估算
4、基本放大器的频率特性分析
§5-1 放大电路频率特性的基本概念
一、频率特性和通频带 1、什么叫频率特性 频率特性是指放大器放大倍数的数值以及输出信号和输入 信号的相位差随输入信号的频率而变化的函数关系。
Au ( j ) | Au ( j ) | e
j ( )
e
Re
Ce RL
RC // RL Aum gm R L rbe
2、低频段增益函数AuL（s）
放大器的AuL(s)由低频段的小信号模型导出， 耦合电容、旁路电容等大电容不能忽略， 而极间电容视为开路。
Rb1
C1
RC
VCC
C2
1 C1 高通电路 1 / C1 (1 ) / Ce
1 GB 2 ( RS rbb )Cbe
任何放大电路都有一个确定的通频带，我们在使用一个放大电路时 应了解其信号频率的适用范围；在设计放大电路时，应能满足信号频率 范围的要求。
§5-2 放大电路的复频域分析
分析放大电路频率特性的方法：分频段复频率分析法
分频段 ：将电路按低频段、中频段和高频段分别进行分析。
m m 1
xi(S) 线性网络 xO (S)
X O ( s ) bm s bm 1 s b1 s b0 H ( s) n n 1 X i ( s) an s an1 s a1 s a0
求出零点和极点后，上式可以表示为：
常数
零点
极点
( s z i) ( s z1 )( s z2 )( s zm ) i 1 K n H ( s) K ( s p1 )( s p2 )( s pn ) ( s pj )
uO ( s ) i 1 K n Au ( s ) ui ( s ) ( s p j )
j 1
(s z i)
m
（2）放大电路增益函数的特点
① 零点数目肯定不会大于极点数目。
（放大电路是可实现的线性时不变系统）
mn
② 所有极点都位于复平面的左半平面上。
（放大电路应该是稳定的系统）
幅频特性： Au ( ) | Au ( j ) | 放大电路对不同频率的信号呈现出不同的放大倍数和相位 差，以阻容耦合放大电路为例： 低频区增 中频区增 高频区增 －－放大倍数的幅值与频
益下降 益最高 益下降 率的关系。 仿真 VCC 信号 放大 相位差 R Rb1 C 相频特性： ( ) C2 频率 倍数 C1 －－输出信号与输入信号的 500Hz 相位差与频率的关系。 产生滞后 25 -105º 产生超前 相差约 RS 附加相移 Rb2 180 附加相移 + RL 30kHz 76 -180º uS C e Re
幅频特性的纵坐标： 60 20 0.1 -40 10 20lg|Au( )|(dB)
幅频特性
20lgA () (dB)
102 103
104 105 106 (rad/s)
相频特性
135 相频特性的纵坐标：
( )/°
10 102 103 104 105 106 (rad/s)
( ),线性刻度（º ）
③ 极点数目等于电路中“独立”电抗元件的数目。（P189）
二、高通电路和低通电路
1、高通电路
U Au o Ui
R 1 R j C
1 1 1 jRC
U i
U o
1 1 令 L ； RC
L 1 fL ； 2 2RC
Au
1
L 1 j
30MHz
44
-225º (4ห้องสมุดไป่ตู้ º )
2、阻容耦合放大电路的频率特性－－定性分析
ZC 1 / C
在中频范围： 大电容的容抗小，视为短路；小电容的容抗大， 视为开路。交流通路是一个纯阻性的电路，电路参数Au、Ri、 RO等均为与频率无关的常数。 在低频段： 耦合、旁路电容的容抗增大，分压作用增大，旁路 作用减弱，导致增益下降并产生超前附加相移。 低频段主要受耦合 高频段主要受三极管的 在高频段： 极间电容、分布电容等容抗减小，分流作用增大， 电容旁路电容影响 结电容或极间电容影响 而且β下降，导致增益下降并产生附加相移。 仿真
1 fL 1 j f
f j fL f 1 j fL
2、低通电路
1 U 1 j C o Au 1 Ui 1 jRC R j C
U i
U o
1 1 令 H ； RC
H 1 fH ； 2 2RC
1
Au
1
1 j H
f 1 j fH
rbb b ib R S R S R s + u u S u s
S
C Cbe 1 | Aum | Cbc
C' C'' Rb rbe i r b e b rce RC RL R R gmube C L e
1 | Aum | C Cbc | Aum |
j=1
m
m 2 2 2 1+ j / z | | 1 ( ) 1+ j / z ( ) 1 ( ) 1 ( ) i …… i z 1 z zm i=1 2 i=1 幅频特性： =A | A( ) | A A 0 n 00 n 2 2 2| ) ( ) …… 1+ / p |1 j/1 pj ( 1 (1+) j ( )j
低频区增 益下降
产生超前 附加相移
中频区增 益最高
高频区增 益下降
Rb1 C1
RC
VCC C2 CO
相差约 180
RS 产生滞后 + Rb2 Ci Re 附加相移 u S
Ce RL
3、通频带以及上、下限截止频率的概念
Au 0 Au 0 2
BW fL
在低频段和高频段，增益的幅值下 降至中频增益Au0的70.7%（即下降 3dB)时所对应的频率分别称为下限 截止频率和上限截止频率。 下限截止频率fL ，简称下限频率
在每个频段分析时，根据其工作特点抓住影响该频段的主要参 数对电路进行简化，得到各频段的微变等效电路。
复频率分析法 ：将电阻、电容、电感用复阻抗表示，得到各频
段增益的传输函数，进而得到频率特性，最后将三个频段的结 果综合起来就得到电路的全频段响应。
一、复频域中放大电路的传输函数
1、线性网络的复频域传输函数与频率特性 线性网络复频域传输函数的一般表达式
f L 0, BW f 0.7 f H
仿真 Rb1 RS + Rb2 Ci uS Re VCC BW
RC C2
CO
fH
RL
二、频率失真和增益带宽积
1、频率失真（线性失真）：
基波
二次谐波
幅频失真： 放大电路对输入信号不同频率
分量的幅值不是等同放大而产 生的输出波形失真。
相频失真： 放大电路对输入信号不同频率
j 1 m
m
j z i ) ( i 1 令S = j，系统的稳态频率响应：H ( j ) K n ( j p j )
j 1
2、放大电路的增益函数及其特点 对于放大器，增益就是放大器的传输函数， ui(s) （1）放大电路增益函数的通式：
放大器 uO (s) A（s）
0.1 -90
45
1、作图思路
（稳态响应）
( s z i ) A(s ) K n ( s pj )
m n
m
s j
( j z i) A( j) K n
变换为作图标准式
m
( j p j )
A( j )
A0
( 1+j/zi ) i=1
( 1+j/pj )
1 AuH ( jf ) Aum 1 j( f / f H )
4、全频段增益函数Au（s）
j( f / f L1 ) 1 Au ( jf ) Aum 1 j( f / f L1 ) 1 j( f / f H )
Au ( jf ) Aum
1 fL f (1 j )(1 j ) f fH
ib1 b C' c C2 RS R RC RS S Rb rr + be + be ib rce R RLR C L uS u uS ibRC S e
RS Rb2 + uS
Re
Ce RL
C1 b ib Rb
c
C2
rbe
Re
ib rce R R C L Ce e
j( f / f L1 ) j( f / f L2 ) AuL ( jf ) Aum 1 j( f / f L1 ) 1 j( f / f L2 )
3、高频段增益函数AuH（s）
AuH(s)由高频小信号模型导出，耦合、旁路 电容视为短路，极间电容不能忽略。
Rb1
RS Rb2 + Ci uS Re
RC
VCC
C2
b rbb RS uS r b e Rb ube C
+
Cbc
c
CO
Ce RL
b e
gmube rce RC RL e 低通电路 c
fH
上限截止频率fH ，简称上限频率 （也称为3dB截止频率、半功率点） 通频带BW（3dB带宽） ：
BW f 0.7 f H f L
4、直接耦合放大电路的频率特性－－定性分析
直接耦合放大器没有耦合或旁路电容，在低频段不会因大电容 上压降的增大而使电压放大倍数降低，也不会产生附加相移。
四、放大电路波特图的近似画法