AI中级教程VIP设计进阶班
霍格沃兹测试开发学社软件测试进阶班Python班培训课程大纲

进阶班测试开发介绍 Python课程介绍测试开发进阶班是一个面向有测试经验,具有基础 Python 编程能力,想要提升测试开发、自动化测试能力的测试开发工程师的班级,课程以服务测试行业的社招需求为出发点,涵盖测试框架、Web/App 自动化测试、接口自动化测试、性能测试、安全测试、Docker/K8s、持续集成/持续交付、测试平台开发等方向。
学习计划整体课程持续 19 周技术体系时长(周)第一阶段测试开发体系/Git 代码管理/Linux 与 Bash1编程语言1测试框架1第二阶段用户端 Web 自动化测试2用户端 App 自动化测试2第三阶段接口测试1接口自动化测试2性能测试实战1第四阶段Docker 容器技术1K8s 容器编排1持续集成实战1持续交付实战1第五阶段自动化测试框架开发1测试平台开发1算法与设计模式1测试左移/测试右移1直播训练营主课:包含对应课程的录播与直播,需要完成配套作业。
赠课:提供对应课程的录播与直播。
直播训练营测试开发进阶学习路线Web 测试用例设计赠课App 测试用例设计赠课测试流程实战赠课直播训练营测试开发进阶学习路线Linux 命令与 Bash 脚本赠课Python 或 Java 编程语言赠课单元测试与集成测试框架主课用户端(Web)自动化测试-企业微信主课用户端(Web)自动化测试-飞书主课用户端(App)自动化测试-企业微信主课用户端(App)自动化测试-雪球主课专项测试赠课小程序测试赠课接口协议抓包分析主课接口自动化测试-企业微信主课接口自动化测试-飞书主课性能测试主课安全测试主课算法与设计模式主课持续集成/持续交付主课Docker 容器技术与 K8S主课测试框架开发主课测试平台开发主课测试左移/白盒测试/单元测试/覆盖率/代码审计赠课测试右移/性能监控/质量监控赠课测试开发体系介绍测试体系介绍-L1教学目标掌握软件测试的基础概念了解测试行业经典的测试方法与经典书籍知识点形式章节描述软件测试基础概念软件测试的原则、对象、作用,缺陷的介绍知识点知识软件开发流程SCRUM、XP、持续集成/持续交付/DevOps点知识测试流程体系传统测试流程、测试左移、测试右移点知识测试技术体系分层测试体系、单元测试、UI 测试、接口测试、白盒测试点形式章节描述知识点常用测试平台用例管理平台、Bug 管理平台、代码管理平台、持续集成平台知识点流程管理平台常用流程管理平台介绍,jira、redmine知识点项目管理与跨部门沟通协作与产品经理、研发、上下游测试的配合知识点测试经典书籍拆分讲解全程软件测试、探索式测试、持续交付、Google 测试之道、不测的秘密等测试体系介绍-L2教学目标掌握测试方案设计方法。
智能计算平台应用开发(初级)-实验手册-AI全流程开发初体验实验手册-学员用书

AI全流程开发初体验实验手册学员用书1 目录1参考资料与工具 (1)1.1参考资料与工具 (1)2 AI全流程开发初体验 (3)2.1课程介绍 (3)2.2教学目标 (3)2.3学员分组 (3)2.4案例背景 (4)2.5任务 (4)演练场景一:项目规划 (5)演练场景二:项目实施与验收 (8)2.6评分表 (12)1 参考资料与工具1.1 参考资料与工具文档中所列出地命令以与参考文档,请根据实际环境中地不同产品版本使用对应地命令以与文档。
参考文档:1. 《华为ModelArts配置指南》,获取地址:2. 《如何购买OBS》登录华为IT产品信息服务平台获取方式:《华为ModelArts配置指南》见附录一。
软件工具(二选一):1. 公有云:云服务ModelArts,AI引擎:选择“TensorFlow”/“TF-1.13.1-python3.6”规格:“CPU(2U)”“GPU(P100)”2. 单机:Python3.6与以上CPU型号:酷睿4代或更新学习链接:1. 华为IT产品信息服务平台2. AI开发平台ModelArts专有名词解释:数据标注:给图片打标签。
比如,图片里有小狗,则可手动命名图片地标签为“dog”。
模型:可粗略理解为用量化地方式描述事件。
参数:影响模型效果地因素。
训练:反复调整模型中地参数地过程。
训练集:用于训练模型地数据集合。
测试集:用于检验模型地数据集合。
部署上线:将模型部署为在线服务,可添加图片或代码进行服务测试,也可使用URL接口调用。
2 AI全流程开发初体验2.1 课程介绍人工智能触发地产业变革,已涉与多数行业。
智慧交通将大大提升通行效率,个性化教育降低因材施教地执行难度,精准预防性治疗有望延长人类地寿命,实时多语言翻译交流再无障碍,自动驾驶与电动汽车将颠覆汽车产业等等。
人工智能是ICT产业60年发展地总成果,正在帮助各行各业降本增效,企业是否具备真正地人工智能思维,是否以人工智能地理念与技术解决现在与未来地问题,是能否在未来构筑领先竞争力地关键。
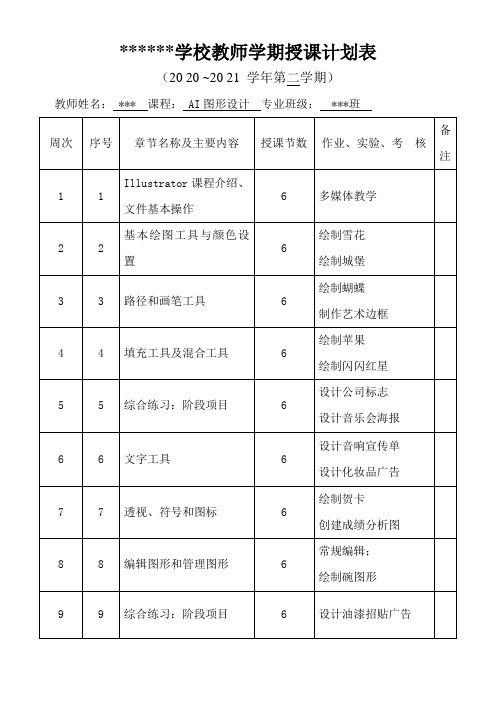
AI(Adobe illustrate图形设计)授课计划
制作艺术边框
4
4
填充工具及混合工具
6
绘制苹果
绘制闪闪红星
5
5
综合练习:阶段项目
6
设计公司标志
设计音乐会海报
6
6
文字工具
6
设计音响宣传单
设计化妆品广告
7
7
透视、符号和图标
6
绘制贺卡
创建成绩分析图
8
8
编辑图形和管理图形
6
常规编辑;
绘制碗图形
9
9
综合练习:阶段项目
6
设计油漆招贴广告
10
10
辅助功能
******学校教师学期授课计划表
(2020~2021学年第二学期)
教师姓名:***课程:AI图形设计专业班级:***班
周次
序号
章节名称及主要内容
授课节数
作业、实验、考 核
备注
1
1
IllusLeabharlann rator课程介绍、文件基本操作6
多媒体教学
2
2
基本绘图工具与颜色设置
6
绘制雪花
绘制城堡
3
3
路径和画笔工具
6
6
图层和蒙版
节目单排版
11
11
综合练习:阶段项目
6
绘制齿轮;
设计蛋糕包装
12
12
综合练习:阶段项目
6
绘制香港区徽
绘制牡丹花
13
13
效果的应用
6
制作爆炸效果
制作花卉图案
14
14
综合练习:阶段项目
6
特殊logo设计
15
15
课程简介模板

附件1:2020年湖北省中小学电脑制作活动骨干教师线上培训班课程简介一、综合课程1.《“互联网+”条件下的创意智造增智模式---2020年湖北省中小学电脑制作活动创客项目解读》。
2. 《“实践探索与创新”---2020年湖北省中小学电脑制作活动机器人项目及人工智能项目解读》。
3. 2020年湖北省电脑制作活动概述、在线培训有关要求、平台操作有关说明等。
二、通识课程(一)设计思维创意课程 ---《建模及数字加工创意设计》3Done建模及数字加工为青少年创客、机器人活动必不可少的创意设计能力,其内容包含三维创意设计及二维切割设计。
培训拟从设计思维、设计工具使用、优秀创意设计国赛获奖作品解析等层面,培训提升教师基于3D及二维设计的数字化加工技术与水平。
(二)人工智能实践课程 ---《机甲大师基础课程》机甲大师机器人项目着重培养青少年参与科技活动的兴趣,提升工程技术的实践能力。
培训课程将从机器底盘的运动控制、视觉标签识别、智能巡线、击打目标、FPV模式等知识、技能入手,系统讲解EP项目活动的详细规则、各任务模块的知识难点,并开放SDK、解锁隐藏等功能,拓展创造空间。
通过与扩展硬件(micro:bit、掌控板)连接的相关实践案例学习,提升工程实践能力。
(三)计算思维应用课程---《人工智能足球世界》本课程秉承国际上具有影响力的FIRA和RoboCup两大世界杯机器人足球赛的核心理念,融趣味性、观赏性、科普性为一体,引入全新的人机协作对抗概念,在充满变数和协作对抗的动态学习环境中,了解和掌握机器人视觉、无线通信等人工智能知识,提升计算思维的实践能力和素养。
三、赛项课程(一)创客项目课程1.《创意智造》课程本课程提供图文教程和视频教程供学员学习,配套的资源包有丰富的插件和大量的源代码程序,Arduino入门到高级项目制作,玩转蓝牙和物联网。
通过APPInventor 学习,编写Android 手机APP 程序,利用语音识别、语音合成、图像识别等技术,再通过Mind+编写单片机程序,连接Arduino 开源硬件,实现“创意智造”完成人工智能作品。
产教融合背景下开展高校人工智能师资培训的实践探索

第 6 期2021 年 6 月 10 日计算机教育Computer Education中图分类号:G642110文章编号:1672-5913(2021)06-0110-05第一作者简介:罗丽,女,在读硕士研究生,研究方向为新媒体与未来教育,****************。
产教融合背景下开展高校人工智能师资培训的 实践探索罗 丽1,涂 涛1,计湘婷2,李轩涯2(1.西南大学 教育学部,重庆 400715;2.百度在线网络技术(北京)有限公司,北京 100085)摘 要:分析高校人工智能课程建设的现状,进一步从理性层面分析校企合作开展的人工智能师资培训,再从教学实践层面探讨校企如何联合开展人工智能师资培训,最后针对目前的师资培训情况给出优化建议。
关键词:人工智能;师资培训;校企合作;教师;高校0 引 言目前世界上部分国家已经将发展人工智能作为国家战略,并着手系统布局和全面推进人工智能产业发展和人才培养。
我国人工智能行业已经进入产业化阶段,高校作为我国人工智能领域科技创新和人才培养的主要阵地,也在加快人工智能领域的人才培养,高校师资水平直接决定着人才培养的质量和高度,因此高校师资队伍的建设显得尤为重要。
1 高校人工智能课程建设的现状分析1.1 开课情况通过查阅教育局公布的普通高等学校本科专业备案和审批结果可以发现,截至2020年,共有215所高校成功申报人工智能专业,可见,申报人工智能专业已经成为国内高校的主流趋势。
为了了解高校人工智能及深度学习相关课程的开设情况,以便更好地配合学校开展教学实践和师资培训,清华大学出版社通过网络问卷调查的方式开展了调研,除了调研已备案的215所申报人工智能专业的高校,还调研了其他219所高校人工智能相关课程的开展情况,调研主要面向这些学校的人工智能、计算机及相关专业的教师,调研情况如图1所示。
值得一提的是,一些其他专业(非人工智能、计算机专业)也在积极开展其专业与人工智能学科的跨专业课程,可见高校正在火热开展人工智能课程的建设,参与调研的大部分高校(91%)都已经开设或者正在建设人工智能课程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
江西省南昌市2015-2016学年度第一学期期末试卷(江西师大附中使用)高三理科数学分析一、整体解读试卷紧扣教材和考试说明,从考生熟悉的基础知识入手,多角度、多层次地考查了学生的数学理性思维能力及对数学本质的理解能力,立足基础,先易后难,难易适中,强调应用,不偏不怪,达到了“考基础、考能力、考素质”的目标。
试卷所涉及的知识内容都在考试大纲的范围内,几乎覆盖了高中所学知识的全部重要内容,体现了“重点知识重点考查”的原则。
1.回归教材,注重基础试卷遵循了考查基础知识为主体的原则,尤其是考试说明中的大部分知识点均有涉及,其中应用题与抗战胜利70周年为背景,把爱国主义教育渗透到试题当中,使学生感受到了数学的育才价值,所有这些题目的设计都回归教材和中学教学实际,操作性强。
2.适当设置题目难度与区分度选择题第12题和填空题第16题以及解答题的第21题,都是综合性问题,难度较大,学生不仅要有较强的分析问题和解决问题的能力,以及扎实深厚的数学基本功,而且还要掌握必须的数学思想与方法,否则在有限的时间内,很难完成。
3.布局合理,考查全面,着重数学方法和数学思想的考察在选择题,填空题,解答题和三选一问题中,试卷均对高中数学中的重点内容进行了反复考查。
包括函数,三角函数,数列、立体几何、概率统计、解析几何、导数等几大版块问题。
这些问题都是以知识为载体,立意于能力,让数学思想方法和数学思维方式贯穿于整个试题的解答过程之中。
二、亮点试题分析1.【试卷原题】11.已知,,A B C 是单位圆上互不相同的三点,且满足AB AC →→=,则AB AC →→⋅的最小值为( )A .14-B .12-C .34-D .1-【考查方向】本题主要考查了平面向量的线性运算及向量的数量积等知识,是向量与三角的典型综合题。
解法较多,属于较难题,得分率较低。
【易错点】1.不能正确用OA ,OB ,OC 表示其它向量。
2.找不出OB 与OA 的夹角和OB 与OC 的夹角的倍数关系。
【解题思路】1.把向量用OA ,OB ,OC 表示出来。
2.把求最值问题转化为三角函数的最值求解。
【解析】设单位圆的圆心为O ,由AB AC →→=得,22()()OB OA OC OA -=-,因为1OA OB OC ===,所以有,OB OA OC OA ⋅=⋅则()()AB AC OB OA OC OA ⋅=-⋅-2OB OC OB OA OA OC OA =⋅-⋅-⋅+ 21OB OC OB OA =⋅-⋅+设OB 与OA 的夹角为α,则OB 与OC 的夹角为2α所以,cos 22cos 1AB AC αα⋅=-+2112(cos )22α=--即,AB AC ⋅的最小值为12-,故选B 。
【举一反三】【相似较难试题】【2015高考天津,理14】在等腰梯形ABCD 中,已知//,2,1,60AB DC AB BC ABC ==∠= ,动点E 和F 分别在线段BC 和DC 上,且,1,,9BE BC DF DC λλ==则AE AF ⋅的最小值为 .【试题分析】本题主要考查向量的几何运算、向量的数量积与基本不等式.运用向量的几何运算求,AE AF ,体现了数形结合的基本思想,再运用向量数量积的定义计算AE AF ⋅,体现了数学定义的运用,再利用基本不等式求最小值,体现了数学知识的综合应用能力.是思维能力与计算能力的综合体现. 【答案】2918【解析】因为1,9DF DC λ=12DC AB =,119199918CF DF DC DC DC DC AB λλλλλ--=-=-==, AE AB BE AB BC λ=+=+,19191818AF AB BC CF AB BC AB AB BC λλλλ-+=++=++=+,()221919191181818AE AF AB BC AB BC AB BC AB BCλλλλλλλλλ+++⎛⎫⎛⎫⋅=+⋅+=+++⋅⋅ ⎪ ⎪⎝⎭⎝⎭19199421cos1201818λλλλ++=⨯++⨯⨯⨯︒2117172992181818λλ=++≥+= 当且仅当2192λλ=即23λ=时AE AF ⋅的最小值为2918. 2.【试卷原题】20. (本小题满分12分)已知抛物线C 的焦点()1,0F ,其准线与x 轴的交点为K ,过点K 的直线l 与C 交于,A B 两点,点A 关于x 轴的对称点为D . (Ⅰ)证明:点F 在直线BD 上; (Ⅱ)设89FA FB →→⋅=,求BDK ∆内切圆M 的方程. 【考查方向】本题主要考查抛物线的标准方程和性质,直线与抛物线的位置关系,圆的标准方程,韦达定理,点到直线距离公式等知识,考查了解析几何设而不求和化归与转化的数学思想方法,是直线与圆锥曲线的综合问题,属于较难题。
【易错点】1.设直线l 的方程为(1)y m x =+,致使解法不严密。
2.不能正确运用韦达定理,设而不求,使得运算繁琐,最后得不到正确答案。
【解题思路】1.设出点的坐标,列出方程。
2.利用韦达定理,设而不求,简化运算过程。
3.根据圆的性质,巧用点到直线的距离公式求解。
【解析】(Ⅰ)由题可知()1,0K -,抛物线的方程为24y x =则可设直线l 的方程为1x my =-,()()()112211,,,,,A x y B x y D x y -,故214x my y x =-⎧⎨=⎩整理得2440y my -+=,故121244y y m y y +=⎧⎨=⎩则直线BD 的方程为()212221y y y y x x x x +-=--即2222144y y y x y y ⎛⎫-=- ⎪-⎝⎭令0y =,得1214y yx ==,所以()1,0F 在直线BD 上.(Ⅱ)由(Ⅰ)可知121244y y m y y +=⎧⎨=⎩,所以()()212121142x x my my m +=-+-=-,()()1211111x x my my =--= 又()111,FA x y →=-,()221,FB x y →=-故()()()21212121211584FA FB x x y y x x x x m →→⋅=--+=-++=-,则28484,93m m -=∴=±,故直线l 的方程为3430x y ++=或3430x y -+=213y y -===±,故直线BD 的方程330x -=或330x -=,又KF 为BKD ∠的平分线,故可设圆心()(),011M t t -<<,(),0M t 到直线l 及BD 的距离分别为3131,54t t +--------------10分 由313154t t +-=得19t =或9t =(舍去).故圆M 的半径为31253t r +== 所以圆M 的方程为221499x y ⎛⎫-+= ⎪⎝⎭【举一反三】【相似较难试题】【2014高考全国,22】 已知抛物线C :y 2=2px(p>0)的焦点为F ,直线y =4与y 轴的交点为P ,与C 的交点为Q ,且|QF|=54|PQ|.(1)求C 的方程;(2)过F 的直线l 与C 相交于A ,B 两点,若AB 的垂直平分线l′与C 相交于M ,N 两点,且A ,M ,B ,N 四点在同一圆上,求l 的方程.【试题分析】本题主要考查求抛物线的标准方程,直线和圆锥曲线的位置关系的应用,韦达定理,弦长公式的应用,解法及所涉及的知识和上题基本相同. 【答案】(1)y 2=4x. (2)x -y -1=0或x +y -1=0. 【解析】(1)设Q(x 0,4),代入y 2=2px ,得x 0=8p,所以|PQ|=8p ,|QF|=p 2+x 0=p 2+8p.由题设得p 2+8p =54×8p ,解得p =-2(舍去)或p =2,所以C 的方程为y 2=4x.(2)依题意知l 与坐标轴不垂直,故可设l 的方程为x =my +1(m≠0). 代入y 2=4x ,得y 2-4my -4=0. 设A(x 1,y 1),B(x 2,y 2), 则y 1+y 2=4m ,y 1y 2=-4.故线段的AB 的中点为D(2m 2+1,2m), |AB|=m 2+1|y 1-y 2|=4(m 2+1).又直线l ′的斜率为-m ,所以l ′的方程为x =-1m y +2m 2+3.将上式代入y 2=4x ,并整理得y 2+4m y -4(2m 2+3)=0.设M(x 3,y 3),N(x 4,y 4),则y 3+y 4=-4m,y 3y 4=-4(2m 2+3).故线段MN 的中点为E ⎝ ⎛⎭⎪⎫2m2+2m 2+3,-2m ,|MN|=1+1m 2|y 3-y 4|=4(m 2+1)2m 2+1m 2.由于线段MN 垂直平分线段AB ,故A ,M ,B ,N 四点在同一圆上等价于|AE|=|BE|=12|MN|,从而14|AB|2+|DE|2=14|MN|2,即 4(m 2+1)2+⎝ ⎛⎭⎪⎫2m +2m 2+⎝ ⎛⎭⎪⎫2m 2+22=4(m 2+1)2(2m 2+1)m 4,化简得m 2-1=0,解得m =1或m =-1, 故所求直线l 的方程为x -y -1=0或x +y -1=0.三、考卷比较本试卷新课标全国卷Ⅰ相比较,基本相似,具体表现在以下方面: 1. 对学生的考查要求上完全一致。
即在考查基础知识的同时,注重考查能力的原则,确立以能力立意命题的指导思想,将知识、能力和素质融为一体,全面检测考生的数学素养,既考查了考生对中学数学的基础知识、基本技能的掌握程度,又考查了对数学思想方法和数学本质的理解水平,符合考试大纲所提倡的“高考应有较高的信度、效度、必要的区分度和适当的难度”的原则. 2. 试题结构形式大体相同,即选择题12个,每题5分,填空题4 个,每题5分,解答题8个(必做题5个),其中第22,23,24题是三选一题。
题型分值完全一样。
选择题、填空题考查了复数、三角函数、简易逻辑、概率、解析几何、向量、框图、二项式定理、线性规划等知识点,大部分属于常规题型,是学生在平时训练中常见的类型.解答题中仍涵盖了数列,三角函数,立体何,解析几何,导数等重点内容。
3. 在考查范围上略有不同,如本试卷第3题,是一个积分题,尽管简单,但全国卷已经不考查了。
四、本考试卷考点分析表(考点/知识点,难易程度、分值、解题方式、易错点、是否区分度题)。
