平面简谐波的表达式
合集下载
10-2平面简谐波函数
y
0.1m
t t0
u x
o
y0 0.1cos(t )
解:
ห้องสมุดไป่ตู้
y0 0.1cos(t )
2
t 0
2
y
t 0
y0 0.1 cos[ (t t0 )
0.1m
t t0
2
]
u
t t0
A o
2
o x
x
x y ( x, t ) 0.1cos[ (t t0 ) ] u 2
推广至三维空间
2 2 2
2
——波函数
2
1 2 2 2 2 2 x y z u t
任何物理量 ，不管是力学量、电学量、热 普遍 意义 学量或其它的量，只要它与时间和坐标的关 系满足上述方程，这一物理量就以波的形式 传播，而偏导数 2 t 2的系数的倒数的平 方根就是这种波的传播速度。
u
M
o
x t 0 2
x
x
点P在 t 时刻的位移为
y P A cos[ t 0 2
x
]
沿OX轴正向传播的平面简谐波的波函数
x y ( x, t ) A cos[ (t ) 0 ] u
沿OX轴负向传播的平面简谐波的波函数
y
x y ( x, t ) A cos[ (t ) 0 ] u
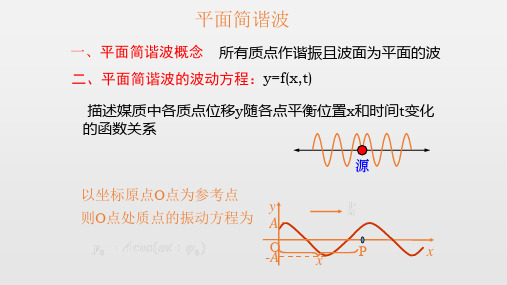
*§10.2 平面简谐波的波函数
平面简谐波：在均匀、无吸收的介质中，当波 源作简谐振动时，在介质中所形成的平面波。 一、波的表达式（波函数）
数学上如何描述简谐波？？
8-3平面简谐波的表达式
已知：波线上任一点 的振动方程 已知：波线上任一点O的振动方程 Ψ o 波速u, 波速 向右传播 求：该平面简谐波波函数 Ψ = Ψ ( x, t )
= A cos(ωt + ϕ 0 )
解： 以参考点 为坐标原点，波速u的方向为 建 以参考点O为坐标原点，波速 的方向为 的方向为+x,建 为坐标原点 立一维坐标。 为波线上任意一点， 立一维坐标。 设P为波线上任意一点，坐标 x 为波线上任意一点
= ⋯⋯
λ
1) 当 x 给定 (x = x0) 时 即x0 处质点的振动方程
x0 Ψ( x0 , t ) = Ψ(t ) = A cos[ω (t − ) + ϕ0 ] u
2) 当 t 给定 (t = t0) 时
x Ψ( x, t0 ) = Ψ( x ) = A cos[ω (t0 − ) + ϕ 0 ] u
O
x(m)
(2) 以O′为坐标原点 ′ P离参考点距离 离参考点距离
x′′ x+5 Ψ = A cos[ω (t − ) + ϕ ] = A cos[ω (t − ) +ϕ] u u
x′′ = x + 5
将xB = −13代入
− 13 + 5 8 ΨB = A cos[ω ( t − ) + ϕ ] = A cos[ω ( t + ) + ϕ ] u u
p
Ψ0 = A cos( ω t + ϕ 0 )
Ψ P (t ) = Ψ 0 (t + ∆ t ) x Ψ ( x, t ) = A cos[ω (t + ) + ϕ 0 ] u x = A cos(ωt + ϕ 0 + 2π ) λ
平面简谐波概念
解：
•
（1）T 2， 40，u 2０，A 10， 2
T
T
且t 0时：yo 5，vo 0
O
2 3
(2) OB长度
Y(cm)
10 •
u
-5 •
解：O B （O B）2
oB
C
20
-5
x(cm)
•
t 0时：yB 0，vB 0
O
-A
x
P
x
P点比O点超前时间 反向波波函数
y
O
P
x
x
以波线上x0处点为参考点
y
则Q点处质点的振动方程为 A x0 Q
O -A
x
P
x
Q点的任一振动状态传到P点，需要时间
则波动方程：
其中：x xo u
— 表示x处质元的振动落后(或超前）xo处质元
振动的时间
(
x u
xo
)
—
表示x处质元的振动落后(或超前）于xo处质元
(2)同一时刻,沿波线各质元振动状态不同,各质元相位 依次落后
*u
=
T
=
u由介质的性质决定
T T振
振 由振源决定.
得波动方程:
当x确定: y(t)——x处质元的振动方程 当t确定： y(x)——t时刻的波形
二、波的强度
1、能流P : 单位时间通过某一面积的波能 P su
—单位:焦耳/秒米2
波动在无吸收的、均匀无限大介质中传播，
1、平面波：A保持不变。
1
2
2、球面波：A与r成反比。 证明：1、 无吸收， P1 P2
14-2平面简谐波的波动方程
u
振动曲线 图形
A O
波形曲线
t A O t 0 P
t0 P
T
v
v
u x
研究 某质点位移随时间 对象 变化规律
由振动曲线可知
某时刻，波线上各质点 位移随位置变化规律
由波形曲线可知 该时刻各质点位移 波长 , 振幅A 只有t=0时刻波形才能提供初相
物理 周期 T 振幅 A 初相 0 意义
14-2 平面简谐波的波动方程
一、波函数的建立
波函数(wave function): 描述波传播媒质中不同质点的 运动规律,又称波动表达式(或波动方程).
y f x, t
依据：各质点沿波传播方 向相位依次落后. 平面波在传播过程中,波 线上的各质点都作同频率 同振幅的简谐运动—叫做 平面简谐行波(traveling wave). 波面为平面 传播中的波(相对于“驻波”而言)
x y A cos t u
(1)
P为任意点,波动表达式为
u O P( x )
x
方法2 波线上沿传播方向每走一个,相位落后2
P点相位比O落后
y P A cos(t
即
x
2π
x
y A cos(t
2π
P在 t=0 时刻过平衡位置向负向运动 ——波向左移
y(m)
0.2 O 1
t=0 P
2
yP(m) x(m)
0.2 O 0.1 0.2
t (s)
3 yO 0.2 cos(10πt π) 2 x 3 波向-x方向传播 y 0.2 cos[10 π(t ) π] 10 2 π π b) 以 P 为参考点 P yP 0 2cos( 10π t ) 2 2 波向-x方向传播 x 1 π 0 2 cos[10 π(t x ) π ] y 0 2 cos[10 π(t ) ] 10 2 10 2
平面简谐波 波动方程
3
式中x以m计。
§5-3 波的能量
能流
弹性波传播到介质中的某处，该处将具有动能和势 能。在波的传播过程中，能量从波源向外传播。
1. 波的能量
考虑棒中的体积V，其质量为m(m=V )。 当波动传播到该体积元时，将具有动能 Wk和弹性势 能Wp。
x 平面简谐波 y ( x, t ) A cos t u
在t1和t1+Δt时刻，对应的位移用x(1) 和x(2)表示，则
y(t1 )
x(1) A cos t1 0 u
x( 2) A cos t1 t 0 u
y(t1 t )
u
S
平均能流密度或波的强度 通过与波传播方向垂直的 单位面积的平均能流，用I 来表示，即
1 平均能流： P w Su uSA2 2 2
2 2 2
u
I wu u A 2 z A 2
2
波的强度
其中介质的特性阻抗 z u 。 I 的单位：瓦特/米2 (W.m-2) 平面余弦行波振幅不变的意义:
加速度
y x 2 A cos t 0 , 2 t u
2
任何物理量y ，若它与时间、坐标间的关系满足上 式，则这一物理量就按波的形式传播。
波动方程的推导
例题 频率为=12.5kHz的平面余弦纵波沿细长的金属棒传播， 棒的杨氏模量为 Y =1.91011N/m2，棒的密度 =7.6103kg/m3。 如以棒上某点取为坐标原点，已知原点处质点振动的振幅为A =0.1mm，试求:(1)原点处质点的振动表式，(2)波动表式，(3) 离原点 10cm 处质点的振动表式， (4) 离原点 20cm 和 30cm 两点 处质点振动的相位差，(5)在原点振动0.0021s时的波形。
式中x以m计。
§5-3 波的能量
能流
弹性波传播到介质中的某处，该处将具有动能和势 能。在波的传播过程中，能量从波源向外传播。
1. 波的能量
考虑棒中的体积V，其质量为m(m=V )。 当波动传播到该体积元时，将具有动能 Wk和弹性势 能Wp。
x 平面简谐波 y ( x, t ) A cos t u
在t1和t1+Δt时刻，对应的位移用x(1) 和x(2)表示，则
y(t1 )
x(1) A cos t1 0 u
x( 2) A cos t1 t 0 u
y(t1 t )
u
S
平均能流密度或波的强度 通过与波传播方向垂直的 单位面积的平均能流，用I 来表示，即
1 平均能流： P w Su uSA2 2 2
2 2 2
u
I wu u A 2 z A 2
2
波的强度
其中介质的特性阻抗 z u 。 I 的单位：瓦特/米2 (W.m-2) 平面余弦行波振幅不变的意义:
加速度
y x 2 A cos t 0 , 2 t u
2
任何物理量y ，若它与时间、坐标间的关系满足上 式，则这一物理量就按波的形式传播。
波动方程的推导
例题 频率为=12.5kHz的平面余弦纵波沿细长的金属棒传播， 棒的杨氏模量为 Y =1.91011N/m2，棒的密度 =7.6103kg/m3。 如以棒上某点取为坐标原点，已知原点处质点振动的振幅为A =0.1mm，试求:(1)原点处质点的振动表式，(2)波动表式，(3) 离原点 10cm 处质点的振动表式， (4) 离原点 20cm 和 30cm 两点 处质点振动的相位差，(5)在原点振动0.0021s时的波形。
机械波一章习题解答
5m
习题 13―7 图
X(m)
y P = A cos(ω t + ϕ )
由所给的波形图容易得到： λ = 10 m ，A=0.10m，u=20m/s，而振动的圆频率
ω=
2πu 2π × 20 = = 4π rad/s λ 10
因为波是自左向右传播的， 由此可以判断出 P 点在 t=0 时刻正在最大位移一半处 且向 Y 轴负向运动，所以， P 点振动的初位相为 ϕ = π 3 。这样，P 处介质质点 的振动方程为
Y
B P C A PX
0 (B)
习题 13─11
如图所示，为一向右传
Y
0
X
播的简谐波在 t 时刻的波形图，BC 为 波密介质的反射面，波由 P 点反射。 则反射波在 t 时刻的波形图为： ［ ］ 解：因为 BC 为波密介质的反 射面，所以在反射时有“半波损失” ， 故反射波在 P 点引起的振动与入射波 在 P 点引的振动在位相上刚好相反，
(A) y P = 0.10 cos(4πt + π 3) 。 (B) y P = 0.10 cos(4πt − π 3) 。 (C) y P = 0.10 cos(2πt + π 3) 。 (D) y P = 0.10 cos(2πt + π 6) 。 解：设 P 点处的振动方程为
u=20m/s P
y0 = A cos(ω t ′ + φ )
由 t=3s 时的波形曲线可知 A = 2 × 10 −2 m , λ = 20 m，所以
ω = 2πν =
2πu π = rad/s λ 2
t ′ = 0 时，原点处质元处于负的最大位移处，则其位相为 φ = π ，所以，
故 x=0 处的振动方程为
平面简谐波波函数
大学物理
波动学基础
第2讲 平面简谐波波函数
平面简谐波波函数
平面简谐波波函数
在均匀的、无吸收的介质中, 波源作简谐运动而形成 平面简谐波.
如何描述一维平面简谐波即建立波动表达式?其所表 示的物理意义是什么?
平面简谐波波函数
(一)波函数的建立 y = y(x，t )
任选参考点 O 为 x 轴的坐标原点, O 点处 质点的简谐运动方程 为
y
∆x
O x1
x2 x
y
=
A cos ω⎜⎛ t1 ⎝
−
x u
⎞ ⎟ ⎠
相位差为
∆ϕ
= ϕ1
−ϕ2
=
2π⎜⎛ t ⎝T
−
x1 λ
⎞ ⎟
−
2π⎜⎛
t
⎠ ⎝T
−
x2 λ
⎞ ⎟ ⎠
=
2π
x2
− λ
x1
波程差 ∆x = x2 − x1 相位差和波程差的关系： ∆ϕ = 2π ∆x
λ
平面简谐波波函数
(3)当 t , x 都变时, y = y(x, t), 表示所有质元在任意时刻 的位移情况.
解: 由图得
A = 2.5cm = 0.025m，λ = 40m，
T = 4s，ω = 2π = π s−1，u = λ = 10m ⋅s−1
y (cm )
T2
Tuv
20
5
x(m )
OP
波动表达式为
y
=
A
cos
⎡ ⎢ω ⎣
⎜⎛ t ⎝
−
x u
⎞ ⎟ ⎠
+
⎤ ϕ⎥
⎦
代入 t = 0, x = 0 , y = 0 ⇒ cosϕ = 0
波动学基础
第2讲 平面简谐波波函数
平面简谐波波函数
平面简谐波波函数
在均匀的、无吸收的介质中, 波源作简谐运动而形成 平面简谐波.
如何描述一维平面简谐波即建立波动表达式?其所表 示的物理意义是什么?
平面简谐波波函数
(一)波函数的建立 y = y(x，t )
任选参考点 O 为 x 轴的坐标原点, O 点处 质点的简谐运动方程 为
y
∆x
O x1
x2 x
y
=
A cos ω⎜⎛ t1 ⎝
−
x u
⎞ ⎟ ⎠
相位差为
∆ϕ
= ϕ1
−ϕ2
=
2π⎜⎛ t ⎝T
−
x1 λ
⎞ ⎟
−
2π⎜⎛
t
⎠ ⎝T
−
x2 λ
⎞ ⎟ ⎠
=
2π
x2
− λ
x1
波程差 ∆x = x2 − x1 相位差和波程差的关系： ∆ϕ = 2π ∆x
λ
平面简谐波波函数
(3)当 t , x 都变时, y = y(x, t), 表示所有质元在任意时刻 的位移情况.
解: 由图得
A = 2.5cm = 0.025m，λ = 40m，
T = 4s，ω = 2π = π s−1，u = λ = 10m ⋅s−1
y (cm )
T2
Tuv
20
5
x(m )
OP
波动表达式为
y
=
A
cos
⎡ ⎢ω ⎣
⎜⎛ t ⎝
−
x u
⎞ ⎟ ⎠
+
⎤ ϕ⎥
⎦
代入 t = 0, x = 0 , y = 0 ⇒ cosϕ = 0
平面简谐波的波动方程
方向的运动情况.
y
u
t 时刻
tt时刻
O
xx
x
从t时到t+∆x时 : 波线上各质点的相位均向前传播 ∆x 即:
xu t （行波）
例1 已知波动方程如下，求波长、周期和波速.
y ( 5 c) c m π [ o 2 (s - .) 1 t5 ( 0 .0 0 c- 1 s ) m 1 x ].
t
u
a 2 t2 y 2 A co (t su x )[ ]
严格区分两种速度(波速和振动速度)
波速(相速)
u
T
v y A si (n t x [ ) ]
t
u
二 波动方程的物理意义
y A co ( t x ) s ] [A c2 o π ( t s x ) [ ]
y co ( t x s ) u [ ] c2 o ( t s T x ) [] m
u2
222
2）求t1 .0 s波形图.
y 1 .0 co 2π (st[x)π ] m 2 .02 .0 2
t 1 .0 s
波形方程
y1.0coπsπ (x) m 2
1.0siπ nx)( m
波形图为 y / m
pO
2π
x
p 2 π x 2 π T x u u x ypA co ts (p)
点 P 振动方程
ypAcos(tu x)
如果原点的 初相位不为零
y A
u
x0,0 O A
x
点 O 振动方程 y O A co t s)(
波 yAco(st [x)]u沿x轴正向
动 方
yAco(st [u x)]u沿 x轴负向
u
T
y
u
t 时刻
tt时刻
O
xx
x
从t时到t+∆x时 : 波线上各质点的相位均向前传播 ∆x 即:
xu t （行波）
例1 已知波动方程如下，求波长、周期和波速.
y ( 5 c) c m π [ o 2 (s - .) 1 t5 ( 0 .0 0 c- 1 s ) m 1 x ].
t
u
a 2 t2 y 2 A co (t su x )[ ]
严格区分两种速度(波速和振动速度)
波速(相速)
u
T
v y A si (n t x [ ) ]
t
u
二 波动方程的物理意义
y A co ( t x ) s ] [A c2 o π ( t s x ) [ ]
y co ( t x s ) u [ ] c2 o ( t s T x ) [] m
u2
222
2）求t1 .0 s波形图.
y 1 .0 co 2π (st[x)π ] m 2 .02 .0 2
t 1 .0 s
波形方程
y1.0coπsπ (x) m 2
1.0siπ nx)( m
波形图为 y / m
pO
2π
x
p 2 π x 2 π T x u u x ypA co ts (p)
点 P 振动方程
ypAcos(tu x)
如果原点的 初相位不为零
y A
u
x0,0 O A
x
点 O 振动方程 y O A co t s)(
波 yAco(st [x)]u沿x轴正向
动 方
yAco(st [u x)]u沿 x轴负向
u
T
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
x2 x1 x21 12 1 2 2 π 2π
2π
x
3 若 x, t 均变化，波函数表示波形沿传播方 向的运动情况（行波）.
y
O
u
t
时刻
t t 时刻
x
x x
t x y A cos 2 π ( ) (t , x) (t t , x x) T t x t x t t x x x ut 2π ( ) 2π ( ) T T T
平面简谐波的表达式
一 平面简谐波的波函数 介质中任一质点（坐标为 x）相对其平衡位置的 位移（坐标为 y）随时间的变化关系，即 y ( x, t ) 称 为波函数.
y y ( x, t )
各质点相对平 衡位置的位移
波线上各质点 平衡位置
简谐波：在均匀的、无吸收的介质中，波源作 简谐运动时，在介质中所形成的波. 平面简谐波：波面为平面的简谐波.
x2 x1 200 cm T t2 t1 0.8 s
例2 一平面简谐波沿 O x 轴正方向传播， 已知振 幅 A 1.0m ， 2.0s ， 2.0m . 在 t 0 时坐标 T 原点处的质点位于平衡位置沿 O y 轴正方向运动 . 求 波动方程
解 写出波动方程的标准式
点 P 振动方程
x y p A cos [(t ) ] u
波 函 数
x y A cos[ (t ) ] u 沿 x 轴正向 u x y A cos[ (t ) ] u 沿 x 轴负向
u
波动方程的其它形式
t x y ( x,t ) A cos[ 2 π( ) ] T λ 2π y( x, t ) A cos(t kx ) (角波数 k )
t 0 x0
t x y A cos[ 2π ( ) ] T
π 2 y cos[π(t x) / 2]
A cos 0 2A sin 0 T
y y 0, v 0 t
作业
P266:5-5,5-7,5-9
下次内容： １．波的能量，能流密度（§５－３） ２．惠更斯原理（§５－４）
2cm 2 1 200 cm u 250 cm s T s 0.8 s T 0.01 2.5
例1 已知波动方程如下，求波长、周期和波速.
y (5cm) cosπ [(2.50s )t (0.01cm ) x].
-1 -1
解：方法二（由各物理量的定义解之）. 波长是指同一时刻 t ，波线上相位差为 2π 的两 点间的距离.
质点的振动速度，加速度
y x v A sin[ (t ) ] t u 2 y x 2 a 2 A cos[ (t ) ] t u
二
波函数的物理意义
x t x y A cos[ (t ) ] A cos[ 2 π( ) ] u T
t 时刻点 P 的运动
波函数 点 O 振动方程
x y A cos [(t ) ] u
y A
O
yo A cos[t ]
相位落后法
u
P
A
x
*
x
x 点 P 比点 O 落后的相位 p O 2 π x x x p 2π 2π Tu u
1. 当 x 固定时， 波函数表示该点的简谐运动方程， 并给出该点与点 O 振动的相位差.
x x 2 π u λ y ( x, t ) y( x, t T ) （波具有时间周期性）
波线上各点的简谐运动图
x t x y A cos[ (t ) ] A cos[ 2 π( ) ] u T
例1 已知波动方程如下，求波长、周期和波速.
y (5cm) cosπ [(2.50s )t (0.01cm ) x].
-1 -1
解：方法一（比较系数法）.
t x y A cos 2π ( ) T
把题中波动方程改写成
比较得
2.50 -1 0.01 -1 y (5cm ) cos 2π [( s )t ( cm ) x] 2 2
-1 -1 π [(2.50s )t (0.01cm-1 ) x1 ] π [(2.50s )t
(0.01cm ) x2 ] 2π
-1
x2 x1 200 cm
x2 x1 u 250 cm s 1 t2 t1
周期为相位传播一个波长所需的时间
-1 -1 π [(2.50s )t1 (0.01cm-1 ) x1 ] π [(2.50s )t2 (0.01cm-1 ) x2 ]
2 当 t 一定时，波函数表示该时刻波线上各点 相对其平衡位置的位移，即此刻的波形.
y ( x, t ) y ( x , t ) （波具有空间的周期性）
x1 t x1 1 (t ) 2 π ( ) u T x2 t x2 2 (t ) 2 π ( ) u T
以速度u 沿 x 轴正向传播的平面简谐波 为例. 令原点O 的初 相为φ其振动 方程
yO A cos(t )
时间推 迟方法
yO A cos t
点O 的振动状态
t-x/u时刻点O 的运动
点P 振动方程
x y P A cos[ (t ) ] u
x t u
点P