电阻三角形与星形的等效变换
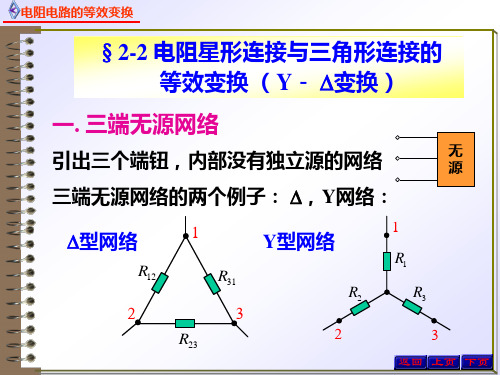
电阻星形连接与三角形连接的等效变换
i1
u12 R12
u31 R31
i2
u23 R23
u12 R12
(1)
i3
u31 R31
u23 R23
由等效条件,比较式(3)与式(1),得由Y接接的变换结果
R12
R1 R2
R2 R3 R3
R3 R1
R23
R1 R2
R2 R3 R1
R3
R1
或
R31
R1 R2
R2 R3 R2
R3
R1
d
h
b
f
a
e
c
g
b
f
返回 上页 下页
电阻电路的等效变换
d
将等电位点短接,
a
e
画出等效电路:
h
c
g
b
f
b de a
cf h
Rag
R 3
R 6
R 3
g
5
R
6
返回 上页 下页
电阻电路的等效变换
(2)求Rab
d
由电路对称性,
h
找出等电位点:
a c
b
a
e
d、e等电位
c、f等电位
g
7
f
Rab 12 R
hg
1.5 (0.6 1.4)(1 1) 2.5 0.6 1.4 1 1
求得: i 10 10 4 R 2.5
返回 上页 下页
电阻电路的等效变换
+
10V -
i1
3 2
2
1.4
3
图(a)
5 Y→△ +
4
10V
-
1
i1
3
2
2.11 星形与三角形电阻电路的等效

3
等效变换——星形与三角形电阻电路的等效
双 端
口 i1பைடு நூலகம்
网 络
i3 i2
端口v-i关系相同
i12
i1 i31 i23 i2
星形(Y)
端
v13 i1R1 i3R3
口 伏
v23 i2 R2 i3R3
安 关
i3 i1 i2
系
v13 AY i1 BY i2
v23 CY i1 DY i2
三角形(Δ)
双
端
Y
口
网
络
Y
等效关系式
R12
R1R2
R2 R3 R3
R3 R1
R23
R1R2
R2 R3 R1
R3 R1
R31
R1R2
R2 R3 R2
R3 R1
当R1 R2 R3 RY时, 得R12 R23 R31 3RY
R1
R31R12 R12+R23+R31
R2
R12 R23 R12+R23+R31
R3
R23R31 R12+R23+R31
当R12 R23 R31 R时, 得R1 R2 R3 R / 3
电工电子教学基地 电路分析教学组
1
2
3 外三内一
5
等效变换——星形与三角形电阻电路的等效 Y-Δ电阻电路等效的应用
有缘学习更多+谓ygd3076或关注桃报:奉献教育(店 铺)
电工电子教学基地 电路分析教学组
6
v13 i31R31 v23 i23R23
i31 i1 i12 i23 i2 i12
AY A , BY B CY C , DY D
等效条件
i12 (v13 v23 ) / R12
电阻的星形连接与三角形连接的等效变换

Rc2 Rc2 Rd4
I
40 51A 4060
电子发烧友 电子技术论坛
第2章 直流电阻电路的分析计算
例 2.5(六)
为了求得R1、R3、R5的电流, 从图2.10(b)求得
U a cR a I R c I2 2 5 0 4 3 1V 1
回到图2.10(a)电路, 得
I1
Uac1122.8A R1 40
I2 R2
R5 I4
I
R3
R4
R0
+ Us -
R
a
I
I2
R c
R2
R
d
R0
I4 R4
+ Us -
(a)
(b)
图2.10例2.5图 电子发烧友 电子技术论坛
第2章 直流电阻电路的分析计算
例 2.5(三)
解 将△形连接的R1, R3, R5等效变换为Y形连接的 Ra, Rc、Rd, 如图2.10(b)所示, 代入式(2.8)求得
第2章 直流电阻电路的分析计算
⒉ 三角形、星形等效的条件
端口电压U12、U23、U31 和电流I1、I2 、I3都 分别相等,则三角形星形等效。
电子发烧友 电子技术论坛
第2章 直流电阻电路的分析计算
3.已知三角形连接电阻求星形连接电阻
R1
R 12
R 12 R 31 R 23
R 31
R2
R 12
⒈三角形连接和星形连接
三角形连接:三个电阻元件首尾相接构成一
个三角形。如下图a所示。 星形连接:三个电阻元件的一端连接在一起,
另一端分别连接到电路的三个节点。如上图b所 示。
I1
I1 1
1
I12
电路原理2.2.1电阻的星形联结和三角形联结的等效变换 - 电阻星形连接与三角形连接的等效变换
返回 上页 下页
电阻电路的等效变换
由式(2)解得:
i1Y
u12Y R3 u31Y R2 R1R2 R2 R3 R3 R1
i2Y
u23Y R 1 u12Y R1R2 R2 R3
R3 R3
R1
(3)
i3Y
u31Y R2 u23Y R1 R1R2 R2 R3 R3 R1
G12
G1
G1G2 G2 G3
G23
G1
G2G3 G2 G3
G31
G1
G3G1 G2
G3返回
上页
下页
电阻电路的等效变换
由Y接 接的变换结果:
R12
R1 R2
R2 R3 R3
R3 R1
R23
R1 R2
R2 R3 R1
R3
R1
或
R31
R1 R2
R2 R3 R2
R3
R1
4
35 R1 3 2 5 1.5
32 R2 3 2 5 0.6
R3
3
2 2
5
5
1
返回 上页 下页
电阻电路的等效变换
+
10V -
i1
1.5
0.6 1
2
3
1.4
1
再用电阻串联和 并联公式,求出连接 到电压源两端单口的 等效电阻:
4
R 1.5 (0.6 1.4)//(1 1)
5 )
17
R23
(5
2+2 1+1 5
5 )
3.4;
R31
(
5
2+2 1+1 2
5 )
8.5
电阻的Y-△等效变换

等效变换的条件是:三端的电流与任何两 点之间的电压在变换前后保持相同,对外电路 的作用是完全一样的。
Y 联结转换为△联结的变换公式:
R12
R1
R2
R1 R2 R3
R23
R2
R3
R2 R3 R1
§3-8 电阻的Y-△等效变换
学习目标
掌握电阻Y-△等效变换的方法。
一、星形(Y)联结和三角形(△)联结
星形联结——把3个电 阻R1、R2、R3的一端联结 在一起,成为一个节点, 电阻的另外三端分别与电 路的不同部分联结的连接 方式,简称Y联结。
三角形联结——把3 个电阻R12、R23、R31联成 一个闭合的三角形,三角 形的三个顶点分别与电路 的不同部位相联结的联结 方式,简称△联结。
对称的Y联结和△联结的等效变换公式为:
1
RY = 3 RV
或
RV 3RY
[例3-12]
计算下图a所示电桥电路中的总电流I以及通 过桥上的电流IP。
解:由于图a所示电桥电路没有处于平衡状态,
故属于复杂直流电路,若按照一般的复杂直流电路
的解法求解非常复杂,更不能用电阻串并联的方法
求解。仔细观察不难发现,图中的三个电阻R2、R3、 R5正好构成对称的三角形接法,根据Y-△等效变 换原则,可把它们等效为星形接法,接成图b所示
的电路。其中
RY
1 3
RV
9 3
(3 )
这时原来的复杂直流电路已经等效成为简单
直流电路,此时的总电阻为:
Rcd = 15 3 / / 6 3 3=( 9 )
电阻网络中的星形三角形变换分析

电阻网络中的星形三角形变换分析在电阻网络中,星形和三角形连接是常见的连接方式。
这两种连接方式在电路分析和设计中具有重要的作用。
本文将对电阻网络中的星形三角形变换进行详细分析,以帮助读者更好地理解和应用这一概念。
一、星形连接和三角形连接简介1. 星形连接在电路中,星形连接是指将三个或更多的电阻连接在一起,其中一个节点连接到电源正极,其余节点连接到电源负极。
这种连接方式常用于电路中需要提供共地或共点的情况。
2. 三角形连接三角形连接是指将三个电阻以闭合的三角形连接方式相连。
三角形连接常用于电路中需要提供平衡电路或无共地的情况。
二、星形三角形变换原理星形三角形变换是一种将一个电路转换为与它等效的另一个电路的方法。
通过执行星形三角形变换,可以简化电路的分析和计算。
具体变换原理如下:1. 星型到三角形变换将星形连接的电阻网络转换为等效的三角形连接网络。
设星形连接的电阻为R1,R2,R3,其中节点A连接到电源正极,节点B和C连接到电源负极。
则等效的三角形连接电阻可表示为:RT = R1 * R2 / (R1 + R2 + R3)RA = R1 * R3 / (R1 + R2 + R3)RB = R2 * R3 / (R1 + R2 + R3)2. 三角形到星形变换将三角形连接的电阻网络转换为等效的星形连接网络。
设三角形连接的电阻为RT,RA,RB,其中节点A、B、C两两相连,形成闭合的三角形。
则等效的星形连接电阻可表示为:R1 = RA * RB / (RA + RB + RT)R2 = RA * RT / (RA + RB + RT)R3 = RB * RT / (RA + RB + RT)三、星形三角形变换的应用星形三角形变换在电路分析和设计中具有广泛应用,其中包括但不限于以下几个方面:1. 简化电路分析和计算通过执行星形三角形变换,可以将复杂的电路转换为等效的简化电路,从而简化电路的分析和计算。
这种方法尤其适用于涉及大量电阻和复杂连接的电路。
电阻星形联接与三角形联接的等效变换

三个电阻的一端连接在一起构成一个节点O,另一端分别为网络的三个端钮a、b、c,它们分别与外电路相连,这种三端网络叫电阻的星形联接,又叫电阻的Y 联接。
如图2.8(a)所示。
三个电阻串联起来构成一个回路,而三个连接点为网络的三个端钮a、b、c,它们分别与外电路相连,这种三端网络叫电阻的三角形联接,又叫电阻的△联接。
如图2.8(b)所示。
1、将△联接的电阻等效变换为Y联接的电阻为:
2、将Y联接的电阻等效变换为△联接的电阻为:
三个相等电阻的Y、△联接方式叫做Y、△的对称联接。
如果对称Y联接的电阻为RY,则对称△联接的等效电阻R△为:。
电阻连接的等效变换公式

电阻连接的等效变换公式在电路中,电阻是一种常见的元件,用于控制电流的流动。
在实际的电路中,常常需要对电阻的连接方式进行变换和等效处理。
通过合理的变换和等效处理,可以简化电路,使其更易于分析和计算。
本文将介绍几种常见的电阻连接方式的等效变换公式,并给出详细的说明。
1. 串联电阻的等效电阻当若干个电阻按照串联的方式连接在一起时,它们的等效电阻可以通过求和的方式计算。
假设有两个串联电阻R1和R2,则它们的等效电阻R等可以表示为:R等 = R1 + R2当有多个电阻串联时,可以逐个将它们的阻值相加,得到它们的等效电阻。
2. 并联电阻的等效电阻当若干个电阻按照并联的方式连接在一起时,它们的等效电阻可以通过倒数和求和的方式计算。
假设有两个并联电阻R1和R2,则它们的等效电阻R等可以表示为:1/R等 = 1/R1 + 1/R2当有多个电阻并联时,可以逐个将它们的阻值的倒数相加,再取倒数得到它们的等效电阻。
3. 三角形连接电阻的等效电阻在某些电路中,电阻可能按照三角形连接的方式进行连接。
对于三角形连接的电阻,其等效电阻可以通过求和和平均值的方式计算。
假设有三个三角形连接的电阻R1、R2和R3,则它们的等效电阻R 等可以表示为:R等 = (R1 + R2 + R3)/3即将三个电阻的阻值相加,再除以3得到它们的等效电阻。
4. 星形连接电阻的等效电阻在某些电路中,电阻可能按照星形连接的方式进行连接。
对于星形连接的电阻,其等效电阻可以通过求和和平方根的方式计算。
假设有三个星形连接的电阻R1、R2和R3,则它们的等效电阻R等可以表示为:1/R等 = 1/R1 + 1/R2 + 1/R3即将三个电阻的阻值的倒数相加,再取倒数得到它们的等效电阻。
除了上述的几种常见的电阻连接方式的等效变换公式外,还有一些特殊的情况需要特别注意。
比如在电路中存在有限电源电阻和无限电源电阻的情况下,等效电阻的计算方式会有所不同。
此外,在某些复杂的电路中,可能需要进行更复杂的等效变换计算,涉及到网络理论和电路分析方法。
