大连理工大学大学物理静电场习题
大学物理静电场练习题带标准答案
大学物理静电场练习题带答案————————————————————————————————作者：————————————————————————————————日期：大物练习题（一）1、如图，在电荷体密度为ρ的均匀带电球体中，存在一个球形空腔，若将带电体球心O 指向球形空腔球心O '的矢量用a 表示。
试证明球形空腔中任一点电场强度为 . A 、03ρεa B 、0ρεa C 、02ρεa D 、3ρεa2、如图所示的绝缘细线上均匀分布着线密度为λ的正电荷,两直导线的长度和半圆环的半径都等于R ．试求环中心O 点处的场强A 、02πR λε-B 、0πRλε- C 、00ln 22π4λλεε+ D 、00ln 2π2λλεε+3、 如图所示，一导体球半径为1R ,外罩一半径为2R 的同心薄导体球壳, 外球壳所带总电荷为Q ,而内球的电势为0V ，求导体球和球壳之间的电势差 （填写A 、B 、C 或D ，从下面的选项中选取）。
A 、1020214R Q V R R πε⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭ B 、102024R Q V R R πε⎛⎫- ⎪⎝⎭C 、0024Q V R πε- D 、1020214R Q V R R πε⎛⎫⎛⎫+-⎪ ⎪⎝⎭⎝⎭4.如图所示，电荷面密度为1σ的带电无限大板A 旁边有一带电导体B ，今测得导体表面靠近P 点处的电荷面密度为2σ。
求：（1）P 点处的场强 ；（2）导体表面靠近P 点处的电荷元S ∆2σ所受的电场力 。
A 、20σεB 、202σεC 、2202S σε∆D 、220S σε∆5．如图，在一带电量为Q 的导体球外，同心地包有一各向同性均匀电介质球壳，其相对电容率为r ε，壳外是真空，则在壳外P 点处(OP r =)的场强和电位移的大小分别为［ ］Q Opr)（A ）2200,44r Q QE D rr εεε==ππ； （B ）22,44r Q QE D r r ε==ππ； （C ）220,44Q QE D r r ε==ππ； （D ）2200,44Q QE D r r εε==ππ。
大连理工大学大学物理作业3(静电场三)及答案详解
作业3（静电场三）1．电场中某区域内电场线如图所示，将一点电荷从M 移到N 点则必有[ ]。
.A 电场力的功0M N A >.B 电势能M N W W >.C 电势M N U U >.D 电势M N U U <答案：【C 】解：由于静电场的无旋性，电场强度的线积分与路径无关，由M 点到N 点的线积分（即M 点与N 点之间的电势差），可以取任意路径。
现取积分路径为：由M 点到O 点，处处与电场线（电场强度方向）垂直；由O 点到N 点，处处沿着电场线。
则0=⋅=-⎰O M O M l d E U U，0>=⋅=-⎰⎰NONON O Edl l d E U U因此，M 点与N 点的电势差为0)()(>=⋅+⋅=-+-=⋅=-⎰⎰⎰⎰NONOOMN O O M N MN M Edl l d E l d E U U U U l d E U U所以，C 正确，D 错误。
由M 点到O 点，电场力所作的功为（设移动电荷量为q ）⎰⋅=-=N MN M N M l d E q U U q A)( 尽管0>⋅⎰N Ml d E，但不知q 的正负，无法判断NMA 的正负。
当0>q ，即移动正电荷时，电场力作功为正，0>NM A ；如果移动的是负电荷，电场力作功为负，0<NMA 。
电势能是静电场中的带电粒子与电场共同拥有的能量。
定义为，点电荷q 在静电场中M 点时，系统拥有的电势能为：从M 点移动电荷q 到电势零点的过程中，电场力所作的功，MM M M qUl d E q A W =⋅==⎰→0，静电势能等于电荷量与电荷所在点电势的乘积。
电场力所作的功等于静电势能的减少，静电场中M 点与N 点系统的电势能之差，等于移动点电荷q 由M 点到N 点的过程中电场力所作的功)(NM NM N M N M UU q l d E q A W W -=⋅==-⎰→尽管0>-N M U U ，但电势能之差还与电荷q 有关，不能判断N M W W -的正负。
大连理工大学大学物理作业5(静电场五)及答案详解
2．一平行板电容器中充满相对介电常数为r ε的各向同性均匀电介质。
已知介质表面极化电荷面密度为σ'±，则极化电荷在电容器中产生的电场强度的大小为[ ]。
.A0σε' .B 02σε' .C 0r σεε' .D rσε' 答案：【A 】解：极化电荷也是一种电荷分布，除不能自由移动和依赖于外电场而存在外，与自由电荷没有区别。
在产生静电场方面，它们的性质是一样的。
在电容器中，正是极化电荷的存在，产生的静电场与自由电荷产生的静电场方向相反，使得电容器中总的电场强度减弱，提高了电容器储存自由电荷的能力，电容器的电容增大。
或者说，储存等量的自由电荷，添加电介质后，电场强度减弱，电容器两极的电势差减小，电容器的电容增大。
正负极化电荷产生的电场强度的大小都是0/2εσ，方向相同，所以，极化电荷产生的电场的电场强度为0/εσ。
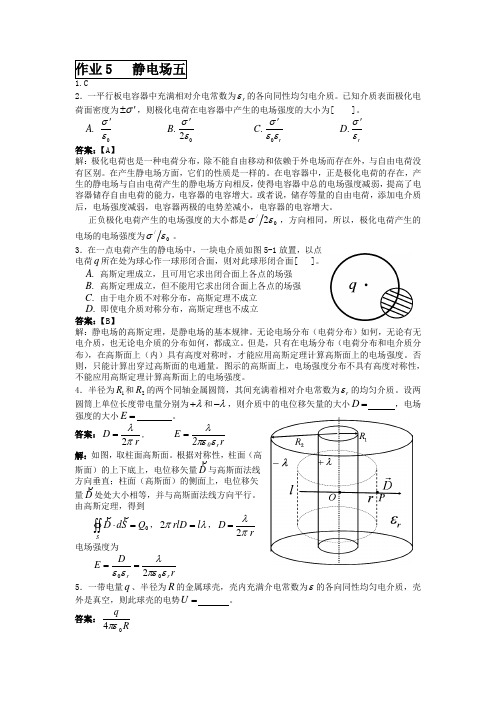
3．在一点电荷产生的静电场中，一块电介质如图5-1放置，以点电荷q 所在处为球心作一球形闭合面，则对此球形闭合面[ ]。
.A 高斯定理成立，且可用它求出闭合面上各点的场强 .B 高斯定理成立，但不能用它求出闭合面上各点的场强 .C 由于电介质不对称分布，高斯定理不成立 .D 即使电介质对称分布，高斯定理也不成立答案：【B 】解：静电场的高斯定理，是静电场的基本规律。
无论电场分布（电荷分布）如何，无论有无电介质，也无论电介质的分布如何，都成立。
但是，只有在电场分布（电荷分布和电介质分布），在高斯面上（内）具有高度对称时，才能应用高斯定理计算高斯面上的电场强度。
否则，只能计算出穿过高斯面的电通量。
图示的高斯面上，电场强度分布不具有高度对称性，不能应用高斯定理计算高斯面上的电场强度。
4．半径为1R 和2R 的两个同轴金属圆筒，其间充满着相对介电常数为r ε的均匀介质。
设两圆筒上单位长度带电量分别为λ+和λ-，则介质中的电位移矢量的大小D = ，电场强度的大小E = 。
静电场习题-参考答案
静电场习题参考答案一、选择题1C 2D 3D 4D 5B 6C 7C 8B 9D 10B 11B 12B 13C 二、填空1. 002-3E ε、0043E ε2. 06q ε3. 不变 减小4. ⎪⎪⎭⎫ ⎝⎛-π00114r r q ε5. ⎪⎭⎫ ⎝⎛-πR r Q 1140ε6.⎪⎪⎭⎫ ⎝⎛-π20114r R Qq ε7.10114q r R ε⎛⎫- ⎪π⎝⎭8. 2202dSU ε 9.204R q επ10. 2021+4q L επ（） 11. C Fd /2 FdC 212. 不变 、 减小三、计算1. 解：设杆的左端为坐标原点O ，x 轴沿直杆方向．带电直杆的电荷线密度为λ=q / L ，在x 处取一电荷元d q = λd x = q d x / L ，它在P 点的场强：()204d d x d L q E -+π=ε()204d x d L L xq -+π=ε 总场强为 ⎰+π=Lx d L xL q E 020)(d 4－ε()d L d q +π=04ε方向沿x 轴，即杆的延长线方向．Ｐ Ldd q x(L+d －d ExO2. 解：选杆的左端为坐标原点，x 轴沿杆的方向．在x 处取一电荷元λd x ，它在点电荷所在处产生场强为：()204d d x d xE +π=ελ整个杆上电荷在该点的场强为：()()l d d lx d x E l+π=+π=⎰00204d 4ελελ 点电荷q 0所受的电场力为：()ld d lq F +π=004ελ＝0.90 N 沿x 轴负向3. 解：设内球上所带电荷为Q ，则两球间的电场强度的大小为204r QE επ= (R 1＜r ＜R 2) 两球的电势差⎰⎰π==212120124d R R R R r dr Q r E U ε⎪⎪⎭⎫ ⎝⎛-π=21114R R Q ε∴ 12122104R R U R R Q -π=ε＝2.14×10-9 C4. (1)由高斯定理 024επQE r =求出 204rQ E πε=21R r R <<)11(421021R R Q Edr U R R -==⎰πε5. 解：由高斯定理当r >R 时，20141r QE πε=当r <R 时，r R Q r r R QE 302330241343441πεπππε==以无穷远处为参考点，球内离球心r 处的P 点的电势为⎰⎰⎰∞∞⋅+⋅=⋅=RR r PP l E l E l E V Pϖϖϖϖϖϖd d d 12q沿径向路径积分得32202030122)3(41d 41d 41d d R r R Q r r Qr r R Q rE r E V P R Rr RRr P PP-=⋅+⋅=⋅+⋅=⎰⎰⎰⎰∞∞πεπεπε6. 解：未插导体片时，极板A 、B 间场强为： E 1=V / d 插入带电荷q 的导体片后，电荷q 在C 、B 间产生的场强为：E 2=q / (2ε0S ) 则C 、B 间合场强为：E ＝E 1＋E 2＝(V / d )＋q / (2ε0S )因而C 板电势为： U ＝Ed / 2＝[V ＋qd / (2ε0S )] / 27. 解：应用动能定理，电场力作功等于粒子的动能增量0212-=v m qEl无限大带电平面的电场强度为： E = σ / (2ε0) 由以上两式得 σ = ε0m v 2 / (ql )8. 解：设试验电荷置于x 处所受合力为零，即该点场强为零．()()0142142020=+π-+-πx qx q εε 得 x 2－6x +1=0, ()223±=x m因23-=x 点处于q 、－2q 两点电荷之间，该处场强不可能为零．故舍去．得 ()223+=x md d。
大学物理静电场习题
习题77.1 选择题(1) 下面说法正确的是： [ ]（A ）若高斯面上的电场强度处处为零，则该面内必无电荷；（B ）若高斯面内无电荷，则高斯面上的电场强度处处为零；（C ）若高斯面上的电场强度处处不为零，则高斯面内必定有电荷；（D ）若高斯面内有净电荷，则通过高斯面的电通量必不为零；（E ）高斯定理仅适用于具有高度对称性的电场。
（2）点电荷Q 被曲面S 所包围 ， 从无穷远处引入另一点电荷q 至曲面外一点，如题7.1（2）图所示，则引入前后, ［ ］(A) 曲面S 的电场强度通量不变，曲面上各点场强不变． (B) 曲面S 的电场强度通量变化，曲面上各点场强不变． (C) 曲面S 的电场强度通量变化，曲面上各点场强变化． (D) 曲面S 的电场强度通量不变，曲面上各点场强变化． 题7.1（2）图（3）在电场中的导体内部的 [ ]（A ）电场和电势均为零； （B ）电场不为零，电势均为零；（C ）电势和表面电势相等； （D ）电势低于表面电势。
（4）两个同心均匀带电球面，半径分别为R a 和R b (R a ＜R b ), 所带电荷分别为Q a 和Q b ．设某点与球心相距r ，当R a ＜r ＜R b 时，该点的电场强度的大小为： ［ ］(A) 2014a b Q Q r ε+⋅π． (B) 2014a b Q Q rε-⋅π． (C) 22014a b b Q Q r R ε⎛⎫⋅+ ⎪⎝⎭π． (D) 2014a Q r ε⋅π．（5）如果某带电体其电荷分布的体密度增大为原来的2倍，则其电场的能量变为原来的 ［ ］(A) 2倍． (B) 1/2倍．(C) 4倍． (D) 1/4倍．7.2 填空题（1）在静电场中，电势不变的区域，场强必定为 。
（2）一个点电荷q 放在立方体中心，则穿过某一表面的电通量为 ，若将点电荷由中心向外移动至无限远，则总的电通量将 。
（3）有一个球形的橡皮膜气球，电荷q 均匀地分布在表面上，在此气球被吹大的过程中，被气球表面掠过的点(该点与球中心距离为r )，其电场强度的大小将由____________变为______．ε的均匀电介质，若测得导体表面附近电场（4）一导体外充满相对介电常量为r强度大小为E，则导体球面上的自由电荷面密度为______.（5）一平板电容器，两板间充满各向同性均匀电介质，已知相对介电常量为ε．若r极板上的自由电荷面密度为σ，则介质中电位移的大小D =____________，电场强度的大小E =____________________.7.3 电量都是q的三个点电荷，分别放在正三角形的三个顶点．试问：(1)在这三角形的中心放一个什么样的电荷，就可以使这四个电荷都达到平衡(即每个电荷受其他三个电荷的库仑力之和都为零)?(2)这种平衡与三角形的边长有无关系?7.4 两小球的质量都是m，都用长为l的细绳挂在同一点，它们带有相同电量，静止时两线夹角为2θ ,如题7.4图所示．设小球的半径和线的质量都可以忽略不计，求每个小球所带的电量．7.5 在真空中有A ，B 两平行板，相对距离为d ，板面积为S ，其带电量分别为+q 和-q ．则这两板之间有相互作用力f ，有人说f =2024dq πε,又有人说，因为f =qE ,S q E 0ε=，所以f =Sq 02ε．试问这两种说法对吗?为什么? f 到底应等于多少?7.7 (1)点电荷q 位于一边长为a 的立方体中心，试求在该点电荷电场中穿过立方体的一个面的电通量；(2)如果该场源点电荷移动到该立方体的一个顶点上，这时穿过立方体各面的电通量是多少?7.8 均匀带电球壳内半径6cm ，外半径10cm ，电荷体密度为2×510-C ·m -3求距球心5cm ，8cm ,12cm 各点的场强．7.9 半径为1R 和2R (2R ＞1R )的两无限长同轴圆柱面，单位长度上分别带有电量λ和-λ,试求:(1)r ＜1R ；(2) 1R ＜r ＜2R ；(3) r ＞2R 处各点的场强．7.10 两个无限大的平行平面都均匀带电，电荷的面密度分别为1σ和2σ，试求空间各处场强．7.11 电荷q 均匀分布在长为2L 细杆上，求在杆外延长线上与杆端距离为a 的P 点的电势（设无穷远处为电势零点）。
大连理工大学大学物理作业5(静电场五)及答案详解
作业5 静电场五2．一平行板电容器中充满相对介电常数为r ε的各向同性均匀电介质。
已知介质表面极化电荷面密度为σ'±，则极化电荷在电容器中产生的电场强度的大小为[ ]。
.A0σε' .B 02σε' .C 0r σεε' .D rσε' 答案：【A 】解：极化电荷也是一种电荷分布，除不能自由移动和依赖于外电场而存在外，与自由电荷没有区别。
在产生静电场方面，它们的性质是一样的。
在电容器中，正是极化电荷的存在，产生的静电场与自由电荷产生的静电场方向相反，使得电容器中总的电场强度减弱，提高了电容器储存自由电荷的能力，电容器的电容增大。
或者说，储存等量的自由电荷，添加电介质后，电场强度减弱，电容器两极的电势差减小，电容器的电容增大。
正负极化电荷产生的电场强度的大小都是0/2εσ，方向相同，所以，极化电荷产生的电场的电场强度为0/εσ。
3．在一点电荷产生的静电场中，一块电介质如图5-1放置，以点电荷q 所在处为球心作一球形闭合面，则对此球形闭合面[ ]。
.A 高斯定理成立，且可用它求出闭合面上各点的场强 .B 高斯定理成立，但不能用它求出闭合面上各点的场强 .C 由于电介质不对称分布，高斯定理不成立 .D 即使电介质对称分布，高斯定理也不成立答案：【B 】解：静电场的高斯定理，是静电场的基本规律。
无论电场分布（电荷分布）如何，无论有无电介质，也无论电介质的分布如何，都成立。
但是，只有在电场分布（电荷分布和电介质分布），在高斯面上（内）具有高度对称时，才能应用高斯定理计算高斯面上的电场强度。
否则，只能计算出穿过高斯面的电通量。
图示的高斯面上，电场强度分布不具有高度对称性，不能应用高斯定理计算高斯面上的电场强度。
4．半径为1R 和2R 的两个同轴金属圆筒，其间充满着相对介电常数为r ε的均匀介质。
设两圆筒上单位长度带电量分别为λ+和λ-，则介质中的电位移矢量的大小D = ，电场强度的大小E = 。
大学物理第9章静电场习题参考答案
第9章 静电场9-1 两小球处于如题9-1图所示的平衡位置时，每小球受到张力T ，重力mg 以及库仑力F 的作用，则有mg T =θcos 和F T =θsin ,∴θmgtg F =,由于θ很小，故lxmgmg mg x q F 2sin tg 41220=≈==θθπε ∴3/1022⎪⎪⎭⎫⎝⎛mg l q πε9-2 设q 1,q 2在C 点的场强分别为1E 和2E，则有210141AC r q E πε=14299m V 108.103.0108.1109--⋅⨯=⨯⨯⨯=方向沿AC 方向 220241BC r q E πε=14299m V 107.204.0108.1109--⋅⨯=⨯⨯⨯= 方向沿CB 方向∴ C 点的合场强E的大小为：24242221)107.2()108.1(⨯+⨯=+=E E E 14m V 1024.3-⋅⨯=设E 的方向与CB 的夹角为α，则有︒===--7.337.28.11211tg E E tg α 9-3 坐标如题9-3图所示，带电圆弧上取一电荷元l q d d λ=，它在圆心O 处的场强为201d 41d RlE λπε=，方向如题9-3图所示，由于对称性，上、下两带电圆弧中对应电荷元在圆心O 处产生的d E 1和d E 2在x 方向分量相互抵消。
习题9-1图习题9-3图习题9-2图0=∴x E ，圆心O 处场强E 的y 分量为⎪⎪⎭⎫⎝⎛-===⎰⎰2312sin d 412sin d 412026260R R R R lE y πελθθλπεθλπεππ方向沿y 轴正向。
9-4 （1）如题9-4图(a)，取与棒端相距d 1的P 点为坐标原点,x 轴向右为正。
设带电细棒电荷元x q d d λ=至P 点的距离x ，它在P 点的场强大小为 20d 41d x xE P λπε=方向沿x 轴正向各电荷元在P 点产生的场强方向相同，于是 ⎰⎰-+-==11)(20d 41d d L d P P xxE E πε 132289110m V 1041.2102811081103109114----⋅⨯=⎪⎭⎫⎝⎛⨯-⨯⨯⨯⨯=⎪⎪⎭⎫ ⎝⎛+-=L d d πελ方向沿x 轴方向。
大连理工大学大学物理作业4(静电场四)及答案详解
作业４ 静电场四它们离地球很远,内球壳用细导线穿过外球壳上得绝缘小孔与地连接,外球壳上带有正电荷,则内球壳上[ ]。
不带电荷 带正电 带负电荷外表面带负电荷,内表面带等量正电荷答案：【C 】解:如图,由高斯定理可知,内球壳内表面不带电。
否则内球壳内得静电场不为零。
如果内球壳外表面不带电(已经知道内球壳内表面不带电)，则两壳之间没有电场,外球壳内表面也不带电;由于外球壳带正电,外球壳外表面带正电;外球壳外存在静电场。
电场强度由内球壳向外得线积分到无限远,不会为零。
即内球壳电势不为零。
这与内球壳接地(电势为零）矛盾。
因此,内球壳外表面一定带电。
设内球壳外表面带电量为(这也就就是内球壳带电量),外球壳带电为，则由高斯定理可知,外球壳内表面带电为,外球壳外表面带电为。
这样,空间电场强度分布,(两球壳之间：) ,(外球壳外:)其她区域（,）,电场强度为零。
内球壳电势为041)11(4ˆ4ˆ4)()(403202020214324322=++-=⋅++⋅=⋅+⋅=⋅=⎰⎰⎰⎰⎰∞∞∞R Qq R R q r d r rQq r d rr q r d r E r d r E l d E U R R R R R R R πεπεπεπε则,由于,,所以即内球壳外表面带负电,因此内球壳负电。
2.真空中有一组带电导体,其中某一导体表面某处电荷面密度为,该处表面附近得场强大小为,则。
那么,就是［ ］。
该处无穷小面元上电荷产生得场 导体上全部电荷在该处产生得场 所有得导体表面得电荷在该处产生得场 以上说法都不对 答案:【C 】解:处于静电平衡得导体，导体表面附近得电场强度为,指得就是:空间全部电荷分布，在该处产生得电场,而且垂直于该处导体表面。
注意:由高斯定理可以算得，无穷小面元上电荷在表面附近产生得电场为；无限大带电平面产生得电场强度也为,但不就是空间全部电荷分布在该处产生得电场。
3.一不带电得导体球壳半径为，在球心处放一点电荷。
大连理工大学大学物理静电场习题-推荐下载
带
电细线，弯成图示形状，若圆弧半径为 R ，试求 O 点的场强。
8．一个金属球带上正电荷后，质量有所增大？减小？不变？
9．以点电荷为中心，半径为 R 的球面上，场强的大小一定处处相等吗？
对全部高中资料试卷电气设备，在安装过程中以及安装结束后进行高中资料试卷调整试验；通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术通关，1系电过，力管根保线据护敷生高设产中技工资术艺料0不高试仅中卷可资配以料置解试技决卷术吊要是顶求指层，机配对组置电在不气进规设行范备继高进电中行保资空护料载高试与中卷带资问负料题荷试2下卷2，高总而中体且资配可料置保试时障卷，各调需类控要管试在路验最习；大题对限到设度位备内。进来在行确管调保路整机敷使组设其高过在中程正资1常料中工试，况卷要下安加与全强过，看度并22工且22作尽22下可22都能22可地护以缩1关正小于常故管工障路作高高；中中对资资于料料继试试电卷卷保破连护坏接进范管行围口整，处核或理对者高定对中值某资，些料审异试核常卷与高弯校中扁对资度图料固纸试定，卷盒编工位写况置复进.杂行保设自护备动层与处防装理腐置，跨高尤接中其地资要线料避弯试免曲卷错半调误径试高标方中高案资等，料，编试要5写、卷求重电保技要气护术设设装交备备置底4高调、动。中试电作管资高气，线料中课并敷3试资件且、设卷料中拒管技试试调绝路术验卷试动敷中方技作设包案术，技含以来术线及避槽系免、统不管启必架动要等方高多案中项；资方对料式整试，套卷为启突解动然决过停高程机中中。语高因文中此电资，气料电课试力件卷高中电中管气资壁设料薄备试、进卷接行保口调护不试装严工置等作调问并试题且技，进术合行，理过要利关求用运电管行力线高保敷中护设资装技料置术试做。卷到线技准缆术确敷指灵设导活原。。则对对：于于在调差分试动线过保盒程护处中装，高置当中高不资中同料资电试料压卷试回技卷路术调交问试叉题技时，术，作是应为指采调发用试电金人机属员一隔，变板需压进要器行在组隔事在开前发处掌生理握内；图部同纸故一资障线料时槽、，内设需，备要强制进电造行回厂外路家部须出电同具源时高高切中中断资资习料料题试试电卷卷源试切，验除线报从缆告而敷与采设相用完关高毕技中，术资要资料进料试行，卷检并主查且要和了保检解护测现装处场置理设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况，然后根据规范与规程规定，制定设备调试高中资料试卷方案。
大连工大静电场习题
静电场一．选择题（每题3分）1．一电场强度为E的均匀电场，E的方向与X轴正向平行如图所示，则通过图中一半径为R的半球面的电场强度通量为[ ]。
（A）πR2E (B) 1/2πR2E (C)2πR2E (D) 0X2．真空中有一均匀带电球体和一均匀带电球面，如果它们的半径和所带的电量都相等，则它们的静电能之间的关系是[ ]。
（A）球体的静电能等于球面的静电能。
（B）球体的静电能大于球面的静电能。
（C）球体的静电能小于球面的静电能。
（D）球体内的静电能大于球面内的静电能，球体外的静电能小于球面外的静电能。
3．已知一高斯面所包围的体积内的电量的代数和∑q=0，则可肯定[ ]（A）高斯面上各点的场强均为零。
（B）穿过高斯面上每一面元的电通量均为零。
（C）穿过整个高斯面的电通量为零。
（D）以上说法都不对。
4．如图所示，各图中所有电荷均与原点等距，且电量相等。
设无穷远为零电势，则各图中电势和场强均为零的是[ ]。
+q +q +q +q+q -q –q -q –q -q +q +q-q -q +q +q （A）图1 （B）图2 （C）图3 （D）图45．一均匀带电球面，若球内电场强度处处为零，则球面上带电量为σds的面元在球面内产生的电场强度是[ ] 。
（A）处处为零（B）不一定为零（C）一定不为零（D）是常数6．在一个点电荷+Q的电场中，一个检验电荷+q，从A点分别移到B，C，D 点，B，C，D点在+Q为圆心的圆周上，如图所示，则电场力做功是[ ]。
（A ） 从A 到B 电场力做功最大。
（B ） 从A 到C 电场力做功最大。
（C ） 从A 到D 电场力做功最大。
B （D ） 电场力做功一样大。
7．空心导体球壳，外半径为R 2，内半径为R 1，中心有点电荷q ，球壳上总电荷q ，以无穷远处为电势零点，则导体壳的电势为[ ]。
（A ）0114q R πε（B ）0214q R πε （C ）01124q R πε （D ）02124qR πε8．平行板电容器极板上每单位面积受到的静电力F 与加在电容器两极板间的电压V 的关系是 [ ]。
大学物理静电场练习题带答案
大物练习题（一）1、如图，在电荷体密度为ρ的均匀带电球体中，存在一个球形空腔，若将带电体球心O 指向球形空腔球心O '的矢量用a 表示。
试证明球形空腔中任一点电场强度为 . A 、03ρεa B 、0ρεa C 、02ρεa D 、3ρεa2、如图所示的绝缘细线上均匀分布着线密度为λ的正电荷,两直导线的长度和半圆环的半径都等于R ．试求环中心O 点处的场强A 、02πR λε-B 、0πRλε- C 、00ln 22π4λλεε+ D 、00ln 2π2λλεε+3、 如图所示，一导体球半径为1R ,外罩一半径为2R 的同心薄导体球壳, 外球壳所带总电荷为Q ,而内球的电势为0V ，求导体球和球壳之间的电势差 （填写A 、B 、C 或D ，从下面的选项中选取）。
A 、1020214R Q V R R πε⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭ B 、102024R Q V R R πε⎛⎫- ⎪⎝⎭C 、0024Q V R πε- D 、1020214R Q V R R πε⎛⎫⎛⎫+- ⎪ ⎪⎝⎭⎝⎭4.如图所示，电荷面密度为1σ的带电无限大板A 旁边有一带电导体B ，今测得导体表面靠近P 点处的电荷面密度为2σ。
求：（1）P 点处的场强 ；（2）导体表面靠近P 点处的电荷元S ∆2σ所受的电场力 。
A 、20σεB 、202σεC 、2202S σε∆D 、220S σε∆5．如图，在一带电量为Q 的导体球外，同心地包有一各向同性均匀电介质球壳，其相对电容率为r ε，壳外是真空，则在壳外P 点处(OP r =)的场强和电位移的大小分别为［ ］（A ）2200,44r Q QE D rr εεε==ππ； （B ）22,44r Q QE D r r ε==ππ； （C ）220,44Q QE D r r ε==ππ； （D ）2200,44Q QE D r r εε==ππ。
6、在一点电荷产生的静电场中，一块电介质如图放置，以点电荷所在处为球心作一球形闭合面，则对此球形闭合面： （A ）高斯定理成立，且可用它求出闭合面上各点的场强；（B ）高斯定理成立，但不能用它求出闭合面上各点的场强； （C ）由于电介质不对称分布，高斯定理不成立； （D ）即使电介质对称分布，高斯定理也不成立。
大连理工大学大学物理作业5(静电场五)及答案详解
2．一平行板电容器中充满相对介电常数为r ε的各向同性均匀电介质。
已知介质表面极化电荷面密度为σ'±，则极化电荷在电容器中产生的电场强度的大小为[ ]。
.A0σε' .B 02σε' .C 0r σεε' .D rσε' 答案：【A 】解：极化电荷也是一种电荷分布，除不能自由移动和依赖于外电场而存在外，与自由电荷没有区别。
在产生静电场方面，它们的性质是一样的。
在电容器中，正是极化电荷的存在，产生的静电场与自由电荷产生的静电场方向相反，使得电容器中总的电场强度减弱，提高了电容器储存自由电荷的能力，电容器的电容增大。
或者说，储存等量的自由电荷，添加电介质后，电场强度减弱，电容器两极的电势差减小，电容器的电容增大。
正负极化电荷产生的电场强度的大小都是0/2εσ，方向相同，所以，极化电荷产生的电场的电场强度为0/εσ。
3．在一点电荷产生的静电场中，一块电介质如图5-1放置，以点电荷q 所在处为球心作一球形闭合面，则对此球形闭合面[ ]。
.A 高斯定理成立，且可用它求出闭合面上各点的场强 .B 高斯定理成立，但不能用它求出闭合面上各点的场强 .C 由于电介质不对称分布，高斯定理不成立 .D 即使电介质对称分布，高斯定理也不成立答案：【B 】解：静电场的高斯定理，是静电场的基本规律。
无论电场分布（电荷分布）如何，无论有无电介质，也无论电介质的分布如何，都成立。
但是，只有在电场分布（电荷分布和电介质分布），在高斯面上（内）具有高度对称时，才能应用高斯定理计算高斯面上的电场强度。
否则，只能计算出穿过高斯面的电通量。
图示的高斯面上，电场强度分布不具有高度对称性，不能应用高斯定理计算高斯面上的电场强度。
4．半径为1R 和2R 的两个同轴金属圆筒，其间充满着相对介电常数为r ε的均匀介质。
设两圆筒上单位长度带电量分别为λ+和λ-，则介质中的电位移矢量的大小D = ，电场强度的大小E = 。
大学物理第五章 静电场部分的习题及答案
第五章 静电场一、简答题1、为什么在无电荷的空间里电场线不能相交?答案：由实验和理论知道，静电场中任一给定点上，场强是唯一确定的，即其大小和方向都是确定的．用电场线形象描述静电场的空间分布时，电场线上任一点的切线方向表示该点的场强方向．如果在无电荷的空间里某一点上有几条电场线相交的话，则过此交点对应于每一条电场线都可作出一条切线，这意味着交点处的场强有好几个方向，这与静电场中任一给定点场强具有唯一确定方向相矛盾，故无电荷的空间里电场线不能相交．2、简述静电场中高斯定理的文字内容和数学表达式。
答案：在真空中的静电场内，通过任意封闭曲面的电通量等于该封闭曲面所包围的所有电荷电量的代数和的01ε倍。
0ε∑⎰=⋅内S Sq S d E3、写出静电场的环路定理，并分别说明其物理意义。
答案：静电场中，电场强度的环流总是等于零(或0l=⋅⎰l d E )，静电场是保守场。
4、感生电场与静电场有哪些区别和联系?二、选择题1、如图所示，两个同心均匀带电球面，内球面半径为1R 、带有电荷1Q ，外球面半径为2R 、带有电荷2Q ，则在外球面外面、距离球心为r 处的P 点的场强大小E 为 ( A ) A.20214r Q Q επ+ B.()()2202210144R r Q R r Q -π+-πεε C.()2120214R R Q Q -+επ D.2024r Q επ 2、半径为R 的均匀带电球体的静电场中各点的电场强度的大小E 与距球心的距离r 的关系曲线为：( B )3、图示一均匀带电球体，总电荷为Q +，其外部同心地罩一内、外半径分别为1r 、2r 的金属球壳．设无穷远处为电势零点，则在球壳内半径为r 的P 点处的场强和电势为： ( D )A.204r QE επ=，r Q U 04επ= B.0=E ，104r Q U επ= C. 0=E ，r Q U 04επ=D.0=E ，204r Q U επ= 4、图中实线为某电场中的电场线，虚线表示等势(位)面，由图可看出：( D )A.C B A E E E >>，C B A U U U >>B.C B A E E E <<，C B A U U U <<C.C B A E E E >>，C B A U U U <<D.C B A E E E <<，C B A U U U >>5、面积为S 的空气平行板电容器，极板上分别带电量q ±，若不考虑边缘效应，则两极板间的相互作用力为 ( B )A.S q 02εB.S q 022εC.2022S q εD.202Sq ε 6、一均匀带电球面在球面内各处产生的场强 ( A )A.处处为零B.不一定为零C.一定不为零D.是常数7、已知一高斯面所包围的体积内电量代数和0=∑i q ，则可肯定：( C )A.高斯面上各点场强均为零B.穿过高斯面上每一面元的电通量均为零C.穿过整个高斯面的电通量为零D.以上说法都不对8、下列说法中正确的是 ( D )A.电场强度为0的点，电势也一定为0.B.电场强度不为0的点，电势也一定不为0.C.电势为0的点，则电场强度也一定为0.D.电势在某一区域为常数，则电场强度在该区域也必定为0.9、如图所示，一个带电量为q 的点电荷位于正立方体的中心上，则通过其中一侧面的电场强度通量等于 ( B )：A.04εqB.06εqC.06πεqD.04πεq 三、计算题1、两无限长同轴圆柱面，半径分别为1R 和2R (21R R < )，带有等量异号电荷，单位长度的电量为λ和λ-，求：(1) 1R r <；(2)21R r R <<；(3)r R <2处各点的场强。
《大学物理》静电场习题
S
d
+
=
E3
S
E3
S
ε
0
（3）
7-30 设电势沿 x 轴的变化 曲 线如图所示。试对所示各区间（忽略区间端点的情况）确定电场强度的x分量，并作出 Ex 对 x 的关系图线。
a
g
f
h
e
c
b
d
5
-5
6
12
-12
-6
V/V
x/m
o
-5
-7
<
<
x
-5
-2
x
<
<
-2
2
x
<
<
U
Δ
Ex
=
x
Δ
=-
= -6V/m
01
式中r是到圆柱轴线的距离， ρ0是轴线处的电荷体密度，a 是常量。试计算其场强分布。
02
解：先计算高斯面内的电量
r
dr
由高斯定律：
例2 有一瓦楞状直长均匀带电薄板，面电荷密度为σ,瓦楞的圆半径为 a 试求：轴线中部一点P 处的电场强度。 a L P
解：
q
x
y
o
d
E
d
q
q
a
a
L
l
d
P
.
L
Φ
.
E
S
=
解：（1）
z
x
y
d
o
d
d
d
（2）
7-19 一层厚度为d =0.5cm的无限大平板，均匀带电，电荷体密度为ρ =1.0×10-4 C/m3 。求: （1）这薄层中央的电场强度； （2）薄层内与其表面相距0.1cm处的电场强 度； （3）薄层外的电场强度。
大连理工大学大学物理作业6(静电场六)及答案详解
作业6 静电场六它们的静电能之间的关系是[ ]。
.A 球体的静电能等于球面的静电能 .B 球体的静电能大于球面的静电能 .C 球体的静电能小于面的静电能.D 球体内的静电能大于球面内的静电能，球体外的静电能小于球面外的静电能 答案：【B 】解：设带电量为Q 、半径为R ，球体的电荷体密度为ρ。
由高斯定理，可以求得两种电荷分布的电场强度分布022επQ E r S d E S==⋅⎰⎰，2002r Q E επ=对于球体电荷分布：03223402031>==ερεπρπr rr E ，（R r <）；2022r Q E επ=，（R r >）。
对于球壳电荷分布：0/1=E ，（R r <）；20/22rQ E επ=，（R r >）。
可见，球外：两种电荷分布下，电场强度相等；球内：球体电荷分布，有电场，球壳电荷分布无电场。
静电场能量密度2021E εω=两球外面的场强相同，分布区域相同，故外面静电能相同；而球体(并不是导体)内部也有电荷分布，也是场分布，故也有静电能。
所以球体电荷分布时，球内的静电场能量，大于球面电荷分布时，球内的静电场能量；球体电荷分布时，球外的静电场能量，等于球面电荷分布时，球外的静电场能量。
2．1C 和2C 两空气电容器串联起来接上电源充电，然后将电源断开，再把一电介质板插入1C 中，如图6-1所示，则[ ]。
.A 1C 两端电势差减少，2C 两端电势差增大.B 1C 两端电势差减少，2C 两端电势差不变 .C 1C 两端电势差增大，2C 两端电势差减小 .D 1C 两端电势差增大，2C 两端电势差不变答案：【B 】解：电源接通时，给两个串联的电容器充电。
充电量是相同的，是为Q 。
则两个电容器的电压分别为11C Q U =，22C Q U = 电源断开后，1C 插入电介质，两个电容器的电量不变，仍然都是Q 。
但1C 的电容增大，因此1C 两端的电压降低；而2C 不变，因此，2C 两端的电压不变。
大连理工大学大学物理作业4(静电场四)及答案详解
作业4 静电场四导线穿过外球壳上的绝缘小孔与地连接，外球壳上带有正电荷，则内球壳上[ ]。
.A 不带电荷.B 带正电 .C 带负电荷.D 外表面带负电荷，内表面带等量正电荷答案：【C 】解：如图，由高斯定理可知，内球壳内表面不带电。
否则内球壳内的静电场不为零。
如果内球壳外表面不带电（已经知道内球壳内表面不带电），则两壳之间没有电场，外球壳内表面也不带电；由于外球壳带正电，外球壳外表面带正电；外球壳外存在静电场。
电场强度由内球壳向外的线积分到无限远，不会为零。
即内球壳电势不为零。
这与内球壳接地（电势为零）矛盾。
因此，内球壳外表面一定带电。
设内球壳外表面带电量为q （这也就是内球壳带电量），外球壳带电为Q ，则由高斯定理可知，外球壳内表面带电为q -，外球壳外表面带电为Q q +。
这样，空间电场强度分布r r qr E ˆ4)(201πε=，（两球壳之间：32R r R <<）r r Qq r E ˆ4)(202πε+= ，（外球壳外：r R <4）其他区域（20R r <<，43R r R <<），电场强度为零。
内球壳电势为041)11(4ˆ4ˆ4)()(403202020214324322=++-=⋅++⋅=⋅+⋅=⋅=⎰⎰⎰⎰⎰∞∞∞R Q q R R q r d r rQq r d r r q r d r E r d r E l d E U R R R R R R R πεπεπεπε则04432=++-R QR q R q R q ，4324111R R R R Q q +--=由于432R R R <<，0>Q ，所以0<q即内球壳外表面带负电，因此内球壳负电。
2．真空中有一组带电导体，其中某一导体表面某处电荷面密度为σ，该处表面附近的场强大小为E ，则0E σ=。
那么，E 是[ ]。
.A 该处无穷小面元上电荷产生的场 .B 导体上全部电荷在该处产生的场 .C 所有的导体表面的电荷在该处产生的场 .D 以上说法都不对答案：【C 】解：处于静电平衡的导体，导体表面附近的电场强度为0E σ=，指的是：空间全部电荷分布，在该处产生的电场，而且垂直于该处导体表面。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
05静电场11.关于电场强度定义式，下列说法中哪个是正确的？[]vA. 场强E的大小与试探电荷q0的大小成反比。
一vB. 对场中某点，试探电荷受力F与q0的比值不因q0而变。
C. 试探电荷受力F的方向就是场强E的方向。
D. 若场中某点不放试探电荷q0,则F 0，从而E 0。
2.一个质子，在电场力作用下从A点经C点运动到B点，其运动轨迹如图所示，已知质点运动的速率是递增的，下面关于C点场强方向的四个图示哪个正确？[]3.带电量均为q的两个点电荷分别位于X轴上的a和a位置，如图所示，则v丫轴上各点电场强度的表示式为E = ______ ,场强最大值的位置在y ______ 。
4.如图所示，在一无限长的均匀带点细棒旁垂直放置一均匀带电的细棒MN。
且二棒共面，若二棒的电荷线密度均为，细棒MN长为I，且M端距长直细棒也为I，那么细棒MN受到的电场力为。
+ J IM+2 N1J_ I \+ 久dq = XdxM NI J I j ¥ E 5 o■X dx£y十g十9----- ■—.-a O+Q X5.用不导电的细塑料棒弯成半径为R的圆弧，两端间空隙为II R，若正电荷Q均匀分布在棒上，求圆心处场强的大小和方向。
Q，下半段均6.如图所示，将一绝缘细棒弯成半径为R的半圆形，其上半段均匀带有电荷& 一个金属球带上正电荷后，质量有所增大？减小？不变?9.以点电荷为中心，半径为 R 的球面上，场强的大小一定处处相等吗?7.线电荷密度为 点的场强。
的“无限长”均匀带电细线，弯成图示形状，若圆弧半径为R ，试求O0 i05静电场21 .如图所示，把点电荷q 从高斯面外 P 移到R 处OP OR , O 为S 上一点，贝U []vA. 穿过S 的电通量e 发生改变，0处E 变v vB. e 不变，E 变。
C. e 变，E 不变。
D. e 不变， VE 不变。
2.半径为R 的均匀带电球面上，电荷面密度为 ， 球面上取小面元 S ，则 S 上的电荷受到的电场力为 []。
&如果高斯面内没有净电荷，能否断定高斯面上E 一定处处为零?v v 19.- E dS — Q j 表明静电场具有什么性质?B.二2 0 03.如图所示，一个带电量为 q 的点电荷位于立方体的 则通过侧面abed 的电场强度通量等于[]。
A.且 6 0 A. 0 C. D. A 角上,B. q12 02S4 0R 2ad7 \bqc/ ___q 48 oC.旦 24 04. 一半径为R 长为L 的均匀带电圆柱面， 其单位长度带电量为 ，在带电圆柱的中垂面上有一点 P ，它到轴线距离为r r ______ ，当r L 时， ，当r L 时，E 。
半径为R 的不均匀带电球体，电荷体密度分布为 R , A 为常数，则球体上的总电量 Q _________ 。
如果点电荷Q 只受电场力作用而运动，其轨迹是否就是电场线? 6. D. R ，则P 点的电场强度的大 Ar ，式中r 为离球心的距离 7.10.如图所示，一质量m 1.6 10 6kg的小球，带电= 11量q 2 10 C，悬于一丝线下端，丝线与一块很大的带电平面成30角。
若带电平面上电荷分布均匀，q很小，不影响带电平面上的电荷分布，求带电平面上的电荷面密度。
11.大小两个同心球面，半径分别为R1,R2R R ，小球上带有电荷q q 0，大球上带有电荷Q Q 0。
试分别求出r R1, r R2, R) r R2时，离球心O为r处的电场强度。
12.两个无限长同轴圆柱面，半径分别为R i和R2R2 R，带有等值异号电荷，每单位长度的电量为（即电荷线密度）。
试分别求出r R,r R2,R I r R2时，离轴线为r处的电荷密度。
13.半径为R、电荷体密度为的均匀带电球体内部，有一个不带电的球形空腔，空腔半径为R/，其中心0, 到球心0的距离为a ,如图所示，求00,的延长线上距球心0为r处的电场强度。
05静电场31.电场中某区域内电场线如图所示，将一点电荷从 必有［］。
A. 电场力的功A MN 0 B. 电势能W M W N C. 电势U M U N D. 电势U M U N 2•图中，A 、B 是真空中的两块相互平行的无限大均匀带电平 面，电荷面密度分别为 a 点的电势是［ 3 d M 移到N 点则AN则图中 和 2 ，若将A 板选作电势零点,。
：-2o-A. C.B.」D.刽的电偶极子放在场强为。
求此电偶极子绕垂直于 2 03. 一偶极矩为p ql 中，p 与E 的夹角为 的过程中，电场力做的功。
4. 均匀带电球面，半径为 R ，电荷面密度为 E 的均匀外电场 (p,E)平面的轴沿 增加的方向转过1800 。
试求离球心为r 处一点P 的电势。
设1 P 点在球内。
2 P 点在球面上。
(3) P 点在球面外。
5.一个有小孔的均匀带电球面，所带电荷面密度为，球面半径为R ,小孔面积S 球面面积，则球心处的电场强度E ____________ ；球心处的电势U __________ 。
6.如图所示，两个同心球面。
内球面半径为R1，均匀带电荷Q ;外球面半径为R2，是一个非常薄的导体壳，原先不带电，但与地相连接。
设地为电势零点，求在两球面之间、距离球心为r处的的P点的电场强度及电势。
7.电荷Q均匀分布在半径为R的球体内，试求离球心r处r R的电势。
&半径为R的圆弧ab，所对圆心角，如图所示，圆弧均匀带正电，电荷线密度为试求圆弧中心处的电场强度和电势。
9. 一圆盘，半径R 8.0 10 2m，均匀带电，面密度1求轴线上任一点的电势（该点与盘心的距离为x ）。
2由场强与电势梯度的关系，求该点电场强度。
3计算x 6.0 10 2m的电势和场强。
10.：：• E dl 0表明静电场具有什么性质?L11.电势为零的空间场强一定为零吗?12.电场强度为零的空间电势一定为零吗?52.0 10 5C m静电场41如图所示，两个同心金属球壳，它们离地球很远，内球壳用细导线穿过外球壳上的绝缘小孔与地连接，外球壳上带有正电荷，则内球壳上［］。
A. 不带电荷B. 带正电C. 带负电荷D. 外表面带负电荷，内表面带等量正电荷2.真空中有一组带电导体，其中某一导体表面某处电荷面密度为，该处表面附近的场强大小为E，贝U E 0。
那么，E是［A. 该处无穷小面元上电荷产生的场B.导体上全部电荷在该处产生的场C.所有的导体表面的电荷在该处产生的场D.以上说法都不对3.一不带电的导体球壳半径为R，在球心处放一点电荷。
测得球壳内外的电场。
然后将此点电荷移至距球心R 2处，重新测量电场。
则电荷的移动对电场的影响为［］。
A.对球壳内外电场无影响B.球壳内电场改变，球壳外电场不变C.球壳内电场不变，球壳外电场改变D.球壳内外电场均改变4.半径分别为R及r的两个球形导体r R，用一根很长的细导线将它们连接起来（即两球相距很远），使两个导体带电，则两球表面电荷面密度的比值大球「小球为［］。
A % B% C. % D%5.一面积为S，间距为d 的平行板电容器，若在其中平行插入厚度为 d 2的导体板，则电容为________ 。
6. ___________________________________________________________________________ 两个同心导体球壳，内球壳带电Q ,外球壳原不带电，则现外球壳内表面电量__________________ , 外球壳外表面电量_________ ，外球壳外P点总场强 ___________ 。
Q答案：0内=—Q , Q外=Q , E - ?40r OP7.在一大块金属导体中挖去一半径为R的球形空腔，球心处有一点电荷q。
空腔内一点A到球心的距离为r A，腔外金属块内有一点B，到球心的距离为r B，如图所示。
求代B两点的电场强度。
a,相隔距离为&试计算两根带异号的平行导线单位长度的电容。
假设导线的半径为d d a，导线为无限长，电荷均匀分布。
9.有两个无限大平行面带电导体板，如图所示。
1证明：相向的两面上，电荷面密度总是大小相等而符号相反；相背的两面上，电荷面密度总是大小相等而符号相同。
2若左导体板带电3C m 2,右导体板带电7C m 2,求四个表面上的电荷面密度。
10.将一个中性的导体放在静电场中，导体上感应出来的正负电荷的电量是否一定相等，这时导体是否为等势体？若在电场中将此导体分为分别带正负电的两部分，两者的电势是否仍相等？11.孤立导体带电量Q，其表面附近的场强方向如何？当将另一带电体移近导体时，其表面附近的场强方向有什么变化？导体内部的场强有无变化？，是否可以为系统不带电时电容为零?12.根据电容的定义C QU圆筒上单位长度带电量分别为 和，则介质中的电位移矢量的大小D _____ ，电场强度的大小E ________ 。
5. 一带电量q 、半径为R 的金属球壳，壳内充满介电常数为 的各向同性均匀电介质，壳外是真空，则此球壳的电势 U ________ 。
6.两个点电荷在真空中相距为 r i 时的相互作用力等于在某一“无限大”均匀电介质中相距为「2时的相互作用力，则该电介质的相对介电常数r _____________ 。
7. 半径为R 的均匀带电金属球壳里充满了均匀、各向同性的电介质，球外是真空，此球壳 的电势是否为 ―—?为什么？静电场51.在点电荷—q 的周围，包围了一个有限大的均 匀介质球，其相对介电常数为球心处，如图所示， 的场强大小为[ 那么，球内 A. B. C. D. q E B q 42 >J A4 0 2r rBqE Bq42 ； J A 42 r r BqE Bq42 ；J A4 0 2r rBqE Bq4 02 ；J A42 r r B2.在一点电荷产生的静电场中，一块电介质如图放置，以点电荷 q 所在处为球心作一球形闭合面，则对此球形闭合面[]A. 高斯定理成立，且可用它求出闭合面上各点的场强B. 高斯定理成立，但不能用它求出闭合面上各点的场强C. 由于电介质不对称分布，高斯定理不成立3. 一平行板电容器中充满相对介电常数为 r 的各向同性均匀电介质。
已知介质表面极化电荷面密度为，则极化电荷在电容器中产生的电场强度的大小为 []A.—B. C.——0 r4.半径为R 和R 2的两个同轴金属圆筒，其间充满着相对介电常数为D.—rr 的均匀介质。
设两]。
E A E AE A E A r ，点电荷位于A点与球外B 点&有一同轴电缆，内、外导体用介电系数分别为1和2的两层电介质隔开。
垂直于轴线的某一截面如图所示。
求电缆单位长度的电容。