计算机中的数制
第1讲计算机中常用的数制

练习题
◆ 45D = 101101B
◆ 0.625D = 0.101B
◆ 97.6825D = 1100001.1011B
◆ 0.8D = ?
二、数制之间的相互转换规则 (二)十进制转换成二进制
注:十进制小数不一定都能转 换成完全等值的二进制小数。
二、数制之间的相互转换规则
十进制
八进制
十六进制
一、进位计数制
世上有10种人,一种是懂 二进制的人,一种不懂。
教学内容
1
进位计数制
2
数制之间的相互转换规则
3
二进制数的运算
教学目标
1. 理解数制的概念;
2. 熟练掌握常用数制相互转换规则; 3. 了解二进制数的相关运算。
一、进位计数制
数制:也称进位计数制,是用一组固定的符号和统 一的规则来表示数值大小的方法。 三要素: 1.数码:数制中表示基本数值大小的不同数字符号。 2.基数:数制所使用数码的个数。 3.位权:由位置决定的值,用基数的指数次幂表示。
二进制
二、数制之间的相互转换规则 (三)十六进制转换成二进制
规则:一分为四。
3 A 8 C . 9 D ↓ ↓ ↓ ↓ ↓ ↓ 0011 1010 1000 1100 . 1001 1101 3A8C.9DH=11101010001100.10011101B
二、数制之间的相互转换规则 (四)二进制转换成十六进制
规则:三位一组。以小数点为中心,向左右两方向按三位
一组划分,不足三位的组在各自方向的前面补0,然后将每 组三位二进制数代之以一位8进制数字。
10110101.01101 B
010 110 101 011 010
2 6 5 3 2
计算机中的数制

4
0
2
2
1
1
0.5
0
0.25
0.25
0.125
.0625
0.125 .0625
16 + 8 + 0 + 2 + 1 + 0 + .25 + .125 + .0625 = 27.4375
数 制 的 转 换
例4: 将下面给出的二进制数转换成十六进制的数
二进制数 十六进制数
0010 2 0000 0 0101 5 1010 A 0111 7 1110 E 0100 4
[例]:
[X]原=1 0110100
[X]反=1 1001011
[+0]反=00000000 [-0]反 =11111111 即:数0的反码也不唯一
补码
定义:
若X>0, 则[X]补= [X]反= [X]原 若X<0, 则[X]补= [X]反+1 [例]: X= –52= – 0110100
[X]原=10110100
1.2
计算机中的数制
数制 是人们利用符号来计数的科学方法。数制可以 有很多种,但在计算机的设计和使用上常用的 则为十进制、二机制、八进制和十六进制。 数制的基和位权 数制所使用的数码的个数称为基,数制中每一 固定位置对应的单位值称为“位权”
十进制: 基为“10”,权为以10为底的幂, —D 二进制: 基为“2”,权为以2为底的幂, —B 八进制: 基为“8”,权为以8为底的幂, —O 十六进制:基为“16”,权为以16为底的幂 —H
ASCII码
ASCII码是目前微机中普遍采用的字符编码系统。 字符的编码,一般用7位二进制码表示128个字符和 符号。在需要时可在D7位加校验位。 0~9的ASCII码:30H~39H;
大学计算机基础1.2计算机的数制
0.3125
×
8
2.5000…………2
×8
4.0000…………4
因此: (125.3125)10 = (175.24) 8
注意: 在十进制小数转换成二进制小数过程中,如出现小数部分不 归0的情况,则应按精度要求“0舍1入”。
十进制
二进制
八进制
十六进制
不
0
0
0
0
同
1
1
1
1
数
2
10
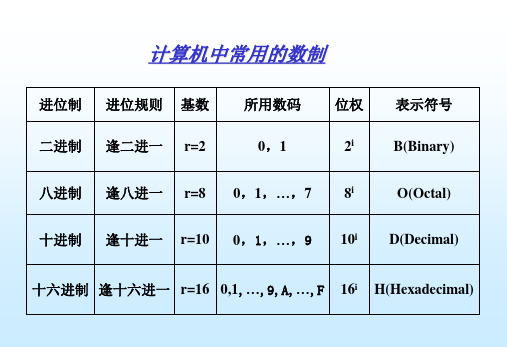
计算机中常用的数制
进位制 进位规则 基数 二进制 逢二进一 r=2
所用数码 0,1
位权 表示符号
2i
B(Binary)
八进制 逢八进一 r=8 0,1,…,7 8i
O(Octal)
十进制 逢十进一 r=10 0,1,…,9 10i D(Decimal)
十六进制 逢十六进一 r=16 0,1,…,9,A,…,F 16i H(Hexadecimal)
三种基本逻辑运算的真值表
a
b
a
a∧b
a∨b
0
0
1
0
0
0
1
0
1
1
0
0
0
1
1
1
0
1
1
若干位二进制数组成的逻辑数据,位与位之间没有“位权”的内 在联系。对两个逻辑数据进行运算时,每位相互独立,按位进 行运算,不存在进位与借位,运算结果也是逻辑量。
逻辑代数是实现逻辑运算的数学工具,逻辑代数有三种基本的逻 辑运算:与、或、非。其它复杂的逻辑关系均可由这三种基本 逻辑运算组合而成。
①与运算(逻辑乘法) 当做一件事情取决于多种因素时,当且仅当所有因素都满足时才去做,
计算机中的数制与编码

计算机中的数制与编码
(2)定点小数 定点小数规定小数点的位置固定在符号位之后,但不占一个二进制位。那么,符号位的右边表示的是一 个纯小数。
定点小数的表示形式
例如,用8位二进制定点整数表示(-0.6875)10,应为: (-0.6875)10=(11011000)2
计算机中的数制与编码
2 浮点数
浮点数是指小数点的位置不固定的数。对于既有整数部分又有小数部分的数,一般用浮点数表示。 任意一个二进制数N都可以表示成如下形式:
微机原理与接口技术
计算机中的数制 与编码
计算机中的数制与编码
1.1 计算机中的数制
1 数制的概念
数制是人们按进位的原则进行计数的一种科学方法。在日常生活中,经常要用到数制,除了最常见的十进 制计数法,有时也采用别的进制来计数。
一种计数制所使用的数字符号的个数称为基数,某个固定位置上的计数单位称为位权。同一数字符号处 在不同位置上所代表的值是不同的,它所代表的实际值等于数字本身的值乘以所在位置上的位权。例如,十 进制数345中的数字3在百位上,表示位权为100,故此时的3表示的是300。又如,十进制数123.45用位权可以 表示为
整数部分:
小数部分:
所以,(69.625)10=(1000101.101)2。
计算机中的数制与编码
② 转换成八进制数
③ 转换成十六Βιβλιοθήκη 制数计算机中的数制与编码3 二进制数与八进制数、十六进制数之间的转换
二进制、八进制、十六进 制之间存在特殊的关系:1位 八进制数对应3位二进制数,1 位十六进制数对应4位二进制 数,因此转换比较容易。
(2)小数部分的转换。
• 小数部分的转换采用“乘基取整法”,方法 是:将十进制数的小数部分反复乘以基数R, 将每次乘积的小数部分作为被乘数,并取得 相应的整数部分,直到乘积的小数部分为0。 将每次得到的整数部分顺序排列在小数点后, 即为转换后的R进制小数。
计算机常用数制及编码

计算机常用数制及编码1.二进制数制:二进制是计算机中最基本的数制,只包含两个数字0和1、它是一种逢二进一的计数法,每位上的数值以2为底数的幂来表示。
例如,二进制数1101表示1*2^3+1*2^2+0*2^1+1*2^0=13、在计算机中,二进制数被广泛应用于存储和运算等操作。
2.八进制数制:八进制使用8个数字0-7来表示。
它是二进制数制的一种压缩表示方法,每3位二进制数可以表示为一位八进制数。
例如,二进制数1101可以表示为八进制数15、八进制数在计算机界并不常见,但在一些特定场景下仍然有一定的应用。
3.十进制数制:十进制是我们常用的数制,使用10个数字0-9来表示数值,每位上的数值以10为底数的幂来表示。
例如,十进制数123表示1*10^2+2*10^1+3*10^0=123、十进制数制通常用于人类的日常计算中,但在计算机中也会涉及到十进制的处理,例如在涉及到金额、日期和时间等数字的场景中。
4.十六进制数制:十六进制使用16个数字0-9和A-F来表示,其中A-F分别表示十进制数10-15、它是二进制数制的另一种压缩表示方法,每4位二进制数可以表示为一位十六进制数。
十六进制数常用于计算机领域,因为它们可以更紧凑地表示二进制数。
例如,二进制数1101可以表示为十六进制数D。
编码系统是为了实现计算机和人类之间的信息交流而发展的。
下面介绍几种常见的编码系统:1.ASCII码:ASCII(American Standard Code for Information Interchange)是最早和最广泛使用的字符编码系统之一、它使用7位二进制数(扩展ASCII使用8位二进制数)来表示128(或256)个字符,包括英文字母、数字、符号等。
ASCII码可以用于存储和表示文本文件中的字符。
2. Unicode编码:3.UTF-8编码:UTF-8(Unicode Transformation Format - 8-bit)是一种对Unicode进行可变长度编码的字符编码系统。
计算机中数制的基本概念

计算机中数制的基本概念数制的三个基本概念数制:记数的方法,指用一组固定的符号和统一的规则来表示数值的方法,如在计数的过程中采用进位的方法则称为进位计数制。
进位计数制有数位、基数、位权3个要素。
数位:指数字符号在一个数中所处的位置。
基数:指在某种进位计数制中数位上所能使用的数字符号的个数,例如,十进制数的基数是10,八进制的基数是8,二进制的基数是2。
不同的数制,可以给数字加上括号,使用下标来表示该数字的数制(当没有下标时默认为十进制)。
C/C++中整数有三种表示形式:1)十进制形式。
如99、-1。
2)八进制形式。
以数字0打头,由0-7构成,如012表示八进制整数12,即12(8)。
3)十六进制形式。
以0x打头,如0x12A,表示十六进制整数12A,即12A(16)。
在数制中,还有一个规则,这就是,N进制必须是逢N进一。
计算机中常用的数制是十进制。
二进制与十进制类似,但是其基数是2,只有两个数字0和1,每超过2时就需要进位。
十进制数的特点是逢十进一。
如下图所示:2.二进制数的特点是逢二进一。
如下图所示:3.八进制数的特点是逢八进一。
如下图所示:4. 十六进制数的特点是逢十六进一。
如下图所示:二进制与十进制之间的转换•十进制转二进制方法为:十进制数除2取余法,即十进制数除2,余数为权位上的数,得到的商值继续除2,依此步骤继续向下运算直到商为0为止。
(具体用法如下图)二进制转十进制方法为:把二进制数按权展开、相加即得十进制数。
具体用法如下图:二进制与十六进制之间的转换二进制转十六进制方法为:与二进制转八进制方法近似,八进制是取三合一,十六进制是取四合一。
(注意事项,4位二进制转成十六进制是从右到左开始转换,不足时补0)。
具体用法如下图:十六进制转二进制方法为:十六进制数通过除2取余法,得到二进制数,对每个十六进制为4个二进制,不足时在最左边补零。
具体用法如下图:。
计算机中的常用数制.

1 计算机中的常用数制进位计数制,按进位的原则计数,超过基数,向左边进位。
日常生活中有10进制、60进制……计算机中有2进制、8进制、16进制等。
1.1 常用的数制数字66是几?先要确定它是几进制数。
在进位计数制中有数位、基数和位权三个要素。
✧数位:是指数码在一个数中所处的位置。
对于任意禁止—J进制,J个数字符号,逢J进一。
例如十进制,逢十进一;✧基数:是指在某种进位计数制中,每个数位上所能使用的数码的个数。
例如十进制,0,1,2,3,4,5,6,7,8,9。
✧位权:在一个形成数的数码序列中,各位上的基数的幂有所不同。
例如十进制数,各数位的位权(由右至左)分别为100,101,102,……最常见,最熟悉的是10进制;计算机用2进制;8进制和16进制都是从2进制“派生”出来的。
1.2数制转换二←→十进制之间的转换是基础。
1)非十进制→十进制a n ...a1a0.a-1...a-m (r) = a n×r n+ …+ a1×r1 + a0×r0 +a-1×r-1+...a-m×r-ma i是某一位上的数码,r是基数,r i是权。
不同的基数,表示是不同的进制数。
r 进制转化成十进制:数码乘以各自的权的累加例:10101=1×24+1×22+1×20=21101.11(B)=22+1+2-1+2-2=5.75101(O)=82+1=6571(O)=7x8+1=57101A(H)=163+16+10=4106注:(B)—表示该数是二进制数;(O)—表示该数是八进制数;(H) —表示该数是16进制数2) 十进制数→非十进制整数部分和小数部分分别计算。
整数—除2取余,到0为止;小数—乘2取整,到0或满足精度为止。
最先算出的数离小数点近。
例:将十进制数转换成二进制数,小数部分和整数部分分别转换:整数部分:小数部分:2 100 0.6252 50 0 离小数点近× 22 25 0 离小数点近1 1.2502 12 1 × 22 6 0 0 0.502 3 0 × 22 1 1 1 1.00 1100.625=1100100.1013) 二、八、十六进制数制间的转换等价关系,3位二进制数对应1位8进制数;4位二进制数对应1位16进制数。
专升本计算机数制及其转换

专升本计算机数制及其转换一、十进制数制十进制数制是我们日常生活中常用的数制,它由0、1、2、3、4、5、6、7、8、9这十个数字组成。
每一位上的数字代表该位上数字的权值,从右往左依次为个位、十位、百位等。
例如,数值1234表示1×10³+2×10²+3×10¹+4×10⁰。
二、二进制数制二进制数制是计算机中最基础的数制,它由0和1这两个数字组成。
每一位上的数字代表该位上数字的权值,从右往左依次为2⁰、2¹、2²等。
例如,数值1011表示1×2³+0×2²+1×2¹+1×2⁰。
三、八进制数制八进制数制是由0、1、2、3、4、5、6、7这八个数字组成。
每一位上的数字代表该位上数字的权值,从右往左依次为8⁰、8¹、8²等。
例如,数值725表示7×8²+2×8¹+5×8⁰。
四、十六进制数制十六进制数制是由0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F这十六个数字组成。
其中,A~F分别表示10~15。
每一位上的数字代表该位上数字的权值,从右往左依次为16⁰、16¹、16²等。
例如,数值3A7表示3×16²+10×16¹+7×16⁰。
五、数制转换在计算机中,经常需要进行不同数制之间的转换。
下面介绍四种常见的数制转换方法。
1. 十进制转二进制:利用除2取余法,将十进制数每次除以2,直到商为0为止,然后将所得余数倒序排列即可得到二进制数。
2. 二进制转十进制:将二进制数从右往左依次乘以2的幂次方,幂次方从0开始递增,然后将乘积相加即可得到十进制数。
3. 十进制转八进制:利用除8取余法,将十进制数每次除以8,直到商为0为止,然后将所得余数倒序排列即可得到八进制数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
计算机中的数制
在数字计算机中,每个数字和字符都是由一系列的电脉冲信号表示的。
在计算机中电路有脉冲时表示“1”,否则表示“0”。
因此,可以用一连串的“0”、“1”代码来表示数字和字符,这样表示的数据容易移动和存储。
一、数制
1.基本概念
表示数的方法称为数制。
通常人们习惯以十进制来计量事物,但在生活中也使用其他的数字系统。
例如:月与年使用12进制来计算。
十进制是我们最熟悉的进制,以十进制为例介绍数制的相关概念。
(1)数码:十进制有0~9十个数字符号组成,0~9这些数字符号称为“数码”。
(2)基数:全部数码的个数称“基数”,十进制的基数为10。
(3)计数原则:“逢十进一”。
即用“逢基数进位”的原则计数,称为进位计数制。
(4)位权:数码所处位置的计数单位为位权,位权的大小以基数为底。
例如,十进制的个位的位权是100,十位上的位权为101,百位上的位权为102,以此类推。
而在小数点后第1位上的位权为10-1。
由此可见,各位上的位权值是基数10的若干次幂。
例如,十进制数234.13用位权表示为:
常用计数制的基数、位权和数字符号如表1所示。
表1 常用数制的基数、位权和数字符号
常用数制的表示方法如表2所示。
表2 常用数制的表示方法
二、数制转换
1. r进制转换为十进制
基数为r的数字,只要将各位数字与它的权相乘,然后按照逢十进位的算法求和,即可将其转换成十进制数。
方法:按位权展开并求和。
(ai为第i位上的数码,r为基数)
(a n…a1a0.a-1…a-m)r=a n×r n+…+a1×r1+a0×r0+a-1×r-1+…+a-m×r-m
【例1】(11011.1011)2=1×24+1×23+0×22+1×21+1×20+1×2-1+0×2-2+1×2-3+1×2-4
=16+8+2+1+0.5+0.125+0.0625
=(27.6875)10
【例2】(576.5)8 =5×82+7×81+6×80+5×8-1
=320+56+6+0.625
=(382.625)10
【例3】(1B2A.5)16=1×163+11×162+2×161+10×160+5×16-1
=4096+2816+32+10+0.31
=(6954.31)10
2.十进制转换为r进制
将十进制数转换为r进制数,可将整数部分与小数部分分别转换,然后相加。
方法:整数部分:整数除以r,取余数,余数倒排序。
小数部分:小数乘以r,取整数,整数正排序。
【例4】将十进制数62.75转换为二进制数(小数部分保留3位)。
求整数部分:
(62)10=(111110)2
求小数部分:
【例5】将十进制数62转换为八进制数。
【例6】将十进制数62转换为十六进制数。
