半导体物理习题课(一)
半导体物理习题课
因此在能量E
E+dE范围,长度为dk内的状态数为:
Na
π
dk =
Na
* mn dE
π
2
E
−
1 2
Na = 2π
* * 1 1 − − 2mn 2 m n E 2 dE = L E 2 dE
因此单位长度晶体中,单位能量间隔的状态数为:
* 1 − 2mn N (E) = E 2
,
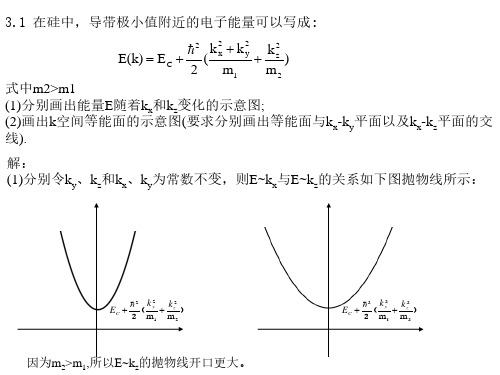
3.9 设硅晶体中电子的纵向有效质量为ml,横向有效质量为mt, (1)如果外加电场沿[100]方向,试分别写出在[100]和[001]方向能谷中电子的加速 度; (2)如果外加电场沿[110]方向,试求出[100]方向能谷中电子的加速度与电场之间 的夹角。 解: y [010] (1)在[100]能谷中,
− eε 2 1 1 m + ml ( + ) − t a ⋅ε mt + ml 2 ml mt ml mt = cosθ = =− = 2 2 2 2 aε 1 1 eε 2 ( ) m + m m + m l t l t ⋅ + ε⋅ 2 2 ml2 mt2 ml mt
于是:
m +m t l θ = π - arc cos 2 2 2(ml + mt )
2 k 2 2 ( k − k1 ) 2 + EC (k ) = 3m m
价带极大值附近的能量Ev(k)为:
2 k12 3 2 k 2 − Ev (k ) = 6m m
式中m为电子质量,k 1 = (1)禁带宽度; (2)导带底电子的有效质量; (3)价带顶空穴的有效质量。
π
a
,a=3.14Å。试求:
半导体物理习题

半导体物理习题 -CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN附: 半导体物理习题第一章 晶体结构1. 指出下述各种结构是不是布拉伐格子。
如果是,请给出三个原基矢量;如果不是,请找出相应的布拉伐格子和尽可能小的基元。
(1) 底心立方(在立方单胞水平表面的中心有附加点的简立方); (2) 侧面心立方(在立方单胞垂直表面的中心有附加点的简立方); (3) 边心立方(在最近邻连线的中点有附加点的简立方)。
2. 证明体心立方格子和面心立方格子互为正、倒格子。
3. 在如图1所示的二维布拉伐格子中,以格点O 为原点,任意选取两组原基矢量,写出格点A 和B 的晶格矢量A R 和B R 。
4. 以基矢量为坐标轴(以晶格常数a 为度量单位,如图2),在闪锌矿结构的一个立方单胞中,写出各原子的坐标。
5.石墨有许多原子层,每层是由类似于蜂巢的六角形原子环组成,使每个原子有距离为a的三个近邻原子。
试证明在最小的晶胞中有两个原子,并画出正格子和倒格子。
第二章晶格振动和晶格缺陷1.质量为m和M的两种原子组成如图3所示的一维复式格子。
假设相邻原子间的弹性力常数都是β,试求出振动频谱。
2.设有一个一维原子链,原子质量均为m,其平衡位置如图4所示。
如果只考虑相邻原子间的相互作用,试在简谐近似下,求出振动频率ω与波矢q之间的函数关系。
3.若把聚乙烯链—CH=CH—CH=CH—看作是具有全同质量m、但力常数是以1β,2β交替变换的一维链,链的重复距离为a,试证明该一维链振动的特征频率为}])(2sin41[1{2/1221221212ββββββω+-±+=qam并画出色散曲线。
第三章 半导体中的电子状态1. 设晶格常数为a 的一维晶格,导带极小值附近的能量)(k E c 为mk k m k k E c 21222)(3)(-+=(3.1)价带极大值附近的能量)(k E v 为mk m k k E v 2221236)( -=(3.2)式中m 为电子质量,14.3,/1==a a k πÅ。
半导体物理课后习题

半导体物理学课后习题第一章 半导体的电子状态1. [能带结构计算]设晶格常数为a 的一维晶格,导带极小值附近能量)(k E c 和价带极大值附近能量)(k E v 分别为()()02120223m k k m k k E c -+= ()022021236m k m k k E v -= 式中,0m 为电子惯性质量,a k /1π=,nm a 314.0=。
试求: ① 禁带宽度;② 导带底电子有效质量; ③ 价带顶电子有效质量;④ 价带顶电子跃迁到导带底时准动量的变化。
解:①先找极值点位置()023201202=-+=m k k m k dk dE c 得出,当143k k =时,0212(min)4m k E c =同理由0=dk dE v 得当0=k 时,0212(max)6m k E v = 所以禁带宽度0212(max)(min)12m k E E E v c g =-==0.636eV ②830222*m dk E d m c nc== ③60222*m dk E d m v nv-==④由①可知,准动量的变化为)(109.7834301291--⋅⋅⨯-=-=⨯-⨯=∆=-=∆s m kg ahk k P P P c v2. [能带动力学相关]晶格常数为0.25nm 的一维晶格,当外加102V/m ,107V/m 的电场时,试分别计算电子能带底运动到能带顶所需要的时间。
解:设晶格常数为a ,则电子从能带底到能带顶过程中准动量的变化为ak π=∆,因为dt dk qE f==,所以qEdt dk =所以所需要的时间为:E =∙∆=∆=∆qa qE k dtdk k t π,当m V /102=E 时,s t 81028.8-⨯=∆ 当m V /107=E 时,s t 131028.8-⨯=∆第二章 半导体中杂质和缺陷能级1. [半导体、杂质概念]实际半导体与理想半导体的主要区别是什么? 解:杂质和缺陷的存在是实际半导体和理想半导体的主要区别。
半导体物理习题课

质浓度为:
3 3 ND = = = 1.7 ×1025 / m3 3 4π r1,n 4π × (2.4 ×10−9 )3 =1.7 ×1019 /cm3 同理 3 3 NA = = = 6.3 × 1025 / m3 3 4π r1,p 4π × (1.56 ×10−9 )3 =6.3 ×1019 /cm3 当施主和受主杂质浓度分别超过以上两值时,相邻杂质原子 的电子轨道(波函数)将明显地交迭。杂质原子有可能在杂质 原子之间作公有化运动,造成杂质带电。
1eV = 1.602 × 10−12 erg , k 0 = 1.38 × 10−16 erg / K = 8.63 × 10−5 eV / K
代入有关数据得:
T= 5.5 − 5 8.63 × 10−5 × ln( 1 − 1) 0.01 = 1261( K )
由费米函数可得:
1 E = EF + k0T ln( − 1) f (E)
当f=0.9时:
1 E1 = E F + 8.63 × 10 × 1261 × ln( − 1) 0.9 =EF -0.24(eV)
−5
1 当f=0. 时:
1 E 2 = EF + 8.63 × 10 × 1261 × ln( − 1) 0.1 =EF +0.24(eV)
−5
能量区间为ΔE=E 2 -E1 =0.48(eV)
习题课
1、半导体硅单晶的相对介电常数εr=11.8,电子和空穴的 有效质量各为mnl=0.97m0(电子纵向有效质量) mnt=0.19m0 (电子横向有效质量), mph=0.53m0(重空穴有效质量),mpl=0.16m0(轻空穴有 效质量),利用类氢模型估算: (1)施主和受主电离能; (2)施主和受主对应的电子、空穴基态轨道半径r1; (3)相邻杂质原子的电子或空穴轨道明显交迭时,施主 和受主浓度各为何值?
半导体物理参考习题和解答

复习思考题与自测题第一章1.原子中的电子和晶体中电子受势场作用情况以及运动情况有何不同, 原子中内层电子和外层电子参与共有化运动有何不同。
答:原子中的电子是在原子核与电子库伦相互作用势的束缚作用下以电子云的形式存在,没有一个固定的轨道;而晶体中的电子是在整个晶体内运动的共有化电子,在晶体周期性势场中运动。
当原子互相靠近结成固体时,各个原子的内层电子仍然组成围绕各原子核的封闭壳层,和孤立原子一样;然而,外层价电子则参与原子间的相互作用,应该把它们看成是属于整个固体的一种新的运动状态。
组成晶体原子的外层电子共有化运动较强,其行为与自由电子相似,称为准自由电子,而内层电子共有化运动较弱,其行为与孤立原子的电子相似。
2.描述半导体中电子运动为什么要引入"有效质量"的概念, 用电子的惯性质量描述能带中电子运动有何局限性。
答:引进有效质量的意义在于它概括了半导体内部势场的作用,使得在解决半导体中电子在外力作用下的运动规律时,可以不涉及半导体内部势场的作用。
惯性质量描述的是真空中的自由电子质量,而不能描述能带中不自由电子的运动,通常在晶体周期性势场作用下的电子惯性运动,成为有效质量3.一般来说, 对应于高能级的能带较宽,而禁带较窄,是否如此,为什么?答:不是,能级的宽窄取决于能带的疏密程度,能级越高能带越密,也就是越窄;而禁带的宽窄取决于掺杂的浓度,掺杂浓度高,禁带就会变窄,掺杂浓度低,禁带就比较宽。
4.有效质量对能带的宽度有什么影响,有人说:"有效质量愈大,能量密度也愈大,因而能带愈窄.是否如此,为什么?答:有效质量与能量函数对于K的二次微商成反比,对宽窄不同的各个能带,1(k)随k的变化情况不同,能带越窄,二次微商越小,有效质量越大,内层电子的能带窄,有效质量大;外层电子的能带宽,有效质量小。
5.简述有效质量与能带结构的关系;答:能带越窄,有效质量越大,能带越宽,有效质量越小。
半导体物理习题答案(1-3章)

第1章 半导体中的电子状态1. 设晶格常数为a 的一维晶格,导带极小值附近能量()c E k 和价带极大值附近能量()v E k 分别为2222100()()3c h k k h k E k m m -=+,22221003()6v h k h k E k m m =-0m 为电子惯性质量,112k a =, 0.314a =nm 。
试求:1) 禁带宽度;2) 导带底电子有效质量; 3) 价带顶电子有效质量;4) 价带顶电子跃迁到导带底时准动量的变化。
解:1) 禁带宽度g E ,根据22100()2()202c dE k h k k h k dk m m -=+=,可求出对应导带能量极小值min E 的k 值:min 134k k =, 由题目中()c E k 式可得:min 12min 3104()4c k k k h E E k k m ====; 根据20()60v dE k h k dk m =-=,可以看出,对应价带能量极大值max E 的k 值为:k max = 0;可得max 221max 00()6v k k h k E E k m ====,所以2221min max 2001248g h k h E E E m m a=-== 2) 导带底电子有效质量m n由于2222200022833c d E h h h dk m m m =+=,所以202238nc m h md E dk== 3) 价带顶电子有效质量vn m由于22206v d E h dk m =-,所以20226v nv m h m d E dk ==- 4) 准动量的改变量min max 133()48hh k h k k hk a∆=-==2. 晶格常数为0.25 nm 的一维晶格,当外加102 V/m 、107 V/m 的电场时,试分别计算电子自能带底运动到能带顶所需的时间。
解:设电场强度为E ,电子受到的力f 为dkf hqE dt==(E 取绝对值),可得h dt dk qE =, 所以12012ta h h t dt dk qE qE a===⎰⎰,代入数据得: 34619106.62108.310()1.6102(2.510)t s E E----⨯⨯==⨯⨯⨯⨯⨯ 当E = 102 V/m 时,88.310t s -=⨯;当E = 107 V/m 时,138.310t s -=⨯。
《半导体物理学》习题库完整

《半导体物理学》习题库完整第1章思考题和习题1. 300K时硅的晶格常数a=5.43?,求每个晶胞所含的完整原⼦数和原⼦密度为多少?2. 综述半导体材料的基本特性及Si、GaAs的晶格结构和特征。
3. 画出绝缘体、半导体、导体的简化能带图,并对它们的导电性能作出定性解释。
4. 以硅为例,简述半导体能带的形成过程。
5. 证明本征半导体的本征费⽶能级E i位于禁带中央。
6. 简述迁移率、扩散长度的物理意义。
7. 室温下硅的有效态密度Nc=2.8×1019cm-3,κT=0.026eV,禁带宽度Eg=1.12eV,如果忽略禁带宽度随温度的变化,求:(a)计算77K、300K、473K 3个温度下的本征载流⼦浓度。
(b) 300K本征硅电⼦和空⽳的迁移率分别为1450cm2/V·s和500cm2/V·s,计算本征硅的电阻率是多少?8. 某硅棒掺有浓度分别为1016/cm3和1018/cm3的磷,求室温下的载流⼦浓度及费⽶能级E FN的位置(分别从导带底和本征费⽶能级算起)。
9. 某硅棒掺有浓度分别为1015/cm3和1017/cm3的硼,求室温下的载流⼦浓度及费⽶能级E FP的位置(分别从价带顶和本征费⽶能级算起)。
10. 求室温下掺磷为1017/cm3的N+型硅的电阻率与电导率。
11. 掺有浓度为3×1016cm-3的硼原⼦的硅,室温下计算:(a)光注⼊△n=△p=3×1012cm-3的⾮平衡载流⼦,是否为⼩注⼊?为什么?(b)附加光电导率△σ为多少?(c)画出光注⼊下的准费⽶能级E’FN和E’FP(E i为参考)的位置⽰意图。
(d)画出平衡下的能带图,标出E C、E V、E FP、E i能级的位置,在此基础上再画出光注⼊时,E FP’和E FN’,并说明偏离E FP的程度是不同的。
12. 室温下施主杂质浓度N D=4×1015 cm-3的N型半导体,测得载流⼦迁移率µn=1050cm2/V·s,µp=400 cm2/V·s,κT/q=0.026V,求相应的扩散系数和扩散长度为多少?第2章思考题和习题1.简述PN结空间电荷区的形成过程和动态平衡过程。
半导体物理习题答案完整版

半导体物理习题答案 HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】第一章半导体中的电子状态例1.证明:对于能带中的电子,K状态和-K状态的电子速度大小相等,方向相反。
即:v(k)= -v(-k),并解释为什么无外场时,晶体总电流等于零。
解:K状态电子的速度为:(1)同理,-K状态电子的速度则为:(2)从一维情况容易看出:(3)同理有:(4)(5)将式(3)(4)(5)代入式(2)后得:(6)利用(1)式即得:v(-k)= -v(k)因为电子占据某个状态的几率只同该状态的能量有关,即:E(k)=E(-k)故电子占有k状态和-k状态的几率相同,且v(k)=-v(-k)故这两个状态上的电子电流相互抵消,晶体中总电流为零。
例2.已知一维晶体的电子能带可写成:式中,a为晶格常数。
试求:(2)能带底部和顶部电子的有效质量。
解:(1)由E(k)关系(1)(2)令得:当时,代入(2)得:对应E(k)的极小值。
当时,代入(2)得:对应E(k)的极大值。
根据上述结果,求得和即可求得能带宽度。
故:能带宽度(3)能带底部和顶部电子的有效质量:习题与思考题:1 什么叫本征激发温度越高,本征激发的载流子越多,为什么试定性说明之。
2 试定性说明Ge、Si的禁带宽度具有负温度系数的原因。
3 试指出空穴的主要特征。
4 简述Ge、Si和GaAs的能带结构的主要特征。
5 某一维晶体的电子能带为其中E0=3eV,晶格常数a=5×10-11m。
求:(2)能带底和能带顶的有效质量。
6原子中的电子和晶体中电子受势场作用情况以及运动情况有何不同原子中内层电子和外层电子参与共有化运动有何不同7晶体体积的大小对能级和能带有什么影响?8描述半导体中电子运动为什么要引入“有效质量”的概念?用电子的惯性质量描述能带中电子运动有何局限性?9 一般来说,对应于高能级的能带较宽,而禁带较窄,是否如此为什么10有效质量对能带的宽度有什么影响?有人说:“有效质量愈大,能量密度也愈大,因而能带愈窄。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.61
3.61
3Байду номын сангаас.1
37.1
13
例5、设二维正方格子的晶格常数为a,若电子 能量可表示为
h2 2 2 E (k ) ( k k x y) 2mn
试求状态密度。
[解] 能量为 E 的等能面方程式可以写成:
2 m 2 2 nE kx k y h2
显然,是一个半径为 R 的圆,其面积为
ΔE D 0.01 116 19 1.6 10 23 k BT 1.3810 T T
* 2(2mn k B )3 2 15 3 2 3 Nc 2 10 T ( cm ) 3 h
2015-1-1 雷天民 7
D Nc 116 D 2 1015 T 3 2 1015 ln ln( ) ln( DT 3 2 ) T 2N D 2N D ND
雷天民
18
由题意,有 EF EA1 0.178 0.045 0.133eV
EF EA2 0.178 0.16 0.018eV
价带空穴p0是由两种杂质电离后提供的,即
N A1 p0 E A1 EF 1 2 exp k T B N A2 E A 2 EF 1 2 exp k T B
[解] 对非简并p型硅,有 EF Ev p0 N v exp k T B 代入数据,计算得
Nv EF Ev k BT ln p 0
2015-1-1
Nv EF Ev k BT ln p Ev 0.178eV 0
2015-1-1
雷天民
15
例6、有一硅样品,施主浓度为ND=2×1014 cm-3, 受主浓度为NA=1014 cm-3,已知施主电离能ED为 0.05eV,试求99%的施主杂质电离时的温度。 [解] 令ND+表示电离施主的浓度,则电中性方程为:
n0 N p0 N
略去价带空穴的贡献,则得:
cos 2 3, cos 0
可知当 B 沿[111]方向时应有两个共振吸收峰; (2)若 B 沿[110]方向则cosθ可以取三组数:
cos 1, cos 0, cos 1 2.
可知当 B 沿[110]方向时应有三个共振吸收峰; (3)若 B 沿[100]方向则cosθ可以取两组数:
所以 N A2
N A1 p0 E A1 EF 1 2 exp k T B
E A2 EF 1 2 exp k T B
代入数据,计算得 N A2 2.31015 / cm3
Semiconductor Physics 雷天民
leitianmin@
半导体物理
例1、锑化铟介电常数ε=17,电子有效质量mn=0.014m, 试计算: 1)浅施主的电离能和基态轨道半径; 2)相邻施主上的基态电子轨道开始交叠时的施 主浓度。当超过这个浓度时,将出现什么效应? (已 知氢的基态电离能E0=13.6eV,玻尔半径a0=0.53Å) [解] 1)利用类氢模型,基态电离能和基态轨道半径分别为
Tn1
116 3 ln Tn 2.3 2
lnTn
5.70
2.92 4.02 3.44 3.70 3.58 3.63
Tn
300
18.6 55.7 31.1 40.6 35.7 37.8
Tn+1
18.6
55.7 31.1 40.6 35.7 37.8 36.9
36.9
37.1
2015-1-1 雷天民
2
2)设想施主杂质均匀地排列成一个立方格子, 那么Nd-1/3 即表示相邻杂质小心的距离。所以
1/ 3 Nd 2a
3 3
1 1 14 3 Nd 5 10 cm 2 8 2a 2 6.4 10 10 当施主浓度越过这个数值时,相邻施主上的基态 电子轨道将发生交叠,这时杂质能级将扩展成一个杂 质能带。即束缚于杂质上的电子,可以在不同杂质原 子之间转移,杂质带表现出一定的导电性。 与晶体能带中的电子相比,杂质带中的电子运动 要困难得多。只是在低温下,当能带中的载流子对电 导的贡献变得很小时,杂质带的导电性才可以表现出 来。 3
ΔE D ND ln k BT Nc
雷天民
116 ND ln T 2 1015 T 3 2
10
2015-1-1
116 ND ln T 2 1015 T 3 2
116 2 1015 T 3 2 ln T ND
若ND=1014cm-3,有
116 3 32 ln( 20T ) ln T ln 20 T 2 116 3 ln T 3 T 2
1 mn 1 4 E 2 E 0 . 014 13 . 6 6 . 6 10 (eV ) 0 2 m0 17 m 1 2 (Å) a a 17 0 . 53 6 . 4 10 m 0 0.014 n
cos 1 / 2 , cos 0.
(4)若 B 沿任意方向,则cosθ可取六 个不同值,所以应有六个共振吸收峰。
2015-1-1 雷天民 6
例4、若锗中杂质电离能△ED=0.01eV,施 主杂质浓度分别为ND=1014cm-3及1017cm-3, 计算:(1)99%电离;(2)90%电离;(3)50% 电离时温度各为多少? [解] 思路:区分电离程度,选择适用条件。 对于强电离,未电离杂质占的百分比为: D N c ΔE D ΔE D nD ND =ln D 2 exp k BT 2N D ND Nc k BT
4
例3:如果 n 型半导体导带极值在[110]轴上及 相应对称方向上,回旋共振实验结果应如何? [解 ] m m m (m sin 2 m cos2 )
n l l t l
思路:确定可取的cosθ,即可确定吸收蜂个数。 据立方对称性,有12个方向上的旋转椭球面
[110],[101 ],[011 ],[ 1 1 0],[ 1 0 1 ],[0 1 1 ]; [1 1 0],[10 1 ],[0 1 1],[ 1 10],[ 1 01],[01 1 ].
D A
A
D
n0 N N (受主杂质全部电离)
Ec EF 式中 n0 N c exp k T B 15 3 2 对硅材料 N c 5.6 10 T
D
由题意,有 N 0.99 N D
2015-1-1 雷天民 16
0.99 N D N A 5.6 10 T
2015-1-1 雷天民 19
例8、计算含有施主杂质浓度ND=9×1015cm-3及 受主杂质浓度为1.1×1016cm-3的硅在300K时的 电子和空穴浓度以及费米能级的位置。 [解]对于硅材料,T=300K时 ni=1.5×1010cm-3
p0 N A N D 2 1015 cm3
116 1015 3 32 3 3 2 ln( DT ) ln(10 T ) ln T 3 ln10 T ND 2
116 3 ln T 6.9 T 2
2015-1-1 雷天民 9
(3)50%电离不属于强电离,不能再用上式
ND nD n 2 ND ND 即 1 ED EF 2 1 exp( ) 2 k BT
2m E R h
2 n 2
2015-1-1 雷天民 14
乘以 k 空间状态密度2S(晶体的面积)即可 得圆内所包含的状态数为:
4Smn E Z (E) h2
取微分,有
4Smn dZ ( E ) dE 2 h
单位能量间隔内的状态数,即状态密度为
dZ ( E ) 4Smn g (E) 2 dE h
D
EF ED kBT ln 2
Ec EF n0 N c exp k T 0
Ec ED k BT ln 2 N D N c exp k0T 2
取对数后得 整理得
Ec ED k BT ln 2 ND ln k BT 2Nc
116 3 ln T 9.2 T 2
2015-1-1 雷天民 8
(2)ND=1014cm-3,90%电离,即D-=1-90%=0.1
116 1015 3 32 32 ln( DT ) ln T ln T T ND 2
116 3 ln T T 2
若ND=1017cm-3,90%电离,D-=0.1
(1) ND=1014cm-3,99%电离,即D-=1-99%=0.01
116 3 1 3 2 ln(10 T ) ln T 2.3 T 2
116 3 ln T 2.3 T 2
若ND=1017cm-3,99%电离,即D-=1-99%=0.01
116 3 4 3 2 ln(10 T ) ln T 4 ln 10 T 2
若ND=1017cm-3,有
116 3 2 3 2 ln( 2 10 T ) ln T ln 2 ln 100 T 2 116 3 ln T 3.9 T 2
2015-1-1 雷天民 11
上述对数方程可用图解法或迭代法解出!
图解法:分别令 116 3 y1 ; y2 ln T Ci (与条件有关) T 2
15
32
Ec EF exp k T B
198
当有99%的施主电离时,说明有1%的施主有 电子占据,即f (ED)=0.01。
1 f ( ED ) ED EF 1 1 exp k T 2 B 0.01
