第一章《直角三角形》导学案(1)
解直角三角形1解直角三角形的概念导学案

解直角三角形1解直角三角形的概念导学案一、导学1.课题导入:如图是意大利的比萨斜塔,设塔顶中心点为B ,塔身中心线与垂直中心线的交点为A ,过B 点向垂直中心线引垂线,垂足为C ,在Rt△ABC 中,∠C=90°,BC=5.2米,AB=54.5米,你能根据上述条件求出图中∠A 的度数吗?这就是我们这节课要研究的问题.2.学习目标(1)知道解直角三角形的概念,理解直角三角形中除直角以外的五个元素之间的关系.(2)能综合运用勾股定理、直角三角形的两个锐角互余及锐角三角函数解直角三角形.3.学习重、难点:重点:直角三角形中除直角以外的五个元素之间的关系,解直角三角形.难点:合理选用三角函数关系式解直角三角形.二、分层学习第一层次学习1.自学指导(1)自学内容:P72—P 73页例题1以前的内容.(2)自学时间:6分钟.(3)自学要求:完成探究提纲.(4)探究提纲:①在直角三角形中,已知有一个角是直角,我们把________________的过程,叫做解直角三角形. ②在直角三角形中,除直角外的五个元素之间有哪些关系?如图,在Rt △ABC 中,∠C=90°,设∠A、∠B、∠C 所对的边分别为a 、b 、c ,则有: ○a 两锐角_________,即∠A+∠B=______°. ○b 三边关系___________,即____________。
. ○c 边角关系:sinA = ,sinB = ; cosA =____;cosB = ;tanA = ;tanB = .③已知直角三角形中不是直角的五个元素中的几个元素,才能求出其余所有未知元素?(提示:可从“确定一个直角三角形,至少需要哪些条件?”来思考).2.自学:学生可参考自学指导进行自学.3.助学:(1)师助生:①明了学情:观察学生自学提纲的答题情况(特别是第②、③题).②差异指导:根据学情进行个别指导或分类指导.(2)生助生:小组内相互交流、研讨、订正结论.4.强化:(1)直角三角形中除直角外的五个元素之间的关系(要板书出来).(2)直角三角形的可解条件:必须已知除直角外的两个元素(至少有一个是边).①已知两边:○a 两直角边;○b 一直角边和斜边; ②已知一边和一锐角:○a 一直角边和一锐角;○b 斜边和一锐角. 第二层次学习 A B Ca b c1.自学指导(1)自学内容:P73页例1,例2.(2)自学时间:8分钟.(3)自学方法:先独立解答,再同桌之间互评互改.(4)自学参考提纲:①在例1中,已知的元素是两条直角边AC、BC,需求出的未知元素是:____________________.BC= _____,∴∠A=_____°,∠B=90°-____=____°.方法1:∵tanA =AC∵AC=2,BC=6∴AB =______.方法2:∵AC=2,BC=6∴由勾股定理可得AB=_____.BC=_____,∴∠A=____°∴∠B=90°-∠A =____°.sinA=AB这里∠B的度数也可用三角函数来求,你会吗?②比较上述解法,体会其优劣.③在例2中,已知的元素是一直角边b和一锐角∠B,则要求的未知元素有__________________.④例2还有别的解法吗?请试一试,并留意你的答案与例题的答案是否存在误差.⑤练习:在Rt△ABC中,∠C=90°,根据下列条件解直角三角形:○a c=202,b=20;○b∠B=60°,c=14;○c∠B=30°,a=7.2.自学:学生可参考自学指导进行自学.3.助学:(1)师助生:①明了学情:关注学生解直角三角形思路是否清晰,是否会选择恰当的三角函数关系式.②差异指导:根据学情对学习有困难的学生进行个别或分类指导.(2)生助生:小组内相互交流、研讨.4.强化:解直角三角形的思路:首先明确已知什么,要求的元素有哪些;其次,合理选择三角函数关系式,并正确进行变形(所选的关系式必须要有两个已知元素);第三,尽可能选用题目的原始数据,以减少误差.三、评价:1.学生学习的自我评价(围绕三维目标):这节课你学到了哪些知识?还有哪些疑问?2.教师对学生的评价:(1)表现性评价:从学生的学习态度、积极性、小组交流状况等等方面进行点评.(2)纸笔评价:课堂评价检测.3.教师的自我评价(教学反思).。
直角三角形(导学案)--八年级数学上册同步备课系列
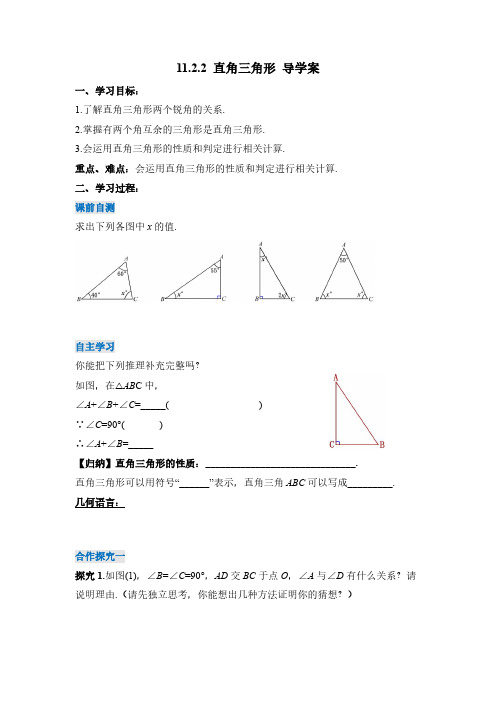
11.2.2直角三角形导学案一、学习目标:1.了解直角三角形两个锐角的关系.2.掌握有两个角互余的三角形是直角三角形.3.会运用直角三角形的性质和判定进行相关计算.重点、难点:会运用直角三角形的性质和判定进行相关计算.二、学习过程:课前自测求出下列各图中x的值.自主学习你能把下列推理补充完整吗?如图,在△AB C中,∠A+∠B+∠C=_____()∵∠C=90°()∴∠A+∠B=_____【归纳】直角三角形的性质:______________________________.直角三角形可以用符号“______”表示,直角三角ABC可以写成_________.几何语言:合作探究一探究1.如图(1),∠B=∠C=90°,AD交BC于点O,∠A与∠D有什么关系?请说明理由.(请先独立思考,你能想出几种方法证明你的猜想?)探究2.如图(2),∠B=∠D=90°,AD交BC于点O,∠A与∠C有什么关系?请说明理由.(解题前请思考下面两个问题①两个图形的相同点和不同点各是什么?②图(1)的两种解答方法能用于图(2)的解答吗?哪个更具一般性?)典例解析例1.如图,∠C=∠D=90°,AD,BC相交于点E,∠CAE与∠DBE有什么关系?为什么?【针对练习】如图,∠ACB=90°,CD⊥AB,垂足为D,∠ACD与∠B有什么关系?为什么?合作探究二我们知道,如果一个三角形是直角三角形,那么这个三角形有两个角互余.反过来,有两个角互余的三角形是直角三角形吗?请你说说理由.提出问题:如图,在△AB C 中,∠A +∠B =90°,那么△ABC 是直角三角形吗?(请你尝试着证明一下,再和小组内其他成员说一说你的做法)【归纳】直角三角形的判定:_________________________________.几何语言:典例解析例2.如图,CE ⊥AD ,垂足为E ,∠A =∠C ,△ABD 是直角三角形吗?为什么?【针对练习】如图,∠C =90°,∠1=∠2,△ADE 是直角三角形吗?为什么?例3.如图所示,有一个三角尺DEF (足够大),其中90EDF ∠=︒,把直角三角尺DEF 放置在锐角ABC 上,三角尺DEF 的两边,DE DF 恰好分别经过点,B C .(1)若35A ∠=︒,则ABC ACB ∠+∠=_________°,DBC DCB ∠+∠=__________°,ABD ACD +=∠∠___________°;(2)若60A ∠=︒,求ABD ACD ∠+∠的度数;(3)请你猜想一下ABD ACD ∠+∠与A ∠所满足的数量关系,并说明理由.达标检测1.已知Rt△ABC的一个锐角为25°,则另一个锐角为______.2.三角形的两个锐角分别为35°和55°,则它是_____三角形.3.已知等腰三角形的顶角是底角的2倍,则这个三角形的顶角为_____,它是____________三角形.4.如图,已知∠1=20°,∠2=25°,∠A=35°,则∠BDC为______.5.如图,∠1+∠2+∠3+∠4=______.6.在三角形中,最大的内角不能小于_____,最小的内角不能大于_____.7.如图,已知等腰三角ABC,底角的平分线BE与底边上的高AD相交与点O,且∠BOD=55°,则∠BAC=______.8.如图,直线a//b,Rt△ABC如图放置,若∠1=28°,∠2=80°,则∠B的度数为() A.62°B.52°C.38°D.28°9.如图,在△AB C中,∠BAC=90°,AD⊥BC于点D,BE平分∠ABC,AD、BE相交于点F.(1)若∠CAD=36°,求∠AEF的度数;(2)试说明:∠AEF=∠AFE.。
直角三角形导学案(1)

1.1.1直角三角形(Ⅰ)导学案(一)【学习目标】 1.了解直角三角形的概念,探索并掌握直角三角形的性质定理:直角三角形的两个锐角互余;直角三角形斜边上的中线等于斜边的一半。
2.掌握有两个锐角互余的三角形是直角三角形。
【强基导学】在前面,我们已经学习了三角形边与边,边与角,角与角之间的一些性质,直角三角形作为一种特殊的三角形,除了具有一般三角形的性质外,它还具有哪些特殊性质呢?说一说:如图1-1,在Rt △ABC 中, ∠C =90°,两锐角的和等于多少呢?在Rt △ABC 中,因为 ∠C =90°,由三角形内角和定理,可得∠A +∠B = °由此得到:直角三角形的两个锐角 .【自主探学】1.有两个锐角互余的三角形是直角三角形吗?如右图,在△ABC 中, ∠A +∠B =90° , 那么△ABC 是直角三角形吗?在△ABC 中,因为 ∠A +∠B +∠C =180°, 又∠A +∠B =90°,所以∠C = °. 于是△ABC 是 三角形.由此得到:有两个角互余的三角形是 三角形.2.探究:画Rt △ABC ,∠C=90º,CD 是斜边AB 上的中线,(l )量一量斜边AB 的长度=__________(2)量一量斜边上的中线CD 的长度=________(3)于是有CD=_ _AB.由此得到:直角三角形斜边上的中线等于斜边的 。
BCB3.互动帮学例1 已知:如图,CD是△ABC的AB边上的中线,且CD=1/2AB。
求证:△ABC是直角三角形【达标评学】1、“直角三角形两锐角互余”逆定律(填:“有”或“没有”)。
2、在RtΔABC中,∠A=30°则∠B=60°最直接的理由是3、在Rt△ABC中,∠C=90度,∠B=15度,则∠A=______度4、如图,Rt△ABC中,CD是斜边AB上的中线,AB=8cm,则AD=____cm, BD=_____cm, CD=________cm5.如图,CD是△ABC的中线,∠ACB=90°,∠CDB=110°,则∠A=__________6.在△ABC中,若∠A=25°,∠B=65°,此三角形为________三角形7.直角三角形中,两锐角的平分线相交所成的角的度数是_________。
直角三角形 导学案

丹凤中学学案28.2解直角三角形(1)主备人:学习目标:(1):理解解直角三角形的概念。
(2):探索解直角三角形至少需要几个元素。
(3):会灵活运用解直角三角形的方法解直角三角形。
学习重点:解直角三角形的方法.学习难点:三角函数在解直角三角形中的灵活运用学习过程:一、复习旧知,引入新课:在Rt△ABC中,∠C=90°,①正弦:=sin____ _ = ;A②余弦:=Atan_____ = ;cos__ ___ = ;③正切:=A如果我们知道∠A=30°并且∠A的对边等于2,能否求得∠A的邻边,斜边及∠B呢?如果∠A=72°呢?那么我们将通过本节课的学习来解决这个问题。
二、展示目标:同上目标1、2、3。
三、出示学法,自主学习自学课本第85页——86页的内容,完成以下问题:1.由直角三角形中__________ 元素,求出其它所有_______•元素的过程,叫做解直角三角形.2.由85页“探究”可知:在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,那么这些元素之间存在有如下关系:(1)三边之间的等量关系:__________________________________.(2)两锐角之间的关系:__________________________________.(3)边与角之间的关系:①正弦:=sin______ = ;或a= .A②余弦:=cos______ = ;或b= .A③正切:=tan_____ = ;或a= .A以上三点正是解直角三角形的依据。
3思考:在直角三角形的六个元素中,除直角外,只要再知道_________(其中至少_________)就可以解这个直角三角形。
4、认真看例1和例2,掌握做题格式及方法。
(时间:12分钟)四、效果检测:1、逐一解决学法中的问题;2、在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,根据下列条件,解直角三角形。
初中数学 导学案1:直角三角形的边角关系

直角三角形的边角关系一、课前小测(限时5分钟): 1.5231---x x = .2. 因式分解:a 3 – 16 a =3. 如图,a ∥b ,∠1 = 65°,那么∠2 = .4. 函数31-=x y 的自变量 x 的取值范围是 . 5. 正比例函数的图象经过点(3,–6),那么它的解析式为 .6. 已知:在△ABC 中,∠A = 35°,∠B = 105°,那么∠C = .7. 圆心角为150°,弧长为20πcm 的扇形面积为 .8. 命题“在同一个三角形中,等边对等角”的逆命题是 . 9. 已知函数()2833my m x -=-+是一次函数,则m 的值为 .10.如图,△ABC 中,D 是AB 上一点,添加什么条件,可使△ABC ∽△ACD?答: 或 或 .二、课标要求:了解(认识)::通过实例认识锐角三角函数(sinA 、cosA 、tanA ),知道已知 30°、 45°、60°角的三角函数值.理解和掌握:会使用计算器由已知锐角,求其相应的三角函数值, 由已知锐角函数值求与其对应的锐角.灵活运用::运用三角函数解决与直角三角形有关的简单的实际问题. 三、复习重点:理解三角函数的概念,并能根据它们的数学意义进行直角三角形的边角关系的计算.四、归纳结构:实际背景锐角三角函数的意义锐角三角函数的计算 利用三角函数解决实际问题五、本课主要知识点:解直角三角形的基本类型及解法:在Rt△ABC 中,∠C = 90° 六、典例示范:1.对锐角三角函数概念的理解.(1) 已知在Rt △ABC 中,∠C =90°, sinB=23,则cosA 的值为( ) A 、21B 、22C 、23D 、33(2)正方形网格中,∠AOB 如图放置,则cos ∠AOB 的值为 ( )A 、55B 、552C 、21D 、230°、 45°、60°角的三角函数一般锐角三角函数值由三角函数值求锐角2.对于特殊角的三角函数值的计算.计算)360tan 2008(45sin 231-+--3.求已知锐角的三角函数值、或求已知三角函数值所对应的角. 已知矩形的两邻边之比是31,则该矩形的两条对角线所夹的锐角度数为 .4.运用三角函数解直角三角形.如图,∠ABC =∠BCD =90°,AB =8,sinA =35 ,CD =2 3 ,求∠CBD的三个三角函数值.思路点拨:解直角三角形所应用的工具有三种:一是通过直角三角形两锐角互余的性质,进行角的计算;二是通过勾股定理进行边的计算;三是应用三角函数进行边与角的计算.在解直角三角形时首先要构造直角三角形,并且常常有用公共边将两个直角三角形联系起来.,5.运用三角函数解决与直角三角形有关的实际问题.(选做)如图所示,某市景区管委会准备在郊外两个景区点A 、B 与该市M 间修建一条笔直的公路,经测量,在A 的北偏西30方向上6km 的C 处的四周1km 范围内是一个重点文物保护区,且又位于景点B 的正北方向,测得AB 的长为5km ,试问能否修这条笔直的公路(精确到,参考数据:73.13,24.25==)?A BCM北思路点拨:关于方向和位置的应用题常涉及解直角三角形和三角函数知识,解决这类问题有把握好三个关键,一是认清方位角,二是确定基点,标清路线角度.三是构造适当的直角三角形七、总结通法:1、在运用直角三角形边角关系解决问题时,应遵循三条原则:一是“知二(直角除外)求三”中至少有一个条件是边;二是尽量使用题目中的原始数据;三是尽量避免除法运算.2、在解决实际问题时,首先要弄清题意,正确画出示意图,将实际问题转化为直角三角形的问题,进而运用三角函数的知识加以解决.3、有些问题涉及的不是直角三角形,这就需要根据条件或图形的特点,适当的引进辅助线,以构造直角三角形,从而将问题转化为直角三角形的问题加以解决.4、解决应用题时要注意弄清仰角、俯角、坡度(坡比)等术语的含义.5、有关锐角三角函数的问题,综合性、技巧性、操作性都比较强,涉及到的知识和方法较多,因此,在综合复习中要体会模型化思想和数形结合等数学思想方法的应用.八、变式训练:1、已知在Rt △ABC 中,∠C =90°,AB=5,AC=2,则cosA 的值为( ) A 、521 B 、52 C 、221 D 、25 2、直角三角形中,∠C =90°,a ,b 分别是∠A ,∠B 的对边,则ab 是角A 的( )A 正弦B 余弦C 正切D 余切3、在Rt △ABC 中,∠C =90°,3a = 3 b ,则∠A = ,sinA = .4、计算: 3 tan30°-1-2 tan60°+tan 260° +cos60°·cos45°.5、已知△ABC 中,∠C =90°,∠A =45°,BD 为AC 边上中线,求sin ∠ABD 和tan ∠ABD 的值.6、如图,甲、乙两栋高楼的水平距离BC 为90米,从甲楼顶部点C 测得乙楼顶部点A 的仰角为30O ,测得乙楼低部点B 的俯角为60O ,求甲、乙两栋高楼各有多高(结果用带根号的数表示)?7、(2006年湖南省张家界市)会堂里竖直挂一条幅,小刚从与成水平的点观察,视角30C =∠,当他沿方向前进米到达到时,视角45ADB =∠,求条幅的长度.ABCD甲乙A BCD8、如图,在某建筑物AC上,挂着“多彩贵州”的宣传条幅BC,小明站在点F处,看条幅顶端B,测得仰角为30°,再往条幅方向前行20米到达点E处,,看到条幅顶端B,测得仰角为60°,求宣传条幅BC的长,(小明的身高不计,结果精确到米)。
浙教版-数学-八年级上册2.6直角三角形 导学案

2.6直角三角形(1)导学案学习目标:1.进一步认识直角三角形.2.会用符号和字母表示直角三角形.3.掌握直角三角形两个锐角互余的性质,直角三角形斜边上的中线等于斜边的一半的性质定理。
4.会运用直角三角形的性质定理解决有关图形的认证、计算等问题。
重点:直角三角形的两个锐角互余的性质及其应用.难点: “直角三角形斜边上的中线等于斜边的一半”的推导以及在例1中的应用。
一、直角三角形的定义:有一个角是_________的三角形叫直角三角形. 用符号“Rt △“表示二、(一)直角三角形的性质定理1的探究: 如图,在Rt △ABC 中,∠C=Rt ∠,完成下面的填空:(1)比较大小:AC_____AB ( )(2)∠A+∠B=______.( ) (3)若∠A=30°, ∠B=_______.归纳:直角三角形的性质定理1:直角三角形的两个锐角___________几何语言:(二)直角三角形性质定理1的应用:1、在直角三角形中,有一个锐角为52.5°,那么另一个锐角的度数为______.2、在Rt △ABC 中,∠C=90°,∠A-∠B=40°,那么∠A=_____,∠B=_____.3、如图,在Rt △ABC 中,∠ACB=900,CD ⊥AB.(1)图中互余的角有_______对,分别是____________________________________.(2)相等的锐角有______对,分别是_______________.4、已知:如图,在△ABC 中,∠ACB=900,CD ⊥AB ,BE 平分∠ABC.则CE 与CF 相等吗?说明理由。
C B A21D C B A F E A BCDE D CB A 三、(一)直角三角形性质定理2的探究: 问题:如图,已知Rt △ABC ,画一条线段把Rt △ABC 分成两个等腰三角形.小明说:当∠A=450时我会画,我的画法是:过点C 画直线CD ,交AB 于D ,使∠ACD=∠ A=450,则线段CD 即为所求.小亮说:当∠A=300时我也会画,我的画法是:过点C 画直线CD ,交AB 于D ,使∠ACD=∠ A= 300,则线段CD 即为所求.小明和小亮的画法正确吗?说明理由当∠A 的度数任意时,你能画出这条线段吗?若能,说说你的画法. 图中你能证明△DCB 是等腰三角形吗?图中的线段CD 是直角三角形的什么线? CD 与AB 有什么数量关系?由此你有什么发现?归纳:直角三角形的性质定理2:直角三角形______上的_______等于________的_________.几何语言:(二)直角三角形性质定理2的应用:1、如图是一副三角尺拼成的四边形ABCD ,E 为BD 的中点.点E 与点A ,C 的距离相等吗?请说明理由.变式1: 如图,已知AD ⊥CD ,AB ⊥BC ,E 为AC 的中点,试判断DE 与BE 是否相等,并说明理由.C BA D D 450AB C D 300C B A600C B A CD B A CD B A 变式2: 如图,已知AD ⊥BD ,AC ⊥BC ,E 为AB 的中点, 试判断DE 与CE 是否相等,并说明理由变式3:如图,已知AD 、BE 分别是△ABC 的BC 、AC 边上的高,F 是DE 的中点,G 是AB 的中点,则FG ⊥DE ,请说明理由。
解直角三角形(第1课时)导学案

课题名称:九年级上册1.4解直角三角形(第1课时)【学习目标】1、掌握直角三角形的边角关系,会运用勾股定理、直角三角形的两个锐角互余及锐角三角函数解直角三角形。
2、通过综合运用勾股定理,直角三角形的两个锐角互余及锐角三角函数解直角三角形,逐步培养分析问题、解决问题的能力。
3、培养数形结合的数学思想,学会用数学解决实际问题。
【教学重、难点】1、解直角三角形的解法。
2、三角函数在解直角三角形中的灵活运用。
【导学流程】一、 自主预习:1、创设情境:(一)锐角三角函数定义 1.结合图形复习锐角三角函数的定义: 在Rt △ABC 中,∠C=90°,求:①sinA= ,a= ,c= ;②cosA= ,b= ,c= ; ③tanA= ,a= ,b= 。
注:三角函数值是一个比值,其大小只与角度的大小有关,与三角形的大小无关。
2.坡度(坡比):我们将坡面的 与 的比称为坡度(坡比)。
(二)特殊角的三角函数值:Ab①若锐角A 与锐角B 互余,则sinA= ,cosA= ,tanA ·tanB= 。
②随着锐角度数的增大,正弦值逐渐 ;余弦值逐渐 ;正切值逐渐 。
2、出示目标:3、学生自主学习,完成预习题: 直角三角形元素间的关系:(1)锐角之间的关系: ; (2)三边之间的关系: ; (3)角与边之间的关系:sinA= = ,cosA= = , tanA= ,tanB= . 解直角三角形的概念:在直角三角形中,知道除直角外的 个元素,(其中至少一个是 ),就可以求出其他元素,由直角三角形中已知的元素,求出其他所有未知的元素的过程,叫做解直角三角形。
4.组内交流质疑:针对预习题目中出现的问题,组内进行交流,互相解答疑惑。
二、展示交流5.小组汇报交流:6.教师精讲点拨: 典例解析:例1、已知如图,在△ABC 中,∠C=90°,a=4,c=8,解这个直角三角形。
例2、在ABC Rt ∆中,∠C=90°,3=a ,3=b ,求:(1)c 的大小;(2)∠A 、∠B 的大小。
八年级直角三角形整章导学案教案共10节(新湘教版)

S1
S2 S3
A.若 a 、 b 、 c 是△ABC 的三边,则 a2 b2 c2 B.若 a 、 b 、 c 是 Rt△ABC 的三边,则 a2 b2 c2
第 4 题图
C.若 a 、 b 、 c 是 Rt△ABC 的三边, A 90 , 则 a2 b2 c2
S3 为________.
5 、 一 个 直 角 三 角 形 的 两 边 长 分 别 为 5cm 和 12cm, 则 第 三 边 的 长
为
。
线, CE AB ,已知 AB 10cm , DE 2.5cm ,求 CD 和 DCE .
五.作业 P11 练习 1 题
课后反思
长乐中学八年级数学导学训练案教案
求线段 AB 的长。
解答过程:
C
B
D
A
例 2:已知:如图,∠B=∠D=90°,∠A=60°,AB=4,CD=2。求:四边形
ABCD 的面积。
解答过程:
A
D
E B
C
三.结 小结:不规则图形的面积,可转化为特殊图形求解,本题通过将图形转
化为直角三角形的方法,把四边形面积转化为三角形面积之差。 四.用 1. 如图,正方形网格中,每个小正方形的边长为 1,则网格上的三角形
- 12 -
ABC 中,边长为无理数的边数是( )
A. 0
B. 1
C. 2
D. 3
A C
B
B
A
7cm
C D
2. 如图所示,在△ABC 中,三边 a,b,c 的大小关系是( )
A.a<b<c
B. c<a<b
C. c<b<a
D. b<a<c
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章《直角三角形》导学案(1)
教学目标
进一步掌握推理证明的方法,发展演绎推理能力;
一、预习导航
1、写出你知道的勾股数
2、勾股定理的内容是:__ ______ _______
它的条件是:______ _______________________ _________;
结论是:______________ ________________。
二、讲授新课
3、将勾股定理的条件和结论分别变成结论和条件,其内容是:下面我们试着将上述命题证明:已知:在△ABC中,AB2+AC2=BC2求证:△ABC是直角三角形。
分析:要△ABC是直角三角形,只须∠A=90°,单独只有一个三角形不能得出结论,那就需用另外作一个Rt△A′B′C′,使∠A′=90°, A′B′=AB, A′C′=AC,通过证三角形全等得到结论。
证明:
定理:如果三角形两边的__________等于______ _ ___,那么这个三角形是直角三角形。
四、合作交流:
1、观察勾股定理及上述定理,它们的条件和结论之间有怎样的关系?然后观察下列每组命题,是否也在类似关系。
(1)如果两个角是对顶角,那么它们相等。
如果两个角相等,那么它们是对顶角。
(2)如果小明患了肺炎,那么他一定会发烧。
如果小明发烧,那么他一定患了肺炎。
(3)三角形中相等的边所对的角相等。
三角形中相等的角所对的边相等。
像上述每组命题我们称为互逆命题,即一个命的条件和结论分别是另一个命题的_________和_________。
2、“想一想”,回答下列问题:
(1)写出命题“如果两个有理数相等,那么它们的平方相等”的逆命题。
它们都是真命题吗?
(2)一个命题是真命题,那么它的逆命题也一定是真命题吗?
互逆定理:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理称为互逆定理,其中一个定理称为另一个定理的逆定理。
(4)是否任何定理都有逆定理?(5)思考我们学过哪些互逆定理?
三、应用深化
1、判断
(1)每个命题都有逆命题,每个定理也都有逆定理。
()
(2)命题正确时其逆命题也正确。
()(3)直角三角形两边分别是3,4,则第三边为5。
()
2、下列长度的三条线段能构成直角三角形的是()
①8、15、17 ②4、5、6、③7.5、4、8.5 ④ 24、25、7 ⑤ 5、8、10
A、①②④
B、②④⑤
C、①③⑤
D、①③④
课下训练:
1、以下命题的逆命题属于假命题的是()
A、两底角相等的两个三角形是等腰三角形。
B、全等三角形的对应角相等。
C、两直线平行,内对角相等。
D、直角三角形两锐角互等。
2、命题:等腰三角形两腰上的高相等的逆命题是_____________________________________________
3、若一个直角两直角边之比为3:4,斜边长20CM,则两直角边为(,)
4、已知直角三角形两直角边长分别为6和8,则斜边长为________,斜边上的高为_________。
5、写出下列命题的逆命题,并判断每对命题的真假:
A、五边形是多边形。
B、两直线平行,同位角相等。
C、如果两个角是对顶角,那么它们相等。
D、如果AB=0,那么A=0,B=0。
6、公园中景点A、B间相距50M,景点A、C间相距40M,景点B、C间相距30M,由这三个景点构成的三角形一定是直角三角形吗?为什么?
7、台风过后,某小学旗杆在B处断裂,旗杆顶A落在离旗杆底部C点8M处,已知旗杆原长16M,则旗杆在距底部几米处断裂。
8、小明将长2.5M的梯子斜靠在竖直的墙上,这时梯子底端B到墙根C的距离是0.7M,如果梯子的顶端垂直下滑0.4M,那么梯子的底端B将向外移动多少米。
中考真题:用四个全等的直角三角形拼成了一个如图所示的图形,其中a表示较短,直角三角形,b表示较长的直角边,c表示斜边,你能用这个图形证明勾股定理。
