大连理工大物作业答案
大连理工大学软件学院大学物理作业及答案详解1-22

大连理工大学大学物理作业及答案详解作业1 (静电场一)1.关于电场强度定义式,下列说法中哪个是正确的?[ ] A .场强E 的大小与试探电荷0q 的大小成反比。
B .对场中某点,试探电荷受力F 与0q 的比值不因0q 而变。
C .试探电荷受力F 的方向就是场强E 的方向。
D .若场中某点不放试探电荷0q ,则0F =,从而0E =。
答案: 【B 】[解]定义。
场强的大小只与产生电场的电荷以及场点有关,与试验电荷无关,A 错;如果试验电荷是负电荷,则试验电荷受的库仑力的方向与电场强度方向相反,C 错;电荷产生的电场强度是一种客观存在的物质,不因试验电荷的有无而改变,D 错;试验电荷所受的库仑力与试验电荷的比值就是电场强度,与试验电荷无关,B 正确。
2.一个质子,在电场力作用下从A 点经C 点运动到B 点,其运动轨迹如图所示,已知质点运动的速率是递增的,下面关于C 点场强方向的四个图示哪个正确?[ ]答案: 【D 】[解]a m E q=,质子带正电且沿曲线作加速运动,有向心加速度和切线加速度。
存在向心加速度,即有向心力,指向运动曲线弯屈的方向,因此质子受到的库仑力有指向曲线弯屈方向的分量,而库仑力与电场强度方向平行(相同或相反),因此A 和B 错;质子沿曲线ACB 运动,而且是加速运动,所以质子受到的库仑力还有一个沿ACB 方向的分量(在C 点是沿右上方),而质子带正电荷,库仑力与电场强度方向相同,所以,C 错,D 正确。
3.带电量均为q +的两个点电荷分别位于X 轴上的a +和a -位置,如图所示,则Y 轴上各点电场强度的表示式为E = ,场强最大值的位置在y = 。
答案:y a qy23220)(2+=πε,2/a y ±= [解]21E E += )(422021y a qE E +==πε关于y 轴对称:θcos 2,01E E E y x ==j y a qyj E E y 23220)(2+==∴πε沿y 轴正向的场强最大处0=dydEy y a y y a dy dE 2)(23)(25222322⨯+-+∝-- 2/a y = 2/a y ±=处电场最强。
大连理工大学大学物理作业3(静电场三)及答案详解

作业3(静电场三)1.电场中某区域内电场线如图所示,将一点电荷从M 移到N 点则必有[ ]。
.A 电场力的功0M N A >.B 电势能M N W W >.C 电势M N U U >.D 电势M N U U <答案:【C 】解:由于静电场的无旋性,电场强度的线积分与路径无关,由M 点到N 点的线积分(即M 点与N 点之间的电势差),可以取任意路径。
现取积分路径为:由M 点到O 点,处处与电场线(电场强度方向)垂直;由O 点到N 点,处处沿着电场线。
则0=⋅=-⎰O M O M l d E U U,0>=⋅=-⎰⎰NONON O Edl l d E U U因此,M 点与N 点的电势差为0)()(>=⋅+⋅=-+-=⋅=-⎰⎰⎰⎰NONOOMN O O M N MN M Edl l d E l d E U U U U l d E U U所以,C 正确,D 错误。
由M 点到O 点,电场力所作的功为(设移动电荷量为q )⎰⋅=-=N MN M N M l d E q U U q A)( 尽管0>⋅⎰N Ml d E,但不知q 的正负,无法判断NMA 的正负。
当0>q ,即移动正电荷时,电场力作功为正,0>NM A ;如果移动的是负电荷,电场力作功为负,0<NMA 。
电势能是静电场中的带电粒子与电场共同拥有的能量。
定义为,点电荷q 在静电场中M 点时,系统拥有的电势能为:从M 点移动电荷q 到电势零点的过程中,电场力所作的功,MM M M qUl d E q A W =⋅==⎰→0,静电势能等于电荷量与电荷所在点电势的乘积。
电场力所作的功等于静电势能的减少,静电场中M 点与N 点系统的电势能之差,等于移动点电荷q 由M 点到N 点的过程中电场力所作的功)(NM NM N M N M UU q l d E q A W W -=⋅==-⎰→尽管0>-N M U U ,但电势能之差还与电荷q 有关,不能判断N M W W -的正负。
大连理工大学大学物理作业5(静电场五)及答案详解
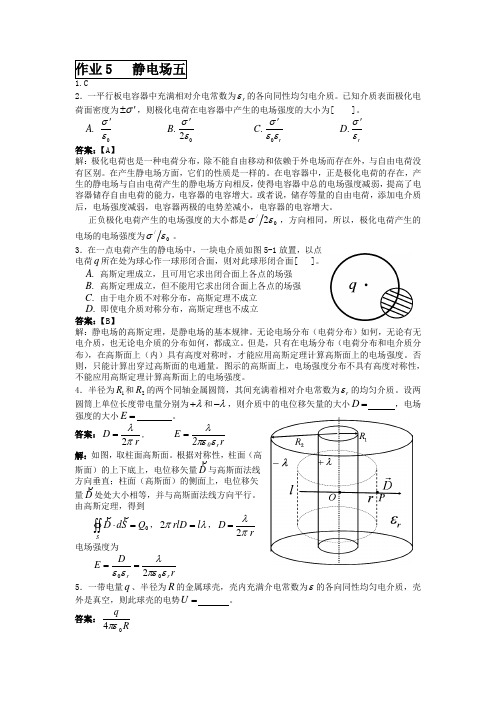
2.一平行板电容器中充满相对介电常数为r ε的各向同性均匀电介质。
已知介质表面极化电荷面密度为σ'±,则极化电荷在电容器中产生的电场强度的大小为[ ]。
.A0σε' .B 02σε' .C 0r σεε' .D rσε' 答案:【A 】解:极化电荷也是一种电荷分布,除不能自由移动和依赖于外电场而存在外,与自由电荷没有区别。
在产生静电场方面,它们的性质是一样的。
在电容器中,正是极化电荷的存在,产生的静电场与自由电荷产生的静电场方向相反,使得电容器中总的电场强度减弱,提高了电容器储存自由电荷的能力,电容器的电容增大。
或者说,储存等量的自由电荷,添加电介质后,电场强度减弱,电容器两极的电势差减小,电容器的电容增大。
正负极化电荷产生的电场强度的大小都是0/2εσ,方向相同,所以,极化电荷产生的电场的电场强度为0/εσ。
3.在一点电荷产生的静电场中,一块电介质如图5-1放置,以点电荷q 所在处为球心作一球形闭合面,则对此球形闭合面[ ]。
.A 高斯定理成立,且可用它求出闭合面上各点的场强 .B 高斯定理成立,但不能用它求出闭合面上各点的场强 .C 由于电介质不对称分布,高斯定理不成立 .D 即使电介质对称分布,高斯定理也不成立答案:【B 】解:静电场的高斯定理,是静电场的基本规律。
无论电场分布(电荷分布)如何,无论有无电介质,也无论电介质的分布如何,都成立。
但是,只有在电场分布(电荷分布和电介质分布),在高斯面上(内)具有高度对称时,才能应用高斯定理计算高斯面上的电场强度。
否则,只能计算出穿过高斯面的电通量。
图示的高斯面上,电场强度分布不具有高度对称性,不能应用高斯定理计算高斯面上的电场强度。
4.半径为1R 和2R 的两个同轴金属圆筒,其间充满着相对介电常数为r ε的均匀介质。
设两圆筒上单位长度带电量分别为λ+和λ-,则介质中的电位移矢量的大小D = ,电场强度的大小E = 。
院大学物理作业题答案及详解1-22

大连理工大学软件学院大学物理作业及答案作业11.关于电场强度定义式,下列说法中哪个是正确的?[ ] A .场强E 的大小与试探电荷0q 的大小成反比。
B .对场中某点,试探电荷受力F 与0q 的比值不因0q 而变。
C .试探电荷受力F 的方向就是场强E 的方向。
D .若场中某点不放试探电荷0q ,则0F =,从而0E =。
答案: 【B 】[解]定义。
场强的大小只与产生电场的电荷以及场点有关,与试验电荷无关,A 错;如果试验电荷是负电荷,则试验电荷受的库仑力的方向与电场强度方向相反,C 错;电荷产生的电场强度是一种客观存在的物质,不因试验电荷的有无而改变,D 错;试验电荷所受的库仑力与试验电荷的比值就是电场强度,与试验电荷无关,B 正确。
2.一个质子,在电场力作用下从A 点经C 点运动到B 点,其运动轨迹如图所示,已知质点运动的速率是递增的,下面关于C 点场强方向的四个图示哪个正确?[ ]答案: 【D 】[解]a m E q=,质子带正电且沿曲线作加速运动,有向心加速度和切线加速度。
存在向心加速度,即有向心力,指向运动曲线弯屈的方向,因此质子受到的库仑力有指向曲线弯屈方向的分量,而库仑力与电场强度方向平行(相同或相反),因此A 和B 错;质子沿曲线ACB 运动,而且是加速运动,所以质子受到的库仑力还有一个沿ACB 方向的分量(在C 点是沿右上方),而质子带正电荷,库仑力与电场强度方向相同,所以,C 错,D 正确。
3.带电量均为q +的两个点电荷分别位于X 轴上的a +和a -位置,如图所示,则Y 轴上各点电场强度的表示式为E = ,场强最大值的位置在y = 。
答案:y a qy23220)(2+=πε,2/a y ±= [解]21E E += )(422021y a qE E +==πε关于y 轴对称:θcos 2,01E E E y x ==j y a qyj E E y 23220)(2+==∴πε沿y 轴正向的场强最大处0=dydEy y a y y a dy dE 2)(23)(25222322⨯+-+∝-- 2/a y = 2/a y ±=处电场最强。
大连理工大学大学物理下答案详解

9 解 :(1) 霍 尔 电 势 差 是 指a、b之 间 的 电 势 差 , 根 据 左 手 定 则 , 电 子 向a端 运 动 , 于 是a端 聚 集 了 大 量 负 电 荷 , 则b点是高电势点 (2)当金属中电子所受磁场的洛伦兹力与电场力平衡时: evd B = eE = e 所以,漂移速度 vd = (3)由ab两端的霍尔电势差:|V | = n= V 4.27 × 10−6 m/s = 1.0675 × 10−4 m/s = Bl 2 × 2 × 10−2 V l
解:(1)曲面上点p的磁感应强度相当于无限长载流直导线产生的磁场,即: B= µ0 I 2πx
由磁场的高斯定理:磁感应线为闭合曲线时,穿过任何一个闭合曲面的磁通量为零,则 Φ=
sБайду номын сангаас
B · dS = 0
2、一电子以速度v 垂直地进入磁感应强度为B 的均匀磁场中,求:穿过此电子运动的轨迹所围的面积的磁通量。 解:电子在磁场中运动的轨迹半径为 r= 运动轨迹所围的面积为 S = πr2 = π ( 所以,穿过此运动轨迹所围面积的磁通量为 Φ=
解:(1)载流圆线圈中心的磁感应强度为 B= µ0 I 2R
图中闭合线圈,只有两半圆弧对中心O的磁场有贡献, 两半圆弧在O点产生的磁场分别为 B1 = µ0 I 4R1
2 方向:垂直于纸面向外 B2 = 方向:垂直于纸面向里 所以 B = B1 − B2 = 方向:垂直纸面向外 (2)线圈的磁矩: m = Isn = 其中n表示垂直纸面向里。 4、 无 限 长 直 导 线 通 电 流I, 分别 弯 成 图25-3(A) 、 (B) 所 示 的 形 状 。 求 :(1) 图 (A) 中O点 磁 感 应 强 度B1 ; (2)图(B)中O点磁感应强度B2 ; 1 2 2 Iπ (R2 − R1 )n 2 µ0 I µ0 I − 4R1 4R2 µ0 I 4R2
大连理工大物2作业答案_40-44

a (2)在− a 5 < x < 5 范围内,粒子出现的概率 2
1 3π cos( ) a 4
2
=
1 2a
p(−
a a <x< )= 5 5
a/5 −a/5
|ψ (x)| dx =
2
1 a
a/5
cos2
−a/5
3πx 1 dx = 2a a
a/5
1 + cos
0
3πx 1 a a 1 1 3 dx = + sin(3π/5) = + sin( a a 5 3π 5 3π
∞
1=
−∞
|ψ (x)| dx = |A|
2
2 0
∞
e−2ax dx =
1 |A|2 24、在宽度为a的一维无限深方势阱中运动的粒子定态波函数为ψ (x) =
2a 求:(1)基态粒子出现在 a 3 < x < 3 范围内的概率; (2)主量子数n = 2的粒子出现概率最大的位置。 解:可知定态波函数已归一化 2a (1)基态粒子出现在 a 3 < x < 3 范围内的概率
2、 粒 子 在 一 维 无 限 深 势 方 阱 中 运 动 , 图42-1 为 粒 子 处 于 某 一 能 态 的 波 函 数ψ (x)的 曲 线 ,(1)写出 粒 子 的 波 函 数;(2)用数学的方法求出粒子出现概率最大的位置。 解:(1)粒子的波函数: ψ (x) = 0,
大连理工大学大学物理 作业及答案详解
丝线与一块很大的带电平面成 30° 角。若带电平面上电荷分布均匀, q 很小,不影响带电平
面上的电荷分布,求带电平面上的电荷面密度。
解:方法一: 受力分析:小球在重力
G
=
mg
(垂直方向),绳中张力
T
(与带电平面成
30
度角)及静电
f = qE(水平方向)的共同作用下而处于受力平衡状态。其中 E 为无限大均匀带电平面(电
电量为 Q1 = 2πRλ )在圆心处产生的场强 E1 与放在空隙处长为 l ,电荷线密度为 − λ 的均 匀带电棒(可以看成是点电荷 q = −λl )在圆心产生的场强 E2 的叠加。即:
E0 = E1 + E2
;
E1
= 0,∴ E0
=
E 2
=
q 4πε 0 R 2
(−Rˆ )
E0
=
− λl 4πε 0 R 2
7.线电荷密度为 λ 的“无限长”均匀带电细线,弯成图示形状,若圆弧半径为 R ,试求 O
点的场强。
答案:按题给坐标, O 点 的场强可以看作是两个半无限长直导线、半圆在 O 点产生场强的 叠加。即: E0 =E1 + E2 + E3
由对称性, E1 和 E2 在 y 方向的矢量和为零;在 x 方向矢量和是单根的 2 倍。 上半无限长导线取电荷元 dq1 = λdx ,它在 O 点的场强沿 x 方向的分量:
答案: 【B】
[解]定义。场强的大小只与产生电场的电荷以及场点有关,与试验电荷无关,A 错;如果
试验电荷是负电荷,则试验电荷受的库仑力的方向与电场强度方向相反,C 错;电荷产生
的电场强度是一种客观存在的物质,不因试验电荷的有无而改变,D 错;试验电荷所受的
大连理工大学大学物理课后答案
作业二十五 稳恒磁场(一)11225-1. 7.210(T)B j −=×GG129.6107.21120(T)B j i −−=×−×G G G25-2.00I 2B Lπ=,方向与水平线成45度角,指向右上方。
25-3.(1)04I 2112(R R R R B μ−=,方向垂直纸面向外。
(2)2221()R 2Im R π=−,方向垂直纸面向内。
25-4.(1)02IB R(2μπ=2−,方向垂直纸面向内。
(2)0062I IB R R(2μμπ=2+2A m )×610(T)−,方向垂直纸面向内。
25-6.2412.55(T )9.3410(B m −==25-7. ,方向垂直纸面向外。
6.37B =×作业二十六 稳恒磁场(二)26-1. I02μB x π=,Φ=0。
26-2. 222m v e B πΦ=26-3. I l 0μ=B d ⋅∫KK 。
26-4.6()Wb −2.1910Φ=×26-5. 2202200(()2()2I r a )()()r a B a r b a I r μπμπ⎧⎪⎪−⎪=≤⎨−⎪⎪≥⎪⎩r b r b ≤≤ 26-6.解:(1)2211)())r D 00(20(NI B D r r μπ⎧⎪⎪=<⎨⎪>⎪⎩D r D << ;2(2)d d Bh r Φ=B 01d ln 2NIh D ND μπΦΦ=∫Φ= 226-7. 用安培环路定理,可以证明图中B 1=B 2;用高斯定理,可以证明图中 B ′1=B ′2。
B 命题得证作业二十七 稳恒磁场(三)27-1. 2R IB M = 方向竖直向上27-2. 02afe Iv πμ=4(/d v m − 27-3.(1)ab 两点间的电势差,b 点电势高。
(2) 1.0710)s ∴=×2835.8410(m )−=×。
大连理工大学大学物理作业5(静电场五)及答案详解
2.一平行板电容器中充满相对介电常数为r ε的各向同性均匀电介质。
已知介质表面极化电荷面密度为σ'±,则极化电荷在电容器中产生的电场强度的大小为[ ]。
.A0σε' .B 02σε' .C 0r σεε' .D rσε' 答案:【A 】解:极化电荷也是一种电荷分布,除不能自由移动和依赖于外电场而存在外,与自由电荷没有区别。
在产生静电场方面,它们的性质是一样的。
在电容器中,正是极化电荷的存在,产生的静电场与自由电荷产生的静电场方向相反,使得电容器中总的电场强度减弱,提高了电容器储存自由电荷的能力,电容器的电容增大。
或者说,储存等量的自由电荷,添加电介质后,电场强度减弱,电容器两极的电势差减小,电容器的电容增大。
正负极化电荷产生的电场强度的大小都是0/2εσ,方向相同,所以,极化电荷产生的电场的电场强度为0/εσ。
3.在一点电荷产生的静电场中,一块电介质如图5-1放置,以点电荷q 所在处为球心作一球形闭合面,则对此球形闭合面[ ]。
.A 高斯定理成立,且可用它求出闭合面上各点的场强 .B 高斯定理成立,但不能用它求出闭合面上各点的场强 .C 由于电介质不对称分布,高斯定理不成立 .D 即使电介质对称分布,高斯定理也不成立答案:【B 】解:静电场的高斯定理,是静电场的基本规律。
无论电场分布(电荷分布)如何,无论有无电介质,也无论电介质的分布如何,都成立。
但是,只有在电场分布(电荷分布和电介质分布),在高斯面上(内)具有高度对称时,才能应用高斯定理计算高斯面上的电场强度。
否则,只能计算出穿过高斯面的电通量。
图示的高斯面上,电场强度分布不具有高度对称性,不能应用高斯定理计算高斯面上的电场强度。
4.半径为1R 和2R 的两个同轴金属圆筒,其间充满着相对介电常数为r ε的均匀介质。
设两圆筒上单位长度带电量分别为λ+和λ-,则介质中的电位移矢量的大小D = ,电场强度的大小E = 。
大连理工大学大学物理作业5(静电场五)及答案详解
作业5 静电场五2.一平行板电容器中充满相对介电常数为r ε的各向同性均匀电介质。
已知介质表面极化电荷面密度为σ'±,则极化电荷在电容器中产生的电场强度的大小为[ ]。
.A0σε' .B 02σε' .C 0r σεε' .D rσε' 答案:【A 】解:极化电荷也是一种电荷分布,除不能自由移动和依赖于外电场而存在外,与自由电荷没有区别。
在产生静电场方面,它们的性质是一样的。
在电容器中,正是极化电荷的存在,产生的静电场与自由电荷产生的静电场方向相反,使得电容器中总的电场强度减弱,提高了电容器储存自由电荷的能力,电容器的电容增大。
或者说,储存等量的自由电荷,添加电介质后,电场强度减弱,电容器两极的电势差减小,电容器的电容增大。
正负极化电荷产生的电场强度的大小都是0/2εσ,方向相同,所以,极化电荷产生的电场的电场强度为0/εσ。
3.在一点电荷产生的静电场中,一块电介质如图5-1放置,以点电荷q 所在处为球心作一球形闭合面,则对此球形闭合面[ ]。
.A 高斯定理成立,且可用它求出闭合面上各点的场强 .B 高斯定理成立,但不能用它求出闭合面上各点的场强 .C 由于电介质不对称分布,高斯定理不成立 .D 即使电介质对称分布,高斯定理也不成立答案:【B 】解:静电场的高斯定理,是静电场的基本规律。
无论电场分布(电荷分布)如何,无论有无电介质,也无论电介质的分布如何,都成立。
但是,只有在电场分布(电荷分布和电介质分布),在高斯面上(内)具有高度对称时,才能应用高斯定理计算高斯面上的电场强度。
否则,只能计算出穿过高斯面的电通量。
图示的高斯面上,电场强度分布不具有高度对称性,不能应用高斯定理计算高斯面上的电场强度。
4.半径为1R 和2R 的两个同轴金属圆筒,其间充满着相对介电常数为r ε的均匀介质。
设两圆筒上单位长度带电量分别为λ+和λ-,则介质中的电位移矢量的大小D = ,电场强度的大小E = 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
p2
h2
Ek = 2m = 2mλ2 = eU
所以
h2
(6.626 × 10−34)2
U = 2mλ2e = 2 × 9.11 × 10−31 × 10−20 × 1.6 × 10−19 ≈ 151V
3、如图41-1所示一束动量为p的电子,通过缝宽为a的狭缝,在距离狭缝为R处放置一荧光屏,求屏上衍射图样中 央明条纹的宽度d.
λmax
=
c ν21
=
1 R(1/12 − 1/22)
=
4 3RΒιβλιοθήκη =4 3 × 1.096776 × 107m−1
=
1.2157 × 10−7m
=
121.57nm
最小波长:从m = ∞到n = 1能级上的跃迁所发射的波长
λ∞1
=
c µ∞1
=
1 R(1/12 − ∞2)
=
1 R
=
0.9118 × 10−7m =
3、设平衡热空腔上一面积为4cm2 的小孔,每分钟向外辐射能量640J ,求空腔内的温度。 (σ = 5.67 × 10−8W/mK˙ , b = 2.898 × 10−3mK˙ ) 解:由斯特藩——波尔兹曼定律知,总辐射出射度为
M = σT 4
故辐射功率
P = AσT 4
因此
T
=
4
P Aσ
=
4
640J/60s 4 × 10−4m2 × 5.67 × 10−8W/m · K
10−31kg,普朗克常数h = 6.63 × 10−34J · s).
解:由于电子所获得的动能Ek = eU12 = 900eV m0c2 = 0.511M eV ,因此可不考虑相对论效应,有
h
6.63 × 10−34
λ= √
=√
≈ 0.0409nm
2meeU12
2 × 9.11 × 10−31 × 1.6 × 10−19 × 900
a/5
cos2
3πx dx
=
1
a/5
3πx
1a a
11 3
1 + cos
dx =
+ sin(3π/5) = + sin(
5
5
−a/5
a −a/5
2a
a0
a
a 5 3π
5 3π
2、粒子在一维无限深势方阱中运动,图42-1 为粒子处于某一能态的波函数ψ(x)的曲线,(1)写出粒子的波函 数;(2)用数学的方法求出粒子出现概率最大的位置。
解:由德布罗意关系知
λ = h/p
单缝衍射暗条纹的条件为
由于R d,所以sin θ1 ≈ d/2R. 于是
a sin θk = ±kλ
d = 2R sin θ1 = 2Rλ/a = 2Rh/pa
4、λ0
=
h me
c
称为电子的康普顿波长(me
为电子的静止质量,h为普朗克常数,c为真空中的光速),已知电子的动能
mnc2 = 1.675 × 10−27 × 9 × 1016 ≈ 9.42 × 108eV
中子的动量p由此决定
Ek = p2c2 + m2nc4 − mnc2
4
因此
p = (1/c) Ek(Ek + 2mnc2)
由德布罗意关系,有热中子的德布罗意波长为
h
hc
λ= =
≈
6.626 × 10−34 × 3 × 108
图42-2中画出其余可能的L矢量,并标明各自对应的m值及Lz 值。 解:(1)角动量
√ L = l(l + 1)¯h = 2(2 + 1)¯h = 6¯h
(2)磁量子数
(3)见右图
m = −2, −1, 0, 1, 2; Lz = m¯h = −2¯h, −h¯, 0, ¯h, 2¯h.
8、原子中电子的波函数与其4个量子数有关,下列波函数都有错,请修正(每个波函数只允许修正一个数)。
2
7、在康普顿散射中,设反冲电子的速度为0.6c,问:在散射过程中电子获得的能量是其静止能量的多少倍? 解:散射过程中电子获得的能量为
Ek = E − E0 = m0c2/ 1 − v2/c2 − m0c2
所以
Ek =
1
−1=
1
− 1 = 0.25
E0
1 − v2/c2
1 − (0.6c)2/c2
<
x
<
a 5
范围内,粒子出现的概率。
解:由波函数的形式可知波函数已经归一化
(1)粒子在x
=
a 2
处出现的概率密度:
p(x = a/2) = |ψ(x = a/2)|2 = 1
3π 2 cos( ) =
1
a
4
2a
(2)在−
a 5
<
x
<
a 5
范围内,粒子出现的概率
a
a
p(− < x < ) =
a/5 |ψ(x)|2 dx = 1
范围内的概率
0
(x < 0, x > a)
2 a
sin
nπx a
(0 ≤ x ≤ a)
,
2a
√
p=
3 a
|ψ1(x)|2 dx =
1 +
3
3 2π
3
6
(2)对于n = 2,可知粒子出现概率最大位置
2πx π 3π =,
a 22
可得
a 3a x= ,
44
5、若氢原子处于主量子数n = 4的状态,(1)写出其轨道角动量所有可能值;(2)对应l = 3的状态,写出其角动量在 外磁场方向的投影可能取值。
=
hc E
=
6.626 × 10−34 × 3 × 108 4.2 × 1.6 × 10−19 m
≈
2.96 × 10−7m
=
296nm
(2)遏制电压
hν
hc
6.622 × 10−34 × 3 × 108
Uc = e − U0 = λ − U0 = 200 × 10−9 × 1.6 × 10−19 − 4.2 ≈ 2V
≈ 2.03 × 10−19m
p
Ek(Ek + 2mnc2)
6.12 × 1012 × (6.12 × 1012 + 2 × 9.42 × 108) × 1.6 × 10−19
注:由于Ek m0c2,因此近似地有λ ≈ hc/Ek. 6、质量为m的电子,由静止起被电势差U12 = 900V 的电场加速,试计算其德布罗意波的波长。(me = 9.11 ×
解:(1)对于处于主量子数n = 4的氢原子 √√ √
l = 0, 1, 2, 3; L = l(l + 1)¯h = 0, 2¯h, 6h¯, 2 3h¯
(2)对应l = 3的状态
m = −3, −2, −1, 0, 1, 2, 3.Lz = m¯h = −3h¯, −2h¯, −h¯, 0, ¯h, 2¯h, 3¯h.
IV. 作业43答案
1、求氢原子光谱的拉曼系中最大波长和最小波长。 解:氢原子光谱的谱线频率:
νmn
=
1 Rc( n2
−
1 m2 ), R
=
1.096776
×
107m−1, m
>
n
n = 1是拉曼系,拉曼系由m ≥ 2到n = 1能级上的跃迁所发射的辐射组成。 最大波长:从m = 2到n = 1能级上的跃迁所发射的波长
≈
3.6
× 10−22kg
· m/s
3
II. 作业41答案
1、设氢原子的质量为m,动能为Ek,不考虑相对论效应,求其德布罗意波长。 解:由
hν h p= =
cλ
知
h
h
λ= = √
p
2mEk
2、欲使电子腔中电子的德布罗意波长为0.1nm,求加速电压。 解:由于电子的波长不是太长,因此可使用非相对论力学
Emin
=
hc λm
=
hc
λ0
+
2h m0 c
=
hc /(1 +
λ0
2(hc/λ) ) = m0c
m0c2 3
≈ 0.17M eV
(2)反冲电子的最大能量
Emax
=
E0
+
hc λ0
−
hc λm
=
m0c2
+
m0c2
−
m0c2 3
=
5 3
m0
c2
最大动能
1 pm = c
Em2 ax
− m20c4
=
4 3 m0c
91.18nm
2、处于第3激发态的氢原子跃迁回低能态时,可以发出的可见光谱线有多少?请画出跃迁能级图。 解:处于第3激发态的氢原子跃迁回低能态时,可以发出的所有光谱线为
1
ψ3,−1,−1,
1 2
,
2
ψ1,1,0,
1 2
,
3
ψ3,1,1,0,
4
ψ1,0,
1 2
,
1 2
。
解:
1
由于l
≤
0,所以应为ψ3,1,−1,
1 2
2
由于l
<
n,所以应为ψ1,0,0,
1 2
.
3
由于mz
=
±1/2,所以应为ψ3,1,1,±
1 2
.
4
由于ml必须为整数,所以应为ψ1,0,0,
1 2
.
7
=
3.19 × 104m
8、若一个电子和一个质子具有同样的动能,哪个粒子的德布罗意波长较大? 解:考虑到相对论效应,有
