2014年海淀区高三数学文科期末考试含答案
北京海淀区2014年高三二模数学(文)详细解析(转载请注明出自易题库教研团队)

A1 B1
侧面 A1 ACC1 是菱形,
AC AC1 , 1
--------------------------------9 分
3
C E
D B
A
由(1)可得 AB AC , 1 A B A 1C , A AC 面 ABC1 , 1 AC BC1 . 1 又 E, F 分别为棱 BC, CC1 的中点, EF // BC1 , . E F A 1C 18. 解: (Ⅰ)由已知可得 f '( x) x 2 2ax 4 .
5 5 或a , 2 2 5 5 综上, a 的取值范围是 (, ) ( , ) . 2 2
即 (5 2a)(5 2a) 0 ,解得 a 19.解:
x2 y 2 1(a 1) --------------------------------------------1 分 2 a 2 a 1 1 2 由e ,可得 e2 ,----------------------------------------------------------------3 分 2 a2 2 2 解得 a 2 , -----------------------------------------------------------4 分 x2 所以椭圆的标准方程为 ----------------------------------------------------5 分 y2 1 . 2 (Ⅱ)法一:
π 6
------------------------------8 分 --------------------------------9 分 ---------------------------------11 分 --------------------------------12 分 -----------------------------13 分
2014年北京市高考数学试卷(文科)及答案
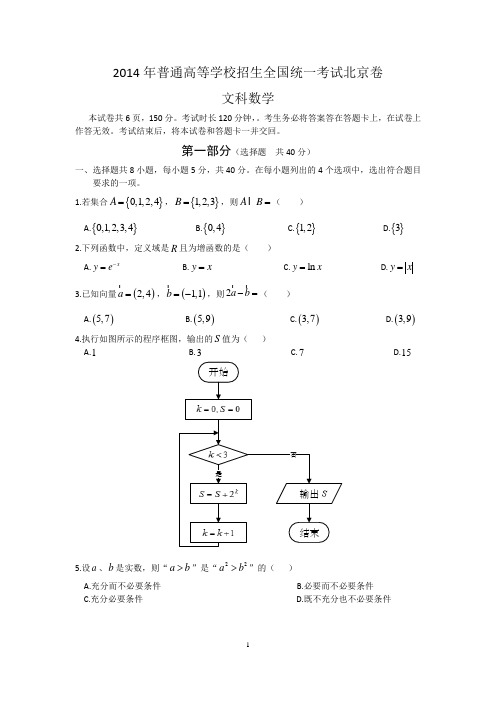
2014年普通高等学校招生全国统一考试北京卷文科数学本试卷共6页,150分。
考试时长120分钟,。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
第一部分(选择题 共40分)一、选择题共8小题,每小题5分,共40分。
在每小题列出的4个选项中,选出符合题目要求的一项。
1.若集合{}0,1,2,4A =,{}1,2,3B =,则AB =( )A.{}0,1,2,3,4B.{}0,4C.{}1,2D.{}3 2.下列函数中,定义域是R 且为增函数的是( )A.xy e -= B.y x = C.ln y x = D.y x = 3.已知向量()2,4a =,()1,1b =-,则2a b -=( )A.()5,7B.()5,9C.()3,7D.()3,9 4.执行如图所示的程序框图,输出的S 值为( )A.1B.3C.7D.15输出5.设a 、b 是实数,则“a b >”是“22a b >”的( )A.充分而不必要条件B.必要而不必要条件C.充分必要条件D.既不充分也不必要条件6.已知函数()26log f x x x=-,在下列区间中,包含()f x 零点的区间是( ) A.()0,1 B.()1,2 C.()2,4 D.()4,+∞7.已知圆()()22:341C x y -+-=和两点(),0A m -,()(),00B m m >,若圆C 上存在点P ,使得90APB ∠=,则m 的最大值为( )A.7B.6C.5D.48.加工爆米花时,爆开且不糊的粒数的百分比称为“可食用率”.在特定条件下,可食用率 p 与加工时间t (单位:分钟)满足的函数关系2p at bt c =++(a 、b 、c 是常数), 下图记录了三次实验的数据.根据上述函数模型和实验数据,可以得到最佳加工时间为( )A.3.50分钟B.3.75分钟C.4.00分钟D.4.25分钟第2部分(非选择题 共110分)二、填空题共6小题,每小题5分,共30分。
【2014海淀一模】北京市海淀区2014届高三下学期期中练习数学文扫描版含答案

海淀区高三年级第二学期期中练习参考答案数学(文科)2014.4 阅卷须知:1.评分参考中所注分数,表示考生正确做到此步应得的累加分数。
2.其它正确解法可以参照评分标准按相应步骤给分。
一、选择题:本大题共8小题,每小题5分,共40分.1.B2.B3.C4.C5.A6.D7. C8.B二、填空题:本大题共6小题,每小题5分,共30分.9. 1 10. 方案三11. 35,712. ③,2()817f x x x=-+13. 15214.π[0,)2{说明:两空的第一空3分,第二空2分;14题的第二空若写成π(0,)2不扣分}三、解答题: 本大题共6小题,共80分.解答应写出文字说明, 演算步骤或证明过程.15.解:(Ⅰ)ππππ()sin sin()6663f=-----------------------------------1分ππsin sin()66=-----------------------------------2分ππsin sin66=+---------------------------------3分π2sin16==---------------------------------4分(Ⅱ)1()sin sin22f x x x x=-+---------------------------------6分1sin2x x=+sin()3xπ=+--------------------------------8分因为ππ22x-≤≤所以ππ5π636x-≤+≤--------------------------------10分所以1πsin()123x -≤+≤ --------------------------------12分所以()f x 的取值范围是1[,1]2- --------------------------------13分16.解:(Ⅰ)答对题目数小于9道的人数为55人,记“答对题目数大于等于9道”为事件A55()10.45100P A =-= --------------------------------5分 (Ⅱ)设答对题目数少于8道的司机为 A 、B 、C 、D 、E ,其中A 、B 为女司机 ,选出两人包含AB 、AC 、AD 、AE 、BC 、BD 、BE 、CD 、CE 、DE 共10种情况,至少有1名女驾驶员的事件为AB 、AC 、AD 、AE 、BC 、BD 、BE 共7种.记“随机选出的两人中至少有1名女驾驶员”为事件M ,则7()0.710P M == --------------------------------13分 17.解:(Ⅰ)因为D ,M 分别为,AC BD 中点,所以DM //EF ---------------------2分 又1EF A EF ⊂平面,1DM A EF ⊄平面所以1//DM A EF 平面. -----------------------4分 (Ⅱ)因为1A E BD ⊥,EF BD ⊥且1A EEF E =所以1BD A EF ⊥平面 -------------7分 又11A F A EF ⊂平面所以1BD A F ⊥ ------------------------9分(Ⅲ)直线1A B 与直线CD 不能垂直 ---------------------------------------10分因为1A BD BCD ⊥平面平面,1A BDBCD BD =平面平面,EF BD ⊥,EF CBD ⊂平面,所以 1EF A BD ⊥平面. ---------------------------------------12分 因为11A B A BD ⊂平面,所以1A B EF ⊥, 又因为//EF DM ,所以1A B DM ⊥. 假设1A B CD ⊥,因为1A B DM ⊥,CDDM D =,所以1A B BCD ⊥平面, ------------------------------------------13分 所以1A B BD ⊥,这与1A BD ∠为锐角矛盾所以直线1A B 与直线CD 不能垂直. ---------------------------------------14分18.解:(Ⅰ) 定义域为()0,+∞ ------------------------------------1分'()ln 1f x x =+ ------------------------------------2分令'()0f x =,得 1ex =------------------------------------3分 '()f x 与()f x 的情况如下:分所以()f x 的单调减区间为1(0,)e ,单调增区间为1(,)e+∞--------------------------6分 (Ⅱ) 证明1:设1()ln g x x x=+,0x > ------------------------------------7分 22111'()x g x x x x-=-= -------------------------------8分 '()g x 与()g x 的情况如下:所以()(1)1g x g ≥=,即 1ln 1x x+≥在0x >时恒成立, ----------------------10分 所以,当1k ≤时,1ln x k x+≥, 所以ln 1x x kx +≥,即ln 1x x kx ≥-,所以,当1k ≤时,有()1f x kx ≥-. ------------------------13分 证明2:令()()(1)ln 1g x f x kx x x kx =--=-+ ----------------------------------7分'()ln 1g x x k =+- -----------------------------------8分令'()0g x =,得1e k x -= -----------------------------------9分'()g x 与()g x 的情况如下:分()g x 的最小值为11(e )1e k k g --=- -------------------11分当1k ≤时,1e 1k -≤,所以11e 0k --≥故()0g x ≥ -----------------------------12分 即当1k ≤时,()1f x kx ≥-. ------------------------------------13分 19.解:(Ⅰ)证明:因为,A B 在椭圆上,所以2211222224,2 4.x y x y ②①ìï+=ïíï+=ïî -----------------------------------1分 因为,A B 关于点(1,0)M 对称,所以12122,0x x y y +=+=, --------------------------------2分将21212,x x y y =-=-代入②得2211(2)24x y -+= ③,由①和③消1y 解得11x =, ------------------------------------------4分 所以 121x x ==. ------------------------------------------5分 (Ⅱ)当直线AB不存在斜率时,(0,A B -,可得AB MA ==∆ABM 不是等边三角形. -----------------------6分当直线AB 存在斜率时,显然斜率不为0.设直线AB :3y kx =+,AB 中点为00(,)N x y ,联立2224,3,x y y kx ⎧+=⎨=+⎩ 消去y 得22(12)12140k x kx +++=, ------------------7分2221444(12)143256k k k ∆=-+⋅=-由0∆>,得到274k >① -----------------------------------8分 又1221212kx x k -+=+, 1221412x x k⋅=+ 所以0002263,31212k x y kx k k -==+=++, 所以 2263(,)1212k N k k-++ -------------------------------------------10分 假设∆ABM 为等边三角形,则有⊥MN AB , 又因为(1,0)M ,所以1MNk k ⨯=-, 即2231216112k k kk +⨯=---+, ---------------------11分 化简 22310k k ++=,解得1=-k 或12k =----------------12分 这与①式矛盾,所以假设不成立.因此对于任意k 不能使得⊥MN AB ,故∆ABM 不能为等边三角形. ------------14分 20.解:(Ⅰ)有序整点列123(0,2),(3,0),(5,2)A A A 与123(0,2),(2,5),(5,2)B B B 互为正交点列.-------------------------1分理由如下:由题设可知 1223(3,2),(2,2)=-=A A A A ,1223(2,3)(33)B B B B ==-,,, 因为 12120=A A B B ,23230=A A B B 所以 12122323⊥⊥A A B B A A B B ,.所以整点列123(0,2),(3,0),(5,2)A A A 与123(0,2),(2,5),(5,2)B B B 互为正交点列. ----------------------------3分 (Ⅱ)证明 :由题意可得 122334(3,1),(3,1)(3,1)A A A A A A ==-=,, 设点列1234,,,B B B B 是点列1234,,,A A A A 的正交点列,则可设121232343(1,3),(1,3)(1,3)B B B B B B λλλ=-==-,,123λλλ∈,,Z 因为1144,与与A B A B 相同,所以有λλλλλλ⎧⎪⎨⎪⎩123123-+-=9①3+3+3=1②因为λλλ∈123,,Z ,方程②不成立,所以有序整点列12340,0),3,1),6,0)(((,9,1)(A A A A 不存在正交点列.----------8分 (Ⅲ)存在无正交点列的整点列(5)A . -------------------------------------------9分当5n =时,设1(,),,,i i i i i i A A a b a b +=∈Z 其中,i i a b 是一对互质整数,1,2,3,4i = 若有序整点列12345,,,,B B B B B 是点列12345,,,,A A A A A 的正交点列, 则1(,),1,2,3,4i i i i i B B b a i λ+=-= ,由441i+1=11+==∑∑i i i i i A AB B得44=1144=11,.i i i i i i i i i i b a a b λλ==⎧-=⎪⎪⎨⎪=⎪⎩∑∑∑∑①②取1,(0,0)A =3,1,2,3,4i a i =,12342,1,1,1b b b b ==-==- 由于12345,,,,B B B B B 是整点列,所以有,1,2,3,4i i λ∈=Z .等式②中左边是3的倍数,右边等于1,等式不成立,所以存在无正交点列的整点列(5)A . -----------------------------------13分。
【2014海淀二模】北京市海淀区2014届高三下学期期末练习 文科数学 Word版含答案-推荐下载

D
代代
C
C1
B1 A1
F B
E A
开始
S=0,n=1
S=S+n
n n2 1
否 n>10
是
输出 S
结束
试卷集合_Wuz
三、解答题: 本大题共 6 小题,共 80 分.解答应写出文字说明, 演算步骤或证明过程.
15.(本小题满分 13 分) 已知函数 f (x) 2 3 sin x cos x 2sin2 x a , a R .
x
x
6.已知向量 AC , AD 和 AB 在正方形网格中的位置如图所示,
若 AC AB AD ,则
A. 2
B. 2
y y
,那么集合
B. x R,x2 x 1 0 D. x R,x2 x 1 0
1 1
C. y cos x
D. (1,1)
D. 3
x
y
1
B AD
C
A
0
2014.5
的距离为
2的 2
① 测量 A,C,b ② 测量 a,b,C
则一定能确定 A, B 间距离的所有方案的序号为
A.①②
B. ②③
试卷集合_Wuz
8. 已知点 E, F 分别是正方体 ABCD A1B1C1D1 的棱 AB, AA1 的中点,点 D1
符合题目要求的一项.
1.
已知全集为
R
,集合
A
{x
|
x
≥ 1}
A.{x | x 1} B.{x | x 1} C.{x | x 1} D.{x | x 1}
2014北京海淀高考二模数学文(含解析)

海淀区高三年级第二学期期末练习 数 学 (文科) 2014.5一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1. 已知全集为R ,集合{}1A x x =≥,那么集合A R ð等于( ).A .{}1x x >B . {}1x x >-C . {}1x x <D . {}1x x <-2. 已知命题:p x ∃∈R ,210x x +-<,则p ⌝为( ).A .2,10x x x ∃∈+->RB . 2,10x x x ∀∈+-≥RC . 2,10x x x ∃∉+-≥RD . 2,10x x x ∀∉+->R3. 下列函数中,既是偶函数又在区间()0,+∞上单调递增的是( ). A.3y x = B.y x C.cos y x = D.2x y =4. 设2log 3a =,4log 3b =,sin 90c =o 则( ).A.a c b << B.b c a << C.c a b << D.c b a <<5. 下面给出的四个点中,位于10,10x y x y ++>⎧⎨-+<⎩表示的平面区域内,且到直线10x y -+=的2). A.()1,1- B.()2,1- C.()0,3 D.()1,16. 已知向量AC uuu r ,AD uuu r 和AB uu u r在正方形网格中的位置如图所示,若AC AB AD λμ=+u u u r u u u r u u u r,则λμ+=( ).A .2B . 2-C . 3D . 3-DCBA7. 如图所示,为了测量某湖泊两侧,A B 间的距离,李宁同学首先选定了与,A B 不共线的一点C ,然后给出了三种测量方案(ABC △的角,,A B C 所对的边分别记为,,a b c ): ①测量当,,A C b ;②测量,,a b C ;③测量,,A B a ,则一定能确定,A B 间的距离的所有方案的序号为( ). A.①②B.②③ C.①③ D.①②③8. 已知点,E F 分别是正方体1111ABCD A B C D -的棱AB ,1AA 的中点,点,M N 分别是线段1D E 与1C F 上的点,则与平面ABCD 垂直的直线MN 有( ). A.0条 B.1条C.2条 D.无数条二、填空题:本大题共6小题,每小题5分,共30分. 9. 复数2i +的模等于_______.10. 若抛物线()220y px p =>的准线经过双曲线221x y -=的左顶点,则p =_______.11. 执行如图所示的程序框图,则输出S 的值为_______.12. 下列函数中:①sin 2y x =-;②cos 2y x =;③π3sin 24y x ⎛⎫=+ ⎪⎝⎭,其图像公通过向左(或向右)平移就能与函数()sin 2f x x =的图像重合的是_______.(填上符合要求的函数对应的序号)BAFE D 1C 1B 1A 1DCBA13. 已知实数0a >且1a ≠,函数(),3,, 3.x a x f x ax b x ⎧<=⎨+≥⎩ 若数列{}n a 满足()()*n a f n n =∈N ,且{}n a 是等差数列,则a =_______,b =_______.14. 农业技术员进行某种作物的种植密度试验,把一块试验田划分为8块面积相等的区域(除了种植密度,其它影响作物生长的因素都保持一致),种植密度和单株产量统计如下:根据上表所提供信息,第____号区域的总产量最大,该区域种植密度为_______株/2m .三、解答题:本大题共6小题,共80分,解答应写出文字说明,演算步骤或证明过程. 15. (本小题满分13分)已知函数()223sin cos 2sin ,f x x x x a a =-+∈R . (I) 求函数()f x 的最小正周期;(II) 若函数()f x 有零点,求实数a 的取值范围.1.2820.20.40.63212下图为某地区2012年1月到2013年1月鲜蔬价格指数的变化情况:记x ∆=本月价格指数-上月价格指数,规定:当0x ∆>时,称本月价格指数环比增长;当0x ∆<时,称本月价格指数环比下降;当0x ∆=时,称本月价格指数环比持平.(I) 比较2012年上半年与下半年鲜蔬价格指数月平均值的大小(不要求计算过程); (II)直接写出从2012年2月到2013年1月的12个月中价格指数环比下降..的月份,若从这12个月中随机选择连续的两个月进行观察,求所选两个月的价格指数都.环比下降的概率;(III) 由图判断从哪个月开始连续三个月的价格指数方差最大?(结论不要求证明)121120136154141130151159138118116151151130901001101201401501601701月12月11月10月9月8月7月6月5月4月3月2月1月如图,在三棱柱111ABC A B C -中, 1AA ⊥底面ABC ,AB AC ⊥,1AC AA =,,E F 分别是棱1,BC CC 的中点.(I) 求证: AB ⊥平面11AA C C ;(II)若线段AC 上的点D 满足平面DEF ∥平面1ABC ,试确定点D 的位置,并说明理由;(III) 证明: 1EF A C ⊥.B 1C 1A 1GFEC AB已知函数()32143f x x ax x b =+++,其中,a b ∈R 且0a ≠.(I) 求证:函数()f x 在点()()0,0f 处的切线与()f x 总有两个不同的公共点; (II) 若函数()f x 在区间()1,1-上有且仅有一个极值点,求实数a 的取值范围.已知椭圆G 2,短轴端点分别为()0,1A,()0,1B-.(I)求椭圆G的标准方程;(II)若,C D是椭圆G上关于y轴对称的两个不同点,直线BC与x轴交于点M,判断以线段MD为直径的圆是否过点A,并说明理由.给定正整数3k ≥,若项数为k 的数列{}n a 满足:对任意的1,2,,i k =L 均有1ki S a k ≤-(其 中12k k S a a a =+++L ),则称数列{}n a 为“Γ数列”. (I) 判断数列DEF 和1ABC ,52a <-,π是否是“Γ数列”,并说明理由;(II) 若{}n a 为“Γ数列”,求证: 0对1,2,,i k =L 恒成立;(III)设{}n b 是公差为d 的无穷项等差数列,若对任意的正整数123,,,,m m b b b ≥L 均构成“Γ数列”,求{}n b 的公差d .海淀区高三年级第二学期期末练习参考答案 数 学 (文科) 2014.5一、选择题:本大题共8小题,每小题5分,共40分. 1.C 2.B 3.D 4.B 5.A 6.A 7.D 8.B 二、填空题:本大题共6小题,每小题5分,共30分.95 10.2 11.8 12.①② 13.2,0 14.5,3.6 {第13,14题的第一空3分,第二空2分} 三、解答题: 本大题共6小题,共80分. 15.解:(Ⅰ)()3sin 2cos21f x x x a ++- ------------------------4分312(2cos 2)12x x a =++- π2sin(2)16x a =++- -------------------------6分∴周期2ππ.2T == --------------------------7分 (Ⅱ)令()0f x =,即π2sin(2)1=06x a ++-, ----------------------------8分则π=12sin(2)6a x -+, ------------------------------9分因为π1sin(2)16x -≤+≤, --------------------------------11分所以π112sin(2)36x -≤-+≤, -------------------------------12分所以,若()f x 有零点,则实数a 的取值范围是[1,3]-. --------------------------13分16.解:(Ⅰ)上半年的鲜疏价格的月平均值大于下半年的鲜疏价格的月平均值.---------------4分 (Ⅱ)从2012年2月到2013年1月的12个月中价格指数环比下降的月份有4月、5月、6月、9月、10月. --------------------------------------6分设“所选两个月的价格指数均环比下降”为事件A , -------------------------------------7分 在这12个月份中任取连续两个月共有11种不同的取法,-----------------------------8分 其中事件A 有(4月,5月),(5月,6月),(9月,10月),共3种情况.-------9分 ∴3().11P A =-----------------------------------------10分 (Ⅲ)从2012年11月开始,2012年11月,12月,2013年1月这连续3个月的价格指数方差最大. ----------------------------------------13分17.解:(I )1A A ⊥Q 底面ABC ,1A A ∴⊥AB , -------------------------2分AB AC ⊥Q ,1A A AC A =I ,AB ∴⊥面11A ACC . --------------------------4分(II )Q 面DEF //面1ABC ,面ABC I 面DEF DE =,面ABC I 面1ABC AB =,AB ∴//DE , ---------------------------7分 Q 在ABC ∆中E 是棱BC 的中点,D ∴是线段AC 的中点. ---------------------------8分(III )Q 三棱柱111ABC A B C -中1A A AC = ∴侧面11A ACC 是菱形,11AC AC ∴⊥, --------------------9分 由(1)可得1AB AC ⊥, Q 1AB AC A =I ,1A C ∴⊥面1ABC , -------------------------------11分 1A C ∴⊥1BC . ---------------------------12分又,E F Q 分别为棱1,BC CC 的中点,EF ∴//1BC , -------------------13分1EF AC ∴⊥. ---------------------14分18. 解:(Ⅰ)由已知可得2'()24f x x ax =++. -------------------------1分'(0)4f ∴=, ------------------2分又(0)f b =()f x ∴在0x =处的切线方程为4y x b =+. -------------------------4分令321443x ax x b x b +++=+,整理得2(3)0x a x +=.0x ∴=或3x a =-, -----------------------5分0a ≠Q 30a ∴-≠, ---------------------6分FD EB 1C 1A 1BAC()f x ∴与切线有两个不同的公共点. -----------------------7分(Ⅱ)()f x Q 在(1,1)-上有且仅有一个极值点,∴2'()24f x x ax =++在(1,1)-上有且仅有一个异号零点, --------------------9分由二次函数图象性质可得'(1)'(1)0f f -<, -------------------------------10分 即(52)(52)0a a -+<,解得52a >或52a <-, ---------------------------12分综上,a 的取值范围是55(,)(,)22-∞-+∞U . ----------------13分19.解:(Ⅰ)由已知可设椭圆G 的方程为:2221(1)x y a a+=> -------------------------------------1分由2e =,可得222112a e a -==,----------------------------------------3分解得22a =, ---------------------------------------4分所以椭圆的标准方程为2212x y +=. -----------------------------------5分(Ⅱ)法一:设00(,),C x y 则000(,),0D x y x -≠ ---------------------------------------6分 因为(0,1),(0,1)A B -, 所以直线BC 的方程为0011y y x x +=-, --------------------------------------------7分 令0y =,得001M x x y =+,所以0(,0)1x M y +. ------------------------------------8分 所以0000(,1),(,1),1x AM AD x y y =-=--+uuu r uuu r--------------------------------9分所以20011x AM AD y y -⋅=-++uuu r uuu r , ---------------------------------10分 又因为2200121x y +=,代入得200002(1)111y AM AD y y y -⋅=+-=-+uuu r uuu r ---------------11分 因为011y -<<,所以0AM AD ⋅≠uuu r uuu r. ------------------------------------------------12分所以90MAN ∠≠o , ---------------------------------------------13分所以点A 不在以线段MN 为直径的圆上. ---------------------------------14分 法二:设直线BC 的方程为1y kx =-,则1(,0)M k . --------------------------------------6分由22220,1,x y y kx ⎧+-=⎨=-⎩化简得到222(1)20x kx +--=,所以22(12)40k x kx +-=,所以12240,21kx x k ==+, ----------------------------8分所以22222421112121k k y kx k k k -=-=-=++, 所以222421(,)2121k k C k k -++,所以222421(,)2121k k D k k --++ ---------------------------------9分所以2221421(,1),(,1),2121k k AM AD k k k --=-=-++u u u r u u u r -----------------------------------10分所以2222421210212121k AM AD k k k ---⋅=-+=≠+++u u u r u u u r , -----------------------------------12分所以90MAN ∠≠o , -------------------------------13分所以点A 不在以线段MN 为直径的圆上. --------------------------14分 20.解: (Ⅰ)①因为5135514S =<-,数列1,3,5,2,4-不是“Γ数列”, -----------------------------2分 ②因为31113311284S =>-,又34是数列2323333,,444中的最大项 所以数列2323333,,444是“Γ数列”. ----------------------------------------------4分(Ⅱ)反证法证明:假设存在某项i a <0,则12111i i k k k i k a a a a a a S a S -+-+++++++=->L L .设12111max{,,,,,,,}j i i k k a a a a a a a -+-=L L ,则12111k i i i k k j S a a a a a a a k a -+--=+++++++L L ≤(-1), 所以(1)j k k a S ->,即1kj S a k >-, 这与“Γ数列”定义矛盾,所以原结论正确. --------------------------8分 (Ⅲ)由(Ⅱ)问可知10,0b d ≥≥.①当0d =时,121m m m S Sb b b m m ====<-L ,符合题设; ---------------------9分 ②当0d >时,12m b b b <<<L 由“Γ数列”的定义可知1m m S b m ≤-,即111(1)[(1)](1)2m b m d mb m m d -+-≤+- 整理得1(1)(2)2m m d b --≤(*)显然当123m b =+时,上述不等式(*)就不成立所以0d >时,对任意正整数3m ≥,1(1)(2)2m m d b --≤不可能都成立. 综上讨论可知{}n b 的公差0d =. -------------------------------------------------13分2014北京市海淀区高三统一测试数学(文科)选填解析一、 选择题 1.【答案】C【解析】解:因为{}1A x x =≥,所以{}|1A x x =<R ð. 故选C .2.【答案】B【解析】解:由存在命题的否定可知“x ∃∈R ,210x x +-<成立”的否定为“x ∀∈R ,有210x x +-≥成立”. 故选B .3.【答案】D【解析】解:A 选项为奇函数,不满足题意;B 选项定义域不满足奇偶性的定义,为非奇非偶函数,不满足题意;C 选项在()0,+∞有增有减,不满足题意. 故选D .4.【答案】B【解析】解:可知22log 3log 21a =>=,44log 3log 41b =<=,sin 901c ==o . 故选B .5.【答案】A【解析】解:把点(1,1)-点带入不等式区域111010111010-++>>⎧⎧⇒⎨⎨--+<-<⎩⎩,满足题意;故不满足题意;利用点到直线距离公式111211d --+==+ 故选A .6.【答案】A【解析】解:建立如图坐标系,则 ()()()2,2,1,2,1,0AC AB AD =-==u u u r u u u r u u u r时,由题可知()()()222,21,21,024λμλλμλμ=+=-⎧⎧-=+⇒⇒⎨⎨-==⎩⎩所以2λμ+=.D CBA yx故选A .7.【答案】D【解析】解:由题可知①②③的三个条件满足三角形全等的判定,所以三角形图像唯一故通过解三角形的知识求出AB . 故选D .8.【答案】B【解析】解:取线段11,FC D E 的中点为,N M ,易证 1MN DD ∥,故满足题意;下证唯一性,假设存在另外一组11,N M ,使得111M N DD ⊥,1111,MN DD M N DD ⊥⊥Q111111,,,,MN M N M M D E N N C F ∴∈∈∥11C FD E ∴四点共面,这与11,C F D E 是异面直线矛盾,故这样的点,N M 只有唯一一组.故选B .二、 填空题 95【解析】解:由222i 215++= 5.10.【答案】2【解析】解:由双曲线的方程可知1a =,而左顶点过抛物线准线,故 122pa p -=-=-⇒=. 故答案为2.11.【答案】8【解析】解:列表S1 3 8 循环结束NMFED 1C 1B 1A 1DCB An1 25 26 输出S故答案为8.12.【答案】①②【解析】解:①②③的周期为π,与()s i n2f xx=的周期一样,而③的取值范围是[]3,3-,不可能通过平移变换得到范围为[]1,1-.故答案为①②.13.【答案】2;0【解析】解:由等差数列通项性质可知当3x ≥时,数列的公差d a =,故221232203a a a a a aa a a ab a b a a ⎧-=-==⎧⎧⎪⇒⇒⎨⎨⎨-==+-=⎪⎩⎩⎩. 故答案为2;0.14.【答案】5;3.6【解析】解:由题可知种植密度的函数表达式()[]()*0.3 2.11,8,f x x x x =+∈∈N ,单株产量的函数表达式为()[]()*0.08 1.361,8,g x x x x =-+∈∈N ,故总产量为()()()20.3 2.10.08 1.360.0240.24 2.856h x x x x x =+-+=-++, 当()0.24520.024x =-=⨯-时取得最大值,此时密度为()50.35 2.1 3.6f =⨯+=.故答案为5;3.6.。
【VIP专享】北京海淀区2014年高三二模数学(文)详细解析(转载请注明出自易题库教研团队)

1解析:根据集合的基本运算性质答案C.2解析:存在命题的否命题是:存在变为任意,条件不变,结论变为对立命题。
3解析:A 是奇函数;B 非奇非偶;C 是偶函数;单在区间上不上一直递增的;D 是偶函数在区间上是单调递增的。
4解析:根据对数函数的性质a>1;0<b<1;c=1;所以答案B.5解析:本题可以通过选项带入求解B,D 不在平面区域;C (0,3)到直线的距离不等于2所以答案为A 。
6解析:以A 为坐标原点,(1,2),(1,0),(2,2)AB AD AC ===-,(2,2)(,2)2λμλλμ-=+∴+=,所以答案A.7解析:本题考察正余弦定理的实际应用,①③知道三个角,一个边,可以应用正弦定理求解A,B 间的距离,②给出的条件可以运用余弦定理求解。
所以三个条件均可以求解AB 间的距离。
8解析:求解与平面ABCD 平行的平面,因为直线11,D E C F 是两条异面直线,所以相当与做面11CDD C 的平行面,当把面11CDD C 平移导面11ABB A 时,一定会与直线11,D E C F 相交与两点,所以与平面ABCD 垂直的直线MN 有一条。
9. 解析:2i +==10.解析:抛物线的准线方程2p x =-,双曲线的左顶点(-1,0)122p p -=-∴= 11.解析:第一次循环S=0,n=1;第二次循环S=1,n=2;第三次循环S=3,n=5;第四次循环S=8,n=26;n>10,输出结果S=812.解析:sin 2y x =-向右平移2π个单位得到sin 2y x =;cos 2y x =向有平移4π个单位得到sin 2y x =;3sin(2)4y x π=+要通过x 不变,y 伸长3倍函数再向右平移8π平移伸缩得到sin 2y x =;所以满足条件的是①②。
13.解析:数列是等差数列,,3(),3n a n f n an b n ⎧<=⎨+≥⎩;21234,,3,4a a a a a a b a a b ===+=+;根据等差数列的中项公式22132;23;a a a a a a b =+=++①23242;64a a a a b a a b =++=++;②解方程①②得b=0.a=2.14.解析:根据题意,种植密度为一次函数,函数经过(1,2.4),(8, 4.5)所以函数的解析式114.5 2.42.4(1),0.3 2.181y x y x --=-=+-;单株产量也满足一次函数,函数经过(1, 1.28),(8,0.72)所以函数的解析式220.72 1.281.28(1),0.08 1.3681y x y x --=-=-+-;所以区域总产量为种植密度乘以单株产量2120.30.08(7)(17)0.30.08(10119)y y y x x x x =⨯=-⨯+-=-⨯--;所以当x=5时,函数有最大值;所以第五号区域的总产量最大;该区域种植密度x=5带入1y ,所以种植密度为3.6.海淀区高三年级第二学期期末练习参考答案数 学 (文科) 2014.5 阅卷须知:1.评分参考中所注分数,表示考生正确做到此步应得的累加分数。
20141104高三海淀区文科数学题

20141104高三海淀区文科数学题1 / 3海淀区高三年级第一学期期中练习数学(文科)2013.11本试卷共4页,150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
一、选择题:本大题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
1. 已知集合{1,0,1,2}A =-,{|1}B x x =≥,则A B =( )A. {2}B. {1,2}C. {1,2}-D. {1,1,2}-2. 下列函数中,为奇函数的是( )A. ()f x =B. ()ln f x x =C. ()2x f x =D. ()sin f x x =3. 已知向量(1,2),(,1)m =-=-a b ,且//a b ,则实数m 的值为( ) A. 2- B. 12-C.12D. 24.“π6α=”是“1sin 2α=”的() A. 充分而不必要条件 B. 必要而不充分条件 C. 充分必要条件D. 既不充分也不必要条件5. 已知数列{}n a 的前n 项和为n S ,且*1110,3()n n a a a n +=-=+∈N ,则n S 取最小值时,n 的值是()A. 3B. 4C. 5D. 66.若函数tan ,0,()2(1)1,0x x f x a x x π⎧-<<⎪=⎨⎪-+≥⎩在π(,)2-+∞上单调递增,则实数a 的取值范围( )A. (0,1]B. (0,1)C. [1,)+∞D. (0,)+∞7.若函数()sin f x x kx =-存在极值,则实数k 的取值范围是( ) A. (1,1)-B. [0,1)C. (1,)+∞D. (,1)-∞-8.已知点(1,0)B ,P 是函数e x y =图象上不同于(0,1)A 的一点.有如下结论: ①存在点P 使得ABP ∆是等腰三角形;2②存在点P 使得ABP ∆是锐角三角形; ③存在点P 使得ABP ∆是直角三角形. 其中,正确的结论的个数为( ) A. 0B.1C. 2D. 3二、填空题:本大题共6小题,每小题5分,共30分。
北京市海淀区2014届高三下学期期末练习(二模)数学文试题 含答案

海淀区高三年级第二学期期末练习参考答案数 学 (文科) 2014.5 阅卷须知:1.评分参考中所注分数,表示考生正确做到此步应得的累加分数。
2.其它正确解法可以参照评分标准按相应步骤给分。
一、选择题:本大题共8小题,每小题5分,共40分.1.C2.B3.D4.B5.A6.A7.D8.B二、填空题:本大题共6小题,每小题5分,共30分.10.2 11.8 12.①② 13.2,0 14.5,3.6{第13,14题的第一空3分,第二空2分}三、解答题: 本大题共6小题,共80分.15.解:(Ⅰ)()2cos21f x x x a =++- --------------------------4分12cos2)12x x a =++- π2sin(2)16x a =++- ---------------------------6分 ∴周期2ππ.2T == ----------------------------7分 (Ⅱ)令()0f x =,即π2sin(2)1=06x a ++-, ------------------------------8分 则π=12sin(2)6a x -+, --------------------------------9分 因为π1sin(2)16x -≤+≤, ---------------------------------11分 所以π112sin(2)36x -≤-+≤, --------------------------------12分 所以,若()f x 有零点,则实数a 的取值范围是[1,3]-. -----------------------------13分 16.解:(Ⅰ)上半年的鲜疏价格的月平均值大于下半年的鲜疏价格的月平均值.--------------------4分 (Ⅱ)从2012年2月到2013年1月的12个月中价格指数环比下降的月份有4月、5月、6月、9月、10月. ------------------------------------------6分设“所选两个月的价格指数均环比下降”为事件A , --------------------------------------7分在这12个月份中任取连续两个月共有11种不同的取法,------------------------------8分其中事件A 有(4月,5月),(5月,6月),(9月,10月),共3种情况. ---------9分 ∴3().11P A = -----------------------------------------10分 (Ⅲ)从2012年11月开始,2012年11月,12月,2013年1月这连续3个月的价格指数方差最大.-----------------------------------------13分17.解:(I )1A A ⊥Q 底面ABC ,1A A ∴⊥AB , -------------------------2分 AB AC ⊥Q ,1A A AC A =I ,AB ∴⊥面11A ACC . --------------------------4分 (II )Q 面DEF //面1ABC ,面ABC I 面DEF DE =,面ABC I 面1ABC AB =, AB ∴//DE , ---------------------------7分Q 在ABC ∆中E 是棱BC 的中点,D ∴是线段AC 的中点. ---------------------------8分 (III )Q 三棱柱111ABC A B C -中1A A AC =∴侧面11A ACC 是菱形, 11AC AC ∴⊥, --------------------------------9分 由(1)可得1AB AC ⊥, Q 1AB AC A =I ,1AC ∴⊥面1ABC , --------------------------------11分 1AC ∴⊥1BC . -------------------------------12分 又,E F Q 分别为棱1,BC CC 的中点,EF ∴//1BC , ------------------------------13分 1EF AC ∴⊥. ------------------------------14分18. 解:(Ⅰ)由已知可得2'()24f x x ax =++. ---------------------------------1分'(0)4f ∴=, ---------------------------------2分 又(0)f b =()f x ∴在0x =处的切线方程为4y x b =+. ---------------------------------4分令321443x ax x b x b +++=+,整理得2(3)0x a x +=. 0x ∴=或3x a =-, -----------------------------------5分 0a ≠Q 30a ∴-≠, ----------------------------------------6分 ()f x ∴与切线有两个不同的公共点. ----------------------------------------7分 (Ⅱ)()f x Q 在(1,1)-上有且仅有一个极值点,∴2'()24f x x ax =++在(1,1)-上有且仅有一个异号零点, ---------------------------9分1由二次函数图象性质可得'(1)'(1)0f f -<, -------------------------------------10分即(52)(52)0a a -+<,解得52a >或52a <-, ----------------------------12分 综上,a 的取值范围是55(,)(,)22-∞-+∞U . -------------------------------13分 19.解:(Ⅰ)由已知可设椭圆G 的方程为:2221(1)x y a a+=> --------------------------------------------1分由e ,可得222112a e a -==,----------------------------------------------------------------3分 解得22a =, -----------------------------------------------------------4分 所以椭圆的标准方程为2212x y +=. ----------------------------------------------------5分 (Ⅱ)法一:设00(,),C x y 则000(,),0D x y x -≠ ------------------------------------------------------6分 因为(0,1),(0,1)A B -,所以直线BC 的方程为0011y y x x +=-, ------------------------------------------------------7分 令0y =,得001M x x y =+,所以00(,0)1x M y +. ----------------------------------------------8分 所以0000(,1),(,1),1x AM AD x y y =-=--+u u u u r u u u r -------------------------------------------9分 所以200011x AM AD y y -⋅=-++u u u u r u u u r , ---------------------------------------------10分 又因为2200121x y +=,代入得200002(1)111y AM AD y y y -⋅=+-=-+u u u u r u u u r --------------------11分 因为011y -<<,所以0AM AD ⋅≠u u u u r u u u r . -----------------------------------------------------------12分所以90MAN ∠≠o , -------------------------------------------------------13分所以点A 不在以线段MN 为直径的圆上. ---------------------------------------------14分 法二:设直线BC 的方程为1y kx =-,则1(,0)M k. ------------------------------------------------6分 由22220,1,x y y kx ⎧+-=⎨=-⎩化简得到222(1)20x kx +--=,所以22(12)40k x kx +-=,所以12240,21k x x k ==+, -------------------------------------8分所以22222421112121k k y kx k k k -=-=-=++, 所以222421(,)2121k k C k k -++,所以222421(,)2121k k D k k --++ ----------------------------------------9分 所以2221421(,1),(,1),2121k k AM AD k k k --=-=-++u u u u r u u u r ---------------------------------------------10分 所以2222421210212121k AM AD k k k ---⋅=-+=≠+++u u u u r u u u r , --------------------------------------12分 所以90MAN ∠≠o , ---------------------------------------13分所以点A 不在以线段MN 为直径的圆上. ------------------------------------14分20.解: (Ⅰ)①因为5135514S =<-,数列1,3,5,2,4-不是“Γ数列”, ---------------------------------2分 ②因为31113311284S =>-,又34是数列2323333,,444中的最大项 所以数列2323333,,444是“Γ数列”. ----------------------------------------------4分 (Ⅱ)反证法证明:假设存在某项i a <0,则12111i i k k k i k a a a a a a S a S -+-+++++++=->L L .设12111max{,,,,,,,}j i i k k a a a a a a a -+-=L L ,则12111k i i i k k j S a a a a a a a k a -+--=+++++++L L ≤(-1),所以(1)j k k a S ->,即1k j S a k >-, 这与“Γ数列”定义矛盾,所以原结论正确. --------------------------8分 (Ⅲ)由(Ⅱ)问可知10,0b d ≥≥.①当0d =时,121m m m S S b b b m m ====<-L ,符合题设; ---------------------9分 ②当0d >时,12m b b b <<<L由“Γ数列”的定义可知1m m S b m ≤-,即111(1)[(1)](1)2m b m d mb m m d -+-≤+- 整理得1(1)(2)2m m d b --≤(*)显然当123m b =+时,上述不等式(*)就不成立所以0d >时,对任意正整数3m ≥,1(1)(2)2m m d b --≤不可能都成立.综上讨论可知{}n b 的公差0d =. --------------------------------------------------13分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
海淀区高三年级第一学期期末练习数学(文科) 2014.01本试卷共4页,150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
一、选择题:本大题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
1.复数i(i 1)+等于A. 1i +B.1i -+C. 1i -D.1i --2.已知直线1:210l x y +-=与直线2:0l mx y -=平行,则实数m 的取值为A. 12-B.12C. 2D.2-3.为了估计某水池中鱼的尾数,先从水池中捕出2000尾鱼,并给每尾鱼做上标记(不影响存活),然后放回水池,经过适当的时间,再从水池中捕出500尾鱼,其中有标记的鱼为40尾,根据上述数据估计该水池中鱼的尾数为A .10000B .20000C .25000D .300004.阅读右边的程序框图,运行相应的程序,输出的S 值为 A.15B.14 C. 7D.65.已知2log 3a =,4log 6b =,4log 9c =,则 A .a b c =<B .a b c << C .a c b =>D .a c b >>6.已知函数22,2,()3,2,x f x x x x ⎧≥⎪=⎨⎪-<⎩若关于x 的方程()f x k =有三个不等的实根,则实数k 的取值范围是A.(3,1)-B. (0,1)C. (2,2)-D. (0,)+∞7.在ABC ∆中,若2a b =,面积记作S ,则下列结论中一定..成立的是 A .30B >B .2A B =C .c b <D .2S b ≤8.如图所示,正方体1111ABCD A B C D -的棱长为1,BD AC O = ,M 是线段1D O 上的动点,过点M 做平面1ACD 的垂线交平面 1111A B C D 于点N ,则点N 到点A 距离的最小值为1A二、填空题:本大题共6小题,每小题5分,共30分。
9.双曲线2213y x -=的离心率为___. 10.某四棱锥的三视图如右图所示,则该四棱锥的体积为__.11.已知点(,)P x y 的坐标满足40,12,0,x y x y +-≤⎧⎪≤≤⎨⎪≥⎩则2z x y =+的最大值为________.12.已知等差数列{}n a 和等比数列{}n b 满足11222,4a b a b ==-==,则满足n na b =的n 的所有取值构成的集合是______.13.某企业三个分厂生产同一种电子产品,三个分厂产量分布如图所示,现在用分层抽样方法从三个分厂生产的该产品中共抽取100件做使用寿命的测试,则第一分厂应抽取的件数为___;由所得样品的测试结果计算出一、二、三分厂取出的产品的使用寿命平均值分别为1020小时,980小时, 1030小时,估计这个企业所生产的该产品的平均使用寿命为___小时.14.直线1x =与抛物线C :24y x =交于,M N 两点,点P 是抛物线C 准线上的一点,记(,)OP aOM bON a b =+∈R,其中O 为抛物线C 的顶点. (1)当OP 与ON平行时,b =________;(2)给出下列命题:①,a b ∀∈R ,PMN ∆不是等边三角形;②∃0a <且0b <,使得OP 与ON垂直;③无论点P 在准线上如何运动,1a b +=-总成立. 其中,所有正确命题的序号是___.三、解答题: 本大题共6小题,共80分。
解答应写出文字说明, 演算步骤或证明过程。
15.(本小题共13分)函数cos2()2sin sin cos xf x x x x=++.(Ⅰ)求π()4f 的值;(Ⅱ)求函数()f x 的最小正周期及其图象的所有对称轴的方程.正视图3左视图俯视图根据以往的成绩记录,甲、乙两名队员射击击中目标靶的环数的频率分布情况如图所示(Ⅰ)求上图中a 的值;(Ⅱ)甲队员进行一次射击,求命中环数大于7环的概率(频率当作概率使用); (Ⅲ)由上图判断甲、乙两名队员中,哪一名队员的射击成绩更稳定(结论不需证明).17.(本小题共14分)如图,在四棱锥P ABCD -中,底面ABCD 是菱形,PA PB =,且侧面PAB ⊥平面ABCD ,点E 是棱AB 的中点. (Ⅰ)求证://CD 平面PAB ; (Ⅱ)求证:PE AD ⊥;(Ⅲ)若CA CB =,求证:平面PEC ⊥平面PAB .18.(本小题共13分)已知函数()()e x f x x a =+,其中a 为常数.(Ⅰ)若函数()f x 是区间[3,)-+∞上的增函数,求实数a 的取值范围; (Ⅱ)若2()e f x ≥在[0,2]x ∈时恒成立,求实数a 的取值范围.a已知椭圆C :22221(0)x y a b a b+=>>的离心率为12,右焦点为F ,右顶点A 在圆F :222(1)(0)x y r r -+=>上. (Ⅰ)求椭圆C 和圆F 的方程;(Ⅱ)已知过点A 的直线l 与椭圆C 交于另一点B ,与圆F 交于另一点P .请判断是否存在斜率不为0的直线l ,使点P 恰好为线段AB 的中点,若存在,求出直线l 的方程;若不存在,说明理由.20.(本小题共13分)如果函数()f x 满足在集合*N 上的值域仍是集合*N ,则把函数()f x 称为N 函数. 例如:()f x x =就是N 函数.(Ⅰ)判断下列函数:①2y x =,②21y x =-,③y =中,哪些是N 函数?(只需写出判断结果); (Ⅱ)判断函数()[ln ]1g x x =+是否为N 函数,并证明你的结论; (Ⅲ)证明:对于任意实数,a b ,函数()[]x f x b a =⋅都不是N 函数.(注:“[]x ”表示不超过x 的最大整数)海淀区高三年级第一学期期末练习数学(文)参考答案及评分标准2014.1阅卷须知:1.评分参考中所注分数,表示考生正确做到此步应得的累加分数。
2.其它正确解法可以参照评分标准按相应步骤给分。
一、选择题(本大题共8小题,每小题5分,共40分)二、填空题(本大题共6小题,每小题5分, 有两空的小题,第一空3分,第二空2分,共30分)三、解答题(本大题共6小题,共80分)15.(本小题共13分)解:(Ⅰ)πcosππ2()2sinππ44sin cos44f=+==+. ------------------------3分(Ⅱ)由sin cos0x x+≠得ππ,4x k k≠-∈Z.因为cos2()2sinsin cosxf x xx x=++22cos sin2sinsin cosx xxx x-=++--------5分cos sinx x=+π)4x=+,----------------7分所以()f x的最小正周期2πT=. -------------------------------------9分因为函数siny x=的对称轴为ππ+,2x k k=∈Z, ------------------------------11分又由πππ+,42x k k+=∈Z,得ππ+,4x k k=∈Z,所以()f x的对称轴的方程为ππ+,4x k k=∈Z.-----------------------------------13分16.(本小题共13分)解:(Ⅰ)由上图可得0.010.190.290.451a++++=, 所以0.06a=. -----4分(Ⅱ)设事件A为“甲队员射击,命中环数大于7环”,它包含三个两两互斥的事件:甲队员射击,命中环数9. 2 10.16 11. 712.{1,2,4}13.50,1015 14.1-;①②③所以()0.290.450.010.75P A =++=. ----------------------------------9分 (Ⅲ)甲队员的射击成绩更稳定. ---------------------------------13分 17.(本小题共14分)解:(Ⅰ)因为底面ABCD 是菱形,所以//CD AB . ----------------------------1分 又因为CD ⊄平面PAB , -------------------3分 所以//CD 平面PAB . --------------------------4分 (Ⅱ)因为PA PB =,点E 是棱AB 的中点,所以PE AB ⊥. ----------------------------------5分 因为平面PAB ⊥平面ABCD ,平面PAB 平面ABCD AB =,PE ⊂平面PAB ,----7分 所以PE ⊥平面ABCD , ------------------------------------8分 因为AD ⊂平面ABCD , 所以PE AD ⊥. ----------9分(Ⅲ)因为CA CB =,点E 是棱AB 的中点, 所以CE AB ⊥. -------10分 由(Ⅱ)可得PE AB ⊥, ---------------------------------11分 所以AB ⊥平面PEC , --------------------------------13分 又因为AB ⊂平面PAB ,所以平面PAB ⊥平面PEC . -------14分 18.(本小题共13分)解:(Ⅰ)'()(1)e x f x x a =++,x ∈R . -------------------------------2分 因为函数()f x 是区间[3,)-+∞上的增函数,所以'()0f x ≥,即10x a ++≥在[3,)-+∞上恒成立.------------------------------3分 因为1y x a =++是增函数,所以满足题意只需310a -++≥,即2a ≥. -------------------------------5分 (Ⅱ)令'()0f x =,解得1x a =-- -------------------------------6分(),'()f x f x 的情况如下:--------------------------------------10分①当10a --≤,即1a ≥-时,()f x 在[0,2]上的最小值为(0)f ,所以此时,2e a ≥; --------------------------------------11分②当012a <--<,即31a -<<-时,()f x 在[0,2]上的最小值为(1)f a --, 若满足题意只需2(1)e f a --≥,求解可得此不等式无解,所以a 不存在; ------------------------12分③当12a --≥,即3a ≤-时,()f x 在[0,2]上的最小值为(2)f , 若满足题意只需2(2)e f ≥,解得1a ≥-,所以此时,a 不存在. ------------------------------13分综上讨论,所求实数a 的取值范围为2[e ,)+∞. 19. (本小题共14分)解:(Ⅰ)由题意可得1c =, ----------------------------------1分 又由题意可得12c a =,所以2a =, --------------2分 所以2223b a c =-=, ----------------------------------3分所以椭圆C 的方程为22143x y +=. ---------------------------------4分所以椭圆C 的右顶点(2,0)A , --------------------------------5分 代入圆F 的方程,可得21r =,所以圆F 的方程为22(1)1x y -+=. ------------------------------6分 (Ⅱ)法1:假设存在直线l :(2)y k x =-(0)k ≠满足条件, -----------------------------7分由22(2),143y k x x y =-⎧⎪⎨+=⎪⎩得2222(43)1616120k x k x k +-+-=----------------------------8分设11(,)B x y ,则21216243k x k +=+, ---------------------------------9分可得中点22286(,)4343k kP k k -++, --------------------------------11分由点P 在圆F 上可得2222286(1)()14343k k k k --+=++化简整理得20k =--------------------------------13分 又因为0k ≠,假设存在直线l 满足题意.由(Ⅰ)可得OA 是圆F 的直径, -----------------------------7分 所以OP AB ⊥. ------------------------------8分 由点P 是AB 中点,可得||||2OB OA ==.--------------------------------9分设点11(,)B x y ,则由题意可得2211143x y +=. --------------------------------10分又因为直线l 的斜率不为0,所以214x <, -------------------------------11分所以22222211111||3(1)3444x x OB x y x =+=+-=+<,-------------------------------13分这与||||OA OB =矛盾,所以不存在满足条件的直线l . --------------------------14分 20. (本小题共13分)解:(Ⅰ)只有y =是N 函数. ----------------------------3分 (Ⅱ)函数()[ln ]1g x x =+是N 函数. 证明如下:显然,*x ∀∈N ,*()[ln ]1g x x =+∈N . ---------------------------------------4分不妨设*[ln ]1,x k k +=∈N ,由[ln ]1x k +=可得1ln k x k -≤<, 即11e e k k x -≤≤<.因为*k ∀∈N ,恒有11e e e (e 1)1k k k ---=->成立, 所以一定存在*x ∈N ,满足1e e k k x -≤<, 所以设*k ∀∈N ,总存在*x ∈N 满足[ln ]1x k +=,所以函数()[ln ]1g x x =+是N 函数. ---------------------------------------8分 (Ⅲ)(1)当0b ≤时,有2(2)[]0f b a =⋅≤,所以函数()[]x f x b a =⋅都不是N 函数. ---------------------------9分(2)当0b >时,① 若0a ≤,有(1)[]0f b a =⋅≤,所以函数()[]x f x b a =⋅都不是N 函数. ------------------10分② 若01a <≤,由指数函数性质易得x b a b a ⋅≤⋅,所以*x ∀∈N ,都有()[][]x f x b a b a =⋅≤⋅所以函数()[]x f x b a =⋅都不是N 函数. -----------------11分③ 若1a >,令12m m b a b a +⋅-⋅>,则2log (1)am b a >⋅-,所以一定存在正整数k 使得12k k b a b a +⋅-⋅>, 所以*12,n n ∃∈N ,使得112k k b a n n b a +⋅<<<⋅, 所以12()(1)f k n n f k <<≤+.又因为当x k <时,x k b a b a ⋅<⋅,所以()()f x f k ≤; 当1x k >+时,1x k b a b a +⋅>⋅,所以()(1)f x f k ≥+, 所以*x ∀∈N ,都有*1{()|}n f x x ∉∈N ,所以函数()[]x f x b a =⋅都不是N 函数.------------------13分综上所述,对于任意实数,a b ,函数()[]x f x b a =⋅都不是N 函数.。
