均相化学反应器
环境工程原理pp第13章均相化学反应器综述PPT文档共71页

11、用道德的示范来造就一个人,显然比用法律来约束他更有价值。—— 希腊
12、法律是无私的,对谁都一视同仁。在每件事上,她都不徇私情。—— 托马斯
13、公正的法律限制不了好的自由,因为好人不会去做法律不允许的事 情。——弗劳德
14、法律是为了保护无辜而制定的。——爱略特 15、像房子一样,法律和法律都是相互依存的。——伯克
▪
28、知之者不如好之者,好之者不如乐之者。——孔子
▪
29、勇猛、大胆和坚定的决心能够抵得上武器的精良。——达·芬奇
▪
30、意志是一个强壮的盲人,倚靠在明眼的跛子肩上。——叔本华
谢谢!
71
▪
26、要使整个人生都过得舒适、愉快,这是不可能的,因为人类必须具备一种能应抱怨环境的心情,化为上进的力量,才是成功的保证。——罗曼·罗兰
第三节 理想均相反应器的计算

间歇搅拌釜式反应器(BSTR) 平推流(活塞流)反应器(PFR) 理想均相反应器 全混流(连续搅拌釜式)反应器(CSTR) 多级全混流反应器(MCSTR)
一、基本原理
1. 物料衡算式:
流入量 = 流出量 + 反应消耗量 + 累积量 2. 热量衡算式: 物料带入量 = 物料带出量 + 反应热效应 + 累积量 3. 反应动力学方程式:
0
c A0 x Af (rA ) f (1 A x Af )
因此,对于变容过程,往往选择标准状况下的体积流量 作为计算空时的基准。
全混釜一般设计方程讨论
5. 动力学特征
1 rA
c A0
1 rA f
1 x Af (rA ) f
1 rA
t c A0
x Af
0
dxA rA
矩形面积
FA0 0.685 1 171 L h 单位时间处理物料的体积量为: 0 c A0 0.004
(3)计算反应体积 V 0 (t t) 171 (8.47 1) 1619L 1.619(m3 ) (4)由装料系数0.75计算反应器体积 V 1.619 VR 2.159(m3 ) 0.75
3.2kmol/m3。该反应为一级,反应温度下的反应速率常数为8×10-3s-1,最 终转化率为98.9%。若加料速率为10kmol/h,则需多大体积的全混流反应 器?若在一个体积为1m3的等温间歇釜中进行,辅助操作时间为30min,求 苯酚的产量和处理10kmol/h过氧化异丙苯时的反应体积?并与全混釜比较。 【思考123】① 恒容过程?变容过程?② 求反应器体积?反应体积? ③ 怎样从设计方程到反应体积?
实验十九 连续均相反应器停留时间分布的测定

实验十九连续均相反应器停留时间分布的测定1 实验目的本实验旨在通过测量连续均相反应器中溶液的进出时间,得到反应器的停留时间分布,并探究不同进料流速对停留时间分布的影响。
2 实验原理连续均相反应器是指反应物在气液、液液或固液两相混合后,在反应器内不断流动,实现反应的一种装置。
在连续均相反应器中,每个质点在反应器内的停留时间是不同的,因此停留时间分布是一个反应器的重要性能参数。
停留时间分布是指质点在反应器内停留时间的概率密度函数,它能反映反应器内的流动特性、物理化学变化。
在本实验中,设计的反应器为塔式反应器,研究单一液相在反应器中的停留时间分布。
反应器内的搅拌器不断搅拌反应液,以保持液体中浓度的均匀分布,使反应均匀进行。
反应器内自上向下分别放置了进料管口、液面计和出料口,通过测量进出管口的时间,可以测定连续均相反应器中质点的停留时间分布。
3 实验步骤3.1 实验器材塔式连续反应器、溶液储罐、液面计、蠕动泵、计时器。
1. 准备实验样品。
将20%的乙醇溶液稀释为5%分数的乙醇溶液,作为实验样品。
2. 设置实验参数。
设定不同的进料流速,包括1.0 mL/min、2.0 mL/min、3.0 mL/min、4.0 mL/min、5.0 mL/min。
3. 注入实验样品。
将实验样品注入液体储罐,设定蠕动泵的流速。
4. 记录出料时间。
在实验操作开始时,记录出料口的时间和液面计读数,随着溶液的流动,不断记录出料时间和液面计读数。
5. 重复实验。
重复同样的实验步骤,至少进行3次以上的实验。
4 实验结果4.1 停留时间分布曲线通过实验数据计算得出不同进料流速下的停留时间分布曲线,如图所示。
图中的横坐标为反应器内质点的停留时间,纵坐标为停留时间的概率密度函数。
根据图中的曲线可以看出,不同进料流速下,停留时间分布的峰值和分布范围都存在差异。
在进料流速较低(≤2.0 m L/min)时,停留时间分布的峰值较窄、分布范围较窄。
化学反应工程-9-第二章-均相理想流动反应器

表1 几种桨叶在不同要求下的不同适用情况
过程 桨叶形状 螺旋桨式 涡轮式 平桨式 螺旋桨式 涡轮式 平桨式 特征参数 容积/mL 0~3.785ⅹ105 0~2.08ⅹ105 0~7.57ⅹ105 固体含量/% 0~50 0~100 65~90 物料流量/ (cm3/s) 0~1.90 0~63 0~0.19 容积/mL 0~39.7ⅹ103 0~75.7ⅹ103 0~189ⅹ103 容积/L 0~3.97ⅹ103 0~37.85ⅹ103 0~37.85ⅹ103 要求 D/d H/D 没有 限制 补充说明
螺旋桨叶:NV=0.5;
NV=0.93D/d,D为釜直径。
六叶涡轮桨叶,叶片宽度和直径之比W/d=1/5 ,当Red>104,
功率数NP、NV和Red之间的关系如下图:
二、釜式反应器内混合概念
对于CSTR,存在两种混合。 1、返混 不同停留时间物料间的混合,即返混。CSTR是返混达到最大 的一种反应器。 问题:完全混合如何判断? 经验标准是:
a b
rS k 2C A2 CB2
a
b
瞬时选择率: 则:
rP SP rP rS
1 1 SP rS k 2 a2 a1 b2 b1 1 C A CB 1 k1 rP
问题:如何提高选择率?
⑴连续操作 ① a1 a2,b1 b 2 对 C A、C B 的控制应使都高,操作方式如下:
螺旋桨 式,平 直叶, 三叶 41.0 0.32
桨叶型 式 KL KT
螺距式, 涡轮式, 三叶 六平叶 43.5 1.00 71.0 6.30
六叶后 掠弯式 70.0 4.80
风扇涡 轮式, 六叶 70.0 1.65
平桨式, 二叶 36.5 1.70
化学反应工程chap 1 均相单一反应动力学和理想反应器

活化能隐含的反应速率对温度敏感程度的度量
例子: 例子:现有两个反应的活化能分别为100kJ/mol和
150kJ/mol ,试计算两者分别(a)温度由300K上 升10K,(b)温度由400K上升10K时速率常数k的 增大倍数。
E(KJ/mol) 100 100 150 150 温度(K) 300-310 400-410 300-310 400-410 速率常数增大倍数 3.64 2.08 6.96 3.00
22
对于体系中只进行一个不可逆反应的过程。 对于体系中只进行一个不可逆反应的过程。
aA+bB→rR + sS
m n −rA = kccAcB
m ⋅ m−3 ⋅s−1 ol
度上,符合阿累尼乌斯关系。 度上,符合阿累尼乌斯关系。
kc为以浓度表示的反应速率常数,随反应级数的不同 为以浓度表示的反应速率常数, 有不同的因次。一般, 是温度的函数, 有不同的因次。一般,kc是温度的函数,在一般工业精
∆nI nI −nI 0 ξ= = aI aI
相应地, 相应地,反应进行到某一时刻
nI = nI 0 + aIξ
10
反应程度的性质
※ ※ ※ ※ 时间的函数, 时间的函数,随反应的进行而不同 积累量,恒大于0 积累量,恒大于0 广度量 与反应式的写法有关
和性,如:功 和性,
广度量:描述体系的广度性质, 广度量:描述体系的广度性质,具有加 强度量:描述体系的强度性质, 强度量:描述体系的强度性质,不具加
7
对于化学反应计量方程 对于化学反应计量方程
aA+bB+L = rR+ sS +L L L
表示化学反应过程中各个组份间量的变化关系。亦 表示化学反应过程中各个组份间量的变化关系。 可以写成其它若干形式: 可以写成其它若干形式:
反应器基础知识—化学反应器的类型
反应过程 进行的条件
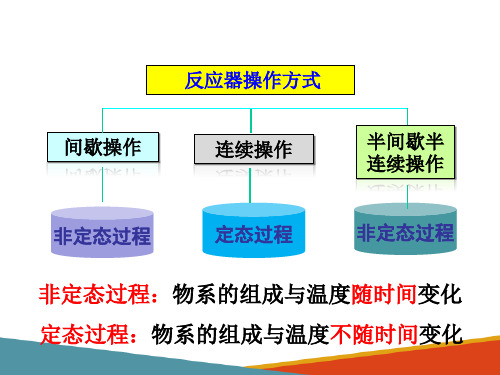
操作温度:等温反应、变温反应。 操作压力:常压反应、加压反应、减压反应。 操作方式:间歌式、连续式、半连续式。 旗热方式:自热式、对外换热式、绝执斗。
相的类别和数目
根据反应过程中所涉及的物料的相态可把反应分为均相反应和 非均相反应。 均相度应:指反应过程中只存在一个相态。如气相反应、液相 反应、固相反应。 均相反应:反应过程中不只存在一个相态。如气液相反应、液固相反应、气-液-固三相反应、气-固相反应。
反应速率除考虑温度、浓度等因素外,还与相间传质速率有关。
2. 按反应器结构分类 (a) 釜式反应器; (b)管式反应器; (c)固定床反应器; (d)流化床反应器; (e)塔式反应器:板式塔、填料塔、鼓泡塔、喷雾塔
实质是按传递过程的特征分类,相同结构反应器内物料具 有相同流动、混和、传质、传热等特征。
。
常见的工业反应器
均相间歇反应器
半间歇反应器
连续搅拌反应器组合
轴向填充床催化反应器
流化床催化反应器
一、化学反应类型:
化学反应类型
操作温度: 操作压力: 操作方式: 换热方式:
均相反应: 非均相反应:
反应特性
反应机理:简单反应(只发生一个化学反应)、复杂反应(不 只发生一个反应,如平行反应、连串反应、自催化反应)。 反应级数:零级反应、一级反应、二级反应、分数级反应等。 不同级数的反应,反应浓度对反应速率的贡献不同。 反应分子数:单分子反应、双分子反应、三分子反应等。 可逆性:可逆反应、不可逆反应。 热效应:吸热反应、放热反应。
均相: 气相:如石油烃管式裂解炉 液相: 如乙酸丁酯的生产
非均相: g-l相:如苯的烷基化 g-s相:如合成氨 l-l相:如已内酰胺缩合 l-s相:如离子交换 g-l-s相:如焦油加氢精制
环境工程原理 均相化学反应器

反应量 -rAV
浓度cA,cB 体积V
积累量:dnA/dt=d(cAV)/dt=cA(dV/dt)+V(dcA/dt) 物料衡算式:
qVcA0=(-rA)V+ cA(dV/dt)+V(dcA/dt) qVcA0=(-rA)V+ cAqV+V(dcA/dt) V=V0+qVt
(13.1.2) (13.1.3)
二、多级串联反应器
(一)多级串联全混流反应器的基本方程
c0
c1
c2
cn
-1/rA
τ=τ1+τ2+···+τn
τ = τ1 +τ2 +τ3 +τ4
τ4 τ3
τ2
τ1
0 cA
c A0
第二节 全混流反应器
在恒容条件下,第i个反应器的基本设计方程为:
τi
=
Vi qV
=
cA(i−1) −cAi − rAi
=
反应器的基本方程
A的输入量=A的输出量+A的反应量+A的积累量 qnA0=qnA+(-rA)ΔV+dnA/dt
第一节 间歇与半间歇反应器
本节的主要内容
一、间歇反应器 二、半间歇反应器
第一节 间歇与半间歇反应器
一、间歇反应器
1. 间歇反应器的操作方法 将反应物料按一定比例一次加到反应器内,然后开始搅
A ⎯⎯k1→ P ⎯⎯k2 → Q
− rA = k1cA rP = k1cA − k2cP
rQ = k2cP
cA
=
cA0
1+ k1τ
cP
=
(1 +
cA0k1τ k1τ )(1+
k2τ )
cQ
均相反应器安全操作及保养规程

均相反应器安全操作及保养规程前言均相反应器是在化学工程、医药等领域中广泛应用的一种实验室器材。
它能够保持反应物在反应中的均相状态,从而提高反应效率。
均相反应器在使用过程中,必须注意安全操作和保养,以保持其长期稳定运行。
本文主要介绍均相反应器的安全操作及保养规程,包括使用前准备、操作过程中的注意事项、使用后的清理保养等内容,以帮助操作人员正确使用和保养均相反应器。
使用前准备1. 安装在使用均相反应器之前,应先检查其安装是否正确。
应将均相反应器放置在平稳的表面上,并连接好电源和水源等相应的设备。
在连接电源和水源时,必须保证其安全可靠,避免发生电漏、水渗漏等不安全因素。
2. 检查仪器检查均相反应器的所有配件是否齐全、无损坏现象,防止在使用过程中发生器材的故障或信息的错误。
3. 开启空气泵通电后,先开启空气泵,同时观察仪表的压力,以判断空气泵是否工作正常。
空气泵开启后,观察出口的气泡是否正常。
4. 开启水泵等空气泵工作正常后,再开启水泵。
用手触摸出水口,检查水流是否正常,是否有渗漏现象。
如果水流过小,应先检查滤芯有无泥沙等杂物阻塞。
5. 预热在进行反应前,首先需要用适量的水和试剂进行清洗,使均相反应器能够达到适宜的反应温度。
均相反应器开始工作后,应进行预热,预热时需根据反应物的特性合理地控制反应温度,以避免均相反应器过热。
操作过程中的注意事项1. 操作前的准备在进行反应操作前,应首先熟悉所需反应物和反应条件,制定相应的实验方案。
操作时应穿着适当的工作服和安全防护服,并保持仪器周围的清洁和整齐,避免杂物占据仪器周围的空间。
2. 使用聚四氟乙烯器皿使用均相反应器时,尽量选择聚四氟乙烯器皿,这样可以降低反应物附着并减少表面张力。
并应注意选择适合聚四氟乙烯器皿的容器大小。
3. 添加试剂在均相反应器中添加试剂时,应逐步加入,避免一次加入过多。
同时,应注重振荡速度和时间的关系,避免振荡速度过快,导致消耗过多的反应物。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
xA 0
(12.2.1)
(12.2.2)
(12.2.3) (12.2.4)(恒容反应)
dxA rA
t
cA
c A0
dcA rA
(12.2.6)(恒容反应)
第一节 间歇与半间歇反应器
间歇反应器的图解设计法
t c A0
xA
0
dxA rA
(12.2.4)
t
A的流入量
qn A0 qVcA0
反应量 -rAV
浓度cA 体积V
qvcA0=(-rA)V+ cAqv+V(dcA/dt)
(13.1.3)
第一节 间歇与半间歇反应器
例题13.1.2
对于由反应 (a) 和 (b) 构成的反应系统,试定性说明在下 述半间歇操作时的反应系统中各组分的浓度变化。 (1)先向反应器中加入A,之后连续加入B。 (2)先向反应器中加入B,之后连续加入A。 A+B→P,r1=k1cAcB A+P→Q,r2=k2cAcP (a) (b)
1 n
[(1 x A )1n 1]
(n 1)
Vm c A rA Km cA
t
1 [c A0 x A K m ln(1 x A )] Vm
c A0 c B c B0 c A ln c B0 B c A0 x A c B0 (1 x A )
A BB P
nA=(nA0+qnA0t)(1-xA)
第一节 间歇与半间歇反应器
2. 半间歇反应器的设计方程
单位时间内A的加入量:qnA0=qvcA0 单位时间内A的排出量:0 反应量:(-rA)V 积累量:dnA/dt=d(cAV)/dt=cA(dV/dt)+V(dcA/dt) 物料衡算式: qvcA0=(-rA)V+ cA(dV/dt)+V(dcA/dt) (13.1.2)
第一节 间歇与半间歇反应器
半间歇操作的特点
(1)与间歇操作一样,是一个非稳态过程 (2)与间歇操作不同之处:反应混合液的体积随时间而 变化。
A的流入量 A的流入量
qn A0 qVcA0
反应量 -rAV 浓度cA 体积V
qn A0 qVcA0
反应量 -rAV A的流出量 浓度cA 体积V A的流出量
q n A q v cA
q n A q v cA
第一节 间歇与半间歇反应器
(二)半间歇反应器的设计计算
1. 转化率的定义
对于二级不可逆反应A+B→P
t时间内反应消耗掉的 A的量 xA A的起始量+t时间内加入的A的量 ( n A 0 qn A 0 t ) n A nA = 1 n A 0 qn A 0 t n A 0 qn A 0 t
cA 0
(t c A0 k )
ln(c A c A0 ) ln(1 x A ) kt
2
A P
rA kcA rA kcA
1 1 kt c A c A0
cA
1 n
t
cA
c A0
dcA rA
n
c A0
1 n
(n 1)kt
c A0
rA kc A c B
ln
(c B0 B c A0 )kt
第一节 间歇与半间歇反应器
例题13.1.1
间歇反应器中发生一级反应A → B(恒容反应),反
应速率常数k为0.35 h-1,要使A的去除率达到90%,则 A在反应器中需反应多少小时?
解:设xA为转化率,则cA的值为
cA=cA0(1-xA)= cA0(1-0.90)=0.10cA0 根据设计方程:cA/cA0=e-kt 有0.10cA0/cA0=e-0.35t 解得t=6.58h
第一节 间歇与半间歇反应器
二、半间歇反应器 (一)半间歇反应器的操作方法 (1) 将两种或两种以上的反应物、或其中的一些组分一次性 放入反应器中,然后将某一种反应物连续加入反应器。
特点:可控制加入成分在反应器中的浓度,便于控制反 应速率
(2) 将反应物料一次性加入反应器,在反应过程中将某个产 物连续取出。 特点:可以使反应产物维持在低浓度水平(利于可逆反 应向生成产物的正方向进行;防止分泌产物对微生物生 长的抑制作用)
反应率达到所定的目标之后,将混合物料排出反应器。之后
再加入物料,进行下一轮操作,如此反复。 2、间歇反应器的设计计算 设计计算的目的
(1)确定达到一定的反应率时需要的反应时间
(2)根据反应时间确定转化率或反应后的各组分浓度
第一节 间歇与半间歇反应器
间歇反应器设计的基本方程及设计方法
dnA rAV dt dx A n A0 rAV dt x A dx A t n A0 0 r V A
第一节 间歇与半间歇反应器
例题
间歇反应器中发生二级反应A +B→ C(恒容反应),实 验测得反应动力学方程为:rA=kcA2,速率常数 k=1.97L/kmol.min,已知:cA0=0.004kmol/L,求A的转化率 分别达到50%、60%、80%、90%,所需反应是多少? 如每天处理2400kgA(分子量146),转化率为80%, 每批操作的非生产时间为1h,计算反应器体积应为多少? 设反应釜装料系数为0.75.
第十三章 均相化学反应器
本章主要内容 第一节 间歇与半间歇反应器
第二节 完全混合流反应器
第三节 平推流反应器
第一节 间歇与半间歇反应器
本节的主要内容 一、间歇反应器 二、半间歇反应器
第一节 间歇与半间歇反应器
一、间歇反应器
1、间歇反应器的操作方法
将反应物料按一定比例一次加到反应器内,然后开始搅
拌,使反应器内物料的浓度和温度保持均匀。反应一定时间,
cA
c A0
dcA rA
(12.2.6)
1 rA
1 rA
面积
0
t c A0
xA
0
面积 t
cA
c A0
表 13.1-1 恒容恒温间歇与平推流反应器的设计方程 反应 反应速率方程 设计方程
rA k
rA kc A
c A0 c A c A0 x A kt (t c A0 k )
第一节 间歇与半间歇应器
A+B→P,r1=k1cAcB A+P→Q,r2=k2cAcP (a) (b)
c
cA
cQ
c
cB
cB
cP
cQ
t (a)先加入A,连续加入B时的变化
