大学物理 几何光学 薄透镜
几何光学综合实验报告

466.7
4
100.0
650.0
232.8
522.1
5
100.0
700.0
221.1
574.5
6
100.0
750.0
215.1
630.9
凸透镜焦距相关计算如下:
= 像屏位置 − 物屏位置
= 小像,透镜位置 − 大像透镜位置
由 =
2 −2
4
得:
表 2 凹透镜焦距
1 (mm)
97.384
2. 自组望远镜
表 3 望远镜数据表
1
物屏位置
(mm)
准直透镜位置
(mm)
物镜位置
(mm)
目镜位置
(mm)
100.0
200.0
811.9
1000.0
3. 自组望远镜并测量凹透镜焦距
表 4 自组望远镜并测量凹透镜焦距数据记录表
缩小实像位置 a(mm)
L2 位置 b(mm)
1
678.9
629.2
2
648.7
主光轴。其它通过透镜光心的直线皆为透镜的附光轴。
2.薄透镜成像公式:
在近轴光束的条件下,薄透镜成像公式为:
1
1
1
= +
…(1)
其中:
u:物距 v:像距 f:焦距
实物、实像时,u,v 为正;虚物、虚像时 u,v 为负。凸透镜 f 为正;凹透镜 f 为负。
3.位移法测凸透镜焦距:
当物体 AB 与像屏 M 的间距 > 4 时,透镜在 D 区间移动,可在屏上两次成像,一次成清晰放大的实像1 1,
同一高度,且连线(光轴)平行于导轨。
几何光学实验

薄透镜焦距测量实验⼀、实验⽬的:1、通过实验深刻理解薄透镜的成像规律;2、熟悉薄透镜焦距测量的⽅法;3、学习和掌握光学系统调节过程中共轴等⾼的调节技巧、各微调光学仪器的使⽤⽅法;4、拓展研究薄透镜在显微系统、望远系统和幻灯⽚系统中的应⽤原理。
⼆、实验原理:透镜是组成各种光学仪器的基本光学元件,焦距则是透镜的⼀个重要参数。
在不同的使⽤场合往往要选择合适的透镜或透镜组,这就需要测定透镜的焦距。
本实验通过不同的实验⽅法来研究薄透镜的成像规律,并确定其焦距。
1. 薄透镜成像公式当透镜的厚度远⽐其焦距⼩的多时,这种透镜称为薄透镜。
在近轴光线的条件下,薄透镜成像的规律可表示为:(1)式中U表示物距,V表示像距,f为透镜的焦距,U、V和f均从透镜的光⼼O点算起。
并且规定U恒取正值;当物和像在透镜异侧时,V为正值;在透镜同侧时,V为负值。
对凸透镜f 为正值,对凹透镜f为负值。
2. 凸透镜焦距的测定(1)⾃准法如图1所示,将物A放在凸透镜的前焦⾯上,这时物上任⼀点发出的光束经透镜后成为平⾏光,由平⾯镜反射后再经透镜会聚于透镜的前焦平⾯上,得到⼀个⼤⼩与原物相同的倒⽴实像A´。
此时,物屏到透镜之间的距离就等于透镜的焦距f。
图1 ⾃准法测薄透镜焦距光路图(2)共轭法如图2所示,固定物与像屏的间距为D(D>4f),当凸透镜在物与像屏之间移动时,像屏上可以成⼀个⼤像和⼀个⼩像,这就是物像共轭。
根据透镜成像公式得知:u 1=v 2 ; u 2=v1(因为透镜的焦距⼀定)若透镜在两次成像时的位移为d ,则从图中可以看出,故 。
由 得: (2)由上式可知只要测出D 和d ,就可计算出焦距f 。
共轭法的优点是把焦距的测量归结为对于可以精确测量的量D 和d 的测量,避免了测量U 和V 时,由于估计透镜光⼼位置不准带来的误差。
3.⾃准法测量凹透镜焦距凹透镜是发散透镜,⽤透镜成像公式测量凹透镜的焦距时,凹透镜成的像为虚象,且虚像的位置在物和凹透镜之间,因⽽⽆法直接测量其焦距,⾃准法来测量。
物理几何光学竞赛讲解及试题

A
F2 B′
A
B
F1 O
A′
B F1
O
F2
L
L
2.一般光线的作图
对于任意一条光线SA,过光心O作副光轴OP平 行于SA,SA与焦平面MN交于P点,连接AP或AP的 反向延长线即为SA的折射光线。
A
M P
S
F1
O F2
N L
M A
S F1
O
F2
PN
L
3.注意:
(1)物点上所发出的任意一条光线,经成像系统作 用后,必定会通过像点;
x1
(n 1)d nf (n 1)d
f
x2
(n 1)d n
11.如图所示,外形一样,折射率均为n的两个薄平凸透 镜,一个透镜的平面镀银,另一个透镜的凸面镀银。 如果光线从未镀银的一面入射,它们的焦距之比为多 少?
f : f′= n : (n-1)
12.如图所示,容器中装有深度为2h的某种液体,其折射
位置成一等大、倒立的像,如图所示。试求出满足上 述要求的配置方案中各透镜的位置。
物
L1
L2
像
取焦距较小的L1放在物右方u处,把焦距较大的L2放
在L1右方d处,其中
d 2 f1 f2
u 2 f1 f2 ( f2 f1 )
9.在焦距为f 的凸透镜L的主光轴上放置 一个发光圆锥
面(如图所示),圆锥的中心轴线与主光轴重合,圆
孔等大,且其主光轴与光屏垂直,再在此透镜的主光
轴上与光心相距为a处置一点光源S,因而在光屏上形 成一个半径为R的圆形光斑。已知a=30cm,b=20cm, r=1cm,R=5cm。试求此透镜的焦距。
(1)若为凸透镜,f=3cm; (2)若为凹透镜,f=-6cm。
大学物理 几何光学 薄透镜.ppt
n0 ni 1
i
ff
ni
(nL
1 1)( 1
r1
1) r2
O i
Qp
nL
d 0
d
p1 Q2 Q1 p2
薄透镜成像公式
1 1 1 p p f
➢ 符号规则:以薄透镜光心为分界点,入射光线方向 为正向,如入射光线自左向右,则当物点、像点、焦点 和薄透镜两面的曲率中心在光心右侧时,物距、像距、 焦距和曲率半径均为正;反之,在左侧则为负 .
r1 0, r2 0 r1 r2
r2 r1 0
r1 0, r2 0 r2 0 r1
r1 0,r2 0 r1 r2
➢ 凹、凸透镜成像图
1
1
h0
hi
2
F
p
2
1
h0
2 3
f
F
F
hi 3
P
p 1 2
➢ 焦平面 过焦点且垂直于主
光轴的平面,平行光线 (近轴)会聚于焦平面.
焦平面
解:第一种情况时有
第二种情况时有
11 1 p1 p1 f
11 1 p2 p2 f
p1 hi 1 p1 h0 2
p2 1 p2
得 p1 3 f
且 p2 p1 100 3 f 100 得 f 100mm
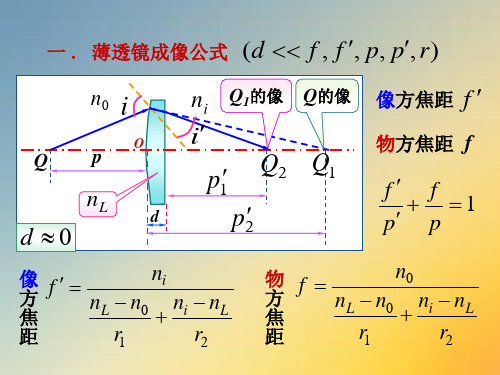
一 . 薄透镜成像公式 (d f , f , p, p, r)
n0 i
O
Qp
nL
d
d 0
ni Q1的像 Q的像
i
p1 Q2 Q1 p2
像方焦距 f
物方焦距 f
f f 1 p p
像 方 焦
f
ni nL n0 ni
nL
薄透镜的实验报告

一、实验目的1. 了解薄透镜的基本成像规律。
2. 掌握光学系统的共轴调节方法。
3. 学会使用自准直法、物距-像距法测量薄凸透镜的焦距。
4. 了解凹透镜的成像特性。
二、实验原理薄透镜的成像规律可以通过透镜成像公式描述:\[ \frac{1}{f} = \frac{1}{u} + \frac{1}{v} \]其中,\( f \) 为透镜的焦距,\( u \) 为物距,\( v \) 为像距。
自准直法是利用透镜将发散光会聚为平行光,通过反射后再会聚,从而确定透镜的焦距。
物距-像距法是利用透镜成像公式,通过测量物距和像距来计算焦距。
凹透镜对光线具有发散作用,当物体位于凹透镜的焦点之外时,所成的像是虚像。
三、实验仪器1. 薄凸透镜2. 凹透镜3. 自准直仪4. 平面反光镜5. 白炽光源6. 狭缝架7. 物屏8. 刻度尺9. 记录本四、实验步骤1. 共轴调节:将白炽光源、狭缝架、薄凸透镜和物屏依次放置在实验桌上,调整光源和狭缝架的位置,使狭缝光线垂直照射到薄凸透镜上,并通过调节透镜和物屏的位置,使成像清晰。
2. 自准直法测量焦距:- 将平面反光镜放置在薄凸透镜的另一侧,调整其角度,使光线经过透镜后反射回狭缝架上。
- 移动薄凸透镜,使狭缝架上的像与狭缝对齐,此时物距等于焦距,记录薄凸透镜的位置。
- 重复上述步骤三次,求平均值。
3. 物距-像距法测量焦距:- 将物屏放置在薄凸透镜的一侧,调整其位置,使成像清晰。
- 使用刻度尺测量物距和像距,记录数据。
- 重复上述步骤三次,求平均值。
- 根据透镜成像公式计算焦距。
4. 凹透镜成像实验:- 将凹透镜放置在白炽光源和狭缝架之间,调整其位置,使成像清晰。
- 使用刻度尺测量物距和像距,记录数据。
- 分析凹透镜的成像特性。
五、实验结果与分析1. 自准直法测量焦距:- 平均焦距:\( f_{avg} = 0.15 \) m- 测量误差:\( \Delta f = 0.01 \) m2. 物距-像距法测量焦距:- 平均焦距:\( f_{avg} = 0.15 \) m- 测量误差:\( \Delta f = 0.01 \) m3. 凹透镜成像实验:- 成像为虚像,且成像位置与物体位置相反。
薄 透 镜

• 薄透镜的光焦度为
n n
f f
• 在国际单位制中,光焦度的单位称屈光度,用 D 表示。
1.2 薄透镜成像的作图法 横向放大率
• 由于过单球面曲率中心 的光线不偏折,故 O即为单球面 的光心。对薄透镜需注意:仅当其处于同一介质,即物方 和像方折射率相同时,过薄透镜光心 的光线才不偏折。 如图所示,薄透镜成像的三条典型光线为:
大学物理
薄透镜 • 1.1薄透镜成像规律
1.1 薄透镜成像规律
• 当 d远小于r1 、r2 及焦距时,可认为 d→0,即 O1、O2
重合在O 。成为最简单的共轴球面系统,称为薄透镜, O 称为光心.薄透镜成像可利用单球面相继成像的方法得到。 因透镜很薄,两个顶点可以看作是重合在一点O。若透镜 两边的折射率相同,则通过O点的光线都不改变原来的方 向,这样的点称为透镜的光心。在薄透镜中量度距离都从 光心算起。
1.1 薄透镜成像规律
• 下面我们利用逐次成像法导出薄透镜成像的公式。
• 设主轴上一物点Q 离薄透镜光心 O的距离为 p1,薄透镜材 料的折射率为nL 。对薄透镜左方第一折射球面,物方折射
率为n1 ,像方折射率为 n1 nL ,得
nL p1
n1 p1
nL n1 r1
1
1
nL
r1
n1
第一折射球面的光焦度
• (1)过物方焦点 的入射光线,其出射光线平行于主轴; • (2)平行于主轴的入射 光线,其出射光线过 像方焦点 ; • (3)对像方和物方为同 一介质中的薄透镜,过光心 的入射光线,其出射光线不发生偏折。
1.2 薄透镜成像的作图法 横向放大率
• 薄透镜由两个单折射球面构成,利用对每个单球面折射逐步成像的方法,不难
薄透镜成像规律的研究

薄透镜成像规律的研究薄透镜是一种常见的光学器件,具有广泛的应用领域,如眼镜、相机、显微镜等。
对于薄透镜成像规律的研究,可以帮助我们更好地理解光学现象,进而应用于实际生活和科学研究中。
一、薄透镜的基本原理薄透镜是由两个或多个用透明介质界面隔开的透镜片组成的。
当光线通过透镜时,会发生折射和聚焦现象,从而形成被称为光的成像。
薄透镜的成像规律可由两条基本光线追迹法确定。
1. 几何光学近似薄透镜的成像规律可采用几何光学近似来描述。
在几何光学中,我们将光线视为直线,不考虑光的波动性,只考虑光线的传播路径。
2. 主光线和次光线在描述薄透镜的成像规律时,我们使用了主光线和次光线的概念。
主光线是指从物体上某一点出发,经过光轴上的光心点,最后到达像上的点的光线。
次光线是指从物体上某一点出发,与光心点平行,折射后通过透镜焦点的光线。
通过主光线和次光线的追踪,可以确定物体和像的位置关系。
二、薄透镜的成像公式薄透镜的成像规律可以通过成像公式来描述。
成像公式可以帮助我们计算出光线通过薄透镜后的物像距离和物像高度的关系。
1. 成像距离公式对于一根从物体上射出的光线经过薄透镜后的成像位置,我们可以使用以下的成像距离公式来描述:1/f = 1/v - 1/u其中,f表示透镜的焦距,v表示成像距离,u表示物距。
2. 物像高度公式薄透镜的成像规律也可通过物像高度公式来描述。
物像高度公式可以帮助我们计算出物体和像的高度之间的关系。
h'/h = -v/u其中,h'表示像的高度,h表示物体的高度。
三、薄透镜成像的类型薄透镜的成像可以分为凸透镜和凹透镜两种类型。
1. 凸透镜成像凸透镜是常见的一种透镜类型。
当物体远离凸透镜时,成像会在凸透镜的焦点附近形成实像。
当物体靠近凸透镜时,成像会在凸透镜的背面形成虚像。
2. 凹透镜成像凹透镜与凸透镜相反,也是一种常见的透镜类型。
当物体经过凹透镜后,成像会在凹透镜的背面形成实像。
无论物体离凹透镜有多远,成像总是在凹透镜的背面形成实像。
1_6_薄透镜

F、 F '
Q 等已知点和已知光线
(2)第一次利用特殊光线作图法做图 (3)以后各次均利用任意光线作图法做图 (4)按比例测量成像后的各个待求量的值
(5)每次均应检验,再进行下一次做图
6.10 例题
n
n' n' n'
n
'
n'
n' n
n'
n
n
(a)
(b)
(c)
(d)
n' n时
n
'
凹透镜是会聚透镜(d), 凸透镜是发散透镜(b)。
n
n' n' n'
n
'
n'
n' n
n'
n
n
(a)
(b)
(c)
(d)
显然,当透镜放在空气中时,薄凸透镜会聚 光束,薄凹透镜发散光束。
c)凸透镜和凹透镜是由透镜的中央和边 缘 的相对厚薄确定的。 中间厚,边缘薄的为凸透镜; 中间薄,边缘厚的为凹透镜。 d)应根据入射光的传播方向正确地选择 r1、r2取值的正负。
2
F1
1
Q1
2
P1
P2
<2>计算法:
第一次成像:
s1 30
f1 20
s'1 60
第二次成像:
1 1 1 , 30 s '1 20
s '1 ,V1 2 倒立、放大实像 s1
1 1 1 20 s '2 40
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
n0 物 f 方 nL n0 ni nL 焦 r1 r2 距
13 - 4 薄透镜 通常情况
物理学教程 (第二版)
n0 ni 1
i
i
ff
ni
1 1 1 (nL 1)( ) r1 r2
薄透镜成像公式
n0
Q p
O
nL
p1
d
Q2 Q1
p2
物理学教程 (第二版)
凹凸透镜 平凸透镜 双凸透镜 平凸透镜 凹凸透镜
r1 0, r2 0 r1 r2
r1 r2 0
r1 0, r2 0
r1 0 r2
r1 0, r2 0 r1 r2
* 第十三章 几何光学
13 - 4 薄透镜 各种形状的透镜 凹透镜(发散)
物理学教程 (第二版)
凹凸透镜 平凹透镜 双凹透镜 平凹透镜 凹凸透镜
r1 0, r2 0 r1 r2
r2 r1 0
r1 0, r2 0
r2 0 r1
r1 0, r2 0 r1 r2
* 第十三章 几何光学
13 - 4 薄透镜 凹、凸透镜成像图 1 1 2
得
1 1 1 p2 p2 f
p1 3 f
且
p2 1 p2 p2 p1 100 3 f 100 得 f 100mm
* 第十三章 几何光学
物理学教程 (第二版)
h0
F
hi
p
1
2
h0
3
2
f
F
F
hi
P
* 第十三章 几何光学
p
3
1
2
13 - 4 薄透镜 焦平面 过焦点且垂直于主 光轴的平面,平行光线 (近轴)会聚于焦平面.
物理学教程 (第二版)
焦平面
F
F
f
h0
F
f
F
hi
* 第十三章 几何光学
13 - 4 薄透镜 2 薄透镜成像特性
物理学教程 (第二版)
凸透镜
fa0
凹透镜
f a
薄透镜成像性质图
* 第十三章 几何光学
13 - 4 薄透镜 3 . 薄透镜的横向放大率
物理学教程 (第二版)
n0 p V ni p
p V p
V
1 放大 1 缩小
当
n0 ni 1 时
V
0 像正立 0 像倒立
d 0
1 1 1 p p f
符号规则:以薄透镜光心为分界点,入射光线方向 为正向,如入射光线自左向右,则当物点、像点、焦点 和薄透镜两面的曲率中心在光心右侧时,物距、像距、 焦距和曲率半径均为正;反之,在左侧则为负 .
* 第十三章 透镜 凸透镜(会聚)
* 第十三章 几何光学
13 - 4 薄透镜
物理学教程 (第二版)
例 有一薄凸透镜对某一实物成一倒立实像,像 高为物高的一半,今将物向透镜移进100mm,则所 得的像与物同样大小,求该薄凸透镜的焦距.
解:第一种情况时有 第二种情况时有
1 1 1 p1 p1 f
hi p1 1 p1 h0 2
13 - 4 薄透镜 一 . 薄透镜成像公式
物理学教程 (第二版)
(d f , f , p, p, r )
Q1的像 Q的像 像方焦距
n0 i
Q p
O
ni i
f
nL
d 0
p1
d
Q2 Q1 p2
物方焦距 f
f f 1 p p
ni 像 f 方 nL n0 ni nL 焦 r1 r2 距
