中考数学专题:圆.(学生版)
中考数学几何模型重点突破讲练专题28 圆中的定弦定角和最大张角模型(学生版)

(1)求“蛋圆”抛物线部分的解析式及“蛋圆”的弦 CD 的长;
(2)已知点 E 是“蛋圆”上的一点(不与点 在“蛋
圆”上,求点 E 坐标;
(3)点 P 是“蛋圆”外一点,满足 BPC 60 ,当 BP 最大时,直接写出点 P 的坐标.
【例 2】数学概念
若点 P 在 ABC 的内部,且 APB 、BPC 和 CPA 中有两个角相等,则称 P 是 ABC 的“等角点”,特别地,
若这三个角都相等,则称 P 是 ABC 的“强等角点”.
理解概念
(1)若点 P 是 ABC 的等角点,且 APB 100 ,则 BPC 的度数是
H ,连接 BH ,点 C 在移动的过程中, BH 的最小值是______.
6.如图,已知 C 、 D 在以 AB 为直径的 O 上,若 CAB 30 ,则 D 的度数是_________.
7.如图,直线 l 与⊙O 相交于点 B、D,点 A、C 是直线 l 两侧的圆弧上的动点,若⊙O 的半径为 1,∠A=
o
.
(2)已知点 D 在 ABC 的外部,且与点 A 在 BC 的异侧,并满足 BDC BAC 180 ,作 BCD 的外接圆
O ,连接 AD ,交圆 O 于点 P .当 BCD 的边满足下面的条件时,求证: P 是 ABC 的等角点.(要求:只选
择其中一道题进行证明!
)
①如图①, DB DC
④若一个三角形存在强等角点,则该点到三角形三个顶点的距离相等;
⑤若一个三角形存在强等角点,则该点是三角形内部到三个顶点距离之和最小的点,其中正确的有
.
(填序号)
一、单选题
1.如图,C,D 是 O 上直径 AB 两侧的两点,若 ABC 20 ,则 ∠BDC 的度数是(
2020年中考数学压轴专题12 圆的有关性质与计算 (学生版)

决胜2020中考数学压轴题全揭秘精品专题12 圆的有关性质与计算【典例分析】【考点1】垂径定理【例1】(2019·湖北中考真题)如图,一条公路的转弯处是一段圆弧,点O 是这段弧所在圆的圆心,40AB m =,点C 是¶AB 的中点,且10CD m =,则这段弯路所在圆的半径为( )A .25mB .24mC .30mD .60m【变式1-1】(2019·四川中考真题)如图,AB ,AC 分别是⊙O 的直径和弦,OD AC ⊥于点D ,连接BD ,BC ,且10AB =,8AC =,则BD 的长为( )A.25B.4 C.213D.4.8【变式1-2】(2019·四川中考真题)如图,Oe的直径AB垂直于弦CD,垂足是点E,22.5∠=o,CAOOC=,则CD的长为( )6A.62B.32C.6 D.12【考点2】弧、弦、圆心角之间的关系【例2】(2019·四川自贡中考真题)如图,⊙O中,弦AB与CD相交于点E,AB CD、.=,连接AD BC求证:⑴»»AD BC=;=.⑵AE CE【变式2-1】(2018·黑龙江中考真题)如图,在⊙O中,,AD⊥OC于D.求证:AB=2AD.【变式2-2】(2019·江苏中考真题)如图,⊙O的弦AB、CD的延长线相交于点P,且AB=CD.求证PA=PC.【考点3】圆周角定理及其推论【例3】(2019·陕西中考真题)如图,AB是⊙O的直径,EF,EB是⊙O的弦,且EF=EB,EF与AB交于点C,连接OF,若∠AOF=40°,则∠F的度数是()A.20°B.35°C.40°D.55°【变式3-1】(2019·北京中考真题)已知锐角∠AOB如图,(1)在射线OA上取一点C,以点O为圆心,OC长为半径作»PQ,交射线OB于点D,连接CD;(2)分别以点C,D为圆心,CD长为半径作弧,交»PQ于点M,N;(3)连接OM,MN.根据以上作图过程及所作图形,下列结论中错误的是()A.∠COM=∠COD B.若OM=MN,则∠AOB=20°C.MN∥CD D.MN=3CD【变式3-2】(2019·湖北中考真题)如图,点A,B,C均在⊙O上,当40∠=︒时,AOBC∠的度数是()A.50︒B.55︒C.60︒D.65︒【考点4】圆内接四边形【例4】(2019·贵州中考真题)如图,四边形ABCD为⊙O的内接四边形,∠A=100°,则∠DCE的度数为_______;【变式4-1】(2019·甘肃中考真题)如图,四边形ABCD内接于Oe,若40∠=︒,则CA∠=()A.110︒B.120︒C.135︒D.140︒【变式4-2】(2019·四川中考真题)如图,正五边形ABCDE内接于⊙O,P为»DE上的一点(点P不与∠的度数为()点D重合),则CPDA.30°B.36︒C.60︒D.72︒【考点5】正多边形和圆【例5】(2019·山东中考真题)如图,五边形 ABCDE 是⊙O 的内接正五边形, AF 是⊙O 的直径,则∠ BDF 的度数是___________°.【变式5-1】(2019·山东中考真题)若正六边形的内切圆半径为2,则其外接圆半径为__________. 【变式5-2】(2019·陕西中考真题)若正六边形的边长为3,则其较长的一条对角线长为___.【考点6】弧长和扇形的面积计算(含阴影部分面积计算)【例6】(2019·广西中考真题)如图,ABC ∆是O e 的内接三角形,AB 为O e 直径,6AB =,AD 平分BAC ∠,交BC 于点E ,交O e 于点D ,连接BD . (1)求证:BAD CBD ∠=∠;(2)若125AEB ∠=︒,求»BD 的长(结果保留π).【变式6-1】(2019·湖北中考真题)如图,等边三角形ABC 的边长为2,以A 为圆心,1为半径作圆分别交AB ,AC 边于D ,E ,再以点C 为圆心,CD 长为半径作圆交BC 边于F ,连接E ,F ,那么图中阴影部分的面积为________.【变式6-2】(2019·四川中考真题)如图,在AOC ∆中,31OA cm OC cm =,=,将△AOC 绕点O 顺时针旋转90o 后得到BOD ∆,则AC 边在旋转过程中所扫过的图形的面积为( )2cm .A .2πB .2πC .178π D .198π 【考点7】与圆锥有关的计算【例7】(2019·湖南中考真题)如图,在等腰ABC △中,120BAC ∠=︒,AD 是BAC ∠的角平分线,且6AD =,以点A 为圆心,AD 长为半径画弧EF ,交AB 于点E ,交AC 于点F ,(1)求由弧EF 及线段FC 、CB 、BE 围成图形(图中阴影部分)的面积;(2)将阴影部分剪掉,余下扇形AEF ,将扇形AEF 围成一个圆锥的侧面,AE 与AF 正好重合,圆锥侧面无重叠,求这个圆锥的高h .【变式7-1】(2019·广西中考真题)已知圆锥的底面半径是115角是_____度.【变式7-2】(2019·辽宁中考真题)圆锥侧面展开图的圆心角的度数为216︒,母线长为5,该圆锥的底面半径为________.【变式7-3】(2019·西藏中考真题)如图,从一张腰长为90cm ,顶角为120︒的等腰三角形铁皮OAB 中剪出一个最大的扇形OCD ,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的底面半径为( )A .15cmB .12cmC .10cmD .20cm【达标训练】一、单选题1.(2019·山东中考真题)如图,ABC ∆是O e 的内接三角形,119A ∠=︒,过点C 的圆的切线交BO 于点P ,则P ∠的度数为( )A .32°B .31°C .29°D .61°2.(2019·广西中考真题)如图,,,,A B C D 是⊙O 上的点,则图中与A ∠相等的角是( )A .B Ð B .C ∠C .DEB ∠D .D ∠3.(2019·吉林中考真题)如图,在O e 中,»AB 所对的圆周角050ACB ∠=,若P 为»AB 上一点,055AOP ∠=,则POB ∠的度数为( )A .30°B .45°C .55°D .60°4.(2019·山东中考真题)如图,BC 是半圆O 的直径,D ,E 是»BC上两点,连接BD ,CE 并延长交于点A ,连接OD ,OE ,如果70A ∠︒=,那么DOE ∠的度数为( )A .35︒B .38︒C .40︒D .42︒5.(2019·贵州中考真题)如图,半径为3的⊙A 经过原点O 和点C (0,2),B 是y 轴左侧⊙A 优弧上一点,则tan ∠OBC 为( )A .13B .22C .2 D .226.(2019·甘肃中考真题)如图,AB 是⊙O 的直径,点C 、D 是圆上两点,且∠AOC =126°,则∠CDB =( )A .54°B .64°C .27°D .37°7.(2018·贵州中考真题)如图,已知圆心角∠AOB=110°,则圆周角∠ACB=( )A .55°B .110°C .120°D .125°8.(2019·浙江中考真题)如图,取两根等宽的纸条折叠穿插,拉紧,可得边长为2的正六边形.则原来的纸带宽为( )A .1B .2C .3D .29.(2019·浙江中考真题)如图,已知正五边形 ABCDE 内接于O e ,连结BD ,则ABD ∠的度数是( )A .60︒B .70︒C .72︒D .144︒10.(2019·宁夏中考真题)如图,正六边形ABCDEF 的边长为2,分别以点,A D 为圆心,以,AB DC 为半径作扇形ABF ,扇形DCE .则图中阴影部分的面积是( )A .4633π-B .8633π-C .41233π-D .41233π-11.(2019·江苏中考真题)如图,正六边形的边长为2,分别以正六边形的六条边为直径向外作半圆,与正六边形的外接圆围成的6个月牙形的面积之和(阴影部分面积)是( )A .63πB .632πC .63πD .632π12.(2019·山东中考真题)如图,在边长为4的正方形ABCD 中,以点B 为圆心,AB 为半径画弧,交对角线BD 于点E ,则图中阴影部分的面积是(结果保留π)( )A .8π-B .162π-C .82π-D .182π-13.(2019·浙江中考真题)若扇形的圆心角为90°,半径为6,则该扇形的弧长为( ) A .32π B .2π C .3π D .6π14.(2019·湖南中考真题)一个扇形的半径为6,圆心角为120°,则该扇形的面积是( ) A .2πB .4πC .12πD .24π15.(2019·浙江中考真题)如图,ABC △内接于圆O ,65B ∠=︒,70C ∠=︒,若22BC =,则弧BC 的长为( )A .πB .2πC .2πD .22π16.(2019·山东中考真题)如图,点A 、B ,C ,D 在⊙O 上,AB =AC ,∠A =40°,BD ∥AC ,若⊙O 的半径为2.则图中阴影部分的面积是( )A .23π3B .23π3C .43π3D .43π2 二、填空题17.(2019·广西中考真题)《九章算术》作为古代中国乃至东方的第一部自成体系的数学专著,与古希腊的《几何原本》并称现代数学的两大源泉.在《九章算术》中记载有一问题“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺,问径几何?”小辉同学根据原文题意,画出圆材截面图如图所示,已知:锯口深为1寸,锯道1AB=尺(1尺=10寸),则该圆材的直径为______寸.18.(2019·江苏中考真题)如图,点A、B、C在⊙O上,BC=6,∠BAC=30°,则⊙O的半径为_______.19.(2019·安徽中考真题)如图,△ABC内接于☉O,∠CAB=30°,∠CBA=45°,CD⊥AB于点D,若☉O 的半径为2,则CD的长为_____20.(2019·辽宁中考真题)如图,AC是⊙O的直径,B,D是⊙O上的点,若⊙O的半径为3,∠ADB=30°,则»BC的长为____.21.(2019·湖南中考真题)《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章计算弧田面积所用的经验公式是:弧田面积12=(弦×矢+矢2).孤田是由圆弧和其所对的弦围成(如图中的阴影部分),公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,运用垂径定理(当半径OC⊥弦AB 时,OC平分AB)可以求解.现已知弦8AB=米,半径等于5米的弧田,按照上述公式计算出弧田的面积为_____平方米.22.(2019·江苏中考真题)如图,点A 、B 、C 、D 、E 在O e 上,且弧AB 为50︒,则E C ∠+∠=________.23.(2019·甘肃中考真题)如图,在平面直角坐标系中,已知D e 经过原点O ,与x 轴、y 轴分别交于A 、B 两点,点B 坐标为(0,23),OC 与D e 交于点C ,30OCA ∠=︒,则圆中阴影部分的面积为_____.24.(2019·湖北中考真题)刘徽是我国魏晋时期卓越的数学家,他在《九章算术》中提出了“割圆术”,利用圆的内接正多边形逐步逼近圆来近似计算圆的面积,如图,若用圆的内接正十二边形的面积1S 来近似估计O e 的面积S ,设O e 的半径为1,则1S S -=__________.25.(2019·江苏中考真题)如图,AC 是⊙O 的内接正六边形的一边,点B 在弧AC 上,且BC 是⊙O 的内接正十边形的一边,若AB 是⊙O 的内接正n 边形的一边,则n=____ .26.(2019·重庆中考真题)如图,在菱形ABCD 中,对角线AC ,BD 交于点O ,∠ABC=60°,AB=2,分别以点A 、点C 为圆心,以AO 的长为半径画弧分别与菱形的边相交,则图中阴影部分的面积为______.(结果保留π)27.(2019·浙江中考真题)如图,一个圆锥形冰激凌外壳(不计厚度).已知其母线长为12cm ,底面圆半径为3cm ,则这个冰激凌外壳的侧面积等于______2cm (计算结果精确到个位).28.(2019·山东中考真题)如图,O 为Rt △ABC 直角边AC 上一点,以OC 为半径的⊙O 与斜边AB 相切于点D ,交OA 于点E ,已知BC=3,AC=3.则图中阴影部分的面积是_____.三、解答题29.(2019·天津中考真题)已知PA ,PB 分别与O e 相切于点A ,B ,80APB ︒∠=,C 为O e 上一点.(Ⅰ)如图①,求ACB ∠的大小;(Ⅱ)如图②,AE 为O e 的直径,AE 与BC 相交于点D ,若AB AD =,求EAC ∠的大小.30.(2019·黑龙江中考真题)图1.2是两张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,线段AC 的两个端点均在小正方形的顶点上;(1)在图1中画出以AC 为底边的等腰直角ABC △,点B 在小正方形顶点上;(2)在图2中画出以AC 为腰的等腰ACD V ,点D 在小正方形的顶点上,且ACD V 的面积为8.31.(2019·河南中考真题)如图,在ABC ∆中,BA BC =,90ABC ︒∠=,以AB 为直径的半圆O 交AC于点D ,点E 是¶BD 上不与点B ,D 重合的任意一点,连接AE 交BD 于点F ,连接BE 并延长交AC 于点G .(1)求证:ADF BDG ∆≅∆; (2)填空:①若=4AB ,且点E 是¶BD的中点,则DF 的长为 ; ②取¶AE的中点H ,当EAB ∠的度数为 时,四边形OBEH 为菱形.32.(2019·江苏中考真题)如图,在Rt △ABC 中,∠ACB=90°,∠A=30°,BC=1,以边AC 上一点O 为圆心,OA 为半径的⊙O 经过点B .(1)求⊙O 的半径;(2)点P 为»AB 中点,作PQ ⊥AC ,垂足为Q ,求OQ 的长; (3)在(2)的条件下,连接PC ,求tan ∠PCA 的值.33.(2019·广西中考真题)如图,五边形ABCDE 内接于O e ,CF 与O e 相切于点C ,交AB 延长线于点F .(1)若,AE DC E BCD =∠=∠,求证:DE BC =; (2)若2,,45OB AB BD DA F ===∠=︒,求CF 的长.34.(2019·辽宁中考真题)如图1,四边形ABCD 内接于圆O ,AC 是圆O 的直径,过点A 的切线与CD 的延长线相交于点P .且APC BCP ∠=∠ (1)求证:2BAC ACD ∠=∠;(2)过图1中的点D 作DE AC ⊥,垂足为E (如图2),当6BC =,2AE =时,求圆O 的半径.35.(2019·内蒙古中考真题)如图,在⊙O 中,B 是⊙O 上的一点,120ABC ∠=o ,弦23AC =弦BM 平分ABC ∠交AC 于点D ,连接,MA MC . (1)求⊙O 半径的长;(2)求证:AB BC BM +=.36.(2019·江苏中考真题)如图,AB 是⊙O 的弦,过点O 作OC ⊥OA ,OC 交于AB 于P ,且CP=CB . (1)求证:BC 是⊙O 的切线;(2)已知∠BAO=25°,点Q 是弧A m B 上的一点. ①求∠AQB 的度数; ②若OA=18,求弧A m B 的长.37.(2019·江苏中考真题)(材料阅读):地球是一个球体,任意两条相对的子午线都组成一个经线圈(如图1中的O e ).人们在北半球可观测到北极星,我国古人在观测北极星的过程中发明了如图2所示的工具尺(古人称它为“复矩”),尺的两边互相垂直,角顶系有一段棉线,棉线末端系一个铜锤,这样棉线就与地平线垂直.站在不同的观测点,当工具尺的长边指向北极星时,短边与棉线的夹角α的大小是变化的. (实际应用):观测点A 在图1所示的O e 上,现在利用这个工具尺在点A 处测得α为31︒,在点A 所在子午线往北的另一个观测点B ,用同样的工具尺测得α为67︒.PQ 是O e 的直径,PQ ON ⊥.(1)求POB ∠的度数;(2)已知6400OP =km ,求这两个观测点之间的距离即O e 上»AB 的长.(π取3.1) 38.(2019·湖北中考真题)如图,点E 是ABC ∆的内心,AE 的延长线和ABC ∆的外接圆圆O 相交于点D ,过D 作直线//DG BC . (1)求证:DG 是圆O 的切线;(2)若6DE =,63BC =,求优弧·BAC 的长.39.(2019·湖南中考真题)如图,AB 为O e 的直径,且3AB =C 是¶AB 上的一动点(不与A ,B 重合),过点B 作O e 的切线交AC 的延长线于点D ,点E 是BD 的中点,连接EC . (1)求证:EC 是O e 的切线;(2)当30D ︒∠=时,求阴影部分面积.40.(2019·贵州中考真题)如图,正六边形ABCDEF内接于⊙O,BE是⊙O的直径,连接BF,延长BA,过F作FG⊥BA,垂足为G.(1)求证:FG是⊙O的切线;(2)已知FG=23,求图中阴影部分的面积.41.(2019·广东中考真题)在如图所示的网格中,每个小正方形的边长为1,每个小正方形的顶点叫格点,∆的三个顶点均在格点上,以点A为圆心的»EF与BC相切于点D,分别交AB、AC于点E、F. ABC∆三边的长;(1)求ABC(2)求图中由线段EB、BC、CF及»FE所围成的阴影部分的面积.。
中考数学专题复习 圆压轴八大模型题(学生用)(word文档良心出品)

圆压轴题八大模型题(一)引言:与圆有关的证明与计算的综合解答题,往往位于许多省市中考题中的倒数第二题的位置上,是试卷中综合性与难度都比较大的习题。
一般都会在固定习题模型的基础上变化与括展,本文结合近年来各省市中考题,整理了这些习题的常见的结论,破题的要点,常用技巧。
把握了这些方法与技巧,就能台阶性地帮助考生解决问题。
类型1 弧中点的运用 在⊙O 中,点C 是⌒AD 的中点,CE ⊥AB 于点E .(1)在图1中,你会发现这些结论吗? ①AP =CP =FP ; ②CH =AD ;②AC 2=AP ·AD =CF ·CB =AE ·A B .(2)在图2中,你能找出所有与△ABC 相似的三角形吗?【典例】(2018·湖南永州)如图,线段AB 为⊙O 的直径,点C ,E 在⊙O 上,=,CD ⊥AB ,垂足为点D ,连接BE ,弦BE 与线段CD 相交于点F . (1)求证:CF =BF ;(2)若cos ∠ABE =,在AB 的延长线上取一点M ,使BM =4,⊙O 的半径为6.求证:直线CM 是⊙O 的切线.【变式运用】1.(2018·四川宜宾)如图,AB 是半圆的直径,AC 是一条弦,D 是AC 的中点,DE ⊥AB 于点E 且DE 交AC 于点F ,DB 交AC 于点G ,若=,OHP F EDCBA(图1)(图1-2)则= .2.(2018·泸州)如图,在平行四边形ABCD 中,E 为BC 边上的一点,且AE 与DE 分别平分∠BAD 和∠ADC 。
(1)求证:AE ⊥DE ;(2)设以AD 为直径的半圆交AB 于F ,连接DF 交AE 于G ,已知CD =5,AE =8,求FGAF值。
3. (2017·泸州)如图,△ABC 内接于⊙O ,AB 是⊙O 的直径,C 是AD 的中点,弦CE ⊥AB 于点H ,连结AD ,分别交CE 、BC 于点P 、Q ,连结BD 。
中考数学几何模型专题09阿氏圆问题(学生版) 知识点+例题
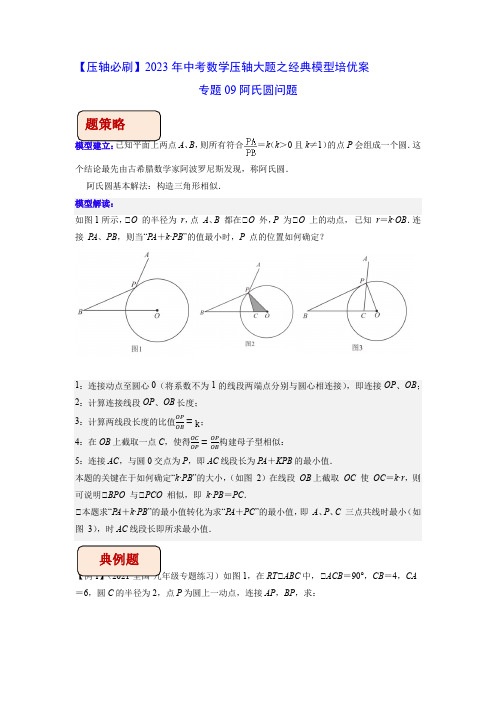
【压轴必刷】2023年中考数学压轴大题之经典模型培优案专题09阿氏圆问题A 、B ,则所有符合=k (k >0且k ≠1)的点P 会组成一个圆.这个结论最先由古希腊数学家阿波罗尼斯发现,称阿氏圆.阿氏圆基本解法:构造三角形相似.模型解读:如图1所示,⊙O 的半径为 r ,点 A 、B 都在⊙O 外,P 为⊙O 上的动点, 已知 r =k ·OB .连接 P A 、PB ,则当“P A +k ·PB ”的值最小时,P 点的位置如何确定?1:连接动点至圆心0(将系数不为1的线段两端点分别与圆心相连接),即连接OP 、OB ; 2:计算连接线段OP 、OB 长度;3:计算两线段长度的比值OP OB =k ;4:在OB 上截取一点C ,使得OC OP =OP OB 构建母子型相似:5:连接AC ,与圆0交点为P ,即AC 线段长为P A +KPB 的最小值.本题的关键在于如何确定“k ·PB ”的大小,(如图 2)在线段 OB 上截取 OC 使 OC =k ·r ,则可说明⊙BPO 与⊙PCO 相似,即 k ·PB =PC .⊙本题求“P A +k ·PB ”的最小值转化为求“P A +PC ”的最小值,即 A 、P 、C 三点共线时最小(如图 3),时AC 线段长即所求最小值.1,在RT ⊙ABC 中,⊙ACB =90°,CB =4,CA =6,圆C 的半径为2,点P 为圆上一动点,连接AP ,BP ,求:BP,⊙AP+12⊙2AP+BP,AP+BP,⊙13⊙AP+3BP的最小值.【例2】(2022·广东惠州·一模)如图1,抛物线y=ax2+bx−4与x轴交于A、B两点,与y.轴交于点C,其中点A的坐标为(−1,0),抛物线的对称轴是直线x=32(1)求抛物线的解析式;(2)若点P是直线BC下方的抛物线上一个动点,是否存在点P使四边形ABPC的面积为16,若存在,求出点P的坐标若不存在,请说明理由;(3)如图2,过点B作BF⊥BC交抛物线的对称轴于点F,以点C为圆心,2为半径作⊙C,点QBQ+FQ的最小值.为⊙C上的一个动点,求√24【例3】(2019秋•山西期末)阅读以下材料,并按要求完成相应的任务.已知平面上两点A、B,则所有符合=k(k>0且k≠1)的点P会组成一个圆.这个结论最先由古希腊数学家阿波罗尼斯发现,称阿氏圆.阿氏圆基本解法:构造三角形相似.【问题】如图1,在平面直角坐标系中,在x轴,y轴上分别有点C(m,0),D(0,n),点P是平面内一动点,且OP=r,设=k,求PC+kPD的最小值.阿氏圆的关键解题步骤:第一步:如图1,在OD上取点M,使得OM:OP=OP:OD=k;第二步:证明kPD=PM;第三步:连接CM,此时CM即为所求的最小值.下面是该题的解答过程(部分):解:在OD上取点M,使得OM:OP=OP:OD=k,又∵∠POD=∠MOP,∴△POM∽△DOP.任务:(1)将以上解答过程补充完整.(2)如图2,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,D为△ABC内一动点,满足CD=2,利用(1)中的结论,请直接写出AD+BD的最小值.【例4】如图,在每个小正方形的边长为1的网格中,△OAB的顶点O,A,B均在格点上,点E在OA上,且点E也在格点上.(I)的值为;(Ⅱ)是以点O为圆心,2为半径的一段圆弧.在如图所示的网格中,将线段OE绕点O逆时针旋转得到OE′,旋转角为α(0°<α<90°)连接E'A,E'B,当E'A+E'B 的值最小时,请用无刻度的直尺画出点E′,并简要说明点E'的位置是如何找到的(不要求证明).一.填空题(共13小题)1.(2022•南召县开学)如图,在△ABC中,∠A=90°,AB=AC=4,点E、F分别是边AB、AC的中点,点P是以A为圆心、以AE为半径的圆弧上的动点,则的最小值为.2.(2021秋•龙凤区期末)如图,在Rt△ABC中,∠C=90°,AC=9,BC=4,以点C为圆心,3为半径做⊙C,分别交AC,BC于D,E两点,点P是⊙C上一个动点,则P A+PB 的最小值为.3.(2022春•长顺县月考)如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,D、E 分别是边BC、AC上的两个动点,且DE=4,P是DE的中点,连接P A,PB,则P A+ PB的最小值为.。
圆的有关计算与证明(共50题)(学生版)--2023年中考数学真题分项汇编(全国通用)

圆的有关计算与证明(50题)一、单选题1.(2023·新疆·统考中考真题)如图,在⊙O 中,若∠ACB =30°,OA =6,则扇形OAB (阴影部分)的面积是()A.12πB.6πC.4πD.2π2.(2023·江苏连云港·统考中考真题)如图,矩形ABCD 内接于⊙O ,分别以AB 、BC 、CD 、AD 为直径向外作半圆.若AB =4,BC =5,则阴影部分的面积是()A.414π-20 B.412π-20 C.20π D.203.(2023·湖北荆州·统考中考真题)如图,一条公路的转弯处是一段圆弧(AC),点O 是这段弧所在圆的圆心,B 为AC上一点,OB ⊥AC 于D .若AC =3003m ,BD =150m ,则AC的长为()A.300πmB.200πmC.150πmD.1003πm4.(2023·山东滨州·统考中考真题)如图,某玩具品牌的标志由半径为1cm 的三个等圆构成,且三个等圆⊙O 1,⊙O 2,⊙O 3相互经过彼此的圆心,则图中三个阴影部分的面积之和为()A.14πcm 2 B.13πcm 2 C.12πcm 2 D.πcm 25.(2023·四川达州·统考中考真题)如图,四边形ABCD 是边长为12的正方形,曲线DA 1B 1C 1D 1A 2⋯是由多段90°的圆心角的圆心为C ,半径为CB 1;C 1D 1 的圆心为D ,半径为DC 1⋯,DA 1 、A 1B 1 、B 1C 1、C 1D 1⋯的圆心依次为A 、B 、C 、D 循环,则A 2023B 2023�的长是()A.4045π2B.2023πC.2023π4D.2022π6.(2023·四川广安·统考中考真题)如图,在等腰直角△ABC 中,∠ACB =90°,AC =BC =22,以点A 为圆心,AC 为半径画弧,交AB 于点E ,以点B 为圆心,BC 为半径画弧,交AB 于点F ,则图中阴影部分的面积是()A.π-2B.2π-2C.2π-4D.4π-47.(2023·江苏苏州·统考中考真题)如图,AB 是半圆O 的直径,点C ,D 在半圆上,CD=DB,连接OC ,CA ,OD ,过点B 作EB ⊥AB ,交OD 的延长线于点E .设△OAC 的面积为S 1,△OBE 的面积为S 2,若S 1S 2=23,则tan ∠ACO 的值为()A.2B.223C.75D.32二、填空题8.(2023·重庆·统考中考真题)如图,在矩形ABCD 中,AB =2,BC =4,E 为BC 的中点,连接AE ,DE ,以E 为圆心,EB 长为半径画弧,分别与AE ,DE 交于点M ,N ,则图中阴影部分的面积为.(结果保留π)9.(2023·黑龙江绥化·统考中考真题)如图,⊙O 的半径为2cm ,AB 为⊙O 的弦,点C 为AB上的一点,将AB沿弦AB 翻折,使点C 与圆心O 重合,则阴影部分的面积为.(结果保留π与根号)10.(2023·重庆·统考中考真题)如图,⊙O 是矩形ABCD 的外接圆,若AB =4,AD =3,则图中阴影部分的面积为.(结果保留π)11.(2023·江苏扬州·统考中考真题)用半径为24cm ,面积为120πcm 2的扇形纸片,围成一个圆锥的侧面,则这个圆锥的底面圆的半径为cm .12.(2023·浙江温州·统考中考真题)若扇形的圆心角为40°,半径为18,则它的弧长为.13.(2023·浙江宁波·统考中考真题)如图,圆锥形烟囱帽的底面半径为30cm ,母线长为50cm ,则烟囱帽的侧面积为cm 2.(结果保留π)14.(2023·天津·统考中考真题)如图,在每个小正方形的边长为1的网格中,等边三角形ABC 内接于圆,且顶点A ,B 均在格点上.(1)线段AB的长为;(2)若点D在圆上,AB与CD相交于点P.请用无刻度的直尺,在如图所示的网格中,画出点Q,使△CPQ为等边三角形,并简要说明点Q的位置是如何找到的(不要求证明).15.(2023·江苏苏州·统考中考真题)如图,在▱ABCD中,AB=3+1,BC=2,AH⊥CD,垂足为H,AH=3.以点A为圆心,AH长为半径画弧,与AB,AC,AD分别交于点E,F,G.若用扇形AEF 围成一个圆锥的侧面,记这个圆锥底面圆的半径为r1;用扇形AHG围成另一个圆锥的侧面,记这个圆锥底面圆的半径为r2,则r1-r2=.(结果保留根号)16.(2023·四川自贡·统考中考真题)如图,小珍同学用半径为8cm,圆心角为100°的扇形纸片,制作一个底面半径为2cm的圆锥侧面,则圆锥上粘贴部分的面积是cm2.三、解答题17.(2023·四川南充·统考中考真题)如图,AB与⊙O相切于点A,半径OC∥AB,BC与⊙O相交于点D,连接AD.(1)求证:∠OCA =∠ADC ;(2)若AD =2,tan B =13,求OC 的长.18.(2023·四川成都·统考中考真题)如图,以△ABC 的边AC 为直径作⊙O ,交BC 边于点D ,过点C 作CE ∥AB 交⊙O 于点E ,连接AD ,DE ,∠B =∠ADE .(1)求证:AC =BC ;(2)若tan B =2,CD =3,求AB 和DE 的长.19.(2023·内蒙古·统考中考真题)如图,AB 是⊙O 的直径,AC 是弦,D 是AC上一点,P 是AB 延长线上一点,连接AD ,DC ,CP .(1)求证:∠ADC -∠BAC =90°;(请用两种证法解答)(2)若∠ACP =∠ADC ,⊙O 的半径为3,CP =4,求AP 的长.20.(2023·辽宁大连·统考中考真题)如图1,在⊙O 中,AB 为⊙O 的直径,点C 为⊙O 上一点,AD 为∠CAB 的平分线交⊙O 于点D ,连接OD 交BC 于点E .(1)求∠BED的度数;(2)如图2,过点A作⊙O的切线交BC延长线于点F,过点D作DG∥AF交AB于点G.若AD= 235,DE=4,求DG的长.21.(2023·浙江杭州·统考中考真题)在边长为1的正方形ABCD中,点E在边AD上(不与点A,D重合),射线BE与射线CD交于点F.(1)若ED=13,求DF的长.(2)求证:AE⋅CF=1.(3)以点B为圆心,BC长为半径画弧,交线段BE于点G.若EG=ED,求ED的长.22.(2023·河北·统考中考真题)装有水的水槽放置在水平台面上,其横截面是以AB为直径的半圆O,AB=50cm,如图1和图2所示,MN为水面截线,GH为台面截线,MN∥GH.计算:在图1中,已知MN=48cm,作OC⊥MN于点C.(1)求OC的长.操作:将图1中的水面沿GH向右作无滑动的滚动,使水流出一部分,当∠ANM=30°时停止滚动,如图2.其中,半圆的中点为Q,GH与半圆的切点为E,连接OE交MN于点D.探究:在图2中(2)操作后水面高度下降了多少?(3)连接OQ 并延长交GH 于点F ,求线段EF 与EQ的长度,并比较大小.23.(2023·湖北武汉·统考中考真题)如图,OA ,OB ,OC 都是⊙O 的半径,∠ACB =2∠BAC .(1)求证:∠AOB =2∠BOC ;(2)若AB =4,BC =5,求⊙O 的半径.24.(2023·湖南·统考中考真题)如图所示,四边形ABCD 是半径为R 的⊙O 的内接四边形,AB 是⊙O 的直径,∠ABD =45°,直线l 与三条线段CD 、CA 、DA 的延长线分别交于点E 、F 、G .且满足∠CFE =45°.(1)求证:直线l ⊥直线CE ;(2)若AB=DG;①求证:△ABC≌△GDE;②若R=1,CE=32,求四边形ABCD的周长.25.(2023·天津·统考中考真题)在⊙O中,半径OC垂直于弦AB,垂足为D,∠AOC=60°,E为弦AB所对的优弧上一点.(1)如图①,求∠AOB和∠CEB的大小;(2)如图②,CE与AB相交于点F,EF=EB,过点E作⊙O的切线,与CO的延长线相交于点G,若OA=3,求EG的长.26.(2023·江苏苏州·统考中考真题)如图,△ABC是⊙O的内接三角形,AB是⊙O的直径,AC= 5,BC=25,点F在AB上,连接CF并延长,交⊙O于点D,连接BD,作BE⊥CD,垂足为E.(1)求证:△DBE∽△ABC;(2)若AF=2,求ED的长.27.(2023·四川达州·统考中考真题)如图,△ABC、△ABD内接于⊙O,AB=BC,P是OB延长线上的一点,∠PAB=∠ACB,AC、BD相交于点E.(1)求证:AP 是⊙O 的切线;(2)若BE =2,DE =4,∠P =30°,求AP 的长.28.(2023·湖南·统考中考真题)如图,AB 是⊙O 的直径,AC 是一条弦,D 是AC的中点,DE ⊥AB 于点E ,交AC 于点F ,交⊙O 于点H ,DB 交AC 于点G .(1)求证:AF =DF .(2)若AF =52,sin ∠ABD =55,求⊙O 的半径.29.(2023·湖南怀化·统考中考真题)如图,AB 是⊙O 的直径,点P 是⊙O 外一点,PA 与⊙O 相切于点A ,点C 为⊙O 上的一点.连接PC 、AC 、OC ,且PC =PA .(1)求证:PC 为⊙O 的切线;(2)延长PC 与AB 的延长线交于点D ,求证:PD ⋅OC =PA ⋅OD ;(3)若∠CAB =30°,OD =8,求阴影部分的面积.30.(2023·四川眉山·统考中考真题)如图,△ABC 中,以AB 为直径的⊙O 交BC 于点E .AE 平分∠BAC ,过点E 作ED ⊥AC 于点D ,延长DE 交AB 的延长线于点P .(1)求证:PE 是⊙O 的切线;(2)若sin ∠P =13,BP =4,求CD 的长.31.(2023·安徽·统考中考真题)已知四边形ABCD 内接于⊙O ,对角线BD 是⊙O 的直径.(1)如图1,连接OA ,CA ,若OA ⊥BD ,求证;CA 平分∠BCD ;(2)如图2,E 为⊙O 内一点,满足AE ⊥BC ,CE ⊥AB ,若BD =33,AE =3,求弦BC 的长.32.(2023·吉林长春·统考中考真题)【感知】如图①,点A 、B 、P 均在⊙O 上,∠AOB =90°,则锐角∠APB 的大小为度.【探究】小明遇到这样一个问题:如图②,⊙O 是等边三角形ABC 的外接圆,点P 在AC上(点P 不与点A 、C 重合),连结PA 、PB 、PC .求证:PB =PA +PC .小明发现,延长PA 至点E ,使AE =PC ,连结BE ,通过证明△PBC ≌△EBA ,可推得PBE 是等边三角形,进而得证.下面是小明的部分证明过程:证明:延长PA 至点E ,使AE =PC ,连结BE ,∵四边形ABCP 是⊙O 的内接四边形,∴∠BAP +∠BCP =180°.∵∠BAP +∠BAE =180°,∴∠BCP =∠BAE .∵△ABC 是等边三角形.∴BA =BC ,∴△PBC ≌△EBA (SAS )请你补全余下的证明过程.【应用】如图③,⊙O 是△ABC 的外接圆,∠ABC =90°,AB =BC ,点P 在⊙O 上,且点P 与点B 在AC的两侧,连结PA 、PB 、PC .若PB =22PA ,则PBPC的值为.33.(2023·四川泸州·统考中考真题)如图,AB 是⊙O 的直径,AB =210,⊙O 的弦CD ⊥AB 于点E ,CD =6.过点C 作⊙O 的切线交AB 的延长线于点F ,连接BC .(1)求证:BC 平分∠DCF ;(2)G 为AD上一点,连接CG 交AB 于点H ,若CH =3GH ,求BH 的长.34.(2023·黑龙江绥化·统考中考真题)如图,MN 为⊙O 的直径,且MN =15,MC 与ND 为圆内的一组平行弦,弦AB 交MC 于点H .点A 在MC 上,点B 在NC 上,∠OND +∠AHM =90°.(1)求证:MH ⋅CH =AH ⋅BH .(2)求证:AC =BC.(3)在⊙O 中,沿弦ND 所在的直线作劣弧ND的轴对称图形,使其交直径MN 于点G .若sin ∠CMN =35,求NG 的长.35.(2023·广东·统考中考真题)综合探究如图1,在矩形ABCD 中(AB >AD ),对角线AC ,BD 相交于点O ,点A 关于BD 的对称点为A ′,连接AA ′交BD 于点E ,连接CA ′.(1)求证:AA ′⊥CA ′;(2)以点O 为圆心,OE 为半径作圆.①如图2,⊙O 与CD 相切,求证:AA ′=3CA ′;②如图3,⊙O 与CA ′相切,AD =1,求⊙O 的面积.36.(2023·山东·统考中考真题)如图,AB 为⊙O 的直径,C 是圆上一点,D 是BC的中点,弦DE ⊥AB ,垂足为点F .(1)求证:BC =DE ;(2)P 是AE上一点,AC =6,BF =2,求tan ∠BPC ;(3)在(2)的条件下,当CP 是∠ACB 的平分线时,求CP 的长.37.(2023·山东·统考中考真题)如图,已知AB 是⊙O 的直径,CD =CB ,BE 切⊙O 于点B ,过点C 作CF ⊥OE 交BE 于点F ,若EF =2BF .(1)如图1,连接BD ,求证:△ADB ≌△OBE ;(2)如图2,N 是AD 上一点,在AB 上取一点M ,使∠MCN =60°,连接MN .请问:三条线段MN ,BM ,DN 有怎样的数量关系?并证明你的结论.38.(2023·浙江杭州·统考中考真题)如图,在⊙O 中,直径AB 垂直弦CD 于点E ,连接AC ,AD ,BC ,作CF ⊥AD 于点F ,交线段OB 于点G (不与点O ,B 重合),连接OF .(1)若BE =1,求GE 的长.(2)求证:BC 2=BG ⋅BO .(3)若FO =FG ,猜想∠CAD 的度数,并证明你的结论.39.(2023·湖北宜昌·统考中考真题)如图1,已知AB 是⊙O 的直径,PB 是⊙O 的切线,PA 交⊙O于点C ,AB =4,PB =3.(1)填空:∠PBA 的度数是,PA 的长为;(2)求△ABC 的面积;(3)如图2,CD ⊥AB ,垂足为D .E 是AC 上一点,AE =5EC .延长AE ,与DC ,BP 的延长线分别交于点F ,G ,求EF FG的值.40.(2023·山东滨州·统考中考真题)如图,点E 是△ABC 的内心,AE 的延长线与边BC 相交于点F ,与△ABC 的外接圆相交于点D .(1)求证:S △ABF :S △ACF =AB :AC ;(2)求证:AB :AC =BF :CF ;(3)求证:AF 2=AB ⋅AC -BF ⋅CF ;(4)猜想:线段DF ,DE ,DA 三者之间存在的等量关系.(直接写出,不需证明.)41.(2023·浙江台州·统考中考真题)我们可以通过中心投影的方法建立圆上的点与直线上点的对应关系,用直线上点的位置刻画圆上点的位置,如图,AB 是⊙O 的直径,直线l 是⊙O 的切线,B 为切点.P ,Q 是圆上两点(不与点A 重合,且在直径AB 的同侧),分别作射线AP ,AQ 交直线l 于点C ,点D .(1)如图1,当AB =6,BP �的长为π时,求BC 的长.(2)如图2,当AQ AB=34,BP =PQ 时,求BC CD 的值.(3)如图3,当sin∠BAQ=64,BC=CD时,连接BP,PQ,直接写出PQBP的值.42.(2023·浙江温州·统考中考真题)如图1,AB为半圆O的直径,C为BA延长线上一点,CD切半圆于点D,BE⊥CD,交CD延长线于点E,交半圆于点F,已知OA=32,AC=1.如图2,连接AF,P为线段AF上一点,过点P作BC的平行线分别交CE,BE于点M,N,过点P作PH⊥AB于点H.设PH=x,MN=y.(1)求CE的长和y关于x的函数表达式.(2)当PH<PN,且长度分别等于PH,PN,a的三条线段组成的三角形与△BCE相似时,求a的值.(3)延长PN交半圆O于点Q,当NQ=154x-3时,求MN的长.43.(2023·新疆·统考中考真题)如图,AB是⊙O的直径,点C,F是⊙O上的点,且∠CBF=∠BAC,连接AF,过点C作AF的垂线,交AF的延长线于点D,交AB的延长线于点E,过点F作FG ⊥AB于点G,交AC于点H.(1)求证:CE是⊙O的切线;(2)若tan E=34,BE=4,求FH的长.44.(2023·云南·统考中考真题)如图,BC是⊙O的直径,A是⊙O上异于B、C的点.⊙O外的点E在射线CB上,直线EA与CD垂直,垂足为D,且DA⋅AC=DC⋅AB.设△ABE的面积为S1,△ACD 的面积为S2.(1)判断直线EA与⊙O的位置关系,并证明你的结论;(2)若BC=BE,S2=mS1,求常数m的值.45.(2023·浙江宁波·统考中考真题)如图1,锐角△ABC内接于⊙O,D为BC的中点,连接AD并延长交⊙O于点E,连接BE,CE,过C作AC的垂线交AE于点F,点G在AD上,连接BG,CG,若BC平分∠EBG且∠BCG=∠AFC.(1)求∠BGC的度数.(2)①求证:AF=BC.②若AG=DF,求tan∠GBC的值,(3)如图2,当点O恰好在BG上且OG=1时,求AC的长.46.(2023·四川遂宁·统考中考真题)如图,四边形ABCD内接于⊙O,AB为⊙O的直径,AD= CD,过点D的直线l交BA的延长线于点M,交BC的延长线于点N,且∠ADM=∠DAC.(1)求证:MN是⊙O的切线;(2)求证:AD2=AB⋅CN;(3)当AB=6,sin∠DCA=33时,求AM的长.47.(2023·四川广安·统考中考真题)如图,以Rt△ABC的直角边AB为直径作⊙O,交斜边AC于点D,点E是BC的中点,连接OE、DE.(1)求证:DE是⊙O的切线.(2)若sin C=4,DE=5,求AD的长.5(3)求证:2DE2=CD⋅OE.48.(2023·浙江嘉兴·统考中考真题)已知,AB是半径为1的⊙O的弦,⊙O的另一条弦CD满足CD=AB,且CD⊥AB于点H(其中点H在圆内,且AH>BH,CH>DH).(1)在图1中用尺规作出弦CD 与点H (不写作法,保留作图痕迹).(2)连结AD ,猜想,当弦AB 的长度发生变化时,线段AD 的长度是否变化?若发生变化,说明理由:若不变,求出AD 的长度;(3)如图2,延长AH 至点F ,使得HF =AH ,连结CF ,∠HCF 的平分线CP 交AD 的延长线于点P ,点M 为AP 的中点,连结HM ,若PD =12AD .求证:MH ⊥CP .49.(2023·浙江·统考中考真题)如图,在⊙O 中,AB 是一条不过圆心O 的弦,点C ,D 是AB的三等分点,直径CE 交AB 于点F ,连结AD 交CF 于点G ,连结AC ,过点C 的切线交BA 的延长线于点H .(1)求证:AD ∥HC ;(2)若OG GC=2,求tan ∠FAG 的值;(3)连结BC 交AD 于点N ,若⊙O 的半径为5①若OF =52,求BC 的长;②若AH =10,求△ANB 的周长;③若HF ⋅AB =88,求△BHC 的面积.50.(2023·四川宜宾·统考中考真题)如图,以AB 为直径的⊙O 上有两点E 、F ,BE =EF,过点E 作直线CD ⊥AF 交AF 的延长线于点D ,交AB 的延长线于点C ,过C 作CM 平分∠ACD 交AE 于点M ,交BE 于点N .(1)求证:CD 是⊙O 的切线;(2)求证:EM =EN ;(3)如果N是CM的中点,且AB=95,求EN的长.。
中考一轮复习 数学专题14 圆与正多边形(学生版)
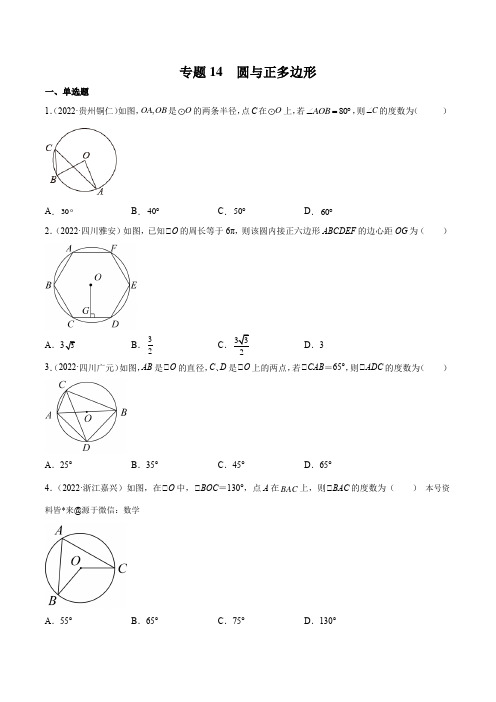
专题14 圆与正多边形一、单选题1.(2022·贵州铜仁)如图,,OA OB 是O 的两条半径,点C 在O 上,若80AOB ∠=︒,则C ∠的度数为( )A .30B .40︒C .50︒D .60︒2.(2022·四川雅安)如图,已知⊙O 的周长等于6π,则该圆内接正六边形ABCDEF 的边心距OG 为( )A .B .32CD .33.(2022·四川广元)如图,AB 是⊙O 的直径,C 、D 是⊙O 上的两点,若⊙CAB =65°,则⊙ADC 的度数为( )A .25°B .35°C .45°D .65°4.(2022·浙江嘉兴)如图,在⊙O 中,⊙BOC =130°,点A 在BAC 上,则⊙BAC 的度数为( ) 本号资料皆*来@源于微信:数学A .55°B .65°C .75°D .130°5.(2022·浙江宁波)已知圆锥的底面半径为4cm,母线长为6cm,则圆锥的侧面积为()A.236πcm B.224πcm C.216πcm D.212πcm6.(2021·广西桂林)如图,AB是⊙O的直径,点C是⊙O上一点,连接AC,BC,则⊙C的度数是()A.60°B.90°C.120°D.150°7.(2021·内蒙古呼伦贝尔)一个正多边形的中心角为30,这个正多边形的边数是()A.8B.12C.3D.68.(2021·吉林)如图,四边形ABCD内接于O,点P为边AD上任意一点(点P不与点A,D重合)连接CP.若120B∠=︒,则APC∠的度数可能为()A.30B.45︒C.50︒D.65︒9.(2021·广西贺州)如图,在边长为2的等边ABC中,D是BC边上的中点,以点A为圆心,AD为半径作圆与AB,AC分别交于E,F两点,则图中阴影部分的面积为()A.π6B.π3C.π2D.2π310.(2021·吉林长春)如图,AB 是O 的直径,BC 是O 的切线,若35BAC ∠=︒,则ACB ∠的大小为( )A .35︒B .45︒C .55︒D .65︒11.(2021·湖南长沙)如图,点A ,B ,C 在⊙O 上,54BAC ∠=︒,则BOC ∠的度数为( )A .27︒B .108︒C .116︒D .128︒12.(2020·广西)如图,AB 是⊙O 的弦,AC 与⊙O 相切于点A ,连接OA ,OB ,若⊙O =130°,则⊙BAC 的度数是( )A .60°B .65°C .70°D .75°13.(2020·重庆)如图,AB 是O 的切线,A 切点,连接OA ,OB ,若20B ∠=︒,则AOB ∠的度数为( )A .40°B .50°C .60°D .70°14.(2020·四川巴中)如图,在O 中,点、、A B C 在圆上,45,ACB AB ︒∠==O 的半径OA 的长是( )AB .2C .D .315.(2020·四川广安)如图,点A ,B ,C ,D 四点均在圆O 上,⊙AOD =68°,AO //DC ,则⊙B 的度数为( )A .40°B .60°C .56°D .68°16.(2020·广西柳州)如图,点A 、B 、C 在⊙O 上,若⊙BOC =70°,则⊙A 的度数为( )A .35°B .40°C .55°D .70°17.(2020·辽宁鞍山)如图,⊙O 是∆ABC 的外接圆,半径为2cm ,若2cm BC =,则A ∠的度数为( )A .30°B .25°C .15°D .10°18.(2020·江苏镇江)如图,AB 是半圆的直径,C 、D 是半圆上的两点,⊙ADC =106°,则⊙CAB 等于( )A .10°B .14°C .16°D .26°19.(2020·四川雅安)如图,ABC 内接于圆,90ACB ∠=︒,过点C 的切线交AB 的延长线于点28P P ∠=︒,.则∠=CAB ( )A .62︒B .31︒C .28︒D .56︒20.(2020·山东淄博)如图,放置在直线l 上的扇形OAB .由图⊙滚动(无滑动)到图⊙,再由图⊙滚动到图⊙.若半径OA =2,⊙AOB =45°,则点O 所经过的最短路径的长是( )A .2π+2B .3πC .52πD .52π+221.(2021·贵州黔西)图1是一把扇形书法纸扇,图2是其完全打开后的示意图,外侧两竹条OA 和OB 的夹角为150︒,OA 的长为30cm ,贴纸部分的宽AC 为18cm ,则CD 的长为( )A .5πcmB .10πcmC .20πcmD .25πcm22.(2021·山东青岛)如图,AB 是O 的直径,点E ,C 在O 上,点A 是EC 的中点,过点A 画O 的切线,交BC 的延长线于点D ,连接EC .若58.5ADB ∠=︒,则ACE ∠的度数为( )A .29.5︒B .31.5︒C .58.5︒D .63︒23.(2021·四川内江)如图,O 是ABC ∆的外接圆,60BAC ∠=︒,若O 的半径OC 为2,则弦BC 的长为( )A .4B .C .3 D24.(2021·山东滨州)如图,O 是ABC 的外接圆,CD 是O 的直径.若10CD =,弦6AC =,则cos ABC ∠的值为( )A .45B .35C .43D .3425.(2021·辽宁鞍山)如图,AB 为O 的直径,C ,D 为O 上的两点,若54ABD ∠︒=,则C ∠的度数为( )A .34︒B .36︒C .46︒D .54︒26.(2021·江苏镇江)如图,⊙BAC =36°,点O 在边AB 上,⊙O 与边AC 相切于点D ,交边AB 于点E ,F ,连接FD ,则⊙AFD 等于( )A .27°B .29°C .35°D .37°27.(2021·湖南湘潭)如图,BC 为⊙O 的直径,弦AD BC ⊥于点E ,直线l 切⊙O 于点C ,延长OD 交l 于点F ,若2AE =,22.5ABC ∠=︒,则CF 的长度为( )A .2B .C .D .428.(2022·广西贺州)某餐厅为了追求时间效率,推出一种液体“沙漏”免单方案(即点单完成后,开始倒转“沙漏”, “沙漏”漏完前,客人所点的菜需全部上桌,否则该桌免费用餐).“沙漏”是由一个圆锥体和一个圆柱体相通连接而成.某次计时前如图(1)所示,已知圆锥体底面半径是6cm ,高是6cm ;圆柱体底面半径是3cm ,液体高是7cm .计时结束后如图(2)所示,求此时“沙漏”中液体的高度为( )A .2cmB .3cmC .4cmD .5cm29.(2022·广西河池)如图,AB 是⊙O 的直径,P A 与⊙O 相切于点A ,⊙ABC =25°,OC 的延长线交P A 于点P ,则⊙P 的度数是( )A .25°B .35°C .40°D .50°30.(2022·内蒙古包头)如图,,AB CD 是O 的两条直径,E 是劣弧BC 的中点,连接BC ,DE .若22ABC ∠=︒,则CDE ∠的度数为( )A .22︒B .32︒C .34︒D .44︒31.(2022·辽宁锦州)如图,线段AB 是半圆O 的直径。
中考数学几何最值模型 专题03 辅助圆模型(学生版+解析版)

辅助圆模型模型讲解一、定点定长1、O为定点,OA=OB,且长度固定,那么O、A、B三点可以确定一个圆,动点P在圆弧AB上运动,如图所示,Q为圆外一定点,当P运动到OQ的连线上时,即:P落到P1处,O、P1、Q三点共线时,PQ最小。
二、定弦定角2、线段AB固定,Q为动点,且∠AQB为定值,那么Q、A、B三点可以确定一个圆,动点Q在圆弧AB上运动,如图所示,R为圆外一定点,当Q运动到OQ的连线上时,即:P落到P1处,O、P1、Q三点共线时,RQ最小。
方法点拨一、题型特征:①动点的运动轨迹为圆②圆外一点到圆上一点的距离最短:即圆外一点与圆心连线与圆的交点③常见确定圆的模型:定点定长、定弦定角。
二、模型本质:两点之间,线段最短。
例题演练1.如图,已知AB=AC=BD=6,AB⊥BD,E为BC的中点,则DE的最小值为()A.3﹣3B.3C.3﹣3D.2【解答】解:取AB的中点O,连接AE,OE,OD.∵AB=AC,BE=EC,∴AE⊥BC,∴∠AEB=90°,∵OA=OB,∴OE=AB=3,∵AB⊥BD,∴∠OBD=90°,∵OB=3,BD=6,∴OD===3,∵DE≥OD﹣OE,∴DE≥3﹣3,∴DE的最小值为3﹣3,故选:C.强化训练1.如图,矩形ABCD中,AB=3,BC=8,点P为矩形内一动点,且满足∠PBC =∠PCD,则线段PD的最小值为()A.5B.1C.2D.3 2.如图,在矩形ABCD中,AB=4,BC=6,E是矩形内部的一个动点,且AE ⊥BE,则线段CE的最小值为.3.如图,△ABC为等边三角形,AB=2.若P为△ABC内一动点,且满足∠P AB =∠ACP,则线段PB长度的最小值为.4.如图,在矩形ABCD中,AB=4,BC=6,E是平面内的一个动点,且满足∠AEB=90°,连接CE,则线段CE长的最大值为.5.如图1,P是⊙O外的一点,直线PO分别交⊙O于点A,B,则P A是点P 到⊙O上的点的最短距离.(1)探究一:如图2,在Rt△ABC中,∠ACB=90°,AC=BC=2,以BC为直径的半圆交AB于D,P是上的一个动点,连接AP,则AP的最小值是.(2)探究二:如图3,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连接A′C,请求出A′C长度的最小值.(3)探究三,在正方形ABCD中,点E,F分别从D,C两点同时出发,以相同的速度在直线DC,CB上移动,连接AE和DF交于点P,由于点E,F的移动,使得点P也随之运动,若AD=4,试求出线段CP的最小值.1.如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′C,则A′C长度的最小值是.辅助圆模型模型讲解一、定点定长1、O为定点,OA=OB,且长度固定,那么O、A、B三点可以确定一个圆,动点P在圆弧AB上运动,如图所示,Q为圆外一定点,当P运动到OQ的连线上时,即:P落到P1处,O、P1、Q三点共线时,PQ最小。
2024中考数学新定义及探究题专题 《圆与新定义》 (含解析)

2024中考数学新定义及探究题专题《圆与新定义》(学生版)通用的解题思路:①对于圆中角度之间的等量关系,主要是两个方面:一是同弧或者等弧所对的圆周角相等,同弧或者等弧所对的圆心角是圆周角的两倍,二是圆内接四边形中外角等于内角的对角。
②对于求圆中的线段长度,主要从两个方向着手,首先看是否可以用垂径定理构建直角三角形,用勾股定理来求线段的长度;如果勾股定理行不通,则尝试着去找相似三角形,用相似三角形的对应线段成比例来求线段的长度。
1.(长沙中考)我们不妨约定:对角线互相垂直的凸四边形叫做“十字形”.(1)①在“平行四边形,矩形,菱形,正方形”中,一定是“十字形”的有;②在凸四边形ABCD 中,AB=AD 且CB≠CD ,则该四边形“十字形”.(填“是”或“不是”)(2)如图1,A ,B ,C ,D 是半径为1的⊙O 上按逆时针方向排列的四个动点,AC 与BD 交于点E ,∠ADB ﹣∠CDB=∠ABD ﹣∠CBD ,当6≤AC 2+BD 2≤7时,求OE 的取值范围;(3)如图2,在平面直角坐标系xOy 中,抛物线y=ax 2+bx+c (a ,b ,c 为常数,a >0,c <0)与x 轴交于A ,C 两点(点A 在点C 的左侧),B 是抛物线与y 轴的交点,点D 的坐标为(0,﹣ac ),记“十字形”ABCD 的面积为S ,记△AOB ,△COD ,△AOD ,△BOC 的面积分别为S 1,S 2,S 3,S 4.求同时满足下列三个条件的抛物线的解析式;①S =1S 2S +;②S 3S 4S +“十字形”ABCD 的周长为10.2.(一中)定义:三角形一边上的点将该边分为两条线段,且这两条线段的积等于这个点到该边所对顶点连线的平方,则称这个点为三角形该边的“好点”.如图1,△ABC中,点D是BC边上一点,连结AD,若2AD BD CD=⋅,则称点D是△ABC中BC边上的“好点”.(1)如图2,△ABC的顶点是43⨯网格图的格点,请仅用直尺画出AB边上的一个“好点”.(2)△ABC中,BC=9,4tan3B=,2tan3C=,点D是BC边上的“好点”,求线段BD的长.(3)如图3,△ABC是O的内接三角形,OH⊥AB于点H,连结CH并延长交O于点D.①求证:点H是△BCD中CD边上的“好点”.②若O的半径为9,∠ABD=90°,OH=6,请直接写出CHDH的值.3.(青竹湖)我们不妨定义:有两边之比为1“勤业三角形”.(1)下列各三角形中,一定是“勤业三角形”的是________;(填序号)①等边三角形;②等腰直角三角形;③含30︒角的直角三角形;④含120︒角的等腰三角形.(2)如图1,△ABC是⊙O的内接三角形,AC为直径,D为AB上一点,且2BD AD=,作DE OA⊥,交线段OA于点F,交⊙O于点E,连接BE交AC于点G.试判断△AED和△ABE是否是“勤业三角形”?如果是,请给出证明,并求出EDBE的值;如果不是,请说明理由;(3)如图2,在(2)的条件下,当AF:FG=2:3时,求BED∠的余弦值.4.(华益)约定:若三角形一边上的中线将三角形分得的两个小三角形中有一个三角形与原三角形相似,我们则称原三角形为关于该边的“华益美三角”.例如,如图1,在ABC 中,AD 为边BC 上的中线,ABD △与ABC 相似,那么称ABC 为关于边BC 的“华益美三角”.(1)如图2,在ABC 中,BC =,求证:ABC 为关于边BC 的“华益美三角”;(2)如图3,已知ABC 为关于边BC 的“华益美三角”,点D 是ABC 边BC 的中点,以BD 为直径的⊙O 恰好经过点A .①求证:直线CA 与O 相切;②若O 的直径为,求线段AB 的长;(3)已知ABC 为关于边BC 的“华益美三角”,4BC =,30B ∠=︒,求ABC 的面积.5.(华益)约定:三角形的一条中线将三角形分成两个小三角形,如果其中的一个小三角形与原三角形相似,那么称原三角形为“华益三角”,这条中线叫做原三角形的“华益中线”,这条中线所在的边叫做“华益边”,原三角形与小三角形的相似比叫做“华益比”.(1)如图1,已知CD 是ABC 边AB 上的中线,若ABC ACD ∽,那么ABC 就是“华益三角”,中线CD 是ABC 的“华益中线”,边AB 就是ABC 的“华益边”.爱思考的你们一定能发现:“华益三角”的“华益比”总是一个定值,以图1为例,求出“华益比”;(2)如图2,已知在ABC 中,45,1AB A AC ∠=︒+,求证:ABC 是“华益三角”;(3)如图3,已知ABC 是“华益三角”,边AB 是ABC 的“华益边”,ABC 的外接圆O 的半径是2.①若A ∠是一个锐角,求sin BC A的值;②记2,AB x BC ==,若1x =,求y 的值.6.(北雅)如图1,⊙O 的半径为r (0r >),若点P '在射线OP 上,满足2OP OP r '⋅=,则称点P '是点P 关于⊙O 的“反演点”.(1)若点A 关于⊙O 的“反演点”是本身,那么点A 与⊙O 的位置关系为()A .点A 在⊙O 内B .点A 在⊙O 上C .点A 在⊙O 外(2)如图1,若⊙O 的半径为4,点P '是点P 关于⊙O 的“反演点”,且6PP '=,过点P 的直线与⊙O 相切于点Q ,求PQ 长.(3)如图2,若⊙O 的半径为4,点Q 在⊙O 上,点A 在⊙O 内,且2OA =,点Q '、A '分别是点Q 、A 关于⊙O 的“反演点”,过点A '作A B A O '⊥'且A B A O '=',连接BQ ',Q A '',求12BQ Q A ''+'的最小值.7.(青竹湖)定义:两个角对应互余,且这两个角的夹边对应相等的两个三角形叫做“青竹三角形”.如图1,在△ABC 和DEF 中,若90A E B D ∠+∠=∠+∠=︒,且AB DE =,则△ABC 和DEF 是“青竹三角形”.45BAC ACD ∴∠=∠=︒(1)以下四边形中,一定能被一条对角线分成两个“青竹三角形”的是;(填序号)①平行四边形;②矩形;③菱形;④正方形.(2)如图2,△ABC ,90ACB ∠=︒,AC BC =,点D 是AB 上任意一点(不与点A 、B 重合),设AD 、BD 、CD 的长分别为a 、b 、c ,请写出图中的一对“青竹三角形”,并用含a 、b 的式子来表示2c ;(3)如图3,⊙O 的半径为4,四边形ABCD 是⊙O 的内接四边形,且△ABC 和△ADC 是“青竹三角形”.①求22AD BC +的值;②若BAC ACD ∠=∠,75ABC ∠=︒,求△ABC 和△ADC 的周长之差.8.(中雅)在平面直角坐标系xOy中,给出如下定义:若点P在图形M上,点Q在图形N 上,称线段PQ长度的最小值为图形M,N的“雅近值”,记为d(M,N),特别地,若图形M,N有公共点,规定d(M,N)=0.(1)如图1,⊙O的半径为2,①点A(1,0),B(3,4),则d(A,⊙O)=______,d(B,⊙O)=______.②已知直线l:y=43x+4与⊙O,求直线l与⊙O的雅近值d(l,⊙O).(2)如图2,C为x轴正半轴上的一点,⊙C的半径为1,直线y=ax+b(a≠0)与x轴交于点D,与y轴交于点E.①若a,b,线段DE与⊙C的“雅近值”d(DE,⊙O)<12,请直接写出圆心C的横坐标m的取值范围;②若b=C的横坐标m DE与⊙C的“雅近值”d(DE,⊙C)=0,求a的取值范围.9.(广益)婆罗摩芨多是公元7世纪古印度伟大的数学家,他在三角形、四边形、零和负数的运算规则,二次方程等方面均有建树,他也研究过对角线互相垂直的圆内接四边形,我们把这类对角线互相垂直的圆内接四边形称为“婆氏四边形”.(1)若平行四边形ABCD是“婆氏四边形”,则四边形ABCD是.(填序号)①矩形;②菱形;③正方形(2)如图1,Rt ABC中,∠BAC=90°,以AB为弦的⊙O交AC于D,交BC于E,连接DE、AE、BD,AB=6,3sin5C ,若四边形ABED是“婆氏四边形”,求DE的长.(3)如图2,四边形ABCD为⊙O的内接四边形,连接AC,BD,OA,OB,OC,OD,已知∠BOC+∠AOD=180°.①求证:四边形ABCD是“婆氏四边形”;②当AD+BC=4时,求⊙O半径的最小值.10.(雅礼)圆内各几何要素之间存在一定的数量关系和位置关系,这也是国内外数学家感兴趣的研究对象,其中就有对角线互相垂直的圆内接四边形.我们把这类对角线互相垂直的圆内接四边形称为“雅系四边形”.(1)若平行四边形ABCD 是“雅系四边形”,则四边形ABCD 是______(填序号);①矩形;②菱形;③正方形(2)如图,四边形ABCD 内接于圆,P 为圆内一点,90APD BPC ∠=∠=︒,且ADP PBC ∠=∠,求证:四边形ABCD 为“雅系四边形”;(3)在(2)的条件下,3BD =,且AB =.①当DC =时,求AC 的长度;②当DC 的长度最小时,请直接写出tan ADP ∠的值.11.(青竹湖)定义:有一组对角互补且一组邻边相等的四边形叫做“完美四边形”.(1)如图1,四边形ABCD 是O 的内接四边形,且对角线BD 平分ABC ∠,四边形ABCD _______(填“是”或者“不是”)“完美四边形”,若90ABC ∠=︒,且2AD =,则O 的直径为;(2)如图2,四边形ABCD 中,AC 平分BAD ∠,CE AB ⊥于E ,AD BE AE +=.求证:四边形ABCD 为“完美四边形”;(3)如图3,在“完美四边形”ABCD 中,AB AD =,8AC =,60BAD ∠=︒,对角线AC 与BD 相交于点P ,设BC x =,CP y =,求y 与x 的函数关系式,并求y 的最大值.12.(师大附中)若凸四边形的两条对角线所夹锐角为60︒,我们称这样的凸四边形为“美丽四边形”.(1)①在“平行四边形、梯形、菱形、正方形”中,一定不是“美丽四边形”的有;②若矩形ABCD 是“美丽四边形”,且3AB =,则BC =;(2)如图1,“美丽四边形”ABCD 内接于⊙O ,AC 与BD 相交于点P ,且对角线AC 为直径,15AP PC ==,,求另一条对角线BD 的长;(3)如图2,平面直角坐标系中,已知“美丽四边形”ABCD 的四个顶点()()3020A C -,、,,B在第三象限,D 在第一象限,AC 与BD 交于点O ,且四边形ABCD 的面积为函数2y ax bx c =++(a 、b 、c 为常数,且0a ≠)的图象同时经过这四个顶点,求a 的值.2024中考数学新定义及探究题专题《圆与新定义》(解析版)通用的解题思路:①对于圆中角度之间的等量关系,主要是两个方面:一是同弧或者等弧所对的圆周角相等,同弧或者等弧所对的圆心角是圆周角的两倍,二是圆内接四边形中外角等于内角的对角。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中考数学试题专题复习:圆 【学生版】
一、选择题
1. (天津3分)已知⊙1O 与⊙2O 的半径分别为3 cm 和4 cm ,若12O O =7 cm ,则⊙1O 与⊙2O 的位置关系是
(A) 相交 (B) 相离 (C) 内切 (D) 外切
2.(内蒙古包头3分)已知两圆的直径分别是2厘米与4厘米,圆心距是3厘米,则这两个圆的位置关系是
A 、相交
B 、外切
C 、外离
D 、内含
3,(内蒙古包头3分)已知AB 是⊙O 的直径,点P 是AB 延长线上的一个动点,
过P 作⊙O 的切线,切点为C ,∠APC 的平分线交AC 于点D ,则∠CDP 等于
A 、30°
B 、60°
C 、45°
D 、50°
4.(内蒙古呼和浩特3分)如图所示,四边形ABCD 中,DC∥AB,BC=1,
AB=AC=AD=2.则BD 的长为 A. 14 B. 15 C. 32 D. 23
5.(内蒙古呼伦贝尔3分)⊙O 1的半径是cm 2,⊙2的半径是cm 5,圆心距是cm 4,则两圆的位置关系为
A. 相交
B. 外切
C.外离
D. 内切
6.(内蒙古呼伦贝尔3分)如图,⊙O 的半径为5,弦AB 的长为8,M 是弦AB 上的动点,
则线段OM 长的最小值为.
A. 5
B. 4
C. .3
D. 2
7.(内蒙古呼伦贝尔3分)如图,AB 是⊙O 的直径,点C 、D 在⊙O 上 ,∠BOD=110°,
AC∥OD,则∠AOC 的度数
A. 70°
B. 60°
C. 50°
D. 40°
8.(内蒙古乌兰察布3分)如图, AB 为 ⊙ O 的直径, CD 为弦, AB ⊥ CD ,
如果∠BOC = 700
,那么∠A 的度数为
A 70 0 B. 350 C. 300 D . 200
17.填空题
1.(天津3分)如图,AD ,AC 分别是⊙O 的直径和弦.且∠CAD=30°.OB⊥AD,交AC
于点B .若OB=5,则BC 的长等于 ▲ 。
2.(河北省3分)如图,点0为优弧¼
ACB所在圆的圆心,∠AOC=108°,点D
在AB延长线上,BD=BC,则∠D=▲.
3.(内蒙古巴彦淖尔、赤峰3分)如图,直线PA过半圆的圆心O,交半圆于A,
B两点,PC切半圆与点C,已知PC=3,PB=1,则该半圆的半径为▲.
4.(内蒙古呼伦贝尔3分)已知扇形的面积为12 ,半径是6,则它的圆心角是▲。
18.解答题
1.(天津8分)已知AB与⊙O相切于点C,OA=OB.OA、OB与⊙O分别交于点D、E.
(I) 如图①,若⊙O的直径为8,AB=10,求OA的长(结果保留根号);
(Ⅱ)如图②,连接CD、CE,若四边形ODCE为菱形.求OD
OA
的值.
2.(河北省10分)如图1至图4中,两平行线AB、CD间的距离均为6,点M为AB上一定点.
思考
如图1,圆心为0的半圆形纸片在AB,CD之间(包括AB,CD),其直径MN在AB上,MN=8,点P为半圆上一点,设∠MOP=α.
当α= ▲度时,点P到CD的距离最小,最小值为▲.
探究一
在图1的基础上,以点M为旋转中心,在AB,CD 之间顺时针旋转该半圆形纸片,直到不能再转动为止,如图2,得到最大旋转角∠BMO=▲度,此时点N到CD的距离是▲.
探究二
将如图1中的扇形纸片NOP按下面对α的要求剪掉,使扇形纸片MOP绕点M在AB,CD之间顺时针旋转.
(1)如图3,当α=60°时,求在旋转过程中,点P到CD的最小距离,并请指出旋转角∠BMO的最大值;
(2)如图4,在扇形纸片MOP旋转过程中,要保证点P能落在直线CD上,请确定α的取值范围.
(参考数椐:sin49°=3
4
,cos41°=
3
4
,tan37°=
3
4
.)
【考点】直线与圆的位置关系,点到直线的距离,平行线之间的距离,切线的性质,旋转的性质,解直角三角形。
3.(内蒙古呼和浩特8分)如图所示,AC为⊙O的直径且PA⊥AC,BC
是⊙O的一条弦,直线PB交直线AC于点D,DB DC2 DP DO3
==.
(1)求证:直线PB是⊙O的切线;
(2)求cos∠BCA的值.
【考点】切线的判定和性质,平行的判定和性质,全等三角形的判
定和性质,相似三角形的判定和性质,锐角三角函数的定义,勾股定理,切线长定理。
4.(内蒙古巴彦淖尔、赤峰12分)如图,等圆⊙O1 和⊙O2 相交于A,B两点,
⊙O2 经过⊙O1 的圆心O1,两圆的连心线交⊙O1于点M,交AB于点N,连接BM,已知
AB=23。
(1)求证:BM是⊙O2的切线;
(2)求⌒
AM的长。
【考点】切线的判定和性质,相交两圆的性质,锐角三角函数,特殊角的三角函数值,弧长的计算。
1
2
N
M
A B
O
O
5.(内蒙古包头12分)如图,已知∠ABC=90°,AB=BC.直线l与以BC为直径的圆O相切于点C.点F是圆O上异于B、C的动点,直线BF与l相交于点E,过点F作AF的垂线交直线BC与点D.
(1)如果BE=15,CE=9,求EF的长;
(2)证明:①△CDF∽△BAF;②CD=CE;
(3)探求动点F在什么位置时,相应的点D位于线段BC的延长线上,且
使BC=3CD,请说明你的理由.
【考点】相似三角形的判定和性质,勾股定理,圆周角定理,切线的性质,
锐角三角函数定义,特殊角的三角函数值。
6.(内蒙古乌兰察布10分)如图,在Rt△ABC中,∠ACB=900D是AB 边上
的一点,以BD为直径的⊙0与边 AC 相切于点E,连结DE并延长,与BC的
延长线交于点 F .
( 1 )求证: BD = BF ;
( 2 )若 BC = 12 , AD = 8 ,求 BF 的长.。
