缓和曲线和圆曲线的有关计算
(完整版)缓和曲线、圆曲线测设计算例题
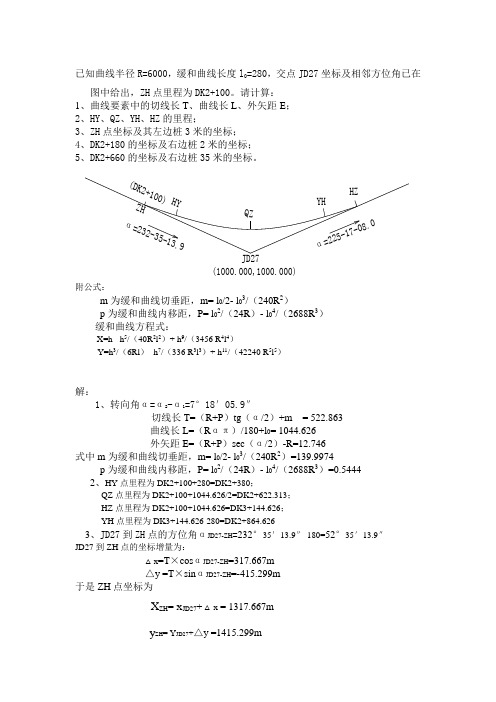
已知曲线半径R=6000,缓和曲线长度l 0=280,交点JD27坐标及相邻方位角已在图中给出,ZH 点里程为DK2+100。
请计算:1、曲线要素中的切线长T 、曲线长L 、外矢距E ;2、HY 、QZ 、YH 、HZ 的里程;3、ZH 点坐标及其左边桩3米的坐标;4、DK2+180的坐标及右边桩2米的坐标;5、DK2+660的坐标及右边桩35米的坐标。
永州α=225-17-08.0JD27(D K 2+100)(1000.000,1000.000)α=232-35-13.9H Z Q ZHZ H Y YH附公式:m 为缓和曲线切垂距,m= l 0/2- l 03/(240R 2)p 为缓和曲线内移距,P= l 02/(24R )- l 04/(2688R 3)缓和曲线方程式:X=h - h 5/(40R 2l 2)+ h 9/(3456 R 4l 4)Y=h 3/(6Rl )- h 7/(336 R 3l 3)+ h 11/(42240 R 5l 5)解:1、转向角α=α2-α1=7°18′05.9″切线长T=(R+P )tg (α/2)+m = 522.863曲线长L=(R απ)/180+l 0= 1044.626外矢距E=(R+P )sec (α/2)-R=12.746式中m 为缓和曲线切垂距,m= l 0/2- l 03/(240R 2)=139.9974p 为缓和曲线内移距,P= l 02/(24R )- l 04/(2688R 3)=0.54442、HY 点里程为DK2+100+280=DK2+380;QZ 点里程为DK2+100+1044.626/2=DK2+622.313;HZ 点里程为DK2+100+1044.626=DK3+144.626;YH 点里程为DK3+144.626-280=DK2+864.6263、JD27到ZH 点的方位角αJD27-ZH =232°35′13.9″-180=52°35′13.9″ JD27到ZH 点的坐标增量为:△x =T ×cos αJD27-ZH =317.667m△y =T ×sin αJD27-ZH =-415.299m于是ZH 点坐标为X ZH = x JD27+ △x = 1317.667my ZH = Y JD27+△y =1415.299mZH点到左边桩3米的方位角αZH-左边桩= 232°35′13.9″-90=142°35′13.9″左边桩3米的坐标为:X左= x ZH+ 3×cosαZH-左边桩= 1315.284mY左= y ZH +3×sinαZH-左边桩=1417.122m4、DK2+180的坐标及右边桩2米的坐标:DK2+180在缓和曲线上,计算过程为:ZH点到JD27的方位角αZH-JD1= =232°35′13.9″DK2+180到ZH点的缓和曲线长度h为180-100=80根据缓和曲线方程式:X=h - h5/(40R2l2)+ h9/(3456 R4l4)=80.000Y=h3/(6Rl)- h7/(336 R3l3)+ h11/(42240 R5l5)=0.0508由X和Y可以求出DK5+900与ZH的距离D和它的偏角δ:D=√(X2+ Y2)=80.000δ=arctg(Y/ X)=0°02′11.0″于是DK2+180的坐标(X1,Y1)为:X1= 1317.667+Dcos(232°35′13.9″-δ)=1269.022Y1 = 1415.299+Dsin(232°35′13.9″-δ)=1351.788DK2+300右边桩2米的坐标(X2,Y2)为:X2= 1269.022+2×cos(232°35′13.9″-3δ+90)=1270.608Y2= 1351.788+2×sin(232°35′13.9″-3δ+90)=1350.5705、圆曲线点DK2+660计算过程为:曲中点QZ的里程推算为DK2+622.313, DK2+660到QZ的圆曲线长度为660-622.313=37.687,所对应的圆心角为O′=(180*37.687)/(πR)=0°21′35.6″, JD27到圆心O的方位角αJD27-O=225°17′08.0″-(180-7°18′05.9″)/2=138°56′10.95″圆心O的坐标为:X3 =1000+(E+R)cos(138°56′10.95″)=-3533.494Y3= 1000+(E+R)sin(138°56′10.95″)=4949.753DK2+660的坐标(X4,Y4)为:X4= X3++ R cos(138°56′10.95″+180- O′)=965.544Y4 = Y3+Rsin(138°56′10.95″+180- O′)=980.035DK2+660右边桩35米的坐标(X5,Y5)为:X5= X3++ (R+35)×cos(138°56′10.95″+180- O′)=991.788Y5= Y3+(R+35)×sin(138°56′10.95″+180- O′)=956.878。
缓和曲线圆曲线计算公式

缓和曲线、竖曲线、圆曲线、匝道(计算公式)一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ,yZ为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ,yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i1(上坡为“+”,下坡为“-”)②第二坡度:i2(上坡为“+”,下坡为“-”)③变坡点桩号:SZ④变坡点高程:HZ⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程:五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x 求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K0③曲线终点桩号:K1④曲线起点坐标:x0,y0⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P0(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”) 求:①线路匝道上点的坐标:xy②待求点的切线方位角:αT计算过程:注:sgn(x)函数是取符号函数,当x0时sgn(x)=1,当x=0时sgn(x)=0。
坐标计算公式

坐标计算公式一、计算公式1、圆曲线坐标计算公式β=180°/π×L/R (L= βπ R/180°)弧长公式β为圆心角△X=sinβ×R△Y=(1-cosβ)×RC= 弦长X=X1+cos (α±β/2)×CY=Y1+sin (α±β/2)×Cβ代表偏角,(既弧上任一点所对的圆心角)。
β/2是所谓的偏角(弦长与切线的夹角)△X、△Y代表增量值。
X、Y代表准备求的坐标。
X1、Y1代表起算点坐标值。
α代表起算点的方位角。
R 代表曲线半径2、缓和曲线坐标计算公式β= L2/2RLS ×180°/πC= L - L5/90R2LS2X=X1+cos (α±β/3)×CY=Y1+sin (α±β/3)×CL代表起算点到准备算的距离。
LS代表缓和曲线总长。
X1、Y1代表起算点坐标值。
3、直线坐标计算公式X=X1+cosα×LY=Y1+sinα×LX1、Y1代表起算点坐标值α代表直线段方位角。
L代表起算点到准备算的距离。
4、左右边桩计算方法X边=X中+cos(α±90°)×LY边=Y中+sin(α±90°)×L在计算左右边桩时,先求出中桩坐标,在用此公式求左右边桩。
如果在线路方向左侧用中桩方位角减去90°,线路右侧加90°,乘以准备算的左右宽度。
二、例题解析例题:直线坐标计算方法α(方位角)=18°21′47″DK184+714.029求DK186+421.02里程坐标X1=84817.831 Y1=352.177 起始里程解:根据公式X=X1+cosα×LX=84817.831+COS18°21′47″×(86421.02—84714.029)=86437.90 1Y=Y1+sinα×LY=352.177+sin18°21′47″×(86421.02—84714.029)=889.943 求DK186+421.02里程左右边桩,左侧3.75m,右侧7.05m.解:根据公式线路左侧计算:X边=X中+cos(α±90°)×LX边=86437.901+cos(18°21′47″- 90°)×3.75=86439.082Y边=Y中+sin(α±90°)×LY边=889.943+sin(18°21′47″- 90°)×3.75=886.384线路右侧计算:X边=X中+cos(α±90°)×LX边=86437.901+cos(18°21′47″+ 90°)×7.05=86435.680Y边=Y中+sin(α±90°)×LY边=889.943+sin(18°21′47″+90°)×7.05=896.634例题:缓和曲线坐标计算方法α(ZH点起始方位角)=18°21′47″ X1=86437.901 Y1=889.941 起始里程DK186+421.02曲线半径2500 缓和曲线长120m求HY点坐标,也可以求ZH点到HY点任意坐标解:根据公式β=L2/2RLS×180°/πβ={1202/(2×2500×120)}×(180°/π)= 1°22′30.36″C=L-L5/90R2LS2C=120-1205/(90×25002×1202)=119.997X=X1+cos(α±β/3)×CX=86437.901+cos(18°21′47″-1°22′30.36″/3)×119.997=86552.086 Y=Y1+sin(α±β/3)×CY=889.941+sin(18°21′47″-1°22′30.36″/3)×119.997=926.832 求DK186+541.02里程左右边桩,左侧3.75m,右侧7.05m.解:根据公式线路左侧计算:X边=X中+cos(α±90°)×LX边=86552.086+cos{(18°21′47″-1°22′30.36″)- 90°}×3.75=86553.182 Y边=Y中+sin(α±90°)×LY边=926.832+sin{(18°21′47″-1°22′30.36″)- 90°}×3.75=923.246 线路右侧计算:X边=X中+cos(α±90°)×LX边=86552.086+cos{(18°21′47″-1°22′30.36″)+ 90°}×7.05=86550.026 Y边=Y中+sin(α±90°)×LY边=926.832+sin{(18°21′47″-1°22′30.36″)+ 90°}×7.05=933.574 缓和曲线方位角计算方法α=(起始方位角±β偏角)= 18°21′47″-1°22′30.36″=16°59′16.64″注:缓和曲线在计算坐标时,此公式只能从两头往中间推,只能从ZH点往HY点推,HZ点往YH点推算,如果YH往HZ点推算坐标,公式里的β为β2/3.例题:圆曲线坐标计算方法α(HY点起始方位角)= 16°59′16.64″ X1=86552.086 Y1=926.832 曲线半径2500 曲线长748.75 起始里程DK186+541.02求YH点坐标,也可以求QZ点坐标或任意圆曲线一点坐标.解:根据公式β=180°/π×L/Rβ= 180°/π×748.75/2500=17°09′36.31″△X=sinβ×R△X=sin17°09′36.31″×2500=737.606△Y=(1-cosβ)×R△Y=(1-cos17°09′36.31″)×2500=111.290C= 弦长C=745.954X=X1+cos(α±β/2)×CX= 86552.086 +cos(16°59′16.64″+360°-17°09′36.31″/2)×745.954=87290.023 Y=Y1+sin(α±β/2)×CY=926.832+ sin(16°59′16.64″+360°-17°09′36.31″/2)×745.954=1035.905圆曲线方位角计算方法α=(起始方位角±β偏角)=16°59′16.64″+360°-17°09′36.31″=359°49′40.33″求DK187+289.77里程左右边桩,左侧3.75m,右侧7.05m.解:根据公式线路左侧计算:X边=X中+cos(α±90°)×LX边=87290.023+cos(359°49′40.33″-90°)×3.75=87290.012 Y边=Y中+sin(α±90°)×LY边=1035.905+sin(359°49′40.33″-90°)×3.75=1032.155线路右侧计算:X边=X中+cos(α±90°)×LX边=87290.023+cos(359°49′40.33″+90°)×7.05=87290.044 Y边=Y中+sin(α±90°)×LY边=1035.905+sin(359°49′40.33″+90°)×7.05=1042.955三、公式解析公式解析一.坐标转换X =A +NCOSα-ESINαY =B +NSINα+ECOSα N=(X-A) COSα±(Y-B)SINα E=(Y-B)COSα±(X-A)SINαA,B为施工坐标系坐标原点α为施工坐标系与北京坐标系X轴的夹角(旋转角)即大地坐标系方位角X,Y为北京坐标值N,E为施工坐标值二.方位角计算1.直线段方位角: α=tanˉ¹ [(Yb-Ya)/(Xb-Xa)]2.交点转角角度: α=2 tanˉ¹ (T/R)计算结果①为﹢且<360,则用原数;②为﹢且>360,则减去360;③为﹣,则加上180.3.缓和曲线上切线角: α=ƟZH±90°*Lo²/(π*R* Ls)α= Lo/(2ρ)=Lo²/(2 A²)=Lo²/(2R*Ls)ρ—该点的曲率半径4.圆曲线上切线角: α=ƟHY±180°*Lo/(π*R)ƟZH—直缓点方位角, ƟHY—缓圆点方位角,注:以计算方向为准,左偏,取"﹣";右偏,取"﹢"。
缓和曲线)计算公式

创作编号:GB8878185555334563BT9125XW创作者:凤呜大王*高速公路的线路(缓和曲线)计算公式一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:x Z,y Z计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反x Z,y Z为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:x Z,y Z计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反x Z,y Z为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i1(上坡为“+”,下坡为“-”)②第二坡度:i2(上坡为“+”,下坡为“-”)③变坡点桩号:S Z④变坡点高程:H Z⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程五、超高缓和过渡段的横坡计算已知:如图,创作编号:GB8878185555334563BT9125XW创作者:凤呜大王*第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K0③曲线终点桩号:K1④曲线起点坐标:x0,y0⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P0(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”)求:①线路匝道上点的坐标:x,y②待求点的切线方位角:αT计算过程:创作编号:GB8878185555334563BT9125XW创作者:凤呜大王*。
圆曲线、缓和曲线计算方法

● 圆曲线方法一:sin (1cos )180i i i i i i x R y R l R ϕϕϕπ⎧⎪=⎪=-⎨⎪︒⎪=⋅⎩——i l 为待定点i P 至起点间的弧长i ϕ为i l 所对的圆心角R 为曲线半径方法二:11802l A R π︒=⋅⋅ 2sin l R A =⋅00cos(/)sin(/)x x l A y y l A =+⋅+-⎧⎨=+⋅+-⎩起点方位角左减右加起点方位角左减右加——00(,)x y 为圆曲线起点坐标方法三:180l A R π︒=⋅ 00cos(/)sin(/)x x R B A y y R B A =+⋅+-⎧⎨=+⋅+-⎩——l 为圆曲线上任意一点距起点距离00(,)x y 为圆曲线圆心坐标B 为圆心到圆曲线起点的方位角,A 为任意点对应的圆心角● 缓和曲线522030406l x l R l ly Rl ⎧=-⎪⎪⎨⎪=⎪⎩——l 为曲线上任一点至起点的曲线长R 曲线半径0l 为缓和曲线全长圆曲线、缓和曲线计算方法1、直线段:先由JD1以及JD2的坐标算出JD1到JD2的方位角,即直线段方位角A ,故可算出HZ 、ZH 坐标及其直线段各点坐标。
2、缓和曲线:以HZ 、ZH 为起点,缓和曲线上任意一点离HZ 、ZH 距离为l ,利用公式522003040()6l x l R l l R ly Rl ⎧=-⎪⎪⎨⎪=⎪⎩为缓和曲线全长,为圆曲线半径算出该点的相对起点坐标,利用arctan y x算出该点相对起点的方位角B ,再根据线路走向及直线段方位角可算出该点的方位角C (顺时针加,逆时针减),用可求出该点相对起点的距离D ,最后用00cos sin x x D C y y D C =+⎧⎨=+⎩可求出该点的坐标。
(00(,)x y 为缓和曲线起点的坐标)3、圆曲线:用上述方法求出圆曲线两端点HY 、YH 坐标,算出HY 到YH 的方位角F ,以及两点间的距离E ,用12arccos ER可算出两端点连线与起点到圆心连线的夹角G ,根据线路走向求出起点到圆心的方位角H (H=F+/-G ),00(,)x y 圆曲线为起点坐标,根据00cos sin x x R H y y R H=+⎧⎨=+⎩,求出圆心坐标。
缓和曲线连同圆曲线的曲线主点测设

缓和曲线连同圆曲线的曲线主点测设一、缓和曲线常数计算曲线要素计算前,应进行必要的常数计算。
缓和曲线的常数包括:缓和曲线、切垂距m(切线增长值)、内移距p。
切线角β缓和曲线切线角——过HY(或YH)点的切线与ZH(或HZ)点的切线组成的角。
即,圆曲线被缓和曲线所代替的那一段弧长对应的圆心角。
向切线作垂线的垂足到缓和曲线起点的距离。
切垂距——由圆心O2内移距——加缓和曲线后,圆曲线相对于切线的内移量。
缓和曲线常数按下式计算:二、缓和曲线要素计算、切曲差q。
各曲线要缓和曲线要素包括:切线长T、曲线总长L、外矢距E素按下式计算:式中 L′——HY点到YH点的曲线长。
三、主点里程计算主点里程计算是根据交点里程和缓和曲线要素推算而得,如图4.5.2所示。
铁路习惯推算方法:公路习惯推算方法:四、主点测设方法举例【例4.6.1】已知某线路,交点里程为DK281+578.59,圆曲线半径R=500m,转向角α右=18°22′00″,缓和曲线长l=40 m。
试计算曲线要素与主点里程。
【解】(1)缓和曲线常数计算:(2)缓和曲线要素计算:(3)主点里程计算:校核:(4)主点测设方法:缓和曲线的圆曲线主点测设与单圆曲线主点测设方法基本相同,ZH、HZ、QZ 的测设方法和精度要求与ZY、YZ、QZ相同。
用直角坐标法(即切线支距法)测设HY、YH点。
如图4.7.1所示,HY、YH点的坐标,按式(4.6.12)、(4.6.13)计算,当l=l0时,则x、y为:置镜于ZH(HZ)点,后视交点方向,沿视线方向测设x,得HY(HY)点的,得HY(HY)垂足,仪器搬到垂足点,后视切线方向,拨90°角,沿视线测设y点。
高速公路线路(缓和曲线、竖曲线、圆曲线、匝道)坐标计算公式

高速公路线路(缓和曲线、竖曲线、圆曲线、匝道)坐标计算公式_★★高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道)一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ,yZ为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ,yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i1(上坡为“+”,下坡为“-”)②第二坡度:i2(上坡为“+”,下坡为“-”)③变坡点桩号:SZ④变坡点高程:HZ⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程:五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x 求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K0③曲线终点桩号:K1④曲线起点坐标:x0,y0⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P0(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”)求:①线路匝道上点的坐标:x,y②待求点的切线方位角:αT计算过程:注:sgn(x)函数是取符号函数,当x<0时sgn(x)=-1,当x>0时sgn(x)=1,当x=0时sgn(x)=0。
缓和曲线计算公式
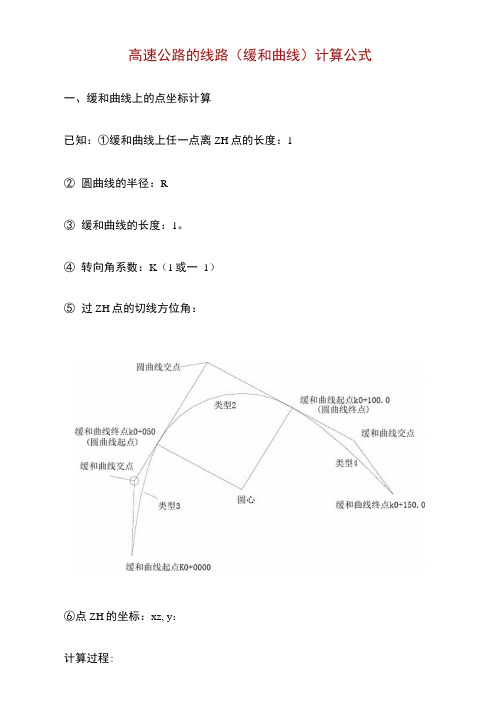
高速公路的线路(缓和曲线)计算公式一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:1②圆曲线的半径:R③缓和曲线的长度:1。
④转向角系数:K(1或一1)⑤过ZH点的切线方位角:⑥点ZH的坐标:xz, y:计算过程:= (工-亠)K6RL 3361JR 54 OR 吒 3456R1⑶ O^ = axctg —+ n.-180冶I4]S=屈十垃⑸ q=y 90I6]X1 = ScosC^(7] y x = Ssina t(8) x = X1 + Xr旧说明:当曲线为左转向时,K 二1,为右转向时,K 二-1, 公式中n 的取值如下:当计算第二缓和曲线上的点坐标时,则:1为到点HZ 的长度a 为过点HZ 的切线方位角再加上180°K 值与计算第一缓和曲线时相反x :, y 二为点HZ 的坐标7 ■二、圆曲线上的点坐标计算 已知:①圆曲线上任一点离ZH 点的长度:1②圆曲线的半径:R③ 缓和曲线的长度:lo 切线角计算公式: I 52R T④转向角系数:K(1或一1)⑤过ZH点的切线方位角:a⑥点ZH的坐标:x:, y:计算过程:[|]2』⑵已)R兀⑵尸——「24R 26SSR3(3)m=^-- +^—2 24OR2 34560丈14]禺二[R(l—cosCl')+p]K(5)y0 = RsinCl 如(6以二arctg如+ml80Xo⑺s二J M+朮(毗二q+a-90(9)x x= Scos(\(10]y x= SsinG,!(I O K=X X+X I忆说明:当曲线为左转向时,K二1,为右转向时,K二-1, 公式中n的取值如下: 当只知道HZ点的坐标时,则:1为到点HZ的长度a为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反X:,穴为点HZ的坐标Q三、曲线要素计算公式12⑴缓曲段任意点转角值:E =2Rlo⑵曲线段任意点转角值:6 = ^^1 = -(P1+P2)L2R1R2 2⑶第一缓曲段总转角值:矗=符⑷第二缓曲段总转角值:內=彩3 F冷 +—-—2 240於34560R"⑸第一曲线顺移量5严屯-⑹第二曲线顺移量:恥=乜- 一E R +—2 240# 34560R⑺第-曲线平移童”施2S88,(8)第二曲线平移童;P2 = ,24R 2688R3⑼第一切线长;T1 = m^ + l(P1 + p2 + 2R)tg- + ini 2辭2 22阿第二切线长;T2=PCPl + £(P1 + P2 + 2R)t g- + m2 2t g°2 22(ID曲线全长度;L = Ra + -(i1+]2)2(12)圆曲线长£:Lo = Rc(-i(L1 + i2) 2個曲线段长度;].=£「=竺些P朵寺闯比]鬼3ZX • CR坳偏禽缓曲D的边势曲线檢度::1=A1 + D^、_公式中各符号说明:1一一任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)11一一第一缓和曲线长度1=一一第二缓和曲线长度10一一对应的缓和曲线长度R—一圆曲线半径R:一一曲线起点处的半径R:一一曲线终点处的半径Pi——曲线起点处的曲率P:——曲线终点处的曲率a一一曲线转角值四、竖曲线上高程计算己知:①第一坡度:h(上坡为“ + ”,下坡为“一”)②第二坡度:込(上坡为“ + ”,下坡为“一”)③变坡点桩号:S:④变坡点高程:比⑤竖曲线的切线长度:T⑥待求点桩号:S(2]R = • • 12 一 la1+—R (ia+iz )B 〕H =压 + L—2R ―丄-扌 Ri 厶第一横坡:i : 第二横坡:i:过渡段长度:L 待求处离第二横坡点(过渡段终点)的距离:xT T⑴耳-期带有符号)2T求:待求处的横坡:i解:d二x/Li二(i厂ij (1-3孑+2占)+血六、匝道坐标计算己知:①待求点桩号:K②曲线起点桩号:Ko③曲线终点桩号:K:④曲线起点坐标:xo,y0⑤曲线起点切线方位角:⑥曲线起点处曲率:P。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
缓和曲线和圆曲线的计算与测设一、缓和曲线的性质缓和曲线是直线与圆曲线间的一种过渡曲线。
它与直线分界处半径为∞,与圆曲线相接处半径与圆曲线半径R 相等。
缓和曲线上任一点的曲率半径ρ∝l1 或ρl=C式中,C 变更率。
当l =0l 时,ρ=R ,所以0Rl =C式中,0l 为缓和曲线总长。
ρl=C 是缓和曲线的必要条件,实用中能满足这一条件的曲线可以作为缓和曲线,如辐射螺旋线、三次抛物线等。
我国缓和曲线均采用辐射螺旋线。
二、缓和曲线方程式按照ρl=C 为必要条件导出的缓和曲线方程为:X=l -2540C l +493456C l +…Y=Cl 63-37336C l +51142240C l + (1)根据测设要求的精度,实际应用中可将高次项舍去,并顾及到0Rl =C ,则上式变为X=l -202540l R lY=036Rl l -3037336l R l (2)式中,x 、y 为缓和曲线上任一点的直角坐标,坐标原点为直缓点(ZH )或缓直点(HZ );通过该点的缓和曲线切线为x 轴,如图2:l 为缓和曲线上任一点P 到ZH (或HZ )的曲线长;0l 为缓和曲线总长度。
当l =0l 时,x=x 0,y=y 0,代入式(2)得:X 0=0l -23040R lY 0=Rl 62-340336Rl (3)式中,x 0 、y 0 为缓圆点(HY )或圆缓点(YH )的坐标。
三、缓和曲线常数计算β0、δ0、m 、p 、 x 0、y 0 等称为缓和曲线常数。
其物理意义及几何关系由下图,图3可得知:β0——缓和曲线的切线角,即HY (或YH )点的切线与ZH (或HZ )点切线的交角;亦即圆曲线一端延长部分所对应的圆心角。
δ0——缓和曲线的总偏角;m —切垂距,即ZH (或HZ )到由圆心O 向切线所作垂线垂足的距离; p —圆曲线内移量,为垂线长与圆曲线半径R 之差。
常数计算公式如下:X 0=0l -23040R lY 0=Rl 62-340336Rlβ0=π18020R lδ0=031β=π 18060R lm=2l -230240R lp=24R l 20-3402688Rl ≈24Rl 20 (4) 下面我们推证常数β0、δ0 、m 、p 、x 0、y 0。
(一) 求β0设β为缓和曲线上任一点的切线角;ρ为该点的曲率半径;l 为该点至ZH 点的缓和曲线长。
如图4d β=d l /ρ,将ρl=0Rl 代入上式,则d β=dl l /0Rl∴ β=∫0l d β=∫0lRl ldl =22Rl l当l =0l ,β=β0 则β0=π18020R l (5)(二)求δ0 由上图可得知,tan δ0=0x y∵δ0很小,故δ0≈tan δ0=00x y 将(3)式代入上式,并略去二次项,∴δ0=R l 60=031β (6)(三)、圆曲线内移值 m如图3 m=c x -0sin β R 运用级数展开,略去高次项=0l -23040R l -R (+-2308612Rl R l …)=2l -230240R l (7)(四) 切垂距p 计算 如图3 p=(R+cos βcy )×0cos β-R =c y -R (1-0cos β) 运用级数展开,略去高次项=Rl62-340336R l -R (1-(1-++44022016241421Rl R l …))=Rl 62-340336Rl -440203848R l R l +=24R l 20-3402688Rl ≈24Rl 20 (8) (五)求x 0、y 0任取一微小变量 dl, 则所对应的x 、y 增量为,dx 、dy, 其对应的关系为 dx= dl βcosdy=dl βsin (9)βcos =1-!β22+!β44-…βsin =β-!β33+!β55-…β=022Rl l(10)将(10)代入(9)式进行积分,并略去高次项得:X=l -202540l R lY=036Rl l -3037336l R l当l=l 0 时X 0=0l -23040R lY 0=Rl 62-340336Rl四、曲线测设(一)曲线综合要素计算由图3可知,曲线综合要素计算如下: 切线长 T=m+(R+p).tan 2α 曲线长 L=20l +1802R 0〕β〔α-π=0l +180R απ 外矢距 E 0=(R+P )2sec α -R切曲差 q=2T -L (11) (二)缓和曲线的偏角计算如图5,缓和曲线上任一点i 的偏角为: δ≈sin δ≈ly (∵δ很小)∵y=036Rl l∴δ=π180602Rl l 又∵β=022Rl l π180∴δ=3β故 b=β-δ=2δ (12)式中,δ为缓和曲线上任一点的正偏角,b 为该点的反偏角。
(三)切线支距法测设曲线坐标计算公式以ZH (或HZ )为坐标原点,以切线为x 轴,垂直切线方向为y 轴。
1、 缓和曲线部分X=l -202540l R lY=036Rl l -3037336l R lδ=π180602Rl l b=2δZHJDHYibb 0弦长 l 弦=22Y X +说明: l —缓和曲线上任意一点至ZH 或HZ 点的距离l 0—缓和曲线长度(单侧) R —圆曲线半径δ—缓和曲线上任一点的正偏角 b —缓和曲线上任一点的反偏角 2、 圆曲线部分 X i =Rsin αi +m Y i =R (1-cos αi )+pαi =Rl L 18001π)-( +β0X i 、Y i —两缓和曲线间圆曲线上某点的支距(原点为ZH 或HZ ) L 1—从ZH 或HZ 点到圆曲线上某点的弧长 l 0—缓和曲线长度(单侧)αi —圆曲线上某点的半径与圆心向切线所作垂线间的夹角。
3、当为圆曲线而无缓和曲线时 X 1=Rsin2φ Y 1=R (1-cos2φ) φ=R2018πl =R90πll 弦=2Rsin φ (弦长)X 1、Y 1—圆曲线上某点的支距(原点为ZY 或YZ ) l —从ZY 或YZ 点到圆曲线上某点的弧长 φ—圆曲线上某点与起点的弦切角。
R —圆曲线半径支距坐标与整体坐标系的转换A 、 当坐标原点与ZH (ZY )或HZ (YZ )点重合时,根据支距坐标与坐标系之间图形的关系,分为四种情况Ⅰ:P (X ,Y )=P ’(X,Y) Ⅱ: P (X ,Y )=P ’(-X,Y) Ⅲ:P (X ,Y )=P ’(-X,-Y) Ⅳ:P (X ,Y )=P ’(X,-Y)支距坐标系整体坐标系ⅡⅠ整体坐标系支距坐标系支距坐标系整体坐标系'ⅢⅣ'整体坐标系支距坐标系缓和曲线加圆曲线切线及法线方位角的计算设自ZH (HZ )(图中为O 点) 指向JD 的起始方位角为0α,(见附图) 1、当所设定的曲线为顺时针偏转时: 缓和曲线上任意点的切线方位角为: A α切线=0α+3δ(方向指向曲线前进方向)OA α=0α+δ缓和曲线上任意点的法线方位角为:A α法线=0α+3δ-90° (方向指向曲线外侧方向)圆曲线上任意点的切线方位角为:B α切线=0α+3δ0+2φ(方向指向曲线前进方向)B HY -α=0α+3δ0+φ 圆曲线上任意点的法线方位角为:B α法线=0α+3δ0+2φ-90° (方向指向曲线外侧方向)2、当所设定的曲线为逆时针偏转时: 缓和曲线上任意点的切线方位角为: A α切线=0α-3δ(方向指向曲线前进方向)OA α=0α-δ缓和曲线上任意点的法线方位角为:A α法线=0α-3δ+90° (方向指向曲线外侧方向)圆曲线上任意点的切线方位角为:B α切线=0α-(3δ0+2φ)(方向指向曲线前进方向) B HY -α=0α-(3δ0+φ) 圆曲线上任意点的法线方位角为:B α法线=0α-(3δ0+2φ)+90° (方向指向曲线外侧方向)以上式中δ=π026180Rl l = 0230Rl l πδ0=πR l 61800 = Rl π300说明: l —缓和曲线上任意一点至ZH 或HZ 点的距离l 0—缓和曲线长度(单侧) R —圆曲线半径δ—ZH 或HZ 处缓和曲线上任意点弦切角δ0—ZH 或HZ 处缓和曲线上HY 或YH 点弦切角 φ=R2018πl =R90πl说明: l —从ZY 或YZ 点到圆曲线上某点的弧长φ—圆曲线上某点与起点的弦切角。
R —圆曲线半径坐标计算方位示意图曲线交点转向角的检核转向角 α=2(δ0+β0+φ0)=6δ0+2φ0=6×R l π 300+2×R 90πR l =R 1800πl +Rl 180Rπ =Rl l 180R 0π〕+〔l 0—缓和曲线长度(单侧) l R —圆曲线长度 R —圆曲线半径算例 长沙疏解线特大桥JD2α=74°36′35″ 圆曲线半径 R=350ml 0=70m , l R =385.76mα=π〕+〔350385.7670180 =74°36′32.1″Δα=3″ 误差在允许范围之内。
一般情况,设计单位都会给出曲线要素,为以防万一,我们需要对设计资料进行必要的复核。
坐标计算X=X 0+r cos α Y=Y 0+r sin α其中 X 0 、Y 0 坐标起始点,r 为增量距离 α 为坐标增量的方位角,在计算时注意方位角的方向,方向是指向计算点的。
竖曲线的设计与计算1、坡长 s=l 2-l 1l 1、l 2 —相邻两变坡点的桩号(l 2 >l 1),单位以m 计;2、坡度 i =%10012 sh h - h 1 、h 2—相邻两变坡点的高程,单位以m 计;3、竖曲线的半径选择A 、切线长控制 R =ωT 2 B 、外距控制 R =28ωEC 、曲线长控制 R =ωl 其中:R —竖曲线半径; T —竖曲线切线长; L —竖曲线长度; E —竖曲线外距;ω—竖曲线处前后坡度差。
4、竖曲线的设计与计算 坡度差:ω=12i i - 曲线长: L=R ω 切线长:T=2L =2ωR 外距:E=2RT 2起点桩号=变坡点桩号-T终点桩号=变坡点桩号+T1i 、2i —变坡点前后两坡段的坡度;R —竖曲线半径; 5、设计标高计算直坡段上:h= h 1+(l -l 1)×1i或h= h 2-(l 2-l )×1i当中桩在竖曲线上时,按该式计算的高程叫切线高程 竖曲线上:设计高程=切线高程±纵距其中纵距y =Rx 22或y =22R x R --L —待求点桩号;l 1、 h 1—前一变坡点桩号和高程; l 2、 h 2—竖曲线对应变坡点桩号和高程;1i 、2i —坡段的坡度;X —待求点与竖曲线起点的桩号差; h —设计标高;“±”—表示竖曲线类型的符号,凹形曲线取“+”,凸形曲线取“-”;2007年7月25日星期三 作者:张华成 (修改于太原)切线高程计算曲线桥梁墩台中线测设一、墩台中线之测设曲线桥梁的线路虽为曲线,但各孔梁仍是直的,将各孔梁联接起来即成折线,各墩中心即是折线的交点。
