学而思网校5年级 超难奥数
学而思教育五年级奥数课程

第一讲分数四则混合运算一、知识点梳理Ø奥数六大模块:计算,计数,应用题,行程,几何,数论。
Ø本讲属于:计算一、小数的运算法则1、加减法:注意小数点对齐,其余和整数相似2、乘法:看乘数和被乘数里共有几位小数,就从积的右边数出几位,点上小数。
3、除法:需要把除数转化为整数,然后按照整数除法进行二、分数的运算法则1、加减法:分母先通分---找到分母的最小公倍数。
然后分子才可以相加减。
2、乘法:分子相乘的积作为结果的分子,分母相乘的积作为结果的分母,最后记住要进行约分。
3、除法:记住:甲除以乙,等于甲乘乙数的倒数。
重要步骤:约分----------找出分子分母的公约数,利用分数基本性质:分子分母同乘(除)一个不为零的数,值不变三、分数与小数的互化:(1)原则:具体化成哪个取决于用分数简单还是用小数简单。
一般是:乘除法运算时,小数化成分数,这样可以约分。
加减法运算时,分数化成小数,这样避免通分。
(2)熟练掌握一些常见的分数和小数互化,如:1=0.5 2,1=0.25,3=0.754,1=0.1258……..等.(3)分数要约分保留最简形式。
四、百分数1、百分数的符号:%,可以看成1100. 也可以看成乘以0.01如:753 75%=0.75==1004五、繁分数1、定义:分子或分母(都)含有四则运算或分数的数,叫繁分数。
最长的分数线叫主分数线,以上叫分子,以下叫分母。
如:122+3,分子是1,分母是22+3。
二、重点例题讲解(按照相关要求,例题只标出题号,不再书写题目,各位家长见谅)例题5:解析:考察了常用的巧算技巧:乘法分配律和其逆运算。
(1)、原式=21233 15125´+´-=212 545 +-=1 4(2)、原式=111388 1212´+´=1113 (8 1212+´=28´=16例题6:解析:考察凑数法,配对法,计算的时候并不一定要按照给定的顺序计算,先观察题目中数字的特点。
学而思五年级计算拓展题目+解析

第7天
挑战时间 ______ 分钟 错 ______ 题 ★青铜新人★
7.8 + 2.3 = _________ 1.49 _ 1 = _________
5 × 0.8 = _________
0.3 × 0.078 = _________
35.92 + 1.357 = _________ 60 _ 13.46 = _________ 0.04 × 9 = _________
0.98 × 0.07 = _________
★★黄金高手★★
0.5 × 0.725 = _________ 0.35 × 0.03 = _________ 0.8 × 0.79 = _________ 0.392 ÷ 0.8 = _________
0.45 × 0.54 = _________ 0.08 × 0.09 = _________ 0.93 × 0.92 = _________ 0.51 ÷ 0.85 = _________
★★★王者大神★★★
4.9 + 5.9 _ 3.992 = _________
19.7 + 0.56 × 3.25 = _________
0.36 ÷ 0.72 × 2 = _________
解方程: x + 0.9 =
4.9
x = _________
27.4 _ 2.96 _ 5.004 = _________ 0.48 × 2.55 _ 0.33 = _________ 0.0943 ÷ 0.23 × 6 = _________ 解方程: 9 × x = 306
0.2 × 0.019 = _________
27.1 + 4.226 = _________ 65.99 _ 18.06 = _________ 0.61 × 9 = _________
学而思奥数5年级秋季班:第1讲《长方体与正方体》讲义

D
【解析】 1、 8 、12 、 6 ; 2、 6 、正方形、相等; 3、 (5 3 4) 4 48 (厘米) ; 4、 6 12 72 (厘米) ; 5、 C .
例2
⑴对长、宽、高分别为 3 厘米、 2 厘米、1厘米的长方体木 块喷漆,喷漆的面积是多大? ⑵制作一个无盖的长方体鱼缸, 长、 宽、 高分别为 3 分米、 2 分米、1分米,需要多少平方分米的玻璃?(不计玻璃之 间粘合的部分) ⑶对左右联通的长方体热水管包一层保护罩,长、宽、高 分别为 3 米、 2 米、1米,需要多少平方米的保护罩?
例4
有一个长方体形状的零件, 中间挖去一个正方体 (如下图, 单位为厘米) . ⑴挖掉这个正方体之后这个长方体的表面积是增大了还 是减小了? ⑵这个挖去一块后得到的图形的表面积为_____平方厘米.
6 2 2 5 8
2
五年级秋季
基础
第 1 讲
【解析】 ⑴这个长方体挖掉一块之后表面积增大了. 挖掉的这个小 正方体的下底面拼在原长方体上表面缺掉的部分恰好可 以拼成完整的长方体, 因此增加的面积可以看成是挖掉的 这个小正方体的四个侧面,它们的面积是 (2 2) 4 16 (平方厘米) ; ⑵原长方体的表面积为: (5 8 5 6 6 8) 2 236 (平 方厘米) .所以挖掉一块的长方体的表面积为 236+16=252 (平方厘米) .
五年级秋季
基础
3
【解析】 ⑴表面积: S表 S长方体 S正方体 S粘贴面积 118 24 4 2 134 (平方 厘米) ; ⑵体积:V V正方体 V长方体 2 2 2 7 5 2 8 70 78 (立方厘米) .
高思奥数导引小学五年级含详解答案第16讲 构造与论证
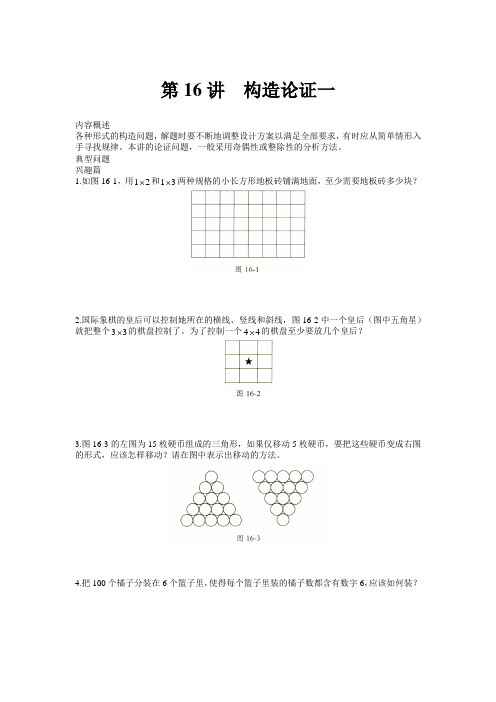
第16讲构造论证一内容概述各种形式的构造问题,解题时要不断地调整设计方案以满足全部要求,有时应从简单情形入手寻找规律。
本讲的论证问题,一般采用奇偶性或整除性的分析方法。
典型问题兴趣篇1.如图16-1,用12⨯两种规格的小长方形地板砖铺满地面,至少需要地板砖多少块?⨯和132.国际象棋的皇后可以控制她所在的横线、竖线和斜线,图16-2中一个皇后(图中五角星)就把整个33⨯的棋盘控制了。
为了控制一个44⨯的棋盘至少要放几个皇后?3.图16-3的左图为15枚硬币组成的三角形,如果仅移动5枚硬币,要把这些硬币变成右图的形式,应该怎样移动?请在图中表示出移动的方法。
4.把100个橘子分装在6个篮子里,使得每个篮子里装的橘子数都含有数字6,应该如何装?5.把正方体的所有棱染成白色或者红色,要求每个面上至少要有一条棱是白色的。
请问:最少有多少条棱是白色的?6.请在9,8,…,3,2,1的相邻两个数之间填入“+”或者“-”(不能改变数的顺序),使得结果是1。
能否使得结果是0呢?987654321= 1987654321=07.如图16-5,能否在三角形的三个顶点各填一个自然数,使得每条边的两个顶点上的数之和都是奇数?如果能,请写出一种填法;如果不能,请说明理由。
8.四位同学进行了一次乒乓球单打比赛,当比赛进行了若干场后,体育老师问他们分别比赛了多少场。
这四全同学回答分别比了1、2、3、3场。
老师说:“你们肯定有人记错了。
”请问:老师是怎么知道的呢?9.有四个算式:□+□=□,□-□=□,⨯□□=□。
如果每一个算式中都至少有1个□□=□,÷偶数和1个奇数,那么12个数中一共有多少个偶数?如果没有前面的限制,这12个数中最少有多少个偶数?最多有多少个偶数?10.有14个孩子,依次给他们编号为1,2,3,…,14。
能否把他们分成三组,使得每组都有一个孩子的编号是该组其它孩子的编号之和。
拓展篇1.图16-6中的左图为21枚硬币组成的三角形,如果仅移动7枚硬币,要把这些硬币变成右图的形状,应该怎样移动?请在图中表示出移动的方法。
五年级奥数学而思专题2、数的整除性(A)备课讲稿

五年级奥数学而思专题2、数的整除性(A)备课讲稿五年级奥数学而思专题2、数的整除性( A)二数的整除性(A)_年级_班姓名_得分一、填空题1. 四位数3AA1”是9的倍数,那么A= ____ .2. 在25口79这个数的□内填上一个数字,使这个数能被11整除,方格内应填_____ .3. 能同时被2、3、5整除的最大三位数是______ .4. 能同时被2、5、7整除的最大五位数是______ .5. 1至100以内所有不能被3整除的数的和是_____ .6. 所有能被3整除的两位数的和是________ .7. 已知一个五位数口691 □能被55整除,所有符合题意的五位数是_____ .8. 如果六位数1992口□能被105整除,那么它的最后两位数是_______ .9. 42 □ 28□是99的倍数,这个数除以99所得的商是 _______ .10. 从左向右编号为1至1991号的1991名同学排成一行,从左向右1至11报数,报数为11的同学原地不动,其余同学出列;然后留下的同学再从左向右1至11报数,报数为11的留下,其余同学出列;留下的同学第三次从左向右1至11报数,报到11的同学留下,其余同学出列,那么最后留下的同学中,从左边数第一个人的最初编号是________ 号.二、解答题11. 173 □是个四位数字.数学老师说:“我在这个□中先后填入3个数字, 所得到的3个四位数,依次可被9、11、6整除.”问:数学老师先后填入的3个数字的和是多少?12 ?在1992后面补上三个数字,组成一个七位数,使它们分别能被2、3、5、11整除,这个七位数最小值是多少?13. 在“改革”村的黑市上人们只要有心,总是可以把两张任意的食品票换成3张其他票券,也可以反过来交换.试问,合作社成员瓦夏能否将100张黄油票换成100张香肠票,并且在整个交换过程中刚好出手了1991张票券?14. 试找出这样的最小自然数,它可被11整除,它的各位数字之和等于13. ----------------------------- 答案------------------------------------1. 7已知四位数3AA1正好是9的倍数,则其各位数字之和3+A+A+1 一定是9的倍数,可能是9的1倍或2倍,可用试验法试之.设3+A+A+1=9,则A=2.5,不合题意.再设3+A+A+仁18,则A=7,符合题意.事实上,3771 9=419.2. 1这个数奇数位上数字和与偶数位上数字和之差是0或是11的倍数,那么这个数能被11整除?偶数位上数字和是5+7=12,因而,奇数位上数字和2+口+9应等于12, □内应填12-2-9=1.3. 990要同时能被2和5整除,这个三位数的个位一定是0.要能被3整除,又要是最大的三位数,这个数是990.4. 99960解法一:能被2、5整除,个位数应为0,其余数位上尽量取9,用7去除999 □ 0,可知方框内应填6.所以,能同时被2、5、7整除的最大五位数是99960.解法二:或者这样想,2,5,7的最小公倍数是70,而能被70整除的最小六位是100030.它减去70仍然是70的倍数,所以能被2,5,7整除的最大五位数是100030-70=99960.5. 3367先求出1~100这100个数的和,再求100以内所有能被3整除的数的和,以上二和之差就是所有不能被3整除的数的和.(1+2+3+ --+100)- (3+6+9+12+?+99)=(1+100) 2 100-(3+99) 2 33=5050-1683=33676. 1665能被3整除的二位数中最小的是12,最大的是99,所有能被3整除的二位数如下:12,15,18,21, …,96, 99这一列数共30个数,其和为12+15+18+-+96+99=(12+99) 30 2=16657. 96910 或46915五位数A691 B能被55整除,即此五位数既能被5整除,又能被11整除.所以B=0或5.当B=0时,A6910能被11整除,所以(A+9+0)-(6+1)= A+2能被11整除, 因此A=9;当B=5时,同样可求出A=4.所以,所求的五位数是96910或46915.8. 90因为105=3 5 7,根据数的整除性质,可知这个六位数能同时被3、5和7 整除。
学而思五年级春季第五讲行程问题

(2)甲乙二人在相同的一段时间内行走,甲速为 10 米每秒,乙速为 12 米每秒,则甲速:乙速=
10:12=5:6;同样我们也可以得到甲乙二人在这段时间内所走的路程关系: 甲: 乙=5:6.
时间一定时,路程与速度成正比例
二、例题讲解
例 1、分析:第一问:速度提高之前与提高之后走的总路程是一样的,那么根据路程一定,速度与时间成
设甲的速度为 x 米/分钟。(x-50)×26=(x+50)×6
x=80
A,B 两地距离为:(80-50)×26=780(米)或者(80+50)×6=780(米)
第五讲 行程问题 5.2
五年级春季班 第五讲 行程问题
曹威
法二:比例法。由图可知(绿线表示同时间内的相遇过程红线表示同时间内的追及过程)
A
4份
B
3份
4份
乙
红色表示相同时间内甲乙走的路程比为 5:4,但此时相遇点距 A,B 两点的距离比为 3:4,
则我们可以统一甲走的路程为 15 份,则 72 千米占 8 份,全程 35 份可求。
例 4、分析:
答案:315 千米
甲
4800
2400 乙
A
B
2880
10 分钟
由图可知速度改变前,相遇时甲走了 4800 米,乙走了 2400 米,则甲乙的速度比为 2:1,
五年级下册数学最难的奥数题

五年级下册数学最难的奥数题1、一个筐子放进4篮苹果后,连筐共重28千克,当倒出3篮苹果后再称,连筐共重10千克,一个筐子重(4)千克2、一块正方形菜地,边长是12米。
如果要把它的面积扩大到原来的2倍,其中一条边增加4米,另一条边增长多少米?(写出过程)3、学校卖3把椅子和4张桌子共用元,未知卖2张桌子的钱可以卖5把椅子,一把椅子多少元?一张桌子多少元?(写下过程)4.一条路长米,从头到尾每隔10米栽1棵梧桐树,共栽多少棵树?5、12棵柳树排列成一排,在每两棵柳树中间种3棵桃树,共种多少棵桃树?6、一根厘米长的木条,要锯成10厘米长的小段,需要锯几次?7、.蚂蚁爬到树枝,每上时一节须要10秒钟,从第一节爬到至第13节须要多少分钟?8.在花圃的周围方式菊花,每隔1米放1盆花。
花圃周围共20米长。
需放多少盆菊花?9、从发电厂至闹市区一共存有根电线杆,每相连两根电线杆之间就是30米。
从发电厂至闹市区存有多离?10、.王老师把月收入的一半又20元留做生活费,又把剩余钱的一半又50元储蓄起来,这时还剩40元给孩子交学费书本费。
他这个月收入多少元?11.一个人沿着小骗走了全长的一半后,又跑了剩的一半,还剩1千米,问:小加全长多少千米?12.甲在加工一批零件,第一天加工了这堆零件的一半又10个,第二天又加工了剩下的一半又10个,还剩下25个没有加工。
问:这批零件有多少个?13.一条毛毛虫由幼虫短至成虫,每天短一倍,16天能长至16厘米。
反问它几天可以短至4厘米?14.一桶水,第一次倒出一半,然后倒回桶里30千克,第二次倒出桶中剩下水的一半,第三次倒出千克,桶中还剩下80千克。
桶里原来有水多少千克?15、甲、乙两书架共计图书本,甲书架的图书数比乙书架的3倍太少16本。
甲、乙两书架上各存有图书多少本?16、甲、乙、丙三人年龄之和是94岁,且甲的2倍比丙多5岁,乙2倍比丙多19岁,问:甲、乙、丙三人各多大?17.小明、小华捉住完鱼。
第九届学而思综合能力测评五年级数学试卷及答案解析

量为: (20 + 10) × 5 = 150 ;10 天吃完需要牛的头数是:150 ÷10 −10 = 5 (头).
第二大题(解答题共 4 道,其中两题为必做题,两题为附加题选做.请同学们把解题过程写清楚)
1. (10 分)8 个人站队,冬冬必须站在小悦和阿奇的中间(不一定相邻),小慧和大智不能相邻,小光 和大亮必须相邻,满足要求的站法一共有多少种? 答案:2400 提示:冬冬要站在小悦和阿奇的中间,就意味着只要为这三个人选定了三个位置,中间的位置就一定要留 给冬冬,而两边的位置可以任意地分配给小悦和阿奇. 小慧和大智不能相邻的互补事件是小慧和大智必须相邻 小光和大亮必须相邻,则可以将两人捆绑考虑 只满足第一、三个条件的站法总数为:
S+ BFD
=
1 16
S, ABCD
=
1 16
×10 ×10
=
6.25
(平方厘米).
8. 在新年联欢会上,某班组织了一场飞镖比赛.如右图,飞镖的靶子分为三块区域,分别对应17 分、11
分和 4 分.每人可以扔若干次飞镖,脱靶不得分,投中靶子就可以得到相应的分数.若恰好投在两块(或
三块)区域的交界线上,则得两块(或三块)区域中分数最高区域的分数.如果比赛规定恰好投中120 分才能
平方厘米
答案:74
提示:要使大正方体的表面上白色部分最多,相当于要使大正方体表面上黑色部分最少,那么就要使得黑
色小正方体尽量不露出来. 在整个大正方体中,没有露在表面的小正方体有 (4 − 2)3 = 8 (个),用黑色的;在面上但不在边上的小正方
体有 (4 − 2)2 × 6 = 24 (个),其中 30 − 8 = 22 个用黑色.
【解析】 log2 4+ log2 16 = log2 64 , loga (M ⋅ N ) = loga M + loga N ,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数列找规律
【例1】
一块白白的豆腐,帅帅“咣咣咣···咔咔咔”切了六刀,最多能切成多少块?
【例2】
有一个国家的钱币仅有六元和七元两种,在这个国家里人们买东西时会出现找不开钱的情况。
⑴出现这种情况的价格共有多少种?
⑵其中最贵的价格是多少元?
【例3】
“不好吃”肉串店老板送给帅帅十张优惠券(从1到10分各1张)。
在一个风雨交加的下午,帅帅拿着优惠券喜滋滋的去吃肉串了,结果看见了老板在店门口给帅帅留了一个牌子:
【例4】
下列⑴~(20)的二十个加法算式是按一定规律排出的,得数最小的算式是哪个?请写出它的得数。
组合专题:超难组合数学㈠
1.一棱柱以五边形A1A2A3A4A5与B1B2B3B4B5为上、下底,这两个多边形的每一条边及每一条线段A i B j(i,j=1,2,3,4,5)分别涂上红色或绿色。
若每一个以棱柱顶点为顶点的、以已涂色的线段为边的三角形均有两条边颜色不同。
证明上、下底10条边颜色一定相同。
2.设在空间给出20个点,其中某些点涂黄色,其余点涂红色。
已知在任何一个平面上同色点不超过3个。
求证:存在一个四面体,它的四个顶点同色,且至少有一个侧面内不含异色点。
3.某一天有若干读者去过图书馆。
他们是单独去的,但是在任何三个读者中,至少有两个人这天在图书馆相遇。
证明:一定可以找到这样两个时刻,使得在这一天到过图书馆的任何一个读者,至少在这两个时刻中的一个时刻是在图书馆的。
4.每一个参加循环赛的人和其余参加比赛的人都要比赛一次。
已知任何一次比赛都没有出现平局。
证明:可以找到这样的运动员,其他人或被他战胜,或被他胜过的人战胜。
测试题
1.一棱柱以四边形F1I1H1G1与K1L1J1E1为下、上底,这两个多边形的每一条边及每一条线段(所有连接顶点的线段)分别涂上红色或绿色。
若每一个以棱柱顶点为顶点的、以已涂色的线段为边的三角形均有两条边颜色不同。
证明上、下底8条边颜色一定相同。
答案及解析
证明:
先证明上底下底分别同色
假如底边有不同色线段,那么假设F1I1为红F1G1为绿,由F1点连三条线段分别为F1E1,F1J1,F1L1,三条线段中必然有两条颜色相同,假设F1J1,F1L1都为红色,那么三角形L1I1J1为全绿三角形,矛盾,假设F1J1,F1L1都为都为绿色,那么三角形G1L1J1为全红三角形,矛盾,所以下底边颜色全部相同。
类似可得上底边颜色全部相同。
再来证明上底下底有同色边,
假设上底边为红,下底边为绿,然后类似的F1E1,F1J1,F1L1必然有两条同色,假设F1J1,F1L1都为都为绿色,那么三角形G1L1J1为全红三角形,矛盾,假设E1F1,L1F1为红,那么三角形G1J1I1为全红三角形,矛盾。
所以上下8条边颜色相同。
几何专题:综合型
【例1】
如图,四边形PQRS与长方形ABCD的内侧相接,AP=4厘米,AS=2厘米,QC=7厘米,RC=3厘米,∠SPQ=90°,∠QRS=45°。
请求出四边形PQRS的面积。
【例2】
如图所示,下午6:30在北方的上空有北极星N和组成等腰直角三角形的三颗星A、B、C(N 的左方是B,B的上方是C,C的左方是A,NB=BC=CA)。
数小时后,星A和星B同时沉入地平线下。
后来,星C也沉下去了。
如果星A、B、C逆时针绕北极星一周需24小时,请问:星C沉下去的时刻是几点?(地平线是水平的直线)
【例3】
如图,在△ABC中,AB=11厘米,AC=9厘米。
首先,在BC边上,取点H,∠BHA=90°;然后在BC边上,在H与C之间取点D,使∠BAD=60°;这样,∠DAC是∠HAD的2倍。
请问:这时线段BH的长度是线段CH的长
度的几倍?
【作业】
如图1,图中的三个四边形ABHG、CDIH和EFGI都是正方形,当其面积分别是10平方厘米、13平方厘米、29平方厘米时,请问:
⑴如图2,有16个边长为1厘米的正方形方格,在图中连结这些方格的顶点,画出四边形ABHG;
⑵请求出六边形ABCDEF的面积。
奇偶靠联想
【例1】
三个相邻偶数的乘积是一个六位数8****2,求这三个偶数。
【例2】
已知,a、b、c、d、e这5个质数互不相同,并且符合下面的算式:(a+b)(c+d)e=2890,那么,这5个数当中最大的数至多是______。
【例3】
请问多位数nnn n会不会是一个完全平方数?说明理由。
【例4】
如果n个奇质数中,任意奇数个数的和仍是质数,那么这个数组可称之为“完美质数组”,
⑴证明,n的最大值为4。
⑵当n=4时,求4个质数的乘积的最小值。
测试题
1.在11张卡片上各写有一个不超过5的数字,将这些卡片排成一行,得到一个11位数;
再将它们按另一种顺序排成一行,又得到一个11位数。
请证明这两个11位数的和至少有一位数字是偶数。
2.甲、乙两人将正整数5至11分别写在7张卡片上。
他们将卡片背面朝上,任意混合后,甲取走3张,乙取走2张,剩下的2张卡片他们谁也没看。
甲看了手里的3张卡片后对乙说“你的2张卡片上的数之和是偶数”。
试问:甲手里的是哪三个数?答案是否唯一?
答案:
1.【分析】如果在求和时发生进位现象,那么考虑从右往左数的第一次进位,由于是第一次进位,所以这一个数位上没有进位过来的,那么这只有这一个数位上的两个数字
都是5时才有可能成立,而这一位向上一位进1后,所得的和的这一位上的数字
是0,是个偶数。
也就是说如果发生进位,那么所得的和至少有一个数字是偶数;
如果这两个11位数在求和时不发生进位现象,由于没有进位,那么每一位上的
两个数字相加就得到和数的一个数字,于是这两个11位数的各位数字之和的和
就等于这两个11位数的和的各位数字之和,而前者是两个相同的数相加,是个
偶数;后者是11个数相加,那么其中必有偶数(否则,11个奇数相加,仍是奇数),
所以不发生进位时仍然至少有一位数字是偶数。
2.【分析】甲知道其余4张卡片上分别写了哪些数,但不知道它们之中的哪两张落到了乙的手中。
因此,只有在它们之中任何两张卡片上的数的和是偶数时,甲才能说出自
己的断言.而这就意味着这4 张卡片上的数的奇偶性相同,即或者都是偶数,或
者都是奇数。
但由于一共只有3张卡片上写的是偶数,所以它们不可能都是偶数,
只能是奇数。
所以3张写着偶数的卡片全部在甲的手里。
穷举用技巧
【例1】
N是一个各位数字互不相等的自然数,它能被它的每个数字整除。
N的最大值是。
【例2】
如果连续N个自然数,每个自然数的数字和都不是11的倍数,则称这连续的N个自然数为一条“龙”,n为这条龙的长度。
比如1,2,3,…,28就是一条龙,它的长度是28。
问:龙的长度最长可以为多少?写出一条最长的龙。
【例3】
黑板上写有1、2、3、……、100这100个自然数,甲、乙二人轮流每次每人划去一个数,直到剩下两个数为止。
如剩下的两数互质则判甲胜,否则判乙胜。
⑴乙先划甲后划,谁有必胜策略?必胜策略是怎样的?
⑵甲先划乙后划,谁有必胜策略?必胜策略是怎样的?
【例4】
如果一个自然数的2004倍恰有2004个约数,这个自然数自己最少有多少个约数?
测试题
【例1】求所有能被30整除,且恰有30个不同约数的自然数。
【例2】在1到100中,恰好有6个约数的数有多少个?
答案: 【例1】【分析】
由于30235=⨯⨯,从质数的观点看整除,如果自然数N 能被30整除,那么自然数N 至少含有三个质因数2,3,5。
设:312235r r r N =⨯⨯⨯。
自然数N 恰有30个不同的因数,根据约数的个数公式:12311130235r r r +⨯+⨯+⨯==⨯⨯()()()。
注意到235⨯⨯是三个约数之积,由此可知自然数N 中质因数的个数恰好有3个。
因此
123111235r r r +⨯+⨯+=⨯⨯()()(),由此可知123r r r (,,)必是124(, , )的一个排列。
综上所述,所求的自然数有:24235⨯⨯,42235⨯⨯,24235⨯⨯,42235⨯⨯,
42235⨯⨯,24235⨯⨯。
【例2】【分析】
6只能表示为()51+或()()1121++,所以恰好有6个约数的数要么能表示成某个质
数的5次方,要么表示为某个质数的平方再乘以另一个质数,100以内符合前者的只有32,符合后者的数枚举如下:
222222222222222232527211213217219223832353731145253272
1⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯种种
种种
所以符合条件的自然数一共有1842116++++=(种)。
