高一数学指数函数知识点及练习题(含答案).
高一数学上册第二章--指数函数知识点及练习题(含答案)

课时 4 指数函数一 . 指数与指数幂的运算( 1)根式的观点①假如xna, a R, x R, n 1,且 nN ,那么 x 叫做 a 的 n 次方根. 当 n 是奇数时, a 的 n 次方根用符号 na 表示;当 n 是偶数时,正数 a 的正的 n 次方根用符号na 表示,负的 n 次方根用符号na表示; 0 的 n 次方根是 0;负数 a 没有 n 次方根.②式子 n a 叫做根式,这里 n 叫做根指数, a 叫做被开方数.当n 为奇数时, a 为随意实数;当 n 为偶数时, a.③根式的性质: (na )n a ;当 n 为奇数时, n a n a ;当 n 为偶数时, n a n | a |a (a 0) .a (a 0)( 2)分数指数幂的观点mna m (a①正数的正分数指数幂的意义是:a n 0, m,n N , 且 n 1) .0 的正分数指数幂等于0.②m(1m1 ) m( a正数的负分数指数幂的意义是:a n)n n (0, m, n N , 且 n1) .0 的负分数指aa数幂没存心义. 注意口诀: 底数取倒数,指数取相反数.( 3)分数指数幂的运算性质①a r a s a r s (a 0, r , s R)② (ar) sa rs (a 0, r , s R)③(ab)ra rb r (a0,b 0, rR)二 . 指数函数及其性质( 4)指数函数函数名称指数函数定义函数 ya x (a 0 且 a1) 叫做指数函数a 1a 1yy a xya xy图象y1y1(0,1)(0,1)OxOx定义域 R值域(0,+ ∞)过定点 图象过定点(0,1 ),即当 x=0 时, y=1.奇偶性非奇非偶单一性在 R 上是增函数在 R 上是减函数函数值的 y > 1(x > 0), y=1(x=0), 0< y < 1(x < 0)y > 1(x < 0), y=1(x=0), 0< y < 1(x > 0)变化状况a 变化对在第一象限内, a 越大图象越高,越凑近 y 轴; 在第一象限内, a 越小图象越高,越凑近 y 轴; 图象影响在第二象限内,a 越大图象越低,越凑近x 轴.在第二象限内,a 越小图象越低,越凑近x 轴.三 .例题剖析1.设 a 、 b 知足 0<a<b<1,以下不等式中正确的选项是 ( C)A.a a <a bB.b a <b bC.a a <b aD.b b <a b 分析: A 、B 不切合底数在 (0,1) 之间的单一性 ; C 、 D 指数同样 , 底小值小 . 应选 C. 2.若 0<a<1,则函数 y=a x 与 y=(a-1)x 2 的图象可能是 (D )分析: 当 0<a<1 时 ,y=a x 为减函数 ,a-1<0, 因此 y=(a-1)x2张口向下 , 应选 D.3.设指数函数 f(x)=a x (a>0 且 a ≠ 1),则以下等式中不正确的选项是 ( D )A.f(x+y)=f(x)f(y)f (x)B.f(x-y)=f ( y)C.f(nx)= [ f(x) ] nD.f [ (xy) n ] =[ f(x) ] n [ f(y) ] n (n ∈ N * )分析: 易知 A 、 B 、 C 都正确 .对于 D,f [(xy)n] =a (xy)n , 而[ f(x) ] n ·[f(y) ] n =(a x ) n ·(a y ) n =a nx+ny , 一般状况下 D 不建立 .11 34.设 a= ( 3) 3,b= ( 4)4,c= ( 3) 4,则 a 、b 、 c 的大小关系是 ( B )43 2A.c<a<b3分析: a= ( )B.c<b<aC.b<a<cD.b<c<a1 111(8133( 4)3 ( 4) 4=b, b=(4) 4)4(3) 4 =c.∴ a>b>c.3 332725.设 f(x)=4 x -2x+1,则 f -1 (0)=______1____________. 分析: 令 f -1 (0)=a, 则 f(a)=0 即有 4a -2 · 2a =0.2a · (2 a -2)=0, 而 2a >0,∴ 2a =2 得 a=1.6.函数 y=a x-3 +4(a>0 且 a ≠ 1)的反函数的图象恒过定点 ______(5,3)____________.分析: 因 y=a x 的图象恒过定点 (0,1), 向右平移 3 个单位 , 向上平移 4 个单位获得 y=a x-3 +4 的图象 , 易知恒过定点 (3,5).故其反函数过定点 (5,3).10 x 10 x.证明 f(x) 在 R 上是增函数 .7.已知函数 f(x)=x10 x10x1010x102x1,设 x 1<x 2∈ R,则f(x 1)-f(x2)=10x 1 1010x 1 10x 110x 210 x 2102 x 11 102 x 21 2(102 x 1102 x2).x 110x2 10x2 102 x1 1102 x21(102 x11)(102 x 2 1)∵ y=10 x是增函数 ,∴ 10 2x 1 10 2x 2 <0.而 10 2x 1 +1>0, 102 x 2 +1>0,故当 x <x 时 ,f(x)-f(x )<0,1212即 f(x 1)<f(x 2). 因此 f(x) 是增函数 .8.若定义运算 a b=b, ab,则函数 f(x)=3 x3-x 的值域为 ( A )a, a b,A.(0,1]B. [ 1,+∞ )C.(0,+ ∞ )D.(- ∞ ,+∞ )分析: 当 3x ≥3-x , 即 x ≥ 0 时 ,f(x)=3-x∈(0,1 ] ;x-x, 即 x<0 时 ,f(x)=3x∈ (0,1).3 x , x 0, 当 3<3∴ f(x)=x值域为 (0,1).3x ,0,9.函数 y=a x 与 y=-a -x (a>0,a ≠1) 的图象 ( C )A. 对于 x 轴对称B.对于 y 轴对称C.对于原点对称D.对于直线 y=-x 对称分析: 可利用函数图象的对称性来判断两图象的关系.10.当 x ∈[ -1,1]时 ,函数 f(x)=3 x-2 的值域为 _______[ -5,1 ] ___________.3分析: f(x) 在[ -1,1 ]上单一递加 .11.设有两个命题 :(1)对于 x 的不等式 x 2+2ax+4>0对全部 x ∈ R 恒建立 ;(2) 函数 f(x)=-(5-2a) x是减函数 .若命题 (1)和 (2)中有且仅有一个是真命题 ,则实数 a 的取值范围是 _______(- ∞ ,-2)__________.分析: (1) 为真命题=(2a) 2-16<0-2<a<2. (2)为真命题 5-2a>1 a<2.若 (1) 假 (2) 真 , 则 a ∈ (- ∞ ,-2]. 若 (1) 真 (2) 假, 则 a ∈ (-2,2)∩[ 2,+ ∞]=.故 a 的取值范围为 (- ∞ ,-2).12.求函数 y=4 -x -2-x +1,x ∈[ -3,2]的最大值和最小值 .解: 设 2-x=t, 由 x ∈[ -3,2 ]得 t ∈[ 1,8 ] , 于是 y=t 2-t+1=(t-1)2+3. 当 t= 1时 ,y3 .424有最小值 这时 x=1.当 t=8 时 ,y 有最大值57.这时 x=-3.2413.已知对于 x 的方程 2a2x-2-7a x-1 +3=0 有一个根是 2,求 a 的值和方程其他的根 . 解: ∵ 2 是方程 2a2x-2-9a x-1+4=0 的根 , 将 x=2 代入方程解得 a= 1或 a=4.2(1) 当 a= 1时 , 原方程化为 2· ( 1)2x-2-9(1) x-1 +4=0.①222x-1 2令 y=( 1) , 方程①变成 2y -9y+4=0,2解得 y 1=4,y 2= 1.∴ ( 1) x-1 =42x=-1,2( 1 ) x-1 = 1x=2.22(2) 当 a=4 时 , 原方程化为 2· 42x-2 -9 · 4x-1 +4=0. ②令 t=4 x-1 , 则方程②变成 2t 2-9t+4=0. 解得 t 1=4,t 2= 1.x-12=4x=2,∴44x-1 = 1x=- 1 .22故方程此外两根是当 a= 1时 ,x=-1;1 .2当 a=4 时 ,x=-214.函数 y= (1) 3 4xx 2的单一递加区间是 ( D )3A. [ 1,2]B.[ 2,3]C.(-∞ ,2]D.[ 2,+∞ )分析: 由于 y=3x2-4x+3 , 又 y=3t 单一递加 ,t=x 2-4x+3 在 x ∈[ 2,+ ∞ ) 上递加 , 故所求的递加区间为[ 2,+ ∞ ).15.已知 f(x)=3 x-b (2≤ x ≤ 4,b 为常数 ) 的图象经过点 (2,1), 则 F(x)=f 2(x)-2f(x) 的值域为 ( B )A. [ -1,+∞ )B. [ -1,63)C.[ 0,+∞ )D.(0,63 ]分析: 由 f(2)=1, 得 32-b =1,b=2,f(x)=3 x-2.∴ F (x)= [ f(x)-1 ]2-1=(3 x-2 -1) 2-1. 令 t=3 x-2 ,2 ≤x ≤4.2∴g(t)=(t-1) - 1,t ∈[ 1,9 ].2.1 指数函数练习1.以下各式中建立的一项A . ( n)71n 7 m 7B .12 ( 3)433m3C . 4 x 3y 3( x y) 4D .393321111 1 52.化简 (a 3 b 2 )( 3a 2 b 3 ) ( a 6 b 6 ) 的结果3D . 9a 2 A . 6aB . aC . 9a3.设指数函数 f ( x)a x ( a 0, a1) ,则以下等式中不正确的选项是f (x) A . f(x+y)=f(x) ·f(y)B . f ( x y )f ( y)C . f (nx)[ f ( x)]n (nQ )D . f ( xy) n [ f ( x)] n ·[f ( y)] n1 4.函数 y (x5) 0 ( x 2)2A . { x | x 5, x 2}B . { x | x 2}C . { x | x 5}D . { x | 2 x 5或 x 5}()()()(n N )( )5.若指数函数 y a x 在 [- 1,1]上的最大值与最小值的差是1,则底数 a 等于 ()A .15 B .1 5 C .15D .5 122 226.当 a0 时,函数 y axb 和 yb ax 的图象只可能是()7.函数 f ( x)2 |x| 的值域是()A . (0,1]B . (0,1)C . (0, )D . R8.函数 f ( x)2 x 1, x 0,知足 f ( x)1的 x 的取值范围1x 2 , x()A . ( 1,1)B . ( 1, )C . { x | x 0或 x2}D . { x | x 1或 x1}9.函数 y(1) x 2x2得单一递加区间是2()A .[ 1,1]B . ( , 1]C .[2,)D .[ 1,2]2exe x210.已知 f ( x)()2 ,则以下正确的选项是A .奇函数,在 R 上为增函数B .偶函数,在 R 上为增函数C .奇函数,在 R 上为减函数D .偶函数,在 R 上为减函数11.已知函数 f (x)的定义域是(1, 2),则函数 f (2 x ) 的定义域是.12.当 a >0 且 a ≠1 时,函数 f (x)=a x -2- 3 必过定点.三、解答题:13.求函数 y1的定义域 .x5 x 1114.若 a >0, b > 0,且 a+b=c ,求证: (1) 当r >1时, a r +b r < c r ; (2) 当r < 1时, a r +b r > c r .a x 1 15.已知函数 f ( x)(a >1) .a x1( 1)判断函数 f (x) 的奇偶性;( 2)证明 f (x)在 (-∞, +∞ )上是增函数 .xa16.函数 f(x) = a (a>0 ,且 a ≠1) 在区间 [1,2] 上的最大值比最小值大2,求 a 的值.参照答案一、 DCDDD AADDA二、 11. (0,1);12. (2,- 2) ;三、 13. 解:要使函数存心义一定:x 1 0x 1x0 x 0x 1∴ 定义域为 : x xR 且 x0, x 1a rrrb r此中a1,0b114. 解:ba,c rcccc.r >1 ,a rb ra b 1,r r r当因此+b< c ;时c c c crrrrr当 r < 1 时, aba b1, 因此 a +b >c .ccc c15. 解 :(1)是奇函数 .(2) 设x <x ,则 f (x 1 )ax11 ax21 。
指数函数习题(经典含答案及详细解析)

指数函数习题一、选择题1.概念运算⎩⎨⎧>≤=⊗ba b b a a b a ,那么函数x x f 21)(⊗=的图象大致为( )2.函数f (x )=x 2-bx +c 知足f (1+x )=f (1-x )且f (0)=3,那么f (b x )与f (c x )的大小关系是( )A .f (b x )≤f (c x )B .f (b x )≥f (c x )C .f (b x )>f (c x )D .大小关系随x 的不同而不同3.函数y =|2x -1|在区间(k -1,k +1)内不单调,那么k 的取值范围是( )A .(-1,+∞)B .(-∞,1)C .(-1,1)D .(0,2)4.设函数f (x )=ln[(x -1)(2-x )]的概念域是A ,函数g (x )=lg(a x -2x -1)的概念域是B ,假设A ⊆B ,那么正数a 的取值范围( )A .a >3B .a ≥3C .a > 5D .a ≥ 55.已知函数⎩⎨⎧>≤--=-77)3)(3()(6x a x x a x f x ,假设数列{a n }知足a n =f (n )(n ∈N *),且{a n }是递增数列,那么实数a 的取值范围是( )A .[94,3) B .(94,3) C .(2,3)D .(1,3) 6.已知a >0且a ≠1,f (x )=x 2-a x ,当x ∈(-1,1)时,均有f (x )<12,那么实数a 的取值范围是( ) A .(0,12]∪[2,+∞) B .[14,1)∪(1,4] C .[12,1)∪(1,2] D .(0,14)∪[4,+∞) 二、填空题7.函数y =a x (a >0,且a ≠1)在[1,2]上的最大值比最小值大a 2,那么a 的值是________. 8.假设曲线|y |=2x +1与直线y =b 没有公共点,那么b 的取值范围是________.9.(2020·滨州模拟)概念:区间[x 1,x 2](x 1<x 2)的长度为x 2-x 1.已知函数y =2|x |的概念域为[a ,b ],值域为[1,2],那么区间[a ,b ]的长度的最大值与最小值的差为________.三、解答题10.求函数y =2342x x ---+的概念域、值域和单调区间.11.(2020·银川模拟)假设函数y =a 2x +2a x -1(a >0且a ≠1)在x ∈[-1,1]上的最大值为14,求a 的值.12.已知函数f (x )=3x ,f (a +2)=18,g (x )=λ·3ax -4x 的概念域为[0,1].(1)求a 的值;(2)假设函数g (x )在区间[0,1]上是单调递减函数,求实数λ的取值范围.指数函数答案1.解析:由a ⊗b =⎩⎪⎨⎪⎧ a a ≤b b a >b 得f (x )=1⊗2x =⎩⎪⎨⎪⎧ 2x x ≤0,1 x >0.答案:A2. 解析:∵f (1+x )=f (1-x ),∴f (x )的对称轴为直线x =1,由此得b =2.又f (0)=3,∴c =3.∴f (x )在(-∞,1)上递减,在(1,+∞)上递增.若x ≥0,那么3x ≥2x ≥1,∴f (3x )≥f (2x ).若x <0,那么3x <2x <1,∴f (3x )>f (2x ).∴f (3x )≥f (2x ).答案:A3.解析:由于函数y =|2x -1|在(-∞,0)内单调递减,在(0,+∞)内单调递增,而函数在区间(k -1,k +1)内不单调,因此有k -1<0<k +1,解得-1<k <1.答案:C4. 解析:由题意得:A =(1,2),a x -2x >1且a >2,由A ⊆B 知a x -2x >1在(1,2)上恒成立,即a x -2x -1>0在(1,2)上恒成立,令u (x )=a x -2x -1,那么u ′(x )=a x ln a -2x ln2>0,因此函数u (x )在(1,2)上单调递增,那么u (x )>u (1)=a -3,即a ≥3.答案:B5. 解析:数列{a n }知足a n =f (n )(n ∈N *),那么函数f (n )为增函数,注意a 8-6>(3-a )×7-3,因此⎩⎪⎨⎪⎧ a >13-a >0a 8-6>3-a ×7-3,解得2<a <3.答案:C6. 解析:f (x )<12⇔x 2-a x <12⇔x 2-12<a x ,考查函数y =a x 与y =x 2-12的图象,当a >1时,必有a -1≥12,即1<a ≤2, 当0<a <1时,必有a ≥12,即12≤a <1, 综上,12≤a <1或1<a ≤2. 答案:C7. 解析:当a >1时,y =a x 在[1,2]上单调递增,故a 2-a =a 2,得a =32.当0<a <1时,y =a x 在[1,2]上单调递减,故a -a 2=a 2,得a =12.故a =12或32. 答案:12或328. 解析:别离作出两个函数的图象,通过图象的交点个数来判定参数的取值范围.曲线|y |=2x +1与直线y =b 的图象如下图,由图象可得:若是|y |=2x +1与直线y =b 没有公共点,那么b 应知足的条件是b ∈[-1,1]. 答案:[-1,1]9. 解析:如图知足条件的区间[a ,b ],当a =-1,b =0或a =0,b =1时区间长度最小,最小值为1,当a =-1,b =1时区间长度最大,最大值为2,故其差为1. 答案:110. 解:要使函数成心义,那么只需-x 2-3x +4≥0,即x 2+3x -4≤0,解得-4≤x ≤1.∴函数的概念域为{x |-4≤x ≤1}.令t =-x 2-3x +4,那么t =-x 2-3x +4=-(x +32)2+254, ∴当-4≤x ≤1时,t max =254,现在x =-32,t min =0,现在x =-4或x =1. ∴0≤t ≤254.∴0≤-x 2-3x +4≤52. ∴函数y =2341()2x x --+[28,1].由t =-x 2-3x +4=-(x +32)2+254(-4≤x ≤1)可知, 当-4≤x ≤-32时,t 是增函数, 当-32≤x ≤1时,t 是减函数. 依照复合函数的单调性知:y =1()2在[-4,-32]上是减函数,在[-32,1]上是增函数. ∴函数的单调增区间是[-32,1],单调减区间是[-4,-32]. 11. 解:令a x =t ,∴t >0,那么y =t 2+2t -1=(t +1)2-2,其对称轴为t =-1.该二次函数在[-1,+∞)上是增函数.①若a >1,∵x ∈[-1,1],∴t =a x ∈[1a,a ],故当t =a ,即x =1时,y max =a 2+2a -1=14,解得a =3(a =-5舍去).②假设0<a <1,∵x ∈[-1,1],∴t =a x ∈[a ,1a ],故当t =1a,即x =-1时, y max =(1a+1)2-2=14. ∴a =13或-15(舍去). 综上可得a =3或13. 12. 解:法一:(1)由已知得3a +2=18⇒3a =2⇒a =log 32.(2)现在g (x )=λ·2x -4x ,设0≤x 1<x 2≤1,因为g (x )在区间[0,1]上是单调减函数,因此g (x 1)-g (x 2)=(2x 1-2x 2)(λ-2x 2-2x 1)>0恒成立,即λ<2x 2+2x 1恒成立.由于2x 2+2x 1>20+20=2,因此实数λ的取值范围是λ≤2.法二:(1)同法一.(2)现在g (x )=λ·2x -4x ,因为g (x )在区间[0,1]上是单调减函数,因此有g ′(x )=λln2·2x -ln4·4x =ln2[-2·(2x )2+λ·2x ]≤0成立.设2x =u ∈[1,2],上式成立等价于-2u 2+λu ≤0恒成立.因为u ∈[1,2],只需λ≤2u 恒成立,因此实数λ的取值范围是λ≤2.。
高一数学指数与指数函数试题答案及解析

高一数学指数与指数函数试题答案及解析1.函数的图像过一个定点,则定点的坐标是【答案】(2,2)【解析】当x=2时,f(2)=a2-2+1=a0+1=2,∴函数y=a x-2+1的图象一定经过定点(2,2).故答案为:(2,2).【考点】含有参数的函数过定点的问题.2.函数的图象与函数的图象所有交点的横坐标之和等于()A.4B.6C.8D.10【答案】C【解析】由数形结合可知,两函数图像在直线两侧各有4个交点,其两两关于对称。
不妨令。
则所有交点横坐标之和为。
故C正确。
【考点】1函数图像;2余弦函数的周期;3数形结合思想。
3.已知幂函数的图象过点,则.【答案】4【解析】因为为幂函数,所以设因为过点,所以本题易错点在将幂函数的定义写成指数函数的形式,即【考点】幂函数定义,指数的运算4.(1)计算.(2)若,求的值.【答案】(1);(2).【解析】(1)利用对数恒等式、换底公式、对数的运算性质进行计算;(2)首先对已知等式进行平方求得的值,再对其平方可求得的值,最后代入所求式即可求得结果.试题解析:(1)原式=.(2)∵,∴,∴,∴,∴,∴原式.【考点】1、对数的运算性质;2、对数的换底公式;3、指数的运算性质.5.已知函数,则=.【答案】【解析】根据题题意:,,故.【考点】1.分段函数;2.指数、对数运算.6.三个数,,的大小顺序是 ( )A.B.C.D.【答案】C【解析】因为,,,所以,故选C.【考点】1.指数函数的单调性;2.对数函数的单调性.7.计算的值为_________.【答案】2【解析】原式【考点】根式、指数、对数的运算8.三个数大小的顺序是()A.B.C.D.【答案】A【解析】由题意得,.,,,,故选A【考点】考察指数函数,和对数函数,分别与1和0的之对比.9.若实数,满足,则关于的函数的图象形状大致是()【答案】B【解析】由等式,可得,根据指数函数的图像可知(或者根据函数的奇偶性、单调性、特殊值来判断),正确答案为B.【考点】1.对数式与指数式的互化;2.指数函数图像、奇偶性、单调性.10.若a<0,>1,则( )A.a>1,b>0B.a>1,b<0C.0<a<1,b>0D.0<a<1,b<0【答案】D【解析】是上的增函数,由,所以是上的减函数, 由,所以故选D【考点】指数函数,对数函数的单调性.11.三个数的大小关系为()A.B.C.D.【答案】D【解析】判断几个数的大小多用构造函数单调性来解题.因为是上的减函数,所以因为是上的减函数,所以因为是上的增函数,所以故选D【考点】用指数函数与对数函数单调性比较大小,转化思想应用.12.若,则函数的图象一定过点_______________.【答案】【解析】由函数过定点,令,即时,恒等于-3,故函数图像过定点;故答案为:.【考点】指数函数的图像和性质.13.设,,,则的大小关系是()A.B.C.D.【答案】D【解析】由对数函数的性质知:,所以答案选.【考点】1.指数大小比较;2.对数函数的性质.14.计算:(1);(2)【答案】(1)6;(2).【解析】(1)直接采用换底公式计算即可;(2)利用指数幂的运算性质逐个运算即可.试题解析:(1)原式=(2)原式=【考点】1.换底公式的应用;2.指数幂的化简求值.15.函数的图象一定过点()A.B.C.D.【答案】B【解析】根据题意,由于函数,令x-1=0,x=1,可知函数值为2,故可知函数一定过点,选B.【考点】指数函数点评:本试题主要是考查了指数函数恒过(0,1)点的运用,属于基础题。
高一数学指数运算及指数函数试题(有答案)

高一数学指数运算及指数函数试题一.选择题1.若xlog 23=1,则3x+9x的值为(B)A.3B.6C.2D.解:由题意x=,所以3x==2,所以9x=4,所以3x+9x=6故选B2.若非零实数a、b、c满足,则的值等于(B)A.1B.2C.3D.4解答:解:∵,∴设=m,a=log5m,b=log2m,c=2lgm,∴==2lgm(log m5+log m2)=2lgm•log m10=2.故选B.3.已知,则a等于()A.B.C. 2 D. 4解:因为所以解得a=4故选D4.若a>1,b>1,p=,则a p等于()A.1B.b C.l og b a D.a log b a解:由对数的换底公式可以得出p==log a(log b a),因此,a p等于log b a.故选C.5.已知lg2=a,10b=3,则log125可表示为(C)A.B.C.D.解:∵lg2=a,10b=3,∴lg3=b,∴log125===.故选C.6.若lgx﹣lgy=2a,则=(C)A.3a B.C.a D.解:∵lgx﹣lgy=2a,∴lg﹣lg=lg﹣lg=(lg﹣lg)=lg=(lgx﹣lgy)=•2a=a;故答案为C.7.已知函数,若实数a,b满足f(a)+f(b﹣2)=0,则a+b= A.﹣2 B.﹣1 C.0D.2解:f(x)+f(﹣x)=ln(x+)+ln(﹣x+=0∵f(a)+f(b﹣2)=0∴a+(b﹣2)=0∴a+b=2故选D.8.=()A.1B.C.﹣2 D.解:原式=+2×lg2+lg5=+lg2+lg5=+1=,故选B.9.设,则=()A.1B.2C.3D.4解:∵,∴==()+()+()==3故选C10.,则实数a的取值区间应为(C)A.(1,2)B.(2,3)C.(3,4)D.(4,5)解:=log34+log37=log328∵3=log327<log328<log381=4∴实数a的取值区间应为(3,4)故选C.11.若lgx﹣lgy=a,则=(A)A.3a B.C.a D.解:=3(lgx﹣lg2)﹣3(lgy﹣lg2)=3(lgx﹣lgy)=3a故选A.12.设,则()A.0<P<1 B.1<P<2 C.2<P<3 D.3<P<4 解:=log112+log113+log114+log115=log11(2×3×4×5)=log11120.∴log1111=1<log11120<log11121=2.故选B.13.已知a,b,c均为正数,且都不等于1,若实数x,y,z满足,则abc的值等于(A)A.1B.2C.3D.4解:∵a,b,c均为正数,且都不等于1,实数x,y,z满足,∴设a x=b y=c z=k(k>0),则x=log a k,y=log b k,z=log c k,∴=log k a+log k b+log k c=log k abc=0,∴abc=1.故选A.14.化简a2•••的结果是(C)A.a B.C.a2D.a3解:∵a2•••=a2•••==a2,故选C15.若x,y∈R,且2x=18y=6xy,则x+y为()A.0B.1C.1或2 D.0或2解:因为2x=18y=6xy,(1)当x=y=0时,等式成立,则x+y=0;(2)当x、y≠0时,由2x=18y=6xy得,xlg2=ylg18=xylg6,由xlg2=xylg6,得y=lg2/lg6,由ylg18=xylg6,得x=lg18/lg6,则x+y=lg18/lg6+lg2/lg6=(lg18+lg2)/lg6=lg36/lg6=2lg6/lg6=2.综上所述,x+y=0,或x+y=2.故选D.16.若32x+9=10•3x,那么x2+1的值为(D)A.1B.2C.5D.1或5解:令3x=t,(t>0),原方程转化为:t2﹣10t+9=0,所以t=1或t=9,即3x=1或3x=9所以x=0或x=2,所以x2+1=1或5故选Dx x2A.﹣2<a<2 B.C.D.解;令t=2x,则t>0若二次函数f(t)=t2﹣at+a2﹣3在(0,+∞)上有2个不同的零点,即0=t2﹣at+a2﹣3在(0,+∞)上有2个不同的根∴解可得,即故选D18.若关于x的方程=3﹣2a有解,则a的范围是(A)A.≤a<B.a≥C.<a<D.a>解:∵1﹣≤1,函数y=2x在R上是增函数,∴0<≤21=2,故0<3﹣2a≤2,解得≤a<,故选A.二.填空题19.,则m=10.解:由已知,a=log2m,b=log5m.∴+=log m2+log m5=log m10=1∴m=10故答案为:10.20.已知x+y=12,xy=9,且x<y,则=.解:由题设0<x<y∵xy=9,∴∴x+y﹣2==12﹣6=6x+y+2==12+6=18∴=,=∴=故答案为:21.化简:=(或或).解:====.故答案为:(或或).22.=1.解:===1.故答案为:1.23.函数在区间[﹣1,2]上的值域是[,8].解:令g(x)=x2﹣2x=(x﹣1)2﹣1,对称轴为x=1,∴g(x)在[﹣1,1]上单调减,在[1,8]上单调递增,又f(x)=2g(x)为符合函数,∴f(x)=2g(x)在[﹣1,1]上单调减,在[1,,2]上单调递增,∴f(x)min=f(1)==;又f(﹣1)==23=8,f(2)==1,∴数在区间[﹣1,2]上的值域是[,8].故答案为:[,8].24.函数的值域为(0,8].解:令t=x2+2|x|﹣3==结合二次函数的性质可得,t≥﹣3∴,且y>0故答案为:(0,8].25.函数(﹣3≤x≤1)的值域是[3﹣9,39],单调递增区间是(﹣2,+∞)..解:可以看做是由y=和t=﹣2x2﹣8x+1,两个函数符合而成,第一个函数是一个单调递减函数,要求原函数的值域,只要求出t=﹣2x2﹣8x+1,在[1,3]上的值域就可以,t∈[﹣9,9]此时y∈[3﹣9,39]函数的递增区间是(﹣∞,﹣2],故答案为:[3﹣9,39];(﹣2,+∞)三.解答题26.计算:(1);(2).解:(1)==(2)===2+2﹣lg3+lg2+lg3﹣lg2+2=627.(1)若,求的值;(2)化简(a>0,b>0).解:(1)∵,∴x+x﹣1=9﹣2=7,x2+x﹣2=49﹣2=47,∴==3×6=18,∴==.(2)∵a >0,b >0,∴====.28.已知函数f (x )=4x ﹣2x+1+3. (1)当f (x )=11时,求x 的值;(2)当x ∈[﹣2,1]时,求f (x )的最大值和最小值.解:(1)当f (x )=11,即4x ﹣2x+1+3=11时,(2x )2﹣2•2x ﹣8=0 ∴(2x ﹣4)(2x +2)=0 ∵2x >02x +2>2,∴2x ﹣4=0,2x =4,故x=2﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(4分) (2)f (x )=(2x )2﹣2•2x +3 (﹣2≤x ≤1) 令∴f (x )=(2x ﹣1)2+2当2x =1,即x=0时,函数的最小值f min (x )=2﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(10分)当2x =2,即x=1时,函数的最大值f max (x )=3﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(12分)29.已知函数||22)(x x x f -=. (1)若2)(=x f ,求x 的值;(2)若0)()2(2≥+t mf t f t 对于]2,1[∈t 恒成立,求实数m 的取值范围。
高一数学指数运算及指数函数试题(有答案)

高一数学指数运算及指数函数试题一.选择题x x=22.若非零实数a、b、c满足,则的值等于(B)∴设=3.已知,则a等于()解:因为4.若a>1,b>1,p=,则a p等于()p=b.6.若lgx﹣lgy=2a,则=(C)lg lg=lg﹣lg=lg﹣lglg(=7.已知函数,若实数a,b满足f(a)+f(b﹣2)=0,则a+b=x+8.=()×+1=9.设,则=()解:∵∴(()10.,则实数a的取值区间应为(C)=log11.若lgx﹣lgy=a,则=(A)解:12.设,则()13.已知a,b,c均为正数,且都不等于1,若实数x,y,z满足,满足=log14.化简a2•••的结果是(C)••x y xy2x x2x x2解可得,18.若关于x的方程=3﹣2a有解,则a的范围是(A)≤a<≥<a<≤≤,二.填空题19.,则m=10.+=log20.已知x+y=12,xy=9,且x<y,则=.=x+y+2=12+6=18,故答案为:21.化简:=(或或)..故答案为:(或或22.=1.23.函数在区间[﹣1,2]上的值域是[,8].=;=[,[24.函数的值域为(0,8].25.函数(﹣3≤x≤1)的值域是[3﹣9,39],单调递增区间是(﹣2,+∞)..y=三.解答题26.计算:(1);(2).)27.(1)若,求的值;(2)化简(a>0,b>0).=3=..28.已知函数f (x )=4x﹣2x+1+3. (1)当f (x )=11时,求x 的值;(2)当x ∈[﹣2,1]时,求f (x )的最大值和最小值.29.已知函数||22)(x x x f -=. (1)若2)(=x f ,求x 的值;(2)若0)()2(2≥+t mf t f t 对于]2,1[∈t 恒成立,求实数m 的取值范围。
(1)当0<x 时,0)(=x f ;当0≥x 时,x x x f 212)(-=. 由条件可知 2212=-x x ,即 012222=-⋅-x x , 解得 212±=x . 02>x ,()21log 2+=∴x . (2)当]2,1[∈t 时,021*******≥⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-t t t t t m , 即 ()()121242--≥-t t m . 0122>-t , ∴ ()122+-≥t m . ()]5,17[21],2,1[2--∈+-∴∈t t ,故m 的取值范围是),5[∞+-.30.如果函数)1,0(122≠>-+=a a a ay x x 在区间[—1,1]上的最大值是14,求a 的值。
高一数学上册 指数函数知识点及练习题含答案
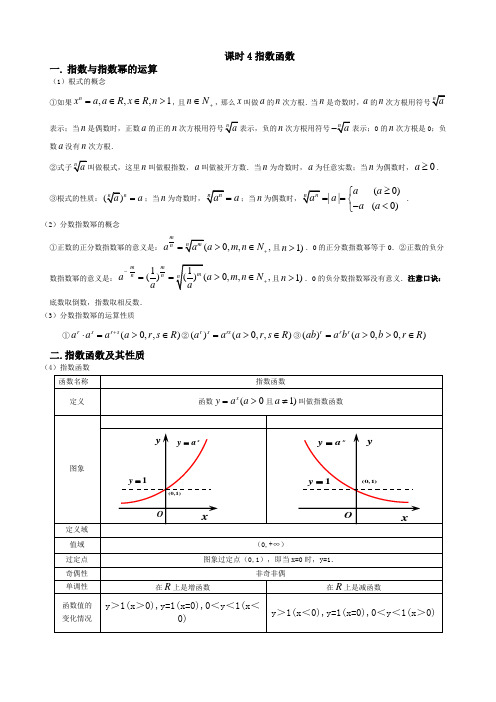
课时4指数函数一. 指数与指数幂的运算(1)根式的概念 ①如果,,,1nxa a R x R n =∈∈>,且n N +∈,那么x 叫做a 的n 次方根.当n 是奇数时,a 的n表示;当n 是偶数时,正数a 的正的nn次方根用符号0的n 次方根是0;负数a 没有n 次方根.n 叫做根指数,a 叫做被开方数.当n 为奇数时,a 为任意实数;当n 为偶数时,0a ≥.③根式的性质:n a =;当na =;当n(0)|| (0)a a a a a ≥⎧==⎨-<⎩.(2)分数指数幂的概念①正数的正分数指数幂的意义是:0,,,m naa m n N +=>∈且1)n >.0的正分数指数幂等于0.②正数的负分数指数幂的意义是: 1()0,,,m m nn aa m n N a -+==>∈且1)n >.0的负分数指数幂没有意义.注意口诀:底数取倒数,指数取相反数. (3)分数指数幂的运算性质①(0,,)rs r s aa a a r s R +⋅=>∈②()(0,,)r s rs a a a r s R =>∈③()(0,0,)r r r ab a b a b r R =>>∈二.指数函数及其性质(4)指数函数a 变化对图象影响在第一象限内,a 越大图象越高,越靠近y 轴; 在第二象限内,a 越大图象越低,越靠近x 轴. 在第一象限内,a 越小图象越高,越靠近y 轴; 在第二象限内,a 越小图象越低,越靠近x 轴.三.例题分析1.设a 、b 满足0<a<b<1,下列不等式中正确的是(C) A.a a <a b B.b a <b b C.a a <b a D.b b <a b解析:A 、B 不符合底数在(0,1)之间的单调性;C 、D 指数相同,底小值小.故选C. 2.若0<a<1,则函数y=a x 与y=(a-1)x 2的图象可能是(D)解析:当0<a<1时,y=a x为减函数,a-1<0,所以y=(a-1)x 2开口向下,故选D.3.设指数函数f(x)=a x (a>0且a ≠1),则下列等式中不正确的是(D) A.f(x+y)=f(x)f(y)B.f(x-y)=)()(y f x f C.f(nx)=[f(x)]n D.f [(xy)n ]=[f(x)]n [f(y)]n (n ∈N *) 解析:易知A 、B 、C 都正确. 对于D,f [(xy)n]=a(xy)n,而[f(x)]n·[f(y)]n=(a x )n·(a y)n=anx+ny,一般情况下D 不成立.4.设a=31)43(-,b=41)34(-,c=43)23(-,则a 、b 、c 的大小关系是(B)A.c<a<bB.c<b<aC.b<a<cD.b<c<a解析:a=413131)34()34()43(>=-=b,b=434141)23()278()34(-=>=c.∴a>b>c.5.设f(x)=4x -2x+1,则f -1(0)=______1____________. 解析:令f -1(0)=a,则f(a)=0即有4a-2·2a=0.2a·(2a-2)=0,而2a>0,∴2a=2得a=1.6.函数y=a x-3+4(a>0且a ≠1)的反函数的图象恒过定点______(5,3)____________.解析:因y=a x的图象恒过定点(0,1),向右平移3个单位,向上平移4个单位得到y=a x-3+4的图象,易知恒过定点(3,5).故其反函数过定点(5,3).7.已知函数f(x)=xx xx --+-10101010.证明f(x)在R 上是增函数.证明:∵f(x)=1101101010101022+-=+---x x xx x x , 设x 1<x 2∈R ,则f(x 1)-f(x 2)=)110)(110()1010(21101101101101010101010101010212122112222111122222222++-=+--+-=+--+-----x x x x x x x x x x x x x x x x . ∵y=10x 是增函数, ∴21221010x x -<0. 而1210x +1>0,2210x +1>0, 故当x 1<x 2时,f(x 1)-f(x 2)<0, 即f(x 1)<f(x 2). 所以f(x)是增函数.8.若定义运算a ⊗b=⎩⎨⎧<≥,,,,b a a b a b 则函数f(x)=3x ⊗3-x 的值域为(A)A.(0,1]B.[1,+∞)C.(0,+∞)D.(-∞,+∞)解析:当3x ≥3-x ,即x ≥0时,f(x)=3-x ∈(0,1];当3x<3-x,即x<0时,f(x)=3x∈(0,1).∴f(x)=⎩⎨⎧<≥-,0,3,0,3x x x x 值域为(0,1).9.函数y=a x 与y=-a -x (a>0,a ≠1)的图象(C) A.关于x 轴对称B.关于y 轴对称 C.关于原点对称D.关于直线y=-x 对称解析:可利用函数图象的对称性来判断两图象的关系.10.当x ∈[-1,1]时,函数f(x)=3x -2的值域为_______[-35,1]___________. 解析:f(x)在[-1,1]上单调递增.11.设有两个命题:(1)关于x 的不等式x 2+2ax+4>0对一切x ∈R 恒成立;(2)函数f(x)=-(5-2a)x 是减函数.若命题(1)和(2)中有且仅有一个是真命题,则实数a 的取值范围是_______(-∞,-2)__________.解析:(1)为真命题⇔Δ=(2a)2-16<0⇔-2<a<2.(2)为真命题⇔5-2a>1⇔a<2.若(1)假(2)真,则a ∈(-∞,-2].若(1)真(2)假,则a ∈(-2,2)∩[2,+∞]=∅. 故a 的取值范围为(-∞,-2).12.求函数y=4-x -2-x +1,x ∈[-3,2]的最大值和最小值. 解:设2-x =t,由x ∈[-3,2]得t ∈[41,8],于是y=t 2-t+1=(t-21)2+43.当t=21时,y 有最小值43.这时x=1.当t=8时,y 有最大值57.这时x=-3. 13.已知关于x 的方程2a 2x-2-7a x-1+3=0有一个根是2,求a 的值和方程其余的根. 解:∵2是方程2a 2x-2-9a x-1+4=0的根,将x=2代入方程解得a=21或a=4. (1)当a=21时,原方程化为2·(21)2x-2-9(21)x-1+4=0.① 令y=(21)x-1,方程①变为2y 2-9y+4=0, 解得y 1=4,y 2=21.∴(21)x-1=4⇒x=-1,(21)x-1=21⇒x=2. (2)当a=4时,原方程化为2·42x-2-9·4x-1+4=0.② 令t=4x-1,则方程②变为2t 2-9t+4=0.解得t 1=4,t 2=21. ∴4x-1=4⇒x=2, 4x-1=21⇒x=-21. 故方程另外两根是当a=21时,x=-1; 当a=4时,x=-21. 14.函数y=243)31(x x -+-的单调递增区间是(D) A.[1,2]B.[2,3]C.(-∞,2]D.[2,+∞)解析:因为y=3x2-4x+3,又y=3t 单调递增,t=x 2-4x+3在x∈[2,+∞)上递增,故所求的递增区间为[2,+∞).15.已知f(x)=3x-b (2≤x ≤4,b 为常数)的图象经过点(2,1),则F(x)=f 2(x)-2f(x)的值域为(B) A.[-1,+∞)B.[-1,63) C.[0,+∞)D.(0,63]解析:由f(2)=1,得32-b =1,b=2,f(x)=3x-2. ∴F(x)=[f(x)-1]2-1=(3x-2-1)2-1. 令t=3x-2,2≤x≤4.∴g(t)=(t -1)2-1,t∈[1,9]. ∴所求值域为[-1,63].2.1指数函数练习1.下列各式中成立的一项()A .7177)(m n mn= B .31243)3(-=-C .43433)(y x y x +=+D .3339=2.化简)31()3)((656131212132b a b a b a ÷-的结果()A .a 6B .a -C .a 9-D .29a3.设指数函数)1,0()(≠>=a a a x f x ,则下列等式中不正确的是() A .f (x +y )=f(x )·f (y ) B .)()(y f x f y x f =-)( C .)()]([)(Q n x f nx f n∈=D .)()]([·)]([)(+∈=N n y f x f xy f n n n4.函数21)2()5(--+-=x x y()A .}2,5|{≠≠x x xB .}2|{>x xC .}5|{>x xD .}552|{><<x x x 或5.若指数函数x a y =在[-1,1]上的最大值与最小值的差是1,则底数a 等于 ()A .251+B .251+- C .251± D .215± 6.当a ≠0时,函数y ax b =+和y b ax =的图象只可能是 ()7.函数||2)(x x f -=的值域是()A .]1,0(B .)1,0(C .),0(+∞D .R8.函数⎪⎩⎪⎨⎧>≤-=-0,0,12)(21x x x x f x ,满足1)(>x f 的x 的取值范围 ()A .)1,1(-B .),1(+∞-C .}20|{-<>x x x 或D .}11|{-<>x x x 或9.函数22)21(++-=x x y 得单调递增区间是 ()A .]21,1[-B .]1,(--∞C .),2[+∞D .]2,21[10.已知2)(xx e e x f --=,则下列正确的是 ()A .奇函数,在R 上为增函数B .偶函数,在R 上为增函数C .奇函数,在R 上为减函数D .偶函数,在R 上为减函数 11.已知函数f (x )的定义域是(1,2),则函数)2(x f 的定义域是. 12.当a >0且a ≠1时,函数f (x )=a x -2-3必过定点. 三、解答题:13.求函数y x x =--1511的定义域.14.若a >0,b >0,且a +b =c ,求证:(1)当r >1时,a r +b r <c r ;(2)当r <1时,a r +b r >c r .15.已知函数11)(+-=x x a a x f (a >1).(1)判断函数f (x )的奇偶性;(2)证明f (x )在(-∞,+∞)上是增函数.16.函数f(x)=a x(a>0,且a ≠1)在区间[1,2]上的最大值比最小值大,求a 的值.参考答案一、DCDDDAADDA二、11.(0,1);12.(2,-2); 三、13.解:要使函数有意义必须:∴定义域为:{}x x R x x ∈≠≠且01,14.解:rrrrr c b c a c b a ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=+,其中10,10<<<<cbc a . 当r >1时,1=+<⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛c b c a c b c a rr,所以a r +b r <c r; 当r <1时,1=+>⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛c b c a c b c a rr ,所以a r +b r >c r . 15.解:(1)是奇函数.(2)设x 1<x 2,则1111)()(221121+--+-=-x x x x a a a a x f x f 。
(完整版)指数函数及对数函数复习(有详细知识点及习题详细讲解)

指数函数与对数函数总结与练习一、指数的性质(一)整数指数幂n 1.整数指数幂概念:a =a ⋅Λ⋅a (n ∈N )a 0=1(a ≠0)1⋅4a 243*n 个aa-n=1a ≠0,n ∈N *)n(a 2.整数指数幂的运算性质:(1)a m ⋅a n =a m +n (m ,n ∈Z )(2)a (3)(ab )=a ⋅b n n n ()mn=a mn(m ,n ∈Z )(n ∈Z )其中a ÷a =a ⋅a m n m -n =a m -n a n ⎛a ⎫-1nn -n , ⎪=(a ⋅b)=a ⋅b =n .b ⎝b ⎭n 3.a 的n 次方根的概念即:若x n 一般地,如果一个数的n 次方等于a n >1,n ∈N ),那么这个数叫做a 的n 次方根,=a ,则x 叫做a 的n 次方根,(n >1,n ∈N )**(说明:①若n 是奇数,则a 的n 次方根记作n a ;若a >0则n a >0,若a <o 则n a <0;②若n 是偶数,且a >0则a 的正的n 次方根记作n a ,a 的负的n 次方根,记作:-n a ;(例如:8的平方根±8=±2216的4次方根±416=±2)③若n 是偶数,且a <0则n a 没意义,即负数没有偶次方根;④Θ0=0n >1,n ∈N nn (*)∴n 0=0;⑤式子a 叫根式,n 叫根指数,a 叫被开方数。
∴(a )nn=a ..4.a 的n 次方根的性质一般地,若n 是奇数,则n a n =a ;若n 是偶数,则n a n =a =⎨5.例题分析:例1.求下列各式的值:(1)3-8⎧a⎩-aa ≥0a <0.(3)(2)(-10)*2(3)4(3-π)(4)4例2.已知a <b <0,n >1,n ∈N ,化简:n (a -b )+n (a +b ).n n (二)分数指数幂1051231.分数指数幂:5a =a =a102(a >0)3a =a =a124(a >0)即当根式的被开方数能被根指数整除时,根式可以写成分数指数幂的形式;如果幂的运算性质(2)a 3()kn=akn 对分数指数幂也适用,442255⨯3⨯4⎛2⎫⎛⎫2532例如:若a >0,则 a 3⎪=a 3=a , a 4⎪=a 4=a ,∴a =a 3⎝⎭⎝⎭a =a .545即当根式的被开方数不能被根指数整除时,根式也可以写成分数指数幂的形式。
高一数学指数函数试题答案及解析

高一数学指数函数试题答案及解析1.函数的单调递减区间【答案】【解析】因为,根据复合函数的单调性可知该函数的单调递减区间为.【考点】本小题主要考查复合函数的单调区间的求法.点评:考查复合函数的单调性时,要注意“同增异减”,还要注意函数的定义域.2.设a,b,c∈R,且3= 4= 6,则( ).A.=+B.=+C.=+D.=+【答案】B【解析】设3= 4= 6= k,则a = log k,b= log k,c = log k,从而= log 6 = log3+log 4 =+,故=+,所以选(B).3.设指数函数,则下列等式中不正确的是()A.f(x+y)=f(x)·f(y)B.C.D.【答案】D【解析】根据指数幂的运算律知:A,B,C正确;。
故选D4.若函数是定义在R上的奇函数,则函数的图象关于()A.轴对称B.轴对称C.原点对称D.以上均不对【答案】B【解析】因为函数是定义在R上的奇函数,所以则所以是偶函数。
故选B5.三个数,,之间的大小关系为()A.B.C.D.【答案】B【解析】因为,,,所以,故应选.【考点】1、指数与指数函数;2、对数与对数函数;6.定义运算为:,例如:,则的取值范围是__________.【答案】【解析】由题意可得,,∵时,,综上可得,的取值范围是,故答案为.7.已知,则三者的大小关系是A.B.C.D.【答案】A【解析】由函数的图象与性质可知:;由函数的图象与性质可知:;∴故选:A8.若,则等于A.B.C.D.【答案】A【解析】因为,故选A.9.已知函数(,且).(1)若函数在上的最大值为2,求的值;(2)若,求使得成立的的取值范围.【答案】(1)或;(2).【解析】(1)分类讨论和两种情况,结合函数的单调性可得:或;(2)结合函数的解析式,利用指数函数的单调性可得,求解对数不等式可得的取值范围是.试题解析:(1)当时,在上单调递增,因此,,即;当时,在上单调递减,因此,,即.综上,或.(2)不等式即.又,则,即,所以.10.已知,,,则,,的大小关系是()A.B.C.D.【答案】C【解析】因为,,,所以,故选C.11.若3<a<4,化简的结果是()A.7-2a B.2a-7C.1D.-1【答案】C【解析】∵,∴,。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
指数函数
2.1.1指数与指数幂的运算
(1)根式的概念 ①如果,,,1n
x
a a R x R n =∈∈>,且n N +∈,那么x 叫做a 的n 次方根.当n 是奇数时,a 的n 次
当n 是偶数时,正数a 的正的n
负的n
次方根用符号表示;0的n 次方根是0;负数a 没有n 次方根.
n 叫做根指数,a 叫做被开方数.当n 为奇数时,a 为任意实数;当n 为偶数
时,0a ≥.
n a =;当n
a =;当n
(0)|| (0)
a a a a a ≥⎧==⎨-<⎩.
(2)分数指数幂的概念
①正数的正分数指数幂的意义是:
0,,,m n
a a m n N +=>∈且1)n >.0的正分数指数幂等于0.②
正数的负分数指数幂的意义是:
1()0,,,m
m n
n a
a m n N a -+==>∈且1)n >.0
的负分数指
数幂没有意义. 注意口诀:底数取倒数,指数取相反数. (3)分数指数幂的运算性质
2.1指数函数练习
1.下列各式中成立的一项
( )
A .71
7
7)(m n m
n =
B .31243)3(-=-
C .4
3433)(y x y x +=+
D .
33
39=
2.化简)3
1
()3)((65
61
3
12
12
13
2b a b a b a ÷-的结果
( )
A .a 6
B .a -
C .a 9-
D .2
9a
3.设指数函数)1,0()(≠>=a a a x f x
,则下列等式中不正确的是
( )
A .f (x +y )=f(x )·f (y )
B .)
()
(y f x f y x f =-)
( C .)()]
([)(Q n x f nx f n
∈=
D .)()]([·
)]([)(+∈=N n y f x f xy f n
n
n
4.函数2
10
)
2()5(--+-=x x y
( )
A .}2,5|{≠≠x x x
B .}2|{>x x
C .}5|{>x x
D .}552|{><<x x x 或 5.若指数函数x
a y =在[-1,1]上的最大值与最小值的差是1,则底数a 等于
( )
A .
2
5
1+
B .
2
5
1+- C .
2
5
1± D .
2
1
5± 6.当a ≠0时,函数y a x b =+和y b a x
=的图象只可能是 ( )
7.函数|
|2)(x x f -=的值域是
( ) A .]1,0(
B .)1,0(
C .),0(+∞
D .R
8.函数⎪⎩⎪
⎨⎧>≤-=-0
,0
,12)(21x x x x f x ,满足1)(>x f 的x 的取值范围
( )
A .)1,1(-
B . ),1(+∞-
C .}20|{-<>x x x 或
D .}11|{-<>x x x 或 9.函数2
2)2
1(++-=x x y 得单调递增区间是
( ) A .]2
1,1[-
B .]1,(--∞
C .),2[+∞
D .]2,2
1[
10.已知2
)(x
x e e x f --=,则下列正确的是
( )
A .奇函数,在R 上为增函数
B .偶函数,在R 上为增函数
C .奇函数,在R 上为减函数
D .偶函数,在R 上为减函数
11.已知函数f (x )的定义域是(1,2),则函数)2(x
f 的定义域是 . 12.当a >0且a ≠1时,函数f (x )=a x -2-3必过定点 . 三、解答题: 13.求函数y x x =
--15
1
1
的定义域.
14.若a >0,b >0,且a +b =c ,
求证:(1)当r >1时,a r +b r <c r ;(2)当r <1时,a r +b r >c r .
15.已知函数1
1
)(+-=x x a a x f (a >1).
(1)判断函数f (x )的奇偶性;(2)证明f (x )在(-∞,+∞)上是增函数.
16.函数f(x)=a x
(a>0,且a ≠1)在区间[1,2]上的最大值比最小值大a 2,求a 的值.
参考答案
一、DCDDD AAD D A
二、11.(0,1); 12.(2,-2); 三、13. 解:要使函数有意义必须:
x x x x x -≠-≠⎧⎨⎪
⎩
⎪⇒≠≠⎧⎨
⎩101010
∴定义域为:{}
x x R x x ∈≠≠且01,
14. 解:r
r r
r
r c b c a c b a ⎪⎭
⎫ ⎝⎛+⎪⎭
⎫ ⎝⎛=+,其中10,10<<<<
c
b
c a . 当r >1时,1=+<⎪
⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛c b c a c b c a r
r
,所以a r +b r <c r
; 当r <1时,1=+>⎪⎭
⎫ ⎝⎛+⎪⎭⎫ ⎝⎛c b c a c b c a r
r
,所以a r +b r >c r .
15.解:(1)是奇函数.
(2)设x 1<x 2,则1111)()(221121+--
+-=-x x x x a a a a x f x f 。
=)
1)(1()1)(1()1)(1(212
121++-+-+-x x x x x x a a a a a a ∵a >1,x 1<x 2,∴a 1x <a
2
x . 又∵a 1x +1>0,a
2
x +1>0,
∴f (x 1)-f (x 2)<0,即f (x 1)<f (x 2).
函数f(x)在(-∞,+∞)上是增函数.
16、 (1)若a>1,则f(x)在[1,2]上递增,
∴a 2-a =a 2,即a =3
2或a =0(舍去).
(2)若0<a<1,则f(x)在[1,2]上递减,
∴a -a 2=a 2,即a =1
2
或a =0(舍去),
综上所述,所求a 的值为12或3
2
.。
