勾股定理知识点总结(经典、实用)
勾股定理全章知识点总结大全

勾股定理全章知识点总结大全一.基础知识点:1:勾股定理:反映了直角三角形三边之间的关系,是直角三角形的重要性质之一,其主要应用:直角三角形两直角边a 、b 的平方和等于斜边c 的平方。
(即:a 2+b 2=c 2) (1)已知直角三角形的两边求第三边(在ABC ∆中,90C ∠=︒,则22c a b =+,22b c a =-,22a c b =-)(2)已知直角三角形的一边与另两边的关系,求直角三角形的另两边(3)利用勾股定理可以证明线段平方关系的问题 2:勾股定理的逆定理如果三角形的三边长:a 、b 、c ,则有关系a 2+b 2=c 2,那么这个三角形是直角三角形。
要点诠释:勾股定理的逆定理是判定一个三角形是否是直角三角形的一种重要方法,它通过“数转化为形”来确定三角形的可能形状,在运用这一定理时应注意: (1)首先确定最大边,不妨设最长边长为:c ;(2)验证c 2与a 2+b 2是否具有相等关系,若c 2=a 2+b 2,则△ABC 是以∠C 为直角的直角三角形(若c 2>a 2+b 2,则△ABC 是以∠C 为钝角的钝角三角形;若c 2<a 2+b 2,则△ABC 为锐角三角形)。
(3)注意:定理中a ,b ,c 及222a b c +=只是一种表现形式,不可认为是唯一的,如若三角形三边长a ,b ,c 满足222a c b +=,那么以a ,b ,c 为三边的三角形是直角三角形,但是b 为斜边) 3:勾股定理与勾股定理逆定理的区别与联系区别:勾股定理是直角三角形的性质定理,而其逆定理是判定定理; 联系:勾股定理与其逆定理的题设和结论正好相反,都与直角三角形有关。
4:勾股定理的证明勾股定理的证明方法很多,常见的是拼图的方法。
用拼图的方法验证勾股定理的思路是:①图形进过割补拼接后,只要没有重叠,没有空隙,面积不会改变;②根据同一种图形的面积不同的表示方法,列出等式,推导出勾股定理。
勾股定理知识点精典总结

勾股定理知识点一:勾股定理及其证明一.勾股定理:在ABC Rt ∆中,︒=∠90C1.角与角之间有怎样的关系?︒=∠+∠90B A 直角三角形两锐角互余2.边与边之间有怎样的关系?(1)斜边最长; (2)任意两边之和大于第三边,任意两边之差小于第三边(3)勾股定理: a 2+b 2=c 2对这个等式可以变形为:22b a c += 22a c b -= 22b c a -=1、填空题⑴在Rt △ABC ,∠C=90°,a=8,b=15,则c= 。
⑵在Rt △ABC ,∠B=90°,a=3,b=4,则c= 。
⑶在Rt △ABC ,∠C=90°,c=10,a :b=3:4,则a= ,b= 。
⑷一个直角三角形的三边为三个连续偶数,则它的三边长分别为 。
⑸已知直角三角形的两边长分别为3cm 和5cm ,,则第三边长为 。
⑹已知等边三角形的边长为2cm ,则它的高为 ,面积为 。
⑺在Rt △ABC ,∠C=90°,如果a=7,c=25,则b= 。
⑻在Rt △ABC ,∠C=90°,如果∠A=30°,a=4,则b= 。
⑼在Rt △ABC ,∠C=90°,如果∠A=45°,a=3,则c= 。
⑽在Rt △ABC ,∠C=90°,如果c=10,a-b=2,则b= 。
⑾在Rt △ABC ,∠C=90°,如果a 、b 、c 是连续整数,则a+b+c= 。
⑿在Rt △ABC ,∠C=90°,如果b=8,a :c=3:5,则c= 。
二.选择题1.在△ABC 中,AB=15,AC=13,BC 上的高AD 长为12,则△ABC 的面积为 ( ).(A )84 (B )24 (C )24或84 (D )84或242.如下图,线段AB=√2、CD=√5,那么,线段EF 的长度为( )A 、√7B 、√11C 、√13D 、√153.如图,点1为单位正方形内一点,且AE=BE=AB ,延长AE 交CD 于F ,作FG ⊥AB 于点G ,则EG 的长度为( )A 、B 、C 、D 、4.如图,两个高度相等的圆柱形水杯,甲杯装满液体,乙杯是空杯.若把甲杯中的液体全部倒入乙杯,则乙杯中的液面与图中点P 的距离是 ( )A .2cm B .4√3cm C .6cm D .8cm5.如图所示,有一个长、宽各2米,高为4米且封闭的长方体纸盒,一只昆虫从顶点要爬到顶点,那么这只昆虫爬行的最短路程为( )A 、3米 B 、 5米 C 、4√2米 D 、2√10米6.如图,在△ABC 中,∠ACB =90º,AC >BC ,分别以AB 、BC 、CA 为一边向△ABC 外作正方形ABDE 、BCMN 、CAFG ,连接EF 、GM 、ND ,设△AEF 、△BND 、△CGM 的面积分别为S 1、S 2、S 3,则下列结论正确的是 A .S 1=S 2=S 3 B .S 1=S 2<S 3 C .S 1=S 3<S 2 D .S 2=S 3<S 1二.填空题1. 如下图,数轴上点A 表示的数为________;2.已知:在Rt △ABC 中,∠C=90°,CD ⊥AB 于D ,∠A=60°,CD=√3,求线段AB 长。
勾股定理(知识点+题型分类练习)

ABCabc弦股勾勾股定理(知识点)【知识要点】1. 勾股定理的概念:如果直角三角形的两直角边长分别为a,b,斜边长为c,那么 a2+b2=c2. 即直角三角形两直角边的平方和等于斜边的平方。
常用关系式由三角形面积公式可得:AB·CD=AC·BC2. 勾股定理的逆定理:如果三角形的三边长a,b,c有下面关系:a2+b2=c2,那么这个三角形是直角三角形,其中c为斜边。
3. 勾股数:①满足a2+b2=c2的三个正整数叫做勾股数(注意:若a,b,c、为勾股数,那么ka,kb,kc同样也是勾股数组。
)②记住常见的勾股数可以提高解题速度,如3,4,5;6,8,10;5,12,13;7,24,25;8,15,17等③用含字母的代数式表示n组勾股数:221,2,1n n n -+(2,n ≥n 为正整数); 2221,22,221n n n n n ++++(n 为正整数)2222,2,m n mn m n -+(,m n >m ,n 为正整数)4.判断直角三角形:(1)有一个角为90°的三角形是直角三角形。
(2)有两个角互余的三角形是直角三角形。
(3)如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形。
(4)如果三角形的三边长a 、b 、c 满足a 2+b 2=c 2 ,那么这个三角形是直角三角形。
(经典直角三角形:勾三、股四、弦五)用勾股定理逆定理判断三角形是否为直角三角形的一般步骤是: (1)确定最大边(不妨设为c );(2)若c 2=a 2+b 2,则△ABC 是以∠C 为直角的三角形;若a 2+b 2<c 2,则此三角形为钝角三角形(其中c 为最大边); 若a 2+b 2>c 2,则此三角形为锐角三角形(其中c 为最大边)5.直角三角形的性质(1)直角三角形的两个锐角互余。
可表示如下:∠C=90°⇒∠A+∠B=90°B(2)在直角三角形中,30°角所对的直角边等于斜边的一半。
勾股定理知识点总结

17.1勾股定理考点一:勾股定理直角三角形两直角边a 、b 的平方和等于斜边c 的平方。
(即:a 2+b 2=c 2) 技巧归纳:勾股定理反映了直角三角形三边之间的关系,是直角三角形的重要性质之一,其主要应用:(1)已知直角三角形的两边求第三边(在ABC ∆中,90C ∠=︒,则22c a b =+,22b c a =-,22a c b =-)(2)已知直角三角形的一边与另两边的关系,求直角三角形的另两边(3)利用勾股定理可以证明线段平方关系的问题考点二:勾股定理的证明一般是通过剪拼,借助面积进行证明。
其中的依据是图形经过割补拼接后,只要没有重叠,没有空隙,面积不变。
图1是由4个全等三角形拼成的,得到一个以a+b 为边长的大正方形和以直角三角形斜边c 为边长的小正方形。
则大正方形的面积可表示为(a+b)2,又可表示为12ab ·4+c 2,所以(a+b)2=12ab ·4+c 2,整理得a 2+b 2=c 2在图2的另一种拼法中,以c 为边长的正方形的面积可表示成四个全等的直角三角形与边长为(b-a)的正方形的面积的和,所以12ab ·4+(b-a)2=c 2,整理得a 2+b 2=c 2.考点三:勾股定理的应用(1)勾股定理的应用条件勾股定理只适用于直角三角形,所以常作辅助线——高,构造直角三角形。
(2)勾股定理的实际应用勾股定理反映了直角三角形3条边之间的关系,利用勾股定理,可以解决直角三角形的有关计算和证明.例如:已知直角三角形的两条直角边可求斜边;已知直角三角形的斜边和一条直角边,可求另一条直角边。
勾股定理还可以解决生产生活中的一些实际问题。
在解决问题的过程中,往往利用勾股定理列方程(组),将实际问题转化成直角三角形的模型来解决。
(3)利用勾股定理作长为 n (n 为大于1的整数)的线段实数与数轴上的点是一一对应的,有理数在数轴上较易找到与它对应的点,而若要在数轴上直接标出无理数对应的点则较难。
勾股定理知识点总结(经典、实用)

勾股定理知识点总结(经典、实用) Chapter 3: Pythagorean Theorem1.Key Points:1.1 Pythagorean TheoremThe Pythagorean Theorem states that in a right triangle。
the square of the hypotenuse (the longest side) is equal to the sum of the squares of the other two sides。
In other words。
if the two legs of a right triangle are a and b。
and the hypotenuse is c。
then a^2 + b^2 = c^2.The formula can also be rearranged to solve for a or b: a^2 = c^2 - b^2 or b^2 = c^2 - a^2.Note: This theorem only applies to right triangles。
where one angle is 90 degrees.1.2 Proof of Pythagorean TheoremThere are many ways to prove the Pythagorean Theorem。
but one common method is to use the concept of area。
By showing that two different shapes have the same area。
we can derive the formula for the theorem。
Another method is to use a puzzle-like diagram to rearrange the squares of the sides.Two common methods are shown below:Method 1: 4 SquaresIn the diagram。
(完整版)勾股定理知识点、经典例题
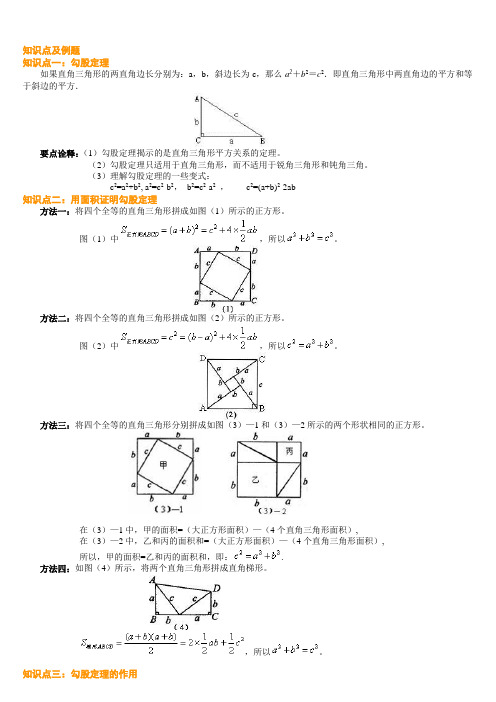
知识点及例题知识点一:勾股定理如果直角三角形的两直角边长分别为:a,b,斜边长为c,那么a2+b2=c2.即直角三角形中两直角边的平方和等于斜边的平方.要点诠释:(1)勾股定理揭示的是直角三角形平方关系的定理。
(2)勾股定理只适用于直角三角形,而不适用于锐角三角形和钝角三角。
(3)理解勾股定理的一些变式:c2=a2+b2, a2=c2-b2,b2=c2-a2,c2=(a+b)2-2ab知识点二:用面积证明勾股定理方法一:将四个全等的直角三角形拼成如图(1)所示的正方形。
图(1)中,所以。
方法二:将四个全等的直角三角形拼成如图(2)所示的正方形。
图(2)中,所以。
方法三:将四个全等的直角三角形分别拼成如图(3)—1和(3)—2所示的两个形状相同的正方形。
在(3)—1中,甲的面积=(大正方形面积)—(4个直角三角形面积),在(3)—2中,乙和丙的面积和=(大正方形面积)—(4个直角三角形面积),所以,甲的面积=乙和丙的面积和,即:.方法四:如图(4)所示,将两个直角三角形拼成直角梯形。
,所以。
知识点三:勾股定理的作用1.已知直角三角形的两条边长求第三边;2.已知直角三角形的一条边,求另两边的关系;3.用于证明平方关系的问题;4.利用勾股定理,作出长为的线段。
2. 在理解的基础上熟悉下列勾股数满足不定方程x2+y2=z2的三个正整数,称为勾股数(又称为高数或毕达哥拉斯数),显然,以x,y,z为三边长的三角形一定是直角三角形。
熟悉下列勾股数,对解题是会有帮助的:①3、4、5②5、12、13;③8、15、17;④7、24、25;⑤10、24、26;⑥9、40、41.如果(a,b,c)是勾股数,当t>0时,以at,bt,ct为三角形的三边长,此三角形必为直角三角形。
经典例题透析类型一:勾股定理的直接用法1、在Rt△ABC中,∠C=90°(1)已知a=6,c=10,求b,(2)已知a=40,b=9,求c;(3)已知c=25,b=15,求a.思路点拨:写解的过程中,一定要先写上在哪个直角三角形中,注意勾股定理的变形使用。
勾股定理知识点总结及练习

第 课时第十八章 勾股定理一.基础知识点: 1:勾股定理直角三角形两直角边a 、b 的平方和等于斜边c 的平方。
(即:a 2+b 2=c 2) 要点诠释:勾股定理反映了直角三角形三边之间的关系,是直角三角形的重要性质之一,其主要应用:(1)已知直角三角形的两边求第三边(在ABC ∆中,90C ∠=︒,则22c a b =+,22b c a =-,22a cb =-)(2)已知直角三角形的一边与另两边的关系,求直角三角形的另两边 (3)利用勾股定理可以证明线段平方关系的问题2:勾股定理的证明勾股定理的证明方法很多,常见的是拼图的方法 用拼图的方法验证勾股定理的思路是①图形进过割补拼接后,只要没有重叠,没有空隙,面积不会改变 ②根据同一种图形的面积不同的表示方法,列出等式,推导出勾股定理 常见方法如下: 方法一:4EFGH S S S ∆+=正方形正方形ABCD ,2214()2ab b a c ⨯+-=,化简可证.方法二:四个直角三角形的面积与小正方形面积的和等于大正方形的面积.四个直角三角形的面积与小正方形面积的和为221422S ab c ab c =⨯+=+ 大正方形面积为222()2S a b a ab b =+=++ 所以222a b c +=方法三:1()()2S a b a b =+⋅+梯形,2112S 222ADE ABE S S ab c ∆∆=+=⋅+梯形,化简得证3:勾股数①能够构成直角三角形的三边长的三个正整数称为勾股数,即222a b c +=中,a ,b ,c 为正整数时,称a ,b ,c 为一组勾股数②记住常见的勾股数可以提高解题速度,如3,4,5;6,8,10;5,12,13;7,24,25等 ③用含字母的代数式表示n 组勾股数:221,2,1n n n -+(2,n ≥n 为正整数);2221,22,221n n n n n ++++(n 为正整数)2222,2,m n mn m n -+(,m n >m ,n 为正整数)规律方法指导1.勾股定理的证明实际采用的是图形面积与代数恒等式的关系相互转化证明的。
(完整版)勾股定理知识点+对应类型
第二章勾股定理、平方根专题第一节勾股定理一、勾股定理:1、勾股定理定义:如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2. 即直角三角形两直角边的平方和等于斜边的平方ABCabc弦股勾勾:直角三角形较短的直角边股:直角三角形较长的直角边弦:斜边勾股定理的逆定理:如果三角形的三边长a,b,c有下面关系:a2+b2=c2,那么这个三角形是直角三角形。
2. 勾股数:满足a2+b2=c2的三个正整数叫做勾股数(注意:若a,b,c、为勾股数,那么ka,kb,kc同样也是勾股数组。
)*附:常见勾股数:3,4,5; 6,8,10; 9,12,15; 5,12,133. 判断直角三角形:如果三角形的三边长a、b、c满足a2+b2=c2 ,那么这个三角形是直角三角形。
(经典直角三角形:勾三、股四、弦五)其他方法:(1)有一个角为90°的三角形是直角三角形。
(2)有两个角互余的三角形是直角三角形。
用它判断三角形是否为直角三角形的一般步骤是:(1)确定最大边(不妨设为c);(2)若c 2=a 2+b 2,则△ABC 是以∠C 为直角的三角形; 若a 2+b 2<c 2,则此三角形为钝角三角形(其中c 为最大边); 若a 2+b 2>c 2,则此三角形为锐角三角形(其中c 为最大边)4.注意:(1)直角三角形斜边上的中线等于斜边的一半(2)在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半。
(3)在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30°。
5. 勾股定理的作用:(1)已知直角三角形的两边求第三边。
(2)已知直角三角形的一边,求另两边的关系。
(3)用于证明线段平方关系的问题。
(4)利用勾股定理,作出长为n 的线段二、平方根:(11——19的平方)1、平方根定义:如果一个数的平方等于a ,那么这个数就叫做a 的平方根。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章、勾股定理 一、知识要点:
1、勾股定理
勾股定理:直角三角形两直角边的平方和等于斜边的平方。
也就是说:如果直角三角形的两直角边为a 、b ,斜边为c ,那么 a 2 + b 2= c 2。
公式的变形:a 2 = c 2- b 2, b 2= c 2-a 2 。
符号语言:
注意:前提一定是直角三角形.
a ,
b 也可能是斜边,分清斜边直角边.
勾股定理的证明 :勾股定理的证明方法很多,常见的的方法是面积相等---根据同一种图形的面积不同的表示方法,列出等式,推导出勾股定理
勾股定理的证明方法很多,常见的是拼图的方法 常见方法如下: 方法一:4EFGH
S S S ∆+=正方形正方形ABCD ,221
4()2
ab b a c ⨯+-=,化简可证.
方法二:
四个直角三角形的面积与小正方形面积的和等于大正方形的面积.
四个直角三角形的面积与小正方形面积的和为221
422S ab c ab c =⨯+=+
大正方形面积为222()2S a b a ab b =+=++ 所以222a b c +=
方法三:1()()2S a b a b =+⋅+梯形,211
2S 222
ADE ABE S S ab c ∆∆=+=⋅+梯形,化简得证
勾股定理的适用范围 : 勾股定理揭示了直角三角形三条边之间所存在的数量关系,它只适用于直角三角形,对于锐角三角形和钝角三角形的三边就不具有这一特征。
2、勾股定理的逆定理
如果三角形ABC 的三边长分别是a ,b ,c ,且满足a 2 + b 2= c 2,那么三角形ABC 是直角三角形。
这个定理叫做勾股定理的逆定理.
该定理在应用时,同学们要注意处理好如下几个要点: ① 已知的条件:某三角形的三条边的长度.
②满足的条件:最大边的平方=最小边的平方+中间边的平方.
③得到的结论:这个三角形是直角三角形,并且最大边的对角是直角. ④如果不满足条件,就说明这个三角形不是直角三角形。
c
b a
H
G F E
D
C
B A b
a
c
b
a
c c
a
b
c
a
b a b
c
c b
a
E
D C
B
A
(分类讨论,数形结合)
最大边的平方<最小边的平方+中间边的平方是锐角三角形 最大边的平方>最小边的平方+中间边的平方是钝角三角形
说明:勾股定理的逆定理是判定一个三角形是否是直角三角形的一种重要方法,它通过“数转化为形”来确定三角形的可能形状,在运用这一定理时应注意:
(1)首先确定最大边,不妨设最长边长为:c ;
(2)分别求出c 2与a 2+b 2,判定c 2与a 2+b 2是否具有相等关系,若c 2=a 2+b 2
,则△ABC
是以∠C 为直角的直角三角形(若c 2>a 2+b 2
,则△ABC 是以∠C 为钝角的钝角三角形;若c 2<a 2+b 2
,则△ABC 为锐角三角形)。
(定理中a ,b ,c 及222a b c +=只是一种表现形式,不可认为是唯一的,如若三角形三边长a ,b ,c 满足222a c b +=,那么以a ,b ,c 为三边的三角形是直角三角形,但是b 为斜边)
3、勾股数
满足a 2 + b 2= c 2的三个正整数,称为勾股数。
注意:①勾股数必须是正整数,不能是分数或小数。
② 一组勾股数扩大相同的正整数倍后,仍是勾股数。
缩小后仍满足a 2 + b 2=
c 2
常见勾股数有:用常见(3,4,5 )(5,12,13 ) ( 6,8,10 ) ( 7,24,25 ) ( 8,15,17 )(9,12,15 )
含字母的代数式表示n 组勾股数:22
1,2,1n n n -+(2,n ≥n 为正整数);
2221,22,221n n n n n ++++(n 为正整数)2222,2,m n mn m n -+(,m n >m ,n 为正整数)
勾股定理与勾股定理逆定理的区别与联系
区别:勾股定理是直角三角形的性质定理,而其逆定理是判定定理;
联系:勾股定理与其逆定理的题设和结论正好相反,都与直角三角形有关。
1.勾股定理的证明实际采用的是图形面积与代数恒等式的关系相互转化证明的。
2.勾股定理反映的是直角三角形的三边的数量关系,可以用于解决求解直角三角形边边关系的题目。
3.勾股定理在应用时一定要注意弄清谁是斜边谁直角边,这是这个知识在应用过程中易犯的主要错误。
4. 勾股定理的逆定理:如果三角形的三条边长a ,b ,c 有下列关系:a 2+b 2=c 2
,•那么这个三角形是直角三角形;该逆定理给出判定一个三角形是否是直角三角形的判定方法.
5.•应用勾股定理的逆定理判定一个三角形是不是直角三角形的过程主要是进行代数运算,通过学习加深对“数形结合”的理解.
我们把题设、结论正好相反的两个命题叫做互逆命题。
如果把其中一个叫做原命题,那么另一个叫做它的逆命题。
(例:勾股定理与勾股定理逆定理)
4.勾股定理的应用
解决求直角三角形中的边长或直角三角形中线段之间的关系的证明问题
① 已知直角三角形的任意两边长,求第三边。
② ②已知一边和关系,设未知数通过勾股定理得方程求解。
典型问题:最短距离问题:主要运用的依据是两点之间线段最短。
注:解决实际问题
思想:把实际问题转化为纯数学问题
方法:(1)抓主要信息。
1.抓已知条件,2.抓数量关系3.抓所求问题同时(2)画图,标注图,分析图.把题目中的已知数量,关系,所求都标注在图形中,分析他们之间关系。
当不能直接求解时,往往先设出未知数,用未知数表示出其他量,也要标注在图形中。
通过分析图形,找关系,想方法,找出解题思路。
(3)从已知出发,一步一步用符号语言书写推理过程。
推理就是,由已知,先能求出什么,再求出的基础上再求什么,----最后求出结果。
技巧:锁定基本图形。
能力:阅读能力,读题要慢读细读,边读边思考,不明白时,再读。
理解能力,把题目信息,动脑想,弄明白,理解怎么用。
胆大心细,多动手,多分析,从多个角度思考分析。
类型:1.勾股定理求线段长度
2.利用列方程求线段的长(方程思想)
3.折叠问题
4.网格问题
5.最短类问题
6.判断类问题
7.云梯问题
8.地摊问题
9小鸟问题
10航海问题
11路径问题。
