微分方程解析近似解的符号计算研究
使用Matlab进行微分方程求解的方法

使用Matlab进行微分方程求解的方法引言微分方程是数学中非常重要的一部分,广泛应用于物理、经济、工程等领域。
对于大部分微分方程的解析解往往难以求得,而数值解法则成为了一种常用的解决手段。
Matlab作为一种强大的科学计算软件,也提供了丰富的工具和函数用于求解微分方程,本文将介绍一些常见的使用Matlab进行微分方程求解的方法。
一、数值求解方法1. 欧拉方法欧拉方法是最简单的一种数值求解微分方程的方法,它将微分方程的微分项用差分的方式进行近似。
具体的公式为:y(n+1) = y(n) + hf(x(n), y(n))其中,y(n)表示近似解在第n个点的值,h为步长,f(x, y)为微分方程的右端项。
在Matlab中使用欧拉方法进行求解可以使用ode113函数,通过设定不同的步长,可以得到不同精度的数值解。
2. 中点法中点法是较为精确的一种数值求解微分方程的方法,它的计算公式为:k1 = hf(x(n), y(n))k2 = hf(x(n) + h/2, y(n) + k1/2)y(n+1) = y(n) + k2中点法通过计算两个斜率的平均值来得到下一个点的值,相较于欧拉方法,中点法能提供更精确的数值解。
3. 4阶龙格库塔法龙格库塔法是一类高阶数值求解微分方程的方法,其中4阶龙格库塔法是最常用的一种。
它的计算公式为:k1 = hf(x(n), y(n))k2 = hf(x(n) + h/2, y(n) + k1/2)k3 = hf(x(n) + h/2, y(n) + k2/2)k4 = hf(x(n) + h, y(n) + k3)y(n+1) = y(n) + (k1 + 2k2 + 2k3 + k4)/64阶龙格库塔法通过计算多个斜率的加权平均值来得到下一个点的值,相较于欧拉方法和中点法,它的精度更高。
二、Matlab函数和工具除了可以使用以上的数值方法进行微分方程求解之外,Matlab还提供了一些相关的函数和工具,方便用户进行微分方程的建模和求解。
微分方程解析近似解的符号计算研究

微分方程解析近似解的符号计算研究引言:微分方程作为数学的一个分支,在实际科学与工程中具有广泛的应用。
然而,很多微分方程并没有明确的解析解,而是需要通过近似方法来得到解。
在研究微分方程的解析近似解时,符号计算成为一种非常有效的工具。
本文将对微分方程解析近似解的符号计算研究进行探讨。
一、背景介绍:符号计算是一种利用计算机代数系统进行数学符号计算的方法。
相比于传统的数值计算方法,符号计算具有更高的精度和更广泛的适用范围。
因此,在微分方程的解析近似解研究中,符号计算成为一种重要的工具。
二、符号计算的基本原理:符号计算基于数学符号的表达和运算,通过代数运算、微分运算、积分运算等方法,能够对复杂的数学表达式进行分析和计算。
符号计算使用一套规则和算法,可以对微分方程的解进行求解和近似计算。
三、符号计算在微分方程解析近似解中的应用:1.级数近似法:符号计算可以通过级数展开的方法,将微分方程转化为一系列级数的和,然后通过截断级数得到近似解。
2.泰勒展开法:符号计算可以使用泰勒展开的方法,将微分方程转化为多项式的形式,然后通过多项式的近似计算得到近似解。
3.变分法:符号计算可以通过变分法,将微分方程转化为一个变分问题,然后通过求解极值得到近似解。
4.对称性方法:符号计算可以利用微分方程的对称性,简化微分方程的求解过程,得到近似解。
5.简化方法:符号计算可以通过符号运算的方法,将微分方程进行化简,得到近似解。
四、符号计算研究的发展和挑战:符号计算在微分方程解析近似解的研究中取得了一系列重要的成果,如级数近似法、变分法和对称性方法等。
然而,符号计算研究中仍然存在一些挑战,如计算复杂度、收敛性和算法设计等问题,需要进一步的探索和研究。
五、结论:微分方程解析近似解的符号计算研究是数学和计算机科学交叉领域的一个重要研究方向。
通过符号计算的方法,可以对微分方程的解进行精确的分析和计算。
未来,符号计算研究仍然有许多挑战和机遇,需要与数学和计算机科学领域的其他研究者进行深入合作,共同推动研究的进展。
微分的意义和作用

微分的意义和作用微分是微积分中的一个重要概念,它在数学和物理学中有着广泛的应用。
微分的意义和作用是研究函数的局部变化情况,通过微分可以求得函数在某一点的斜率,从而揭示函数的变化规律和性质。
微分的意义在于能够描述函数在某一点的瞬时变化率。
在数学中,函数的微分可以看作是函数在某一点附近的线性逼近。
通过对函数进行微分,可以得到函数在该点的切线斜率,这个斜率反映了函数在该点附近的变化趋势。
通过研究函数的微分,可以揭示函数的增减性、极值点、拐点等重要信息。
微分的作用十分广泛。
首先,在几何学中,微分广泛应用于曲线的研究。
通过对曲线的微分,可以得到曲线在某一点的切线方程,从而研究曲线的几何性质。
此外,在物理学中,微分也被广泛应用于描述物理量的变化。
例如,速度和加速度可以通过对位移函数进行微分得到。
微分还可以用于解决最优化问题,通过求解函数的极值点,可以得到函数的最大值和最小值。
微分的概念可以追溯到17世纪的牛顿和莱布尼茨。
牛顿和莱布尼茨分别独立发展了微积分学,他们的贡献被称为牛顿-莱布尼茨公式。
微分的计算通常使用导数的定义或者基本的微分法则。
导数的定义是通过极限来定义的,它表示函数在某一点的瞬时变化率。
基本的微分法则包括常数法则、幂法则、指数法则、对数法则等,这些法则可以简化微分的计算。
微分的计算方法有多种,常见的方法有数值微分、符号微分和微分方程。
数值微分是通过数值逼近来计算微分,它适用于函数没有解析表达式的情况。
符号微分是通过对函数的表达式进行代数运算来求得微分,它适用于函数具有解析表达式的情况。
微分方程是描述函数导数与自变量之间关系的方程,通过求解微分方程可以得到函数的解析表达式。
微分作为微积分的重要概念,在数学和物理学中有着广泛的应用。
它可以描述函数的局部变化情况,揭示函数的性质和规律。
微分的计算方法有多种,可以根据具体的问题选择合适的方法。
微分的研究对于深入理解数学和物理学的原理和应用具有重要意义。
华东师范大学信息科学技术学院计算机科学技术系历年培养研究生学位论文情况

王成道
博士
系统科学
系统分析与集成
模糊系统,遗传算法,规则抽取,参数估计,多目标优化,可解释性与精度,多Agent系统,近似推理,交互影响,模糊积分
论文题目
论文作者
论文时间
指导教师
论文层次
(硕士、博士)
学科
专业
论文关键词
基于Nutch的学校信息垂直搜索引擎的研究与实现
王可
2009
朱敏
专业硕士
专业学位
物流系统模型和算法研究
戴树贵
2007
潘荫荣
博士
系统科学
系统分析与集成
物流;选址问题;车辆路径安排问题;库存系统仿真;遗传算法;蚁群算法;离散事件系统
对等网络中的信任感知和可信协同商务洽谈关键技术研究
江红
2007
顾君忠
博士
系统科学
系统分析与集成
对等网络,信任感知,可信,协同商务洽谈,信任协商策略,信誉,信任模型,信任反馈,有色Petri网系统,BN_CPN
微分方程解析近似解的符号计算研究
杨沛
2010
李志斌
博士
系统科学
系统分析与集成
微分方程,微分差分方程,解析近似解,符号计算,孤立子
动态UML子图的形式语义研究
赵也非
2010
杨宗源
博士
计算机科学与技术
计算机应用技术
UML,进程代数,概率模型检测,XMI,一致性检查,量化分析,实时并发系统
无线传感器网络若干关键安全技术的研究
面向复杂自适应系统的本体构造方法及其若干关键技术研究
杨德仁
2008
顾君忠
博士
系统科学
系统分析与集成
符号计算国内外研究概况

国内外研究概况一、国外研究概况:1.1885年,Backlund在研究负常曲率曲面时发现了SG方程的两个不同解之间的Backlund变换.它在后来的孤子理论中发挥了重要的作用.2.19世纪50年代,Hopf与Cole提出了将非线性Burgers方程线性化的Hopf-Cole变换. Hopf-Cole变换将非线性Burgers方程与线性热传导方程联系起来,可看作两个方程之间的Backlund变换.此后,人们发现了很多Backlund变换可以将非线性微分方程线性化,如Kumei 和Bluman利用群论的方法使得非线性微分方程线性化.3.1967年,Gardner,Greener,Kruskal和Miura(GGKM)提出逆散射方法,求解了KdV 方程的初值问题.该方法的提出是应用数学的一次重大突破.它不仅为应用数学开拓了一个新领域,而且也为孤子物理学的研究提供了数学工具.4.1968年,Lax将GGKM的思想进行分析,给出了方程的Lax对,提出了用逆散射方法求解非线性模型更一般的框架.1973年,Ablowitz,Kaup,Newell与Segur提出了可求解一大类有物理意义的非线性模型初值问题的AKNS程序。
5.1971年,Hirota提出了双线性方法.通过适当的因变量变换,将非线性模型转化为双线性方程,然后借助形式参数展开法求解非线性模型的精确解.6.1979年,Satsuma给出了Kdy方程Wronski行列式形式的解.此后,Freeman和Nimmo 基于双线性形式,提出了求解非线性模型Wronski行列式解的Wronskian技巧.7.1983年,Weiss、Tabor和Carnevale将常微分方程的Painleve可积的判定方法进行了推广,提出了偏微分方程Painleve可积的判定法.8.1991年,Hirota和Ohta发展了一种寻找原非线性发展方程新的可积系统的程序称为pfaffian程序.9.1995年,Wang等人提出了齐次平衡法,求解了大批的非线性模型.1996年,Gao和Tian改进了此方法来研究高维方程的求解问题.10.2000年,Lou等人提出了多线性分离变量法研究高维非线性模型的解.11.2006年,Hu和Wang提出了另外一种系统化的构造新可积模型的方法一源推广程序.此方法主要是基于无源双线性孤子方程带有任意常数的Pfaffian或行列式形式的N孤子解.二、国内研究概述:在我国,孤子理论的研究开始于20世纪70年代.当时,李政道、杨振宁、陈省身等教授向国内同行介绍孤子理论的研究进展,并指出它的重要性,随后在国内相继开展了这方面的研究工作.目前国内许多科研院所与高校都有关于孤子理论研究的团队.中国科学院数学与物理学部院士郭柏灵在非线性发展方程方面,对力学及物理学中的一些重要方程进行了系统深入的研究,其中包括Landau-Lifshitz方程、Benjamin-Ono方程等非线性发展方程的大初值的整体可解性、解的唯一性、正则性、渐近行为以及爆破现象等,给出了系统而深刻的数学理论。
微分方程的符号解与数值解
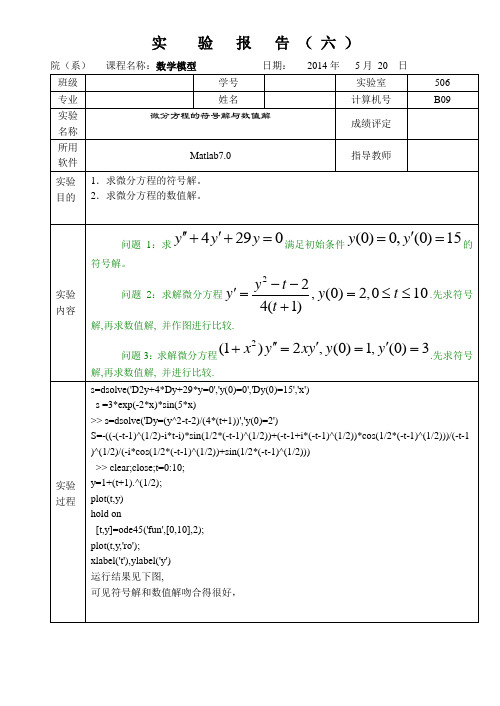
实验报告(六)院(系)课程名称:数学模型日期:2014年5月20 日班级学号实验室506 专业姓名计算机号B09实验名称微分方程的符号解与数值解成绩评定所用软件Matlab7.0 指导教师实验目的1.求微分方程的符号解。
2.求微分方程的数值解。
实验内容问题1:求4290y y y'''++=满足初始条件(0)0,(0)15y y'==的符号解。
问题2:求解微分方程22,(0)2,0104(1)y ty y tt--'==≤≤+.先求符号解,再求数值解, 并作图进行比较.问题3:求解微分方程2(1)2,(0)1,(0)3x y xy y y''''+===.先求符号解,再求数值解, 并进行比较.实验过程s=dsolve('D2y+4*Dy+29*y=0','y(0)=0','Dy(0)=15','x')s =3*exp(-2*x)*sin(5*x)>> s=dsolve('Dy=(y^2-t-2)/(4*(t+1))','y(0)=2')S=-((-(-t-1)^(1/2)-i*t-i)*sin(1/2*(-t-1)^(1/2))+(-t-1+i*(-t-1)^(1/2))*cos(1/2*(-t-1)^(1/2)))/(-t-1 )^(1/2)/(-i*cos(1/2*(-t-1)^(1/2))+sin(1/2*(-t-1)^(1/2)))>> clear;close;t=0:10;y=1+(t+1).^(1/2);plot(t,y)hold on[t,y]=ode45('fun',[0,10],2);plot(t,y,'ro');xlabel('t'),ylabel('y')运行结果见下图,可见符号解和数值解吻合得很好,>> s=dsolve('(1+x^2)*D2y=2*x*Dy','y(0)=1','Dy(0)=3','x') s =1+x^3+3*x>> clearx=0:0.5:10;y=1+x.^3+3*x;plot(x,y)hold onxs=[0,10];y0=[3,1];[x,y]=ode45('ill',xs,y0);plot(x,y(:,2),'ro')运行结果见下图,可见符号解和数值解吻合得很好心得体会这次实验很难,我是在同学的帮助下完成的。
非线性微分方程对称和无穷级数解的符号计算研究的开题报告

非线性微分方程对称和无穷级数解的符号计算研究的开题报告一、选题背景和意义在物理、化学、生物、工程等领域中,许多现象和系统都可以用非线性微分方程来描述。
尤其是对于涉及到相变、非线性波动、混沌现象等复杂系统,非线性微分方程的重要性更加凸显。
然而,常常由于方程的复杂性和难以求解的问题,研究人员在实际问题中往往无法直接解决这些方程。
在这种情况下,对于非线性微分方程的对称性进行研究显得尤为重要。
利用对称性可以有效地简化方程求解的难度,获得更多有用的信息和结论,提高求解效率。
此外,采用无穷级数解来描述非线性微分方程的解也是一种十分常见和有效的方法。
因此,对于非线性微分方程的对称和无穷级数解进行符号计算的研究具有重要的理论和应用价值。
二、主要研究内容本文的研究旨在针对一些常见的非线性微分方程,如Korteweg-de Vries方程、Burgers方程、Sine-Gordon方程等,进行对称和无穷级数解的符号计算研究。
具体研究内容如下:1. 对称分析方法研究:介绍经典的对称分析方法,如Lie方法和Kovalevskaya 方法,并探讨如何应用这些方法找到非线性微分方程的对称性。
2. 非线性微分方程的对称性研究:应用上述对称分析方法,找到几个常见的非线性微分方程的对称性,并根据对称性获得其精确或近似解。
3. 无穷级数解法研究:介绍一些常用的无穷级数求解方法,如Painleve展开和Frobenius方法,并利用这些方法求解一些常见的非线性微分方程。
4. 数值方法和计算求解研究:介绍一些计算求解方法,如有限元法和谱方法,并利用Mathematica等数学软件对上述研究结果进行计算验证。
三、预期结果预期研究结果如下:1. 建立非线性微分方程的对称性分析方法,并应用该方法找到几个常见非线性微分方程的对称性。
2. 发现非线性微分方程中的无穷级数解,并探究该类无穷级数解在实际应用中的作用和意义。
3. 发现非线性微分方程的符号计算方法,并能够以计算的方式验证得到的结果。
常微分方程的数值解与解析解

一、 常微分方程的解析解常微分方程的解析解也就是常微分方程的精确解,也称为常微分方程的符号解;一般可理解为求微分方程的通解或者特解的解析式或表达式;但只有少数的微分方程存在解析解。
在MA TLAB 中,由函数dsolve()求解常微分方程(组)的解析解,其具体格式如下: X=dsolve(‘方程1’,‘方程2’,…‘方程n ’,‘初始条件’,‘自变量’)函数dsolve 用来解符号常微分方程、方程组,如果没有初始条件,则求出通解,如果有初始条件,则求出特解。
例1:求解常微分方程1dy dx x y =+的MA TLAB 程序为:dsolve('Dy=1/(x+y)','x'),注意,系统缺省的自变量为t ,因此这里要把自变量写明。
结果为:-lambertw(-C1*exp(-x-1))-x-1其中:Y=lambertw(X)表示函数关系Y*exp(Y)=X 。
例2:求解常微分方程2'''0yy y -=的MA TLAB 程序为:Y2=dsolve('y*D2y-Dy^2=0’,’x’) 结果为:Y2 =[ exp((x+C2)/C1)][ C2]我们看到有两个解,其中一个是常数。
例3:求常微分方程组253t tdx x y e dt dy x y e dt ⎧++=⎪⎪⎨⎪--=⎪⎩通解的MA TLAB 程序为:[X,Y]=dsolve('Dx+5*x+y=exp(t),Dy-x-3*y=exp(2*t)','t')例4:求常微分方程组020210cos ,224,0t t t dx dy x t x dt dt dx dy y e y dt dt =-=⎧+-==⎪⎪⎨⎪++==⎪⎩通解的MA TLAB 程序为:[X,Y]=dsolve('Dx+2*x-Dy=10*cos(t),Dx+Dy+2*y=4*exp(-2*t)','x(0)=2','y(0)=0')二、 常微分方程的数值解在生产和科研中所处理的微分方程往往很复杂且大多得不出一般解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
微分方程解析近似解的符号计算研究
【摘要】:本文基于数学机械化思想,借助于符号计算软件,以非线性方程为对象,系统地研究了适用于强非线性问题的解析近似方法:Adomian分解方法(ADM)和同伦分析方法(HAM)的应用和机械化实现。
第一章是与本文相关的研究背景。
简要综述了计算机代数和孤立子理论的发展进程,针对性地介绍了近年来解析近似方法的研究成果和现状。
第二章改进了Adomian分解方法,能够获得修正Korteweg-deVries(mKdV)方程和Kadomtsev-Petviashvili(KP)方程的双孤子解。
通过引入自变量变换和行波变换,将Degasperis-Procesi(DP)方程短波模型化为常微分方程,应用Adomian分解方法求解之,获得其闭合形式的解析解,再经过反变换,能够获得其环状孤子解。
以上结果表明了Adomian分解方法在求解方程特殊孤子解方面的有效性。
对Adomian分解方法进行了推广,解决了方程中离散变量不同于连续方程中的变量问题,并与Pade近似结合,能够获得几个经典的非线性微分差分方程组的孤子解,显著提高了方程解析近似解的精度。
同时,我们还讨论了Pade有理近似中出现的伪极点问题,给出了合适选择Pade 近似阶数的指导原则。
获得的解析近似解与精确解符合得很好,表明了Adomian分解方法对复杂强非线性问题的有效性。
第三章通过引入自变量变换和行波变换,将偏微分方程化为常微分方程,通过同伦分析方法求解之,再经过反变换,能够获得DP方程短波模型的环状孤子解和Camassa-Holm(CH)方程短波模型的尖状孤子解,结果表明了同伦
分析方法在求解方程特殊孤子解方面的有效性。
对同伦分析方法进行了推广,解决了方程中离散变量不同于连续方程中的变量问题,改进了同伦分析方法选择初始猜测解的方法,能够获得离散修正KdV方程的亮孤子解,获得的解析近似解与精确解符合得很好,表明了同伦分析方法对复杂强非线性问题的有效性。
第四章在计算机代数系统Maple 上实现了Biazar提出的求解Adomian多项式的算法,编制了构造微分方程(组)和积分方程(组)解析近似解的自动推导软件包,这个算法避免了Adomian多项式的计算膨胀问题,降低了计算难度并显著提高了计算速度,通过大量实例说明了该软件包的有效性和实用性。
【关键词】:微分方程微分差分方程解析近似解符号计算孤立子
【学位授予单位】:华东师范大学
【学位级别】:博士
【学位授予年份】:2010
【分类号】:O175
【目录】:摘要6-7Abstract7-11第一章绪论11-181.1数学机械化与计算机代数12-131.2孤立子理论13-141.3求解非线性方程的解析近似方法14-161.3.1Adomian分解方法14-151.3.2同伦分析方法15-161.4本文的选题和主要工作16-18第二章Adomian分解方法在非线性系统中的应用18-592.1Adomian分解方法求解非线性微分方程18-322.1.1
基本原理简介18-202.1.2修正KdV方程及其双孤子解20-242.1.3KP 方程及其双孤子解24-292.1.4Degasperis-Procesi方程的短波模型及其环状孤子解29-322.2Adomian分解方法求解非线性微分差分方程组32-562.2.1基本原理简介32-342.2.2Pade近似基本原理简介34-362.2.3Belov-Chaltikian格方程及其孤子解36-412.2.4非线性自偶网格方程及其扭状孤子解41-482.2.5Blaszak-Marciniak3-场格方程及其孤子解48-512.2.6Blaszak-Marciniak4-场格方程及其孤子解51-562.3本章小结56-59第三章同伦分析方法在非线性系统中的应用59-813.1基本原理简介59-613.2同伦分析方法求解非线性微分方程61-743.2.1Camassa-Holm方程的短波模型及其尖状孤子解61-673.2.2Degasperis-Procesi方程的短波模型及其环状孤子解67-743.3同伦分析方法求解非线性微分差分方程74-803.3.1离散修正KdV方程及其孤子解74-803.4本章小结80-81第四章Adomian分解方法软件包BZAdm81-944.1基本原理简介81-834.2算法描述834.3BZ 算法在Maple系统上的实现:BZAdm软件包83-854.3.1求解微分方程(组)的模块及其功能844.3.2求解积分方程(组)的模块及其功能84-854.4BZAdm软件包的应用85-914.4.1微分方程(组)的求解85-894.4.2积分方程(组)的求解89-914.5效率评估91-924.6本章小结92-94第五章结束语94-95参考文献95-104致谢104-105在读期间完成的论文目录105 本论文购买请联系页眉网站。
