数学分析课后习题答案--高教第二版(陈纪修)--11章
数学分析上册chp11习题解答
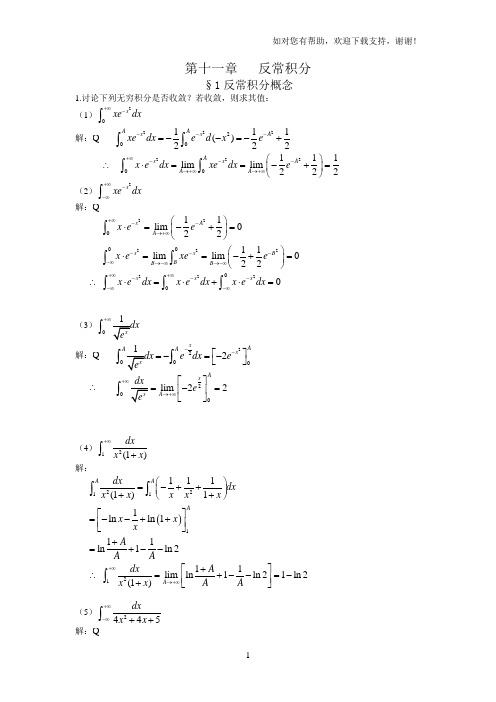
第十一章 反常积分§1反常积分概念1.讨论下列无穷积分是否收敛?若收敛,则求其值: (1)2x xe dx +∞-⎰解:222200111()222AA x x A xe dx e d x e ---=--=-+⎰⎰ ∴ 22200111lim lim 222A x x A A A x e dx xe dx e+∞---→+∞→+∞⎛⎫⋅==-+= ⎪⎝⎭⎰⎰ (2)2x xe dx +∞--∞⎰解:2222200011lim 02211lim lim 022x A A x x B B B B x e e x e xe e +∞--→+∞----∞→-∞→-∞⎛⎫⋅=-+= ⎪⎝⎭⎛⎫⋅==-+= ⎪⎝⎭⎰⎰⎰ ∴ 2220x x x x e dx x e dx x e dx +∞+∞----∞-∞⋅=⋅+⋅=⎰⎰⎰(3)0+∞⎰解:22002xAAA x e dx e --⎡⎤=-=-⎣⎦⎰⎰∴2l i m 22AxA e →+∞+∞⎡⎤-=⎢⎥⎣⎦=⎰(4)21(1)dxx x +∞+⎰解:()22111111(1)11ln ln 111ln 1ln 2AA Adx dx x x x x x x x x A A A ⎛⎫=-++ ⎪++⎝⎭⎡⎤=--++⎢⎥⎣⎦+=+--⎰⎰ ∴ 21lim 11ln 1ln 21ln 2(1)A dx A x x A A →+∞+∞+⎡⎤=⎢⎥=+--⎣-⎦+⎰ (5)2445dxx x +∞-∞++⎰解:2202001445(21)lim lim 1lim arcta 2(2n 1)82AA A A AA dx x x x x π→+∞→+∞→+∞==+++++=⎰⎰2220001445(21)2(21)l i m l i m 1l i m a r c t a n 41l i m a r c t a 1)48n(2B B B B B B Bdx dx x x x x B π→-∞→-∞→-∞→-∞=+++++=+=⎡⎤-=⎢⎥⎣⎦⎰⎰ ∴ 002224454454l i m l m 4i 5884A B A B dx dx dxx x x x x x πππ→++∞-→∞∞-∞=+++++=+=++⎰⎰⎰(6)0sin x e xdx +∞-⎰解:()0sin sin 1sin co limim s l 22AxA x x A A e xdx e xdxe x x →+∞→++---∞∞==--=⎰⎰(7)sin x e xdx +∞--∞⎰解:limsin sin AA x x e xdx e xdx →++∞∞=⎰⎰0sin limcos 2AA x x →+∞-= ()1sin lim cos 12A A A →+∞=-+发散 而limsin sin B xx Be xdx e xdx →∞--∞⋅=⎰⎰0sin limcos 2BB x x →-∞-=发散∴sin x e xdx +∞--∞⎰发散(8)+∞⎰解:0limli m A A A A →+∞→+∞=⎰发散故+∞⎰2. 讨论下列瑕积分是否收敛?若收敛,则求其值:(1)()bp a dxx a -⎰解:()21()f x x a =-在(,]a b 上连续, 从而在(,]a b 上可积,x a =为其瑕点由瑕积分定义,知111lim()()lim ()()1lim ()11lim ()()1bb p pau u a bp uu a p bu u a p pu a dx dx x a x a x a d x a x a pb a u a p →-→-→--→=--=--=--⎡⎤=---⎣⎦-⎰⎰⎰显然当1p <时,上式收敛于1()1pb a p---,其瑕积分也收敛,其值为1()1pb a p---若1p ≥,则上式发散,其瑕积分也发散(2)1201dx x -⎰解:122001010010011lim 11111lim 211111lim 21111lim ln 1ln 12211lim ln 1ln 122u u u u u u u u u u u dxdx x x dx x x dx dx x x x x u u →→→→→=--⎛⎫=+ ⎪-+⎝⎭⎡⎤=+⎢⎥-+⎣⎦⎧⎫=-⎡-⎤+⎡+⎤⎨⎬⎣⎦⎣⎦⎩⎭⎡⎤=--++⎢⎥⎣⎦⎰⎰⎰⎰⎰ 上式的极限不存在,故瑕积分1201dxx -⎰发散(3)2⎰解:()()()()()()212001112221111222011112211lim 1lim 1lim 21lim 21lim 212lim 2214uuu u u uu u u u x dx x dxx x u u --→→--→→--→→=+=-+-⎡⎤=--+-⎢⎥⎣⎦⎡⎤⎡⎤=--++--⎢⎥⎢⎥⎣⎦⎣⎦=⎰⎰⎰⎰⎰故瑕积分收敛,其值为4 (4)1⎰解:()()()()())11122201222112201111121lim 1121lim 12lim11u u uu u x d x x d x x --→-→→=---=---=--=-=⎰⎰⎰ 故瑕积分收敛,其值为1 (5)1ln xdx ⎰解:()111100ln lim ln lim ln lim ln 11u u u u u u xdx xdxx x dx u u u +++→→→=⎡⎤=-⎢⎥⎣⎦=--+=-⎰⎰⎰故瑕积分收敛,其值为-1(6)⎰解:令21xt x=-,则()20200020202lim 1lim 21lim arctan 12tdt t t t t t εεεπ+++→→→=+⎡⎢=⎢+⎣⎦⎛=- +⎝=⎰故瑕积分收敛,其值为2π(7)1⎰解:()()()()1111121211210200lim lim lim arcsin 21lim arcsin 21lim arcsin 21lim arcsin 21122x x εεεεεεεεεεεεπππ++++++-→→-→→→→==+=-+-=--+---⎡⎤⎡⎤⎣⎦⎣⎦=+=⎰⎰⎰⎰故瑕积分收敛,其值为π (8)10ln (ln )p d x x ⎰解:()()1112100211210211112100211100ln (ln )ln (ln )ln (ln )lim (ln 2)ln lim (ln )ln 11lim (ln )lim (ln )11111lim ln ln lim ln 1121p p p p p p p p p d x x d x x d x x d x x d xx x ppp p εεεεεεεεεεεε++++++-----→→---→→---→→=+=+=+--⎡⎤⎛⎫=-+-⎢⎥ ⎪--⎝⎭⎢⎥⎣⎦⎰⎰⎰⎰⎰11ln 2pp -⎡⎤⎛⎫-⎢⎥ ⎪⎝⎭⎢⎥⎣⎦上面极限式发散,故瑕积分发散3. 举例说明:瑕积分⎰badx x f )(收敛时,⎰badx x f )(2不一定收敛。
复旦大学数学系陈纪修《数学分析》 第二版 习题答案ex

− x ≤ sup S ,即 x ≥ − sup S ;同时对任意 ε > 0,存在 y ∈ S ,使得 y > sup S − ε ,
于是 − y ∈ T ,且 − y < − sup S + ε 。所以 − sup S 为集合 T 的下确界,即
inf T = − sup S 。
5. 证明有界数集的上、下确界唯一。 证 设 sup S 既等于 A ,又等于 B ,且 A < B 。取 ε = B − A > 0 ,因为 B 为
m
可能:
(i)⎜⎛ n ⎟⎞2 < 3 ,由(1)可知存在充分小的有理数 r > 0 ,使得 ⎜⎛ n + r ⎟⎞2 < 3 ,
⎝m⎠
⎝m ⎠
这说明 n + r ∈ S ,与 sup S = n 矛盾;
m
m
(ii) ⎜⎛ n ⎟⎞2 > 3 ,取有理数 r > 0 充分小,使得 4r − r 2 < ⎜⎛ n ⎟⎞2 − 3 ,于是
m +1
n < n < n + 1 ,所以 maxC 与 minC 都不存在。
m+1 m m+1
3. A, B 是两个有界集,证明:
(1) A ∪ B 是有界集;
(2) S = { x + y | x ∈ A, y ∈ B} 也是有界集。 证 (1)设 ∀x ∈ A ,有 x ≤ M1 , ∀x ∈ B ,有 x ≤ M 2 ,则 ∀x ∈ A ∪ B ,有
xn+k
= a。
证
设 lim n→∞
xn
=
a
,则 ∀ε
>
陈纪修数学分析答案

陈纪修数学分析答案【篇一:陈纪修教授《数学分析》九讲学习笔记与心得】class=txt>云南分中心 ? 昆明学院 ? 周兴伟此次听陈教授的课,收益颇多。
陈教授的这些讲座,不仅是在教我们如何处理《数学分析》中一些教学重点和教学难点,更是几堂非常出色的示范课。
我们不妨来温习一下。
第一讲、微积分思想产生与发展的历史法国著名的数学家h.庞加莱说过:“如果我们想要预见数学的将来,适当的途径是研究这门科学的历史和现状。
” 那么,如果你要学好并用好《数学分析》,那么,掌故微积分思想产生与发展的历史是非常必要的。
陈教授就是以这一专题开讲的。
在学校中,我不仅讲授《数学分析》,也讲授《数学史》,所以我非常赞同陈教授在教学中渗透数学史的想法,这应该也是提高学生数学素养的有效途径。
在这一讲中,陈教授脉络清晰,分析精当,这是我自叹不如的。
讲《数学史》也有些年头,但仅满足于史料的堆砌,没有对一些精彩例子加以剖析。
如陈教授对祖暅是如何用“祖暅原理”求出球的体积的分析,这不仅对提高学生的学习兴趣是有益的(以疑激趣、以奇激趣),而且有利于提高学生的民族自豪感(陈教授也提到了这一点)。
第二讲、实数系的基本定理在这一讲中,陈教授从《实变函数》中对集合基数的讨论展开,对实数系的连续性作了有趣的讨论。
首先是从绅士开party的礼帽问题,带我们走进了“无穷的世界”。
我在开《数学赏析》时有一个专题就是“无穷的世界”,我给学生讲礼帽问题、也讲希尔伯特无穷旅馆问题,但遗憾的是,当我剖析“若无穷旅馆住满了人,再来两个时,可将住1号房间的移往3号房间,住2号房间的移往4号房间,从而空出两个房间”时,学生对我“能移”表示怀疑。
这一点我往往只能遗憾的说“跳不出有限的圈子,用有限的眼光来看无限,只能是‘只在此山中,云深不知处’”。
当然,我还是会进一步考虑如何来讲好这一讲。
若陈教授或其他老师有好的建议,能指点一下,则不胜感激。
对于集合[0,1]与(0,1)的对等关系,包括q与R的对等关系,或者说他们之间双射的构造。
陈纪修《数学分析》(第2版)(下册)名校考研真题-Euclid空间上的极限和连续(圣才出品)

第11章Euclid空间上的极限和连续一、判断题1.若f(x,y)在D内对x和y都是连续的,则f(x,y)对(x,y)∈D为二元连续函数.[重庆大学研]【答案】错【解析】举反例:,很明显但是不存在,如果选取路径y=kx趋于0,有不唯一.二、填空题(1)函数的定义域是______,它是______区域;(2)函数的定义域是______;(3)函数的定义域是______;(4)二元函数的定义域是______;(5)函数的定义域是______.[西安交通大学研]【答案】(1)(2)(3)椭圆与抛物线所围的区域;(4)(5)三、解答题1.设f(x)为定义在上的连续函数,α是任意实数,有证明:E是开集,F是闭集.[江苏大学2006研]证明:对任意的,有.因为f(x)在上连续,所以由连续函数的局部保号性知,存在的一个邻域使得当时有,从而,故E是开集.设为F 的任意一个聚点,则存在F中的点列使得.由于f(x)在上连续,所以,又,从而,即,故F是闭集.2.求.[南京大学研、厦门大学研、山东科技大学研]解:方法一由于令,有所以方法二由于,,所以,故有3.设f(x,y)在[a,b]×[c,d]上连续,证明:在[c,d]上连续.[南京理工大学研、华东师范大学研]证明:反证法.假设g(y)在某点处不连续,则存在及点列,使得因为f(x,y)在[a,b]×[c,d]上连续,故在[a,b]×[c,d]上一致连续.于是对,存在δ>0,当时恒有.特别当时,即.固定y,让x在[a,b]上变化,取最大值,可得即时,.因为,所以对δ>0,存在N >0,当n>N时有,从而有,这与一开始得到的不等式矛盾,结论得证.4.设,为有界闭集,试证:开集W、V,使得A证明:A、B为有界闭集.[四川大学研]令显然W、V为开集.5.设试讨论下面三种极限:[南京工学院研]解:由于在y=0和x=0的函数极限不存在,故在(0,0)点的两个累次极限都不存在.6.设f(x,y是区域D:|x|≤1,|y|≤1上的有界k次齐次函数(k≥1),问极限是否存在?若存在,试求其值.[南京大学研]解:令x=rcosθ,y=rsinθ.由于f(x,y)是区域D上的有界k次齐次函数7.设二元函数f(x,y)在正方形区域[0,1]×[0,1]上连续.记J=[0,1].(1)试比较的大小并证明之;(2)给出并证明使等式成立的(你认为最好的)充分条件.[浙江大学研]解:(1),有上式对于任意的x都成立,则由y的任意性可知(2)若,使下面证明上面条件为充分条件显然8.设为n维欧氏空间,A是的非空子集,定义x到A的距离为证明:上的一致连续函数.[南京大学研] 证明:有对使故对时,即上的一致连续函数.9.[暨南大学2013研] 解:设,则。
数学分析原理答案

数学分析原理答案数学分析原理答案【篇一:数学分析教材和参考书】:《数学分析》(第二版),陈纪修,於崇华,金路编高等教育出版社, 上册:2004年6月,下册:2004年10月参考书:(1)《数学分析习题全解指南》,陈纪修,徐惠平,周渊,金路,邱维元高等教育出版社, 上册:2005年7月,下册:2005年11月(2)《高等数学引论》(第一卷),华罗庚著科学出版社(1964)(3)《微积分学教程》,菲赫金哥尔兹编,北京大学高等数学教研室译,人民教育出版社(1954)(4)《数学分析习题集》,吉米多维奇编,李荣译高等教育出版社(1958)(5)《数学分析原理》,卢丁著,赵慈庚,蒋铎译高等教育出版社(1979)(6)《数学分析》,陈传璋等编高等教育出版社(1978)(7)《数学分析》(上、下册),欧阳光中,朱学炎,秦曾复编,上海科学技术出版社(1983)(8)《数学分析》(第一、二、三卷),秦曾复,朱学炎编,高等教育出版社(1991)(9)《数学分析新讲》(第一、二、三册),张竹生编,北京大学出版社(1990)(10)《数学分析简明教程》(上、下册),邓东皋等编高等教育出版社(1999)(11)《数学分析》(第三版,上、下册),华东师范大学数学系,高等教育出版社(2002)(12)《数学分析教程》常庚哲,史济怀编,江苏教育出版社(1998)(13)《数学分析解题指南》林源渠,方企勤编,北京大学出版社(2003)(14)《数学分析中的典型问题与方法》裴礼文编,高等教育出版社(1993)复旦大学数学分析全套视频教程全程录像,asf播放格式,国家级精品课程,三学期视频全程教师简介:陈纪修-基本信息博士生导师教授姓名:陈纪修任教专业:理学-数学类在职情况:在性别:男所在院系:数学科学学院陈纪修-本人简介姓名:陈纪修性别:男学位:博士职称:教授(博士生导师)高校教龄22年,曾获2001年上海市教学成果一等奖、获2001年国家级教学成果二等奖、获2002年全国普通高等学校优秀教材一等奖、2002年获政府特殊津贴;获宝钢教育奖(优秀教师奖);被评为“九五”国家基础科学人才培养基金实施和基地建设先进工作者。
数学分析课后习题答案--高教第二版(陈纪修)--13章

F (x, y) = f (x) , (x, y) ∈ D 。
证明 F (x, y) 在 D 上可积。
证 将[a,b] 、[c, d ] 分别作划分:
a = x0 < x1 < x2 < < xn−1 < xn = b
和
m c = y0 < y1 < y2 < < ym−1 < ym = d , o 则 D 分成了 nm 个小矩形 ∆Dij (i = 1,2, , n, j = 1,2, , m) 。
2π 3
≤
∫∫∫
Ω
1
+
dxdxdz x2 + y2 +
z
2
≤
4π 3
。
m 4.计算下列重积分:
co (1) ∫∫(x3 + 3x2 y + y3 )dxdy ,其中 D 为闭矩形[0,1] × [0,1] ;
. D
aw (2) ∫∫ xy ex2+y2 dxdy ,其中 D 为闭矩形[a,b] × [c,d ];
课 证明
H ( x, y) = max{ f ( x, y), g( x, y)}
和
h( x, y) = min{ f ( x, y), g( x, y)}
也在 D 上可积。
证 首先我们有
H (x, y) = 1 ( f (x, y) + g(x, y) + f (x, y) − g(x, y) ), 2
D
khd (3)
∫∫∫ Ω
dxdydz (x + y + z)3
,其中
Ω
为长方体 [1,2]
×
[1,2]
数学分析课后习题答案--高教第二版(陈纪修)--9章
习
∞
数项级数
数项级数的收敛性
∞
题
9.1
1. 讨论下列级数的收敛性。收敛的话,试求出级数之和。
1 ; ⑴ ∑ n =1 n ( n + 2) ∞ 1 ; ⑶ ∑ n =1 n ( n + 1)( n + 2) ∞ 1
⑵ ⑷
∑ 3n + 1 ; ∑⎜ ⎝2
n =1 ∞
2n
⑸ ⑺ ⑼
∑
n =1 ∞ n =1 ∞
2n − 1 , 3n
;
co m
(3)当 x = 1 时显然级数收敛;当 x ≠ 1 时 ∑ x n (1 − x) = (1 − x) ∑ x n ,收敛
n =1
∞
∞
n =1
范围是 x ∈ (−1,1) ;所以当 x ∈ (− 1,1] 时级数收敛。 3. 求八进制无限循环小数 (36.0736073607 … )8 的值。 解 (36.0736073607 … )8
n→∞ n→∞
3. 证明: (1) lim ( x n + y n ) ≥ lim x n + lim y n ;
n→∞ n→∞ n→∞
(2) 若 lim x n 存在,则
n →∞
lim ( x n + y n )= lim x n + lim y n 。
n→∞
n→∞
n→∞
证 (1)记 lim x n = h1 , lim y n = h2 ,则对任意给定的 ε > 0 ,存在正整
h − ε < yn < H + ε 。
min{( x − ε )( H + ε ), ( x + ε )( H + ε )} < x n y n < max{( x − ε )(h − ε ), ( x + ε )(h − ε )},
数学分析第二版答案
数学分析第二版答案LtD数学分析第二版答案【篇一:?数学分析?第三版全册课后答案(1)】class=txt>------------------------------------------------- 密---------------------------------- 封----------------------------- 线---------------------------------------------------------第页(共)------------------------------------------------- 密---------------------------------- 封----------------------------- 线---------------------------------------------------------【篇二:复旦大学数学分析课后习题解陈纪修】> 4.〔1〕?x|?2?x?3?;〔2〕?(x,y)|x?0且y?0?;〔3〕?x|0?x?1且x?q?;〔4〕?x|x?k2,k?z?.?7.〔1〕不正确。
x?a?b?x?a或者x?b;〔2〕不正确。
x?a?b?x?a并且x?b.第2节2.〔1〕f:[a,b]?[0,1] x?y?x?ab?a.〔2〕f:(0,1)?(??,??) x?tan[x(?12)?]3.〔1〕y?log2a(x?3),定义域:,?33,,值域:(??,??);〔2〕y?arcsin3x,定义域:,0?,值域:???0,??;2??〔3〕y?tanx,定义域:k?k?z?2,k2?,值域:??0,;〔4〕y?x?1x?1,定义域:,?11,,值域:?0,11,. 5.〔1〕定义域:??2k?,(2k?1)??,值域:,0?;k?z〔2〕定义域:?2k??,2k,值域:?0,1?;k?z?22?1〔3〕定义域:??4,1?,值域:0,;?25??32 〔4〕定义域:,00,,值域:?,???2??. ??7.〔1〕f(x)?2x3?21x2?77x?97;〔2〕f(x)?2x?14x?1。
数学分析课后习题答案--高教第二版(陈纪修)--12章
5
aw .
⎛ x2 y2 + 2 2 b ⎝a
co m
解
在 ( x, y ) ≠ (0,0) 点, 函数值增长最快的方向为 grad f = ( y, x) ; 在 (0,0) 点, 由于梯度为零向量,不能直接从梯度得出函数值增长
最快的方向。设沿方向 v = (cos α , sin α ) 自变量的改变量为
⎛ x2 ∂z 2 x = sec 2 ⎜ ⎜ y ∂x y ⎝
2 ⎞ ∂z x2 2⎛ x ⎞ ⎜ ⎟。 ⎟, = − sec ⎜ y ⎟ ⎟ ∂y y2 ⎝ ⎠ ⎠
∂z 1 x y y x y x y x x y 1 ∂z = cos cos + 2 sin sin , = − 2 cos cos − sin sin 。 ∂x y y x x y x y x ∂y y x x y
案
网
n ∂u = ∑ aij xi , ∂y j i =1
∂u = ai , i = 1,2, " , n 。 ∂xi
n
∑ aij y j , i = 1,2,", n ,
ww
x
z z z ∂u ∂u ∂u = zy z −1 x y ln x , = y z x y −1 , = y z x y ln x ln y 。 ∂x ∂y ∂z
(6) u = ln( x 2 + y 2 + z 2 ) 。
co m
5. 求下列函数在指定点的全微分: (1) f ( x, y ) = 3 x 2 y − xy 2 ,在点 (1,2) ; (2) f ( x, y ) = ln(1 + x 2 + y 2 ) ,在点 (2,4) ;
数学分析课后习题答案--高教第二版(陈纪修)--10章
第十章 函数项级数习 题 10. 1 函数项级数的一致收敛性1. 讨论下列函数序列在指定区间上的一致收敛性。
⑴ S n (x ) = , (i) x nx −e ∈)1,0(, (ii) x ∈; ),1(+∞ ⑵ S n (x ) = x , x nx −e ∈),0(+∞;⑶ S n (x ) = sin nx , (i)x ∈),(+∞−∞, (ii) x ∈],[A A −(); 0>A ⑷ S n (x ) = arctan nx , (i)x ∈)1,0(, (ii) x ∈; ),1(+∞ ⑸ S n (x ) =221nx +, x ∈),(+∞−∞; ⑹ S n (x ) = nx (1 - x )n , x ∈]1,0[;⑺ S n (x ) =n x ln n x, (i) x ∈)1,0(, (ii) x ∈);),1(+∞ ⑻ S n (x ) = nnx x +1, (i) x ∈)1,0(, (ii) x ∈;),1(+∞ ⑼ S n (x ) = (sin x )n , x ∈],0[π;⑽ S n (x ) = (sin x )n1, (i) x ∈[0,]π, (ii) x ∈],[(0>δ);δπδ− ⑾ S n (x ) = nn x ⎟⎠⎞⎜⎝⎛+1, (i) x ∈),0(+∞, (ii)x ∈],0(A (); 0>A ⑿ S n (x ) = ⎟⎟⎠⎞⎜⎜⎝⎛−+x n x n 1, (i) x ∈),0(+∞, (ii)[)0,,>+∞∈δδx 。
解 (1)(i) ,0)(=x S )()(sup ),()1,0(x S x S S S d n x n −=∈1= ─/→ 0(∞→n ), 所以{}()n S x 在上非一致收敛。
(0,1) (ii) ,0)(=x S )()(sup ),(),1(x S x S S S d n x n −=+∞∈n e −=)(0∞→→n ,所以{}()n S x 在上一致收敛。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解 (1) S = {( x, y ) x > 0, y ≠ 0}; ∂ S = {( x, y ) x = 0或 x > 0, y = 0};
S = {( x, y ) x ≥ 0}。
2 2 2 2 2 2 (2) S = ( x, y ) 0 < x + y < 1 ; ∂ S = ( x, y ) x + y = 0或 x + y = 1 ;
(1)S = ⎨(−1) k
⎧
解 (1) S' = {± 1} 。 (2) S' = ∅ 。
以x为极限,产生矛盾。 7. 设 U 是 R 2 上的开集,是否 U 的每个点都是它的聚点。对于 R 2 中 的闭集又如何呢? 解 开集 U 中的每个点 x 一定是它的内点,所以 x 的任意邻域都有 U 中的无限个点,所以 x 一定是 U 的聚点。 由于 S = {(0, 0)} 是 R 2 上的闭集,而 S 只有一个点,所以无聚点, 即闭集中的点不一定是它的聚点。 8. 证明 S ⊂ R n 的所有内点组成的点集 S 必是开集。 证 假 设 x ∈ S , 则 ∃δ > 0 , O ( x , δ ) ⊂ S 。 而 ∀y ∈ O ( x , δ ) , 由 于
网
lim (αx k + β y k ) = α lim x k + β lim y k 。
k →∞ k →∞
后 答
案
4.
求下列 R 中子集的内部、边界与闭包: (1)S = {( x, y ) | x > 0, y ≠ 0} ; (2)S = {( x, y ) | 0 < x 2 + y 2 ≤ 1} ;
第十一章 Euclid 空间上的极限和连续
习题 11.1 Euclid 空间上的基本定理
1. 证明定理 11.1.1: 距离满足正定性、对称性和三角不等式。 证 (a)显然有 | x − y |≥ 0 ,而且 | x − y |= 0 ⇔ xi = yi (i = 1, 2, … , n) ⇔ x = y 。 (b) 由距离定义直接可得 | x − y |=| y − x | 。 (c) 由于
案
网
ww
5
w. kh d
如果 S 无聚点,即 S ' = ∅ ,则 S 为 S = S ,即 S 为有界闭集,从而由
aw .
co m
习题
(1) u = ln( y − x) +
x
11.2
;
多元连续函数
(2) u =
1 x + 1 y + 1 z
1. 确定下列函数的自然定义域:
1− x2 − y2
;
0
δ
1 k
0
1 k = 0,1, ⎩k
1 ⎫ ,[ ]⎬ , δ ⎭
存在 {Uα } 中 U α ,使得 ∈ Uα , k = 0,1, ,[ ] 。于是
k
1 k
1
k
δ
⎧ ⎨Uα0 , Uα k ⎩
k = 0,1,
1 ⎫ ,[ ]⎬ 构成 S 的有限开覆盖,所以 S 为紧集。 δ ⎭
15. 应用 Heine-Borel 定理直接证明: R n 上有界无限点集必有聚点。 证 假定 S 为 R n 上有界无限点集,则由习题 9, S = S ∪ S′ 必是闭集。
{ S ={ ( x, y ) x
⎧ ⎩
课
(3)S = {( x, y) | 0 < x ≤ 1, y = sin } 。
}
ww
1 x
| (α xk + β yk ) − (α x + β y ) |≤| α || xk − x | + | β || yk − y | < (| α | + | β |)ε ,
co m
14. 用定义证明点集 {0} ∪ ⎨
⎧1 ⎩k ⎧1 ⎩k
⎫ k = 1,2, ⎬ 是 R 中的紧集。 ⎭ ⎫ k = 1,2, ⎬ 的任一开覆盖。设 0 ∈ Uα0 , ⎭
1
证 假定 {Uα } 为点集 S= {0} ∪ ⎨
则 ∃δ > 0 : O (0, δ ) ⊂ Uα , 于是当 k > 时, ∈ Uα 。 对于 ⎧ ⎨
课
后 答
案
再证唯一性。假设 y ∈ ∩ Sk ,则 x − y ≤ diam Sk → 0 ( k → ∞ ) ,所以
k =1
网
k =1
k =1
∞
xk +1 − xk = lim 解 xk = ∑ 1 ∈ R ,则 lim k →∞ k →∞
i =1
k
i
{xk}不收敛。 13. 设 E, F ⊂ R n 为紧集,证明 E ∩ F 和 E ∪ F 为紧集。 证 因为 E, F ⊂ R n 为紧集, 所以 E, F 为有界闭集, 于是可知 E ∩ F 和 E ∪ F 也都是有界闭集,即紧集。
i =1
n
∑ ai 2 +
i =1
n
∑b
i =1
n
2
i
。
令 ai = xi − yi , bi = yi − zi ,则有
| x − z |=
∑ ( xi − zi )2 =
i =1
n
∑ (a + b )
i =1 i i
n
2
1
aw .
所以关于上述两次三项式的判别式有
co m
f (t ) = ∑ (ai − tbi ) 2 =t 2 ∑ bi 2 − 2t ∑ ai bi + ∑ ai 2 ≥ 0 ,
ww
k 1 = 0 ,而 |xk|= ∑ 1 → +∞ ,所以 k +1 i =1 i
w. kh d
4
立 xm − xn ≤ diam Sk ,于是 { xk } 是基本序列,从而收敛,设其极限为 x 。
aw .
以及 lim diam S k = 0 。任取 xk ∈ S k ,则当 m, n>k 时, xm , xn ∈ Sk ,从而成 k →∞
f ( x − 1) = x − 1 = ( x − 1 + 1) 2 − 1 ,
所以
f ( x) = ( x + 1) 2 − 1 = x 2 + 2 x ,
5.
求下列点集的全部聚点:
⎫ k k = 1,2, ⎬ ; k +1 ⎩ ⎭ ⎫ ⎧ 2kπ 2kπ ⎞ , sin (2)S = ⎨⎛ ⎜ cos ⎟ k = 1,2, ⎬ ; 5 5 ⎠ ⎭ ⎩⎝ 2 2 2 2 (3)S = {( x, y ) | ( x + y )( y − x + 1) ≤ 0} 。
{
w. kh d
⎫ ⎭
2
∃N1 , ∀k > N1 :| xk − x |< ε ,
aw .
}
⎫ ⎭
证
设 lim xk = x, lim yk = y,则 ∀ε > 0 ,
2
+ y2 ≤ 1 。
⎧ ⎩
}
1 (3) S = ∅ ; ∂ S = ⎨( x, y ) 0 < x ≤ 1, y = sin x 或x = 0,−1 ≤ y ≤ 1⎬ ;
O ( y , δ − | y − x |) ⊂ O ( x , δ ) ,所以 y 也是 S 的内点,从而 O( x , δ ) ⊂ S o ,于是
S 必是开集。
9. 证明 S ⊂ R n 的闭包 S = S ∪ S′ 必是闭集。 则 x∉ S , 且 x 不是 S 的聚点, 于是在 x 的某邻域 O ( x , δ ) 证 假设 x ∈ S c , 中至多只有 S 的有限项,故存在 x 的邻域 O( x , δ1 ) 不含 S 的点,即
{
z 。 x + y2
2}Biblioteka 解因为所以
案
网
x3 1 ⎛ y⎞ , = f ⎜ ⎟= 2 3 2 3/ 2 ⎝ x ⎠ (x + y ) 2 2 ⎡ ⎛ y⎞ ⎤ ⎢1 + ⎜ ⎟ ⎥ ⎢ ⎝x⎠ ⎦ ⎥ ⎣
f ( x) = (1 +
3.
若函数
后 答
且当 y = 4 时 z = x + 1 ,求 f ( x) 和 z ( x, y ) 。 解 由 z ( x, 4) = 4 + f ( x − 1) = x + 1 ,可得
3
课
后 答
案
网
ww
充分性:用反证法。假设x不是点集S的聚点,则在x的某邻域 最多只有S的有限个点, 所以 S ∩ O ( x , δ ) − {x} 为有限集, O (x , δ ), δ > 0 中, 于是 d = inf{| y − x | y ∈ S, y ≠ x} > 0 ,故不存在S中满足xk ≠ x的点列{xk}
S1 ⊃ S2 ⊃ ⊃ S k ⊃ S k +1 ⊃
,
对于任意 k,当 m ≥ k 时, xm ∈ Sk ,所以 { xk } 的极限 x ∈ Sk = Sk ,于是
x ∈ ∩ Sk ,所以 ∩ Sk 非空。
∞ ∞
x= y。
x k +1 − x k = 0 的点列{xk}不一定收敛。 12. 举例说明:满足 lim k →∞
于是当 k > max{N1 , N 2 } 时,成立
| x − y |<| xk − x | + | xk − y |< 2ε ,
k →∞
k →∞
k →∞
k →∞
k →∞
∃N 2 , ∀k > N 2 :| yk − y |< ε ,
