【现代测试技术】 作业题解
现代测试技术课后答案

现测课后习题答案第1章1. 直接的直接的 间接的间接的2. 测量对象测量对象 测量方法测量方法 测量设备测量设备3. 直接测量直接测量 间接测量间接测量 组合测量组合测量 直读测量法直读测量法 比较测量法比较测量法 时域测量时域测量 频域测量频域测量 数据域测量数据域测量4. 维持单位的统一,保证量值准确地传递维持单位的统一,保证量值准确地传递 基准量具基准量具 标准量具标准量具 工作用量具工作用量具5. 接触电阻接触电阻 引线电阻引线电阻6. 在对测量对象的性质、特点、测量条件(环境)认真分析、全面了解的前提下,根据对测量结果的准确度要求选择恰当的测量方法(方式)和测量设备,进而拟定出测量过程及测量步骤。
度要求选择恰当的测量方法(方式)和测量设备,进而拟定出测量过程及测量步骤。
7. 米(m) 秒(s) 千克(kg) 安培(A) 8. 准备准备 测量测量 数据处理数据处理9. 标准电池标准电池 标准电阻标准电阻 标准电感标准电感 标准电容标准电容第2章填空题1. 系统系统 随机随机 粗大粗大 系统系统2. 有界性有界性 单峰性单峰性 对称性对称性 抵偿性抵偿性3. 置信区间置信区间 置信概率置信概率4. 最大引用最大引用 0.6% 5. 0.5×10-1 [100.1[100.1ΩΩ,100.3100.3ΩΩ] 6. ±7.9670×10-4 ±0.04% 7. 测量列的算术平均值测量列的算术平均值8. 测量装置的误差不影响测量结果,但测量装置必须有一定的稳定性和灵敏度测量装置的误差不影响测量结果,但测量装置必须有一定的稳定性和灵敏度 9. ±6Ω10. [79.78V ,79.88V] 计算题 2. 解: (1)该电阻的平均值计算如下:128.504nii xx n===å该电阻的标准差计算如下:该电阻的标准差计算如下:21ˆ0.0331n i in n s ===-å(2)用拉依达准则有,测量值28.40属于粗大误差,剔除,重新计算有以下结果:属于粗大误差,剔除,重新计算有以下结果:28.511ˆ0.018x s ¢=¢=用格罗布斯准则,置信概率取0.99时有,n=15,a=0.01,查表得,查表得0(,) 2.70g n a =所以,所以,0ˆ(,) 2.700.0330.09g n a s =´=可以看出测量值28.40为粗大误差,剔除,重新计算值如上所示。
现代检测技术期末考试试卷及答案全文优选

最新精选全文完整版(可编辑修改)《现代检测技术》期末考试试卷及答案一、名词解释(每题5分,共25分)1、测试系统的灵敏度2、压电效应3、热电偶冷端补偿4、电阻应变效应5、虚拟仪器二、填空题(每空1分,共25分)1、一阶系统的时间常数r表征系统的特性,一阶系统的被止频率表示为。
2、线性度是指。
也称非线性误差,常用的直线拟合方法有理论拟合、和等。
3、常用的应变片有与两大类,其中灵敏度较高的是,线性度较好的是。
4、为了加强居氏小区的安全,可以在小区围墙上加装传感器进行昼夜监控。
5、可以进行转速测量的传感器包括、和;可以进行金属工件厚度测星:的传感器包括、和。
6、在图像测量中,为了确定丄件的角点,常采用方法,它的原理是。
7、光电管、光电倍増管是利用效应工作的,光电池是利用效应工作的,光敏电阻是利用效应工作的。
8、极距变化型的电容式传感器常釆用差动结构,目的是以及。
9、为利用电桥的和差特性,提髙系统的灵敏度,应使桥臂上电阻应变极性相同,桥臂上电阻应变极性相反。
三、简答题(每题10分,共50分)1、基本型现代检测系统包括哪些环节?2、什么是霍尔效应?为什么半导体材料适合于作霍尔元件?3、请从CCD的原理解释图像亮度与曝光时间的关系。
4、如果对1mm左右的微位移量进行检测,请问可以选用什么传感器?列举2种方案,并解释其工作原理。
5、探底雷达可以完成哪些检测任务?在对混凝土构件进行探测时与超声波传感器有何异同?现代检测技术参考答案:一、名词解释1、测试系统的灵敏度一专感器输出变化量与输入变化量之比2、压电效应一一某些材料(如石英)当沿着一定方向施加力变形,由于材料分子不具备中心对称性, 其内部产生极化现象,同时在它的两个表面上产生符号相反的电荷,当外力去掉后,重新恢复到不带电状态,此现象称为正压电效应。
逆压电效应是指当压电材料沿一定方向受到电场作用时,相应的在一定的晶轴方向将产生机械变形或机械应力,又称电致伸缩效应。
现代测试技术 作业题解

第二章习题1.现校准为量程100mV ,表盘刻度为100等份毫伏表,见表。
题1:测量数据 被校表示值U X (mV ) 10 20 30 40 50 60 70 80 90 100标准表示值U 0(mV ) 9.9 20.0 30.4 39.8 50.2 60.4 70.3 79.9 89.7 99.9绝对误差∆U (mV )-0.1 0.0 0.4 -0.2 0.2 0.4 0.3 -0.1 -0.3 -0.1试求:①.计算各校准点的绝对误差,并填入表中; ②.确定被校表的准确度等级; 解: 最大引用误差为:100%0.4%mnm mA A γ∆=⨯=%a nm ≤γ所以应该取a=0.52.某四位半数字电压表,量程为2V ,工作误差为∆= ± (0.025%∙U X +2个字) 用该表测量时,读数分别为0.0345V 和1.8567V ,试求两种情况下的测量误 差。
从计算结果中可得到什么启示?解:四位半仪表在2V 量程下的显示范围是 0~1.9999V ,分辨率为0.0001V 。
当测量值为0.0345V 时绝对误差和相对误差分别为:()411110.025%0.03450.00012 2.110100%0.6%X VA γ-∆=±⨯+⨯=±⨯∆=⨯=±当测量值为1.8567V 时绝对误差和相对误差分别为:()422220.025% 1.85670.00012710100%0.04%X VA γ-∆=±⨯+⨯=±⨯∆=⨯=±可以看出,测量结果的测量误差不仅和仪表的准确度有关,而且和量程的选择有关。
测量值与量程越近,测量误差越小。
3.对某直流电压源的输出电压U 进行10次 ,读数如表所示。
题3:测量数据次数 12 3 4 5 6 7 8 9 10 U/V 5.003 5.011 5.006 4.998 5.015 4.996 5.009 4.999 5.010 5.007① 求输出电压x U 的算术平均值U 及其标准差()U s .。
现代测试技术计算题习题集(附答案)1

补充习题参考答案1、 有一个电容测微仪,两极板介质为空气,其圆形极板半径r = 4 mm ,工作初始间隙δ=0.2 mm ,已知 ε0=8.58×10-12F/m ,ε=1,问:1)、工作时,如果传感器与工件的间隙变化量Δδ=1μm 时,电容变化量是多少?2)、如果测量电路的灵敏度S 1=100mV/pF ,读数仪表的灵敏度S 2=5格/mV ,在Δδ=1μm 时,读数仪表的指示值变化多少格?解:1)、ΔC=εε0A ×Δδ/-δ2=1×8.58×10-12(F/m )×3.14×(0.004)2(m 2)×1×10-6(m )=-4.94×10-3pF2)、S=ΔC ×S 1×S 2=-4.94×10-3(pF) ×100(mv/pF )×5(格/mv)=-2.47格≈-2.5格2、 应变片的计算:已知试件尺寸如图,试件材料为45#钢,E=2.0×10+7N/cm 2,应变片电阻R=120Ω,K=2.0,康铜电阻丝的电阻温度系数α=-50×10-6/℃,温度线膨胀系数β2=15×10-6/℃,45#钢的温度线膨胀系数β1=11×10-6/℃。
求:(1)、不考虑温度的影响,当P=10吨时,求电阻应变片的电阻相对变化量ΔR/R 和绝对变化量ΔR。
(2)、当P=0,环境温度在-20℃变到+20℃时,求电阻应变片的相对变化量ΔR/R 和绝对变化量ΔR。
解:(1)拉伸变形 A E A P εδ== 得EAP=ε 所以005.012100.210100.263=⨯⨯⨯⨯⨯===∆EA KP K R R ε R ∆=0.005×120=0.6 Ω (2)当p =0,t ∆=20-(-20)=40 ℃时Ω-=⨯⨯-⨯+⨯-⨯∆⨯-+=∆--2784.040]10)1511(0.21050[120t)]([6621=ββαK R R31032.21202784.0-⨯-=-=∆R R 3、 脱粒机滚筒轴上,沿与轴线方向成45º方向贴一应变片,在工作时应变片的阻值从120Ω增加到120.006Ω,试问滚筒轴所承受的工作扭矩是多少?已知轴的直径为40mm ,E=2.1×10+6kg/cm 2,μ=0.3,应变片又ΔR/R=k ε→ε=ΔR/R*k=0.006/120×2.0=25×10-6所以M k=ㄧ2.1×10-6(kg/cm 2) ×25×10-6/(1+0.3)ㄧ×3.14×(4 cm)3/16 =507.2kg.cm=5.072kg.m=50.72N.m4、 如图所示,在左端固定的悬臂梁的右端部,沿X-X 轴,Y-Y 轴,Z-Z 轴分别作用有P x 、P y 、P z 三个力,且P x 、5、 已知条件如图,试件为45号钢,E=2.0×10+7N/cm 2,应变片的电阻为R1=R2=120欧,K=2.0, 由.281Ω,ΔR2=-0.281Ω的电阻变化,求P=?⎩⨯⨯=WE M ε其中W 是抗弯截面系数,矩形截面的W =bh 2/6又μεεε117021120281.01=⨯=⨯∆=∆K R R K R R =即 则NLh b E P 01.492064.06.110117010262662≈⨯⨯⨯⨯⨯=⨯⨯⨯=-ε6、 如图所示,弹性元件为钢材,E=2.0×10+5N/mm 2, 贴片处的断面积为400mm 2,泊松比μ=0.3,R1=R2=R3=R4=120欧,K=2.0,力P=50000N ,求电桥的输出电压UBD =?解:弹性元件拉伸变形A E A P εδ== 得μεε62510625)(400)/(100.2)(50006224=⨯=⨯⨯==-+mm mm kg kg EAP根据布片、接桥规则(如图所示):mVU K U BD 875.4610625)3.01(0.221)1(26=⨯⨯⨯+⨯⨯=+=-εμ17、 图示为圆轴销,其端部受有一力P ,轴上贴有两应变片R 1=R 2=120Ω,K=2.0,两片之间的距离L=100mm ,圆轴直径d=20 mm ,E=2.0×10+5N/mm 2,若测得半桥的指示应变为2000με 。
现代测试技术习题解答 第二章 信号的描述与分析 - 副本

所以
所以x(t+)=y(t++T)
令t1=t++T,代入上式得
x(t1- T)=y(t1),即y(t) =x(t- T)
结果说明了该系统将输入信号不失真地延迟了T时间。
2-12已知信号的自相关函数为Acos,请确定该信号的均方值x2和均方根值xrms。
解:Rx()=Acos
根据以上分析结论,便可由自相关函数图中确定均值(即常值分量)和周期分量的周期及幅值,参见下面的图。例如:如果 ,则 。
所以
解法3:直接按Rxy()定义式计算(参看下图)。
参考上图可以算出图中方波y(t)的自相关函数
2-11某一系统的输人信号为x(t)(见图5-25),若输出y(t)与输入x(t)相同,输入的自相关函数Rx()和输入—输出的互相关函数Rx()之间的关系为Rx()=Rxy(+T),试说明该系统起什么作用?
2- 19假定有一个信号x(t),它由两个频率、相角均不相等的余弦函数叠加而成,其数学表达式为x(t)=A1cos(1t+1)+A2cos(2t+2)求该信号的自相关函数。
解:设x1(t)=A1cos(1t+1);x2(t)=A2cos(2t+2),则
因为12,所以 , 。又因为x1(t)和x2(t)为周期信号,所以
x2=Rx(0)=A
2-13已知某信号的自相关函数,求均方值、和均方根值 。
2-14已知某信号的自相关函数,求信号的均值 、均方根值、功率谱。
2-15已知某信号的自相关函数,求信号的自功率谱。
解:采样序列x(n)
2-18对三个正弦信号x1(t)=cos2t、x2(t)=cos6t、x3(t)=cos10t进行采样,采样频率fs=4Hz,求三个采样输出序列,比较这三个结果,画出x1(t)、x2(t)、x3(t)的波形及采样点位置,并解释频率混叠现象。
现代测试技术习题例题
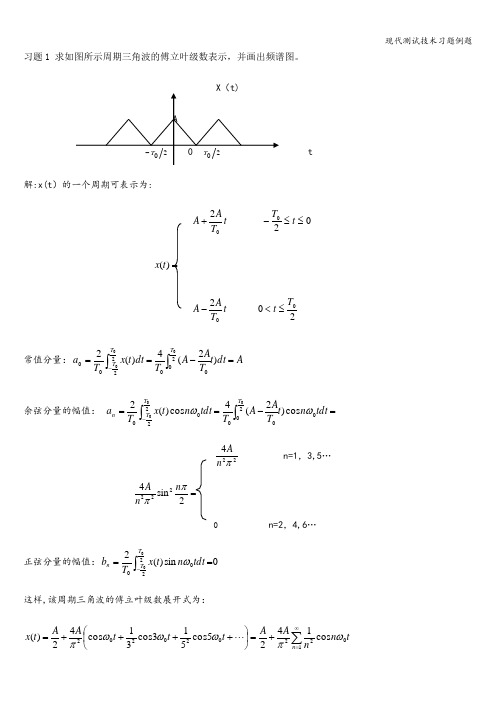
习题1 求如图所示周期三角波的傅立叶级数表示,并画出频谱图。
解:x(t )的一个周期可表示为:t T AA 02+020≤≤-t T=)(t xt T AA 02-200T t ≤<常值分量:A dt t T AA T dt t x T a TT T =-==⎰⎰-)2(4)(220022000000余弦分量的幅值: =-==⎰⎰-tdt n t T AA T tdt n t x T a TT T n 020022000cos )2(4cos )(2000ωω224πn An=1,3,5… =2sin 4222ππn n A 0n=2,4,6…正弦分量的幅值:0sin )(2220000⎰-==T T n tdt n t x T b ω这样,该周期三角波的傅立叶级数展开式为:t n nA A t t t A A t x n 0122020202cos 1425cos 513cos 31cos 42)(ωπωωωπ∑∞=+=⎪⎭⎫ ⎝⎛++++=000练习2 求指数衰减振荡信号t e t x at 0si n )(ω-=的频谱函数. 解一:22000)()(000)(00)(121)(1)(1221][221)()(2sin sin 21sin 21)(0000ωωπωωωωππωωωπωπωωωωωωωωω++=⎥⎦⎤⎢⎣⎡-+-++=-=-===⎰⎰⎰∞-+-++--∞+-∞--j a j j a j j a j dt e e j X e e j t tdte dtte e X tj j a t j j a t j t j t j a t j at 解二:[])()(22sin 000f f f f jt f --+⇔δδπ fj a e at π21+⇔-)()()(T t x T t t x ±=±*δ)()()()(f Y f X t y t x *⇔•[]⎥⎦⎤⎢⎣⎡-+-++=--+*+⇔∴-000002)2(12)2(12)()(2212sin f j f j a f j f j a j f f f f j f j a t f eatππππδδππ4. 求指数衰减函数的频谱函数,().并定性画出信号及其频谱图形.解:(1)求单边指数函数的傅里叶变换及频谱(2)求余弦振荡信号的频谱。
现代测试技术习题解答第二章信号的描述与分析副本
第二章 信号的描述与分析补充题2-1-1 求正弦信号0()sin()x t x ωt φ=+的均值x μ、均方值2x ψ和概率密度函数p (x )。
解答: (1)00011lim ()d sin()d 0TT x T μx t t x ωt φt TT →∞==+=⎰⎰,式中02πT ω=—正弦信号周期(2)2222220000111cos 2()lim()d sin ()d d 22TT T xT x x ωt φψx t t x ωt φt t TT T →∞-+==+==⎰⎰⎰(3)在一个周期内012ΔΔ2Δx T t t t =+=0002Δ[()Δ]limx x T T T tP x x t x x T T T →∞<≤+===22Δ0Δ0000[()Δ]2Δ2d ()limlim ΔΔd x x P x x t x x t t p x x T x T x πx x →→<≤+====-x (t )正弦信号xx +ΔxΔtΔtt2-8 求余弦信号0()sin x t x ωt 的绝对均值x μ和均方根值rms x 。
2-1 求图示所示锯齿波信号的傅里叶级数展开。
2-4周期性三角波信号如图所示,求信号的直流分量、基波有效值、信号有效值及信号的平均功率。
2-1 求图示所示锯齿波信号的傅里叶级数展开。
补充题2-1-2 求周期方波(见图1-4)的傅里叶级数(复指数函数形式),划出|c n|–ω和φn–ω图,并与表1-1对比。
解答:在一个周期的表达式为00 (0)2() (0)2T A t x t T A t ⎧--≤<⎪⎪=⎨⎪≤<⎪⎩积分区间取(-T/2,T/2)00000002202002111()d =d +d =(cos -1) (=0, 1, 2, 3, )T T jn tjn tjn t T T n c x t et Aet Ae tT T T Ajn n n ωωωππ-----=-±±±⎰⎰⎰所以复指数函数形式的傅里叶级数为001()(1cos )jn tjn t n n n Ax t c ejn e n∞∞=-∞=-∞==--∑∑ωωππ,=0, 1, 2, 3, n ±±±。
现代检测技术~电子测量~作业及答案整理版本
选择1.欲测量一个标称频率f=1MHZ的石英振荡器,要求测量准确度优于10*-6,选用的计数器标准频率准确度和闸门时间应为(1*10e-7,T=1s)2.用计数器测频的误差主要包括:()B. 量化误差、标准频率误差3.在通用计数器测量低频信号的频率时,采用倒数计数器是为了()D.减小测频时的量化误差影响4.调制域描述的是( )之间的关系。
D.时间-频率5.在用计数式频率计测量频率比N=Fa/Fb,选用的门控信号由()产生。
B.Fb放大后的信号6.从基本的测量对象来看,电子测量是对( ) 的测量。
A.电信号C.电系数7.测量系统的理想静态特性为().B.y=Sx8.电子信息技术应用在电子测量中的优点有()A.速度极快B. 分辨力高C.范围宽D.利于信息传递9.下列参量中有源量有()B.功率D.信号频率10.已知系统输入量的拉氏变换为X(S),输出量的拉氏变换为Y(S),则测量系统的传递函数为()。
D.Y(S)/ X(S )11.频谱分析仪的频率范围是____。
A: 频谱仪可测得最大/最小频率值之差12.两个等幅信号的频率间距为30KHz,至少需要______的分辨率带宽才能分辨出两个峰。
B: 30KHz13.以下哪些因素对频率分辨率有贡献?C: RBW D: 相位噪声14.在进行阿伦方差的测量时,组与组之间以及组内两次测量之间必须都是连续的。
(错)15.用计数器直接测周的误差主要有三项:即量化误差、触发误差以及标准频率误差。
(对)16.在通用计数器测量低频信号的频率时,采用倒数计数器是为了克服转换误差。
(错)17.当计数器进行自校时,从理论上来说不存在±1个字的量化误差。
(对)18.为了减少测量误差,应使被测量的数值尽可能地在仪表满量程的2/3 以上。
(对),因为当示值X越接近于满度值Xm时,其测量准确度越高。
19.粗大误差具有随机性,可采用多次测量,求平均的方法来消除或减少。
(错)因为粗大误差明显的歪曲了测量结果,应该剔除不用20.通过多次测量取平均值的方法可减弱随机误差对测量结果的影响。
现代测试技术试卷及部分答案
一、填空题(每小题1 分,共 10 分)1. 当测试系统的输出)(t y 与输入)(t x 之间的关系为)()(00t t x A t y -=,其中0A 、0t 为常数时,该系统就能实现对信号的( 不失真 )测试。
2. 测试系统动态特性的描述函数主要有脉冲响应函数、传递函数和( 频率响应函数 )。
3. 周期信号的频域分析采用的数学工具是( 傅里叶级数 )。
4. 有源传感器一般是将非电量转换为电能量,称之为能量( 转换 )型传感器。
5. 压电式振动加速度传感器是利用某些材料的( 压电效应 )原理工作的。
6. 交流电桥的平衡条件是( 两相对臂阻抗的乘机相等 )。
7. 电容式传感器分为( 极距变化 )型电容传感器、面积变化型电容传感器和介质变化型电容传感器三大类。
8. 振动的激励方式通常有稳态正弦激振、( 随机激振 )和瞬态激振。
9. 随机信号的自功率谱密度函数的物理含义是( 随机信号的自相关函数的傅里叶变换 )。
二、单项选择题(每小题 1 分,共 15 分)1.传感器在非电量电测系统中的作用是( C )。
(A) 将被测电量转换为电参量(B) 将被测非电量转换为非电参量(C) 将被测非电量转换为电参量2. ( C )不属于测试系统的静态特性指标。
(A )回程误差(B )灵敏度(C )阻尼系数3. 频率响应函数H (j ω)是在( A )描述测试系统对正弦信号稳态响应特征的函数。
(A )频率域内(B ) 时间域内(C )幅值域内4. 压电式传感器目前多用于测量( B )。
(A )静态的力(B )物体运动速度(C )瞬态的力5. 振动子FC6-1200的固有频率为1200Hz ,问用该振动子能不失真记录信号的频率范围是( C )。
(A )0 - 1200 Hz(B )>1200Hz (C )0 - 600 Hz6. 不能用涡流式传感器进行检测的是( A )。
(A)非金属材料(B)金属材质鉴别(C)金属材料无损探伤7.变气隙高度型电感式传感器在实际应用时常采用差动工作方式,这是为了(A )。
现代测试技术试卷A答案
现代测试技术试卷A 答案一、填空题。
1、传感技术、通信技术、计算机技术。
2、电阻式、电感式、电容式、压电式、光电式。
3、灵敏度、非线性度、回程误差。
4、可以用数学关系式或图表精确描述的信号。
5、模拟式和数字式传感器。
6、电桥、放大器、滤波器、调制器和模数转换器。
7、单臂工况、相邻半桥工况和全桥工况。
8、计算机、仪器硬件和应用软件。
二、判断题。
1、×2、√3、×4、√5、×6、√7、×8、√9、√三、单项选择题。
1、C2、D3、C4、C5、D四、多项选择题1、A 、C2、A 、B 、C3、A 、B 、C 、D4、A 、D五、简答题1、如果一测试装置的输入x(t)和输出y(t)满足方程00()()y t A x t t =-,其中A 0和t 0均为常量,则称此测试装置为不失真测试装置。
它必须满足以下两个条件: 考察其传递函数0000()()()()()st st A e X s Y s H s A e X s X s --===,相应的频率响应函数为: 00()jt H j A e ωω-=,其幅频与相频特性分别为:00()()()()A H j A H j t ωωϕωωω===∠=- 可见,要实现不失真测试,测试装置的幅频特性应为常数,相频特性应为直线(线性)。
2、信号是信息的载体,是物质,具备能量;信息是信号所载的内容,不等于物质,不具备能量。
同一个信息,可以用不同的信号来运载,反过来,同一种信号也可以运载不同的信息。
3、直流电桥的特点是平衡电路简单,对联接导线的要求较低,可采用直流仪表测量,直流电源的稳定度容易保证;但要求后接比较复杂的直流放大器。
而交流电桥要求工作电源的电压波形没有畸变,频率必须稳定,否则电桥对基波调平衡后,仍会有高次谐波的电压输出。
交流电桥后接电路采用简单的交流放大器,但其容易受寄生参数和外界因素的影响。
4、虚拟仪器是指在通用的计算机平台上加上一组软件或硬件或接通其他仪器,用户根据自己的需要定义和设计仪器的测试功能,以实现对被测对象的数据采集、信号分析、数据处理、数据存储和可视化显示等功能,完成测试、测量和控制等任务。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章习题1.现校准为量程100mV ,表盘刻度为100等份毫伏表,见表。
题1:测量数据 被校表示值U X (mV ) 10 20 30 40 50 60 70 80 90 100标准表示值U 0(mV ) 9.9 20.0 30.4 39.8 50.2 60.4 70.3 79.9 89.7 99.9绝对误差∆U (mV )-0.1 0.0 0.4 -0.2 0.2 0.4 0.3 -0.1 -0.3 -0.1试求:①.计算各校准点的绝对误差,并填入表中; ②.确定被校表的准确度等级; 解: 最大引用误差为:100%0.4%mnm mA A γ∆=⨯=%a nm ≤γ所以应该取a=0.52.某四位半数字电压表,量程为2V ,工作误差为∆= ± (0.025%∙U X +2个字) 用该表测量时,读数分别为0.0345V 和1.8567V ,试求两种情况下的测量误 差。
从计算结果中可得到什么启示?解:四位半仪表在2V 量程下的显示范围是 0~1.9999V ,分辨率为0.0001V 。
当测量值为0.0345V 时绝对误差和相对误差分别为:()411110.025%0.03450.00012 2.110100%0.6%X VA γ-∆=±⨯+⨯=±⨯∆=⨯=±当测量值为1.8567V 时绝对误差和相对误差分别为:()422220.025% 1.85670.00012710100%0.04%X VA γ-∆=±⨯+⨯=±⨯∆=⨯=±可以看出,测量结果的测量误差不仅和仪表的准确度有关,而且和量程的选择有关。
测量值与量程越近,测量误差越小。
3.对某直流电压源的输出电压U 进行10次 ,读数如表所示。
题3:测量数据次数 12 3 4 5 6 7 8 9 10 U/V 5.003 5.011 5.006 4.998 5.015 4.996 5.009 4.999 5.010 5.007① 求输出电压x U 的算术平均值U 及其标准差()U s .。
② 在正态分布、置信概率为99%的情况下,输出电压的真值应在什么范围内。
解: ① 测量数据的平均值为:101 5.00510n n U U V -=⎛⎫ ⎪⎝⎭==∑测量数据的标准差为()10211ˆ()0.006101nn U U U V σ-==-=-∑ 测量数据平均值的标准差为:ˆ()/100.002U s U V σ-⎛⎫== ⎪⎝⎭② 当为正态分布,P=99%,取置信因子K=2.58,则置信区间为ˆˆ[(),()][5.000,5.011]U K U U K U V V σσ-----+=4. 用直流电桥对某电阻进行重复测量,测量读数见表。
题4:测量数据次数 12 3 4 5 6 7 8 9 10 R/Ω 156.6 156.8 157.1 156.5 156.8 156.9 156.5 157.0 156.8 156.9已知直流电桥的允许误差x R ⨯±=∆%2.0,试求: ①.被测电阻的平均值x R 。
②.被测电阻的A 类不确定度()R u A 和B 类不确定度()R u B 。
③ 被测电阻的合成不确定度()R u c 。
④ 在3=k 时,被测电阻的扩展不确定度U 和测量结果的完整表达式。
解:① 被测电阻的平均值:101156.810n n x R R -=⎛⎫⎪⎝⎭==Ω∑② 被测电阻的标准差:10211ˆ()0.20101x R nn R R σ-==-=Ω-∑A 类不确定度为ˆˆ()()()/100.06A x x u R R R σσ--===ΩB 类不确定度为()0.2%0.1833xB R u R -∆⨯===Ω③ 合成不确定度x R 的 A 类不确定度和B 类不确定度属于独立误差分量,误差传递系数为1,所以x R 的合成不确定度为:22()()()0.19C A B u R u R u R ---=+=Ω④ 当k=3时,x R 的扩展不确定度Ω==-57.0)(*R u k U c最后的测量结果Ω±=±=-)57.08.156(U R R5. 铜电阻的电阻值R 与温度t 之间关系为(1)t o R R t α=+,在不同温度下,测得铜电阻的电阻值如下表所示。
题5:测量数据/o i t C 19.1 25.0 30.1 36.0 40.0 45.1 50.0 /ti r Ω 76.3 77.8 79.75 80.80 82.35 83.90 85.10① 试估计0o C 时的铜电阻的电阻值0R 和铜电阻的电阻温度系数α,并估计出0R 和α的标准差。
② 实际测量中,可根据测得的电阻由(1)t o R R t α=+的反函数求出被测温度。
已知电阻t R =81.0Ω,t R 的测量误差为0.2%,求被测温度x T 。
③ 计算②被测温度x T 的合成标准不确定度()x c T u 和置信因子为2.5时的扩展不确定度U 。
解:① 将上表数据两两一组,分成6组,每一组使用最小二乘法可以得到一个R 0和α(2,1t t r r ) (3,2t t r r ) (4,3t t r r ) (5,4t t r r ) (6,5t t r r ) (7,6t t r r ) R 0 71.44 68.24 74.39 66.85 70.19 72.85 α 0.00350.00560.0024.000580.00430.003466.700=R 0042.0=-α14.130)(6200^=-=∑-R RR σ 00054.030)(62^=-=∑-αασα② 由题给关系可得)1(1-=R R t tα当Rt=81.0时, t=35.5C ︒③ 类不确定度有和A R α0,类不确定度有B R t39.3t t =∂∂=t R R C88.3t00=∂∂=R C R6.8295t =∂∂=ααC094.03%2.0*81)(==t B R u合成不确定度=++=-2322)10*54.0*6.8295()14.1*89.3()094.0*39.3(C u 5.93现代测试技术习题二1、一个测压记录系统框图如下:已知:S 1=10-4mv ·[P a ]-1, S 2=10, 分度值K=50mv ·cm -1,记录仪最大记录幅度L m =5cm , 最小可分辨幅度ΔL=0.5mm, 求系统可测量最大压力与分辨率。
解:传感系统的灵敏度4410*51501*10*10*10*--==∆∆∆∆=∆∆=U P P U P L S cm/Pa最大可测量压力:5410*5.210*2.05==-S L m pa 分辨率: Ls ∆=340.05 2.5*100.2*10-=pa 2、某测量环节的微分方程为:()mnp d r rq dt s sφ+= 试问:4.是几阶测量系统? 一阶系统5.时间常数τ=? qm np=τ6.写出传递函数; 11)(+=s s H τ7.写出频率(响应)特性; 11)(+=ωτωj j H8.若可使参量P 缩小10倍,即10'pp = ,q 增大10倍,即q ’=10q ,那么该系统的时间常数τ’将有何变化?系统的工作频带将有何变化?解:ττ10011010'==q p m n转折频率:τωτ1=,所以工作频带扩展100倍 3、 已知某测量环节的传函数W 1(S)、W 2(S)。
()110411+-=s s W ()11052.02101012+-⨯+-=s s s W(1)试求相应的K 、ωτ、f τ、τ 或K 、ω0、ζ值。
解:W1:K=1, s 410-=τ,410=τω ,Hz f 6.15912==πωττW2:K=1, 5010=ω,1.0=ζ压力传感放大器 X-Y 记录ΔP S 1 S 2 K ΔL(2)由W 1(S)、W 2(S)组成一测量系统。
试问:当工作信号频率KH z f H 9.15=时将有多大的幅值动态误差?γ解:这个测量系统是由一个一阶系统和一个二阶系统组成的,s rad f H /1002==πω1)(11*)2(])(1[1202020-++-=ωωωωζωωγ=-50.2%4、某测量环节的输入信号为一方波,其频率f=6HZ ,在示波器上观察到方波幅值有40格,再用示波器观察该测量环节的输出波形(阶跃响应)y(t)及其数值如下:时间t1t ’ 2t ’ 3t ’ 4t ’ 5t ’ 6t ’ 7t ’ 8t ’响应y(t)格19.0 27.5 32.5 35.0 37.0 38.5 39.0 39.5 试判断该测量环节是否为一阶系统? 它的时间常数τ=? 转折频率?=f τ 该系统之(通)频带是多少? 若输入被测信号的频率为f τ时, 输出信号的幅值频率误差 γ=? 若被测信号的频率为10f τ, 输出信号幅值将有多大变化? 写出频率特性表达式及微分方程式。
40格T/2y(t)0'3t'5t'7t'9t'11t'解:一阶系统响应 : )1()(τte A t y --=40)(=∞=y A令τt Z -= 可得 ])(1ln[At y Z -= 列出Z-t 关系如下 t 1t ’ 2t ’ 3t ’ 4t ’ 5t ’ 6t ’ 7t ’ 8t ’ Z -0.644 -1.163 -1.674 -2.079 -2.590 -3.283 -3.689 -4.382绘制Z-t 图可以近似看做是一条直线,所以该系统是一阶系统。
由题图可知:11s T t 1212'== s t 1321'=s Z t015.0=∆∆=τ s rad /7.661==τωτHz f 6.102==πωττ 293.01)(112-=-+=τωωγ当被测信号的频率为10f τ 90.01)(112-=-+=τωωγ该系统频率特性表达式H (ωj )=ωj 015.011+5、已知一热电偶的时间常数10=τs, 如果用它来测量一台炉子的温度,炉内温度在 540℃和500℃之间按近似正弦曲线波动,周期为80s ,静态灵敏度k=1,试求该热电偶输出的最大值和最小值,以及输入与输出信号之间的相位差和滞后时间。
解:题给条件可知: s rad /40802ππω==炉内温度函数 520)40sin(20+=t T π热电偶的频率特性:ωωj j H 1011)(+=786.0)(=ωj H ︒-=15.38))((ωϕj H热电偶测得的温度为:()52020sin(38.15)*0.78652015.7sin(38.15)y t t t ωω=+-=+-max 52015.7535.7y =+= min 52015.7504.3y =-=时间滞后:38.15*808.5360t s ︒∆==第4章作业题解1.某热电阻的特性为2100(10.38510) t R t -=+⨯Ω,测量系统见下图,电流源输出5 mA ,标准电阻100 Ω,A/D 转换器的输入电压0 ~ 2 V ,测温上限200︒C ,试计算:①.要求分辨率为0.2︒C 时,A/D 转换器的位数; ②.放大器的放大倍数;③.如果改用单恒流源会带来什么问题?解:(1)若需分辨力为0.2℃, 则20010000.2x == 所以n 取10位就可以满足 210=1024>1000(2)分辨力为102 1.95322Rn V Q mV === 因为放大器前端输入电压(双电流源输出电压)与温度t 的关系为 20051000.38510 1.9251.9250.20.3855U I R T mA t tU mV U K Q Q K Uα-==⨯⨯⨯=∆=⨯=∆⨯===∆所以,所以(3)如果改为单恒流源,则00(1)U I R T α=+在输入T 为0时,仍有输出电压U=I 0R 0会进入A/D 转换器,从而造成A/D 转换器中有一部分量程未用,浪费了。
